19.1.2函数的图象 同步练习 (无答案)2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 19.1.2函数的图象 同步练习 (无答案)2023-2024学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 234.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 16:16:19 | ||
图片预览

文档简介
19.1.2函数的图象
一、单选题
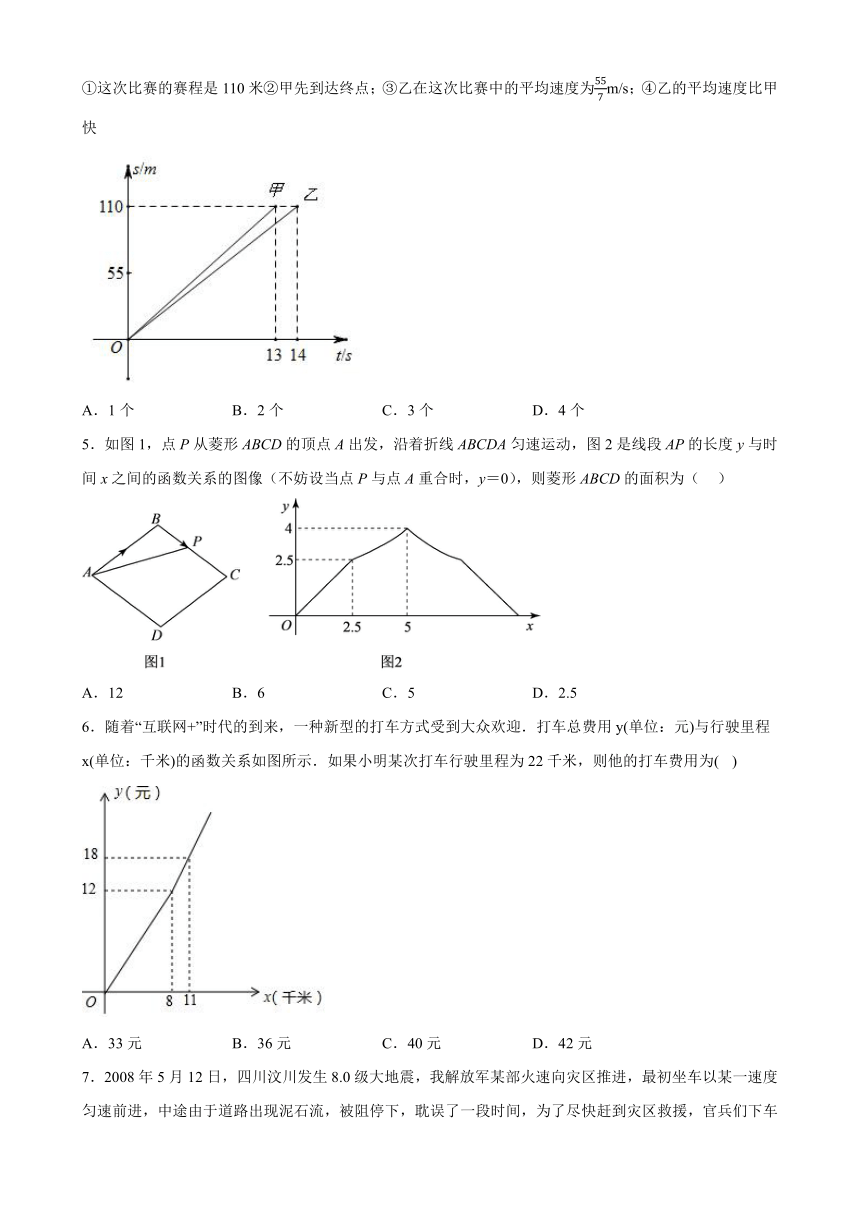
1.如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
A. B. C. D.
2.如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
A. B. C. D.
3.小强和小敏练短跑,小敏在小强前面12米.如图,、分别表示小强、小敏在短跑中的距离(单位:米)与时间(单位:秒)的变量关系的图象.根据图象判断小强的速度比小敏的速度每秒快
A.2.5米 B.2米 C.1.5 D.1米
4.甲、乙两人在一次跨栏比赛中,路程s(m)与时间t(s)的函数关系如图所示,根据图形下列说法正确的个数为( )
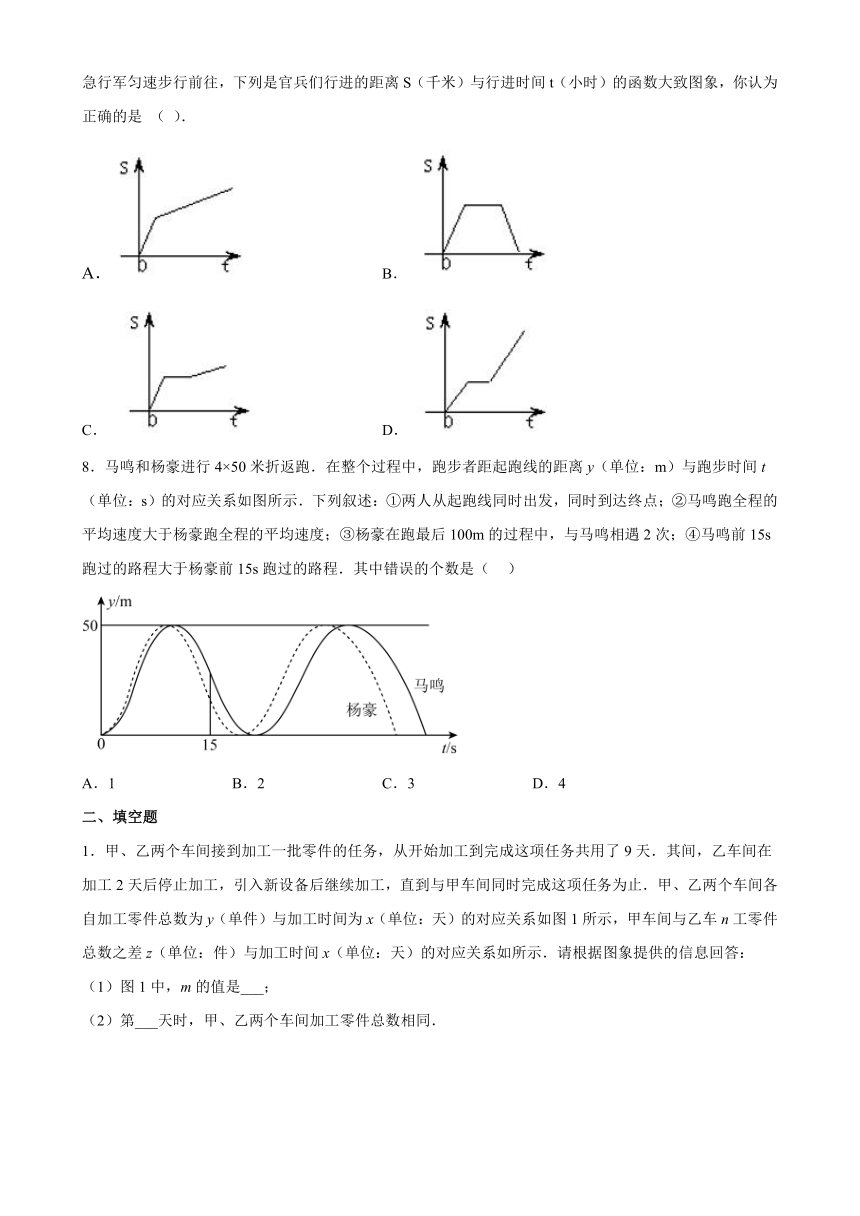
①这次比赛的赛程是110米②甲先到达终点;③乙在这次比赛中的平均速度为m/s;④乙的平均速度比甲快
A.1个 B.2个 C.3个 D.4个
5.如图1,点P从菱形ABCD的顶点A出发,沿着折线ABCDA匀速运动,图2是线段AP的长度y与时间x之间的函数关系的图像(不妨设当点P与点A重合时,y=0),则菱形ABCD的面积为( )
A.12 B.6 C.5 D.2.5
6.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元 B.36元 C.40元 D.42元
7.2008年5月12日,四川汶川发生8.0级大地震,我解放军某部火速向灾区推进,最初坐车以某一速度匀速前进,中途由于道路出现泥石流,被阻停下,耽误了一段时间,为了尽快赶到灾区救援,官兵们下车急行军匀速步行前往,下列是官兵们行进的距离S(千米)与行进时间t(小时)的函数大致图象,你认为正确的是 ( ).
B.
C. D.
8.马鸣和杨豪进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图所示.下列叙述:①两人从起跑线同时出发,同时到达终点;②马鸣跑全程的平均速度大于杨豪跑全程的平均速度;③杨豪在跑最后100m的过程中,与马鸣相遇2次;④马鸣前15s跑过的路程大于杨豪前15s跑过的路程.其中错误的个数是( )
A.1 B.2 C.3 D.4
二、填空题
1.甲、乙两个车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天.其间,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止.甲、乙两个车间各自加工零件总数为y(单件)与加工时间为x(单位:天)的对应关系如图1所示,甲车间与乙车n工零件总数之差z(单位:件)与加工时间x(单位:天)的对应关系如所示.请根据图象提供的信息回答:
(1)图1中,m的值是___;
(2)第___天时,甲、乙两个车间加工零件总数相同.
2.如图,OA、BA分别表示甲、乙两名学生运动的一次函数图象,图中s(m)和t(s)分别表示运动路程和时间,根据图象,判断快者的速度比慢者的速度每秒快____________.
3.如图,是嘉淇在体育课上投掷铅球的曲线图,其中表示铅球与投掷点的水平距离,表示铅球在投掷过程中的高度.在铅球出手时,铅球的高度为_________,嘉淇投掷铅球的成绩为_________.
4.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,AB=8cm,点P从B出发,沿折线BE ED DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则b=_______.
5.甲,乙两车在笔直的公路上行驶,乙车从之间的地出发,到达终点地停止行驶,甲车从起点地与乙车同时出发,到达地休息半小时后立即以另一速度返回地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车之间的距离(千米)与乙车行驶的时间(小时)之间的关系如图所示,则乙车到达终点时,甲车离地还有_____千米.
三、解答题
1.如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程、与时间的关系,观察图象并回答下列问题:
(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙有事耽搁,停下来时间为 小时;
(3)甲从出发起,经过 小时与乙相遇;
(4)甲行走的平均速度是多少千米小时?
2某人沿一条直路行走,此人离出发地的距离(千米)与行走时间(分钟)的函数关系如图所示,请根据图像提供的信息回答下列问题:
(1)此人离开出发地最远距离是________________千米;
(2)此人在这次行走过程中,停留所用的时间为______________分钟;
(3)由图中线段可知,此人在这段时间内行走的速度是每分钟__________千米;并写出对应的函数解析式__________________;
(4)此人在120分钟内共走了_____________千米.
3.某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.
(1)分别求出甲、乙两条生产线各自总产量(吨)与从乙开始投产以来所用时间(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
4.如图,在直角梯形中,动点从点出发,沿匀速运动,设点运动的路程为,三角形的面积为,图象如图所示.
(1)在这个变化中,自变量、因变量分别是______、______;(用字母表示)
(2)当点运动的路程时,三角形的面积______;
(3)的长为______,梯形的面积为______;
(4)当点运动的路程______时,三角形的面积.
5.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示)与x之间的函数关系.根据图象进行以下探究:
[信息读取]
(1)甲,乙两地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需______小时,普通列车的速度是______千米/小时:
[解决问题]
(3)求动车的速度:
(4)求点C的坐标.
6.描点画图是探究未知函数图象变化规律的一个重要方法,下面是通过描点画图感知函数图象的变化规律的过程:
(1)下表是与的几组对应值.
0 1 2 3 4 …
0 1 2 …
其中,的值为 ;
(2)已知,是函数图象上的任意两点(在的左侧),将,同时向右平移1个单位得到点,,再将,同时向上平移个单位后得到点,,若刚好落在函数的图象上,则与函数图象的位置关系是( )
A. 是图象上的点
B. 在图象的上方
C. 在图象的下方
一、单选题
1.如图,在Rt△PMN中,∠P=90°,PM=PN,MN=6cm,矩形ABCD中AB=2cm,BC=10cm,点C和点M重合,点B、C(M)、N在同一直线上,令Rt△PMN不动,矩形ABCD沿MN所在直线以每秒1cm的速度向右移动,至点C与点N重合为止,设移动x秒后,矩形ABCD与△PMN重叠部分的面积为y,则y与x的大致图象是( )
A. B. C. D.
2.如图1,动点P从矩形ABCD的顶点A出发,在边AB,BC上沿A→B→C的方向,以1cm/s的速度匀速运动到点C,的面积S(cm2)随运动时间t(s)变化的函数图象如图2所示,则AB的长是( )
A. B. C. D.
3.小强和小敏练短跑,小敏在小强前面12米.如图,、分别表示小强、小敏在短跑中的距离(单位:米)与时间(单位:秒)的变量关系的图象.根据图象判断小强的速度比小敏的速度每秒快
A.2.5米 B.2米 C.1.5 D.1米
4.甲、乙两人在一次跨栏比赛中,路程s(m)与时间t(s)的函数关系如图所示,根据图形下列说法正确的个数为( )
①这次比赛的赛程是110米②甲先到达终点;③乙在这次比赛中的平均速度为m/s;④乙的平均速度比甲快
A.1个 B.2个 C.3个 D.4个
5.如图1,点P从菱形ABCD的顶点A出发,沿着折线ABCDA匀速运动,图2是线段AP的长度y与时间x之间的函数关系的图像(不妨设当点P与点A重合时,y=0),则菱形ABCD的面积为( )
A.12 B.6 C.5 D.2.5
6.随着“互联网+”时代的到来,一种新型的打车方式受到大众欢迎.打车总费用y(单位:元)与行驶里程x(单位:千米)的函数关系如图所示.如果小明某次打车行驶里程为22千米,则他的打车费用为( )
A.33元 B.36元 C.40元 D.42元
7.2008年5月12日,四川汶川发生8.0级大地震,我解放军某部火速向灾区推进,最初坐车以某一速度匀速前进,中途由于道路出现泥石流,被阻停下,耽误了一段时间,为了尽快赶到灾区救援,官兵们下车急行军匀速步行前往,下列是官兵们行进的距离S(千米)与行进时间t(小时)的函数大致图象,你认为正确的是 ( ).
B.
C. D.
8.马鸣和杨豪进行4×50米折返跑.在整个过程中,跑步者距起跑线的距离y(单位:m)与跑步时间t(单位:s)的对应关系如图所示.下列叙述:①两人从起跑线同时出发,同时到达终点;②马鸣跑全程的平均速度大于杨豪跑全程的平均速度;③杨豪在跑最后100m的过程中,与马鸣相遇2次;④马鸣前15s跑过的路程大于杨豪前15s跑过的路程.其中错误的个数是( )
A.1 B.2 C.3 D.4
二、填空题
1.甲、乙两个车间接到加工一批零件的任务,从开始加工到完成这项任务共用了9天.其间,乙车间在加工2天后停止加工,引入新设备后继续加工,直到与甲车间同时完成这项任务为止.甲、乙两个车间各自加工零件总数为y(单件)与加工时间为x(单位:天)的对应关系如图1所示,甲车间与乙车n工零件总数之差z(单位:件)与加工时间x(单位:天)的对应关系如所示.请根据图象提供的信息回答:
(1)图1中,m的值是___;
(2)第___天时,甲、乙两个车间加工零件总数相同.
2.如图,OA、BA分别表示甲、乙两名学生运动的一次函数图象,图中s(m)和t(s)分别表示运动路程和时间,根据图象,判断快者的速度比慢者的速度每秒快____________.
3.如图,是嘉淇在体育课上投掷铅球的曲线图,其中表示铅球与投掷点的水平距离,表示铅球在投掷过程中的高度.在铅球出手时,铅球的高度为_________,嘉淇投掷铅球的成绩为_________.
4.已知:如图①,长方形ABCD中,E是边AD上一点,且AE=6cm,AB=8cm,点P从B出发,沿折线BE ED DC匀速运动,运动到点C停止.P的运动速度为2cm/s,运动时间为t(s),△BPC的面积为y(cm2),y与t的函数关系图象如图②,则b=_______.
5.甲,乙两车在笔直的公路上行驶,乙车从之间的地出发,到达终点地停止行驶,甲车从起点地与乙车同时出发,到达地休息半小时后立即以另一速度返回地并停止行驶,在行驶过程中,两车均保持匀速,甲、乙两车之间的距离(千米)与乙车行驶的时间(小时)之间的关系如图所示,则乙车到达终点时,甲车离地还有_____千米.
三、解答题
1.如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程、与时间的关系,观察图象并回答下列问题:
(1)乙出发时,乙与甲相距 千米;
(2)走了一段路程后,乙有事耽搁,停下来时间为 小时;
(3)甲从出发起,经过 小时与乙相遇;
(4)甲行走的平均速度是多少千米小时?
2某人沿一条直路行走,此人离出发地的距离(千米)与行走时间(分钟)的函数关系如图所示,请根据图像提供的信息回答下列问题:
(1)此人离开出发地最远距离是________________千米;
(2)此人在这次行走过程中,停留所用的时间为______________分钟;
(3)由图中线段可知,此人在这段时间内行走的速度是每分钟__________千米;并写出对应的函数解析式__________________;
(4)此人在120分钟内共走了_____________千米.
3.某车间有甲、乙两条生产线.在甲生产线已生产了200吨成品后,乙生产线开始投入生产,甲、乙两条生产线每天分别生产20吨和30吨成品.
(1)分别求出甲、乙两条生产线各自总产量(吨)与从乙开始投产以来所用时间(天)之间的函数关系式.
(2)作出上述两个函数在如图所示的直角坐标系中的图象,观察图象,分别指出第10天和第30天结束时,哪条生产线的总产量高?
4.如图,在直角梯形中,动点从点出发,沿匀速运动,设点运动的路程为,三角形的面积为,图象如图所示.
(1)在这个变化中,自变量、因变量分别是______、______;(用字母表示)
(2)当点运动的路程时,三角形的面积______;
(3)的长为______,梯形的面积为______;
(4)当点运动的路程______时,三角形的面积.
5.一列动车从甲地开往乙地,一列普通列车从乙地开往甲地,两车同时出发,设普通列车行驶的时间为x(小时),两车之间的距离为y(千米),如图中的折线表示)与x之间的函数关系.根据图象进行以下探究:
[信息读取]
(1)甲,乙两地相距______千米,两车出发后______小时相遇;
(2)普通列车到达终点共需______小时,普通列车的速度是______千米/小时:
[解决问题]
(3)求动车的速度:
(4)求点C的坐标.
6.描点画图是探究未知函数图象变化规律的一个重要方法,下面是通过描点画图感知函数图象的变化规律的过程:
(1)下表是与的几组对应值.
0 1 2 3 4 …
0 1 2 …
其中,的值为 ;
(2)已知,是函数图象上的任意两点(在的左侧),将,同时向右平移1个单位得到点,,再将,同时向上平移个单位后得到点,,若刚好落在函数的图象上,则与函数图象的位置关系是( )
A. 是图象上的点
B. 在图象的上方
C. 在图象的下方
