2.3平行线的性质讲义(无答案)2023—2024学年北师大版数学七年级下册
文档属性
| 名称 | 2.3平行线的性质讲义(无答案)2023—2024学年北师大版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 236.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 18:54:03 | ||
图片预览

文档简介
平行线的性质讲义
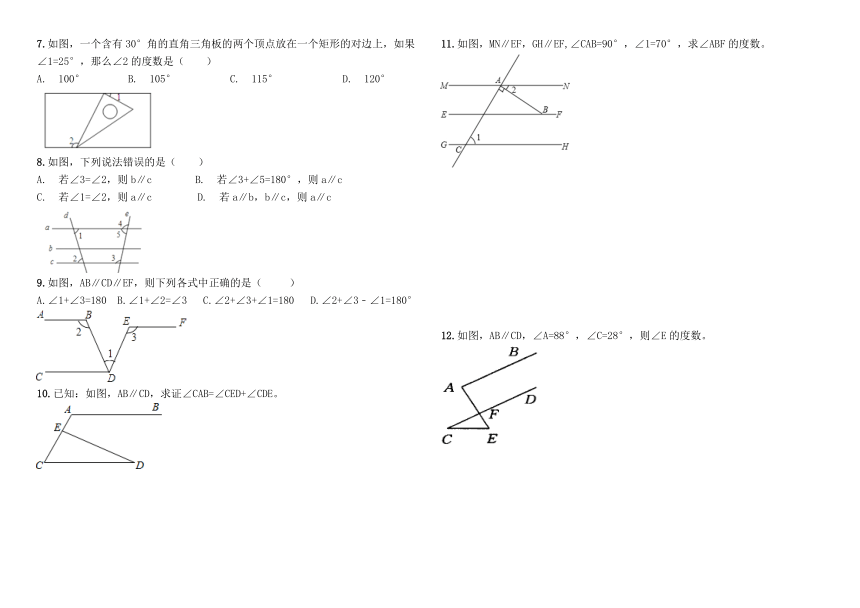
例1:如图,点P为∠AOB的边OA上的一点,过点P作直线EF∥OB。(用尺规作图,不写作法,保留作图痕迹)
如图,AB∥CD,则下列各式等于180°的是( )
A.∠1+∠2+∠3 B.∠2-∠1+∠3 C.∠1-∠2+∠3 D.∠1+∠2-∠3
如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐的角∠A是1200,第二次拐的角∠B是1500第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A.1200 B.1300 C.1400 D.150
如图,下列推理不正确的是( )
A. ∵AB∥CD, ∴∠ABC+∠C=180 B. ∵∠1=∠2, ∴AD∥BC
C. ∵AD∥BC,∴∠3=∠4 D. ∵∠A+∠ADC=180, ∴AB∥CD
已知两个角的两边分别平行,且其中一个角比另一个角的3倍多360,则这两个角的度数是( )
A.200和 960 B.360和1440 C.400和1560 D.不能确定
如图,AB∥CD,∠3=∠4,下列结论不成立的是( )
A.∠1=∠4 B.∠3=∠5 C.∠1=∠5 D.∠2+∠4=180°
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为( )
A.20° B. 25° C.30° D. 35°
如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=25°,那么∠2的度数是( )
A. 100° B. 105° C. 115° D. 120°
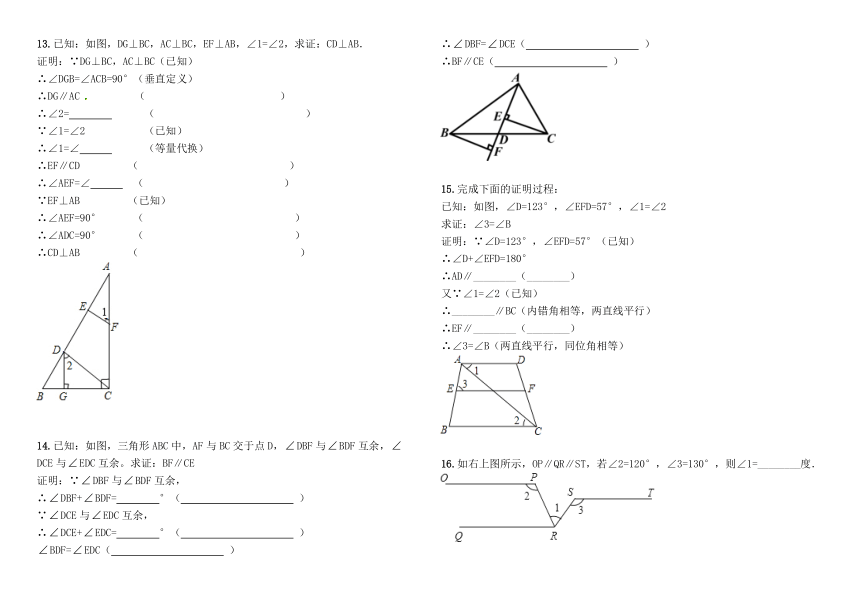
如图,下列说法错误的是( )
A. 若∠3=∠2,则b∥c B. 若∠3+∠5=180°,则a∥c
C. 若∠1=∠2,则a∥c D. 若a∥b,b∥c,则a∥c
如图,AB∥CD∥EF,则下列各式中正确的是( )
A.∠1+∠3=180 B.∠1+∠2=∠3 C.∠2+∠3+∠1=180 D.∠2+∠3﹣∠1=180°
已知:如图,AB∥CD,求证∠CAB=∠CED+∠CDE。
如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求∠ABF的度数。
如图,AB∥CD,∠A=88°,∠C=28°,则∠E的度数。
已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC ( )
∴∠2= ( )
∵∠1=∠2 (已知)
∴∠1=∠ (等量代换)
∴EF∥CD ( )
∴∠AEF=∠ ( )
∵EF⊥AB (已知)
∴∠AEF=90° ( )
∴∠ADC=90° ( )
∴CD⊥AB ( )
已知:如图,三角形ABC中,AF与BC交于点D,DBF与BDF互余,DCE与EDC互余。求证:BF∥CE
证明:∵DBF与BDF互余,
∴DBF+BDF= °( )
∵DCE与EDC互余,
∴DCE+EDC= °( )
BDF=EDC( )
∴DBF=DCE( )
∴BF∥CE( )
完成下面的证明过程:
已知:如图,∠D=123°,∠EFD=57°,∠1=∠2
求证:∠3=∠B
证明:∵∠D=123°,∠EFD=57°(已知)
∴∠D+∠EFD=180°
∴AD∥________(________)
又∵∠1=∠2(已知)
∴________∥BC(内错角相等,两直线平行)
∴EF∥________(________)
∴∠3=∠B(两直线平行,同位角相等)
如右上图所示,OP∥QR∥ST,若∠2=120°,∠3=130°,则∠1=________度.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,试判断DG与BC的位置关系,并说明理由.
如图所示,已知∠1=∠2,∠3=∠4,∠5=∠C,求证:DE//BF
如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)请你判断∠1与∠BDC的数量关系,并说明理由;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
如图1,已知直线l1∥l2 , 且l1、l2分别相交于A、B两点,l4和l1、l2分别交于C、D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3.点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________.
(2)试找出∠1、∠2、∠3之间的等量关系,并说明理由.
(3)应用(2)中的结论解答下列问题: 如图2,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数.
(4)如果点P在直线l3上且在A、B两点外侧运动时,其他条件不变,试探究∠1、∠2、∠3之间的关系(点P和A、B两点不重合),直接写出结论即可.
探究题:如图,直线AC∥BD,点P是一个动点,连接PA、PB,构成∠PAC、∠APB、∠PBD三个角。
(1)当动点P落在AC、BD内部如图①的位置时,则∠PAC、∠APB、∠PBD三个角存在等量关系:_______________________。(提示:可以过点P作AC的平行线)
(2)当动点P落在AC的上方如图②的位置时,∠PAC、∠APB、∠PBD三个角存在等量关系:_______________________。
(3)当动点P落在BD的下方如图③的位置时,∠PAC、∠APB、∠PBD三个角存在等量关系:_______________________。
图① 图② 图③
出门考
1.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于________°.
2.如图所示,AB∥CD,∠1=120°,∠2=130°,则∠3的度数为________°.
3.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 。
5.如右图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC
∴∠EFB=∠ADB=90°
∴EF∥AD ( )
∴∠1=∠BAD ( )
又∵∠1=∠2
∴∠_____=∠______(等量代换)
∴DG∥BA .( )
6.如图,已知∠3+∠ADC=180°,且DG//AB,试证明∠1=∠2。
例1:如图,点P为∠AOB的边OA上的一点,过点P作直线EF∥OB。(用尺规作图,不写作法,保留作图痕迹)
如图,AB∥CD,则下列各式等于180°的是( )
A.∠1+∠2+∠3 B.∠2-∠1+∠3 C.∠1-∠2+∠3 D.∠1+∠2-∠3
如图,一条公路修到湖边时,需拐弯绕湖而过;如果第一次拐的角∠A是1200,第二次拐的角∠B是1500第三次拐的角是∠C,这时的道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A.1200 B.1300 C.1400 D.150
如图,下列推理不正确的是( )
A. ∵AB∥CD, ∴∠ABC+∠C=180 B. ∵∠1=∠2, ∴AD∥BC
C. ∵AD∥BC,∴∠3=∠4 D. ∵∠A+∠ADC=180, ∴AB∥CD
已知两个角的两边分别平行,且其中一个角比另一个角的3倍多360,则这两个角的度数是( )
A.200和 960 B.360和1440 C.400和1560 D.不能确定
如图,AB∥CD,∠3=∠4,下列结论不成立的是( )
A.∠1=∠4 B.∠3=∠5 C.∠1=∠5 D.∠2+∠4=180°
如图,直线l∥m,将含有45°角的三角板ABC的直角顶点C放在直线m上,若∠1=25°,则∠2的度数为( )
A.20° B. 25° C.30° D. 35°
如图,一个含有30°角的直角三角板的两个顶点放在一个矩形的对边上,如果∠1=25°,那么∠2的度数是( )
A. 100° B. 105° C. 115° D. 120°
如图,下列说法错误的是( )
A. 若∠3=∠2,则b∥c B. 若∠3+∠5=180°,则a∥c
C. 若∠1=∠2,则a∥c D. 若a∥b,b∥c,则a∥c
如图,AB∥CD∥EF,则下列各式中正确的是( )
A.∠1+∠3=180 B.∠1+∠2=∠3 C.∠2+∠3+∠1=180 D.∠2+∠3﹣∠1=180°
已知:如图,AB∥CD,求证∠CAB=∠CED+∠CDE。
如图,MN∥EF,GH∥EF,∠CAB=90°,∠1=70°,求∠ABF的度数。
如图,AB∥CD,∠A=88°,∠C=28°,则∠E的度数。
已知:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:CD⊥AB.
证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=∠ACB=90°(垂直定义)
∴DG∥AC ( )
∴∠2= ( )
∵∠1=∠2 (已知)
∴∠1=∠ (等量代换)
∴EF∥CD ( )
∴∠AEF=∠ ( )
∵EF⊥AB (已知)
∴∠AEF=90° ( )
∴∠ADC=90° ( )
∴CD⊥AB ( )
已知:如图,三角形ABC中,AF与BC交于点D,DBF与BDF互余,DCE与EDC互余。求证:BF∥CE
证明:∵DBF与BDF互余,
∴DBF+BDF= °( )
∵DCE与EDC互余,
∴DCE+EDC= °( )
BDF=EDC( )
∴DBF=DCE( )
∴BF∥CE( )
完成下面的证明过程:
已知:如图,∠D=123°,∠EFD=57°,∠1=∠2
求证:∠3=∠B
证明:∵∠D=123°,∠EFD=57°(已知)
∴∠D+∠EFD=180°
∴AD∥________(________)
又∵∠1=∠2(已知)
∴________∥BC(内错角相等,两直线平行)
∴EF∥________(________)
∴∠3=∠B(两直线平行,同位角相等)
如右上图所示,OP∥QR∥ST,若∠2=120°,∠3=130°,则∠1=________度.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.∠1=∠2,试判断DG与BC的位置关系,并说明理由.
如图所示,已知∠1=∠2,∠3=∠4,∠5=∠C,求证:DE//BF
如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)请你判断∠1与∠BDC的数量关系,并说明理由;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
如图1,已知直线l1∥l2 , 且l1、l2分别相交于A、B两点,l4和l1、l2分别交于C、D两点,∠ACP=∠1,∠BDP=∠2,∠CPD=∠3.点P在线段AB上.
(1)若∠1=22°,∠2=33°,则∠3=________.
(2)试找出∠1、∠2、∠3之间的等量关系,并说明理由.
(3)应用(2)中的结论解答下列问题: 如图2,点A在B处北偏东40°的方向上,在C处的北偏西45°的方向上,求∠BAC的度数.
(4)如果点P在直线l3上且在A、B两点外侧运动时,其他条件不变,试探究∠1、∠2、∠3之间的关系(点P和A、B两点不重合),直接写出结论即可.
探究题:如图,直线AC∥BD,点P是一个动点,连接PA、PB,构成∠PAC、∠APB、∠PBD三个角。
(1)当动点P落在AC、BD内部如图①的位置时,则∠PAC、∠APB、∠PBD三个角存在等量关系:_______________________。(提示:可以过点P作AC的平行线)
(2)当动点P落在AC的上方如图②的位置时,∠PAC、∠APB、∠PBD三个角存在等量关系:_______________________。
(3)当动点P落在BD的下方如图③的位置时,∠PAC、∠APB、∠PBD三个角存在等量关系:_______________________。
图① 图② 图③
出门考
1.如图,AB∥EF∥CD,∠ABC=46°,∠CEF=154°,则∠BCE等于________°.
2.如图所示,AB∥CD,∠1=120°,∠2=130°,则∠3的度数为________°.
3.一大门的栏杆如图所示,BA垂直于地面AE于A,CD平行于地面AE,则∠ABC+∠BCD= 。
5.如右图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.
证明:∵AD⊥BC,EF⊥BC
∴∠EFB=∠ADB=90°
∴EF∥AD ( )
∴∠1=∠BAD ( )
又∵∠1=∠2
∴∠_____=∠______(等量代换)
∴DG∥BA .( )
6.如图,已知∠3+∠ADC=180°,且DG//AB,试证明∠1=∠2。
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
