2023-2024学年苏科版九年级下册数学第12周滚动练习卷二(无答案)
文档属性
| 名称 | 2023-2024学年苏科版九年级下册数学第12周滚动练习卷二(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 270.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 20:27:43 | ||
图片预览

文档简介
2023--2024学年第二学期初三数学第12周滚动练习卷二
几何基础题练习
一.选择题(共8小题)
1.实数与数轴上的点一一对应,小明在构造数轴上的点时,将一个直角边长为1的等腰直角三角形放在数轴上,直角顶点C与原点重合,点A与数轴上表示﹣1的点重合.如图,小明以点A为圆心,AB长为半径画弧,与数轴的负半轴交于点D,则点D表示的实数为( )
A. B. C. D.
第1题第2题
2.如图在△ABC,△CDE中,∠ACB=∠DCE=90°,AC=BC,CD=CE.连接BD,AE交于点F.以下四个结论:①BD=AE;②BD⊥AE;③∠AEC+∠DBC=45°;④FC平分∠BFE,其中结论正确的个数为( )
A.1 B.2 C.3 D.4
3.如图,已知矩形ABCD的一边AB长为12,点P为边AD上一动点,连接BP、CP,且满足∠BPC=30°,则BC的值可能是( )
A.6 B.6.8 C. D.
4.两个三角形相似比是2:3,其中小三角形的周长为18,则另一个大三角形的周长是( )
A.12 B.18 C.24 D.27
第3题第5题第6题
5.如图,Rt△ABC中,∠ACB=90°,∠CAB=37°,,,BC=1,直线MN经过点C,交边AB于点D,分别过点A,B作 AF⊥MN,BE⊥MN,垂足分别为E,F,设线段BE,AF的长度分别为d1,d2.若直线MN从与CB重合位置开始顺时针绕着点C旋转,至与CA重合时停止,在旋转过程中,d1+d2的最大值为( )
A. B.1 C. D.
6.如图,点O为正六边形ABCDEF对角线FD上一点,假设可以随机在正六边形中取点,那么这个点取在阴影部分的概率是( )
A. B. C. D.
7.某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )
A.众数是80; B.中位数是75; C.平均数是80; D.极差是15
8.如图①,在矩形ABCD中,AB>BC,点P从点B出发沿线段BC向点C运动,线段AP的垂直平分线分别交AB,DC于点M,N,设BM=y,BP=x,y与x之间的函数图象如图②所示,则图②中的a的值为( )
A.8 B.12 C.9 D.
二.填空题(共8小题)
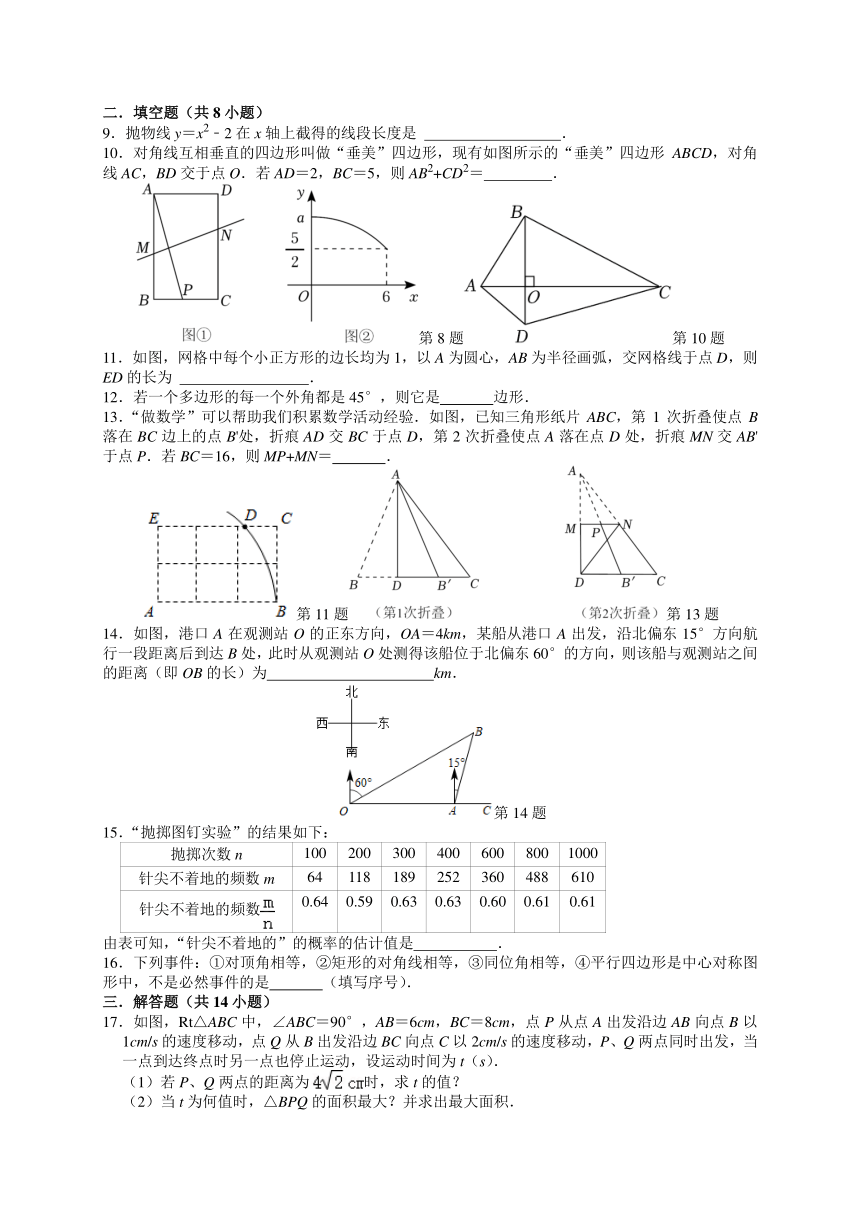
9.抛物线y=x2﹣2在x轴上截得的线段长度是 .
10.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=2,BC=5,则AB2+CD2= .
第8题第10题
11.如图,网格中每个小正方形的边长均为1,以A为圆心,AB为半径画弧,交网格线于点D,则ED的长为 .
12.若一个多边形的每一个外角都是45°,则它是 边形.
13.“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片ABC,第1次折叠使点B落在BC边上的点B'处,折痕AD交BC于点D,第2次折叠使点A落在点D处,折痕MN交AB'于点P.若BC=16,则MP+MN= .
第11题第13题
14.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船与观测站之间的距离(即OB的长)为 km.
第14题
15.“抛掷图钉实验”的结果如下:
抛掷次数n 100 200 300 400 600 800 1000
针尖不着地的频数m 64 118 189 252 360 488 610
针尖不着地的频数 0.64 0.59 0.63 0.63 0.60 0.61 0.61
由表可知,“针尖不着地的”的概率的估计值是 .
16.下列事件:①对顶角相等,②矩形的对角线相等,③同位角相等,④平行四边形是中心对称图形中,不是必然事件的是 (填写序号).
三.解答题(共14小题)
17.如图,Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,点P从点A出发沿边AB向点B以1cm/s的速度移动,点Q从B出发沿边BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一点到达终点时另一点也停止运动,设运动时间为t(s).
(1)若P、Q两点的距离为时,求t的值?
(2)当t为何值时,△BPQ的面积最大?并求出最大面积.
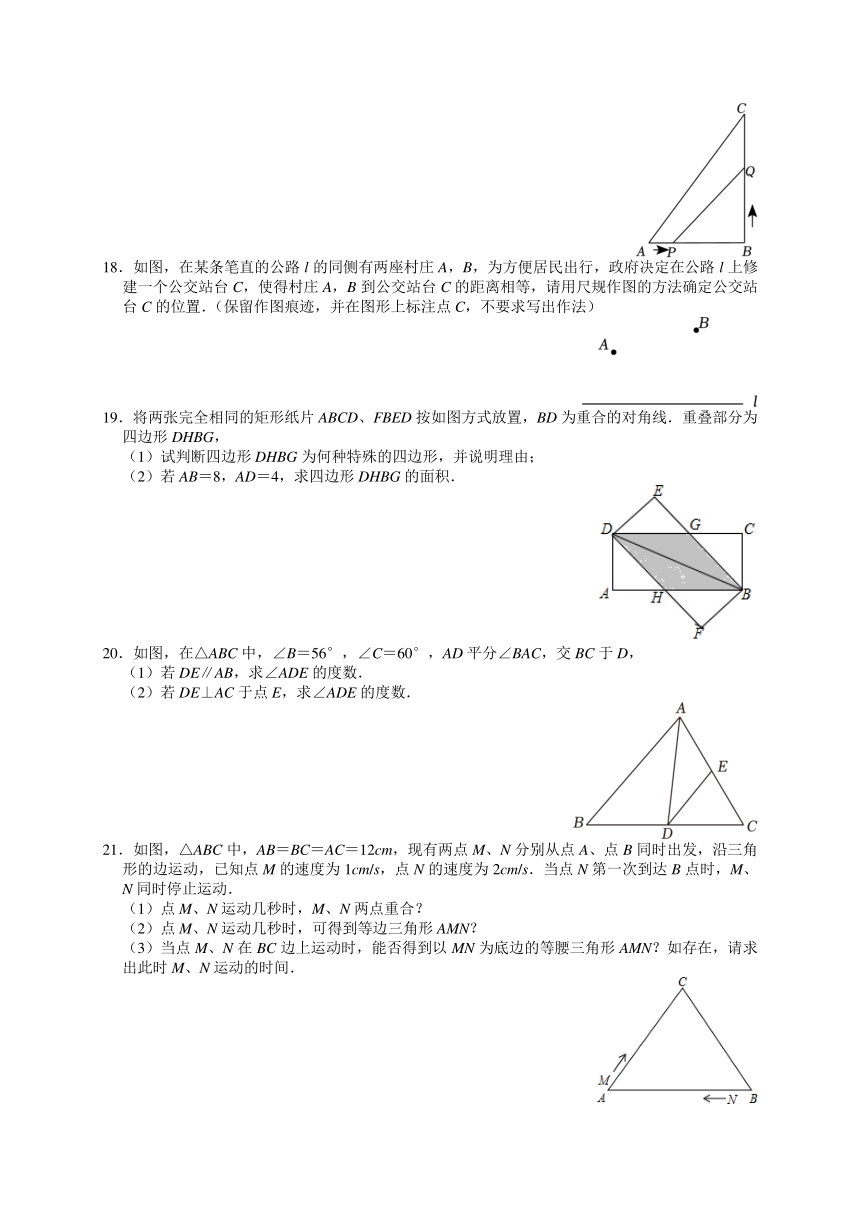
18.如图,在某条笔直的公路l的同侧有两座村庄A,B,为方便居民出行,政府决定在公路l上修建一个公交站台C,使得村庄A,B到公交站台C的距离相等,请用尺规作图的方法确定公交站台C的位置.(保留作图痕迹,并在图形上标注点C,不要求写出作法)
19.将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
20.如图,在△ABC中,∠B=56°,∠C=60°,AD平分∠BAC,交BC于D,
(1)若DE∥AB,求∠ADE的度数.
(2)若DE⊥AC于点E,求∠ADE的度数.
21.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒时,M、N两点重合?
(2)点M、N运动几秒时,可得到等边三角形AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
22.如图,四边形ABCD中,AD∥BC,E是BC的中点,AD=10,BC=24,CD=,∠C=45°,点P是边BC上的一动点,设PB的长为x.
(1)当x的值为多少时,以点P、A、D、E为顶点的四边形为平行四边形;
(2)点P在边BC上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
23.如图,在△ABC中,点D在BC边上,∠DAC=∠B.点E在AD边上,CD=CE.
(1)求证:△ABD∽△CAE;
(2)若AB=6,AC=,BD=2,求AE的长.
24.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A与点D重合,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并画出AB边上的中线CG;
(2)若连接AD、BE,则这两条线段之间的关系是 ;
(3)△DEF的面积为 .
25.生活中,折纸是一种大家喜欢的活动、在数学中,我们可以通过折纸进行探究,探寻数学奥秘.
【纸片规格】
三角形纸片ABC,∠ACB=120°,CA=CB,点D是底边AB上一点.
【换作探究】
(1)如图1,若AC=6,AD=2,连接CD,求CD的长度;
(2)如图2,若AC=6,连接CD,将△ACD沿CD所在直线翻折得到△ECD,点A的对应点为点E.若DE所在的直线与△ABC的一边垂直,求AD的长;
(3)如图3,将△ACD沿CD所在直线翻折得到△ECD,边CE与边AB交于点F,且DE∥BC,再将△DFE沿DF所在直线翻折得到△DFG,点E的对应点为点G,DG与CE、BC分别交于H,K,若KH=1,请直接写出AC边的长.
26.如图,在边长为1的小正方形网格中,点A,B,C均落在格点上.
(1)画出△ABC关于直线l的轴对称图形△A'B'C';
(2)连接A'B,C'B,则△A'BC'的面积为 ;
(3)在直线l上找一点P,使PA+PC最小,在直线l上标出点P的位置.
27.某校组织1000名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机抽取一些学生在评比中的成绩制成的统计图表如下:
频数分布表
分数段 频数 百分比
80≤x<85 a 20%
85≤x<90 80 b
90≤x<95 60 30%
95≤x<100 20
根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a= ,b= ;
(2)补全频数分布表和频数分布直方图;
(3)如果评比成绩在95分以上的可以获得一等奖,试估计该校参加此次活动获得一等奖的人数.
28.田忌赛马的故事为我们熟知,小王与小方学习概率初步知识后设计了如下游戏:小王手中有方块9、6、5三张扑克牌,小方手中有方块8、7、4三张扑克牌.每人从各自手中取出一张牌进行比较,数字大的为本“局”获胜,每次取得牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小方本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小王的三张牌出牌顺序为先出5,再出6,最后出9时,小方随机出牌应对,用列举的方法求出小方本次比赛获胜的概率.
29.不透明的袋子中装有红球、黄球、蓝球各一个,这些球除颜色外无其他差别.
(1)从袋子中随机摸出一个球,摸到蓝球的概率是 ;
(2)从袋子中随机摸出一个球后,放回并摇匀,再随机摸出一个球.求两次摸到的球的颜色为“一红一黄”的概率.
30.某校九年级开展男、女学生数学学习竞赛.从全体九年级学生中随意抽取男生、女生各10名同学,进行“十分制”(满分10分)答题对抗赛,竞赛成绩结果(单位:分)如下:
男生:2,4,6,8,7,7,8,9,9,10:
女生:9,6,7,6,2,7,7,9,8,9.
(1)男女两组学生的对抗赛成绩的方差各是多少?
(2)规定成绩较稳定者胜出,你认为哪一组应胜出?说明理由.
几何基础题练习
一.选择题(共8小题)
1.实数与数轴上的点一一对应,小明在构造数轴上的点时,将一个直角边长为1的等腰直角三角形放在数轴上,直角顶点C与原点重合,点A与数轴上表示﹣1的点重合.如图,小明以点A为圆心,AB长为半径画弧,与数轴的负半轴交于点D,则点D表示的实数为( )
A. B. C. D.
第1题第2题
2.如图在△ABC,△CDE中,∠ACB=∠DCE=90°,AC=BC,CD=CE.连接BD,AE交于点F.以下四个结论:①BD=AE;②BD⊥AE;③∠AEC+∠DBC=45°;④FC平分∠BFE,其中结论正确的个数为( )
A.1 B.2 C.3 D.4
3.如图,已知矩形ABCD的一边AB长为12,点P为边AD上一动点,连接BP、CP,且满足∠BPC=30°,则BC的值可能是( )
A.6 B.6.8 C. D.
4.两个三角形相似比是2:3,其中小三角形的周长为18,则另一个大三角形的周长是( )
A.12 B.18 C.24 D.27
第3题第5题第6题
5.如图,Rt△ABC中,∠ACB=90°,∠CAB=37°,,,BC=1,直线MN经过点C,交边AB于点D,分别过点A,B作 AF⊥MN,BE⊥MN,垂足分别为E,F,设线段BE,AF的长度分别为d1,d2.若直线MN从与CB重合位置开始顺时针绕着点C旋转,至与CA重合时停止,在旋转过程中,d1+d2的最大值为( )
A. B.1 C. D.
6.如图,点O为正六边形ABCDEF对角线FD上一点,假设可以随机在正六边形中取点,那么这个点取在阴影部分的概率是( )
A. B. C. D.
7.某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )
A.众数是80; B.中位数是75; C.平均数是80; D.极差是15
8.如图①,在矩形ABCD中,AB>BC,点P从点B出发沿线段BC向点C运动,线段AP的垂直平分线分别交AB,DC于点M,N,设BM=y,BP=x,y与x之间的函数图象如图②所示,则图②中的a的值为( )
A.8 B.12 C.9 D.
二.填空题(共8小题)
9.抛物线y=x2﹣2在x轴上截得的线段长度是 .
10.对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形ABCD,对角线AC,BD交于点O.若AD=2,BC=5,则AB2+CD2= .
第8题第10题
11.如图,网格中每个小正方形的边长均为1,以A为圆心,AB为半径画弧,交网格线于点D,则ED的长为 .
12.若一个多边形的每一个外角都是45°,则它是 边形.
13.“做数学”可以帮助我们积累数学活动经验.如图,已知三角形纸片ABC,第1次折叠使点B落在BC边上的点B'处,折痕AD交BC于点D,第2次折叠使点A落在点D处,折痕MN交AB'于点P.若BC=16,则MP+MN= .
第11题第13题
14.如图,港口A在观测站O的正东方向,OA=4km,某船从港口A出发,沿北偏东15°方向航行一段距离后到达B处,此时从观测站O处测得该船位于北偏东60°的方向,则该船与观测站之间的距离(即OB的长)为 km.
第14题
15.“抛掷图钉实验”的结果如下:
抛掷次数n 100 200 300 400 600 800 1000
针尖不着地的频数m 64 118 189 252 360 488 610
针尖不着地的频数 0.64 0.59 0.63 0.63 0.60 0.61 0.61
由表可知,“针尖不着地的”的概率的估计值是 .
16.下列事件:①对顶角相等,②矩形的对角线相等,③同位角相等,④平行四边形是中心对称图形中,不是必然事件的是 (填写序号).
三.解答题(共14小题)
17.如图,Rt△ABC中,∠ABC=90°,AB=6cm,BC=8cm,点P从点A出发沿边AB向点B以1cm/s的速度移动,点Q从B出发沿边BC向点C以2cm/s的速度移动,P、Q两点同时出发,当一点到达终点时另一点也停止运动,设运动时间为t(s).
(1)若P、Q两点的距离为时,求t的值?
(2)当t为何值时,△BPQ的面积最大?并求出最大面积.
18.如图,在某条笔直的公路l的同侧有两座村庄A,B,为方便居民出行,政府决定在公路l上修建一个公交站台C,使得村庄A,B到公交站台C的距离相等,请用尺规作图的方法确定公交站台C的位置.(保留作图痕迹,并在图形上标注点C,不要求写出作法)
19.将两张完全相同的矩形纸片ABCD、FBED按如图方式放置,BD为重合的对角线.重叠部分为四边形DHBG,
(1)试判断四边形DHBG为何种特殊的四边形,并说明理由;
(2)若AB=8,AD=4,求四边形DHBG的面积.
20.如图,在△ABC中,∠B=56°,∠C=60°,AD平分∠BAC,交BC于D,
(1)若DE∥AB,求∠ADE的度数.
(2)若DE⊥AC于点E,求∠ADE的度数.
21.如图,△ABC中,AB=BC=AC=12cm,现有两点M、N分别从点A、点B同时出发,沿三角形的边运动,已知点M的速度为1cm/s,点N的速度为2cm/s.当点N第一次到达B点时,M、N同时停止运动.
(1)点M、N运动几秒时,M、N两点重合?
(2)点M、N运动几秒时,可得到等边三角形AMN?
(3)当点M、N在BC边上运动时,能否得到以MN为底边的等腰三角形AMN?如存在,请求出此时M、N运动的时间.
22.如图,四边形ABCD中,AD∥BC,E是BC的中点,AD=10,BC=24,CD=,∠C=45°,点P是边BC上的一动点,设PB的长为x.
(1)当x的值为多少时,以点P、A、D、E为顶点的四边形为平行四边形;
(2)点P在边BC上运动的过程中,以P、A、D、E为顶点的四边形能否构成菱形?试说明理由.
23.如图,在△ABC中,点D在BC边上,∠DAC=∠B.点E在AD边上,CD=CE.
(1)求证:△ABD∽△CAE;
(2)若AB=6,AC=,BD=2,求AE的长.
24.在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A与点D重合,点E、F分别是B、C的对应点.
(1)请画出平移后的△DEF,并画出AB边上的中线CG;
(2)若连接AD、BE,则这两条线段之间的关系是 ;
(3)△DEF的面积为 .
25.生活中,折纸是一种大家喜欢的活动、在数学中,我们可以通过折纸进行探究,探寻数学奥秘.
【纸片规格】
三角形纸片ABC,∠ACB=120°,CA=CB,点D是底边AB上一点.
【换作探究】
(1)如图1,若AC=6,AD=2,连接CD,求CD的长度;
(2)如图2,若AC=6,连接CD,将△ACD沿CD所在直线翻折得到△ECD,点A的对应点为点E.若DE所在的直线与△ABC的一边垂直,求AD的长;
(3)如图3,将△ACD沿CD所在直线翻折得到△ECD,边CE与边AB交于点F,且DE∥BC,再将△DFE沿DF所在直线翻折得到△DFG,点E的对应点为点G,DG与CE、BC分别交于H,K,若KH=1,请直接写出AC边的长.
26.如图,在边长为1的小正方形网格中,点A,B,C均落在格点上.
(1)画出△ABC关于直线l的轴对称图形△A'B'C';
(2)连接A'B,C'B,则△A'BC'的面积为 ;
(3)在直线l上找一点P,使PA+PC最小,在直线l上标出点P的位置.
27.某校组织1000名学生参加“展示我美丽祖国”庆国庆的自拍照片的评比活动.随机抽取一些学生在评比中的成绩制成的统计图表如下:
频数分布表
分数段 频数 百分比
80≤x<85 a 20%
85≤x<90 80 b
90≤x<95 60 30%
95≤x<100 20
根据以上图表提供的信息,解答下列问题:
(1)写出表中a、b的数值:a= ,b= ;
(2)补全频数分布表和频数分布直方图;
(3)如果评比成绩在95分以上的可以获得一等奖,试估计该校参加此次活动获得一等奖的人数.
28.田忌赛马的故事为我们熟知,小王与小方学习概率初步知识后设计了如下游戏:小王手中有方块9、6、5三张扑克牌,小方手中有方块8、7、4三张扑克牌.每人从各自手中取出一张牌进行比较,数字大的为本“局”获胜,每次取得牌不能放回.
(1)若每人随机取手中的一张牌进行比赛,求小方本“局”获胜的概率;
(2)若比赛采用三局两胜制,即胜2局或3局者为本次比赛获胜者.当小王的三张牌出牌顺序为先出5,再出6,最后出9时,小方随机出牌应对,用列举的方法求出小方本次比赛获胜的概率.
29.不透明的袋子中装有红球、黄球、蓝球各一个,这些球除颜色外无其他差别.
(1)从袋子中随机摸出一个球,摸到蓝球的概率是 ;
(2)从袋子中随机摸出一个球后,放回并摇匀,再随机摸出一个球.求两次摸到的球的颜色为“一红一黄”的概率.
30.某校九年级开展男、女学生数学学习竞赛.从全体九年级学生中随意抽取男生、女生各10名同学,进行“十分制”(满分10分)答题对抗赛,竞赛成绩结果(单位:分)如下:
男生:2,4,6,8,7,7,8,9,9,10:
女生:9,6,7,6,2,7,7,9,8,9.
(1)男女两组学生的对抗赛成绩的方差各是多少?
(2)规定成绩较稳定者胜出,你认为哪一组应胜出?说明理由.
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
