第18章 勾股定理 单元检测题(含答案)2023-2024学年沪科版数学八年级下册
文档属性
| 名称 | 第18章 勾股定理 单元检测题(含答案)2023-2024学年沪科版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 400.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 00:00:00 | ||
图片预览


文档简介
第18章《勾股定理》单元检测题2023-2024学年八年级下册数学沪科版
一、单选题(共10小题,满分40分)
1.如图,钓鱼竿的长为5.4米,露在水面上的鱼线长为1.8米.当钓鱼者把钓鱼竿转到的位置时,露在水面上的鱼线长为4.2米,则的长为( )
A.米 B.米 C.米 D.米
2.《九章算术》提供了许多勾股数如,等一组勾股数最大的数称为“弦数”.经研究,若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个数组成勾股数,若m是大于1的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1,得到两个整数,那么m与这两个数组成勾股数,根据上面的规律,由10生成的勾股数的“弦数”是( )
A.16 B.24 C.26 D.32
3.如图,有一根电线杆在离地面9米A处断裂,电线杆顶部C落在离电线杆底部B点12米远的地方,则电线杆断裂之前的长度为( )米.
A.12 B.15 C.21 D.24
4.下列命题是真命题的是( )
A.是无理数
B.三个连续的整数不能构成直角三角形的三边长
C.一次函数的图象不可能同时经过三、四象限
D.二元一次方程的解一定是整数解
5.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要多长. ( )
A.10n B. C. D.
6.《算法统宗》是中国古代数学名著,作者是明代数学家程大位.书中记载了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地;送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉;良工高士素好奇,算出索长有几?”
译文:“秋千静止的时候,踏板离地1尺,将它往前推送两步(两步10尺)时,此时踏板升高离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长?”
若设秋千绳索长为x尺,则可列方程为( ).
A. B.
C. D.
7.如图,在平面直角坐标系xOy中,已知点P(m,m),过点P作OP的垂线交函数(k>1)的图象于点Q.若Q的横坐标为1,且OP2﹣PQ2=6,则k的值为( )
A.2 B.3 C. D.4
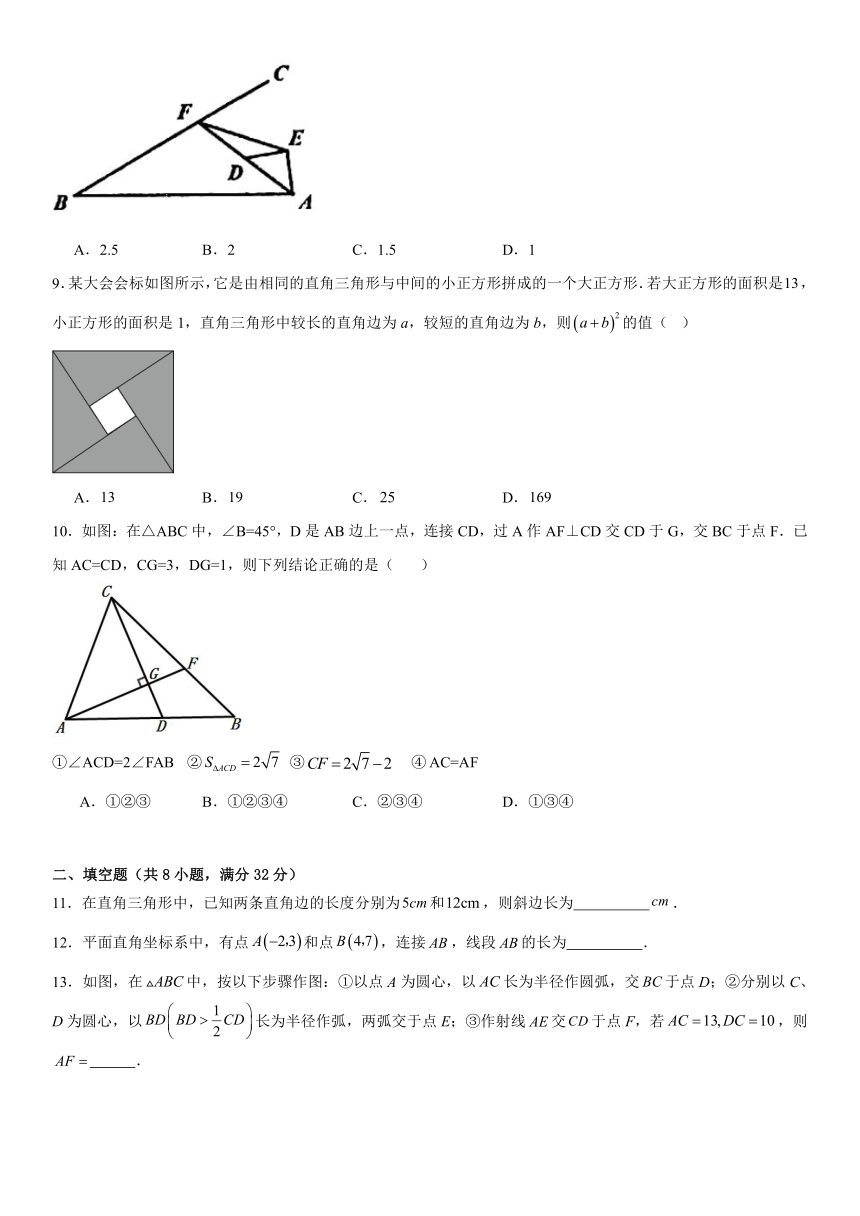
8.如图,是射线上一动点,为线段中点,以为斜边做等腰直角,连结,当最短时,的面积为( )
A.2.5 B.2 C.1.5 D.1
9.某大会会标如图所示,它是由相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是,小正方形的面积是1,直角三角形中较长的直角边为a,较短的直角边为b,则的值( )
A. B. C. D.
10.如图:在△ABC中,∠B=45°,D是AB边上一点,连接CD,过A作AF⊥CD交CD于G,交BC于点F.已知AC=CD,CG=3,DG=1,则下列结论正确的是( )
①∠ACD=2∠FAB ② ③ ④ AC=AF
A.①②③ B.①②③④ C.②③④ D.①③④
二、填空题(共8小题,满分32分)
11.在直角三角形中,已知两条直角边的长度分别为和,则斜边长为 .
12.平面直角坐标系中,有点和点,连接,线段的长为 .
13.如图,在中,按以下步骤作图:①以点A为圆心,以长为半径作圆弧,交于点D;②分别以C、D为圆心,以长为半径作弧,两弧交于点E;③作射线交于点F,若,则 .
14.如图,在ΔABC中,∠A=90°,∠B=30°,AD为中线,AD=1,则BC= ,AB= .
15.两直角边a , b满足,则斜边长为 .
16.如图,,点M,N分别是射线,上的动点,平分,且,当的周长取最小值时,的长为 .
17.如图,在中,,,的平分线交于点,若,则 .
18.如图,点,把线段分割成,和,若以,,为边的三角形是一个直角三角形,则称点,是线段的“勾股分割点”.已知点,是线段的“勾股分割点”,若,,则的长为 .
三、解答题(共6小题,每题8分,满分48分)
19.如图,在△ABC 中,∠B=30°,∠C=45°,AC=2.求 BC 边上的高及△ABC 的面积.
20.在我国古代数学著作《九章算术》的“勾股”章中,有一题:“今有开门去阃一尺,不合二寸,向门广几何"大意如下:如图,推开两扇门(和),门边缘D,C两点到门槛的距离为1尺(1尺寸),两扇门间的缝隙为2寸,问门的宽度(两扇门宽度的和)为多少尺?
21.在△ABC中,AB=2,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
22.如图,A、B两个小集镇在河流的同侧,分别到河的距离为千米,千米,且千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
23.在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°,
(1)如图1,当点A、C、D在同一条直线上时,AC=4,EC=3,
①求证:AF⊥BD ; ②AF的长度为 直接写出答案);
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,则∠FCD+∠FEC= (直接写出答案)
24.如图,直线经过点,与轴交于点,点在轴上.
(1)求的值;
(2)动点在线段上运动,连接、.设的面积为,求出与之间函数关系式,并写出的取值范围;
(3)能否为等腰三角形;若能,求出点的坐标;若不能,请说明理由.
参考答案:
1.C
2.C
3.D
4.C
5.B
6.D
7.B
8.D
9.C
10.B
11.
12.
13.12
14. 2; .
15.
16.
17.
18.或
19.2,2+2.
20.尺
21.2或2或3
22.75
23.(1)AF=5.6;(2)略;(3) 45°
24.(1)
(2)
(3)能,点坐标为或或或
一、单选题(共10小题,满分40分)
1.如图,钓鱼竿的长为5.4米,露在水面上的鱼线长为1.8米.当钓鱼者把钓鱼竿转到的位置时,露在水面上的鱼线长为4.2米,则的长为( )
A.米 B.米 C.米 D.米
2.《九章算术》提供了许多勾股数如,等一组勾股数最大的数称为“弦数”.经研究,若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个数组成勾股数,若m是大于1的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1,得到两个整数,那么m与这两个数组成勾股数,根据上面的规律,由10生成的勾股数的“弦数”是( )
A.16 B.24 C.26 D.32
3.如图,有一根电线杆在离地面9米A处断裂,电线杆顶部C落在离电线杆底部B点12米远的地方,则电线杆断裂之前的长度为( )米.
A.12 B.15 C.21 D.24
4.下列命题是真命题的是( )
A.是无理数
B.三个连续的整数不能构成直角三角形的三边长
C.一次函数的图象不可能同时经过三、四象限
D.二元一次方程的解一定是整数解
5.如图,长方体的底面边长分别为1cm和3cm,高为6cm.如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要多长. ( )
A.10n B. C. D.
6.《算法统宗》是中国古代数学名著,作者是明代数学家程大位.书中记载了一道“荡秋千”问题:“平地秋千未起,踏板一尺离地;送行二步与人齐,五尺人高曾记;仕女佳人争蹴,终朝笑语欢嬉;良工高士素好奇,算出索长有几?”
译文:“秋千静止的时候,踏板离地1尺,将它往前推送两步(两步10尺)时,此时踏板升高离地5尺,秋千的绳索始终拉得很直,试问秋千绳索有多长?”
若设秋千绳索长为x尺,则可列方程为( ).
A. B.
C. D.
7.如图,在平面直角坐标系xOy中,已知点P(m,m),过点P作OP的垂线交函数(k>1)的图象于点Q.若Q的横坐标为1,且OP2﹣PQ2=6,则k的值为( )
A.2 B.3 C. D.4
8.如图,是射线上一动点,为线段中点,以为斜边做等腰直角,连结,当最短时,的面积为( )
A.2.5 B.2 C.1.5 D.1
9.某大会会标如图所示,它是由相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是,小正方形的面积是1,直角三角形中较长的直角边为a,较短的直角边为b,则的值( )
A. B. C. D.
10.如图:在△ABC中,∠B=45°,D是AB边上一点,连接CD,过A作AF⊥CD交CD于G,交BC于点F.已知AC=CD,CG=3,DG=1,则下列结论正确的是( )
①∠ACD=2∠FAB ② ③ ④ AC=AF
A.①②③ B.①②③④ C.②③④ D.①③④
二、填空题(共8小题,满分32分)
11.在直角三角形中,已知两条直角边的长度分别为和,则斜边长为 .
12.平面直角坐标系中,有点和点,连接,线段的长为 .
13.如图,在中,按以下步骤作图:①以点A为圆心,以长为半径作圆弧,交于点D;②分别以C、D为圆心,以长为半径作弧,两弧交于点E;③作射线交于点F,若,则 .
14.如图,在ΔABC中,∠A=90°,∠B=30°,AD为中线,AD=1,则BC= ,AB= .
15.两直角边a , b满足,则斜边长为 .
16.如图,,点M,N分别是射线,上的动点,平分,且,当的周长取最小值时,的长为 .
17.如图,在中,,,的平分线交于点,若,则 .
18.如图,点,把线段分割成,和,若以,,为边的三角形是一个直角三角形,则称点,是线段的“勾股分割点”.已知点,是线段的“勾股分割点”,若,,则的长为 .
三、解答题(共6小题,每题8分,满分48分)
19.如图,在△ABC 中,∠B=30°,∠C=45°,AC=2.求 BC 边上的高及△ABC 的面积.
20.在我国古代数学著作《九章算术》的“勾股”章中,有一题:“今有开门去阃一尺,不合二寸,向门广几何"大意如下:如图,推开两扇门(和),门边缘D,C两点到门槛的距离为1尺(1尺寸),两扇门间的缝隙为2寸,问门的宽度(两扇门宽度的和)为多少尺?
21.在△ABC中,AB=2,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
22.如图,A、B两个小集镇在河流的同侧,分别到河的距离为千米,千米,且千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
23.在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°,
(1)如图1,当点A、C、D在同一条直线上时,AC=4,EC=3,
①求证:AF⊥BD ; ②AF的长度为 直接写出答案);
(2)如图2,当点A、C、D不在同一条直线上时,求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,则∠FCD+∠FEC= (直接写出答案)
24.如图,直线经过点,与轴交于点,点在轴上.
(1)求的值;
(2)动点在线段上运动,连接、.设的面积为,求出与之间函数关系式,并写出的取值范围;
(3)能否为等腰三角形;若能,求出点的坐标;若不能,请说明理由.
参考答案:
1.C
2.C
3.D
4.C
5.B
6.D
7.B
8.D
9.C
10.B
11.
12.
13.12
14. 2; .
15.
16.
17.
18.或
19.2,2+2.
20.尺
21.2或2或3
22.75
23.(1)AF=5.6;(2)略;(3) 45°
24.(1)
(2)
(3)能,点坐标为或或或
