人教版五年级下册数学第八单元数学广角—找次品解答题训练(含答案)
文档属性
| 名称 | 人教版五年级下册数学第八单元数学广角—找次品解答题训练(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 444.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
人教版五年级下册数学第八单元 数学广角—找次品解答题训练
1.有11盒饼干,其中10盒质量相同,另有1盒少了几块。如果用天平称,至少几次可以保证找出这盒饼干?
2.有28个乒乓球,其中有1个球是次品,但不知道比正品轻,还是重。如果只利用没有砝码的天平来判断哪个球是次品,至少要称几次能知道这个次品球是轻还是重?
3.有15盒糖果,其中14盒质量相同,另有1盒少了几颗。如果用天平称,至少称几次能保证找出这盒糖果?请写出过程。
4.有3袋白糖,其中2袋每袋500克,另1袋不是500克,但不知道比500克重还是轻。你能用天平找出来吗?
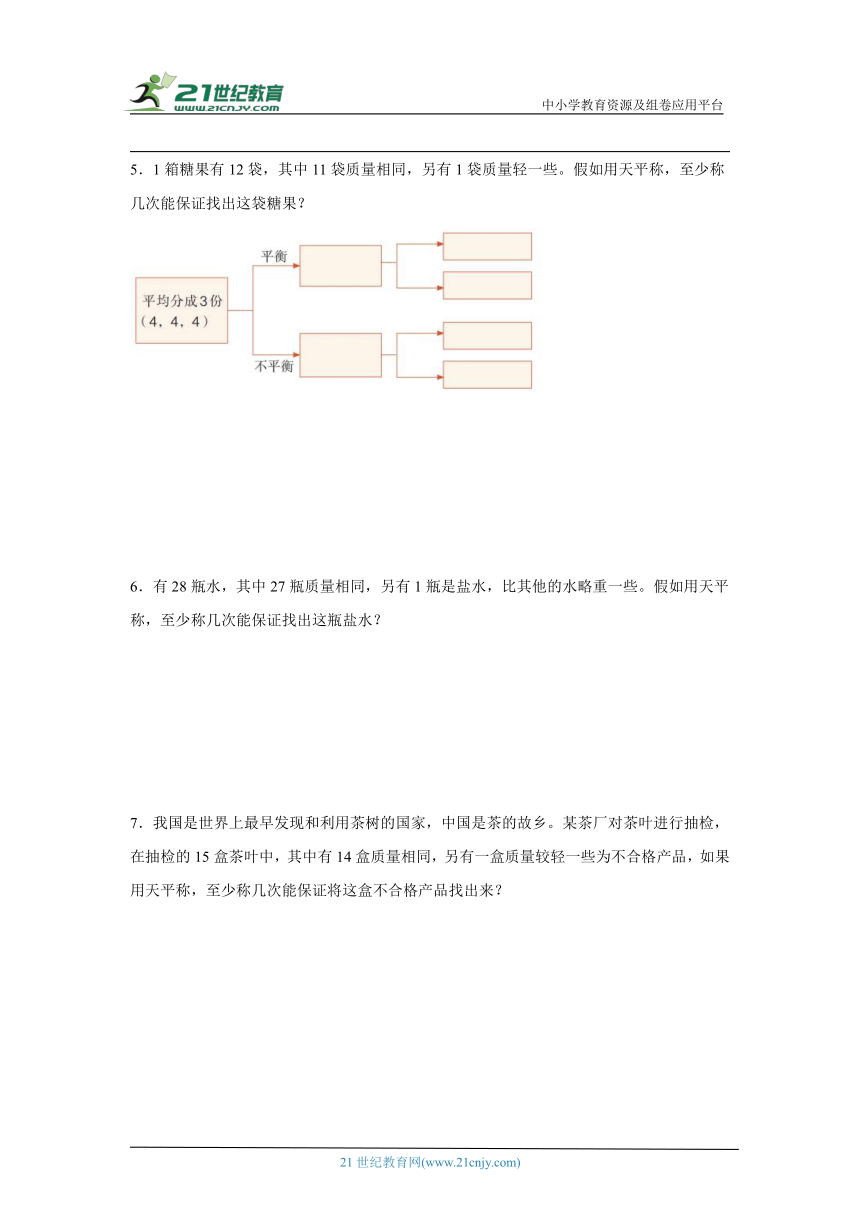
5.1箱糖果有12袋,其中11袋质量相同,另有1袋质量轻一些。假如用天平称,至少称几次能保证找出这袋糖果?
6.有28瓶水,其中27瓶质量相同,另有1瓶是盐水,比其他的水略重一些。假如用天平称,至少称几次能保证找出这瓶盐水?
7.我国是世界上最早发现和利用茶树的国家,中国是茶的故乡。某茶厂对茶叶进行抽检,在抽检的15盒茶叶中,其中有14盒质量相同,另有一盒质量较轻一些为不合格产品,如果用天平称,至少称几次能保证将这盒不合格产品找出来?
8.张叔叔加工了25个形状、大小完全一样的零件,其中有一个质量较轻的不合格产品,你能用天平只称3次帮他找出这个不合格产品吗?(请写出简要过程)
9.在9枚一模一样的金币中,有一枚比真金币轻的假金币。如果用天平称,至少称几次能保证找出这枚假金币?请把称的过程写下来。
10.技术监督部门抽检一批网球的质量,看是否符合比赛要求。在抽检的15个网球中,有1个是次品,且次品的质量较重,如果用天平称,至少称几次能保证找出次品?
11.黄阿姨买了9盒饼干,其中1盒少了6块。
(1)如果用天平称,至少称几次可以把它找出来?
(2)如果天平两边各放4盒,称一次有可能找出来吗?
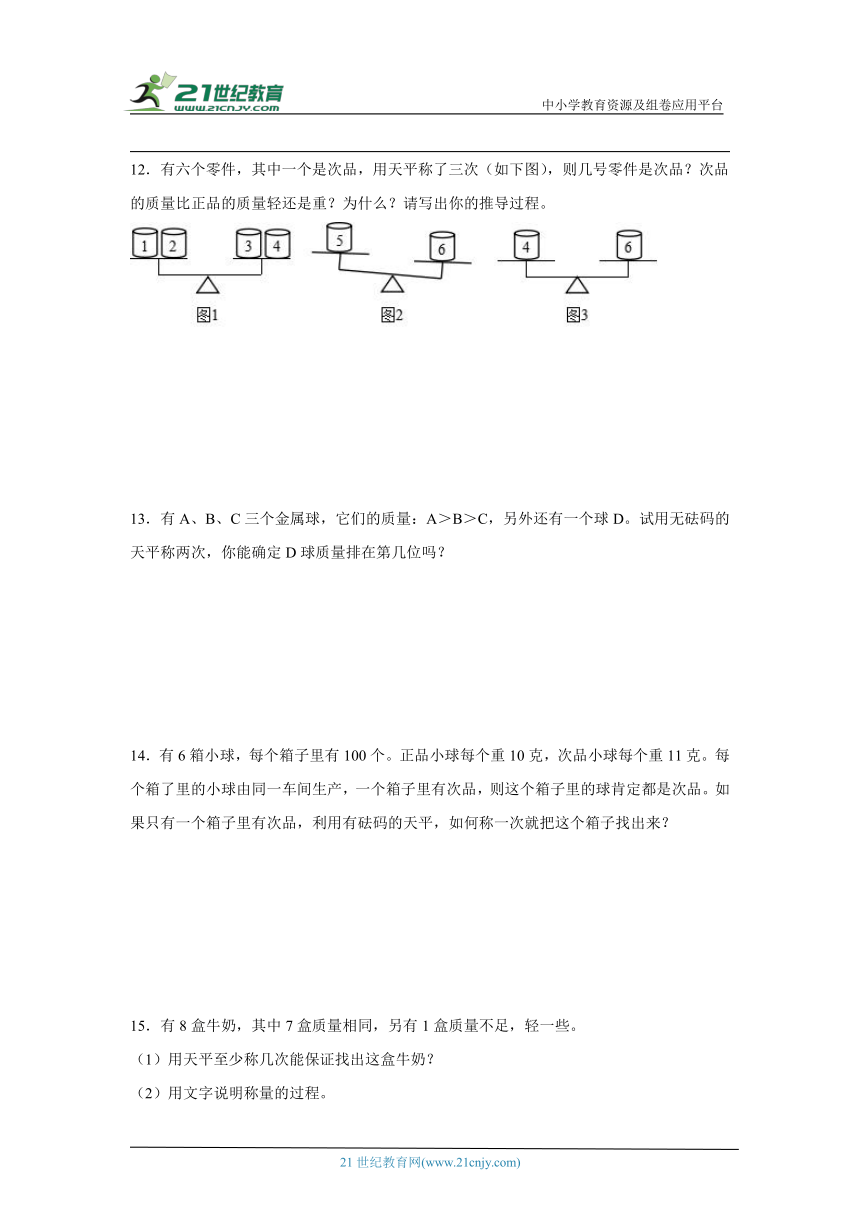
12.有六个零件,其中一个是次品,用天平称了三次(如下图),则几号零件是次品?次品的质量比正品的质量轻还是重?为什么?请写出你的推导过程。
13.有A、B、C三个金属球,它们的质量:A>B>C,另外还有一个球D。试用无砝码的天平称两次,你能确定D球质量排在第几位吗?
14.有6箱小球,每个箱子里有100个。正品小球每个重10克,次品小球每个重11克。每个箱了里的小球由同一车间生产,一个箱子里有次品,则这个箱子里的球肯定都是次品。如果只有一个箱子里有次品,利用有砝码的天平,如何称一次就把这个箱子找出来?
15.有8盒牛奶,其中7盒质量相同,另有1盒质量不足,轻一些。
(1)用天平至少称几次能保证找出这盒牛奶?
(2)用文字说明称量的过程。
16.质监部门对某企业的产品进行质量抽检。在抽查的19盒产品中有1盒不合格(质量稍轻一些)。
(1)至少称几次能保证将这盒产品找出来?
(2)如果在天平的左右两端各放9盒的话,称一次有可能称出来吗?为什么?
17.一个古玩商店经理不小心将一枚假铜币混入了10个真铜币中,这10枚真铜币外形、质量完全相同,假铜币外形与真铜币一样,只是质量不一样,但不知道比真铜币轻还是重。如果用天平称,至少称几次,就能保证帮助经理从11枚铜币中找出假铜币?你能用画图和文字写出你的称法吗?
18.有7盒巧克力,其中有一盒少了几块,其余的质量相同,如果用天平称,至少称几次可以找出这盒巧克力?
(1)如果天平两边各放3盒,称一次有可能称出来吗?
(2)如果用天平称,你打算怎么称?(用表示巧克力,表示称的过程)
19.现有A、B、C、D四袋奶糖,A袋最重,C袋最轻.试用无砝码的天平称一次,将四袋奶糖按照从轻到重的顺序排一排,说说你是怎样称量的.
20.有101枚硬币,其中100枚质量相同,另一枚是假币,现在不知道假币比真币重还是轻.
(1)利用天平,至少称几次就一定可以判断出假币比真币重还是轻?
(2)至少再称几次就一定能找出那枚假币?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.3次
2.2次
4.能
5.3次,
6.4次
7.3次
8.能;
9.2次,
10.3次
11.(1)2次;
(2)可能
12.5号是次品,次品比正品质量轻
13.能;
14.给每个箱子编号1到6,从编号为1到6的箱子里分别取出1、2、3、4、5、6个球,并编号。与对应箱号相同,共21个。称21个球的重量(如果都是正品,共重210克)。重量比210克重几克,则对应箱子里的就是次品。
15.(1)2次
(2)把8盒牛奶分成3盒、3盒、2盒,第一次天平两侧各放3盒,如果平衡,那么质量不足的在余下的2盒中,再称一次即可;如果不平衡,那么把轻的3盒在天平两侧各放1盒,如果平衡,那么余下的1盒是质量不足的,如果不平衡,那么轻的为质量不足的。
16.(1)3次
(2)有可能,因为如果在天平的左右两侧各放9盒,天平正好平衡,那么最后剩下的一盒就是次品。
17.至少称4次;
将11枚硬币分成(4、4、3),先称两个4枚,①平衡,次品在3个中,将3个分成(1、1、1),称两个,平衡剩下一个是次品,不平衡,随便拿下一个与剩下的称,即可找出次品;②不平衡,次品在4个中,随便拿出一个放到3个里,确定在哪4个,再称两次确定次品是轻还是重,再称一次即可。
18.(1)有可能。
(2)
如果平衡,剩下一盒为次品;如果不平衡,将轻的一端的3盒,天平两端各放一盒,若平衡,剩下一盒即为次品,如果不平衡,低的那端是次品。
19.把B、D两袋奶糖放在天平上称一次,如果D袋比B袋轻,那么按照从轻到重的顺序排列依次为:C<D<B<A;如果D袋比B袋重,那么按照从轻到重的顺序排列依次为:C<B<D<A
20.(1)2次 (2)4次
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
人教版五年级下册数学第八单元 数学广角—找次品解答题训练
1.有11盒饼干,其中10盒质量相同,另有1盒少了几块。如果用天平称,至少几次可以保证找出这盒饼干?
2.有28个乒乓球,其中有1个球是次品,但不知道比正品轻,还是重。如果只利用没有砝码的天平来判断哪个球是次品,至少要称几次能知道这个次品球是轻还是重?
3.有15盒糖果,其中14盒质量相同,另有1盒少了几颗。如果用天平称,至少称几次能保证找出这盒糖果?请写出过程。
4.有3袋白糖,其中2袋每袋500克,另1袋不是500克,但不知道比500克重还是轻。你能用天平找出来吗?
5.1箱糖果有12袋,其中11袋质量相同,另有1袋质量轻一些。假如用天平称,至少称几次能保证找出这袋糖果?
6.有28瓶水,其中27瓶质量相同,另有1瓶是盐水,比其他的水略重一些。假如用天平称,至少称几次能保证找出这瓶盐水?
7.我国是世界上最早发现和利用茶树的国家,中国是茶的故乡。某茶厂对茶叶进行抽检,在抽检的15盒茶叶中,其中有14盒质量相同,另有一盒质量较轻一些为不合格产品,如果用天平称,至少称几次能保证将这盒不合格产品找出来?
8.张叔叔加工了25个形状、大小完全一样的零件,其中有一个质量较轻的不合格产品,你能用天平只称3次帮他找出这个不合格产品吗?(请写出简要过程)
9.在9枚一模一样的金币中,有一枚比真金币轻的假金币。如果用天平称,至少称几次能保证找出这枚假金币?请把称的过程写下来。
10.技术监督部门抽检一批网球的质量,看是否符合比赛要求。在抽检的15个网球中,有1个是次品,且次品的质量较重,如果用天平称,至少称几次能保证找出次品?
11.黄阿姨买了9盒饼干,其中1盒少了6块。
(1)如果用天平称,至少称几次可以把它找出来?
(2)如果天平两边各放4盒,称一次有可能找出来吗?
12.有六个零件,其中一个是次品,用天平称了三次(如下图),则几号零件是次品?次品的质量比正品的质量轻还是重?为什么?请写出你的推导过程。
13.有A、B、C三个金属球,它们的质量:A>B>C,另外还有一个球D。试用无砝码的天平称两次,你能确定D球质量排在第几位吗?
14.有6箱小球,每个箱子里有100个。正品小球每个重10克,次品小球每个重11克。每个箱了里的小球由同一车间生产,一个箱子里有次品,则这个箱子里的球肯定都是次品。如果只有一个箱子里有次品,利用有砝码的天平,如何称一次就把这个箱子找出来?
15.有8盒牛奶,其中7盒质量相同,另有1盒质量不足,轻一些。
(1)用天平至少称几次能保证找出这盒牛奶?
(2)用文字说明称量的过程。
16.质监部门对某企业的产品进行质量抽检。在抽查的19盒产品中有1盒不合格(质量稍轻一些)。
(1)至少称几次能保证将这盒产品找出来?
(2)如果在天平的左右两端各放9盒的话,称一次有可能称出来吗?为什么?
17.一个古玩商店经理不小心将一枚假铜币混入了10个真铜币中,这10枚真铜币外形、质量完全相同,假铜币外形与真铜币一样,只是质量不一样,但不知道比真铜币轻还是重。如果用天平称,至少称几次,就能保证帮助经理从11枚铜币中找出假铜币?你能用画图和文字写出你的称法吗?
18.有7盒巧克力,其中有一盒少了几块,其余的质量相同,如果用天平称,至少称几次可以找出这盒巧克力?
(1)如果天平两边各放3盒,称一次有可能称出来吗?
(2)如果用天平称,你打算怎么称?(用表示巧克力,表示称的过程)
19.现有A、B、C、D四袋奶糖,A袋最重,C袋最轻.试用无砝码的天平称一次,将四袋奶糖按照从轻到重的顺序排一排,说说你是怎样称量的.
20.有101枚硬币,其中100枚质量相同,另一枚是假币,现在不知道假币比真币重还是轻.
(1)利用天平,至少称几次就一定可以判断出假币比真币重还是轻?
(2)至少再称几次就一定能找出那枚假币?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
参考答案:
1.3次
2.2次
4.能
5.3次,
6.4次
7.3次
8.能;
9.2次,
10.3次
11.(1)2次;
(2)可能
12.5号是次品,次品比正品质量轻
13.能;
14.给每个箱子编号1到6,从编号为1到6的箱子里分别取出1、2、3、4、5、6个球,并编号。与对应箱号相同,共21个。称21个球的重量(如果都是正品,共重210克)。重量比210克重几克,则对应箱子里的就是次品。
15.(1)2次
(2)把8盒牛奶分成3盒、3盒、2盒,第一次天平两侧各放3盒,如果平衡,那么质量不足的在余下的2盒中,再称一次即可;如果不平衡,那么把轻的3盒在天平两侧各放1盒,如果平衡,那么余下的1盒是质量不足的,如果不平衡,那么轻的为质量不足的。
16.(1)3次
(2)有可能,因为如果在天平的左右两侧各放9盒,天平正好平衡,那么最后剩下的一盒就是次品。
17.至少称4次;
将11枚硬币分成(4、4、3),先称两个4枚,①平衡,次品在3个中,将3个分成(1、1、1),称两个,平衡剩下一个是次品,不平衡,随便拿下一个与剩下的称,即可找出次品;②不平衡,次品在4个中,随便拿出一个放到3个里,确定在哪4个,再称两次确定次品是轻还是重,再称一次即可。
18.(1)有可能。
(2)
如果平衡,剩下一盒为次品;如果不平衡,将轻的一端的3盒,天平两端各放一盒,若平衡,剩下一盒即为次品,如果不平衡,低的那端是次品。
19.把B、D两袋奶糖放在天平上称一次,如果D袋比B袋轻,那么按照从轻到重的顺序排列依次为:C<D<B<A;如果D袋比B袋重,那么按照从轻到重的顺序排列依次为:C<B<D<A
20.(1)2次 (2)4次
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
