北京市平谷五中2023~2024学年第二学期初二期中数学试卷(无答案)
文档属性
| 名称 | 北京市平谷五中2023~2024学年第二学期初二期中数学试卷(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 571.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-14 23:59:00 | ||
图片预览



文档简介
平谷五中2023~2024学年度第二学期期中试卷
2024.5 初二数学
一、选择题(每小题2分,共16分)
1、下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2、点P的坐标为(3,-5),则点P在( )
A、 第一象限 B、第二象限 C、第三象限 D、第四象限
3、已知点(-2,)和点(3,)在直线上,则( )
A、 B、 C、 D不能确定
4、如图,在ABCD中,对角线AC,BD相交于点0,且AB≠AD,则下列式子不正确的是( )
A AC⊥BD B AB=CD C BO=OD D ∠BAD=∠BCD
5、如图,平行四边形OABC的顶点O,A,C的坐标分别是(0,0),(3,0),(2,3),则顶点B的坐标是( )
A、(5,3) B、(3,3) C、(4,3) D(3,5)
6、下列命题中正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线互相平分且相等的四边形是矩形
C.对角线相等的四边形是矩形
D.对角线相等的平行四边形是正方形
7、一次函数y=3x+21的图像不经过的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8、在平面直角坐标系中,矩形,,,,点在边上,.点在边上运动,连接,点A关于直线的对称点为.若,,下列图像能大致反映与的函数关系的是().
A. B.
C. D.
二、填空题(每空2分,共18分)
9、函数的自变量x的取值范围为 ,函数的自变量x的取值
范围为 。
10、点关于x轴对称点的坐标为 .
11、如图,中∠A的度数为45°,则∠B的度数为 .
12、如图,为了测量池塘边上A,B两点间的距离,在池塘外选一点C,分别连接CA和CB并延长到点D,E,使AD=AC,BE=BC,连接DE.若测得DE=20m,则A,B两点间距离是 m.
13、如图,在□ABCD中,E,F分别是边AD,BC上的点,连接AF,CE,只需添加一个条件即可证明四边形AFCE是平行四边形,这个条件可以是 (写出一个即可).
14、如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠BAD=120°,OA=2,则菱形的面积为 .
15、如图,直线与直线交于点P,则不等式的解集为__________.
16、在中,,平分交于点,交于点,交于点.有以下结论:
①四边形一定是平行四边形;
②连接所得四边形一定是平行四边形;
③保持的大小不变,改变的长度可使成立;
④保持的长度不变,改变的大小可使成立.
共中所有的正确结论是:______.(填序号即可)
三、解答题
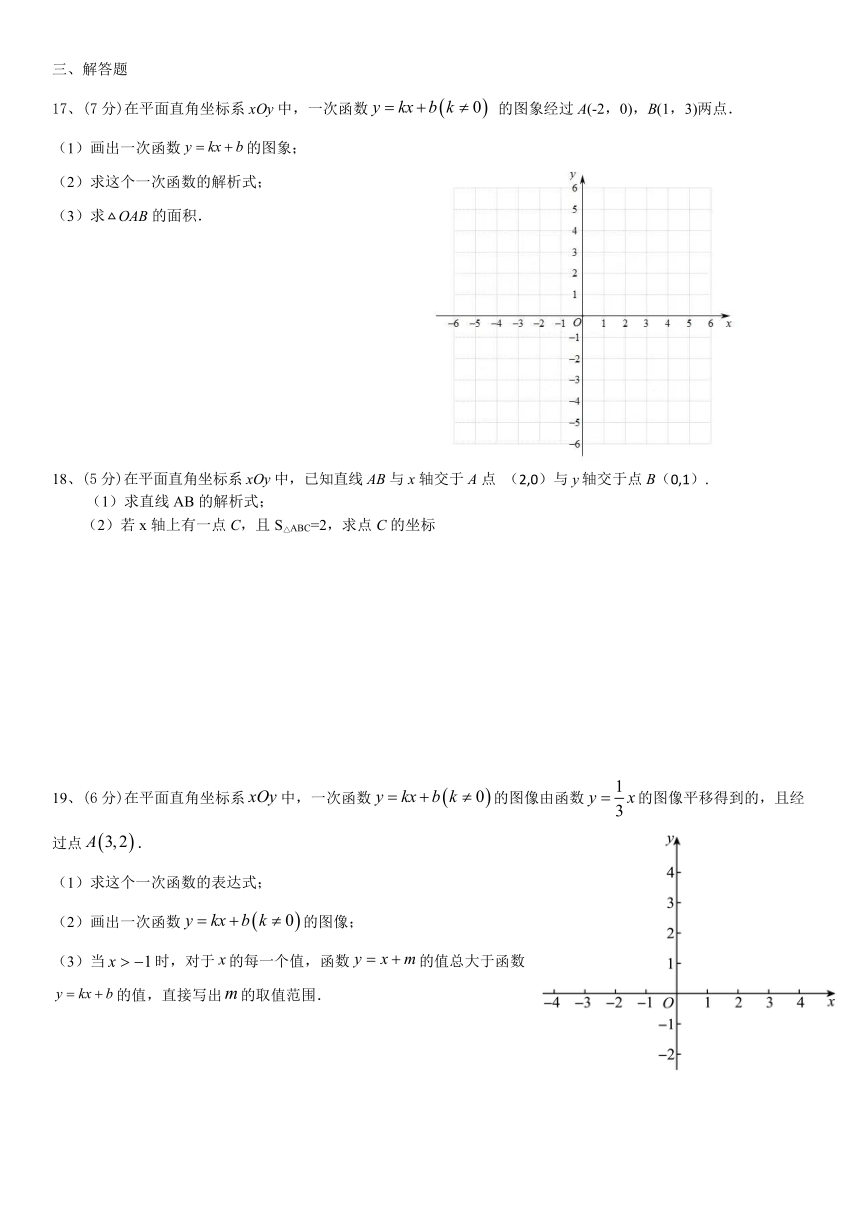
17、(7分)在平面直角坐标系xOy中,一次函数 的图象经过A(-2,0),B(1,3)两点.
(1)画出一次函数的图象;
(2)求这个一次函数的解析式;
(3)求OAB的面积.
18、(5分)在平面直角坐标系xOy中,已知直线AB与x轴交于A点 (2,0)与轴交于点B(0,1).
(1)求直线AB的解析式;
(2)若x轴上有一点C,且S△ABC=2,求点C的坐标
19、(6分)在平面直角坐标系中,一次函数的图像由函数的图像平移得到的,且经过点.
(1)求这个一次函数的表达式;
(2)画出一次函数的图像;
(3)当时,对于的每一个值,函数的值总大于函数的值,直接写出的取值范围.
20、(5分)下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.已知:四边形ABCD是平行四边形.求作:菱形ABEF(点E在BC上,点F在AD上).作法:①以点A为圆心,AB长为半径作弧,交AD于点F;②以点B为圆心,AB长为半径作弧,交BC于点E;③连接EF.所以四边形ABEF为所求作的菱形.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明,
证明:∵AF=AB,BE=AB,
∴ = ,
在□ABCD中,AD∥BC,即AF∥BE,
∴四边形ABEF为 形,
∵AF=AB,
∴四边形ABEF为菱形( )(填依据).
21、(5分)如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF, FA.
求证:四边形AECF是平行四边形.
22、(5分)已知:如图,正方形ABCD,E,F分别为DC,BC中点.求证:AE=AF.
23、(5分)下面是证明直角三角形斜边中线定理的两种添加辅助线的方法,选择其中一种,完成证明.
直角三角形斜边的中线等于斜边的一半. 已知:如图,中,,点为中点. 求证:
方法一 证明:如图,取AC中点E,连接DE. 方法二 证明:如图,延长至点,使,连接、.
24、(5分)如图,在直角△中,点,,分别是边,, 的中点.
(1)求证:四边形为矩形;
(2)若,,求出矩形的周长.
25、(5分)如图,□ABCD中, AE⊥BD于点E,CF⊥BD于点F.
(1)求证:BF=DE;
(2)如果,, BC=2,求BD的长.
26、(5分)有这样一个问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数的自变量x的取值范围是 .
(2)下表是y与x的几组对应值,m的值为 .
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点根据描出的点,画出该函数的图象:
(4)结合函数的图象,写出该函数的一条性质: .
(5)结合函数图象估计的解的个数为 .
27、(7分)如图,在正方形ABCD中,E是边AB上的一动点,点F在边BC的延长线上,且CF=AE,连接DE、DF.
(1)求证:DE⊥DF;
(2)连接EF,取EF中点G,连接DG并延长交BC于H,连接BG.
①依题意,补全图形;
②求证:BG=DG;
③若∠EGB=45°,用等式表示线段BG、HG与AE之间的数量关系,并证明.
28、(6分)在平面直角坐标系xOy中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为垂距等点.如图所示P、Q两点即为垂距等点.
已知点A的坐标为(-2,3).
① 在点M(1,4),N(7,-2),T(-5,0)中,为点A的垂距等点的是 ;
② 若点B在y轴的负半轴上,且A、B两点为垂距等点,则点B的坐标为 ;
(2)直线l:y=x-4与x轴交于点C,与y轴交于点D.
① 当E为线段CD上一点时,若在直线x=n上存在点F,使得E、F两点为垂距等点,
求n的取值范围.
② 已知正方形HPKQ的边长为2,(t,0)是对角线HK、PQ的交点,且正方形的任何
一条边均与某条坐标轴垂直.当E为直线l上一动点时,若该正方形的边上存在点G,使
得E、G两点为垂距等点,直接写出t的取值范围.
2024.5 初二数学
一、选择题(每小题2分,共16分)
1、下列图形中,既是轴对称图形又是中心对称图形的是( )
A. B. C. D.
2、点P的坐标为(3,-5),则点P在( )
A、 第一象限 B、第二象限 C、第三象限 D、第四象限
3、已知点(-2,)和点(3,)在直线上,则( )
A、 B、 C、 D不能确定
4、如图,在ABCD中,对角线AC,BD相交于点0,且AB≠AD,则下列式子不正确的是( )
A AC⊥BD B AB=CD C BO=OD D ∠BAD=∠BCD
5、如图,平行四边形OABC的顶点O,A,C的坐标分别是(0,0),(3,0),(2,3),则顶点B的坐标是( )
A、(5,3) B、(3,3) C、(4,3) D(3,5)
6、下列命题中正确的是( )
A.对角线互相垂直的四边形是菱形
B.对角线互相平分且相等的四边形是矩形
C.对角线相等的四边形是矩形
D.对角线相等的平行四边形是正方形
7、一次函数y=3x+21的图像不经过的象限是
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8、在平面直角坐标系中,矩形,,,,点在边上,.点在边上运动,连接,点A关于直线的对称点为.若,,下列图像能大致反映与的函数关系的是().
A. B.
C. D.
二、填空题(每空2分,共18分)
9、函数的自变量x的取值范围为 ,函数的自变量x的取值
范围为 。
10、点关于x轴对称点的坐标为 .
11、如图,中∠A的度数为45°,则∠B的度数为 .
12、如图,为了测量池塘边上A,B两点间的距离,在池塘外选一点C,分别连接CA和CB并延长到点D,E,使AD=AC,BE=BC,连接DE.若测得DE=20m,则A,B两点间距离是 m.
13、如图,在□ABCD中,E,F分别是边AD,BC上的点,连接AF,CE,只需添加一个条件即可证明四边形AFCE是平行四边形,这个条件可以是 (写出一个即可).
14、如图,在菱形ABCD中,对角线AC与BD相交于点O,若∠BAD=120°,OA=2,则菱形的面积为 .
15、如图,直线与直线交于点P,则不等式的解集为__________.
16、在中,,平分交于点,交于点,交于点.有以下结论:
①四边形一定是平行四边形;
②连接所得四边形一定是平行四边形;
③保持的大小不变,改变的长度可使成立;
④保持的长度不变,改变的大小可使成立.
共中所有的正确结论是:______.(填序号即可)
三、解答题
17、(7分)在平面直角坐标系xOy中,一次函数 的图象经过A(-2,0),B(1,3)两点.
(1)画出一次函数的图象;
(2)求这个一次函数的解析式;
(3)求OAB的面积.
18、(5分)在平面直角坐标系xOy中,已知直线AB与x轴交于A点 (2,0)与轴交于点B(0,1).
(1)求直线AB的解析式;
(2)若x轴上有一点C,且S△ABC=2,求点C的坐标
19、(6分)在平面直角坐标系中,一次函数的图像由函数的图像平移得到的,且经过点.
(1)求这个一次函数的表达式;
(2)画出一次函数的图像;
(3)当时,对于的每一个值,函数的值总大于函数的值,直接写出的取值范围.
20、(5分)下面是小明设计的“在一个平行四边形内作菱形”的尺规作图过程.已知:四边形ABCD是平行四边形.求作:菱形ABEF(点E在BC上,点F在AD上).作法:①以点A为圆心,AB长为半径作弧,交AD于点F;②以点B为圆心,AB长为半径作弧,交BC于点E;③连接EF.所以四边形ABEF为所求作的菱形.根据小明设计的尺规作图过程.
(1)使用直尺和圆规,补全图形(保留作图痕迹);
(2)完成下面的证明,
证明:∵AF=AB,BE=AB,
∴ = ,
在□ABCD中,AD∥BC,即AF∥BE,
∴四边形ABEF为 形,
∵AF=AB,
∴四边形ABEF为菱形( )(填依据).
21、(5分)如图,平行四边形ABCD,E、F两点在对角线BD上,且BE=DF,连接AE,EC,CF, FA.
求证:四边形AECF是平行四边形.
22、(5分)已知:如图,正方形ABCD,E,F分别为DC,BC中点.求证:AE=AF.
23、(5分)下面是证明直角三角形斜边中线定理的两种添加辅助线的方法,选择其中一种,完成证明.
直角三角形斜边的中线等于斜边的一半. 已知:如图,中,,点为中点. 求证:
方法一 证明:如图,取AC中点E,连接DE. 方法二 证明:如图,延长至点,使,连接、.
24、(5分)如图,在直角△中,点,,分别是边,, 的中点.
(1)求证:四边形为矩形;
(2)若,,求出矩形的周长.
25、(5分)如图,□ABCD中, AE⊥BD于点E,CF⊥BD于点F.
(1)求证:BF=DE;
(2)如果,, BC=2,求BD的长.
26、(5分)有这样一个问题:探究函数的图象与性质.小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
(1)函数的自变量x的取值范围是 .
(2)下表是y与x的几组对应值,m的值为 .
(3)如下图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点根据描出的点,画出该函数的图象:
(4)结合函数的图象,写出该函数的一条性质: .
(5)结合函数图象估计的解的个数为 .
27、(7分)如图,在正方形ABCD中,E是边AB上的一动点,点F在边BC的延长线上,且CF=AE,连接DE、DF.
(1)求证:DE⊥DF;
(2)连接EF,取EF中点G,连接DG并延长交BC于H,连接BG.
①依题意,补全图形;
②求证:BG=DG;
③若∠EGB=45°,用等式表示线段BG、HG与AE之间的数量关系,并证明.
28、(6分)在平面直角坐标系xOy中,对于P、Q两点给出如下定义:若点P到两坐标轴的距离之和等于点Q到两坐标轴的距离之和,则称P、Q两点为垂距等点.如图所示P、Q两点即为垂距等点.
已知点A的坐标为(-2,3).
① 在点M(1,4),N(7,-2),T(-5,0)中,为点A的垂距等点的是 ;
② 若点B在y轴的负半轴上,且A、B两点为垂距等点,则点B的坐标为 ;
(2)直线l:y=x-4与x轴交于点C,与y轴交于点D.
① 当E为线段CD上一点时,若在直线x=n上存在点F,使得E、F两点为垂距等点,
求n的取值范围.
② 已知正方形HPKQ的边长为2,(t,0)是对角线HK、PQ的交点,且正方形的任何
一条边均与某条坐标轴垂直.当E为直线l上一动点时,若该正方形的边上存在点G,使
得E、G两点为垂距等点,直接写出t的取值范围.
同课章节目录
