沪教版九年级数学上册24.1放缩与相似形试题 (含解析)
文档属性
| 名称 | 沪教版九年级数学上册24.1放缩与相似形试题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 348.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-15 07:16:52 | ||
图片预览


文档简介
24.1放缩与相似形
一、单选题
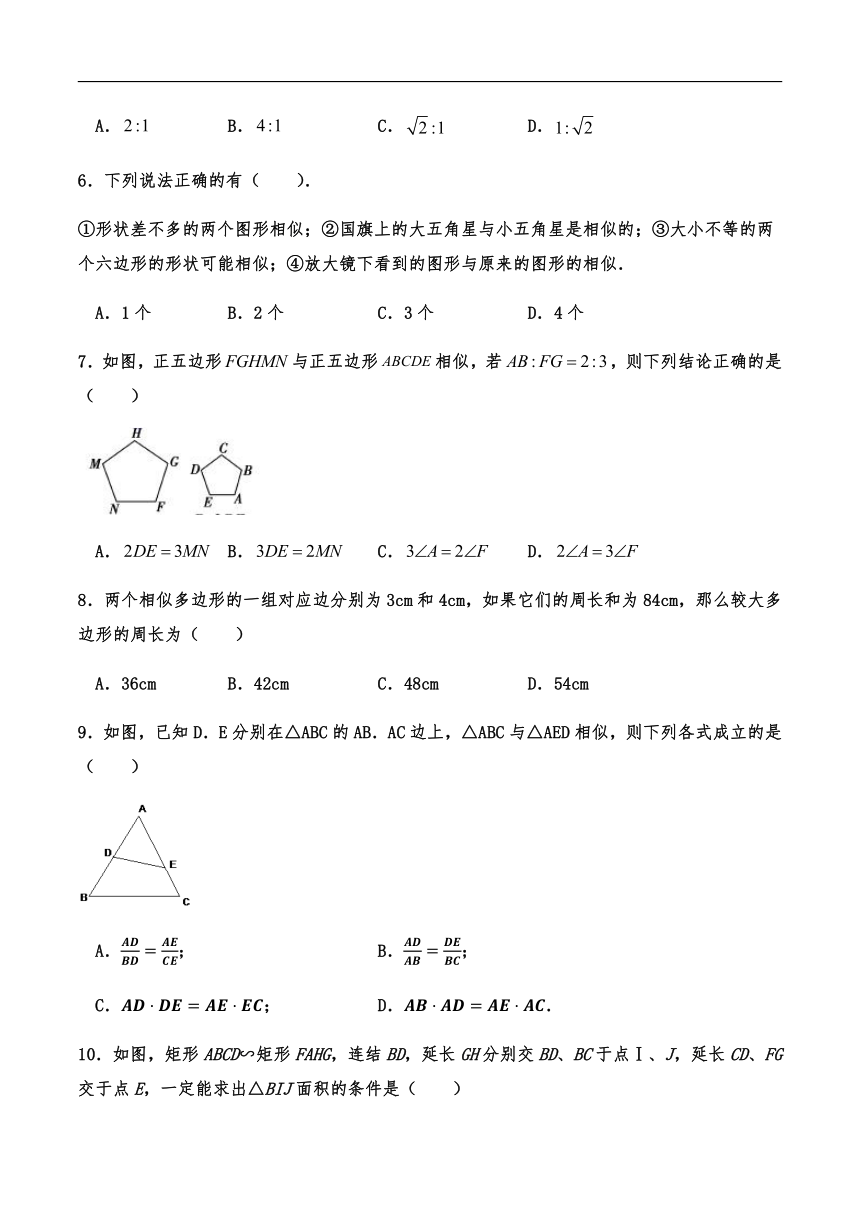
1.对一个图形进行放缩时,下列说法中正确的是( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变、角的大小可以改变
D.图形中线段的长度可以改变、角的大小保持不变
2.下列说法正确的是( )
A.所有矩形都相似 B.所有等腰三角形都相似
C.角相等的四边形都相似 D.等边三角形都相似
3.下列各组图形中,不一定相似的是( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
4.一个长方形各边按扩大后,得到的图形与原图形比较,下列说法中正确的是( )
A.周长扩大原来的16倍 B.周长缩小原来的
C.面积扩大原来的16倍 D.面积缩小原来的
5.若一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是( ).
A. B. C. D.
6.下列说法正确的有( ).
①形状差不多的两个图形相似;②国旗上的大五角星与小五角星是相似的;③大小不等的两个六边形的形状可能相似;④放大镜下看到的图形与原来的图形的相似.
A.1个 B.2个 C.3个 D.4个
7.如图,正五边形与正五边形相似,若,则下列结论正确的是( )
A. B. C. D.
8.两个相似多边形的一组对应边分别为3cm和4cm,如果它们的周长和为84cm,那么较大多边形的周长为( )
A.36cm B.42cm C.48cm D.54cm
9.如图,已知D.E分别在△ABC的AB.AC边上,△ABC与△AED相似,则下列各式成立的是( )
A.; B.;
C.; D..
10.如图,矩形ABCD∽矩形FAHG,连结BD,延长GH分别交BD、BC于点Ⅰ、J,延长CD、FG交于点E,一定能求出△BIJ面积的条件是( )
A.矩形ABJH和矩形HJCD的面积之差
B.矩形ABJH和矩形HDEG的面积之差
C.矩形ABCD和矩形AHGF的面积之差
D.矩形FBJG和矩形GJCE的面积之差
二、填空题
11.ABC与DEF相似,∠A=72°,∠B=48°,∠F=60°,则∠E=_________.
12.相似的两个图形,它们的大小_________(填“一定”,“不一定”,“一定不”)相同.
13.已知两个三角形是相似形,其中一个三角形的两个角分别为25 、55 ,则另一个三角形的最大内角的度数为__________.
14.四边形和四边形是相似图形,点分别与对应,已知,,,那么的长是__________.
15.在矩形中,点分别在上(点与点不重合)矩形与矩形相似,那么的长为________.
16.已知:四边形ABCD∽四边形A′B′C′D′,它们的周长分别为5m和3m,则S四边形ABCD:S四边形A′B′C′D′=______.
17.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为、、,另一个三角形框架的一条短边长为,则另外一个三角形的周长为________.
18.如图,如果两个相似多边形任意一组对应顶点P、P′所在的直线都是经过同一点O,且有OP′=k·OP(k≠0),那么我们把这样的两个多边形叫位似多边形,点O叫做位似中心,已知△ABC与△A′B′C′是关于点O的位似三角形,OA′=3OA,则△ABC与△A′B′C′的周长之比是________.
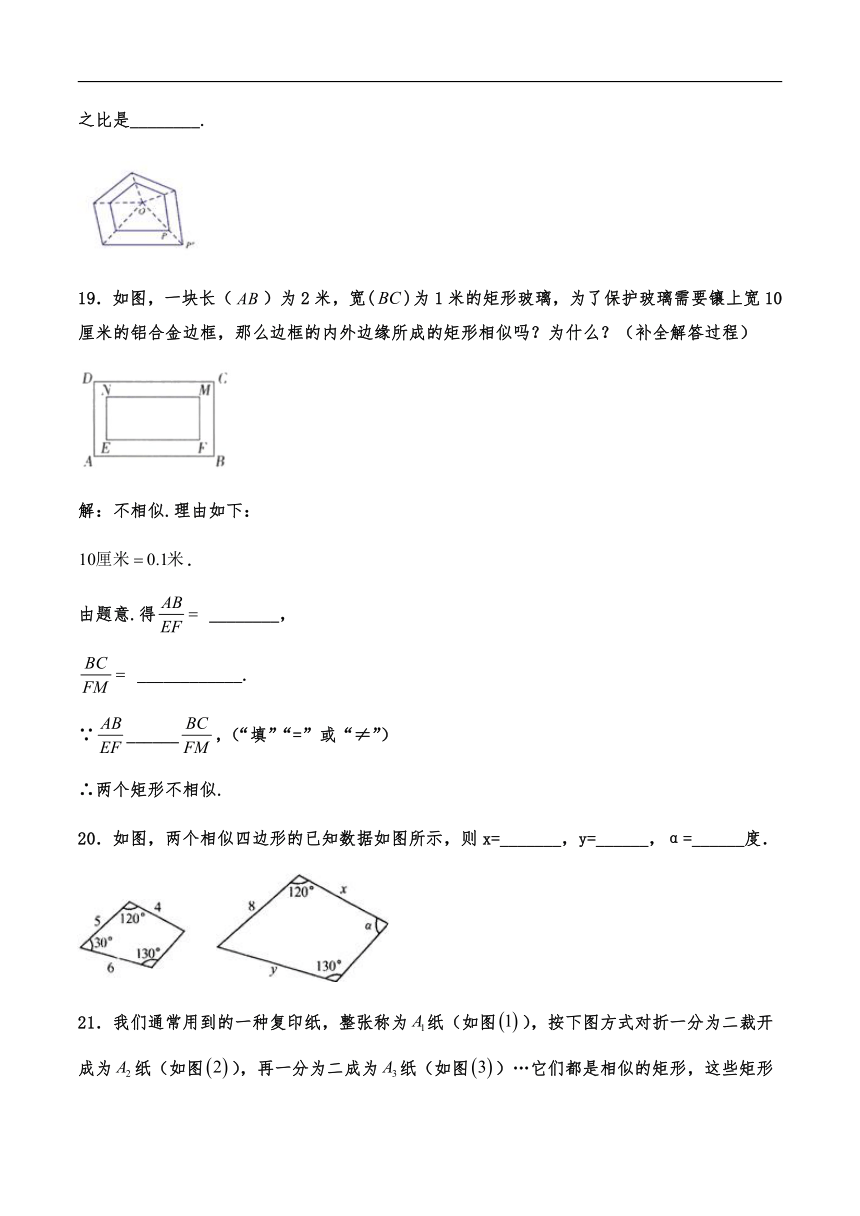
19.如图,一块长()为2米,宽()为1米的矩形玻璃,为了保护玻璃需要镶上宽10厘米的铝合金边框,那么边框的内外边缘所成的矩形相似吗?为什么?(补全解答过程)
解:不相似.理由如下:
.
由题意.得 ________,
____________.
∵______,(“填”“=”或“≠”)
∴两个矩形不相似.
20.如图,两个相似四边形的已知数据如图所示,则x=_______,y=______,α=______度.
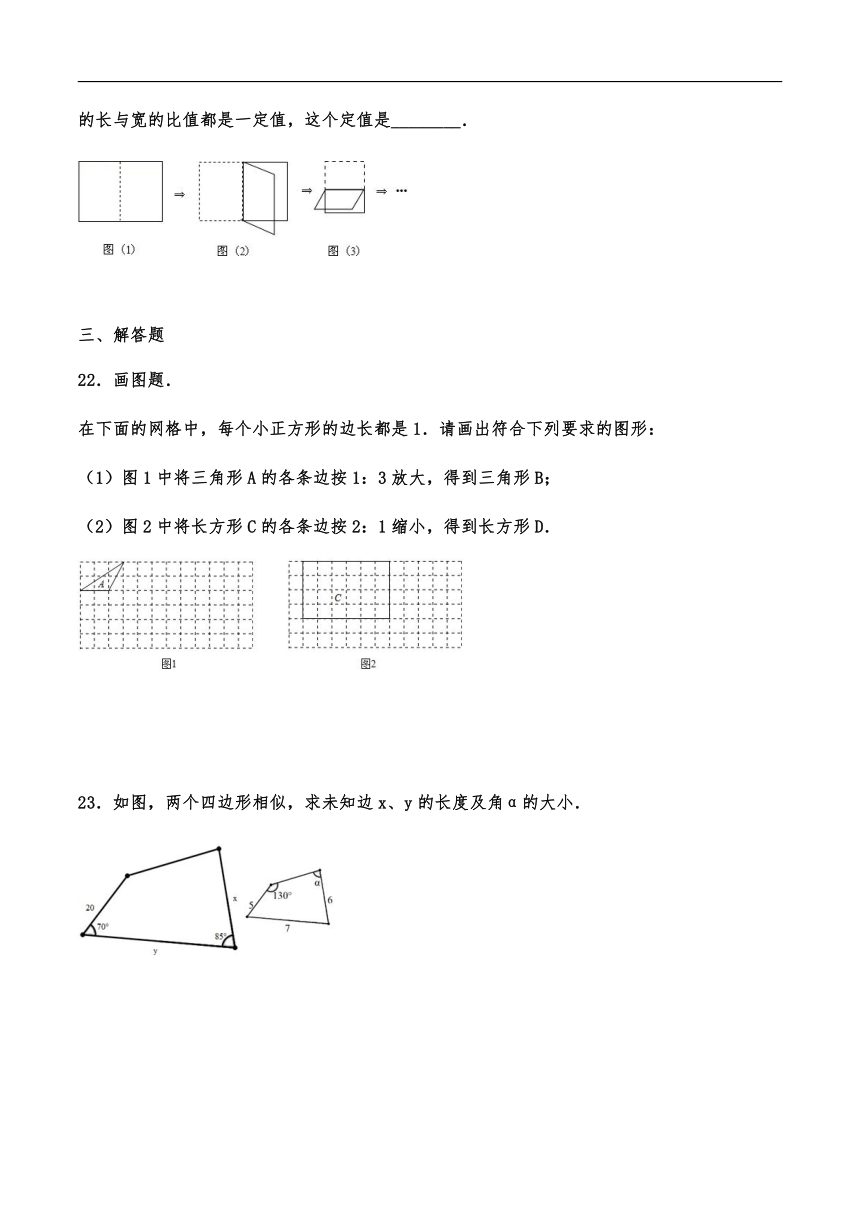
21.我们通常用到的一种复印纸,整张称为纸(如图),按下图方式对折一分为二裁开成为纸(如图),再一分为二成为纸(如图)…它们都是相似的矩形,这些矩形的长与宽的比值都是一定值,这个定值是________.
三、解答题
22.画图题.
在下面的网格中,每个小正方形的边长都是1.请画出符合下列要求的图形:
(1)图1中将三角形A的各条边按1:3放大,得到三角形B;
(2)图2中将长方形C的各条边按2:1缩小,得到长方形D.
23.如图,两个四边形相似,求未知边x、y的长度及角α的大小.
24.在相同时刻的物高与影长成正比例,如果在某时,旗杆在地面上的影长为10米,此时身高是米的小明的影长是米,求旗杆的高度.
25.设四边形与四边形是相似的图形,且与、与、与是对应点,已知,,求四边形的周长.
26.如图,△ABC在方格中.
(1)请在方格纸上建立平面直角坐标系,使A、C两点坐标依次为 (1,2)、 (3,1),并写出点B坐标为 ;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形.
27.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形是矩形的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为,时,它是否存在“减半”矩形?请作出判断,并说明理由.
(2)边长为的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
答案
一、单选题
1.D
【解析】
根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,可知对一个图形进行收缩时,图形中线段的长度改变,角的大小不变,
故选D.
2.D
【解析】
根据相似图形的定义对各选项分析判断后利用排除法求解.
解:A、矩形的四个角相等,四条边不一定对应成比例,所以不一定相似,故本选项错误;
B、所有等腰三角形不一定相似,只有顶角对应相等或底角对应相等才相似,故本选项错误;
C、角相等的四边形,四条边不一定对应成比例,所以不一定相似,故本选项错误;
D、等边三角形三个角均相等且对应边成比例,符合相似三角形的判定;故本选项正确.
故选:D.
3.D
【解析】
根据相似图形的定义,以及等边三角形的性质对各选项分析判断求解.
【详解】
A、各有一个角是100°的两个等腰三角形,100°的角只能是顶角,夹顶角的两边成比例,所以一定相似;
B、两个等腰直角三角形,对应边的比相等,锐角都是45°,相等,所以一定相似;
C、各有一个角是60°的两个等腰三角形,是等边三角形,有两对对应角相等,所以一定相似;
D、各有一个角是50°的两个等腰三角形,可能是顶角为50°,也可能底角为50°,所以对应角不一定相等,所以不一定不相似;
故选:D.
4.C
【解析】
相似矩形的周长比等于相似比,相似矩形的面积比等于相似比的平方,据此进行求解即可.
【详解】
一个长方形按放大后,得到的图形与原图形相似,边长扩大到原来的4倍,
所以周长扩大到原来的4倍,面积扩大到原来的16倍,
所以A、B、D错误,C正确,
故选C.
5.C
【解析】
根据相似图形对应边成比例列出关系式即可求解.
【详解】
如图,矩形ABCD对折后所得矩形与原矩形相似,则矩形ABCD∽矩形BFEA,
设矩形的长边长是a,短边长是b,则AB=CD=EF=b,AD=BC=a,BF=AE=,
根据相似多边形对应边成比例得:,即
∴
∴
故选C.
6.C
【解析】
根据相似图形的定义,对各项进行分析即可得出答案.
【详解】
①形状相同的两个图形是相似图形,形状差不多的两个图形,不是相似图形,故①说法错误;
②国旗上的大五角星与小五角星,形状相同,是相似图形,故②说法正确;
③当大小不等两个六边形的对应角相等,对应边成比例式时,这两个六边形相似,故③说法正确;
④放大镜下看到的图形与原来的图形形状相同,是相似图形,故④说法正确;
②③④说法正确,故选C.
7.B
【解析】
根据相似多边形的定义:各边对应成比例,各角对应相等的多边形叫做相似多边形,逐一分析即可.
【详解】
解:因为相似多边形的对应角相等,对应边成比例,
所以,故可排除C和D
所以.故排除A
故选B.
8.C
【解析】
根据相似三角形的周长的比等于相似比,设较大多边形的周长为x,表示出较小的多边形的周长,再根据它们的周长的和等于84cm列式求解即可.
【详解】
解:设较大多边形的周长为x,则
较小多边形的周长:x=3:4,
∴较小多边形的周长为x,
∵它们的周长和为84cm,
∴x+x=84,
解得x=48cm
故选:C.
9.D
【解析】
根据相似三角形的对应边成比例列式解答即可.
【详解】
∵△ABC与△AED相似,
∴,
∴.
故选D.
10.B
【解析】
设矩形的边AH=x,GH=y,EG=a,DC=b,根据平行线分线段成比例可得JI=,根据相似多边形的性质可得=,然后表示出S阴影的面积和S矩形ABJH﹣S矩形HDEG的值即可求解.
【详解】
解:设矩形的边AH=x,GH=y,EG=a,DC=b,
则BJ=x,JC=a,
∵JI//CD,
∴=即JI=,
∵矩形ABCD∽矩形FAHG,
∴=,
即=,
∴x+a=,
∴S阴影=BJ JI
=x
=xy.
∵S矩形ABJH﹣S矩形HDEG
=xb﹣ay
=x ﹣ay
=xy.
∴S阴影△BIJ=(S矩形ABJH﹣S矩形HDEG).
所以一定能求出△BIJ面积的条件是矩形ABJH和矩形HDEG的面积之差.
故选:B.
二、填空题
11.48°或72°
【解析】
根据相似三角形的性质解答即可.
【详解】
∵ABC与DEF相似,且,∠B≠∠A≠∠F,
∴∠E=∠B或∠E=∠A,
∵∠B=48°,∠A=72°
∴∠E=48°或72°,
故答案为:48°或72°.
12.不一定
【解析】
根据相似图形的定义判断即可.
【详解】
相似的两个图形形状相同,但大小不一定相等,只有两个图形全等时大小才相等,全等是相似的一种特殊情况.
故答案为:不一定.
13.
【解析】
先根据三角形的内角和定理得出一个三角形的最大内角度数,再根据相似三角形的对应角相等得出另一个三角形最大内角度数.
【详解】
解:∵一个三角形的两个角分别为25°、55°,
∴第三个角,即最大角为180°-(25°+55°)=100°,
∵两个三角形相似,
∴另一个三角形的最大内角度数为100°,
故答案为:100°.
14.1.6
【解析】
相似多边形的对应边成比例,根据相似多边形的性质即可解决问题.
【详解】
∵四边形ABCD∽四边形A'B'C'D',
∴CD:C′D′=BC:B′C′,
∵BC=3,CD=2.4,B'C′=2,
∴C′D′=1.6,
故答案为:1.6.
15.
【解析】
由矩形的对边相等,可得CD=AB=2,由相似多边形的性质可得AB:BC=ED:CD,求解即可.
【详解】
解:如图,
∵矩形ABCD中,AB=2,BC=3,
∴CD=AB=2,
∵矩形CDEF与矩形ABCD相似,
∴AB:BC=ED:CD,
即2:3=ED:2,
∴ED=.
故答案为:.
16.25:9.
【解析】
首先确定相似多边形的相似比,然后根据相似多边形面积的比等于相似比的平方求解.
【详解】
∵四边形ABCD∽四边形A′B′C′D′,它们的周长分别为5m和3m,
∴相似比为5:3,
∴S四边形ABCD:S四边形A′B′C′D′=25:9
故答案为:25:9.
17.
【解析】
根据三角形的三边长是4、5、6,即可求得此三角形的周长,又由相似三角形周长的比等于相似比,即可求得另一个三角形的周长.
【详解】
设另外一个三角形的周长是x,
∵一个三角形的三边长是4、5、6,
∴这个三角形的周长为:4+5+6=15,
∵与它相似的另一个三角形最短的一边长是2,
∴,
解得:x=7.5,
∴另一个三角形的周长是7.5.故答案为7.5.
18.1:3
【解析】
分析:根据相似三角形的周长比等于相似比解答.
详解:∵△ABC与△A′B′C′是关于点O的位似三角形,∴△ABC∽△A′B′C′.∵OA′=3OA,∴△ABC与△A′B′C′的周长之比是:OA:OA′=1:3.故答案为1:3.
19.
【解析】
两个矩形的四个角为直角相等,但先求出边框的内外边缘所成的矩形长的比与宽的比,然后根据相似多边形的定义进行判断即可.
【详解】
不相似.理由如下:
.
由题意.得,
.
∵≠,(“填”“=”或“≠”)
∴两个矩形不相似.
故答案为:(1). (2). (3).
20.6.4, 9.6, 80°.
【解析】
根据相似形对应角相等,对应边的比相等,即可求解.
【详解】
解:∵两个四边形相似,∴==;
解得:x==6.4.y==9.6.
α=360°﹣120°﹣30°﹣130°=80°
故答案为(1). 6.4, (2). 9.6, (3). 80°.
21.
【解析】
分别设A1纸的长为a,宽为b,A2纸的长为b,宽为再由相似多边形的对应边成比例列出比例式,求出的值即可.
【详解】
解:设A1纸的长为a,宽为b,A2纸的长为b,宽为,由A1、A2纸的长与宽对应比成比例得=,
故==.
故答案为.
三、解答题
22.解:(1)如图1,三角形B为所作;
(2)如图2,长方形D为所作;
23.∵两个四边形相似,
∴20:5=x:6=y:7,
解得:x=24,y=28,
∵四边形内角和等于360°,
∴α= =75°,
∴x=24,y=28,α=75°.
24.解:设此时高为x米的旗杆的影长为10m,
根据题意得,
解得x=12.
所以此时高为12米的旗杆的影长为10m.
25.解:∵四边形ABCD与四边形A1B1C1D1是相似的图形,
∴,
又∵AB=12,BC=18,CD=18,AD=9,A1B1=8,
∴,
∴B1C1=12,C1D1=12,D1A1=6,
∴四边形A1B1C1D1的周长=8+12+12+6=38.
26.(1)如图所示:
则B的坐标为:(2,0);
故答案为:(2,0);
(2)如图所示:△A′B′C′即为所求.
27.解:(1)存在
假设存在,不妨设“减半”矩形的长和宽分别为,,则,
由①,得:,③
把③代入②,得,
解得,.
所以“减半”矩形长和宽分别为与.
(2)不存在
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.
一、单选题
1.对一个图形进行放缩时,下列说法中正确的是( )
A.图形中线段的长度与角的大小都保持不变
B.图形中线段的长度与角的大小都会改变
C.图形中线段的长度保持不变、角的大小可以改变
D.图形中线段的长度可以改变、角的大小保持不变
2.下列说法正确的是( )
A.所有矩形都相似 B.所有等腰三角形都相似
C.角相等的四边形都相似 D.等边三角形都相似
3.下列各组图形中,不一定相似的是( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
4.一个长方形各边按扩大后,得到的图形与原图形比较,下列说法中正确的是( )
A.周长扩大原来的16倍 B.周长缩小原来的
C.面积扩大原来的16倍 D.面积缩小原来的
5.若一个矩形对折后所得矩形与原矩形相似,则此矩形的长边与短边的比是( ).
A. B. C. D.
6.下列说法正确的有( ).
①形状差不多的两个图形相似;②国旗上的大五角星与小五角星是相似的;③大小不等的两个六边形的形状可能相似;④放大镜下看到的图形与原来的图形的相似.
A.1个 B.2个 C.3个 D.4个
7.如图,正五边形与正五边形相似,若,则下列结论正确的是( )
A. B. C. D.
8.两个相似多边形的一组对应边分别为3cm和4cm,如果它们的周长和为84cm,那么较大多边形的周长为( )
A.36cm B.42cm C.48cm D.54cm
9.如图,已知D.E分别在△ABC的AB.AC边上,△ABC与△AED相似,则下列各式成立的是( )
A.; B.;
C.; D..
10.如图,矩形ABCD∽矩形FAHG,连结BD,延长GH分别交BD、BC于点Ⅰ、J,延长CD、FG交于点E,一定能求出△BIJ面积的条件是( )
A.矩形ABJH和矩形HJCD的面积之差
B.矩形ABJH和矩形HDEG的面积之差
C.矩形ABCD和矩形AHGF的面积之差
D.矩形FBJG和矩形GJCE的面积之差
二、填空题
11.ABC与DEF相似,∠A=72°,∠B=48°,∠F=60°,则∠E=_________.
12.相似的两个图形,它们的大小_________(填“一定”,“不一定”,“一定不”)相同.
13.已知两个三角形是相似形,其中一个三角形的两个角分别为25 、55 ,则另一个三角形的最大内角的度数为__________.
14.四边形和四边形是相似图形,点分别与对应,已知,,,那么的长是__________.
15.在矩形中,点分别在上(点与点不重合)矩形与矩形相似,那么的长为________.
16.已知:四边形ABCD∽四边形A′B′C′D′,它们的周长分别为5m和3m,则S四边形ABCD:S四边形A′B′C′D′=______.
17.要制作两个形状相同的三角形框架,其中一个三角形框架的三边长分别为、、,另一个三角形框架的一条短边长为,则另外一个三角形的周长为________.
18.如图,如果两个相似多边形任意一组对应顶点P、P′所在的直线都是经过同一点O,且有OP′=k·OP(k≠0),那么我们把这样的两个多边形叫位似多边形,点O叫做位似中心,已知△ABC与△A′B′C′是关于点O的位似三角形,OA′=3OA,则△ABC与△A′B′C′的周长之比是________.
19.如图,一块长()为2米,宽()为1米的矩形玻璃,为了保护玻璃需要镶上宽10厘米的铝合金边框,那么边框的内外边缘所成的矩形相似吗?为什么?(补全解答过程)
解:不相似.理由如下:
.
由题意.得 ________,
____________.
∵______,(“填”“=”或“≠”)
∴两个矩形不相似.
20.如图,两个相似四边形的已知数据如图所示,则x=_______,y=______,α=______度.
21.我们通常用到的一种复印纸,整张称为纸(如图),按下图方式对折一分为二裁开成为纸(如图),再一分为二成为纸(如图)…它们都是相似的矩形,这些矩形的长与宽的比值都是一定值,这个定值是________.
三、解答题
22.画图题.
在下面的网格中,每个小正方形的边长都是1.请画出符合下列要求的图形:
(1)图1中将三角形A的各条边按1:3放大,得到三角形B;
(2)图2中将长方形C的各条边按2:1缩小,得到长方形D.
23.如图,两个四边形相似,求未知边x、y的长度及角α的大小.
24.在相同时刻的物高与影长成正比例,如果在某时,旗杆在地面上的影长为10米,此时身高是米的小明的影长是米,求旗杆的高度.
25.设四边形与四边形是相似的图形,且与、与、与是对应点,已知,,求四边形的周长.
26.如图,△ABC在方格中.
(1)请在方格纸上建立平面直角坐标系,使A、C两点坐标依次为 (1,2)、 (3,1),并写出点B坐标为 ;
(2)以原点O为位似中心,相似比为2,在第一象限内将△ABC放大,画出放大后的图形.
27.阅读理解:给定一个矩形,如果存在另一个矩形,它的周长和面积分别是已知矩形的周长和面积的一半,则这个矩形是给定矩形的“减半”矩形.如图,矩形是矩形的“减半”矩形.
请你解决下列问题:
(1)当矩形的长和宽分别为,时,它是否存在“减半”矩形?请作出判断,并说明理由.
(2)边长为的正方形存在“减半”正方形吗?如果存在,求出“减半”正方形的边长;如果不存在,请说明理由.
答案
一、单选题
1.D
【解析】
根据相似多边形的性质:相似多边形的对应边成比例,对应角相等,可知对一个图形进行收缩时,图形中线段的长度改变,角的大小不变,
故选D.
2.D
【解析】
根据相似图形的定义对各选项分析判断后利用排除法求解.
解:A、矩形的四个角相等,四条边不一定对应成比例,所以不一定相似,故本选项错误;
B、所有等腰三角形不一定相似,只有顶角对应相等或底角对应相等才相似,故本选项错误;
C、角相等的四边形,四条边不一定对应成比例,所以不一定相似,故本选项错误;
D、等边三角形三个角均相等且对应边成比例,符合相似三角形的判定;故本选项正确.
故选:D.
3.D
【解析】
根据相似图形的定义,以及等边三角形的性质对各选项分析判断求解.
【详解】
A、各有一个角是100°的两个等腰三角形,100°的角只能是顶角,夹顶角的两边成比例,所以一定相似;
B、两个等腰直角三角形,对应边的比相等,锐角都是45°,相等,所以一定相似;
C、各有一个角是60°的两个等腰三角形,是等边三角形,有两对对应角相等,所以一定相似;
D、各有一个角是50°的两个等腰三角形,可能是顶角为50°,也可能底角为50°,所以对应角不一定相等,所以不一定不相似;
故选:D.
4.C
【解析】
相似矩形的周长比等于相似比,相似矩形的面积比等于相似比的平方,据此进行求解即可.
【详解】
一个长方形按放大后,得到的图形与原图形相似,边长扩大到原来的4倍,
所以周长扩大到原来的4倍,面积扩大到原来的16倍,
所以A、B、D错误,C正确,
故选C.
5.C
【解析】
根据相似图形对应边成比例列出关系式即可求解.
【详解】
如图,矩形ABCD对折后所得矩形与原矩形相似,则矩形ABCD∽矩形BFEA,
设矩形的长边长是a,短边长是b,则AB=CD=EF=b,AD=BC=a,BF=AE=,
根据相似多边形对应边成比例得:,即
∴
∴
故选C.
6.C
【解析】
根据相似图形的定义,对各项进行分析即可得出答案.
【详解】
①形状相同的两个图形是相似图形,形状差不多的两个图形,不是相似图形,故①说法错误;
②国旗上的大五角星与小五角星,形状相同,是相似图形,故②说法正确;
③当大小不等两个六边形的对应角相等,对应边成比例式时,这两个六边形相似,故③说法正确;
④放大镜下看到的图形与原来的图形形状相同,是相似图形,故④说法正确;
②③④说法正确,故选C.
7.B
【解析】
根据相似多边形的定义:各边对应成比例,各角对应相等的多边形叫做相似多边形,逐一分析即可.
【详解】
解:因为相似多边形的对应角相等,对应边成比例,
所以,故可排除C和D
所以.故排除A
故选B.
8.C
【解析】
根据相似三角形的周长的比等于相似比,设较大多边形的周长为x,表示出较小的多边形的周长,再根据它们的周长的和等于84cm列式求解即可.
【详解】
解:设较大多边形的周长为x,则
较小多边形的周长:x=3:4,
∴较小多边形的周长为x,
∵它们的周长和为84cm,
∴x+x=84,
解得x=48cm
故选:C.
9.D
【解析】
根据相似三角形的对应边成比例列式解答即可.
【详解】
∵△ABC与△AED相似,
∴,
∴.
故选D.
10.B
【解析】
设矩形的边AH=x,GH=y,EG=a,DC=b,根据平行线分线段成比例可得JI=,根据相似多边形的性质可得=,然后表示出S阴影的面积和S矩形ABJH﹣S矩形HDEG的值即可求解.
【详解】
解:设矩形的边AH=x,GH=y,EG=a,DC=b,
则BJ=x,JC=a,
∵JI//CD,
∴=即JI=,
∵矩形ABCD∽矩形FAHG,
∴=,
即=,
∴x+a=,
∴S阴影=BJ JI
=x
=xy.
∵S矩形ABJH﹣S矩形HDEG
=xb﹣ay
=x ﹣ay
=xy.
∴S阴影△BIJ=(S矩形ABJH﹣S矩形HDEG).
所以一定能求出△BIJ面积的条件是矩形ABJH和矩形HDEG的面积之差.
故选:B.
二、填空题
11.48°或72°
【解析】
根据相似三角形的性质解答即可.
【详解】
∵ABC与DEF相似,且,∠B≠∠A≠∠F,
∴∠E=∠B或∠E=∠A,
∵∠B=48°,∠A=72°
∴∠E=48°或72°,
故答案为:48°或72°.
12.不一定
【解析】
根据相似图形的定义判断即可.
【详解】
相似的两个图形形状相同,但大小不一定相等,只有两个图形全等时大小才相等,全等是相似的一种特殊情况.
故答案为:不一定.
13.
【解析】
先根据三角形的内角和定理得出一个三角形的最大内角度数,再根据相似三角形的对应角相等得出另一个三角形最大内角度数.
【详解】
解:∵一个三角形的两个角分别为25°、55°,
∴第三个角,即最大角为180°-(25°+55°)=100°,
∵两个三角形相似,
∴另一个三角形的最大内角度数为100°,
故答案为:100°.
14.1.6
【解析】
相似多边形的对应边成比例,根据相似多边形的性质即可解决问题.
【详解】
∵四边形ABCD∽四边形A'B'C'D',
∴CD:C′D′=BC:B′C′,
∵BC=3,CD=2.4,B'C′=2,
∴C′D′=1.6,
故答案为:1.6.
15.
【解析】
由矩形的对边相等,可得CD=AB=2,由相似多边形的性质可得AB:BC=ED:CD,求解即可.
【详解】
解:如图,
∵矩形ABCD中,AB=2,BC=3,
∴CD=AB=2,
∵矩形CDEF与矩形ABCD相似,
∴AB:BC=ED:CD,
即2:3=ED:2,
∴ED=.
故答案为:.
16.25:9.
【解析】
首先确定相似多边形的相似比,然后根据相似多边形面积的比等于相似比的平方求解.
【详解】
∵四边形ABCD∽四边形A′B′C′D′,它们的周长分别为5m和3m,
∴相似比为5:3,
∴S四边形ABCD:S四边形A′B′C′D′=25:9
故答案为:25:9.
17.
【解析】
根据三角形的三边长是4、5、6,即可求得此三角形的周长,又由相似三角形周长的比等于相似比,即可求得另一个三角形的周长.
【详解】
设另外一个三角形的周长是x,
∵一个三角形的三边长是4、5、6,
∴这个三角形的周长为:4+5+6=15,
∵与它相似的另一个三角形最短的一边长是2,
∴,
解得:x=7.5,
∴另一个三角形的周长是7.5.故答案为7.5.
18.1:3
【解析】
分析:根据相似三角形的周长比等于相似比解答.
详解:∵△ABC与△A′B′C′是关于点O的位似三角形,∴△ABC∽△A′B′C′.∵OA′=3OA,∴△ABC与△A′B′C′的周长之比是:OA:OA′=1:3.故答案为1:3.
19.
【解析】
两个矩形的四个角为直角相等,但先求出边框的内外边缘所成的矩形长的比与宽的比,然后根据相似多边形的定义进行判断即可.
【详解】
不相似.理由如下:
.
由题意.得,
.
∵≠,(“填”“=”或“≠”)
∴两个矩形不相似.
故答案为:(1). (2). (3).
20.6.4, 9.6, 80°.
【解析】
根据相似形对应角相等,对应边的比相等,即可求解.
【详解】
解:∵两个四边形相似,∴==;
解得:x==6.4.y==9.6.
α=360°﹣120°﹣30°﹣130°=80°
故答案为(1). 6.4, (2). 9.6, (3). 80°.
21.
【解析】
分别设A1纸的长为a,宽为b,A2纸的长为b,宽为再由相似多边形的对应边成比例列出比例式,求出的值即可.
【详解】
解:设A1纸的长为a,宽为b,A2纸的长为b,宽为,由A1、A2纸的长与宽对应比成比例得=,
故==.
故答案为.
三、解答题
22.解:(1)如图1,三角形B为所作;
(2)如图2,长方形D为所作;
23.∵两个四边形相似,
∴20:5=x:6=y:7,
解得:x=24,y=28,
∵四边形内角和等于360°,
∴α= =75°,
∴x=24,y=28,α=75°.
24.解:设此时高为x米的旗杆的影长为10m,
根据题意得,
解得x=12.
所以此时高为12米的旗杆的影长为10m.
25.解:∵四边形ABCD与四边形A1B1C1D1是相似的图形,
∴,
又∵AB=12,BC=18,CD=18,AD=9,A1B1=8,
∴,
∴B1C1=12,C1D1=12,D1A1=6,
∴四边形A1B1C1D1的周长=8+12+12+6=38.
26.(1)如图所示:
则B的坐标为:(2,0);
故答案为:(2,0);
(2)如图所示:△A′B′C′即为所求.
27.解:(1)存在
假设存在,不妨设“减半”矩形的长和宽分别为,,则,
由①,得:,③
把③代入②,得,
解得,.
所以“减半”矩形长和宽分别为与.
(2)不存在
因为两个正方形是相似图形,当它们的周长比为时,面积比必定是,
所以正方形不存在“减半”正方形.
