沪教版九年级数学上册试题第二十五章锐角的三角比单元测试(含解析)
文档属性
| 名称 | 沪教版九年级数学上册试题第二十五章锐角的三角比单元测试(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-15 00:00:00 | ||
图片预览



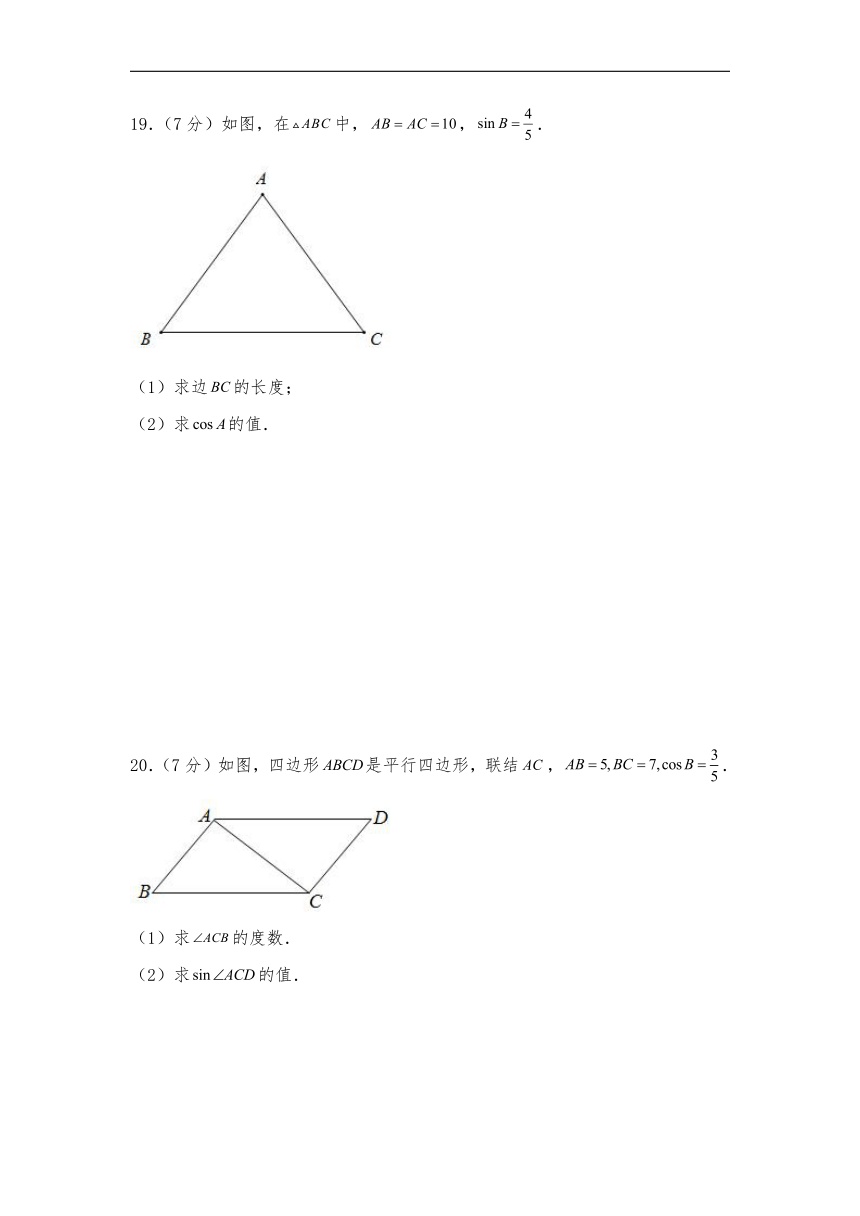
文档简介
第二十五章《锐角的三角比 》单元测试
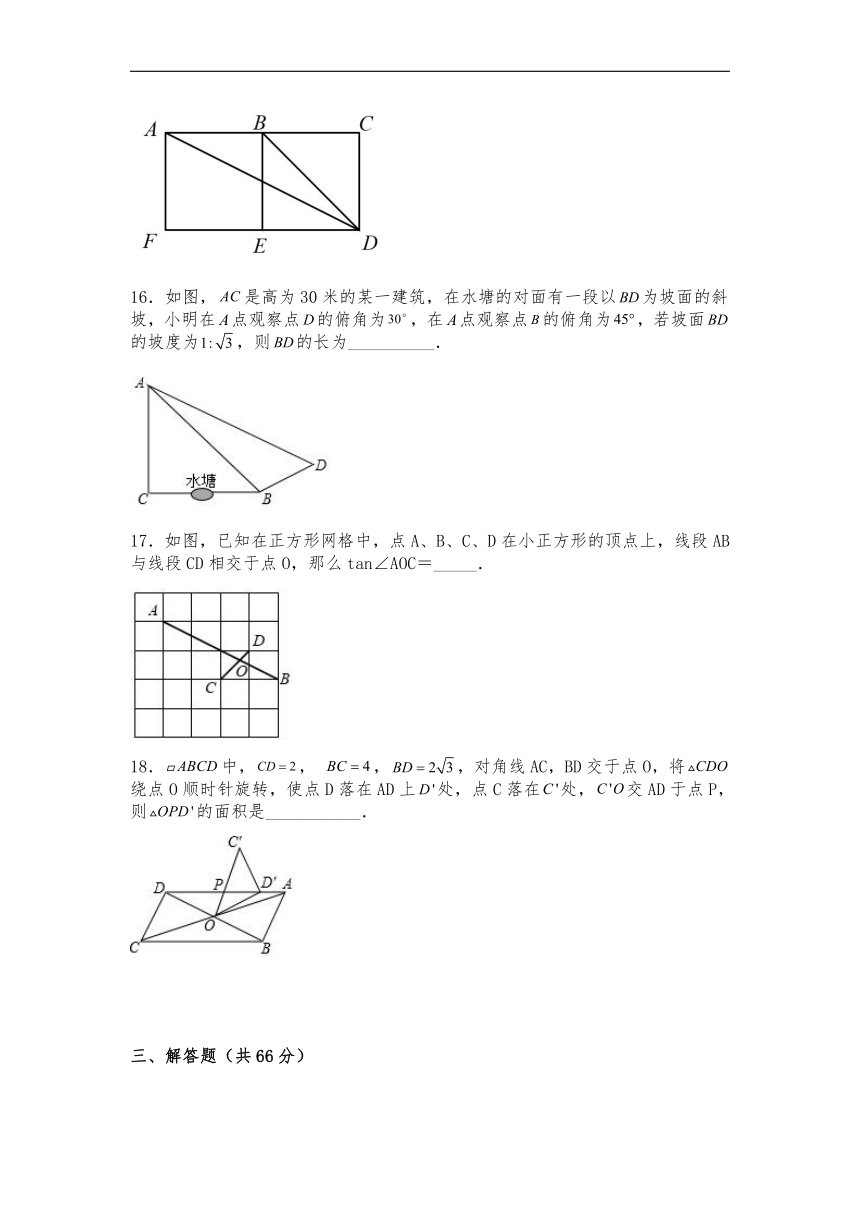
一、单选题(每题3分,共10分)
1.在△中,,,,则的值是( )
A. B. C. D.
2.在中,,那么锐角的正弦等于( )
A. B. C. D..
3.在中,,,,那么下列结论正确的是( )
A. B. C. D.
4.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴y的夹角α的余切值是( )
A. B. C. D.
5.如图,在中,,,的垂直平分线交于,连接,若,则的长是( ).
A. B. C. D.
6.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )
A.5 米 B.5米 C.2米 D.4米
7.如图,中,,已知,,,则的长可表示为( )
A. B.
C. D.
8.共享单车为市民出行提供了便利.图1为单车实物图,图2为单车示意图,与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线方向调节.已知,,,车轮半径为,,小明体验后觉得当坐垫C离地面高度为时骑着比较舒适,此时的长约为( )(结果精确到,参考数据:,,)
A. B. C. D.
9.如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为( )
A.千米 B.千米
C.千米 D.千米
10.如图,已知中,,,分别为,的中点,连结,过作的平行线与的角平分线交于点,连结,若,,则的正弦值为( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.计算:(﹣π)0+()﹣1﹣sin60°=_____.
12.在Rt△ABC中,∠C=90°,AC=5,AB=10,则∠B=_____.
13.在中,,,,那么AB的长为__.
14.如图,在中,,,,将绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF=_________.
15.如图,正方形和正方形的边长相等,点A、B、C在同一条直线上.连接、,那么的值为______.
16.如图,是高为30米的某一建筑,在水塘的对面有一段以为坡面的斜坡,小明在点观察点的俯角为,在点观察点的俯角为,若坡面的坡度为,则的长为__________.
17.如图,已知在正方形网格中,点A、B、C、D在小正方形的顶点上,线段AB与线段CD相交于点O,那么tan∠AOC=_____.
18.中,, ,,对角线AC,BD交于点O,将绕点O顺时针旋转,使点D落在AD上处,点C落在处,交AD于点P,则的面积是___________.
三、解答题(共66分)
19.(7分)如图,在中,,.
(1)求边的长度;
(2)求的值.
20.(7分)如图,四边形是平行四边形,联结,.
(1)求的度数.
(2)求的值.
21.(9分)如图,在中,是边上的高,.
求:(1)线段的长;
(2)的值.
22.(9分)如图是某地摩天轮(图1)和示意图(图2),已知线段经过圆心且垂直于地面,垂足为点,当座舱在点时,测得摩天轮顶端点的仰角为,同时测得点的俯角为,又知摩天轮的半径为米,求摩天轮顶端与地面的距离.(精确到米)
参考数据:,
23.(10分)如图,甲、乙两栋楼的高度均为90 m.冬至日正午,太阳光线与水平面所成的角为30°,甲楼在乙楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为53°,甲楼在乙楼墙面上的影高为AD.已知CD=40 m,若每层楼的高度均为3 m,求点C位于第几层.(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,≈1.73,≈1.41)
24.(12分)在一次对某水库大坝设计中,李设计师对修建一座长80米的水库大坝提出了以下方案:大坝的横截面为等腰梯形,如图,∥,坝高10米,迎水坡面的坡度1:,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面的坡度进行修改,修改后的迎水坡面的坡度1:.
(1)求原方案中此大坝迎水坡的长(结果保留根号);
(2)如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿方向拓宽2.7米,求坝底将会沿方向加宽多少米?
25.(12分)已知点P为线段AB上的一点,将线段AP绕点A逆时针旋转60°,得到线段AC;再将线段绕点B逆时针旋转120°,得到线段BD;点M是AD的中点,联结BM、CM.
(1)如图1,如果点P在线段CM上,求证:;
(2)如图1,如果点P在线段CM上,求证:;
(3)如果点P不在线段CM上(如图12),当点P在线段AB上运动时,的正切值是否发生变化?如果发生变化,简述理由;如果不发生变化,请求出的正切值.
答案
一、单选题
1.A
【分析】
直接利用正弦函数的定义即可求解.
【解析】
解:在Rt△ABC中,AB=13 , BC=5,
∴sinA= =,
故选:A.
2.B
【分析】
根据锐角三角函数的定义可直接得出结果.
【解析】
在中,,那么锐角的正弦=,
故选:B.
3.D
【分析】
先根据勾股定理解出AB,再逐项根据三角函数的定义判断即可.
【解析】
根据勾股定理可得:,
则;;;;
故选:D.
4.B
【分析】
过点A作AB⊥x轴,构造直角三角形,由坐标得出OB=2,AB=3,再根据余切的意义求出结果即可.
【解析】
解:过点A作AB⊥x轴,垂足为B,则OB=2,AB=3,
在Rt△OAB中,cot∠AOB=cotα=,
故选:B.
5.B
【分析】
要求出BC的长,可以先求出CD和BD的长,再利用勾股定理求得,可以设CD=xcm, 再根据,建立关于x的方程即可求出CD和BD的长.
【解析】
∵MN是AB的垂直平分线,
∴AD=BD.
设CD=xcm,则AD=BD=(8-x)cm,
在Rt△BCD中,,
得 ,
解得x=3,
则8-x=5,
∴BD=5cm,CD=3cm.
在Rt△BCD中,BC= =4cm.
故选B.
6.C
【分析】
如图,斜坡AB的坡度为1:2,可设DE=x,AE=2x,在Rt△ADE中,利用勾股定理列方程求解即可.
【解析】
如图,斜坡AB的坡度为1:2,设DE=x,AE=2x,
在Rt△ADE中,
∵AE2+DE2=AD2,
∴(2x)2+x2=102,
解之得
x= 2,或x= -2(舍去).
故选C.
7.C
【分析】
利用锐角三角函数关系分别表示出BC,DC的长进而得出答案.
【解析】
解:∵∠C=90°,∠B=α,∠ADC=β,AB=a,
∴cosB=cosα==,
则BC=a cosα,
sinB=sinα==,
故AC=a sinα,
则tanβ=,
故DC==,
则BD=BC-DC=a cosα-,
故选:C.
8.B
【分析】
过点C作CN⊥AB,交AB于M,通过构建直角三角形解答即可.
【解析】
解:过点C作CN⊥AB,交AB于M,交地面于N
由题意可知MN=30cm,当CN=90cm时,CM=60cm,
∵Rt△BCM中,∠ABE=70°,sin∠ABE=sin70°=≈0.9,
∴BC≈67cm,
∴CEBC BE=67 40=27cm.
故选B.
9.A
【分析】
根据锐角三角函数的概念进行作答.
【解析】
在P点做一条直线垂直于直线AB且交于点O,由锐角三角函数知,AO=PO,BO=PO,又AB=m=AO-BO= PO- PO= . 所以答案选A.
10.A
【分析】
根据题意延长DF交AB于H,过F作FT⊥AB于T,连接CF,设DF=x,运用三角形中位线定理、全等三角形的性质以及锐角三角函数定义构建方程,求出x即可得出答案.
【解析】
解:延长DF交AB于H,过F作FT⊥AB于T,连接CF,
设DF=x,
∵DH∥AC,D为BC的中点,
∴H为AB的中点,
∴BH=AH,
∴DH是△ABC的中位线,
∴DH=AC=1,
∴FH=1-x,
∵FA平分∠CAB,FE⊥AC,FT⊥AB,
∴FE=FT,
∵E为AC的中点,FE⊥AC,
∴CF=AF,
在Rt△CFE和Rt△AFT中,
,
∴Rt△CFE≌Rt△AFT(HL),
∴AE=AT=1,
∵∠FAE=∠AFH=∠FAH,
∴FH=AH=BH=1-x,
∴TH=1-(1-x)=x,
∵∠C=∠BDH=∠TFH,
∴sin∠C=sin∠TFH,
∴,
解得:或(舍去),
∴,
∵DE=,
∴.
故选:A.
二、填空题
11.
【分析】
先运用零次幂、负整数指数幂以及特殊角的三角函数值化简,然后计算即可.
【解析】
解:(﹣π)0+()﹣1﹣sin60°
=1+2﹣×
=3﹣
=.
故填:.
12.60°
【分析】
利用正弦定义计算即可.
【解析】
解:如图,
∵sinB=,
∴∠B=60°,
故答案为:60°.
13.8
【分析】
根据余弦函数的定义即可直接求解.
【解析】
解:∵,
∴AB===8,
故答案为:8.
14.
【分析】
如图,过点F作FG⊥AC于G,设FG=x,由旋转得∠D=∠B,求出,,利用FG∥BC,求得FG=2AG,由此列得x=2(2x-3),求出FG=2,AG=1,利用勾股定理求出AF,即可求得答案.
【解析】
如图,过点F作FG⊥AC于G,
设FG=x,
由旋转得∠D=∠B,
∴,
∴,
∴,
∵AD=AB=3,
∴,
∵∠FGA=,
∴FG∥BC,
∴∠AFG=∠B,
∴,
∴FG=2AG,
∴x=2(2x-3)
解得x=2
∴FG=2,AG=1,
∴,
∴,
故答案为:.
15.3
【分析】
先构造以∠ADB为内角的直角三角形,根据余切的定义求解即可.
【解析】
解:如图,作正方形ABEF关于直线AB对称的正方形ABGH,连接AG,BH,相交于点O;
∵正方形ABGH,
∴∠AOD=90°,OA=OB=AG,
∵正方形和正方形的边长相等,
∴正方形和正方形的边长相等,
∴AG=BD=2OA,
∴OD=OB+BD=3OA,
∴在Rt△AOD中,
==3.
故答案为3.
16.
【分析】
延长CB、AD交于F点,作,由题意得:,,,,设,则,,,解出即可得出答案.
【解析】
解:延长CB、AD交于F点,作
小明在点观察点的俯角为,在点观察点的俯角为
在中,
又坡面的坡度为
则
设,则,
解得:
(米)
故答案为:.
17.3
【分析】
如图,取格点E、F,连接AE、AF、BE,通过计算得到等腰三角形△ABE,利用等腰三角形的三线合一得出AF⊥BE,接着推出∠AOC=∠ABF.在Rt△ABF中,由勾股定理求出两直角边的长,再依据正切值的意义可求解.
【解析】
解:如图,取格点E、F,连接AE、AF、BE,可知AF经过点C,BE经过点F,
设网格中的小正方形的边长为1,
则AE=AB=,
∵F是BE的中点,
∴AF⊥BE.
由题意:∠DCB=∠CBE=45°.
∴CD∥BE,
∴∠AOC=∠ABF.
∴tan∠AOC=tan∠ABF.
∵BF=,
AF=,
∴tan∠ABF=.
∴tan∠AOC=3.
故答案为:3.
18.
【分析】
过点作,作,,,,为垂足,根据,,,可证是直角三角形,,可求△各边长,以及的长,由可求的长,即可求的面积.
【解析】
解:过点作,作,,,,为垂足,
,,,
,
,
.
,
,
,
是平行四边形,
,,,
,
在中,,
旋转,
,,,,
,,
,,
,,
,
,,
,
,
,,
,
,
且,
,
,
故答案为.
三、解答题
19.
(1)作,垂足为点E.
∵,AB=10,
∴,
∴=6,
∴;
(2)作,
∵AB=AC,
∴∠B=∠C,
∴cosC=,
∴,
∴,
∴,
∴.
.
20.
解:(1)过点A作,
中
;
(2)过点作,如图,
四边形是平行四边形,
中,
.
21.
解:(1)∵AD是BC边上的高,
∴∠D=90°,
在Rt△ABD中,
∵sinB=,
∴,
又∵AD=12,
∴AB=15,
∴BD==9,
又∵BC=4,
∴CD=BD-BC=9-4=5;
答:线段CD的长为5;
(2)如图,过点C作CE⊥AB,垂足为E,
∵S△ABC=BC AD=AB CE
∴×4×12=×15×CE,
∴CE=,
在Rt△AEC中,
∴sin∠BAC=,
答:sin∠BAC的值为.
22.
解:连接AB、AD、AC,过点A作AE⊥BC于E,
则∠AEB=∠AEC=90°,
由题意得:点A、B在圆D上,
∴DB=DA,
在Rt△ABE中,∠BAE=15°,
∴∠DBA=∠DAB=75°,∠DAE=60°,
∵OA=10米,
∴AE=5(米),
∴BE=AE×tan15°≈5×0.27=1.35(米),
∵∠EAC=76°,
∴CE=AE×tan76°≈5×4.01=20.05(米),
∴BC=BE+CE=1.35+20.05≈21(米),
答:摩天轮顶端B与地面的距离约为21米.
23.
解:如图,过点C作CE⊥PB于点E,过点D作DF⊥PB于点F,
则∠CEP=∠DFP=90°.
设楼间距为x m.
∵∠PCE=30°,∠PDF=53°,
∴PE=CE·tan 30°=x m,PF=DF·tan 53°≈1.33x m.
∵EF=CD=40 m,
∴PF-PE=40 m,
即1.33x-x=40,
解得x≈53.1,
∴PE=x≈30.6(m),
∴AC=BE=PB-PE=90-30.6=59.4(m).
∵每层楼高为3 m,59.4÷3=198,
∴点C位于第20层.
24.
(1)过点作于.
在△中,1∶,,且米.
∴米.
∴米.
(2)如图,延长至点,至点,连接,过点作于.
在△中,1∶,且米,
∴米,米.
∵方案修改前后,修建大坝所需土石方总体积不变.
∴.
即.
∴.
米.
答:坝底将会沿方向加宽米.
25.
解:(1)如图1中,
由题意可得,∠CAP=60°,且AP=AC,
∴△APC是等边三角形,
∴∠APC=60°,
∴∠BPM=60°,
又∵∠PBD=120°,
∴∠BPM+∠PBD=180°,
∴PM∥BD;
(2)如图1中,∵AM=MD,PM∥BD,
∴AP=PB,
∴PM= BD,
∵PA=PC=PB=BD,
∴PC=2PM;
(3)结论:tan∠BCM=.理由如下:
如图2,延长BM至点G,使得MG=MB,连接AG,BC,GC,PC,GD,
∵AM=MD,GM=BM,
∴四边形AGDB是平行四边形,
∴AG=BD,AG∥BD,
∴∠BAG=180°-∠ABD=60°,
∴∠CAG=120°,
∵△APC是等边三角形,
∴AC=CP,∠CPB=120°,
∵PB=DB=AG,
∴△CAG≌△CPB(SAS),
∴CG=CB,∠ACG=∠PCB,
∴∠GCB=60°,
∴△CBG是等边三角形,
∵GM=BM,
∴∠BCM=∠BCG=30°,
∴tan∠BCM=.
一、单选题(每题3分,共10分)
1.在△中,,,,则的值是( )
A. B. C. D.
2.在中,,那么锐角的正弦等于( )
A. B. C. D..
3.在中,,,,那么下列结论正确的是( )
A. B. C. D.
4.如图,已知在平面直角坐标系xOy内有一点A(2,3),那么OA与x轴正半轴y的夹角α的余切值是( )
A. B. C. D.
5.如图,在中,,,的垂直平分线交于,连接,若,则的长是( ).
A. B. C. D.
6.如图,传送带和地面所成斜坡AB的坡度为1:2,物体从地面沿着该斜坡前进了10米,那么物体离地面的高度为( )
A.5 米 B.5米 C.2米 D.4米
7.如图,中,,已知,,,则的长可表示为( )
A. B.
C. D.
8.共享单车为市民出行提供了便利.图1为单车实物图,图2为单车示意图,与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线方向调节.已知,,,车轮半径为,,小明体验后觉得当坐垫C离地面高度为时骑着比较舒适,此时的长约为( )(结果精确到,参考数据:,,)
A. B. C. D.
9.如图,一架飞机在点A处测得水平地面上一个标志物P的俯角为α,水平飞行m千米后到达点B处,又测得标志物P的俯角为β,那么此时飞机离地面的高度为( )
A.千米 B.千米
C.千米 D.千米
10.如图,已知中,,,分别为,的中点,连结,过作的平行线与的角平分线交于点,连结,若,,则的正弦值为( )
A. B. C. D.
二、填空题(每题3分,共24分)
11.计算:(﹣π)0+()﹣1﹣sin60°=_____.
12.在Rt△ABC中,∠C=90°,AC=5,AB=10,则∠B=_____.
13.在中,,,,那么AB的长为__.
14.如图,在中,,,,将绕着点A顺时针旋转后,点B恰好落在射线CA上的点D处,点C落在点E处,射线DE与边AB相交于点F,那么BF=_________.
15.如图,正方形和正方形的边长相等,点A、B、C在同一条直线上.连接、,那么的值为______.
16.如图,是高为30米的某一建筑,在水塘的对面有一段以为坡面的斜坡,小明在点观察点的俯角为,在点观察点的俯角为,若坡面的坡度为,则的长为__________.
17.如图,已知在正方形网格中,点A、B、C、D在小正方形的顶点上,线段AB与线段CD相交于点O,那么tan∠AOC=_____.
18.中,, ,,对角线AC,BD交于点O,将绕点O顺时针旋转,使点D落在AD上处,点C落在处,交AD于点P,则的面积是___________.
三、解答题(共66分)
19.(7分)如图,在中,,.
(1)求边的长度;
(2)求的值.
20.(7分)如图,四边形是平行四边形,联结,.
(1)求的度数.
(2)求的值.
21.(9分)如图,在中,是边上的高,.
求:(1)线段的长;
(2)的值.
22.(9分)如图是某地摩天轮(图1)和示意图(图2),已知线段经过圆心且垂直于地面,垂足为点,当座舱在点时,测得摩天轮顶端点的仰角为,同时测得点的俯角为,又知摩天轮的半径为米,求摩天轮顶端与地面的距离.(精确到米)
参考数据:,
23.(10分)如图,甲、乙两栋楼的高度均为90 m.冬至日正午,太阳光线与水平面所成的角为30°,甲楼在乙楼墙面上的影高为CA;春分日正午,太阳光线与水平面所成的角为53°,甲楼在乙楼墙面上的影高为AD.已知CD=40 m,若每层楼的高度均为3 m,求点C位于第几层.(参考数据:sin 53°≈0.80,cos 53°≈0.60,tan 53°≈1.33,≈1.73,≈1.41)
24.(12分)在一次对某水库大坝设计中,李设计师对修建一座长80米的水库大坝提出了以下方案:大坝的横截面为等腰梯形,如图,∥,坝高10米,迎水坡面的坡度1:,审核组专家看后,从力学的角度对此方案提出了建议,李设计师决定在原方案的基础上,将迎水坡面的坡度进行修改,修改后的迎水坡面的坡度1:.
(1)求原方案中此大坝迎水坡的长(结果保留根号);
(2)如果方案修改前后,修建大坝所需土石方总体积不变,在方案修改后,若坝顶沿方向拓宽2.7米,求坝底将会沿方向加宽多少米?
25.(12分)已知点P为线段AB上的一点,将线段AP绕点A逆时针旋转60°,得到线段AC;再将线段绕点B逆时针旋转120°,得到线段BD;点M是AD的中点,联结BM、CM.
(1)如图1,如果点P在线段CM上,求证:;
(2)如图1,如果点P在线段CM上,求证:;
(3)如果点P不在线段CM上(如图12),当点P在线段AB上运动时,的正切值是否发生变化?如果发生变化,简述理由;如果不发生变化,请求出的正切值.
答案
一、单选题
1.A
【分析】
直接利用正弦函数的定义即可求解.
【解析】
解:在Rt△ABC中,AB=13 , BC=5,
∴sinA= =,
故选:A.
2.B
【分析】
根据锐角三角函数的定义可直接得出结果.
【解析】
在中,,那么锐角的正弦=,
故选:B.
3.D
【分析】
先根据勾股定理解出AB,再逐项根据三角函数的定义判断即可.
【解析】
根据勾股定理可得:,
则;;;;
故选:D.
4.B
【分析】
过点A作AB⊥x轴,构造直角三角形,由坐标得出OB=2,AB=3,再根据余切的意义求出结果即可.
【解析】
解:过点A作AB⊥x轴,垂足为B,则OB=2,AB=3,
在Rt△OAB中,cot∠AOB=cotα=,
故选:B.
5.B
【分析】
要求出BC的长,可以先求出CD和BD的长,再利用勾股定理求得,可以设CD=xcm, 再根据,建立关于x的方程即可求出CD和BD的长.
【解析】
∵MN是AB的垂直平分线,
∴AD=BD.
设CD=xcm,则AD=BD=(8-x)cm,
在Rt△BCD中,,
得 ,
解得x=3,
则8-x=5,
∴BD=5cm,CD=3cm.
在Rt△BCD中,BC= =4cm.
故选B.
6.C
【分析】
如图,斜坡AB的坡度为1:2,可设DE=x,AE=2x,在Rt△ADE中,利用勾股定理列方程求解即可.
【解析】
如图,斜坡AB的坡度为1:2,设DE=x,AE=2x,
在Rt△ADE中,
∵AE2+DE2=AD2,
∴(2x)2+x2=102,
解之得
x= 2,或x= -2(舍去).
故选C.
7.C
【分析】
利用锐角三角函数关系分别表示出BC,DC的长进而得出答案.
【解析】
解:∵∠C=90°,∠B=α,∠ADC=β,AB=a,
∴cosB=cosα==,
则BC=a cosα,
sinB=sinα==,
故AC=a sinα,
则tanβ=,
故DC==,
则BD=BC-DC=a cosα-,
故选:C.
8.B
【分析】
过点C作CN⊥AB,交AB于M,通过构建直角三角形解答即可.
【解析】
解:过点C作CN⊥AB,交AB于M,交地面于N
由题意可知MN=30cm,当CN=90cm时,CM=60cm,
∵Rt△BCM中,∠ABE=70°,sin∠ABE=sin70°=≈0.9,
∴BC≈67cm,
∴CEBC BE=67 40=27cm.
故选B.
9.A
【分析】
根据锐角三角函数的概念进行作答.
【解析】
在P点做一条直线垂直于直线AB且交于点O,由锐角三角函数知,AO=PO,BO=PO,又AB=m=AO-BO= PO- PO= . 所以答案选A.
10.A
【分析】
根据题意延长DF交AB于H,过F作FT⊥AB于T,连接CF,设DF=x,运用三角形中位线定理、全等三角形的性质以及锐角三角函数定义构建方程,求出x即可得出答案.
【解析】
解:延长DF交AB于H,过F作FT⊥AB于T,连接CF,
设DF=x,
∵DH∥AC,D为BC的中点,
∴H为AB的中点,
∴BH=AH,
∴DH是△ABC的中位线,
∴DH=AC=1,
∴FH=1-x,
∵FA平分∠CAB,FE⊥AC,FT⊥AB,
∴FE=FT,
∵E为AC的中点,FE⊥AC,
∴CF=AF,
在Rt△CFE和Rt△AFT中,
,
∴Rt△CFE≌Rt△AFT(HL),
∴AE=AT=1,
∵∠FAE=∠AFH=∠FAH,
∴FH=AH=BH=1-x,
∴TH=1-(1-x)=x,
∵∠C=∠BDH=∠TFH,
∴sin∠C=sin∠TFH,
∴,
解得:或(舍去),
∴,
∵DE=,
∴.
故选:A.
二、填空题
11.
【分析】
先运用零次幂、负整数指数幂以及特殊角的三角函数值化简,然后计算即可.
【解析】
解:(﹣π)0+()﹣1﹣sin60°
=1+2﹣×
=3﹣
=.
故填:.
12.60°
【分析】
利用正弦定义计算即可.
【解析】
解:如图,
∵sinB=,
∴∠B=60°,
故答案为:60°.
13.8
【分析】
根据余弦函数的定义即可直接求解.
【解析】
解:∵,
∴AB===8,
故答案为:8.
14.
【分析】
如图,过点F作FG⊥AC于G,设FG=x,由旋转得∠D=∠B,求出,,利用FG∥BC,求得FG=2AG,由此列得x=2(2x-3),求出FG=2,AG=1,利用勾股定理求出AF,即可求得答案.
【解析】
如图,过点F作FG⊥AC于G,
设FG=x,
由旋转得∠D=∠B,
∴,
∴,
∴,
∵AD=AB=3,
∴,
∵∠FGA=,
∴FG∥BC,
∴∠AFG=∠B,
∴,
∴FG=2AG,
∴x=2(2x-3)
解得x=2
∴FG=2,AG=1,
∴,
∴,
故答案为:.
15.3
【分析】
先构造以∠ADB为内角的直角三角形,根据余切的定义求解即可.
【解析】
解:如图,作正方形ABEF关于直线AB对称的正方形ABGH,连接AG,BH,相交于点O;
∵正方形ABGH,
∴∠AOD=90°,OA=OB=AG,
∵正方形和正方形的边长相等,
∴正方形和正方形的边长相等,
∴AG=BD=2OA,
∴OD=OB+BD=3OA,
∴在Rt△AOD中,
==3.
故答案为3.
16.
【分析】
延长CB、AD交于F点,作,由题意得:,,,,设,则,,,解出即可得出答案.
【解析】
解:延长CB、AD交于F点,作
小明在点观察点的俯角为,在点观察点的俯角为
在中,
又坡面的坡度为
则
设,则,
解得:
(米)
故答案为:.
17.3
【分析】
如图,取格点E、F,连接AE、AF、BE,通过计算得到等腰三角形△ABE,利用等腰三角形的三线合一得出AF⊥BE,接着推出∠AOC=∠ABF.在Rt△ABF中,由勾股定理求出两直角边的长,再依据正切值的意义可求解.
【解析】
解:如图,取格点E、F,连接AE、AF、BE,可知AF经过点C,BE经过点F,
设网格中的小正方形的边长为1,
则AE=AB=,
∵F是BE的中点,
∴AF⊥BE.
由题意:∠DCB=∠CBE=45°.
∴CD∥BE,
∴∠AOC=∠ABF.
∴tan∠AOC=tan∠ABF.
∵BF=,
AF=,
∴tan∠ABF=.
∴tan∠AOC=3.
故答案为:3.
18.
【分析】
过点作,作,,,,为垂足,根据,,,可证是直角三角形,,可求△各边长,以及的长,由可求的长,即可求的面积.
【解析】
解:过点作,作,,,,为垂足,
,,,
,
,
.
,
,
,
是平行四边形,
,,,
,
在中,,
旋转,
,,,,
,,
,,
,,
,
,,
,
,
,,
,
,
且,
,
,
故答案为.
三、解答题
19.
(1)作,垂足为点E.
∵,AB=10,
∴,
∴=6,
∴;
(2)作,
∵AB=AC,
∴∠B=∠C,
∴cosC=,
∴,
∴,
∴,
∴.
.
20.
解:(1)过点A作,
中
;
(2)过点作,如图,
四边形是平行四边形,
中,
.
21.
解:(1)∵AD是BC边上的高,
∴∠D=90°,
在Rt△ABD中,
∵sinB=,
∴,
又∵AD=12,
∴AB=15,
∴BD==9,
又∵BC=4,
∴CD=BD-BC=9-4=5;
答:线段CD的长为5;
(2)如图,过点C作CE⊥AB,垂足为E,
∵S△ABC=BC AD=AB CE
∴×4×12=×15×CE,
∴CE=,
在Rt△AEC中,
∴sin∠BAC=,
答:sin∠BAC的值为.
22.
解:连接AB、AD、AC,过点A作AE⊥BC于E,
则∠AEB=∠AEC=90°,
由题意得:点A、B在圆D上,
∴DB=DA,
在Rt△ABE中,∠BAE=15°,
∴∠DBA=∠DAB=75°,∠DAE=60°,
∵OA=10米,
∴AE=5(米),
∴BE=AE×tan15°≈5×0.27=1.35(米),
∵∠EAC=76°,
∴CE=AE×tan76°≈5×4.01=20.05(米),
∴BC=BE+CE=1.35+20.05≈21(米),
答:摩天轮顶端B与地面的距离约为21米.
23.
解:如图,过点C作CE⊥PB于点E,过点D作DF⊥PB于点F,
则∠CEP=∠DFP=90°.
设楼间距为x m.
∵∠PCE=30°,∠PDF=53°,
∴PE=CE·tan 30°=x m,PF=DF·tan 53°≈1.33x m.
∵EF=CD=40 m,
∴PF-PE=40 m,
即1.33x-x=40,
解得x≈53.1,
∴PE=x≈30.6(m),
∴AC=BE=PB-PE=90-30.6=59.4(m).
∵每层楼高为3 m,59.4÷3=198,
∴点C位于第20层.
24.
(1)过点作于.
在△中,1∶,,且米.
∴米.
∴米.
(2)如图,延长至点,至点,连接,过点作于.
在△中,1∶,且米,
∴米,米.
∵方案修改前后,修建大坝所需土石方总体积不变.
∴.
即.
∴.
米.
答:坝底将会沿方向加宽米.
25.
解:(1)如图1中,
由题意可得,∠CAP=60°,且AP=AC,
∴△APC是等边三角形,
∴∠APC=60°,
∴∠BPM=60°,
又∵∠PBD=120°,
∴∠BPM+∠PBD=180°,
∴PM∥BD;
(2)如图1中,∵AM=MD,PM∥BD,
∴AP=PB,
∴PM= BD,
∵PA=PC=PB=BD,
∴PC=2PM;
(3)结论:tan∠BCM=.理由如下:
如图2,延长BM至点G,使得MG=MB,连接AG,BC,GC,PC,GD,
∵AM=MD,GM=BM,
∴四边形AGDB是平行四边形,
∴AG=BD,AG∥BD,
∴∠BAG=180°-∠ABD=60°,
∴∠CAG=120°,
∵△APC是等边三角形,
∴AC=CP,∠CPB=120°,
∵PB=DB=AG,
∴△CAG≌△CPB(SAS),
∴CG=CB,∠ACG=∠PCB,
∴∠GCB=60°,
∴△CBG是等边三角形,
∵GM=BM,
∴∠BCM=∠BCG=30°,
∴tan∠BCM=.
