第18章 平行四边形 习题课件 (共89张PPT) 2023—2024学年人教版数学八年级下册
文档属性
| 名称 | 第18章 平行四边形 习题课件 (共89张PPT) 2023—2024学年人教版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-15 09:43:16 | ||
图片预览




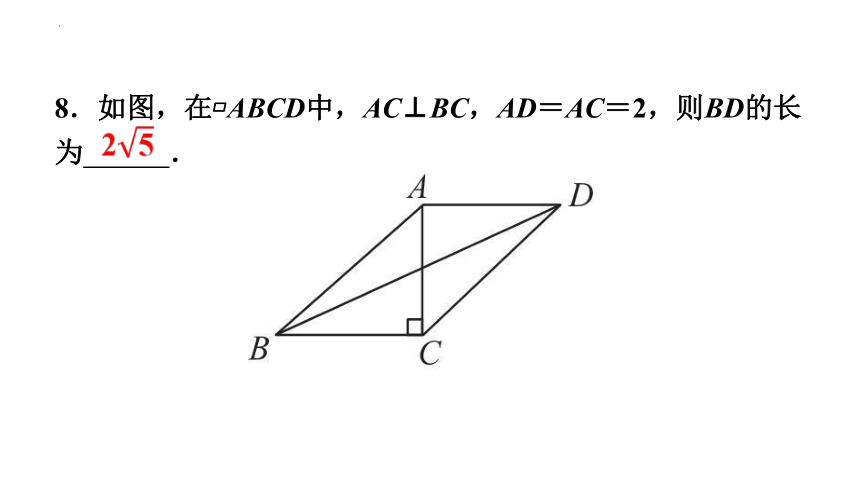

文档简介
(共89张PPT)
第1节 平行四边形的性质
1.平行四边形的周长为10 cm,其中一边长为3 cm,则它的邻边长为 ( )
A.2 cm B.3 cm
C.4 cm D.7 cm
A层 基础练
A
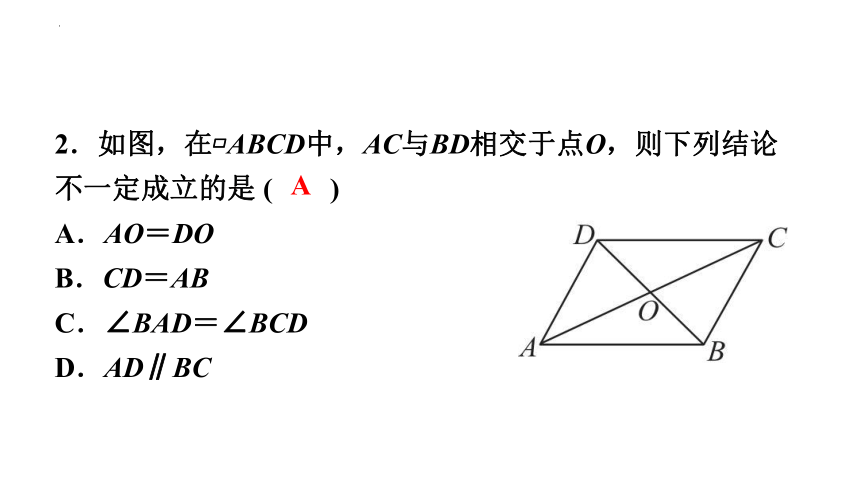
2.如图,在 ABCD中,AC与BD相交于点O,则下列结论不一定成立的是 ( )
A.AO=DO
B.CD=AB
C.∠BAD=∠BCD
D.AD∥BC
A
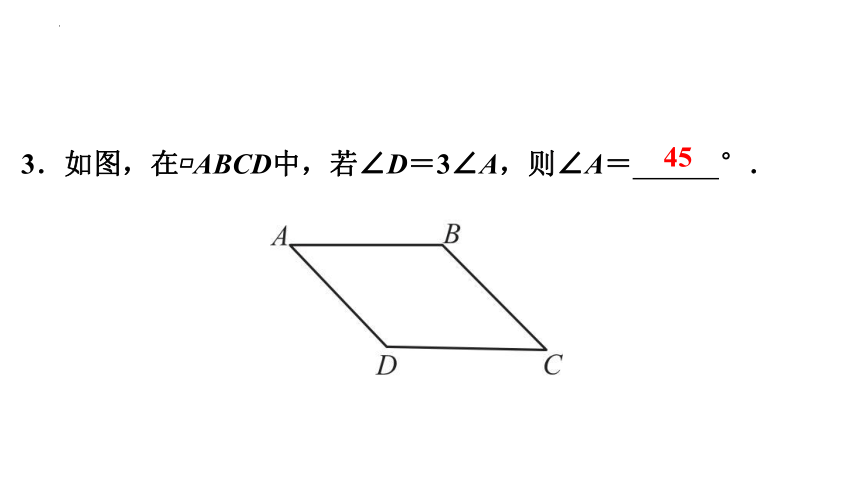
3.如图,在 ABCD中,若∠D=3∠A,则∠A= °.
45
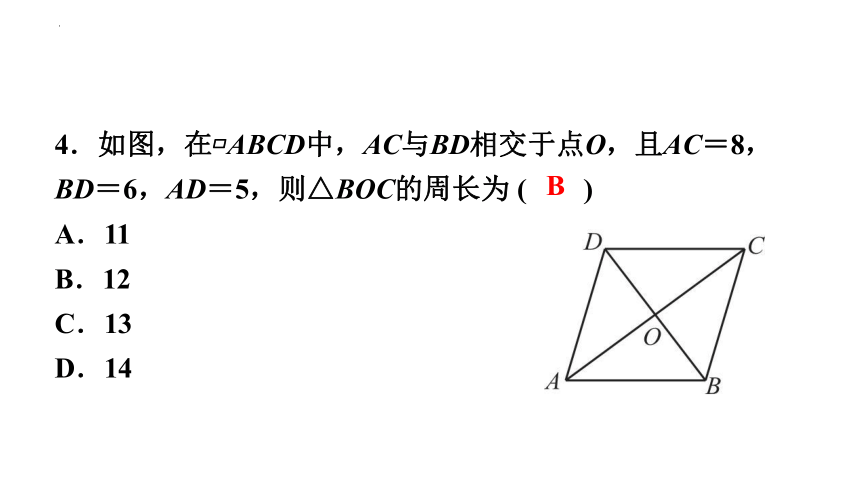
4.如图,在 ABCD中,AC与BD相交于点O,且AC=8,BD=6,AD=5,则△BOC的周长为 ( )
A.11
B.12
C.13
D.14
B
5.在 ABCD中,若∠A+∠C=100°,则∠D的度数为 ( )
A.100° B.130° C.140° D.150°
B
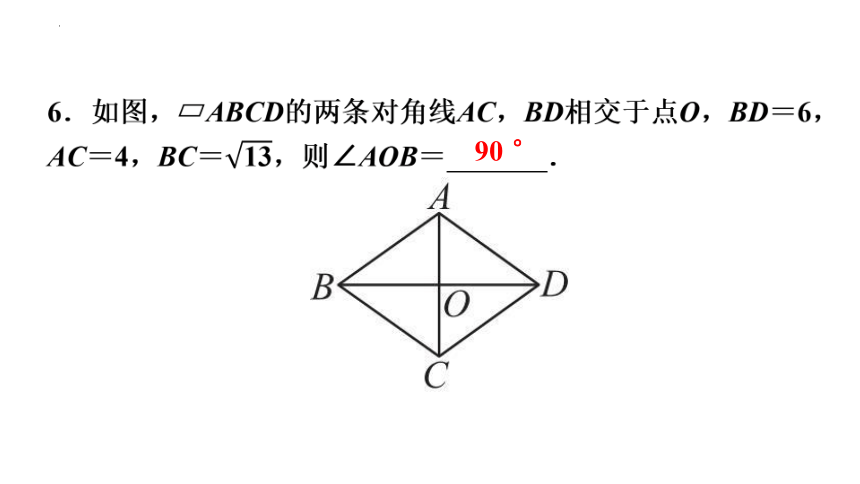
6.如图, ABCD的两条对角线AC,BD相交于点O,BD=6,AC=4,BC=,则∠AOB= .
90 °
7. ABCD的周长为28 cm,且AB∶BC=2∶5,那么AB=
cm,AD= cm.
10
4
8.如图,在 ABCD中,AC⊥BC,AD=AC=2,则BD的长为 .
2
9.如图,在 ABCD中,BE平分∠ABC交AD于点E,BC=4,DE=1,则 ABCD的周长是 .
14
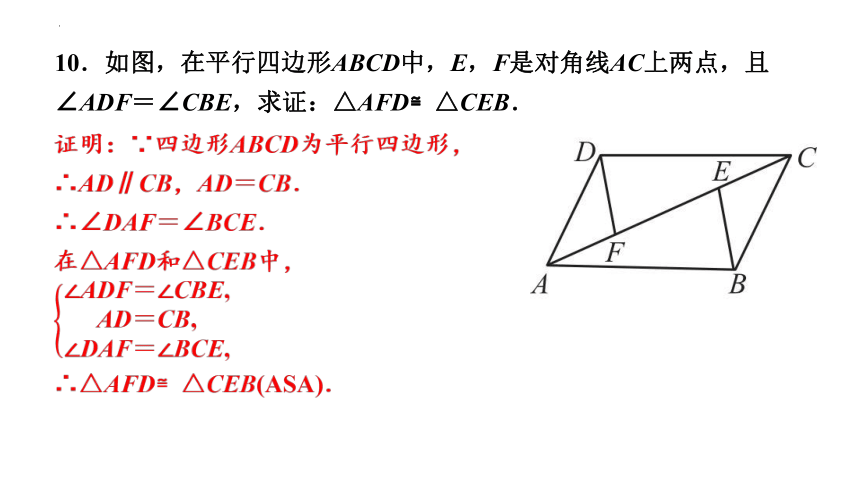
10.如图,在平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,求证:△AFD≌△CEB.
证明:∵四边形ABCD为平行四边形,
∴AD∥CB,AD=CB.
∴∠DAF=∠BCE.
在△AFD和△CEB中,
∴△AFD≌△CEB(ASA).
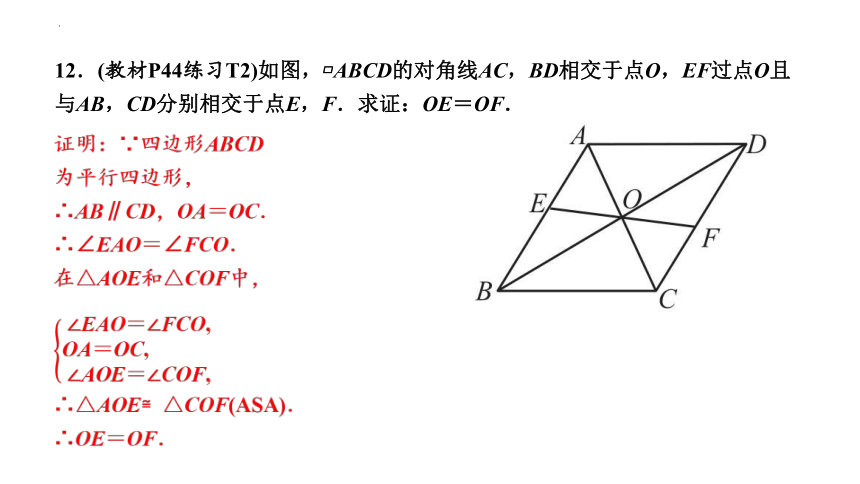
12.(教材P44练习T2)如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.求证:OE=OF.
证明:∵四边形ABCD
为平行四边形,
∴AB∥CD,OA=OC.
∴∠EAO=∠FCO.
在△AOE和△COF中,
∴△AOE≌△COF(ASA).
∴OE=OF.
B层 提升练
13.如图,在 ABCD中,M是CD的中点,AB=2BC,若BM=1,AM=2,则CD的长为 .
14.如图,在 ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点M,N,若△CON的面积为2,△DOM的面积为4,则△AOB的面积为 .
B层 提升练
6
15.如图, ABCD的顶点A,B,D的坐标分别是(2,0),
(-4,0),(0,3),则顶点C的坐标是___________.
(-6,3)
16.如图,在 ABCD中,分别以边BC,CD为腰作等腰三角形BCF和等腰三角形CDE,使BC=BF,CD=ED,∠CBF=∠CDE,连接AF,AE.
(2)延长AB与CF相交于点G,若AF⊥AE,求证:BF⊥BC.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠CBG=∠DAB.
∵△ABF≌△EDA,
∴∠AFB=∠EAD.
∴∠GBF=∠BAF+∠AFB=∠BAF+∠EAD.
∵AF⊥AE,
∴∠EAD+∠DAB+∠BAF=90°.
∴∠GBF+∠CBG=90°,即∠FBC=90°.
∴BF⊥BC.
C层 拓展练
17.如图,在 ABCD中,分别以边BC,CD为腰作等腰三角形BCF和等腰三角形CDE,使BC=BF,CD=ED,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,DA=BC,∠ABC=∠CDA.
又BC=BF,CD=ED,
∴AB=ED,BF=DA.
∵∠CBF=∠CDE,
∴360°-∠ABC-∠CBF=360°-∠CDA-∠CDE,
即∠ABF=∠EDA.
∴△ABF≌△EDA(SAS).
C层 拓展练
18.如图,已知在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,求AC的长.
解:过A,C两点分别作AD⊥l3于点D,CE⊥l3于点E.
由题意,得AD=3,CE=2+3=5.
∵AD⊥l3,∠ABC=90°,
∴∠DAB+∠ABD=90°,∠ABD+∠EBC=90°.
∴∠DAB=∠EBC.
又∠ADB=∠BEC=90°,AB=BC,
∴△ABD≌△BCE(AAS).
∴BD=CE=5.
在Rt△ABD中,∠ADB=90°,
由勾股定理,得AB2=AD2+BD2=32+52=34.
在Rt△ABC中,∠ABC=90°.
由勾股定理,得
AC==2.
答图
第十八章 平行四边形
第2节 平行四边形的判定
A.AB∥CD,AB=CD
B.AB=CD,AD=BC
C.∠B+∠DAB=180°,AB=CD
D.∠B=∠D,∠BCA=∠DAC
1.如图,下列给出的条件中,不能判定四边形ABCD是平行四边形的是 ( )
A层 基础练
C
2.下列不能判定四边形ABCD为平行四边形的条件是 ( )
A.AB∥CD,AD=BC
B.AB∥CD,∠A=∠C
C.AD∥BC,AD=BC
D.∠A=∠C,∠B=∠D
A
A.20°
B.45°
C.65°
D.70°
3.如图,M,N分别是△ABC的边AB,AC的中点,若∠A=65°,∠ANM=45°,则∠B= ( )
D
4.如图,在四边形ABCD中,OA=OC,BD=16 cm,则当OB= cm时,四边形ABCD是平行四边形.
8
5.如图,在△ABC中,AC=6 cm,BC=8 cm,AB=10 cm,D,E,F分别是AB,BC,CA的中点,则△EDF的周长是
cm.
12
6.如图,在四边形ABCD中,AC,BD相交于点O,请从给定的四个条件:①AB=CD;②AD∥BC;③∠BAD=∠BCD;④BO=DO中选择两个,使得构成的四边形可判定为平行四边形.你的选择是 .(填序号)
②③或②④
7.如图,四边形ABCD的对角线AC,BD交于点O,∠CAD=∠ACB,OA=OC,求证:四边形ABCD是平行四边形.
证明:在△AOD和△COB中,
∴△AOD≌△COB(ASA).
∴OD=OB.
∴四边形ABCD是平行四边形.
8.如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,求△BDC的面积.
解:∵E,F分别是AB,AD的中点,EF=2,
∴BD=2EF=4.
∵BD2+CD2=42+32=52,BC2=52,
∴BD2+CD2=BC2.
∴△BDC是直角三角形,∠BDC=90°.
∴S△BDC=BD·CD=×4×3=6.
9.如图,在 ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°.
∴∠ADE=∠CBF=60°.
∵AE=AD,CF=CB,
∴△AED,△CFB是等边三角形.
∴∠E=∠DAE=∠F=∠BCF=60°.
∴∠EAF=∠FCE=120°.
∴四边形AFCE是平行四边形.
10.如图,已知四边形ABCD中,CD⊥AC,AB⊥AC,垂足分别为C,A,AD=CB.
(1)求证:Rt△ACD≌Rt△CAB.
(2)求证:四边形ABCD是平行四边形.
证明:(1)在Rt△ACD和Rt△CAB中,
∴Rt△ACD≌Rt△CAB(HL).
(2)∵△ACD≌△CAB,
∴CD=AB.
又AD=CB,
∴四边形ABCD是平行四边形.
11.如图,在 ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠BAC=∠DCA.
又AE平分∠BAC,CF平分∠ACD,
∴∠EAC=∠BAC,∠ACF=∠DCA.
∴∠EAC=∠ACF.
∴AE∥CF.
∴四边形AECF是平行四边形.
12.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,若EF=4,则DE的长为 .
B层 提升练
2
13.如图,在 ABCD中,E,F分别是边AB,DC的中点,求证:EF=BC.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
又E,F分别是边AB,DC的中点,
∴BE=AB,CF=CD.
∴BE=CF.
∴四边形BCFE是平行四边形.
∴EF=BC.
14.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,且AE=CF,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO.
又∠AOE=∠COF,AE=CF,
∴△AEO≌△CFO(AAS).
∴AO=CO.
在△ABO和△CDO中,
∴△ABO≌△CDO(ASA).
∴AB=CD.
∵∠BAC=∠DCA,∴AB∥DC.
∴四边形ABCD是平行四边形.
15.如图,在△ABC中,AD是BC边的中线,F是AC上一点,且满足CF=2AF,连接BF与AD相交于点E.若G为线段BF上一动点,试分析当点G在何位置时,四边形AFDG为平行四边形?
解:当点G为线段BF的中点时,四边形AFDG为平行四边形.
理由如下:∵AD是BC边的中线,
∴BD=CD.
∵G为线段BF的中点,
∴DG是△BCF的中位线.
∴DG∥CF,DG=CF.
∵CF=2AF,
∴DG=AF.
∴四边形AFDG为平行四边形.
16.如图,在△ABC中,D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF.求证:四边形ADEF是平行四边形.
证明:∵D,E分别是边BC,AC的中点,
∴DE∥BF,DE=AB.
∵AF=AB,
∴DE=AF.
∴四边形ADEF是平行四边形.
17. 如图, ABCD的对角线AC,BD相交于点O.
E,F分别是OA,OC的中点.求证:BE∥DF.
证明:连接BF,DE.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
∴OE=OA,OF=OC.
∴OE=OF.
∴四边形BFDE是平行四边形.
∴BE∥DF.
答图
18.如图,在四边形ABCD中,M是边BC的中点,AM,BD互相平分并交于点O.求证:四边形AMCD是平行四边形.
证明:连接DM.
∵AM,BD互相平分,
∴四边形ABMD是平行四边形.
∴AD=BM,AD∥BM.
∵M是边BC的中点,
∴BM=CM.
∴AD=CM.
又AD∥CM,
∴四边形AMCD是平行四边形.
答图
C层 拓展练
19.如图,在四边形ABCD中,CD=,∠C=30°,M为AD的中点,动点P从点B出发沿BC向终点C运动,连接AP,DP,取AP的中点N,连接MN,则线段MN的最小值为
.
20.如图,平行四边形ABCD中,AB=8 cm,AD=12 cm.点P在AD边上以每秒1 cm的速度从点A向点D运动,点Q以每秒3 cm的速度从点D出发,沿DC,CB向点B运动,两个点同时出发,在运动多少秒时,以P,D,Q,B四点组成的四边形是平行四边形.
解:设运动时间为t秒.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=8 cm,BC=AD=12 cm.
当点Q在BC上,且PD=BQ时,以P,D,Q,B四点组成的四边形是平行四边形,则
12-t=12+8-3t,
解得t=4.
∴运动4秒时,以P,D,Q,B四点组成的四边形是平行四边形.
21.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD,CE相交于点O.求证:OB=2OD.
证明:分别取OB,OC的中点F,G,连接DE,EF,FG,GD.
∴FG∥BC,FG=BC.
又D,E分别是AC,AB的中点,
∴ED∥BC,ED=BC.
∴ED∥FG,ED=FG.
∴四边形DEFG是平行四边形.
∴OF=OD.
又OF=OB,
∴OB=2OD.
答图
22.如图,在 ABCD中,连接BD,点E,F在线段BD上,连接AE,EC,CF,FA.
(1)请你添加一个条件: ,使四边形AECF是平行四边形;(只填一个)
BE=DF(答案不唯一 )
(2)根据已知及(1)中你所添加的条件,求证:四边形AECF是平行四边形.
(2)证明:如图,连接AC,交BD于点O.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF,
∴BO-BE=DO-DF,即EO=FO.
∴四边形AECF是平行四边形.
答图
第十八章 平行四边形
第3节 矩形的性质和判定
A.4
B.4
C.2
D.2
1.如图,矩形ABCD的对角线AC,BD交于点O,AC=4,∠AOD=120°,则AB的长为 ( )
A层 基础练
D
A.∠ABC=90°
B.AC=BD
C.AD=AB
D.∠BAD=∠ADC
2.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件后,不能判定平行四边形ABCD为矩形的是 ( )
C
3.如图,在矩形ABCD中,O是对角线AC,BD的交点,E,F分别是OD,OC的中点.若AC=10,BC=6,则EF的长为
.
4
4.如图,在矩形ABCD中,E是AD上一点,F,G,H分别是BE,BC,CE的中点,若AF=3,则GH的长为 .
3
5.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的长.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=90°=∠B.
在△ABE和△DFA中,
∴△ABE≌△DFA(AAS).
∴DF=AB.
(2)解:∵∠FDC=30°,∠ADC=90°,
∴∠ADF=60°.
∴∠DAF=30°.
由(1)得,△ABE≌△DFA.
∴DF=AB=4.
∴AD=2DF=8.
6.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,且BE=DF,连接BF.求证:四边形BFDE是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
7.如图,在△ABC中,D,E,F分别是AC,AB,BC的中点,CE=BE.
(1)求证:四边形DCFE为平行四边形;
(2)求证:四边形DCFE为矩形.
证明:(1)∵D,E,F分别是AC,AB,BC的中点,
∴DE∥BC,EF∥AC.
∴四边形DCFE为平行四边形.
(2)∵D,E,F分别是AC,AB,BC的中点,
∴DF=AB=BE.
又CE=BE,
∴CE=DF.
∴平行四边形DCFE为矩形.
B层 提升练
8.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若AB=1,AC=2,则矩形AEFC的面积为
.
9.如图,在△ABC中,CD⊥AB,垂足为D,E为BC边的中点,AB=4,AC=2,DE=,则∠ACD的度数为 ( )
A.15°
B.30°
C.22.5°
D.45°
B
10.如图,矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,且∠CAE=15°.
(1)求证:△AOB为等边三角形;
(2)∠BOE的度数为 .
75°
(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,AC与BD相等且互相平分.
∴OA=OB.
又AE平分∠BAD,
∴∠BAE=∠BAD=45°.
∴∠BAO=∠BAE+∠CAE=60°.
∴△AOB为等边三角形.
11.如图,在平行四边形ABCD中,M,N分别是AD和BC的中点.若AC=CD,求证:四边形AMCN是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵M,N分别是AD和BC的中点,
∴AM=AD,CN=BC.
∴AM=CN.
∵AM∥CN,
∴四边形AMCN是平行四边形.
∵AC=CD,M是AD的中点,
∴CM⊥AD.∴∠AMC=90°.
∴平行四边形AMCN是矩形.
C层 拓展练
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,BC=2AB=8,P是BC上一点,PE⊥AC于点E,PF⊥BD于点F,
若m=PE+PF,则m的值为 .(提示:连接OP)
13.如图,在 ABCD中,对角线AC,BD相交于点O,E是 ABCD外一点,且∠AEC=∠BED=90°,求证:四边形ABCD是矩形.
证明:连接EO.
∵四边形ABCD是平行四边形,
∴O是AC,BD的中点.
∴在Rt△EBD中,EO=BD,
在Rt△AEC中,EO=AC.
∴AC=BD.
∴ ABCD是矩形.
答图
第十八章 平行四边形
第4节 菱形的性质和判定
1.如图,在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE= ( )
A.70° B.40°
C.75° D.30°
A层 基础练
A
2.如图,菱形ABCD的周长为36,且∠B=60°,AC的长为 .
9
3.如图,在菱形ABCD中,E,F分别在边AD,AB上,且DE=BF.求证:EC=FC.
证明:∵四边形ABCD为菱形,
∴∠D=∠B,CD=CB.
在△CDE和△CBF中,
∴△CDE≌△CBF(SAS).
∴EC=FC.
4.如图,在菱形ABCD中,对角线AC,BD交于点O,E为边AD的中点,OE=5,OB=8,求菱形ABCD的面积.
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
∴OD=8,BD=2OD=16.
∵E为AD的中点,
∴OE=AD.
∴ AD=2OE=10.
在Rt△OAD中,
OA==6.
∴AC=2OA=12.
∴S菱形ABCD=AC·BD=×12×16=96.
5.如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线,且BD⊥BC.求证:四边形BEDF是菱形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC.
∵BD⊥BC,
∴BD⊥AD.
∴∠ADB=90°.
∵E是AB的中点,
∴DE=AB=BE.
同理可得BF=CD=DF.
∴DE=BE=BF=DF.
∴四边形BEDF是菱形.
6.如图,在菱形ABCD中,点E,F在对角线AC上,且AE=CF.求证:四边形BEDF是菱形.
证明:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
又AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BEDF是平行四边形.
又EF⊥BD,
∴四边形BEDF是菱形.
7.如图,在菱形ABCD中,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是 ( )
A.BE=DF
B.∠BAE=∠DAF
C.AE=AD
D.∠AEB=∠AFD
B层 提升练
C
8.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF的度数为 .
60°
9.在平面直角坐标系内,点O是原点,点A的坐标是(3,4),点B的坐标是(3,-4),要使四边形AOBC是菱形,则满足条件的点C的坐标是 ( )
A.(-3,0) B.(3,0)
C.(6,0) D.(5,0)
C
10.如图,四边形ABCD的对角线相交于点O,且O是BD的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为 .
24
11.如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(2)当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(2)OE+OF的值不发生变化,理由如下:
如图,连接AO,
则S△ABD=S△ABO+S△ADO,
即BD·AG=AB·OE+AD·OF.
∴BD·AG=AB·OE+AD·OF,
即16×6=10·OE+10·OF,
解得OE+OF=9.6,是定值.
∴当点O在对角线BD上运动时,OE+OF的值不变.
答图
C层 拓展练
12.如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(1)求对角线AC的长;
解:(1)∵四边形ABCD是菱形,边长为10,对角线BD=16,
∴AB=10,AG=CG,
AC⊥BD,BG=BD=8.
由勾股定理,得AG==6.
∴AC=2AG=12.
13.如图,在△ABC中,点D是AB上一点,点E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.
(1)求证:△ADE≌△CFE;
(1)证明:∵CF∥AB,
∴∠ADE=∠CFE,∠DAE=∠FCE.
∵点E是AC的中点,
∴AE=CE.
在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
13.如图,在△ABC中,点D是AB上一点,点E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.
(2)连接AF,CD,如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形?证明你的结论.
(2)解:当AC⊥BC时,四边形ADCF是菱形,证明如下:
∵△ADE≌△CFE,∴AD=CF.
又AD∥CF,∴四边形ADCF是平行四边形.
∵点D,E分别是AB,AC的中点,
∴DF∥BC.
∵AC⊥BC,
∴AC⊥DF.
∴四边形ADCF是菱形.
第十八章 平行四边形
第5节 正方形的性质和判定
1.下列说法不正确的是 ( )
A.矩形的对角线相等且互相平分
B.菱形的对角线互相垂直平分
C.正方形的对角线相等且互相平分
D.平行四边形、矩形、菱形、正方形都是轴对称图形
A层 基础练
D
A.②③
B.②④
C.①②
D.①③
2.下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.从中选取两个作为补充条件,使 ABCD为正方形(如图).现有下列四种选法,其中错误的是
( )
A
3.如图,四边形ABCD是正方形,它的四个顶点都在坐标轴上,且正方形边的长为8,则点A的坐标为 ( )
A.(8,0)
B.(4,0)
C.(4,0)
D.(8,0)
C
4.满足下列条件的四边形是正方形的有 ( )
①对角线互相垂直且相等的平行四边形;
②对角线互相垂直的矩形;
③对角线相等的菱形;
④对角线互相垂直平分且相等的四边形.
A.①③④ B.①②④
C.②③④ D.①②③④
D
5.如图,在矩形纸片ABCD中,AB=3,点E在边BC上,
将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点
F处.若∠EAC=∠ECA,则AC的长是 ( )
A.3 B.6
C.4 D.5
B
6.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 cm2.
8
7.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处;将边CD沿CF折叠,使点D落在AC上的点N处,易证四边形AECF是平行四边形.要使四边形AECF是菱形,则∠BAE的度数是 .
30°
8.既是矩形又是菱形的四边形是 .
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件
,使矩形ABCD是正方形.
AB=AD(答案不唯一)
正方形
10.如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于点F,连接AF.求证:BF=EC.
证明:∵四边形ABCD是正方形,FE⊥AC,
∴∠ACB=45°,∠AEF=∠CEF=∠B=90°.
∴∠EFC=∠ACB=45°.
∴EF=EC.
在Rt△AFE和Rt△AFB中,
∴Rt△AFE≌Rt△AFB(HL).
∴BF=EF.
∴BF=EC.
11.如图,在正方形ABCD中,点E,F分别在BC,CD上,点A到EF的距离AG的长始终保持与AB的长相等,求证:∠EAF=45°.
证明:由题意,可知AB=AG,∠BAD=∠B=90°.
∵AG⊥EF,
∴∠AGE=90°.
又AE=AE,
∴Rt△ABE≌Rt△AGE(HL).
∴∠BAE=∠GAE.
同理Rt△ADF≌Rt△AGF(HL).
∴∠DAF=∠GAF.
∴∠EAF=∠GAE+∠GAF=∠BAG+∠DAG=∠BAD=45°.
12.如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
证明:∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD为矩形,
∴∠ABC=∠BCD=90°.
∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ECB=45°.
∴∠BEC=90°,BE=CE.
∴四边形BECF是正方形.
A.4个 B.3个 C.2个 D.1个
13.如图,点E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:
①AE=BF;②AE⊥BF;③AO=OE;
④.
其中正确的有 ( )
B层 提升练
B
14.如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(10,8).
(1)求CE的长;
(2)写出点E的坐标.
解:(1)∵四边形AOCD为矩形,D(10,8),
∴AD=OC=10,DC=AO=8.
由折叠可得AF=AD=10,DE=EF.
在Rt△AOF中,OF==6.
∴FC=10-6=4.
设CE=x,则DE=EF=8-x.
在Rt△CEF中,EF2=EC2+FC2,
即(8-x)2=x2+42,解得x=3.
即CE的长为3.
(2)∵OC=10,CE=3,
∴点E的坐标为(10,3).
15.如图,已知四边形ABCD是正方形,点E,F分别在AD,DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,H为BF的中点,连接GH.求GH的长.
(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=DA.
在Rt△ABE和Rt△DAF中,
∴Rt△ABE≌Rt△DAF(HL).
(2)证明:∵Rt△ABE≌Rt△DAF,∴∠ABE=∠DAF.
∵∠ABE+∠BEA=90°,∴∠DAF+∠BEA=90°.
∴∠AGE=90°.
∴BE⊥AF.
(3)解:∵BE⊥AF,H为BF的中点,
∴GH=BF.
∵△ABE≌△DAF,
∴DF=AE=2.
在Rt△BCF中,
BC=5,CF=CD-DF=5-2=3.
根据勾股定理,得BF=.
∴GH=
16.如图,在Rt△ABC中,E是两锐角的平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
证明:过点E作EM⊥AB于点M.
∵ED⊥BC,EF⊥AC,∠C是直角,
∴∠CFE=∠CDE=∠C=90°.
∴四边形CDEF是矩形.
∵AE,BE分别平分∠CAB,∠CBA,
∴EF=EM,EM=ED.
∴EF=ED.
∴四边形CDEF是正方形.
答图
C层 拓展练
17.如图,在边长为4的正方形ABCD中,E,F分别是AB,BC的中点,连接CE,DF,G,H分别是CE,DF的中点,连接GH,则GH的长为 .
18.如图,在矩形纸片ABCD中,AB=12,AD=5,点P为DC边上的动点(点P不与点D,C重合),将纸片沿AP折叠,点D落在点D'处,则CD'的最小值为 .
8
19.如图,在平行四边形ABCD中,F是对角线的交点,E是边BC的中点,连接EF.
(1)求证:2EF=CD;
(2)当EF与BC满足什么关系时,四边形ABCD是正方形?并证明你的结论.
(1)证明:∵四边形ABCD是平行四边形,
∴BF=FD.
又E是边BC的中点,
∴EF是△BCD的中位线.
∴2EF=CD.
(2)解:当EF⊥BC,且BC=2EF时,四边形ABCD是正方形.证明如下:
∵EF⊥BC,E是BC的中点,
∴EF垂直平分BC.
∴FB=FC.
∵四边形ABCD是平行四边形,
∴FB=FD,FA=FC.
∴FB=FC=FD=FA.
∴四边形ABCD是矩形.
∵BC=2EF,CD=2EF,
∴BC=CD.
∴四边形ABCD是正方形.
第1节 平行四边形的性质
1.平行四边形的周长为10 cm,其中一边长为3 cm,则它的邻边长为 ( )
A.2 cm B.3 cm
C.4 cm D.7 cm
A层 基础练
A
2.如图,在 ABCD中,AC与BD相交于点O,则下列结论不一定成立的是 ( )
A.AO=DO
B.CD=AB
C.∠BAD=∠BCD
D.AD∥BC
A
3.如图,在 ABCD中,若∠D=3∠A,则∠A= °.
45
4.如图,在 ABCD中,AC与BD相交于点O,且AC=8,BD=6,AD=5,则△BOC的周长为 ( )
A.11
B.12
C.13
D.14
B
5.在 ABCD中,若∠A+∠C=100°,则∠D的度数为 ( )
A.100° B.130° C.140° D.150°
B
6.如图, ABCD的两条对角线AC,BD相交于点O,BD=6,AC=4,BC=,则∠AOB= .
90 °
7. ABCD的周长为28 cm,且AB∶BC=2∶5,那么AB=
cm,AD= cm.
10
4
8.如图,在 ABCD中,AC⊥BC,AD=AC=2,则BD的长为 .
2
9.如图,在 ABCD中,BE平分∠ABC交AD于点E,BC=4,DE=1,则 ABCD的周长是 .
14
10.如图,在平行四边形ABCD中,E,F是对角线AC上两点,且∠ADF=∠CBE,求证:△AFD≌△CEB.
证明:∵四边形ABCD为平行四边形,
∴AD∥CB,AD=CB.
∴∠DAF=∠BCE.
在△AFD和△CEB中,
∴△AFD≌△CEB(ASA).
12.(教材P44练习T2)如图, ABCD的对角线AC,BD相交于点O,EF过点O且与AB,CD分别相交于点E,F.求证:OE=OF.
证明:∵四边形ABCD
为平行四边形,
∴AB∥CD,OA=OC.
∴∠EAO=∠FCO.
在△AOE和△COF中,
∴△AOE≌△COF(ASA).
∴OE=OF.
B层 提升练
13.如图,在 ABCD中,M是CD的中点,AB=2BC,若BM=1,AM=2,则CD的长为 .
14.如图,在 ABCD中,对角线AC,BD相交于点O,过点O的直线分别交AD,BC于点M,N,若△CON的面积为2,△DOM的面积为4,则△AOB的面积为 .
B层 提升练
6
15.如图, ABCD的顶点A,B,D的坐标分别是(2,0),
(-4,0),(0,3),则顶点C的坐标是___________.
(-6,3)
16.如图,在 ABCD中,分别以边BC,CD为腰作等腰三角形BCF和等腰三角形CDE,使BC=BF,CD=ED,∠CBF=∠CDE,连接AF,AE.
(2)延长AB与CF相交于点G,若AF⊥AE,求证:BF⊥BC.
(2)∵四边形ABCD是平行四边形,
∴AD∥BC.
∴∠CBG=∠DAB.
∵△ABF≌△EDA,
∴∠AFB=∠EAD.
∴∠GBF=∠BAF+∠AFB=∠BAF+∠EAD.
∵AF⊥AE,
∴∠EAD+∠DAB+∠BAF=90°.
∴∠GBF+∠CBG=90°,即∠FBC=90°.
∴BF⊥BC.
C层 拓展练
17.如图,在 ABCD中,分别以边BC,CD为腰作等腰三角形BCF和等腰三角形CDE,使BC=BF,CD=ED,∠CBF=∠CDE,连接AF,AE.
(1)求证:△ABF≌△EDA;
证明:(1)∵四边形ABCD是平行四边形,
∴AB=CD,DA=BC,∠ABC=∠CDA.
又BC=BF,CD=ED,
∴AB=ED,BF=DA.
∵∠CBF=∠CDE,
∴360°-∠ABC-∠CBF=360°-∠CDA-∠CDE,
即∠ABF=∠EDA.
∴△ABF≌△EDA(SAS).
C层 拓展练
18.如图,已知在△ABC中,∠ABC=90°,AB=BC,三角形的顶点在相互平行的三条直线l1,l2,l3上,且l1,l2之间的距离为2,l2,l3之间的距离为3,求AC的长.
解:过A,C两点分别作AD⊥l3于点D,CE⊥l3于点E.
由题意,得AD=3,CE=2+3=5.
∵AD⊥l3,∠ABC=90°,
∴∠DAB+∠ABD=90°,∠ABD+∠EBC=90°.
∴∠DAB=∠EBC.
又∠ADB=∠BEC=90°,AB=BC,
∴△ABD≌△BCE(AAS).
∴BD=CE=5.
在Rt△ABD中,∠ADB=90°,
由勾股定理,得AB2=AD2+BD2=32+52=34.
在Rt△ABC中,∠ABC=90°.
由勾股定理,得
AC==2.
答图
第十八章 平行四边形
第2节 平行四边形的判定
A.AB∥CD,AB=CD
B.AB=CD,AD=BC
C.∠B+∠DAB=180°,AB=CD
D.∠B=∠D,∠BCA=∠DAC
1.如图,下列给出的条件中,不能判定四边形ABCD是平行四边形的是 ( )
A层 基础练
C
2.下列不能判定四边形ABCD为平行四边形的条件是 ( )
A.AB∥CD,AD=BC
B.AB∥CD,∠A=∠C
C.AD∥BC,AD=BC
D.∠A=∠C,∠B=∠D
A
A.20°
B.45°
C.65°
D.70°
3.如图,M,N分别是△ABC的边AB,AC的中点,若∠A=65°,∠ANM=45°,则∠B= ( )
D
4.如图,在四边形ABCD中,OA=OC,BD=16 cm,则当OB= cm时,四边形ABCD是平行四边形.
8
5.如图,在△ABC中,AC=6 cm,BC=8 cm,AB=10 cm,D,E,F分别是AB,BC,CA的中点,则△EDF的周长是
cm.
12
6.如图,在四边形ABCD中,AC,BD相交于点O,请从给定的四个条件:①AB=CD;②AD∥BC;③∠BAD=∠BCD;④BO=DO中选择两个,使得构成的四边形可判定为平行四边形.你的选择是 .(填序号)
②③或②④
7.如图,四边形ABCD的对角线AC,BD交于点O,∠CAD=∠ACB,OA=OC,求证:四边形ABCD是平行四边形.
证明:在△AOD和△COB中,
∴△AOD≌△COB(ASA).
∴OD=OB.
∴四边形ABCD是平行四边形.
8.如图,在四边形ABCD中,E,F分别是AB,AD的中点,若EF=2,BC=5,CD=3,求△BDC的面积.
解:∵E,F分别是AB,AD的中点,EF=2,
∴BD=2EF=4.
∵BD2+CD2=42+32=52,BC2=52,
∴BD2+CD2=BC2.
∴△BDC是直角三角形,∠BDC=90°.
∴S△BDC=BD·CD=×4×3=6.
9.如图,在 ABCD中,∠DAB=60°,点E,F分别在CD,AB的延长线上,且AE=AD,CF=CB.求证:四边形AFCE是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴DC∥AB,∠DCB=∠DAB=60°.
∴∠ADE=∠CBF=60°.
∵AE=AD,CF=CB,
∴△AED,△CFB是等边三角形.
∴∠E=∠DAE=∠F=∠BCF=60°.
∴∠EAF=∠FCE=120°.
∴四边形AFCE是平行四边形.
10.如图,已知四边形ABCD中,CD⊥AC,AB⊥AC,垂足分别为C,A,AD=CB.
(1)求证:Rt△ACD≌Rt△CAB.
(2)求证:四边形ABCD是平行四边形.
证明:(1)在Rt△ACD和Rt△CAB中,
∴Rt△ACD≌Rt△CAB(HL).
(2)∵△ACD≌△CAB,
∴CD=AB.
又AD=CB,
∴四边形ABCD是平行四边形.
11.如图,在 ABCD中,AE平分∠BAC交BC于点E,CF平分∠ACD交AD于点F.求证:四边形AECF是平行四边形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AB∥CD.
∴∠BAC=∠DCA.
又AE平分∠BAC,CF平分∠ACD,
∴∠EAC=∠BAC,∠ACF=∠DCA.
∴∠EAC=∠ACF.
∴AE∥CF.
∴四边形AECF是平行四边形.
12.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D,E分别是边AB,AC的中点,延长BC到点F,使CF=BC,若EF=4,则DE的长为 .
B层 提升练
2
13.如图,在 ABCD中,E,F分别是边AB,DC的中点,求证:EF=BC.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD.
又E,F分别是边AB,DC的中点,
∴BE=AB,CF=CD.
∴BE=CF.
∴四边形BCFE是平行四边形.
∴EF=BC.
14.如图,在四边形ABCD中,AE⊥BD,CF⊥BD,且AE=CF,∠BAC=∠DCA.求证:四边形ABCD是平行四边形.
证明:∵AE⊥BD,CF⊥BD,
∴∠AEO=∠CFO.
又∠AOE=∠COF,AE=CF,
∴△AEO≌△CFO(AAS).
∴AO=CO.
在△ABO和△CDO中,
∴△ABO≌△CDO(ASA).
∴AB=CD.
∵∠BAC=∠DCA,∴AB∥DC.
∴四边形ABCD是平行四边形.
15.如图,在△ABC中,AD是BC边的中线,F是AC上一点,且满足CF=2AF,连接BF与AD相交于点E.若G为线段BF上一动点,试分析当点G在何位置时,四边形AFDG为平行四边形?
解:当点G为线段BF的中点时,四边形AFDG为平行四边形.
理由如下:∵AD是BC边的中线,
∴BD=CD.
∵G为线段BF的中点,
∴DG是△BCF的中位线.
∴DG∥CF,DG=CF.
∵CF=2AF,
∴DG=AF.
∴四边形AFDG为平行四边形.
16.如图,在△ABC中,D,E分别是边BC,AC的中点,连接DE,AD,点F在BA的延长线上,且AF=AB,连接EF.求证:四边形ADEF是平行四边形.
证明:∵D,E分别是边BC,AC的中点,
∴DE∥BF,DE=AB.
∵AF=AB,
∴DE=AF.
∴四边形ADEF是平行四边形.
17. 如图, ABCD的对角线AC,BD相交于点O.
E,F分别是OA,OC的中点.求证:BE∥DF.
证明:连接BF,DE.
∵四边形ABCD是平行四边形,
∴OA=OC,OB=OD.
∵E,F分别是OA,OC的中点,
∴OE=OA,OF=OC.
∴OE=OF.
∴四边形BFDE是平行四边形.
∴BE∥DF.
答图
18.如图,在四边形ABCD中,M是边BC的中点,AM,BD互相平分并交于点O.求证:四边形AMCD是平行四边形.
证明:连接DM.
∵AM,BD互相平分,
∴四边形ABMD是平行四边形.
∴AD=BM,AD∥BM.
∵M是边BC的中点,
∴BM=CM.
∴AD=CM.
又AD∥CM,
∴四边形AMCD是平行四边形.
答图
C层 拓展练
19.如图,在四边形ABCD中,CD=,∠C=30°,M为AD的中点,动点P从点B出发沿BC向终点C运动,连接AP,DP,取AP的中点N,连接MN,则线段MN的最小值为
.
20.如图,平行四边形ABCD中,AB=8 cm,AD=12 cm.点P在AD边上以每秒1 cm的速度从点A向点D运动,点Q以每秒3 cm的速度从点D出发,沿DC,CB向点B运动,两个点同时出发,在运动多少秒时,以P,D,Q,B四点组成的四边形是平行四边形.
解:设运动时间为t秒.
∵四边形ABCD是平行四边形,
∴AD∥BC,CD=AB=8 cm,BC=AD=12 cm.
当点Q在BC上,且PD=BQ时,以P,D,Q,B四点组成的四边形是平行四边形,则
12-t=12+8-3t,
解得t=4.
∴运动4秒时,以P,D,Q,B四点组成的四边形是平行四边形.
21.如图,在△ABC中,BD,CE分别是边AC,AB上的中线,BD,CE相交于点O.求证:OB=2OD.
证明:分别取OB,OC的中点F,G,连接DE,EF,FG,GD.
∴FG∥BC,FG=BC.
又D,E分别是AC,AB的中点,
∴ED∥BC,ED=BC.
∴ED∥FG,ED=FG.
∴四边形DEFG是平行四边形.
∴OF=OD.
又OF=OB,
∴OB=2OD.
答图
22.如图,在 ABCD中,连接BD,点E,F在线段BD上,连接AE,EC,CF,FA.
(1)请你添加一个条件: ,使四边形AECF是平行四边形;(只填一个)
BE=DF(答案不唯一 )
(2)根据已知及(1)中你所添加的条件,求证:四边形AECF是平行四边形.
(2)证明:如图,连接AC,交BD于点O.
∵四边形ABCD是平行四边形,
∴AO=CO,BO=DO.
∵BE=DF,
∴BO-BE=DO-DF,即EO=FO.
∴四边形AECF是平行四边形.
答图
第十八章 平行四边形
第3节 矩形的性质和判定
A.4
B.4
C.2
D.2
1.如图,矩形ABCD的对角线AC,BD交于点O,AC=4,∠AOD=120°,则AB的长为 ( )
A层 基础练
D
A.∠ABC=90°
B.AC=BD
C.AD=AB
D.∠BAD=∠ADC
2.如图,在 ABCD中,对角线AC,BD相交于点O,添加下列条件后,不能判定平行四边形ABCD为矩形的是 ( )
C
3.如图,在矩形ABCD中,O是对角线AC,BD的交点,E,F分别是OD,OC的中点.若AC=10,BC=6,则EF的长为
.
4
4.如图,在矩形ABCD中,E是AD上一点,F,G,H分别是BE,BC,CE的中点,若AF=3,则GH的长为 .
3
5.如图,在矩形ABCD中,点E在BC边上,AE=AD,DF⊥AE,垂足为F.
(1)求证:DF=AB;
(2)若∠FDC=30°,且AB=4,求AD的长.
(1)证明:∵四边形ABCD是矩形,
∴AD∥BC.
∴∠DAF=∠AEB.
∵DF⊥AE,
∴∠AFD=90°=∠B.
在△ABE和△DFA中,
∴△ABE≌△DFA(AAS).
∴DF=AB.
(2)解:∵∠FDC=30°,∠ADC=90°,
∴∠ADF=60°.
∴∠DAF=30°.
由(1)得,△ABE≌△DFA.
∴DF=AB=4.
∴AD=2DF=8.
6.如图,在 ABCD中,过点D作DE⊥AB于点E,点F在边CD上,且BE=DF,连接BF.求证:四边形BFDE是矩形.
证明:∵四边形ABCD是平行四边形,
∴AB∥CD.
∵BE∥DF,BE=DF,
∴四边形BFDE是平行四边形.
∵DE⊥AB,
∴∠DEB=90°.
∴四边形BFDE是矩形.
7.如图,在△ABC中,D,E,F分别是AC,AB,BC的中点,CE=BE.
(1)求证:四边形DCFE为平行四边形;
(2)求证:四边形DCFE为矩形.
证明:(1)∵D,E,F分别是AC,AB,BC的中点,
∴DE∥BC,EF∥AC.
∴四边形DCFE为平行四边形.
(2)∵D,E,F分别是AC,AB,BC的中点,
∴DF=AB=BE.
又CE=BE,
∴CE=DF.
∴平行四边形DCFE为矩形.
B层 提升练
8.如图,四边形ABCD和四边形AEFC是两个矩形,点B在EF边上,若AB=1,AC=2,则矩形AEFC的面积为
.
9.如图,在△ABC中,CD⊥AB,垂足为D,E为BC边的中点,AB=4,AC=2,DE=,则∠ACD的度数为 ( )
A.15°
B.30°
C.22.5°
D.45°
B
10.如图,矩形ABCD中,AC,BD相交于点O,AE平分∠BAD交BC于点E,且∠CAE=15°.
(1)求证:△AOB为等边三角形;
(2)∠BOE的度数为 .
75°
(1)证明:∵四边形ABCD是矩形,
∴∠BAD=90°,AC与BD相等且互相平分.
∴OA=OB.
又AE平分∠BAD,
∴∠BAE=∠BAD=45°.
∴∠BAO=∠BAE+∠CAE=60°.
∴△AOB为等边三角形.
11.如图,在平行四边形ABCD中,M,N分别是AD和BC的中点.若AC=CD,求证:四边形AMCN是矩形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC.
∵M,N分别是AD和BC的中点,
∴AM=AD,CN=BC.
∴AM=CN.
∵AM∥CN,
∴四边形AMCN是平行四边形.
∵AC=CD,M是AD的中点,
∴CM⊥AD.∴∠AMC=90°.
∴平行四边形AMCN是矩形.
C层 拓展练
12.如图,在矩形ABCD中,对角线AC,BD相交于点O,BC=2AB=8,P是BC上一点,PE⊥AC于点E,PF⊥BD于点F,
若m=PE+PF,则m的值为 .(提示:连接OP)
13.如图,在 ABCD中,对角线AC,BD相交于点O,E是 ABCD外一点,且∠AEC=∠BED=90°,求证:四边形ABCD是矩形.
证明:连接EO.
∵四边形ABCD是平行四边形,
∴O是AC,BD的中点.
∴在Rt△EBD中,EO=BD,
在Rt△AEC中,EO=AC.
∴AC=BD.
∴ ABCD是矩形.
答图
第十八章 平行四边形
第4节 菱形的性质和判定
1.如图,在菱形ABCD中,∠ABC=80°,BA=BE,则∠BAE= ( )
A.70° B.40°
C.75° D.30°
A层 基础练
A
2.如图,菱形ABCD的周长为36,且∠B=60°,AC的长为 .
9
3.如图,在菱形ABCD中,E,F分别在边AD,AB上,且DE=BF.求证:EC=FC.
证明:∵四边形ABCD为菱形,
∴∠D=∠B,CD=CB.
在△CDE和△CBF中,
∴△CDE≌△CBF(SAS).
∴EC=FC.
4.如图,在菱形ABCD中,对角线AC,BD交于点O,E为边AD的中点,OE=5,OB=8,求菱形ABCD的面积.
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
∴OD=8,BD=2OD=16.
∵E为AD的中点,
∴OE=AD.
∴ AD=2OE=10.
在Rt△OAD中,
OA==6.
∴AC=2OA=12.
∴S菱形ABCD=AC·BD=×12×16=96.
5.如图,在 ABCD中,E,F分别为边AB,CD的中点,BD是对角线,且BD⊥BC.求证:四边形BEDF是菱形.
证明:∵四边形ABCD是平行四边形,
∴AB=CD,AD∥BC.
∵BD⊥BC,
∴BD⊥AD.
∴∠ADB=90°.
∵E是AB的中点,
∴DE=AB=BE.
同理可得BF=CD=DF.
∴DE=BE=BF=DF.
∴四边形BEDF是菱形.
6.如图,在菱形ABCD中,点E,F在对角线AC上,且AE=CF.求证:四边形BEDF是菱形.
证明:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD.
又AE=CF,
∴OA-AE=OC-CF,即OE=OF.
∴四边形BEDF是平行四边形.
又EF⊥BD,
∴四边形BEDF是菱形.
7.如图,在菱形ABCD中,点E,F分别在BC,DC边上,添加以下条件不能判定△ABE≌△ADF的是 ( )
A.BE=DF
B.∠BAE=∠DAF
C.AE=AD
D.∠AEB=∠AFD
B层 提升练
C
8.如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,垂足为E,连接DF,则∠CDF的度数为 .
60°
9.在平面直角坐标系内,点O是原点,点A的坐标是(3,4),点B的坐标是(3,-4),要使四边形AOBC是菱形,则满足条件的点C的坐标是 ( )
A.(-3,0) B.(3,0)
C.(6,0) D.(5,0)
C
10.如图,四边形ABCD的对角线相交于点O,且O是BD的中点.若AB=AD=5,BD=8,∠ABD=∠CDB,则四边形ABCD的面积为 .
24
11.如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(2)当点O在对角线BD上运动时,OE+OF的值是否发生变化?请说明理由.
(2)OE+OF的值不发生变化,理由如下:
如图,连接AO,
则S△ABD=S△ABO+S△ADO,
即BD·AG=AB·OE+AD·OF.
∴BD·AG=AB·OE+AD·OF,
即16×6=10·OE+10·OF,
解得OE+OF=9.6,是定值.
∴当点O在对角线BD上运动时,OE+OF的值不变.
答图
C层 拓展练
12.如图,在边长为10的菱形ABCD中,对角线BD=16,对角线AC,BD相交于点G,点O是直线BD上的动点,OE⊥AB于点E,OF⊥AD于点F.
(1)求对角线AC的长;
解:(1)∵四边形ABCD是菱形,边长为10,对角线BD=16,
∴AB=10,AG=CG,
AC⊥BD,BG=BD=8.
由勾股定理,得AG==6.
∴AC=2AG=12.
13.如图,在△ABC中,点D是AB上一点,点E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.
(1)求证:△ADE≌△CFE;
(1)证明:∵CF∥AB,
∴∠ADE=∠CFE,∠DAE=∠FCE.
∵点E是AC的中点,
∴AE=CE.
在△ADE与△CFE中,
∴△ADE≌△CFE(AAS).
13.如图,在△ABC中,点D是AB上一点,点E是AC的中点,过点C作CF∥AB,交DE的延长线于点F.
(2)连接AF,CD,如果点D是AB的中点,那么当AC与BC满足什么条件时,四边形ADCF是菱形?证明你的结论.
(2)解:当AC⊥BC时,四边形ADCF是菱形,证明如下:
∵△ADE≌△CFE,∴AD=CF.
又AD∥CF,∴四边形ADCF是平行四边形.
∵点D,E分别是AB,AC的中点,
∴DF∥BC.
∵AC⊥BC,
∴AC⊥DF.
∴四边形ADCF是菱形.
第十八章 平行四边形
第5节 正方形的性质和判定
1.下列说法不正确的是 ( )
A.矩形的对角线相等且互相平分
B.菱形的对角线互相垂直平分
C.正方形的对角线相等且互相平分
D.平行四边形、矩形、菱形、正方形都是轴对称图形
A层 基础练
D
A.②③
B.②④
C.①②
D.①③
2.下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.从中选取两个作为补充条件,使 ABCD为正方形(如图).现有下列四种选法,其中错误的是
( )
A
3.如图,四边形ABCD是正方形,它的四个顶点都在坐标轴上,且正方形边的长为8,则点A的坐标为 ( )
A.(8,0)
B.(4,0)
C.(4,0)
D.(8,0)
C
4.满足下列条件的四边形是正方形的有 ( )
①对角线互相垂直且相等的平行四边形;
②对角线互相垂直的矩形;
③对角线相等的菱形;
④对角线互相垂直平分且相等的四边形.
A.①③④ B.①②④
C.②③④ D.①②③④
D
5.如图,在矩形纸片ABCD中,AB=3,点E在边BC上,
将△ABE沿直线AE折叠,点B恰好落在对角线AC上的点
F处.若∠EAC=∠ECA,则AC的长是 ( )
A.3 B.6
C.4 D.5
B
6.如图,正方形ABCD的边长为4 cm,则图中阴影部分的面积为 cm2.
8
7.如图,AC为矩形ABCD的对角线,将边AB沿AE折叠,使点B落在AC上的点M处;将边CD沿CF折叠,使点D落在AC上的点N处,易证四边形AECF是平行四边形.要使四边形AECF是菱形,则∠BAE的度数是 .
30°
8.既是矩形又是菱形的四边形是 .
9.如图,在矩形ABCD中,对角线AC,BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件
,使矩形ABCD是正方形.
AB=AD(答案不唯一)
正方形
10.如图,E是正方形ABCD对角线AC上一点,且AE=AB,EF⊥AC,交BC于点F,连接AF.求证:BF=EC.
证明:∵四边形ABCD是正方形,FE⊥AC,
∴∠ACB=45°,∠AEF=∠CEF=∠B=90°.
∴∠EFC=∠ACB=45°.
∴EF=EC.
在Rt△AFE和Rt△AFB中,
∴Rt△AFE≌Rt△AFB(HL).
∴BF=EF.
∴BF=EC.
11.如图,在正方形ABCD中,点E,F分别在BC,CD上,点A到EF的距离AG的长始终保持与AB的长相等,求证:∠EAF=45°.
证明:由题意,可知AB=AG,∠BAD=∠B=90°.
∵AG⊥EF,
∴∠AGE=90°.
又AE=AE,
∴Rt△ABE≌Rt△AGE(HL).
∴∠BAE=∠GAE.
同理Rt△ADF≌Rt△AGF(HL).
∴∠DAF=∠GAF.
∴∠EAF=∠GAE+∠GAF=∠BAG+∠DAG=∠BAD=45°.
12.如图,在矩形ABCD中,BE平分∠ABC,CE平分∠DCB,BF∥CE,CF∥BE.求证:四边形BECF是正方形.
证明:∵BF∥CE,CF∥BE,
∴四边形BECF是平行四边形.
∵四边形ABCD为矩形,
∴∠ABC=∠BCD=90°.
∵BE平分∠ABC,CE平分∠DCB,
∴∠EBC=∠ECB=45°.
∴∠BEC=90°,BE=CE.
∴四边形BECF是正方形.
A.4个 B.3个 C.2个 D.1个
13.如图,点E,F分别是正方形ABCD的边CD,AD上的点,且CE=DF,AE,BF相交于点O,下列结论:
①AE=BF;②AE⊥BF;③AO=OE;
④.
其中正确的有 ( )
B层 提升练
B
14.如图,在平面直角坐标系中,将矩形AOCD沿直线AE折叠(点E在边DC上),折叠后顶点D恰好落在边OC上的点F处,若点D的坐标为(10,8).
(1)求CE的长;
(2)写出点E的坐标.
解:(1)∵四边形AOCD为矩形,D(10,8),
∴AD=OC=10,DC=AO=8.
由折叠可得AF=AD=10,DE=EF.
在Rt△AOF中,OF==6.
∴FC=10-6=4.
设CE=x,则DE=EF=8-x.
在Rt△CEF中,EF2=EC2+FC2,
即(8-x)2=x2+42,解得x=3.
即CE的长为3.
(2)∵OC=10,CE=3,
∴点E的坐标为(10,3).
15.如图,已知四边形ABCD是正方形,点E,F分别在AD,DC上,BE与AF相交于点G,且BE=AF.
(1)求证:△ABE≌△DAF;
(2)求证:BE⊥AF;
(3)如果正方形ABCD的边长为5,AE=2,H为BF的中点,连接GH.求GH的长.
(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠D=90°,AB=DA.
在Rt△ABE和Rt△DAF中,
∴Rt△ABE≌Rt△DAF(HL).
(2)证明:∵Rt△ABE≌Rt△DAF,∴∠ABE=∠DAF.
∵∠ABE+∠BEA=90°,∴∠DAF+∠BEA=90°.
∴∠AGE=90°.
∴BE⊥AF.
(3)解:∵BE⊥AF,H为BF的中点,
∴GH=BF.
∵△ABE≌△DAF,
∴DF=AE=2.
在Rt△BCF中,
BC=5,CF=CD-DF=5-2=3.
根据勾股定理,得BF=.
∴GH=
16.如图,在Rt△ABC中,E是两锐角的平分线的交点,ED⊥BC,EF⊥AC,垂足分别为D,F,求证:四边形CDEF是正方形.
证明:过点E作EM⊥AB于点M.
∵ED⊥BC,EF⊥AC,∠C是直角,
∴∠CFE=∠CDE=∠C=90°.
∴四边形CDEF是矩形.
∵AE,BE分别平分∠CAB,∠CBA,
∴EF=EM,EM=ED.
∴EF=ED.
∴四边形CDEF是正方形.
答图
C层 拓展练
17.如图,在边长为4的正方形ABCD中,E,F分别是AB,BC的中点,连接CE,DF,G,H分别是CE,DF的中点,连接GH,则GH的长为 .
18.如图,在矩形纸片ABCD中,AB=12,AD=5,点P为DC边上的动点(点P不与点D,C重合),将纸片沿AP折叠,点D落在点D'处,则CD'的最小值为 .
8
19.如图,在平行四边形ABCD中,F是对角线的交点,E是边BC的中点,连接EF.
(1)求证:2EF=CD;
(2)当EF与BC满足什么关系时,四边形ABCD是正方形?并证明你的结论.
(1)证明:∵四边形ABCD是平行四边形,
∴BF=FD.
又E是边BC的中点,
∴EF是△BCD的中位线.
∴2EF=CD.
(2)解:当EF⊥BC,且BC=2EF时,四边形ABCD是正方形.证明如下:
∵EF⊥BC,E是BC的中点,
∴EF垂直平分BC.
∴FB=FC.
∵四边形ABCD是平行四边形,
∴FB=FD,FA=FC.
∴FB=FC=FD=FA.
∴四边形ABCD是矩形.
∵BC=2EF,CD=2EF,
∴BC=CD.
∴四边形ABCD是正方形.
