高中数学课件-充分与必要条件

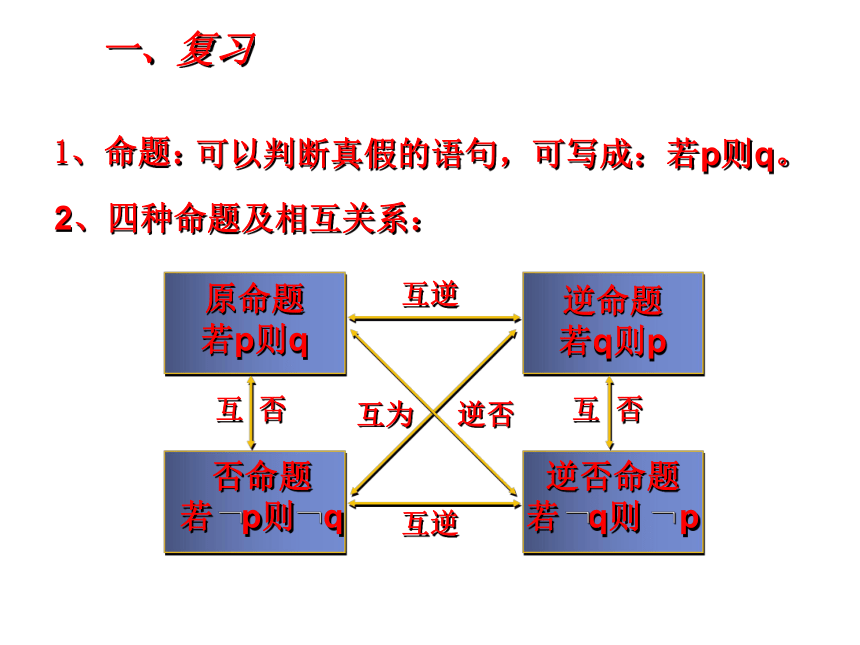
课件15张PPT。1、命题：可以判断真假的语句，可写成：若p则q。 2、四种命题及相互关系：一、复习1.1.2 充分条件与必要条件 （1）若 ，则 ；
（2）若 ，则 ；
（3）全等三角形的面积相等；
（4）对角线互相垂直的四边形是菱形；
判断下列命题是真命题还是假命题： 真真假假（1）若 ，则 ； （3）全等三角形的面积相等； 真真x≥1 x2≥1两三角形全等 两三角形面积相等（2）若 ，则 ；（4）对角线互相垂直的四边形是菱形；假假 若p则q为真 ，记作若p则q为假，记作 新授课 1、充分条件与必要条件：一般地，如果已知 那么就说，p 是q 的充分条件，q 是p 的必要条件．两三角形全等 两三角形面积相等两三角形全等是两三角形面积相等的充分条件．两三角形面积相等是两三角形全等的必要条件．典型例题解: (1) x=y是x2=y2的充分不必要条件. x2=y2是x=y的必要不充分条件.
(2) p是q的充分条件且是必要条件.
q是p充分条件且是必要条件. 2. 充分必要条件
如果p是q的充分条件， p又是q的必
要条件，则称 p是q的充分必要条件，
简称充要条件，记作 ．
3.判断充分、必要条件的基本步骤：
（1）认清条件和结论；
（2）考察 p q 和 q p 的真假。例2．填表典型例题典型例题例3、请用“充分不必要”、“必要不充分”、
“充要”、“既不充分也不必要”填空：
(1)“(x-2)(x-3)=0”是“x=2”的＿＿＿＿＿＿条件.
(2)“同位角相等”是“两直线平行”的＿＿＿条件.
(3)“x=3”是“x2=9”的＿＿＿＿＿＿条件.
(4)“四边形的对角线相等”是“四边形为平行四边形”的＿＿＿＿＿＿＿＿＿＿条件.充分不必要必要不充分充要既不充分也不必要

，相当于 ，即 或
，相当于 ，即 或
，相当于 ，即
4.从集合角度理解充分必要条件：练习：1．课后练习 1、2 3．设p是q的充分不必要条件，则 是 的
条件．D必要不充分课堂小结 （3）判别技巧：
① 可先简化命题；
② 否定一个命题只要举出一个反例即可；
③ 将命题转化为等价的逆否命题后再判断。
（1）充分条件、必要条件、充分必要条件的概念. （2）判断充分、必要条件的基本步骤：
①认清条件和结论；
②考察 p q 和 q p 的真假。