19.2.3-一次函数与方程、不等式 课件(共20张PPT)2023-2024学年人教版数学八年级下册
文档属性
| 名称 | 19.2.3-一次函数与方程、不等式 课件(共20张PPT)2023-2024学年人教版数学八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 316.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-15 10:18:20 | ||
图片预览





文档简介
(共20张PPT)
19.2.3一次函数与方程(组)、不等式
学习目标
1.理解一次函数与一元一次方程、一元一次不等式、二元一次方程组的关系。
2.会用数形结合的方法分析和解决问题。
问题:
(1)解方程2x+20=0
(2)当y=0时,求函数y=2x+20中自变量x的值。
◆从问题本质上看,(1)和(2)有什么关系?
问题:
(1)解方程2x+20=0
(2)当y=0时,求函数y=2x+20中自变量x的值。
◆若作出y=2x+20,(1)和(2)有什么关系?
x
y
o
-10
20
y=2x+20
从“形”的角度看:
(-10,0)
问题:
(1)解方程2x+20=0
(2)当y=0时,求函数y=2x+20中自变量x的值。
结论:这两个问题实际上是同一个问题(只是表达形式不同)
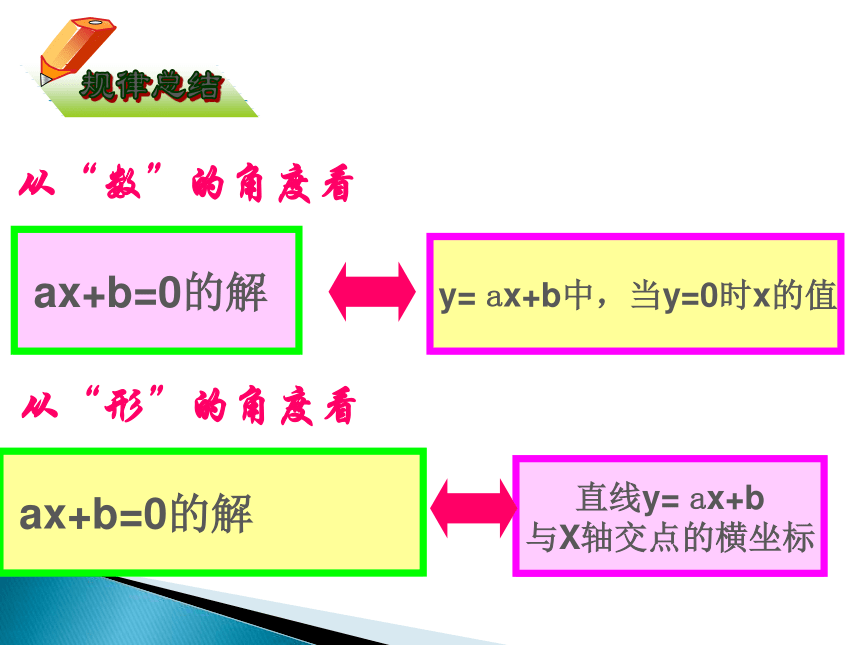
ax+b=0的解
y= ax+b中,当y=0时x的值
直线y= ax+b
与X轴交点的横坐标
从“数”的角度看
从“形”的角度看
ax+b=0的解
规律总结
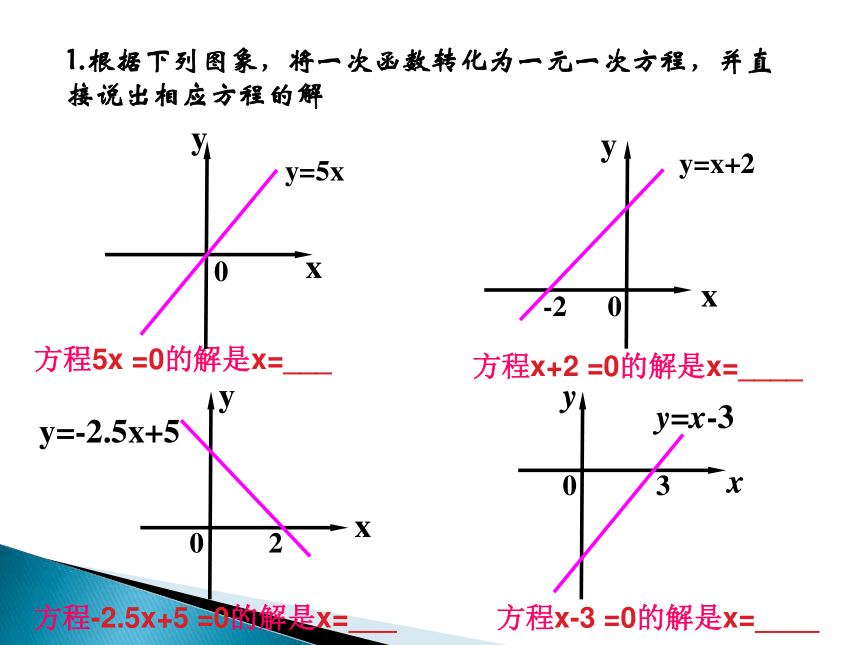
1.根据下列图象,将一次函数转化为一元一次方程,并直接说出相应方程的解
方程5x =0的解是x=___
方程x+2 =0的解是x=____
方程x-3 =0的解是x=____
y=5x
0
x
y
y=x+2
-2
0
x
y
方程-2.5x+5 =0的解是x=___
2
y=-2.5x+5
0
x
y
3
y=x-3
x
0
y
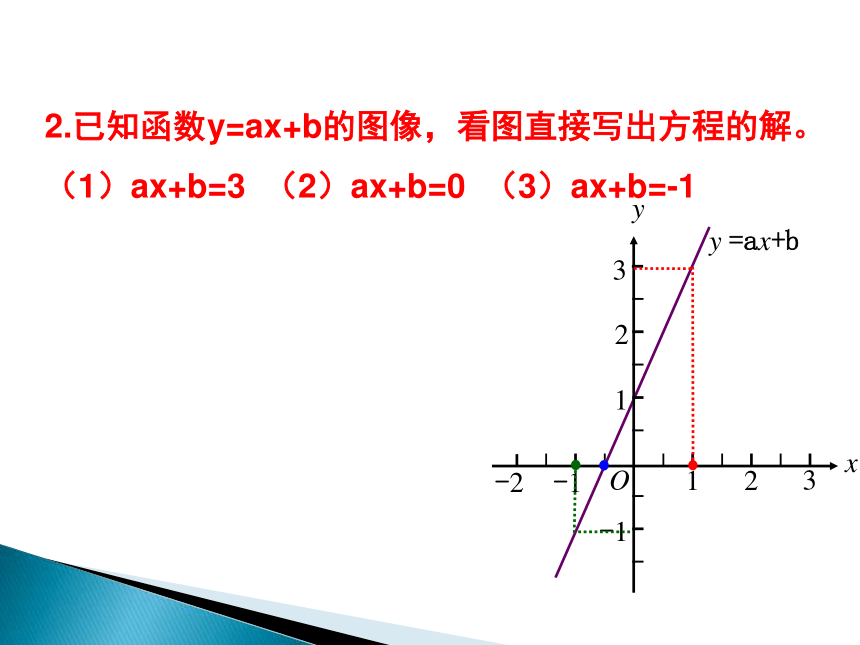
2.已知函数y=ax+b的图像,看图直接写出方程的解。
(1)ax+b=3 (2)ax+b=0 (3)ax+b=-1
y =ax+b
3
2
1
2
1
-2
O
x
y
-1
-1
3
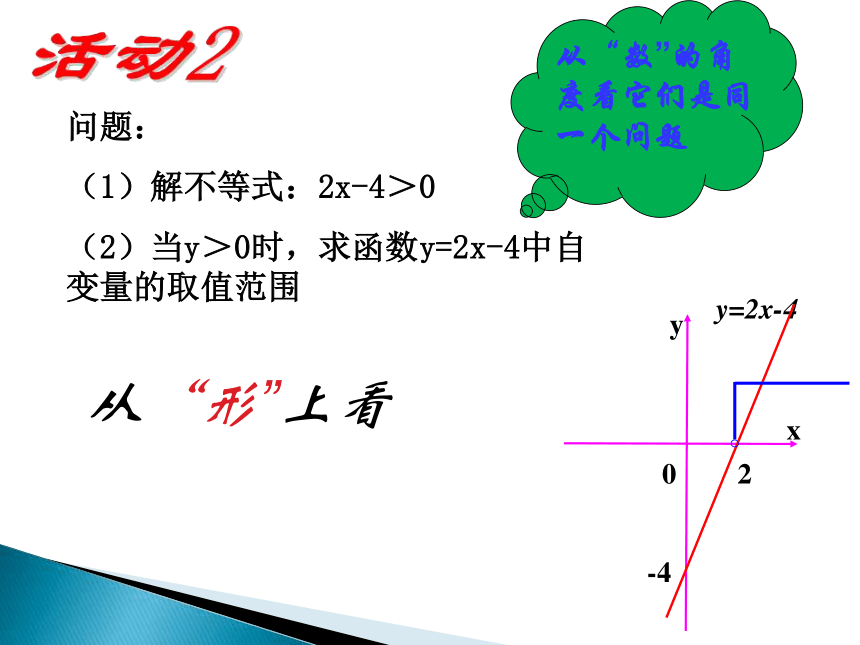
问题:
(1)解不等式:2x-4>0
(2)当y>0时,求函数y=2x-4中自变量的取值范围
从“数”的角度看它们是同一个问题
y
x
y=2x-4
-4
2
0
从“形”上看
ax+b>0
(或<0)的解集
y= ax+b中,y>0(或<0)
时,x的取值范围
y= ax+b在X轴上方(或下方)
图像对应的x取值范围
从数的角度看
从形的角度看
一次函数与一元一次不等式的关系
ax+b>0
(或<0)的解集
归纳
试一试
1、直线y=-3x-3与x轴的交点坐标是 ,不等式-3x-3>0的解集是 ,不等式-3x-3≤0的解集是
x
o
y
-1
y=-3x-3
(-1,0)
x<-1
x≥-1
-2
x
y=3x+6
y
2. 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
3、直线y=mx+n与x轴的交点坐标是(2,0),与y轴的交点坐标是(0,1.5),直接写出下面不等式的解集。
x
o
y
2
y=mx+n
(1)mx+n>0,____________
(2)mx+n<0,____________
(3)mx+n≥1.5,__________
(4)mx+n≤1.5,___________
1.5
x <2
x >2
x ≤0
x ≥0
10
-5
y1=2x+10
2
x
y
0
14
4
4.看图直接写出不等式的解集
(1)2x+10>5x+4 解集是______
(2)2x+10<5x+4 解集是______
x <2
x >2
5.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),写出下列不等式的解集x+b>kx+4,_______
x+by
x
O
y1=x+b
y2=kx+4
P
1
3
x >1
x <1
6.
-2二元一次 方程组与一次函数的关系
任何一个方程组都可以看成是两个一次函数的组合.
对于①,根据方程组解的意义和函数的观点,就是求当x取什么数值时,两个—次函数的y值相等 反映在图象上,直线y=-0.6x+1.6和直线y=2x-1的交点坐标就是方程组的解.
①
二元一次方程组的解就是两个一次函数的图象的交点坐标
活动3
你一定能行的!
巩固练习
做 一 做
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组 的解为 .
2、若二元一次方程组 的解为 ,
则函数 与 的图象的交点坐标为 .
(2,2)
3.根据下列图象,你能说出哪些方程组的解 这些解是什么
1
1
x
y
0
-2
1
x
y
0
综合运用
一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网时间计费;方式B初收月租费20元外再以每分0.05元的价格按上网时间计费.如何选择收费方式能使上网者更合算
解法1:设上网时间为x分,若按方式A则收费y=0.1x元;若按方式B则收费y=0.05x+20元
在同一直角坐标系中分别画出这两个函数的图象
解方程组
所以两图象交于(400,40)
400
当0<x<<400时,直线y=0.1x在直线y=0.05x+20的下方, 0.1x< 0.05x+20,选A种方式合算
当x=400时两者均可。
当x>400时,直线y=0.1x在直线y=0.05x+20的上方, 0.1x>0.05x+20,选B种方式合算
20
y/元
x/分
y=0.1x
y=0.05x+20
0
19.2.3一次函数与方程(组)、不等式
学习目标
1.理解一次函数与一元一次方程、一元一次不等式、二元一次方程组的关系。
2.会用数形结合的方法分析和解决问题。
问题:
(1)解方程2x+20=0
(2)当y=0时,求函数y=2x+20中自变量x的值。
◆从问题本质上看,(1)和(2)有什么关系?
问题:
(1)解方程2x+20=0
(2)当y=0时,求函数y=2x+20中自变量x的值。
◆若作出y=2x+20,(1)和(2)有什么关系?
x
y
o
-10
20
y=2x+20
从“形”的角度看:
(-10,0)
问题:
(1)解方程2x+20=0
(2)当y=0时,求函数y=2x+20中自变量x的值。
结论:这两个问题实际上是同一个问题(只是表达形式不同)
ax+b=0的解
y= ax+b中,当y=0时x的值
直线y= ax+b
与X轴交点的横坐标
从“数”的角度看
从“形”的角度看
ax+b=0的解
规律总结
1.根据下列图象,将一次函数转化为一元一次方程,并直接说出相应方程的解
方程5x =0的解是x=___
方程x+2 =0的解是x=____
方程x-3 =0的解是x=____
y=5x
0
x
y
y=x+2
-2
0
x
y
方程-2.5x+5 =0的解是x=___
2
y=-2.5x+5
0
x
y
3
y=x-3
x
0
y
2.已知函数y=ax+b的图像,看图直接写出方程的解。
(1)ax+b=3 (2)ax+b=0 (3)ax+b=-1
y =ax+b
3
2
1
2
1
-2
O
x
y
-1
-1
3
问题:
(1)解不等式:2x-4>0
(2)当y>0时,求函数y=2x-4中自变量的取值范围
从“数”的角度看它们是同一个问题
y
x
y=2x-4
-4
2
0
从“形”上看
ax+b>0
(或<0)的解集
y= ax+b中,y>0(或<0)
时,x的取值范围
y= ax+b在X轴上方(或下方)
图像对应的x取值范围
从数的角度看
从形的角度看
一次函数与一元一次不等式的关系
ax+b>0
(或<0)的解集
归纳
试一试
1、直线y=-3x-3与x轴的交点坐标是 ,不等式-3x-3>0的解集是 ,不等式-3x-3≤0的解集是
x
o
y
-1
y=-3x-3
(-1,0)
x<-1
x≥-1
-2
x
y=3x+6
y
2. 根据下列一次函数的图像,直接写出下列不等式的解集
3x+6>0
(3) –x+3 ≥0
x
y
3
y=-x+3
(2)3x+6 ≤0
X>-2
(4) –x+3<0
x≤3
X≤-2
x>3
(即y>0)
(即y≤0)
(即y<0)
(即y≥0)
3、直线y=mx+n与x轴的交点坐标是(2,0),与y轴的交点坐标是(0,1.5),直接写出下面不等式的解集。
x
o
y
2
y=mx+n
(1)mx+n>0,____________
(2)mx+n<0,____________
(3)mx+n≥1.5,__________
(4)mx+n≤1.5,___________
1.5
x <2
x >2
x ≤0
x ≥0
10
-5
y1=2x+10
2
x
y
0
14
4
4.看图直接写出不等式的解集
(1)2x+10>5x+4 解集是______
(2)2x+10<5x+4 解集是______
x <2
x >2
5.如图,一次函数y1=x+b与一次函数y2=kx+4的图象交于点P(1,3),写出下列不等式的解集x+b>kx+4,_______
x+b
x
O
y1=x+b
y2=kx+4
P
1
3
x >1
x <1
6.
-2
任何一个方程组都可以看成是两个一次函数的组合.
对于①,根据方程组解的意义和函数的观点,就是求当x取什么数值时,两个—次函数的y值相等 反映在图象上,直线y=-0.6x+1.6和直线y=2x-1的交点坐标就是方程组的解.
①
二元一次方程组的解就是两个一次函数的图象的交点坐标
活动3
你一定能行的!
巩固练习
做 一 做
1、一次函数y=5-x与y=2x-1图象的交点为(2,3),
则方程组 的解为 .
2、若二元一次方程组 的解为 ,
则函数 与 的图象的交点坐标为 .
(2,2)
3.根据下列图象,你能说出哪些方程组的解 这些解是什么
1
1
x
y
0
-2
1
x
y
0
综合运用
一家电信公司给顾客提供两种上网收费方式:方式A以每分0.1元的价格按上网时间计费;方式B初收月租费20元外再以每分0.05元的价格按上网时间计费.如何选择收费方式能使上网者更合算
解法1:设上网时间为x分,若按方式A则收费y=0.1x元;若按方式B则收费y=0.05x+20元
在同一直角坐标系中分别画出这两个函数的图象
解方程组
所以两图象交于(400,40)
400
当0<x<<400时,直线y=0.1x在直线y=0.05x+20的下方, 0.1x< 0.05x+20,选A种方式合算
当x=400时两者均可。
当x>400时,直线y=0.1x在直线y=0.05x+20的上方, 0.1x>0.05x+20,选B种方式合算
20
y/元
x/分
y=0.1x
y=0.05x+20
0
