2023-2024年人教版八年级数学下册第19章 一次函数 单元同步检测试题(含答案)
文档属性
| 名称 | 2023-2024年人教版八年级数学下册第19章 一次函数 单元同步检测试题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-15 11:24:21 | ||
图片预览


文档简介
(
装
订
线
( 装 订 线 内 不 要 答 题 )
)
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.对于次函数y=2x﹣1,下列结论错误的是( )
A.图象过点(0,﹣1)
B.图象与x轴的交点坐标为(,0)
C.图象沿y轴向上平移1个单位长度,得到直线y=2x
D.图象经过第一、二、三象限
2.正比例函数y=kx的图象经过不在同一象限内的两点(a,b)、(b,a),则k的值为( )
A.1 B.﹣1 C.±1 D.无法确定
3.关于直线l:y=kx﹣k(k≠0).下列说法正确的是( )
A.l经过定点(﹣1.0) B.l经过定点(1,0)
C.l经过第二、三、四象限 D.l经过第一、二、三象限
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
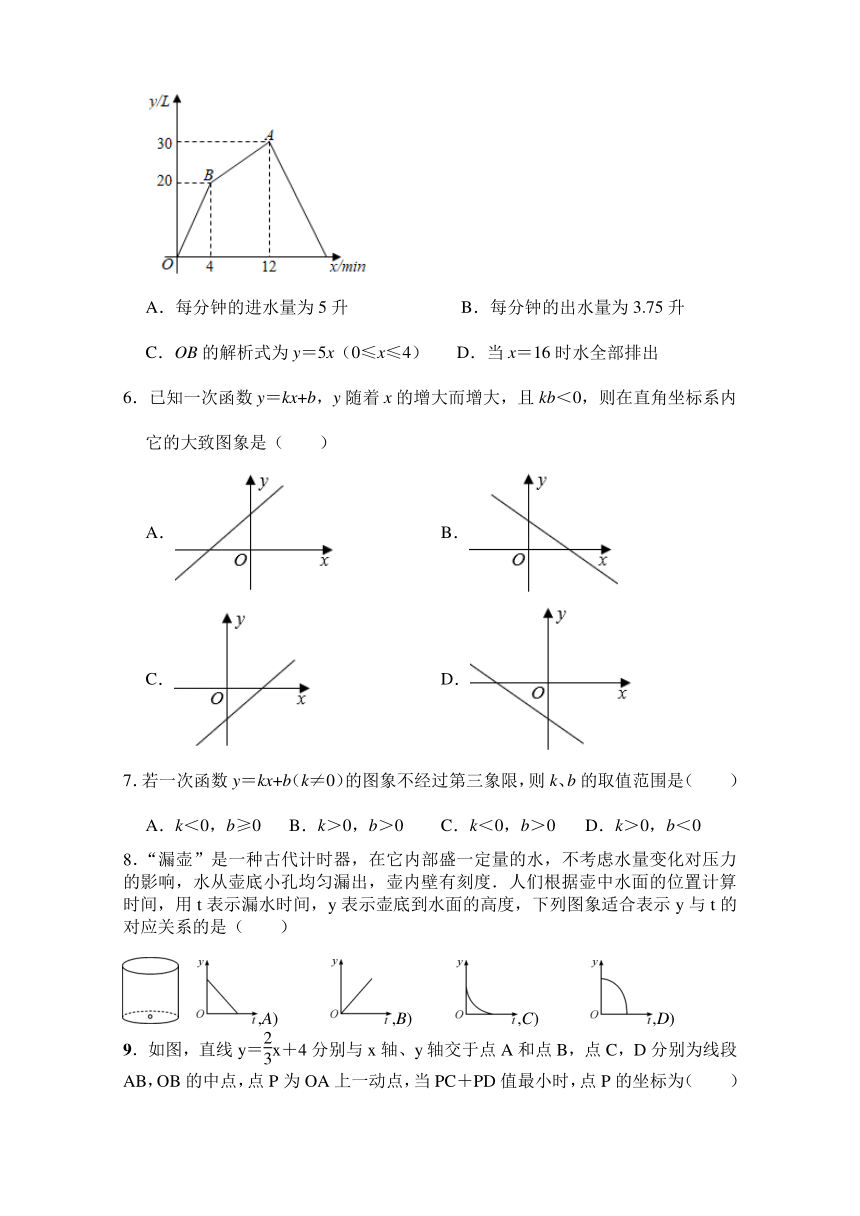
5.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,而后只出水不进水,直到水全部排出.假设每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则下列说法错误的是( )
A.每分钟的进水量为5升 B.每分钟的出水量为3.75升
C.OB的解析式为y=5x(0≤x≤4) D.当x=16时水全部排出
6.已知一次函数y=kx+b,y随着x的增大而增大,且kb<0,则在直角坐标系内它的大致图象是( )
A. B.
C. D.
7.若一次函数y=kx+b(k≠0)的图象不经过第三象限,则k、b的取值范围是( )
A.k<0,b≥0 B.k>0,b>0 C.k<0,b>0 D.k>0,b<0
8.“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与t的对应关系的是( )
,A) ,B) ,C) ,D)
9.如图,直线y=x+4分别与x轴、y轴交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,当PC+PD值最小时,点P的坐标为( )
A.(-3,0) B.(-6,0) C.(-,0) D.(-,0)
10.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10 km;
②出发1.25 h后两人相遇;
③甲每小时比乙多骑行8 km;
④相遇后,乙又骑行了15 min或65 min时两人相距2 km.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共30分)
11.已知一次函数图象过点A(1,5)、B(2,﹣3),则y随x的增大而 .(填“增大”或“减小”)
12.已知一次函数y=(k﹣3)x+1的图象经过第二、一、四象限,请你写出一个符合条件的k的值为 .
13.在平面直角坐标系xOy中,点A的坐标为(﹣1,2),点B的坐标为(m,2),若直线y=x﹣1与线段AB有公共点,则m的值可以为 (写出一个即可).
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
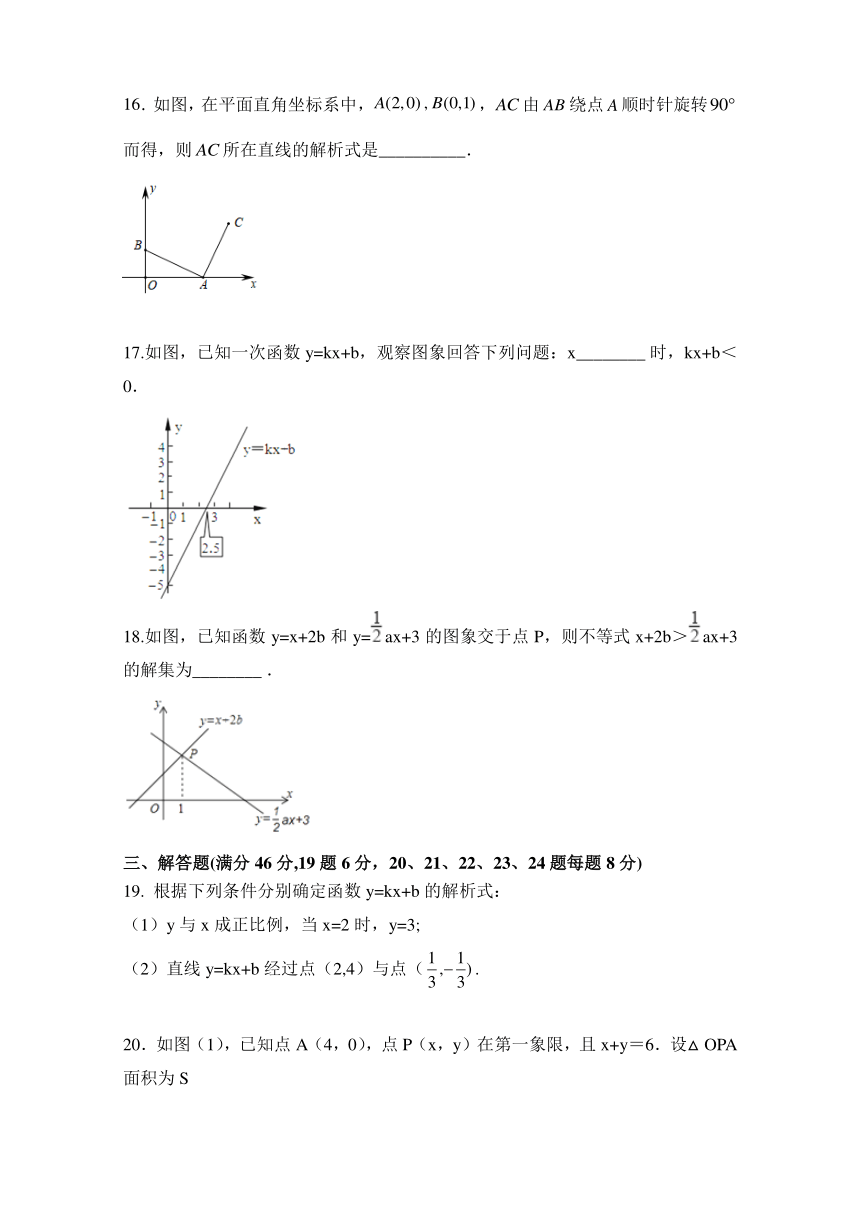
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,已知一次函数y=kx+b,观察图象回答下列问题:x________ 时,kx+b<0.
18.如图,已知函数y=x+2b和y=ax+3的图象交于点P,则不等式x+2b>ax+3的解集为________ .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. 根据下列条件分别确定函数y=kx+b的解析式:
(1)y与x成正比例,当x=2时,y=3;
(2)直线y=kx+b经过点(2,4)与点(.
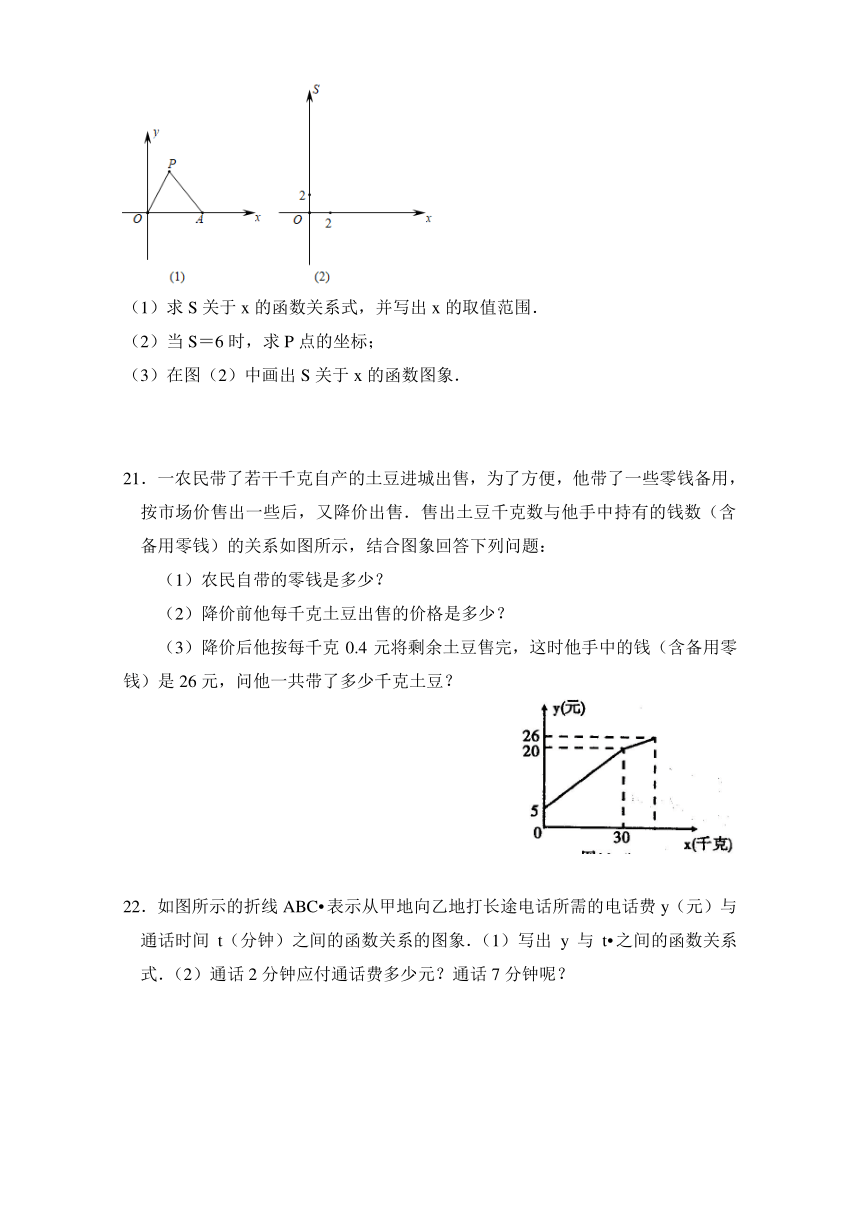
20.如图(1),已知点A(4,0),点P(x,y)在第一象限,且x+y=6.设△OPA面积为S
(1)求S关于x的函数关系式,并写出x的取值范围.
(2)当S=6时,求P点的坐标;
(3)在图(2)中画出S关于x的函数图象.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也在同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:
(1)甲出发 小时后,乙才开始出发;乙的速度为 千米/时:甲骑自行车在全程的平均速度为 千米;
(2)乙出发多少小时后就追上了甲?写出解答过程:
(3)请你自己再提出一个符合题意的问题情境,并解答.
24.如图,直线l1:y=﹣x+b分别与x轴、y轴交于A、B两点,与直线l2:y=kx﹣6交于点C(4,2)
(1)求直线l1和直线l2的解析式;
(2)点E是射线BC上一动点,其横坐标为m,过点E作EF∥y轴,交直线l2于点F,若以O、B、E、F为顶点的四边形是平行四边形,求m值;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得以P、Q、A、B为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D D A C B C A
二、填空题(每题3分,共24分)
11.减小.
12.y=﹣x+1.
13. 4.
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. (1)y=3x/2;(2)y=13x/5-6/5
20. 解:∵S=OA yP
=×4×(6﹣x)
=12﹣2x.
其中0<x<6;
(2)当S=6时,12﹣2x=6,
解得x=3.
把x=3代入x+y=6,得y=3,
∴P点的坐标为(3,3);
(3)如图,
即为S关于x的函数图象.
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.解:(1)从图象中发现乙比甲晚出发1小时,乙1小时走了50千米,速度为50千米/小时,甲的平均速度总路程除以所用总时间,即50÷(5﹣1)=12.5千米/小时.
故答案为:1,50,12.5.
(2)设QR的关系式为:s=kt+b,把Q(2,20),R(5,50)代入得:
解得:k=10,b=0,
∴QR的关系式为:s=10t (2≤t≤5)
同理可求出:MN的关系式为:s=50t﹣100 (2≤t≤3)
∴10t=50t﹣100
∴t=2.5
2.5﹣2=0.5
答:乙出发0.5小时后就追上了甲;
(3)提出问题:“乙出发多少时间,两车相距15千米”
求出PQ的关系式为:s=20t﹣20 (1≤t≤2)
①甲在前乙在后相距15千米,即:10t﹣(50t﹣100)=15,解得:t=,﹣2=小时;
②乙在前甲在后相距15千米,即:50t﹣100﹣10t=15,解得:t=,﹣2=小时;
答:乙出发小时或小时,两车相距15千米.
24.解:(1)将点C的坐标代入l1、l2表达式得:
2=﹣4+b,2=4k﹣6,
解得:b=4,k=2,
故直线l1和直线l2的解析式分别为:y=﹣x+4,y=2x﹣6,
则点A、B的坐标分别为(8,0)、(0,4);
(2)设点E(m,﹣m+4),点F(m,2m﹣6),
当以O、B、E、F为顶点的四边形是平行四边形时,
则EF=OB,即|﹣m+4﹣2m+6|=4,
解得:m=或;
(3)①当AB是菱形的一条边时,
则AP=AB==4,
则点P的坐标为(8+4,0)或(8﹣4,0)或(﹣8,0),
则点Q(4,4)或(﹣4,4)或(0,﹣4);
②当AB是菱形的对角线时,
设点P(m,0),点Q(s,t),
由中点公式得:8=m+s,4=t…①,
由菱形性质知:PA=PB得:(m﹣8)2=m2+16…②,
联立①②并解得:t=4,s=5,
故点Q(5,4),
综上,点Q(4,4)或(﹣4,4)或(5,4)或(0,﹣4).
数学试卷 第15页(共22页) ( 数学试卷 第16页(共22页)
装
订
线
( 装 订 线 内 不 要 答 题 )
)
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.对于次函数y=2x﹣1,下列结论错误的是( )
A.图象过点(0,﹣1)
B.图象与x轴的交点坐标为(,0)
C.图象沿y轴向上平移1个单位长度,得到直线y=2x
D.图象经过第一、二、三象限
2.正比例函数y=kx的图象经过不在同一象限内的两点(a,b)、(b,a),则k的值为( )
A.1 B.﹣1 C.±1 D.无法确定
3.关于直线l:y=kx﹣k(k≠0).下列说法正确的是( )
A.l经过定点(﹣1.0) B.l经过定点(1,0)
C.l经过第二、三、四象限 D.l经过第一、二、三象限
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.一个有进水管和出水管的容器,从某时刻开始4min内只进水不出水,在随后的8min内既进水又出水,而后只出水不进水,直到水全部排出.假设每分钟的进水量和出水量是两个常数,容器内的水量y(L)与时间x(min)之间的关系如图所示,则下列说法错误的是( )
A.每分钟的进水量为5升 B.每分钟的出水量为3.75升
C.OB的解析式为y=5x(0≤x≤4) D.当x=16时水全部排出
6.已知一次函数y=kx+b,y随着x的增大而增大,且kb<0,则在直角坐标系内它的大致图象是( )
A. B.
C. D.
7.若一次函数y=kx+b(k≠0)的图象不经过第三象限,则k、b的取值范围是( )
A.k<0,b≥0 B.k>0,b>0 C.k<0,b>0 D.k>0,b<0
8.“漏壶”是一种古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与t的对应关系的是( )
,A) ,B) ,C) ,D)
9.如图,直线y=x+4分别与x轴、y轴交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,当PC+PD值最小时,点P的坐标为( )
A.(-3,0) B.(-6,0) C.(-,0) D.(-,0)
10.一条公路旁依次有A,B,C三个村庄,甲、乙两人骑自行车分别从A村、B村同时出发前往C村,甲、乙之间的距离s(km)与骑行时间t(h)之间的函数关系如图所示,下列结论:
①A,B两村相距10 km;
②出发1.25 h后两人相遇;
③甲每小时比乙多骑行8 km;
④相遇后,乙又骑行了15 min或65 min时两人相距2 km.
其中正确的个数是( )
A.1 B.2 C.3 D.4
二、填空题(每题3分,共30分)
11.已知一次函数图象过点A(1,5)、B(2,﹣3),则y随x的增大而 .(填“增大”或“减小”)
12.已知一次函数y=(k﹣3)x+1的图象经过第二、一、四象限,请你写出一个符合条件的k的值为 .
13.在平面直角坐标系xOy中,点A的坐标为(﹣1,2),点B的坐标为(m,2),若直线y=x﹣1与线段AB有公共点,则m的值可以为 (写出一个即可).
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,已知一次函数y=kx+b,观察图象回答下列问题:x________ 时,kx+b<0.
18.如图,已知函数y=x+2b和y=ax+3的图象交于点P,则不等式x+2b>ax+3的解集为________ .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. 根据下列条件分别确定函数y=kx+b的解析式:
(1)y与x成正比例,当x=2时,y=3;
(2)直线y=kx+b经过点(2,4)与点(.
20.如图(1),已知点A(4,0),点P(x,y)在第一象限,且x+y=6.设△OPA面积为S
(1)求S关于x的函数关系式,并写出x的取值范围.
(2)当S=6时,求P点的坐标;
(3)在图(2)中画出S关于x的函数图象.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.已知A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也在同日下午骑摩托车按同路从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S(千米)与该日下午时间t(时)之间的关系.根据图象回答下列问题:
(1)甲出发 小时后,乙才开始出发;乙的速度为 千米/时:甲骑自行车在全程的平均速度为 千米;
(2)乙出发多少小时后就追上了甲?写出解答过程:
(3)请你自己再提出一个符合题意的问题情境,并解答.
24.如图,直线l1:y=﹣x+b分别与x轴、y轴交于A、B两点,与直线l2:y=kx﹣6交于点C(4,2)
(1)求直线l1和直线l2的解析式;
(2)点E是射线BC上一动点,其横坐标为m,过点E作EF∥y轴,交直线l2于点F,若以O、B、E、F为顶点的四边形是平行四边形,求m值;
(3)若点P为x轴上一点,则在平面直角坐标系中是否存在一点Q,使得以P、Q、A、B为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D B C D D A C B C A
二、填空题(每题3分,共24分)
11.减小.
12.y=﹣x+1.
13. 4.
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19. (1)y=3x/2;(2)y=13x/5-6/5
20. 解:∵S=OA yP
=×4×(6﹣x)
=12﹣2x.
其中0<x<6;
(2)当S=6时,12﹣2x=6,
解得x=3.
把x=3代入x+y=6,得y=3,
∴P点的坐标为(3,3);
(3)如图,
即为S关于x的函数图象.
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23.解:(1)从图象中发现乙比甲晚出发1小时,乙1小时走了50千米,速度为50千米/小时,甲的平均速度总路程除以所用总时间,即50÷(5﹣1)=12.5千米/小时.
故答案为:1,50,12.5.
(2)设QR的关系式为:s=kt+b,把Q(2,20),R(5,50)代入得:
解得:k=10,b=0,
∴QR的关系式为:s=10t (2≤t≤5)
同理可求出:MN的关系式为:s=50t﹣100 (2≤t≤3)
∴10t=50t﹣100
∴t=2.5
2.5﹣2=0.5
答:乙出发0.5小时后就追上了甲;
(3)提出问题:“乙出发多少时间,两车相距15千米”
求出PQ的关系式为:s=20t﹣20 (1≤t≤2)
①甲在前乙在后相距15千米,即:10t﹣(50t﹣100)=15,解得:t=,﹣2=小时;
②乙在前甲在后相距15千米,即:50t﹣100﹣10t=15,解得:t=,﹣2=小时;
答:乙出发小时或小时,两车相距15千米.
24.解:(1)将点C的坐标代入l1、l2表达式得:
2=﹣4+b,2=4k﹣6,
解得:b=4,k=2,
故直线l1和直线l2的解析式分别为:y=﹣x+4,y=2x﹣6,
则点A、B的坐标分别为(8,0)、(0,4);
(2)设点E(m,﹣m+4),点F(m,2m﹣6),
当以O、B、E、F为顶点的四边形是平行四边形时,
则EF=OB,即|﹣m+4﹣2m+6|=4,
解得:m=或;
(3)①当AB是菱形的一条边时,
则AP=AB==4,
则点P的坐标为(8+4,0)或(8﹣4,0)或(﹣8,0),
则点Q(4,4)或(﹣4,4)或(0,﹣4);
②当AB是菱形的对角线时,
设点P(m,0),点Q(s,t),
由中点公式得:8=m+s,4=t…①,
由菱形性质知:PA=PB得:(m﹣8)2=m2+16…②,
联立①②并解得:t=4,s=5,
故点Q(5,4),
综上,点Q(4,4)或(﹣4,4)或(5,4)或(0,﹣4).
数学试卷 第15页(共22页) ( 数学试卷 第16页(共22页)
