2023--2024学年人教版七年级数学下册第五章相交线与平行线单元复习试题(含答案)
文档属性
| 名称 | 2023--2024学年人教版七年级数学下册第五章相交线与平行线单元复习试题(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 535.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-15 00:00:00 | ||
图片预览



文档简介
人教版数学2023-2024学年度
七年级下第五章《相交线与平行线》复习试题
一.选择题(共10小题)
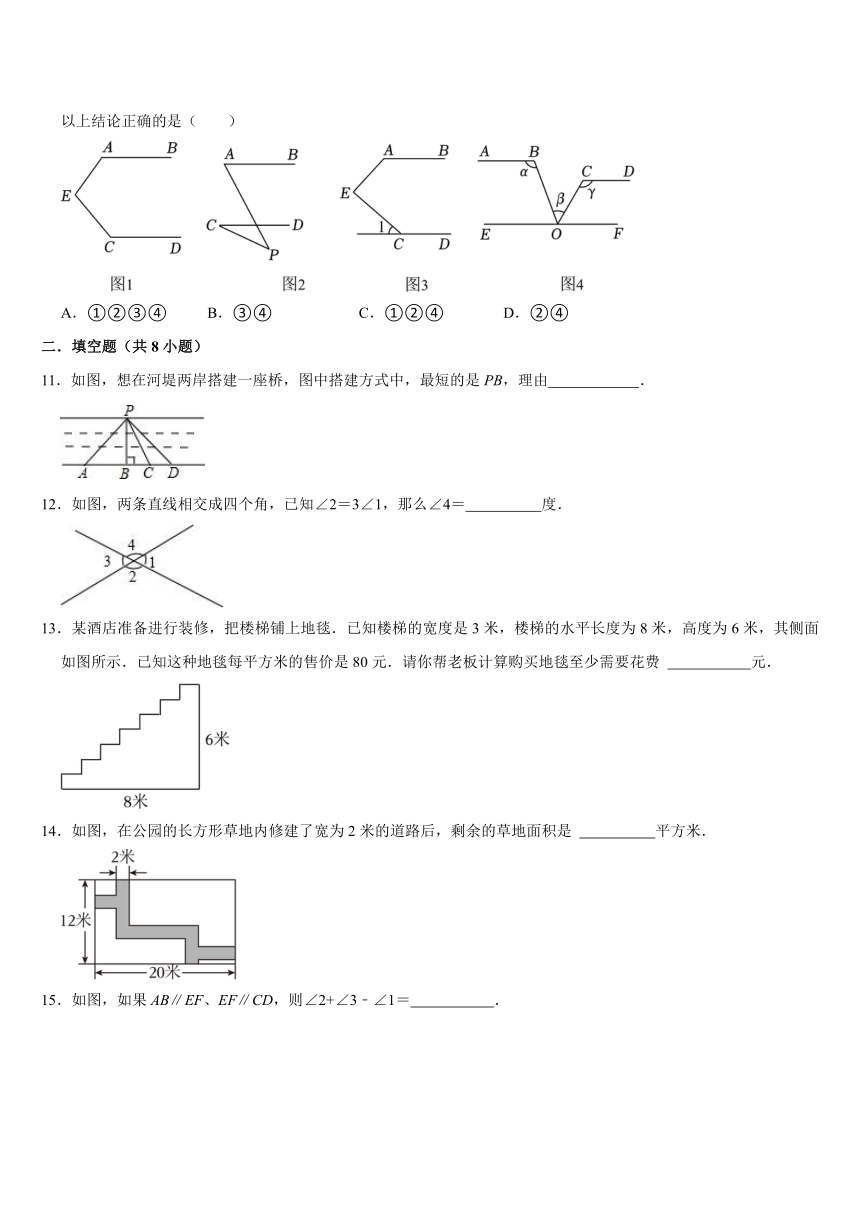
1.如图,哪个可以通过左边图形平移得到( )
A. B. C. D.
2.下列图形中,∠1与∠2不是同位角的是( )
A. B. C. D.
3.直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
A.30° B.36° C.45° D.72°
4.如图,将三角形ABC沿着B到C的方向平移到三角形DEF的位置,AB=10,BC=20,DH=4,BE=8,则阴影部分的面积是( )
A.40 B.32 C.36 D.64
5.下列命题中真命题有( )
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
②两条直线被第三条直线所截,同旁内角互补;
③如果两条直线都与第三条直线垂直,那么这两条直线互相平行;
④在同一平面内,过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
6.如图,已知AB∥CD,∠1=40°,则∠2的度数为( )
A.120° B.130° C.140° D.150°
7.如图,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠3+∠5=180° D.∠2=∠3
8.某人把“抖空竹”的一个姿势抽象成数学问题.如图所示,已知AB∥CD,∠A=85°,∠C=120°,则∠E的度数是( )
A.25° B.35° C.39° D.40°
9.如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:
①∠D=40°;②2∠D+∠EHC=90°;③FD平分∠HFB;④FH平分∠GFD.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.①如图1,AB∥CD,则∠A+∠E+∠C=360°;
②如图2,AB∥CD,则∠P=∠A﹣∠C;
③如图3,AB∥CD,则∠E=∠A+∠1;
④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α﹣∠β+∠γ=180°.
以上结论正确的是( )
A.①②③④ B.③④ C.①②④ D.②④
二.填空题(共8小题)
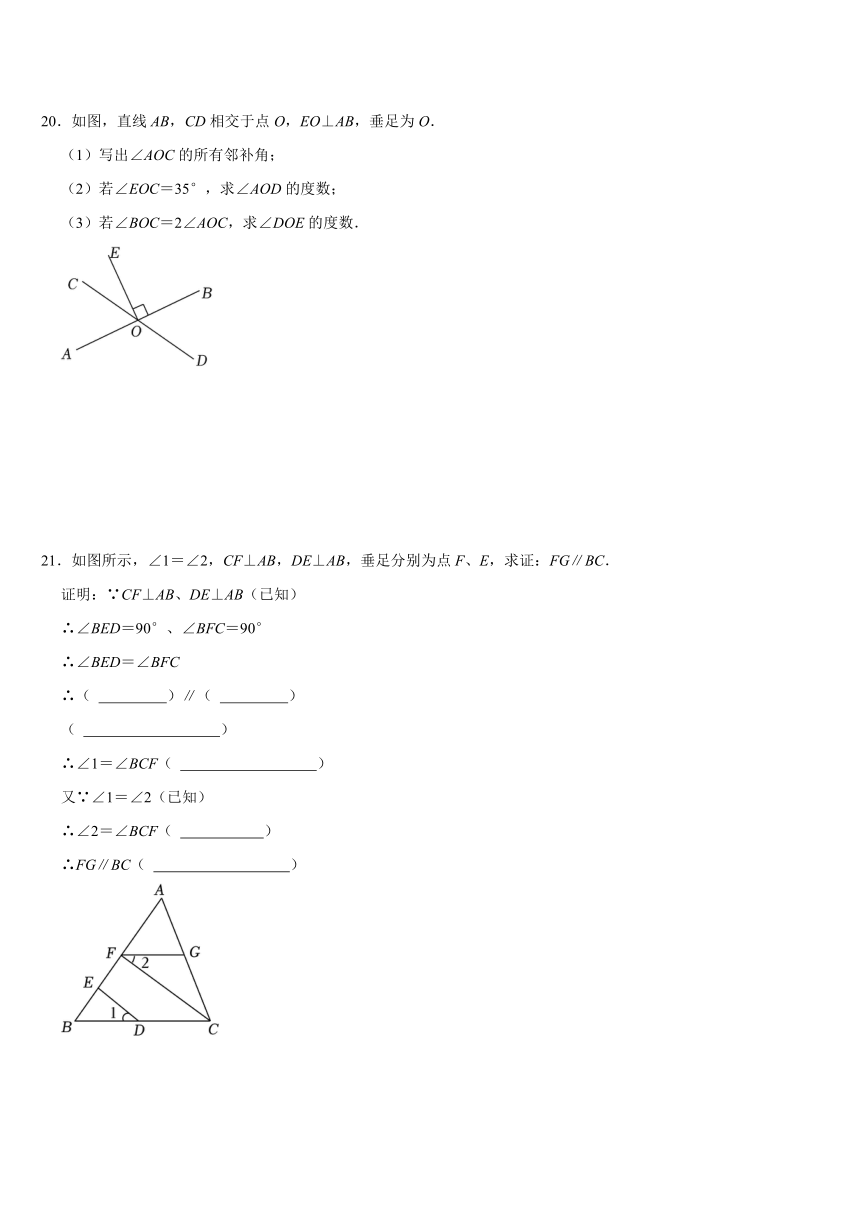
11.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB,理由 .
12.如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4= 度.
13.某酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是3米,楼梯的水平长度为8米,高度为6米,其侧面如图所示.已知这种地毯每平方米的售价是80元.请你帮老板计算购买地毯至少需要花费 元.
14.如图,在公园的长方形草地内修建了宽为2米的道路后,剩余的草地面积是 平方米.
15.如图,如果AB∥EF、EF∥CD,则∠2+∠3﹣∠1= .
16.如图,已知直线AB∥CD,EG平分∠BEF,∠1=40°,则∠2的度数是 .
17.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有 (填正确结论的序号)
18.如图,将长方形ABCD沿EF翻折,再沿ED翻折,若∠FEA″=105°,则∠CFE= 度.
三.解答题(共10小题)
19.如图,点B、O、C三点在同一直线上,∠DOE=90°,
(1)若AO⊥BC,∠AOE=65°,求∠COE的度数;
(2)若∠BOD:∠COE=2:1,求∠COD的度数.
20.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.
(1)写出∠AOC的所有邻补角;
(2)若∠EOC=35°,求∠AOD的度数;
(3)若∠BOC=2∠AOC,求∠DOE的度数.
21.如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴( )∥( )
( )
∴∠1=∠BCF( )
又∵∠1=∠2(已知)
∴∠2=∠BCF( )
∴FG∥BC( )
22.如图,点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D,F,点M,G在AB上,∠AMD=∠AGF,∠1=∠2.
求证:(1)∠2=∠CBD;
(2)MD∥BC.
23.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD;
(2)若FG⊥BC于点H,BC平分∠ABD,∠D=108°,求∠1的度数.
24.如图,在△ABC中,点D,E在AB边上,点F在AC边上,EF∥DC,点H在BC边上,且∠1+∠2=180°.
(1)求证:DH∥AC;
(2)若CD平分∠ACB,∠BHD=66°,求∠2的度数.
25.(1)如图1,已知AB∥CD,∠ABC=45°,可得∠BCD= 度;
(2)如图2,在(1)的条件下,如果CM平分∠BCD,求∠ECM度数;
(3)如图3,在(1)(2)的条件下,如果CN⊥CM,则∠BCN= 度;
(4)尝试解决下面问题:如图4,AB∥CD,∠BCM=20°,CN是∠BCE的平分线,CN⊥CM,求∠B的度数.
26.综合与实践
综合与实践课上,老师让同学们以“平行中的数量关系”为主题开展数学活动.已知AB∥CD,BF为∠ABE的平分线,DF为∠CDE的平分线,BF和DF相交于点F.
探究问题
(1)在图1中,∠BFD,∠ABF,∠CDF之间的数量的关系为 .
∠BFD,∠ABE,∠CDE之间的数量关系为: .
知识迁移
(2)如图2,若∠E+8∠M=360°,,试猜想∠CDM和∠MDF间的数量关系,并加以证明.
27.已知:如图,AB∥CD,线段EF分别与AB,CD相交于点E,F
(1)如图1,已知∠A=30°,∠APC=80°,求∠C的度数;
(2)如图2,当动点P在线段EF上运动时(不包括E,F两点),∠A,∠APC与∠C之间有何数量关系?并证明你的结论;
(3)当动点P在直线EF(线段EF除外)上运动时,(2)中的结论是否仍然成立?如果不成立,请直接写出∠A,∠APC与∠C之间的数量关系.
28.如图,直线l1∥l2,A、N为直线l1上的点,过点A的直线交l2于点B,C在线段BA的延长线上.D、E为直线l2上的两个动点,D在B的右侧,E在D的右侧,连接AD,AE,满足∠AED=∠DAE.点M在l2上,且在点B的左侧.
(1)如图1,若∠BAD=25°,∠AED=50°,则∠ABM的度数为 ;
(2)如图2,射线AF为∠CAD的角平分线.
①用等式表示∠EAF与∠ABD之间的数量关系,并给出证明;
②当∠ABM+∠EAF=150°时,∠EAF的度数为 .
参考答案
一.选择题(共10小题)
1.C.
2.B.
3.A.
4.D.
5.B.
6.C.
7.A.
8.B.
9.A.
10.C.
二.填空题(共8小题)
11.垂线段最短.
12.135
13.3360.
14.180.
15.180°.
16.70°.
17.②③④.
18.155.
三.解答题(共10小题)
19.解:(1)∵AO⊥BC,
∴∠AOC=90°,
∵∠AOE=65°,
∴∠COE=90°﹣∠AOE=25°;
(2)∵∠BOD+∠DOE+∠COE=90°,∠DOE=90°,
∴∠BOD+∠COE=90°,
∵∠BOD:∠COE=2:1,
∴∠BOD=2∠COE,
∴2∠COE+∠COE=90°,
∴∠COE=30°,
∴∠COD=∠COE+∠DOE=120°.
20.解:(1)由图中可得∠AOC的所有邻补角为∠BOC和∠AOD;
(2)∵AB⊥EO,
∴∠BOE=90°.
∵∠EOC=35°,
∴∠BOC=∠AOD=∠EOC+∠BOE=125°;
(3)∵∠BOC=2∠AOC,∠AOC+∠BOC=180°,
∴∠AOC+2∠AOC=180°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠DOE=∠BOE+∠BOD=90°+60°=150°.
21.证明:∵CF⊥AB、DE⊥AB(已知),
∴∠BED=90°,∠BFG=90°,
∴∠BED=∠BFC,
∴(ED)∥(FC)(同位角相等,两直线平行),
∴∠1=∠BCF(两直线平行,同位角相等),
∵∠1=∠2,
∴∠2=∠BCF(等量代换),
∴FG∥BC(内错角相等,两直线平行),
22.证明:(1)∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠2=∠CBD;
(2)∵∠1=∠2,∠2=∠CBD,
∴∠1=∠CBD,
∴GF∥BC,
∵∠AMD=∠AGF,
∴GF∥MD,
∴MD∥BC.
23.(1)证明:∵FG∥AE,
∴∠2=∠FGC,
又∵∠1=∠2,
∴∠1=∠FGC,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠ABD=180°﹣∠D=180°﹣108°=72°,
又∵BC平分∠ABD,
∴,
∵FG⊥BC,
∴∠BHF=90°,
在△BFH中,
∵∠BHF=90°,∠FBH=36°,
∴∠1=180°﹣∠BHF﹣∠FBH=180°﹣90°﹣36°=54°.
24.(1)证明:∵EF∥DC,
∴∠DCF+∠2=180°,
∵∠1+∠2=180°,
∴∠DCF=∠1,
∴DH∥AC;
(2)解:由(1)知DH∥AC,
∴∠∠BHD=∠ACB,
∵∠BHD=66°,
∴∠ACB=66°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=33°,
∵EF∥DC,
∴∠ACD+∠2=180°,
∴∠2=147°.
25.解:(1)∵AB∥CD,∠ABC=45°,
∴∠BCD=∠ABC=45°,
(2)∵AB∥CD,∠ABC=45°,
∴∠BCD=∠ABC=45°,
∵CM平分∠BCD,
∴∠BCM=∠DCM=∠BCD=22.5°,
∵∠ECM+∠DCM=180°,
∴∠ECM=157.5°;
(3)∵AB∥CD,∠ABC=45°,
∴∠BCD=∠ABC=45°,
∵CM平分∠BCD,
∴∠BCM=∠DCM=∠BCD=22.5°,
∵CN⊥CM,
∴∠BCN=90°﹣22.5°=67.5°,
(4)∵CN⊥CM,
∴∠BCN+∠BCM=90°,
∵∠BCM=20°,
∴∠BCN=70°,
∵CN是∠BCE的平分线,
∴∠BCE=2∠BCN=2×70°=140°,
∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠BCE=140°,
∴∠B=180°﹣∠BCE=180°﹣140°=40°.
26.解:(1)如图所示,过点F作FG∥AB,
∵AB∥CD,
∴AB∥FG∥CD,
∴∠ABF=∠BFG,∠CDF=∠DFG,
∵∠BFG+∠DFG=∠BFD,
∴∠BFD=∠ABF+∠CDF;
由上述证明可知,∠BFD=∠ABF+∠CDF,
∵BF为∠ABE的平分线,DF为∠CDE的平分线,
∴,,
∴,
∴∠ABE+∠CDE=2∠BFD;
(2)∠MDF=3∠CDM,理由如下:
如图所示,过点E作EQ∥AB,过点M作MP∥AB,
设∠CDM=x,∠ABM=y,
∵CD∥AB,
∴EQ∥MP∥AB∥CD,
∴∠CDM=∠PMD=x,∠ABM=∠PMB=y,
∵∠ABE+∠QEB=180°,∠CDE+∠QED=180°,
∴∠ABE+∠QEB+∠CDE+∠QED=360°,
∴∠ABE+∠CDE+∠BED=360°,
∴∠BDE=360﹣(∠ABE+∠CDE),
∵∠E+8∠M=360°,即∠BED+8∠BMD=360°,
∴360°﹣(∠ABE+∠CDE)+8∠BMD=360°,
∴8∠BMD=∠ABE+∠CDE,
∵∠BMD=∠PMD+∠PMB=x+y,
∴8∠BMD=8x+8y=∠ABE+∠CDE,
∵,
∴∠EBF=4y,
∵BF为∠ABE的平分线,DF为∠CDE的平分线,
∴∠EBF=∠ABF=4y,∠CDF=∠EDF,
∴∠ABE=8y,
∵∠ABE+∠CDE=8x+8y,
∴∠CDE=8x,
∴∠CDF=∠EDF=4x,
∵∠CDM=x,
∴∠MDF=3x,
∴∠MDF=3∠CDM.
27.解:(1)如图①,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∵∠A=30°,
∴∠APO=∠A=30°,∠C=∠CPO,
∵∠APC=80°
∴∠C=∠CPO=∠APC﹣∠APO=80°﹣30°=50°;
(2)∠A+∠C=∠APC,
证明:如图②,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠APC=∠APO+∠CPO=∠A+∠C;
(3)不成立,关系式是:∠A﹣∠C=∠APC,
理由:如图③,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠A﹣∠C=∠APO﹣∠CPO=∠APC,
即∠A﹣∠C=∠APC.
28.解:(1)如图1:∵l1∥l2,
∴∠ABM=∠BAN,∠NAE=∠AED=50°,
∵∠BAD=25°,∠DAE=∠AED=50°,
∴∠ABM=∠BAN=∠BAD+∠DAE+∠NAE=25°+50°+50°=125°,
(2)①∠ABD=2∠EAF,
证明:∵l1∥l2,
∴∠CAN=∠ABD,∠NAE=∠AED,
又∵AF平分∠CAD,
∴∠DAF=∠CAF=∠CAD,
∵∠DAE=∠AED=∠NAE,
∴∠DAE=∠NAE=(∠DAE+∠NAE)=∠DAN,
∴∠EAF=∠DAF﹣∠DAE=∠CAD﹣∠DAN=∠CAN=∠ABD.
即∠ABD=2∠EAF;
②Ⅰ、如图所示:点D在点B右侧,此时有∠EAF=∠ABD,
∵∠ABM+∠EAF=150°,
∴∠ABM+∠ABD=150°,
又∵∠ABM+∠ABD=180°,
∴∠ABD=180°﹣150°=30°,
∴∠EAF=30°;
Ⅱ如图所示,点D在点B左侧,点E在点B右侧,
∵AE平分∠CAD,
∴∠DAF=∠CAD,
∵l1∥l2,
∴∠AED=∠NAE,∠CAN=∠ABE,
∵∠DAE=∠AED=∠NAE,
∴∠DAE=(∠DAE+∠NAE)=∠DAN,
∴∠EAF=∠DAF+∠DAE=(∠CAD+∠DAN)=×(360°﹣∠CAN)=180°﹣∠ABE,
∵∠ABE+∠ABM=180°,
∴∠EAF=180°﹣(180°﹣∠ABM)=90°+∠ABM,
又∵∠EAF+∠ABM=150°,
∴∠EAF=90°+(150°﹣∠EAF)=165°﹣∠EAF,
∴∠EAF=110°;
Ⅲ如图,D、E均在B点左侧,
此时,∠DAE=∠DAN,∠DAF=∠CAD,
∠EAF=∠DAE+∠DAF=(360°﹣∠CAN)=180°﹣∠ABG=180°﹣(180°﹣∠ABM)=90°+∠ABM,
∴∠EAF=110°.
综上所述:∠EAF=30°或∠EAF=110°.
七年级下第五章《相交线与平行线》复习试题
一.选择题(共10小题)
1.如图,哪个可以通过左边图形平移得到( )
A. B. C. D.
2.下列图形中,∠1与∠2不是同位角的是( )
A. B. C. D.
3.直线AB,CD相交于O,OE平分∠AOC,∠EOA:∠AOD=1:4,∠EOC等于( )
A.30° B.36° C.45° D.72°
4.如图,将三角形ABC沿着B到C的方向平移到三角形DEF的位置,AB=10,BC=20,DH=4,BE=8,则阴影部分的面积是( )
A.40 B.32 C.36 D.64
5.下列命题中真命题有( )
①如果两条直线都与第三条直线平行,那么这两条直线也互相平行;
②两条直线被第三条直线所截,同旁内角互补;
③如果两条直线都与第三条直线垂直,那么这两条直线互相平行;
④在同一平面内,过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
6.如图,已知AB∥CD,∠1=40°,则∠2的度数为( )
A.120° B.130° C.140° D.150°
7.如图,下列条件中不能判定AB∥CD的是( )
A.∠1=∠2 B.∠3=∠4 C.∠3+∠5=180° D.∠2=∠3
8.某人把“抖空竹”的一个姿势抽象成数学问题.如图所示,已知AB∥CD,∠A=85°,∠C=120°,则∠E的度数是( )
A.25° B.35° C.39° D.40°
9.如图,AB∥CD,F为AB上一点,FD∥EH,且FE平分∠AFG,过点F作FG⊥EH于点G,且∠AFG=2∠D,则下列结论:
①∠D=40°;②2∠D+∠EHC=90°;③FD平分∠HFB;④FH平分∠GFD.
其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
10.①如图1,AB∥CD,则∠A+∠E+∠C=360°;
②如图2,AB∥CD,则∠P=∠A﹣∠C;
③如图3,AB∥CD,则∠E=∠A+∠1;
④如图4,直线AB∥CD∥EF,点O在直线EF上,则∠α﹣∠β+∠γ=180°.
以上结论正确的是( )
A.①②③④ B.③④ C.①②④ D.②④
二.填空题(共8小题)
11.如图,想在河堤两岸搭建一座桥,图中搭建方式中,最短的是PB,理由 .
12.如图,两条直线相交成四个角,已知∠2=3∠1,那么∠4= 度.
13.某酒店准备进行装修,把楼梯铺上地毯.已知楼梯的宽度是3米,楼梯的水平长度为8米,高度为6米,其侧面如图所示.已知这种地毯每平方米的售价是80元.请你帮老板计算购买地毯至少需要花费 元.
14.如图,在公园的长方形草地内修建了宽为2米的道路后,剩余的草地面积是 平方米.
15.如图,如果AB∥EF、EF∥CD,则∠2+∠3﹣∠1= .
16.如图,已知直线AB∥CD,EG平分∠BEF,∠1=40°,则∠2的度数是 .
17.如图,点E在AC的延长线上,对于下列给出的四个条件:
①∠3=∠4;②∠1=∠2;③∠A=∠DCE;④∠D+∠ABD=180°.
能判断AB∥CD的有 (填正确结论的序号)
18.如图,将长方形ABCD沿EF翻折,再沿ED翻折,若∠FEA″=105°,则∠CFE= 度.
三.解答题(共10小题)
19.如图,点B、O、C三点在同一直线上,∠DOE=90°,
(1)若AO⊥BC,∠AOE=65°,求∠COE的度数;
(2)若∠BOD:∠COE=2:1,求∠COD的度数.
20.如图,直线AB,CD相交于点O,EO⊥AB,垂足为O.
(1)写出∠AOC的所有邻补角;
(2)若∠EOC=35°,求∠AOD的度数;
(3)若∠BOC=2∠AOC,求∠DOE的度数.
21.如图所示,∠1=∠2,CF⊥AB,DE⊥AB,垂足分别为点F、E,求证:FG∥BC.
证明:∵CF⊥AB、DE⊥AB(已知)
∴∠BED=90°、∠BFC=90°
∴∠BED=∠BFC
∴( )∥( )
( )
∴∠1=∠BCF( )
又∵∠1=∠2(已知)
∴∠2=∠BCF( )
∴FG∥BC( )
22.如图,点E在BC上,BD⊥AC,EF⊥AC,垂足分别为D,F,点M,G在AB上,∠AMD=∠AGF,∠1=∠2.
求证:(1)∠2=∠CBD;
(2)MD∥BC.
23.如图,点F在线段AB上,点E,G在线段CD上,FG∥AE,∠1=∠2.
(1)求证:AB∥CD;
(2)若FG⊥BC于点H,BC平分∠ABD,∠D=108°,求∠1的度数.
24.如图,在△ABC中,点D,E在AB边上,点F在AC边上,EF∥DC,点H在BC边上,且∠1+∠2=180°.
(1)求证:DH∥AC;
(2)若CD平分∠ACB,∠BHD=66°,求∠2的度数.
25.(1)如图1,已知AB∥CD,∠ABC=45°,可得∠BCD= 度;
(2)如图2,在(1)的条件下,如果CM平分∠BCD,求∠ECM度数;
(3)如图3,在(1)(2)的条件下,如果CN⊥CM,则∠BCN= 度;
(4)尝试解决下面问题:如图4,AB∥CD,∠BCM=20°,CN是∠BCE的平分线,CN⊥CM,求∠B的度数.
26.综合与实践
综合与实践课上,老师让同学们以“平行中的数量关系”为主题开展数学活动.已知AB∥CD,BF为∠ABE的平分线,DF为∠CDE的平分线,BF和DF相交于点F.
探究问题
(1)在图1中,∠BFD,∠ABF,∠CDF之间的数量的关系为 .
∠BFD,∠ABE,∠CDE之间的数量关系为: .
知识迁移
(2)如图2,若∠E+8∠M=360°,,试猜想∠CDM和∠MDF间的数量关系,并加以证明.
27.已知:如图,AB∥CD,线段EF分别与AB,CD相交于点E,F
(1)如图1,已知∠A=30°,∠APC=80°,求∠C的度数;
(2)如图2,当动点P在线段EF上运动时(不包括E,F两点),∠A,∠APC与∠C之间有何数量关系?并证明你的结论;
(3)当动点P在直线EF(线段EF除外)上运动时,(2)中的结论是否仍然成立?如果不成立,请直接写出∠A,∠APC与∠C之间的数量关系.
28.如图,直线l1∥l2,A、N为直线l1上的点,过点A的直线交l2于点B,C在线段BA的延长线上.D、E为直线l2上的两个动点,D在B的右侧,E在D的右侧,连接AD,AE,满足∠AED=∠DAE.点M在l2上,且在点B的左侧.
(1)如图1,若∠BAD=25°,∠AED=50°,则∠ABM的度数为 ;
(2)如图2,射线AF为∠CAD的角平分线.
①用等式表示∠EAF与∠ABD之间的数量关系,并给出证明;
②当∠ABM+∠EAF=150°时,∠EAF的度数为 .
参考答案
一.选择题(共10小题)
1.C.
2.B.
3.A.
4.D.
5.B.
6.C.
7.A.
8.B.
9.A.
10.C.
二.填空题(共8小题)
11.垂线段最短.
12.135
13.3360.
14.180.
15.180°.
16.70°.
17.②③④.
18.155.
三.解答题(共10小题)
19.解:(1)∵AO⊥BC,
∴∠AOC=90°,
∵∠AOE=65°,
∴∠COE=90°﹣∠AOE=25°;
(2)∵∠BOD+∠DOE+∠COE=90°,∠DOE=90°,
∴∠BOD+∠COE=90°,
∵∠BOD:∠COE=2:1,
∴∠BOD=2∠COE,
∴2∠COE+∠COE=90°,
∴∠COE=30°,
∴∠COD=∠COE+∠DOE=120°.
20.解:(1)由图中可得∠AOC的所有邻补角为∠BOC和∠AOD;
(2)∵AB⊥EO,
∴∠BOE=90°.
∵∠EOC=35°,
∴∠BOC=∠AOD=∠EOC+∠BOE=125°;
(3)∵∠BOC=2∠AOC,∠AOC+∠BOC=180°,
∴∠AOC+2∠AOC=180°,
∴∠AOC=60°,
∴∠BOD=∠AOC=60°,
∴∠DOE=∠BOE+∠BOD=90°+60°=150°.
21.证明:∵CF⊥AB、DE⊥AB(已知),
∴∠BED=90°,∠BFG=90°,
∴∠BED=∠BFC,
∴(ED)∥(FC)(同位角相等,两直线平行),
∴∠1=∠BCF(两直线平行,同位角相等),
∵∠1=∠2,
∴∠2=∠BCF(等量代换),
∴FG∥BC(内错角相等,两直线平行),
22.证明:(1)∵BD⊥AC,EF⊥AC,
∴BD∥EF,
∴∠2=∠CBD;
(2)∵∠1=∠2,∠2=∠CBD,
∴∠1=∠CBD,
∴GF∥BC,
∵∠AMD=∠AGF,
∴GF∥MD,
∴MD∥BC.
23.(1)证明:∵FG∥AE,
∴∠2=∠FGC,
又∵∠1=∠2,
∴∠1=∠FGC,
∴AB∥CD;
(2)解:∵AB∥CD,
∴∠ABD=180°﹣∠D=180°﹣108°=72°,
又∵BC平分∠ABD,
∴,
∵FG⊥BC,
∴∠BHF=90°,
在△BFH中,
∵∠BHF=90°,∠FBH=36°,
∴∠1=180°﹣∠BHF﹣∠FBH=180°﹣90°﹣36°=54°.
24.(1)证明:∵EF∥DC,
∴∠DCF+∠2=180°,
∵∠1+∠2=180°,
∴∠DCF=∠1,
∴DH∥AC;
(2)解:由(1)知DH∥AC,
∴∠∠BHD=∠ACB,
∵∠BHD=66°,
∴∠ACB=66°,
∵CD平分∠ACB,
∴∠ACD=∠BCD=33°,
∵EF∥DC,
∴∠ACD+∠2=180°,
∴∠2=147°.
25.解:(1)∵AB∥CD,∠ABC=45°,
∴∠BCD=∠ABC=45°,
(2)∵AB∥CD,∠ABC=45°,
∴∠BCD=∠ABC=45°,
∵CM平分∠BCD,
∴∠BCM=∠DCM=∠BCD=22.5°,
∵∠ECM+∠DCM=180°,
∴∠ECM=157.5°;
(3)∵AB∥CD,∠ABC=45°,
∴∠BCD=∠ABC=45°,
∵CM平分∠BCD,
∴∠BCM=∠DCM=∠BCD=22.5°,
∵CN⊥CM,
∴∠BCN=90°﹣22.5°=67.5°,
(4)∵CN⊥CM,
∴∠BCN+∠BCM=90°,
∵∠BCM=20°,
∴∠BCN=70°,
∵CN是∠BCE的平分线,
∴∠BCE=2∠BCN=2×70°=140°,
∵AB∥CD,
∴∠B+∠BCE=180°,
∵∠BCE=140°,
∴∠B=180°﹣∠BCE=180°﹣140°=40°.
26.解:(1)如图所示,过点F作FG∥AB,
∵AB∥CD,
∴AB∥FG∥CD,
∴∠ABF=∠BFG,∠CDF=∠DFG,
∵∠BFG+∠DFG=∠BFD,
∴∠BFD=∠ABF+∠CDF;
由上述证明可知,∠BFD=∠ABF+∠CDF,
∵BF为∠ABE的平分线,DF为∠CDE的平分线,
∴,,
∴,
∴∠ABE+∠CDE=2∠BFD;
(2)∠MDF=3∠CDM,理由如下:
如图所示,过点E作EQ∥AB,过点M作MP∥AB,
设∠CDM=x,∠ABM=y,
∵CD∥AB,
∴EQ∥MP∥AB∥CD,
∴∠CDM=∠PMD=x,∠ABM=∠PMB=y,
∵∠ABE+∠QEB=180°,∠CDE+∠QED=180°,
∴∠ABE+∠QEB+∠CDE+∠QED=360°,
∴∠ABE+∠CDE+∠BED=360°,
∴∠BDE=360﹣(∠ABE+∠CDE),
∵∠E+8∠M=360°,即∠BED+8∠BMD=360°,
∴360°﹣(∠ABE+∠CDE)+8∠BMD=360°,
∴8∠BMD=∠ABE+∠CDE,
∵∠BMD=∠PMD+∠PMB=x+y,
∴8∠BMD=8x+8y=∠ABE+∠CDE,
∵,
∴∠EBF=4y,
∵BF为∠ABE的平分线,DF为∠CDE的平分线,
∴∠EBF=∠ABF=4y,∠CDF=∠EDF,
∴∠ABE=8y,
∵∠ABE+∠CDE=8x+8y,
∴∠CDE=8x,
∴∠CDF=∠EDF=4x,
∵∠CDM=x,
∴∠MDF=3x,
∴∠MDF=3∠CDM.
27.解:(1)如图①,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∵∠A=30°,
∴∠APO=∠A=30°,∠C=∠CPO,
∵∠APC=80°
∴∠C=∠CPO=∠APC﹣∠APO=80°﹣30°=50°;
(2)∠A+∠C=∠APC,
证明:如图②,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠APC=∠APO+∠CPO=∠A+∠C;
(3)不成立,关系式是:∠A﹣∠C=∠APC,
理由:如图③,过P作PO∥AB,
∵AB∥CD,
∴AB∥PO∥CD,
∴∠APO=∠A,∠C=∠CPO,
∴∠A﹣∠C=∠APO﹣∠CPO=∠APC,
即∠A﹣∠C=∠APC.
28.解:(1)如图1:∵l1∥l2,
∴∠ABM=∠BAN,∠NAE=∠AED=50°,
∵∠BAD=25°,∠DAE=∠AED=50°,
∴∠ABM=∠BAN=∠BAD+∠DAE+∠NAE=25°+50°+50°=125°,
(2)①∠ABD=2∠EAF,
证明:∵l1∥l2,
∴∠CAN=∠ABD,∠NAE=∠AED,
又∵AF平分∠CAD,
∴∠DAF=∠CAF=∠CAD,
∵∠DAE=∠AED=∠NAE,
∴∠DAE=∠NAE=(∠DAE+∠NAE)=∠DAN,
∴∠EAF=∠DAF﹣∠DAE=∠CAD﹣∠DAN=∠CAN=∠ABD.
即∠ABD=2∠EAF;
②Ⅰ、如图所示:点D在点B右侧,此时有∠EAF=∠ABD,
∵∠ABM+∠EAF=150°,
∴∠ABM+∠ABD=150°,
又∵∠ABM+∠ABD=180°,
∴∠ABD=180°﹣150°=30°,
∴∠EAF=30°;
Ⅱ如图所示,点D在点B左侧,点E在点B右侧,
∵AE平分∠CAD,
∴∠DAF=∠CAD,
∵l1∥l2,
∴∠AED=∠NAE,∠CAN=∠ABE,
∵∠DAE=∠AED=∠NAE,
∴∠DAE=(∠DAE+∠NAE)=∠DAN,
∴∠EAF=∠DAF+∠DAE=(∠CAD+∠DAN)=×(360°﹣∠CAN)=180°﹣∠ABE,
∵∠ABE+∠ABM=180°,
∴∠EAF=180°﹣(180°﹣∠ABM)=90°+∠ABM,
又∵∠EAF+∠ABM=150°,
∴∠EAF=90°+(150°﹣∠EAF)=165°﹣∠EAF,
∴∠EAF=110°;
Ⅲ如图,D、E均在B点左侧,
此时,∠DAE=∠DAN,∠DAF=∠CAD,
∠EAF=∠DAE+∠DAF=(360°﹣∠CAN)=180°﹣∠ABG=180°﹣(180°﹣∠ABM)=90°+∠ABM,
∴∠EAF=110°.
综上所述:∠EAF=30°或∠EAF=110°.
