2010高中数学会考-直线与平面专题训练
文档属性
| 名称 | 2010高中数学会考-直线与平面专题训练 |  | |
| 格式 | rar | ||
| 文件大小 | 79.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-07-27 16:40:00 | ||
图片预览


文档简介
高中数学会考直线与平面专题训练
一、选择题:(本大题共12小题,每小题4分,共48分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
得分
答案
1、下列图形不一定是平面图形的是
A、三角形 B、梯形 C、四边形 D、平行四边形
2、如图,正方体中,直线和直线所成的角为
A、 B、 C、 D、
3、若直线a与直线b,c所成的角相等,则b,c的位置关系为
A、相交 B、平行
C、异面 D、以上答案都有可能
4、过四条两两平行的直线最多确定平面的个数是
A、3 B、4 C、5 D、6
5、当太阳光线与水平面的倾斜角为60°时,要使一根长为2m的细杆的影子最长,则细杆与水平地面所成的角为
A、15° B、30° C、45° D、60°
6、下图所示的是水平放置的三角形的直观图,D是△ABC中BC边的中点,那么AB、AD、AC三条线段中
A、最长的是AB,最短的是AC
B、最长的是AC,最短的是AB
C、最长的是AB,最短的是AD
D、最长的是AC,最短的是AD
7、已知直线m、n是异面直线,则过直线n且与直线m垂直的平面
A、有且只有一个 B、有一个或无数多个
C、有一个或不存在 D、不存在
8、以下命题(表示直线,表示平面)正确的个数有
①若,则 ; ②若,则
③若,则; ④若,则。
A、0个 B、1个 C、2个 D、3个
9、设是所在平面外的一点,且,则在这个平面的射影是的
A、重心 B、垂心 C、内心 D、外心
10、如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC等于
A.45° B.60° C.90° D.120°
11、在下列条件中,可判断平面α与β平行的是
A、α、β都垂直于平面r.
B、α内存在三点到β的距离相等.
C、l,m是α内两条直线,且l∥β,m∥β.
D、l,m是两条异面直线,且l∥α,m∥α, l∥β,m∥β.
12、正方体中,是的中点,为底面的中心,为棱
上的任意一点,则直线与直线所成的角为
A、 B、 C、 D、与点P的位置有关
二、填空题:(本大题共4小题,每小题4分,共16分)
13、过直线外一点与这条直线平行的直线有_________条,过直线外一点与这条直线平行的平面有_______个。
14、点P在Rt△ACB所在平面外,PC⊥平面ABC,∠C = 90°, 过P作侧面△PAB的高PD,D为垂足,则图中直角三角形有_________个。
15、若两直线a, b在平面α上的射影a', b' 是平行的直线,则a,b的位置关系是 。
16、直线的夹角为,O是空间一点,则过O与都成的直线有 ______ 条。
三、解答题:(本大题共4小题,共36分)
17、(8分)如图,正方体中,E为AB的中点,F为的中点,
求证: 四点共面。
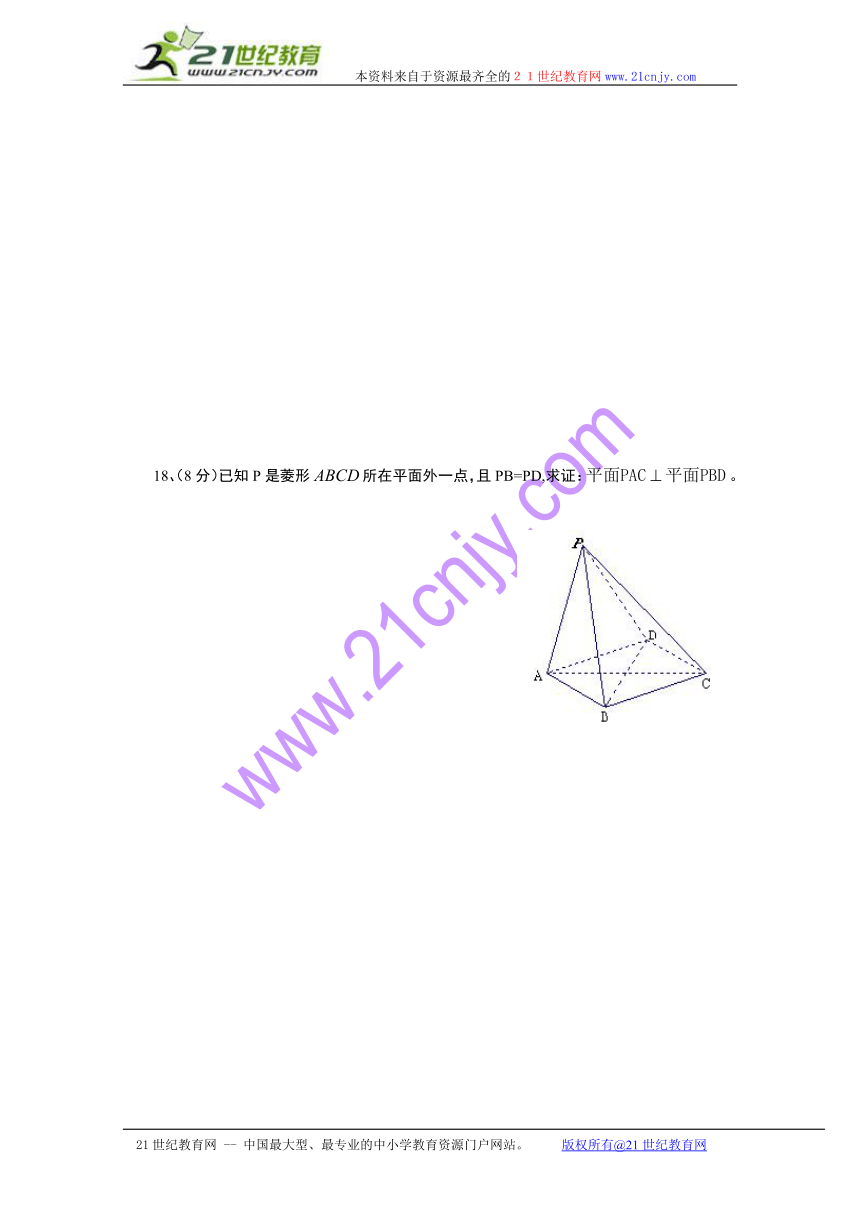
18、(8分)已知P是菱形所在平面外一点,且PB=PD,求证:。
19、(10分)已知长方体ABCD—A1B1C1D1中, A1A=AB, E、F分别是BD1和AD中点.
(1)求异面直线CD1、EF所成的角;
(2)证明EF是异面直线AD和BD1的公垂线.
20、(10分)如图,正方形ABCD和正方形ABEF所在平面互相垂直,M,N分别是对角线AC和BF上的点,且,求证:MN//平面BEC
数学参考答案
十一、直线与平面
一、选择题:CADDB BCBDB DC
二、填空题:13.1, 无数 14.8 15.平行或异面 16. 3
三、解答题
17.证明:在正方体中,
且,
, E、C、、 F 四点共面
18.证明:设AC与BD的交点为O
19.(1)解:∵在平行四边形中,E也是的中点,∴,
∴两相交直线D1C与CD1所成的角即异面直线CD1与EF所成的角.
又A1A=AB,长方体的侧面都是正方形,∴D1CCD1
∴异面直线CD1、EF所成的角为90°.
(2)证:设AB=AA1=a, ∵D1F=∴EF⊥BD1
由平行四边形,知E也是的中点,且点E是
长方体ABCD—A1B1C1D1的对称中心,
∴EA=ED,∴EF⊥AD,
又EF⊥BD1,∴EF是异面直线BD1与AD的公垂线.
20.过点M作于点P,连结 NP,CD
又
由(1)(2)得平面PNM//平面BEC ,.
一、选择题:(本大题共12小题,每小题4分,共48分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
得分
答案
1、下列图形不一定是平面图形的是
A、三角形 B、梯形 C、四边形 D、平行四边形
2、如图,正方体中,直线和直线所成的角为
A、 B、 C、 D、
3、若直线a与直线b,c所成的角相等,则b,c的位置关系为
A、相交 B、平行
C、异面 D、以上答案都有可能
4、过四条两两平行的直线最多确定平面的个数是
A、3 B、4 C、5 D、6
5、当太阳光线与水平面的倾斜角为60°时,要使一根长为2m的细杆的影子最长,则细杆与水平地面所成的角为
A、15° B、30° C、45° D、60°
6、下图所示的是水平放置的三角形的直观图,D是△ABC中BC边的中点,那么AB、AD、AC三条线段中
A、最长的是AB,最短的是AC
B、最长的是AC,最短的是AB
C、最长的是AB,最短的是AD
D、最长的是AC,最短的是AD
7、已知直线m、n是异面直线,则过直线n且与直线m垂直的平面
A、有且只有一个 B、有一个或无数多个
C、有一个或不存在 D、不存在
8、以下命题(表示直线,表示平面)正确的个数有
①若,则 ; ②若,则
③若,则; ④若,则。
A、0个 B、1个 C、2个 D、3个
9、设是所在平面外的一点,且,则在这个平面的射影是的
A、重心 B、垂心 C、内心 D、外心
10、如图,是一个无盖正方体盒子的表面展开图,A、B、C为其上的三个点,则在正方体盒子中,∠ABC等于
A.45° B.60° C.90° D.120°
11、在下列条件中,可判断平面α与β平行的是
A、α、β都垂直于平面r.
B、α内存在三点到β的距离相等.
C、l,m是α内两条直线,且l∥β,m∥β.
D、l,m是两条异面直线,且l∥α,m∥α, l∥β,m∥β.
12、正方体中,是的中点,为底面的中心,为棱
上的任意一点,则直线与直线所成的角为
A、 B、 C、 D、与点P的位置有关
二、填空题:(本大题共4小题,每小题4分,共16分)
13、过直线外一点与这条直线平行的直线有_________条,过直线外一点与这条直线平行的平面有_______个。
14、点P在Rt△ACB所在平面外,PC⊥平面ABC,∠C = 90°, 过P作侧面△PAB的高PD,D为垂足,则图中直角三角形有_________个。
15、若两直线a, b在平面α上的射影a', b' 是平行的直线,则a,b的位置关系是 。
16、直线的夹角为,O是空间一点,则过O与都成的直线有 ______ 条。
三、解答题:(本大题共4小题,共36分)
17、(8分)如图,正方体中,E为AB的中点,F为的中点,
求证: 四点共面。
18、(8分)已知P是菱形所在平面外一点,且PB=PD,求证:。
19、(10分)已知长方体ABCD—A1B1C1D1中, A1A=AB, E、F分别是BD1和AD中点.
(1)求异面直线CD1、EF所成的角;
(2)证明EF是异面直线AD和BD1的公垂线.
20、(10分)如图,正方形ABCD和正方形ABEF所在平面互相垂直,M,N分别是对角线AC和BF上的点,且,求证:MN//平面BEC
数学参考答案
十一、直线与平面
一、选择题:CADDB BCBDB DC
二、填空题:13.1, 无数 14.8 15.平行或异面 16. 3
三、解答题
17.证明:在正方体中,
且,
, E、C、、 F 四点共面
18.证明:设AC与BD的交点为O
19.(1)解:∵在平行四边形中,E也是的中点,∴,
∴两相交直线D1C与CD1所成的角即异面直线CD1与EF所成的角.
又A1A=AB,长方体的侧面都是正方形,∴D1CCD1
∴异面直线CD1、EF所成的角为90°.
(2)证:设AB=AA1=a, ∵D1F=∴EF⊥BD1
由平行四边形,知E也是的中点,且点E是
长方体ABCD—A1B1C1D1的对称中心,
∴EA=ED,∴EF⊥AD,
又EF⊥BD1,∴EF是异面直线BD1与AD的公垂线.
20.过点M作于点P,连结 NP,CD
又
由(1)(2)得平面PNM//平面BEC ,.
同课章节目录
