2024年北京二中高一(下)期中数学(PDF版含解析)
文档属性
| 名称 | 2024年北京二中高一(下)期中数学(PDF版含解析) |  | |
| 格式 | |||
| 文件大小 | 567.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-15 19:17:12 | ||
图片预览



文档简介
2024北京二中高一(下)期中
数 学
班级:___________姓名:___________学号:___________
一、单选题
5
1.复数 = 在复平面内所对应的点位于( )
1 2i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知向量 = ( 1,2), = (1, ),且 // ,那么 =( )
A. 5 B. 4 C. 2 D.0
3.在△ 中,若 = 105°, = 45°, = √2,则 =( )
A.1 B.√3 C.2 D.√6
4.如图,在矩形 中, = 2 , , 分别为 , 的中点, 为 中点,则 =( )
2 1 1
A. + B.
2
+
3
C.
3 2 2
+ D. +
3 3 3 3 4 4 3 3
5.设 、 表示两条不同的直线, 、 表示不同的平面,则下列命题中不正确的是( ).
A. ⊥ , ⊥ ,则 // B. // , ⊥ ,则 ⊥
C. ⊥ , ⊥ ,则 // D. // , ∩ = ,则 //
6.在△ 中,若 + 2 = 0,则△ 的形状一定是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
7.已知平面 , , , ∩ = , ∩ = ,则 ∥ 是 ∥ 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.在正方体 1 1 1 1中,M是 的中点,N是 1 1的中点,则异面直线 1 与 所成角的余弦
值为( )
1 3 3 4
A. B. C. D.
2 5 4 5
9.已知正方形 的边长为2,动点 在以 为圆心且与 相切的圆上,则 的取值范围是( )
A.[ 2√2, 2√2] B.[0,2√2] C.[ 4,4] D.[0,4]
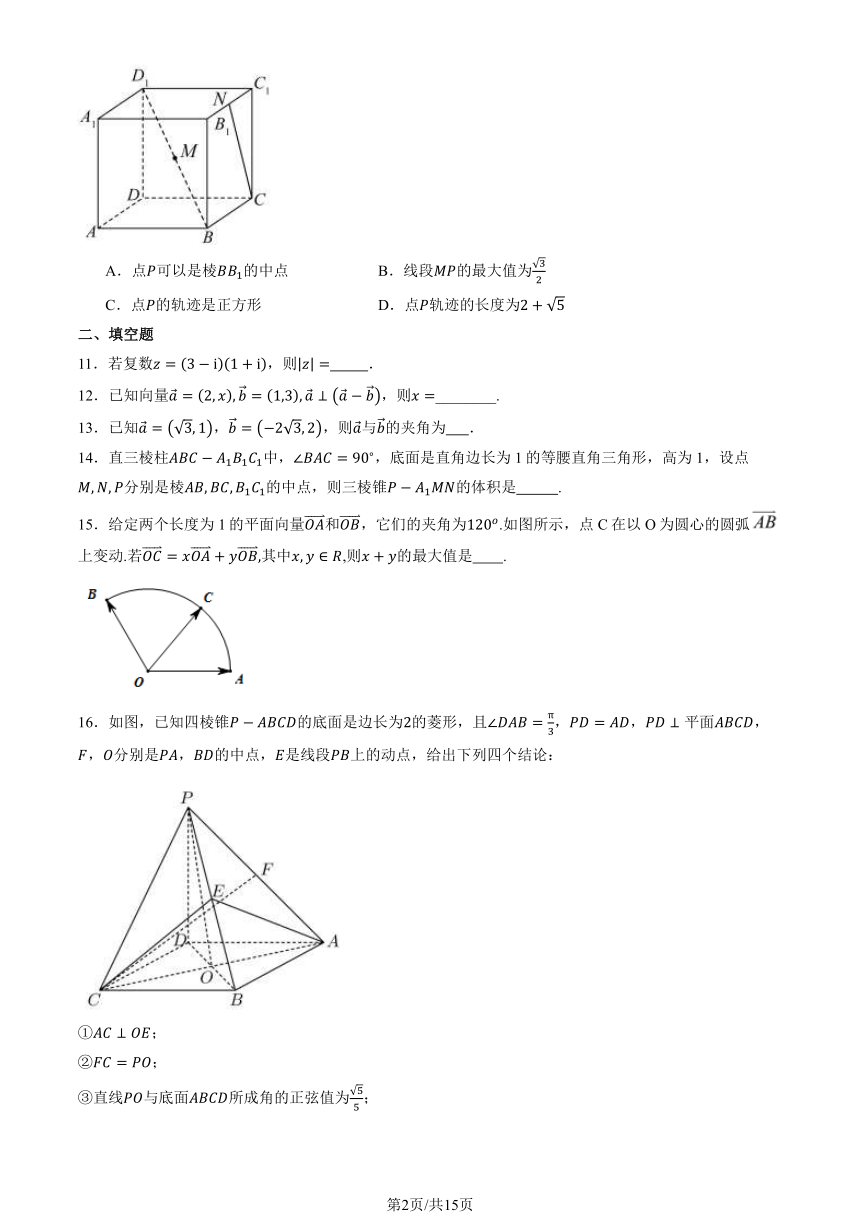
10.在棱长为 1 的正方体 1 1 1 1中, , 分别为 1, 1 1的中点,点 在正方体的表面上运
动,且满足 //平面 1,则下列说法正确的是( )
第1页/共15页
√3
A.点 可以是棱 1的中点 B.线段 的最大值为 2
C.点 的轨迹是正方形 D.点 轨迹的长度为2 + √5
二、填空题
11.若复数 = (3 i)(1 + i),则| | = .
12.已知向量 = (2, ), = (1,3), ⊥ ( ),则 =________.
13.已知 = (√3, 1), = ( 2√3, 2),则 与 的夹角为 .
14.直三棱柱 1 1 1中,∠ = 90
,底面是直角边长为 1 的等腰直角三角形,高为 1,设点
, , 分别是棱 , , 1 1的中点,则三棱锥 1 的体积是 .
15.给定两个长度为 1 的平面向量 和 ,它们的夹角为120 .如图所示,点 C 在以 O 为圆心的圆弧
上变动.若 = + ,其中 , ∈ ,则 + 的最大值是 .
π
16.如图,已知四棱锥 的底面是边长为2的菱形,且∠ = , = , ⊥ 平面 ,
3
, 分别是 , 的中点, 是线段 上的动点,给出下列四个结论:
① ⊥ ;
② = ;
√5
③直线 与底面 所成角的正弦值为 ;
5
第2页/共15页
√6
④△ 面积的取值范围是[ , √15].
2
其中所有正确结论的序号是 .
三、解答题
1
17.如图所示,在四棱锥 中, //平面 , = , 是 的中点.
2
(1)求证: // ;
(2)求证: //平面 ;
18.如图,在正方体 1 1 1 1中, 1 = 2, 为 1的中点, 为 1的中点.
(1)求证:平面 1 1 ⊥平面 1 1;
(2)求证: ⊥平面 1 1;
(3)设 为正方体 1 1 1 1棱上一点,给出满足条件 = √2的点 的个数.(结论不要求证明)
19.如图所示,D为△ 外一点,且∠ = 135 , ⊥ , = √2, = 1, = 2,
(1)求 sin∠ACD的值;
(2)求 BD的长.
20.在△ 中, sin cos = 0.
(1)求 ;
(2)求√2cos + cos 的最大值.
(3)再从条件①、条件②、条件③这三个条件中选择两个作为已知,使△ 存在且唯一确定,求△ 的
面积.
条件①: = √2 ;
第3页/共15页
√10
条件②:sin = ;
10
条件③: = √10.
注:如果选择的条件不符合要求,第(3)问得 0 分;如果选择多个符合要求的条件分别解答,按第一个
解答计分.
a1 b1 c1 d1
*
21.已知 0 = (a0,b0,c0,d0 )和数表 A = a2 b2 c2 d2 ,其中ai ,bi ,ci ,di N (i = 0,1,2,3 ) .若数表A 满足如
a3 b3 c d
3 3
下两个性质,则称数表A 由 0生成.
①任意 i 0,1,2 ,ai+1 ai ,bi+1 bi ,ci+1 ci ,di+1 di 中有三个 1,一个 3;
②存在 k 1,2,3 ,使ak ,bk ,ck ,dk 中恰有三个数相等.
5 6 6 6
(1)判断数表 A = 4 5 5 9 是否由 0 = (6,7,7,3 )生成;(结论无需证明)
3 8 4 8
(2)是否存在数表A 由 0 = (6,7,7,4)生成?说明理由;
0 = (7,12,3,d ) d(3)若存在数表A 由 0 生成,写出 0 所有可能的值.
第4页/共15页
参考答案
1.A
【分析】根据复数的运算法则求出复数即可判断.
5 5(1+2i) 5(1+2i)
【详解】由题意知, = = = = 1 + 2i,
1 2i (1 2i)(1+2i) 5
5
所以 = 在复平面内所对应的点为(1,2),位于第一象限.
1 2i
故选:A.
2.C
【分析】根据向量共线的坐标表示得到方程,解得即可.
【详解】解:因为 = ( 1,2), = (1, ),且 // ,
所以 = 1 × 2,解得 = 2.
故选:C
3.A
【分析】由题意可得 ,再由正弦定理即可得到结果.
【详解】因为 = 105°, = 45°,所以 = 30°,
1
sin √2×
由正弦定理可得 = = 2 = 1.
sin √2
2
故选:A
4.C
【分析】根据向量加法的三角形法则和四边形法则,可得结果.
1
【详解】根据题意: = ( + )
2
又
1
= + = +
2
1
= + = +
2
3 3
所以 = +
4 4
故选:C
【点睛】本题主要考查利用向量的加法法则,熟练掌握向量加法的三角形法则和平行四边形法则,对向量
用其它向量表示有很大的作用,属基础题.
5.D
【详解】A 选项中命题是真命题, ⊥ , ⊥ ,可以推出 // ;
B 选项中命题是真命题, // , ⊥ ,可得出 ⊥ ;
C 选项中命题是真命题, ⊥ , ⊥ ,,利用线面垂直的性质得到 // ;
D 选项中命题是假命题,因为两直线平行或异面.
故选 D.
6.B
第5页/共15页
【分析】先利用数量积运算化简得到 cos = 2,再利用余弦定理化简得解.
【详解】因为 + 2 = 0,所以 cos( ) + 2 = 0,
2+ 2 2
所以 cos = 2,所以 × = 2,
2
所以 2 + 2 = 2,所以三角形是直角三角形.
故选:B
7.A
【分析】结合面面平行的性质定理和线面平行的性质定理即可判断.
【详解】因为 ∥ , ∩ = , ∩ = ,所以由面面平行的性质定理可得 ∥ ,则充分性成立;
因为 ∥ , ∩ = , ∩ = 可知,所以{ ,则 ∥ ,又{ ,则 ∥ ,当 ∩ = 时,由线
面平行的性质定理可知 ∥ ∥ ,则必要性不成立;
综上所述, ∥ 是 ∥ 的充分不必要条件.
故选:A.
8.D
【分析】设正方体棱长为 2,取 中点 E,BC中点 F连接 ,可证得 1 // 1 , // 1 ,则∠ 1 为 1
与 所成角,计算即可求得结果.
【详解】设正方体棱长为 2,取 中点 E,BC中点 F连接 ,
∵ C1D1//MF,C1D1=MF,∴四边形 1 1为平行四边形,∴ 1 // 1 .
∵ C1N//DE,C1N=DE,∴四边形 1为平行四边形,∴ // 1 .
∴ ∠ 1 为 1 与 所成角.
在△ 1 中, 1 = 1 = √5, = √2,
5+5 2 4
∴ cos∠ 1 = = . 2×√5×√5 5
4
∴ 1 与 所成角的余弦值为 . 5
故选:D
9.C
【分析】根据条件可建立直角坐标系,写出点的坐标,根据点坐标得向量坐标,进而根据向量数量积的坐
标运算即可求解.
【详解】以点 为圆心,以 , 分别为 , 轴,建立如图所示的平面直角坐标系,则:
(0,0), (0,2), (2,2), (2,0)
第6页/共15页
圆 的半径为√2,∴设 (√2cos , √2sin ), ∈ R
∴ = (√2cos 2, √2sin 2), = (2, 2),
∴
π
= 2(√2cos 2) 2(√2sin 2) = 4cos( + ),
4
π π
当cos( + ) = 1时, 取最小值 4,当cos( + ) = 1时 取最大值 4
4 4
故选:C
10.B
【分析】
如图,取棱 的中点 ,连接 , 1 , ,进而证明平面 1 //平面 1,再结合题意可知直线 1 必
过 点,进而取 1 1中点 ,连接 1 , , ,证明 ∈平面 1 即可得四边形 1 为点 的轨迹,再根
据几何关系依次判断各选项即可.
【详解】解:如图,取棱 的中点 ,连接 , 1 , ,
因为 , 分别为 1, 1 1的中点,
所以,在△ 1中, // 1,由于 平面 1, 1 平面 1,
所以 //平面 1,
因为 1 // , 1 = ,所以,四边形 1 为平行四边形,
所以 // 1 ,因为 平面 1, 1 平面 1,
所以, 1 //平面 1,
因为 1 ∩ = , 1 , 平面 1 ,
所以,平面 1 //平面 1,
由于 为体对角线 1的中点,
所以,连接 1 并延长,直线 1 必过 点,
故取 1 1中点 ,连接 1 , , ,
所以,由正方体的性质易知 1// , 1 = ,
所以,四边形 1 是平行四边形, // 1, = 1,
1
因为, // 1, = 1, 2
所以, , , 共线,即 ∈平面 1 ,
所以,四边形 1 为点 的轨迹,故 A 选项错误;
√5
由正方体的棱长为1,所以,四边形 1 的棱长均为 ,且对角线为 = √2, 1 = √3,, 2
第7页/共15页
所以,四边形 1 为菱形,周长为2√5,故 CD 选项错误,
1 √3
由菱形的性质知,线段 的最大值为 1 = ,故 B 选项正确. 2 2
故选:B
【点睛】关键点点睛:本题解题的关键在于取棱 的中点 ,进而证明平面 1 //平面 1,再根据面
面平行的性质求解点 轨迹即可求解.
11.2√5
【分析】利用复数乘法运算化简,进而求模即可.
【详解】∵ = (3 i)(1 + i) = 4 + 2i,
∴| | = √16+4=2√5.
故答案为:2√5
12. =1 或者 2
【分析】求出 坐标,再根据 ( ) = 0列方程求解.
→ →
【详解】由已知 = (1, 3),
又 ⊥ ( ),
→ → →
所以 ( ) = 2 + ( 3) = 0,
解得 =1 或者 2
2π
13.
3
【分析】根据题意结合向量的坐标运算求解.
【详解】由题意可知: = 6 + 2 = 4, | | = 2, | | = 4,
1
可得cos , = = ,且 , ∈ [0,π],
| | | | 2
2π
所以 与 的夹角为 .
3
2π
故答案为: .
3
1
14.
24
【分析】根据线面平行,可知 = 1 ,然后根据等体积法即可求解.
【详解】因为 , 分别是棱 , 1 1的中点,所以 // 1 , 平面 , 1 平面 ,所以 1//平
面
第8页/共15页
1 1 1 1
= = = 1 1 = 3 △
= × =
3 8 24
1
故答案为:
24
15.2
1
【详解】 =
2
1
+ =
2
+ = 2( + ) = 2 = 2cos < , >
所以最大值为 2
16.①④
【分析】①通过线面垂直证明线线垂直
②通过计算可得到结果
③通过线面角的定义与计算可得到结果
④通过求 OE的取值范围计算三角形面积的取值范围
【详解】
由 ⊥ , ⊥ 得 ⊥平面 ,因为 平面 ,所以 ⊥ ,①正确
计算可得 = 2√3, = = 2√2, = √2, = √3
2
= √ 2 2 = √(2√2)2 √3 = √5
2 + 2 2 (2√3)2 + (2√2)2 (2√2)2 √6
cos∠ = = =
2| || | 2 × 2√3 × 2√2 4
2 √6
2 = 2 + 2 2| || |cos∠ = √2 + (2√3)2 2 × 2√3 × √2 × = 8
4
所以 = 2√2,②不正确;
2√5
由线面角定义知,∠ 就是直线 与底面 所成的角,sin∠ = ,③不正确;
5
第9页/共15页
1
由 ⊥ 平面 得, ⊥ , △ = = √3 × 2
√2
| |max = √5, ⊥ 时| |最小,| |min = ④正确. 2
故答案为:①④
17.(1)证明见解析
(2)证明见解析
【分析】(1)由题意利用线面平行的性质定理即可证明 // ;
(2)取 的中点 ,连接 , ,由(1)可证明 是平行四边形,再利用线面平行的判定定理即可得
//平面 .
【详解】(1)根据题意可得, //平面 ,
平面 ,且平面 ∩平面 = ,
由线面平行的性质定理可得 // ;
(2)取 的中点为 ,连接 , ,如下图所示:
1
由 是 的中点, 是 的中点,可得 // ,且 = ;
2
1
由(1)知 // ,且 = ,所以 // ,且 = ;
2
所以四边形 是平行四边形,
即 // ,又 平面 , 平面 ;
所以 //平面 .
18.(1)证明见解析,(2)证明见解析,(3)12
【分析】(1)由正方体的性质可得 1 1 ⊥平面 1 1,再由面面垂直的判定定理可证得结论;
(2)连接 1 1,可证得 1 1 ⊥平面 1 1,连接 1,可得 ∥ 1 1,从而可证得结论;
(3)只要求出以 为球心,√2为半径的球与正方体棱的交点个数即可
【详解】(1)证明:在正方体 1 1 1 1中, 1 1 ⊥平面 1 1,
因为 1 1 平面 1 1,
所以平面 1 1 ⊥平面 1 1;
(2)证明:连接 1 1, 1,则 1 1 ⊥ 1 1,
因为 1 ⊥平面 1 1 1 1, 1 1 平面 1 1 1 1,
所以 1 ⊥ 1 1,
因为 1 ∩ 1 1 = 1,所以 1 1 ⊥平面 1 1,
连接 1,因为 为 1的中点,所以 是 1的中点,
因为 为 1的中点,所以 ∥ 1 1,
第10页/共15页
所以 ⊥平面 1 1;
(3)因为在正方体 1 1 1 1中, 1 = 2,且 为正方体体对角线的交点,
所以 到每条棱的距离均为√2,
所以满足条件 = √2的点 的个数为 12
√5
19.(1)
5
√65
(2)
5
【分析】(1)利用余弦定理求出 边的长,用勾股定理得出 边的长,即可求出 sin∠ACD的值;
(2)由正弦定理求出∠ 与∠ 的关系,由余弦定理即可求出 BD的长.
【详解】(1)由题意,
在△ 中,∠ = 135 , = √2, = 1,
由余弦定理得, 2 = 2 + 2 2 cos∠ ,
√2
∴ 2 = 2 + 1 2 × √2 × 1 × ( ).
2
∴ = √5.
∴在Rt △ 中, ⊥ , = 2,
= √ 2 2 = √5 4 = 1,
√5
∴ sin∠ = = .
5
(2)由题意及(1)得,
在△ 中,由正弦定理得, = .
sin∠ sin∠
√2
√2× √5
∴sin∠ = 2 = ,且0 < ∠ < 45 .
√5 5
又0 < ∠ < 90 ,
∴∠ = ∠ ,
1 3
∴cos∠ = cos2∠ = 1 2sin2∠ = 1 2 × = .
5 5
在△ 中, = 1, = 2,
由余弦定理得, 2 = 2 + 2 2 cos∠ ,
3 13
∴ 2 = 1 + 4 2 × 1 × 2 × = ,
5 5
第11页/共15页
√65
∴ = .
5
20.(1) ;
4
(2)答案见解析.
【分析】(1)利用正弦定理得到sin = cos ,由 ∈ (0, ),即可求出 A;
√5 √190+√10 √10
(2)选条件②③:利用正弦定理求得sin = ,再由 AC 求出sin = ≠ ,即可判断出这样的
10 20 10
三角形不存在.
选条件①③:利用余弦定理求得 = √10, = 2√5,满足 2 + 2 = 2,即可判断出三角形存在且唯一,
进而求出三角形的面积.
选条件①②:由正弦定理求得 = √2,由余弦定理求得 = 4, = √10, = √2,这样的三角形存在且唯
一,进而求出三角形的面积.
【详解】(1)在△ 中, sin cos = 0,由正弦定理得:sin sin sin cos = 0.
因为 ∈ (0, ),所以sin ≠ 0,所以sin = cos .
因为 ∈ (0, ),所以 = .
4
√10
(2)选条件②③:在△ 中, = , = √2 ,sin = .
4 10
√2 √10 √5
由正弦定理得:sin = √2sin ,所以sin = × = .
2 10 10
2
√5 √95
因为 = √2 > ,所以 C必为锐角,所以cos = √1 sin2 = √1 ( ) = .
10 10
所以sin = sin( + ) = sin cos + cos sin
√2 √95 √2 √5
= × + ×
2 10 2 10
√190+√10 √10
= ≠ .
20 10
所以这样的三角形不存在.
选条件①③:在△ 中, = , = √2 , = √10.
4
由余弦定理 2 = 2 + 2
2 cos 得:10 = 2 2 + 2 2 × √2 2cos ,解得: = √10.
4
所以 = √2 = 2√5,满足 2 + 2 = 2,即△ 为直角三角形,这样的三角形存在且唯一.
1 1
此时, △ = = × √10 × √10 = 5. 2 2
√10
选条件①②:在△ 中, = ,sin = , = √10.
4 10
√10
sin √10×
由正弦定理 = 得: = = 10 = √2.
sin sin sin √2
2
√2
由余弦定理 2 = 2 + 2 2 cos 得:10 = 2 + 2 2 × √2 × ,
2
解得: = 4( = 2舍去).
= 4, = √10, = √2也满足三角形两边之和大于第三边,两边之差小于第三边.
故这样的三角形存在且唯一.
第12页/共15页
1 1 √10
此时, △ = sin = × √10 × 4 × = 2. 2 2 10
21.(1)是
(2)不存在,理由见解析
(3)3,7,11.
【分析】(1)根据数表A 满足的两个性质进行检验,即可得结论;
(2)采用反证的方法,即若存在这样的数表 A,由性质①推出对任意的 k 1,2,3 ,ak ,bk ,ck ,dk 中均有 2
个奇数,2 个偶数,则推出不满足性质②,即得结论;
(3)判断出 d0 的所有可能的值为 3,7,11,一方面说明 d0 取这些值时可以由 0 = (7,12,3,d0 )生成数表
A,另一方面,分类证明 d0 的取值只能为 3,7,11,由此可得 d0 所有可能的值.
5 6 6 6
【详解】(1)数表 A = 4 5 5 9 是由 0 = (6,7,7,3)生成;
3 8 4 8
检验性质①:
当 i = 0时,5 6 = 1,6 7 = 1,6 7 = 1,6 3 = 3,共三个 1,一个 3;
当 i =1时, 4 5 = 1,5 6 = 1,5 6 = 1,9 6 = 3,共三个 1,一个 3;
当 i = 2时,3 4 = 1,8 5 = 3,4 5 = 1,8 9 = 1,共三个 1,一个 3;
任意 i 0,1,2 ,ai+1 ai ,bi+1 bi ,ci+1 ci ,di+1 di 中有三个 1,一个 3;
检验性质②:
当 k =1时, a1 = 5,b1 = 6,c1 = 6,d1 = 6,恰有 3 个数相等.
(2)不存在数表A 由 0 = (6,7,7, 4)生成,理由如下:
若存在这样的数表 A,由性质①任意 i 0,1,2 ,ai+1 ai ,bi+1 bi ,ci+1 ci ,di+1 di 中有三个 1,一个 3,
则 a ai+1 ai = 3或-1,总有 i+1与 ai 的奇偶性相反,
类似的,bi+1 与bi 的奇偶性相反, ci+1 与 ci 的奇偶性相反,di+1与 d i的奇偶性相反;
因为 a0 = 6,b0 = 7,c0 = 7,d0 = 4中恰有 2 个奇数,2 个偶数,
所以对任意的 k 1,2,3 ,ak ,bk ,ck ,dk 中均有 2 个奇数,2 个偶数,
此时ak ,bk ,ck ,dk 中至多有 2 个数相等,不满足性质②;
综上,不存在数表A 由 0 = (6,7,7,4)生成;
(3) d0 的所有可能的值为 3,7,11.
6 11 2 6
一方面,当 d0 = 3时, (7,12,3,3) 可以生成数表 A = 5 10 5 5 ;
4 13 4 4
6 11 6 6
当 d0 = 7时, (7,12,3,7) 可以生成数表 A = 5 14 5 5 ;
4 17 4 4
第13页/共15页
6 11 6 10
当 d0 =11时, (7,12,3,11)可以生成数表 A = 5 10 9 9 ;
8 9 8 8
另一方面,若存在数表 A由 0 = (7,12,3,d0 )生成,
首先证明: d0 除以 4 余 3;
证明:对任意的 i = 0,1,2,3,令 i = ai bi ,
则Δi+1 Δi = (at+1 bi+1 ) (ai bi ) = (ai+1 ai ) (bi+1 bi ),
分三种情况:(i)若 ai+1 ai = 1,且bi+1 bi = 1,则 i+1 i = 0;
(ii)若ai+1 ai = 1,且bi+1 bi = 3,则 i+1 i = 4;
(iii)若ai+1 ai = 3,且bi+1 bi = 1,则 i+1 i = 4 ;
均有 i+1 与 i 除以 4 的余数相同.
特别的,“存在 k 1,2,3 ,使得 ak = bk ”的一个必要不充分条件为“ a0 ,b0 除以 4 的余数相同”;
类似的,“存在 k 1,2,3 ,使得 ak = ck ”的一个必要不充分条件为“ a0 ,c0除以 4 的余数相同”;
“存在 k 1,2,3 ,使得 ak = dk ”的一个必要不充分条件为“ a0 ,d0 除以 4 的余数相同”;
“存在 k 1,2,3 ,使得bk = ck ”的一个必要不充分条件为“b0 ,c0除以 4 的余数相同”;
“存在 k 1,2,3 ,使得bk = dk ”的一个必要不充分条件为“b0 ,d0 除以 4 的余数相同”;
“存在 k 1,2,3 ,使得 ck = dk ”的一个必要不充分条件为“ c0 ,d0 除以 4 的余数相同”;
所以,存在 k 1,2,3 ,使得ak ,bk ,ck ,dk 中恰有 3 个数相等的一个必要不充分条件是ak ,bk ,ck ,dk 中至少有 3
个数除以 4 的余数相同.
注意到 a0 = 7与 c0 = 3除以 4 余 3,b0 =12除以 4 余 0,故 d0 除以 4 余 3.
其次证明: d0 {3,7,11,15};
证明:只需证明 d0 15;
由上述证明知若 0 = (7,12,3,d0 )可以生成数表 A,则必存在 k 1,2,3 ,
使得 ak = ck = dk ;
若 d0 15,则 d0 c0 15 3 =12, d1 c1 (d0 c0 ) 4 8,d2 c2 (d1 c1 ) 4 4,
d3 c3 (d2 c2 ) 4 0 ,
所以,对任意 k 1,2,3 ,均有 dk ck 0 ,矛盾;
最后证明: d0 15;
证明:由上述证明可得若 0 = (7,12,3,d0 )可以生成数表 A,
则必存在 k 1,2,3 ,使得 ak = ck = dk ,
d0 c0 =15 3 =12,d1 c1 (d0 c0 ) 4 = 8,d2 c2 (d1 c1 ) 4 4,
第14页/共15页
d3 c3 (d2 c2 ) 4 0,
欲使上述等号成立,对任意的 k 1,2,3 , ck+1 ck = 3,dk+1 dk = 1,
6 11 6 14
则 ak+1 ak = 1,bk+1 bk = 1, A = 5 10 9 13 ,
4 9 12 12
经检验,不符合题意;
综上, d0 所有可能的取值为 3,7,11
第15页/共15页
数 学
班级:___________姓名:___________学号:___________
一、单选题
5
1.复数 = 在复平面内所对应的点位于( )
1 2i
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.已知向量 = ( 1,2), = (1, ),且 // ,那么 =( )
A. 5 B. 4 C. 2 D.0
3.在△ 中,若 = 105°, = 45°, = √2,则 =( )
A.1 B.√3 C.2 D.√6
4.如图,在矩形 中, = 2 , , 分别为 , 的中点, 为 中点,则 =( )
2 1 1
A. + B.
2
+
3
C.
3 2 2
+ D. +
3 3 3 3 4 4 3 3
5.设 、 表示两条不同的直线, 、 表示不同的平面,则下列命题中不正确的是( ).
A. ⊥ , ⊥ ,则 // B. // , ⊥ ,则 ⊥
C. ⊥ , ⊥ ,则 // D. // , ∩ = ,则 //
6.在△ 中,若 + 2 = 0,则△ 的形状一定是( )
A.等边三角形 B.直角三角形
C.等腰三角形 D.等腰直角三角形
7.已知平面 , , , ∩ = , ∩ = ,则 ∥ 是 ∥ 的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
8.在正方体 1 1 1 1中,M是 的中点,N是 1 1的中点,则异面直线 1 与 所成角的余弦
值为( )
1 3 3 4
A. B. C. D.
2 5 4 5
9.已知正方形 的边长为2,动点 在以 为圆心且与 相切的圆上,则 的取值范围是( )
A.[ 2√2, 2√2] B.[0,2√2] C.[ 4,4] D.[0,4]
10.在棱长为 1 的正方体 1 1 1 1中, , 分别为 1, 1 1的中点,点 在正方体的表面上运
动,且满足 //平面 1,则下列说法正确的是( )
第1页/共15页
√3
A.点 可以是棱 1的中点 B.线段 的最大值为 2
C.点 的轨迹是正方形 D.点 轨迹的长度为2 + √5
二、填空题
11.若复数 = (3 i)(1 + i),则| | = .
12.已知向量 = (2, ), = (1,3), ⊥ ( ),则 =________.
13.已知 = (√3, 1), = ( 2√3, 2),则 与 的夹角为 .
14.直三棱柱 1 1 1中,∠ = 90
,底面是直角边长为 1 的等腰直角三角形,高为 1,设点
, , 分别是棱 , , 1 1的中点,则三棱锥 1 的体积是 .
15.给定两个长度为 1 的平面向量 和 ,它们的夹角为120 .如图所示,点 C 在以 O 为圆心的圆弧
上变动.若 = + ,其中 , ∈ ,则 + 的最大值是 .
π
16.如图,已知四棱锥 的底面是边长为2的菱形,且∠ = , = , ⊥ 平面 ,
3
, 分别是 , 的中点, 是线段 上的动点,给出下列四个结论:
① ⊥ ;
② = ;
√5
③直线 与底面 所成角的正弦值为 ;
5
第2页/共15页
√6
④△ 面积的取值范围是[ , √15].
2
其中所有正确结论的序号是 .
三、解答题
1
17.如图所示,在四棱锥 中, //平面 , = , 是 的中点.
2
(1)求证: // ;
(2)求证: //平面 ;
18.如图,在正方体 1 1 1 1中, 1 = 2, 为 1的中点, 为 1的中点.
(1)求证:平面 1 1 ⊥平面 1 1;
(2)求证: ⊥平面 1 1;
(3)设 为正方体 1 1 1 1棱上一点,给出满足条件 = √2的点 的个数.(结论不要求证明)
19.如图所示,D为△ 外一点,且∠ = 135 , ⊥ , = √2, = 1, = 2,
(1)求 sin∠ACD的值;
(2)求 BD的长.
20.在△ 中, sin cos = 0.
(1)求 ;
(2)求√2cos + cos 的最大值.
(3)再从条件①、条件②、条件③这三个条件中选择两个作为已知,使△ 存在且唯一确定,求△ 的
面积.
条件①: = √2 ;
第3页/共15页
√10
条件②:sin = ;
10
条件③: = √10.
注:如果选择的条件不符合要求,第(3)问得 0 分;如果选择多个符合要求的条件分别解答,按第一个
解答计分.
a1 b1 c1 d1
*
21.已知 0 = (a0,b0,c0,d0 )和数表 A = a2 b2 c2 d2 ,其中ai ,bi ,ci ,di N (i = 0,1,2,3 ) .若数表A 满足如
a3 b3 c d
3 3
下两个性质,则称数表A 由 0生成.
①任意 i 0,1,2 ,ai+1 ai ,bi+1 bi ,ci+1 ci ,di+1 di 中有三个 1,一个 3;
②存在 k 1,2,3 ,使ak ,bk ,ck ,dk 中恰有三个数相等.
5 6 6 6
(1)判断数表 A = 4 5 5 9 是否由 0 = (6,7,7,3 )生成;(结论无需证明)
3 8 4 8
(2)是否存在数表A 由 0 = (6,7,7,4)生成?说明理由;
0 = (7,12,3,d ) d(3)若存在数表A 由 0 生成,写出 0 所有可能的值.
第4页/共15页
参考答案
1.A
【分析】根据复数的运算法则求出复数即可判断.
5 5(1+2i) 5(1+2i)
【详解】由题意知, = = = = 1 + 2i,
1 2i (1 2i)(1+2i) 5
5
所以 = 在复平面内所对应的点为(1,2),位于第一象限.
1 2i
故选:A.
2.C
【分析】根据向量共线的坐标表示得到方程,解得即可.
【详解】解:因为 = ( 1,2), = (1, ),且 // ,
所以 = 1 × 2,解得 = 2.
故选:C
3.A
【分析】由题意可得 ,再由正弦定理即可得到结果.
【详解】因为 = 105°, = 45°,所以 = 30°,
1
sin √2×
由正弦定理可得 = = 2 = 1.
sin √2
2
故选:A
4.C
【分析】根据向量加法的三角形法则和四边形法则,可得结果.
1
【详解】根据题意: = ( + )
2
又
1
= + = +
2
1
= + = +
2
3 3
所以 = +
4 4
故选:C
【点睛】本题主要考查利用向量的加法法则,熟练掌握向量加法的三角形法则和平行四边形法则,对向量
用其它向量表示有很大的作用,属基础题.
5.D
【详解】A 选项中命题是真命题, ⊥ , ⊥ ,可以推出 // ;
B 选项中命题是真命题, // , ⊥ ,可得出 ⊥ ;
C 选项中命题是真命题, ⊥ , ⊥ ,,利用线面垂直的性质得到 // ;
D 选项中命题是假命题,因为两直线平行或异面.
故选 D.
6.B
第5页/共15页
【分析】先利用数量积运算化简得到 cos = 2,再利用余弦定理化简得解.
【详解】因为 + 2 = 0,所以 cos( ) + 2 = 0,
2+ 2 2
所以 cos = 2,所以 × = 2,
2
所以 2 + 2 = 2,所以三角形是直角三角形.
故选:B
7.A
【分析】结合面面平行的性质定理和线面平行的性质定理即可判断.
【详解】因为 ∥ , ∩ = , ∩ = ,所以由面面平行的性质定理可得 ∥ ,则充分性成立;
因为 ∥ , ∩ = , ∩ = 可知,所以{ ,则 ∥ ,又{ ,则 ∥ ,当 ∩ = 时,由线
面平行的性质定理可知 ∥ ∥ ,则必要性不成立;
综上所述, ∥ 是 ∥ 的充分不必要条件.
故选:A.
8.D
【分析】设正方体棱长为 2,取 中点 E,BC中点 F连接 ,可证得 1 // 1 , // 1 ,则∠ 1 为 1
与 所成角,计算即可求得结果.
【详解】设正方体棱长为 2,取 中点 E,BC中点 F连接 ,
∵ C1D1//MF,C1D1=MF,∴四边形 1 1为平行四边形,∴ 1 // 1 .
∵ C1N//DE,C1N=DE,∴四边形 1为平行四边形,∴ // 1 .
∴ ∠ 1 为 1 与 所成角.
在△ 1 中, 1 = 1 = √5, = √2,
5+5 2 4
∴ cos∠ 1 = = . 2×√5×√5 5
4
∴ 1 与 所成角的余弦值为 . 5
故选:D
9.C
【分析】根据条件可建立直角坐标系,写出点的坐标,根据点坐标得向量坐标,进而根据向量数量积的坐
标运算即可求解.
【详解】以点 为圆心,以 , 分别为 , 轴,建立如图所示的平面直角坐标系,则:
(0,0), (0,2), (2,2), (2,0)
第6页/共15页
圆 的半径为√2,∴设 (√2cos , √2sin ), ∈ R
∴ = (√2cos 2, √2sin 2), = (2, 2),
∴
π
= 2(√2cos 2) 2(√2sin 2) = 4cos( + ),
4
π π
当cos( + ) = 1时, 取最小值 4,当cos( + ) = 1时 取最大值 4
4 4
故选:C
10.B
【分析】
如图,取棱 的中点 ,连接 , 1 , ,进而证明平面 1 //平面 1,再结合题意可知直线 1 必
过 点,进而取 1 1中点 ,连接 1 , , ,证明 ∈平面 1 即可得四边形 1 为点 的轨迹,再根
据几何关系依次判断各选项即可.
【详解】解:如图,取棱 的中点 ,连接 , 1 , ,
因为 , 分别为 1, 1 1的中点,
所以,在△ 1中, // 1,由于 平面 1, 1 平面 1,
所以 //平面 1,
因为 1 // , 1 = ,所以,四边形 1 为平行四边形,
所以 // 1 ,因为 平面 1, 1 平面 1,
所以, 1 //平面 1,
因为 1 ∩ = , 1 , 平面 1 ,
所以,平面 1 //平面 1,
由于 为体对角线 1的中点,
所以,连接 1 并延长,直线 1 必过 点,
故取 1 1中点 ,连接 1 , , ,
所以,由正方体的性质易知 1// , 1 = ,
所以,四边形 1 是平行四边形, // 1, = 1,
1
因为, // 1, = 1, 2
所以, , , 共线,即 ∈平面 1 ,
所以,四边形 1 为点 的轨迹,故 A 选项错误;
√5
由正方体的棱长为1,所以,四边形 1 的棱长均为 ,且对角线为 = √2, 1 = √3,, 2
第7页/共15页
所以,四边形 1 为菱形,周长为2√5,故 CD 选项错误,
1 √3
由菱形的性质知,线段 的最大值为 1 = ,故 B 选项正确. 2 2
故选:B
【点睛】关键点点睛:本题解题的关键在于取棱 的中点 ,进而证明平面 1 //平面 1,再根据面
面平行的性质求解点 轨迹即可求解.
11.2√5
【分析】利用复数乘法运算化简,进而求模即可.
【详解】∵ = (3 i)(1 + i) = 4 + 2i,
∴| | = √16+4=2√5.
故答案为:2√5
12. =1 或者 2
【分析】求出 坐标,再根据 ( ) = 0列方程求解.
→ →
【详解】由已知 = (1, 3),
又 ⊥ ( ),
→ → →
所以 ( ) = 2 + ( 3) = 0,
解得 =1 或者 2
2π
13.
3
【分析】根据题意结合向量的坐标运算求解.
【详解】由题意可知: = 6 + 2 = 4, | | = 2, | | = 4,
1
可得cos , = = ,且 , ∈ [0,π],
| | | | 2
2π
所以 与 的夹角为 .
3
2π
故答案为: .
3
1
14.
24
【分析】根据线面平行,可知 = 1 ,然后根据等体积法即可求解.
【详解】因为 , 分别是棱 , 1 1的中点,所以 // 1 , 平面 , 1 平面 ,所以 1//平
面
第8页/共15页
1 1 1 1
= = = 1 1 = 3 △
= × =
3 8 24
1
故答案为:
24
15.2
1
【详解】 =
2
1
+ =
2
+ = 2( + ) = 2 = 2cos < , >
所以最大值为 2
16.①④
【分析】①通过线面垂直证明线线垂直
②通过计算可得到结果
③通过线面角的定义与计算可得到结果
④通过求 OE的取值范围计算三角形面积的取值范围
【详解】
由 ⊥ , ⊥ 得 ⊥平面 ,因为 平面 ,所以 ⊥ ,①正确
计算可得 = 2√3, = = 2√2, = √2, = √3
2
= √ 2 2 = √(2√2)2 √3 = √5
2 + 2 2 (2√3)2 + (2√2)2 (2√2)2 √6
cos∠ = = =
2| || | 2 × 2√3 × 2√2 4
2 √6
2 = 2 + 2 2| || |cos∠ = √2 + (2√3)2 2 × 2√3 × √2 × = 8
4
所以 = 2√2,②不正确;
2√5
由线面角定义知,∠ 就是直线 与底面 所成的角,sin∠ = ,③不正确;
5
第9页/共15页
1
由 ⊥ 平面 得, ⊥ , △ = = √3 × 2
√2
| |max = √5, ⊥ 时| |最小,| |min = ④正确. 2
故答案为:①④
17.(1)证明见解析
(2)证明见解析
【分析】(1)由题意利用线面平行的性质定理即可证明 // ;
(2)取 的中点 ,连接 , ,由(1)可证明 是平行四边形,再利用线面平行的判定定理即可得
//平面 .
【详解】(1)根据题意可得, //平面 ,
平面 ,且平面 ∩平面 = ,
由线面平行的性质定理可得 // ;
(2)取 的中点为 ,连接 , ,如下图所示:
1
由 是 的中点, 是 的中点,可得 // ,且 = ;
2
1
由(1)知 // ,且 = ,所以 // ,且 = ;
2
所以四边形 是平行四边形,
即 // ,又 平面 , 平面 ;
所以 //平面 .
18.(1)证明见解析,(2)证明见解析,(3)12
【分析】(1)由正方体的性质可得 1 1 ⊥平面 1 1,再由面面垂直的判定定理可证得结论;
(2)连接 1 1,可证得 1 1 ⊥平面 1 1,连接 1,可得 ∥ 1 1,从而可证得结论;
(3)只要求出以 为球心,√2为半径的球与正方体棱的交点个数即可
【详解】(1)证明:在正方体 1 1 1 1中, 1 1 ⊥平面 1 1,
因为 1 1 平面 1 1,
所以平面 1 1 ⊥平面 1 1;
(2)证明:连接 1 1, 1,则 1 1 ⊥ 1 1,
因为 1 ⊥平面 1 1 1 1, 1 1 平面 1 1 1 1,
所以 1 ⊥ 1 1,
因为 1 ∩ 1 1 = 1,所以 1 1 ⊥平面 1 1,
连接 1,因为 为 1的中点,所以 是 1的中点,
因为 为 1的中点,所以 ∥ 1 1,
第10页/共15页
所以 ⊥平面 1 1;
(3)因为在正方体 1 1 1 1中, 1 = 2,且 为正方体体对角线的交点,
所以 到每条棱的距离均为√2,
所以满足条件 = √2的点 的个数为 12
√5
19.(1)
5
√65
(2)
5
【分析】(1)利用余弦定理求出 边的长,用勾股定理得出 边的长,即可求出 sin∠ACD的值;
(2)由正弦定理求出∠ 与∠ 的关系,由余弦定理即可求出 BD的长.
【详解】(1)由题意,
在△ 中,∠ = 135 , = √2, = 1,
由余弦定理得, 2 = 2 + 2 2 cos∠ ,
√2
∴ 2 = 2 + 1 2 × √2 × 1 × ( ).
2
∴ = √5.
∴在Rt △ 中, ⊥ , = 2,
= √ 2 2 = √5 4 = 1,
√5
∴ sin∠ = = .
5
(2)由题意及(1)得,
在△ 中,由正弦定理得, = .
sin∠ sin∠
√2
√2× √5
∴sin∠ = 2 = ,且0 < ∠ < 45 .
√5 5
又0 < ∠ < 90 ,
∴∠ = ∠ ,
1 3
∴cos∠ = cos2∠ = 1 2sin2∠ = 1 2 × = .
5 5
在△ 中, = 1, = 2,
由余弦定理得, 2 = 2 + 2 2 cos∠ ,
3 13
∴ 2 = 1 + 4 2 × 1 × 2 × = ,
5 5
第11页/共15页
√65
∴ = .
5
20.(1) ;
4
(2)答案见解析.
【分析】(1)利用正弦定理得到sin = cos ,由 ∈ (0, ),即可求出 A;
√5 √190+√10 √10
(2)选条件②③:利用正弦定理求得sin = ,再由 AC 求出sin = ≠ ,即可判断出这样的
10 20 10
三角形不存在.
选条件①③:利用余弦定理求得 = √10, = 2√5,满足 2 + 2 = 2,即可判断出三角形存在且唯一,
进而求出三角形的面积.
选条件①②:由正弦定理求得 = √2,由余弦定理求得 = 4, = √10, = √2,这样的三角形存在且唯
一,进而求出三角形的面积.
【详解】(1)在△ 中, sin cos = 0,由正弦定理得:sin sin sin cos = 0.
因为 ∈ (0, ),所以sin ≠ 0,所以sin = cos .
因为 ∈ (0, ),所以 = .
4
√10
(2)选条件②③:在△ 中, = , = √2 ,sin = .
4 10
√2 √10 √5
由正弦定理得:sin = √2sin ,所以sin = × = .
2 10 10
2
√5 √95
因为 = √2 > ,所以 C必为锐角,所以cos = √1 sin2 = √1 ( ) = .
10 10
所以sin = sin( + ) = sin cos + cos sin
√2 √95 √2 √5
= × + ×
2 10 2 10
√190+√10 √10
= ≠ .
20 10
所以这样的三角形不存在.
选条件①③:在△ 中, = , = √2 , = √10.
4
由余弦定理 2 = 2 + 2
2 cos 得:10 = 2 2 + 2 2 × √2 2cos ,解得: = √10.
4
所以 = √2 = 2√5,满足 2 + 2 = 2,即△ 为直角三角形,这样的三角形存在且唯一.
1 1
此时, △ = = × √10 × √10 = 5. 2 2
√10
选条件①②:在△ 中, = ,sin = , = √10.
4 10
√10
sin √10×
由正弦定理 = 得: = = 10 = √2.
sin sin sin √2
2
√2
由余弦定理 2 = 2 + 2 2 cos 得:10 = 2 + 2 2 × √2 × ,
2
解得: = 4( = 2舍去).
= 4, = √10, = √2也满足三角形两边之和大于第三边,两边之差小于第三边.
故这样的三角形存在且唯一.
第12页/共15页
1 1 √10
此时, △ = sin = × √10 × 4 × = 2. 2 2 10
21.(1)是
(2)不存在,理由见解析
(3)3,7,11.
【分析】(1)根据数表A 满足的两个性质进行检验,即可得结论;
(2)采用反证的方法,即若存在这样的数表 A,由性质①推出对任意的 k 1,2,3 ,ak ,bk ,ck ,dk 中均有 2
个奇数,2 个偶数,则推出不满足性质②,即得结论;
(3)判断出 d0 的所有可能的值为 3,7,11,一方面说明 d0 取这些值时可以由 0 = (7,12,3,d0 )生成数表
A,另一方面,分类证明 d0 的取值只能为 3,7,11,由此可得 d0 所有可能的值.
5 6 6 6
【详解】(1)数表 A = 4 5 5 9 是由 0 = (6,7,7,3)生成;
3 8 4 8
检验性质①:
当 i = 0时,5 6 = 1,6 7 = 1,6 7 = 1,6 3 = 3,共三个 1,一个 3;
当 i =1时, 4 5 = 1,5 6 = 1,5 6 = 1,9 6 = 3,共三个 1,一个 3;
当 i = 2时,3 4 = 1,8 5 = 3,4 5 = 1,8 9 = 1,共三个 1,一个 3;
任意 i 0,1,2 ,ai+1 ai ,bi+1 bi ,ci+1 ci ,di+1 di 中有三个 1,一个 3;
检验性质②:
当 k =1时, a1 = 5,b1 = 6,c1 = 6,d1 = 6,恰有 3 个数相等.
(2)不存在数表A 由 0 = (6,7,7, 4)生成,理由如下:
若存在这样的数表 A,由性质①任意 i 0,1,2 ,ai+1 ai ,bi+1 bi ,ci+1 ci ,di+1 di 中有三个 1,一个 3,
则 a ai+1 ai = 3或-1,总有 i+1与 ai 的奇偶性相反,
类似的,bi+1 与bi 的奇偶性相反, ci+1 与 ci 的奇偶性相反,di+1与 d i的奇偶性相反;
因为 a0 = 6,b0 = 7,c0 = 7,d0 = 4中恰有 2 个奇数,2 个偶数,
所以对任意的 k 1,2,3 ,ak ,bk ,ck ,dk 中均有 2 个奇数,2 个偶数,
此时ak ,bk ,ck ,dk 中至多有 2 个数相等,不满足性质②;
综上,不存在数表A 由 0 = (6,7,7,4)生成;
(3) d0 的所有可能的值为 3,7,11.
6 11 2 6
一方面,当 d0 = 3时, (7,12,3,3) 可以生成数表 A = 5 10 5 5 ;
4 13 4 4
6 11 6 6
当 d0 = 7时, (7,12,3,7) 可以生成数表 A = 5 14 5 5 ;
4 17 4 4
第13页/共15页
6 11 6 10
当 d0 =11时, (7,12,3,11)可以生成数表 A = 5 10 9 9 ;
8 9 8 8
另一方面,若存在数表 A由 0 = (7,12,3,d0 )生成,
首先证明: d0 除以 4 余 3;
证明:对任意的 i = 0,1,2,3,令 i = ai bi ,
则Δi+1 Δi = (at+1 bi+1 ) (ai bi ) = (ai+1 ai ) (bi+1 bi ),
分三种情况:(i)若 ai+1 ai = 1,且bi+1 bi = 1,则 i+1 i = 0;
(ii)若ai+1 ai = 1,且bi+1 bi = 3,则 i+1 i = 4;
(iii)若ai+1 ai = 3,且bi+1 bi = 1,则 i+1 i = 4 ;
均有 i+1 与 i 除以 4 的余数相同.
特别的,“存在 k 1,2,3 ,使得 ak = bk ”的一个必要不充分条件为“ a0 ,b0 除以 4 的余数相同”;
类似的,“存在 k 1,2,3 ,使得 ak = ck ”的一个必要不充分条件为“ a0 ,c0除以 4 的余数相同”;
“存在 k 1,2,3 ,使得 ak = dk ”的一个必要不充分条件为“ a0 ,d0 除以 4 的余数相同”;
“存在 k 1,2,3 ,使得bk = ck ”的一个必要不充分条件为“b0 ,c0除以 4 的余数相同”;
“存在 k 1,2,3 ,使得bk = dk ”的一个必要不充分条件为“b0 ,d0 除以 4 的余数相同”;
“存在 k 1,2,3 ,使得 ck = dk ”的一个必要不充分条件为“ c0 ,d0 除以 4 的余数相同”;
所以,存在 k 1,2,3 ,使得ak ,bk ,ck ,dk 中恰有 3 个数相等的一个必要不充分条件是ak ,bk ,ck ,dk 中至少有 3
个数除以 4 的余数相同.
注意到 a0 = 7与 c0 = 3除以 4 余 3,b0 =12除以 4 余 0,故 d0 除以 4 余 3.
其次证明: d0 {3,7,11,15};
证明:只需证明 d0 15;
由上述证明知若 0 = (7,12,3,d0 )可以生成数表 A,则必存在 k 1,2,3 ,
使得 ak = ck = dk ;
若 d0 15,则 d0 c0 15 3 =12, d1 c1 (d0 c0 ) 4 8,d2 c2 (d1 c1 ) 4 4,
d3 c3 (d2 c2 ) 4 0 ,
所以,对任意 k 1,2,3 ,均有 dk ck 0 ,矛盾;
最后证明: d0 15;
证明:由上述证明可得若 0 = (7,12,3,d0 )可以生成数表 A,
则必存在 k 1,2,3 ,使得 ak = ck = dk ,
d0 c0 =15 3 =12,d1 c1 (d0 c0 ) 4 = 8,d2 c2 (d1 c1 ) 4 4,
第14页/共15页
d3 c3 (d2 c2 ) 4 0,
欲使上述等号成立,对任意的 k 1,2,3 , ck+1 ck = 3,dk+1 dk = 1,
6 11 6 14
则 ak+1 ak = 1,bk+1 bk = 1, A = 5 10 9 13 ,
4 9 12 12
经检验,不符合题意;
综上, d0 所有可能的取值为 3,7,11
第15页/共15页
同课章节目录
