26.1.2反比例函数的图像与性质(3课时)
文档属性
| 名称 | 26.1.2反比例函数的图像与性质(3课时) |  | |
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-24 22:05:03 | ||
图片预览



文档简介
课件37张PPT。26.1.2 反比例函数的
图像和性质(1)学习内容和目标1.学习内容:书4页至6页
2.学习目标:
(1)会画反比例函数的图像,会正确辨析反比例函数的增减性
(2)能根据图像,确定反比例函数的解析式
3.学习重点: 重点:会画反比例函数的图像,会正确辨析反比例函数的增减性
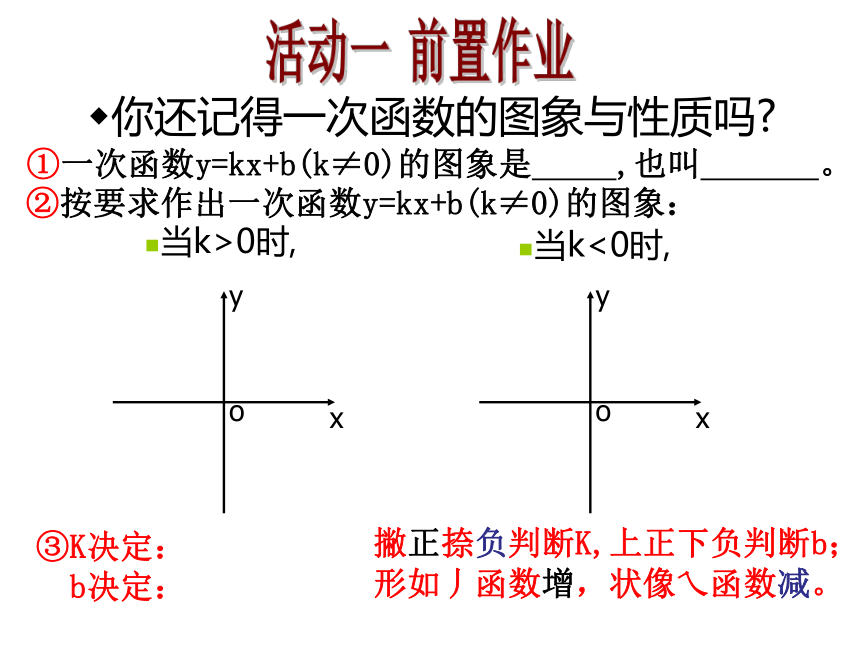
你还记得一次函数的图象与性质吗?①一次函数y=kx+b(k≠0)的图象是 ,也叫 。
当k>0时,当k<0时,活动一 前置作业②按要求作出一次函数y=kx+b(k≠0)的图象:
撇正捺负判断K,上正下负判断b;
形如丿函数增,状像乀函数减。③K决定:
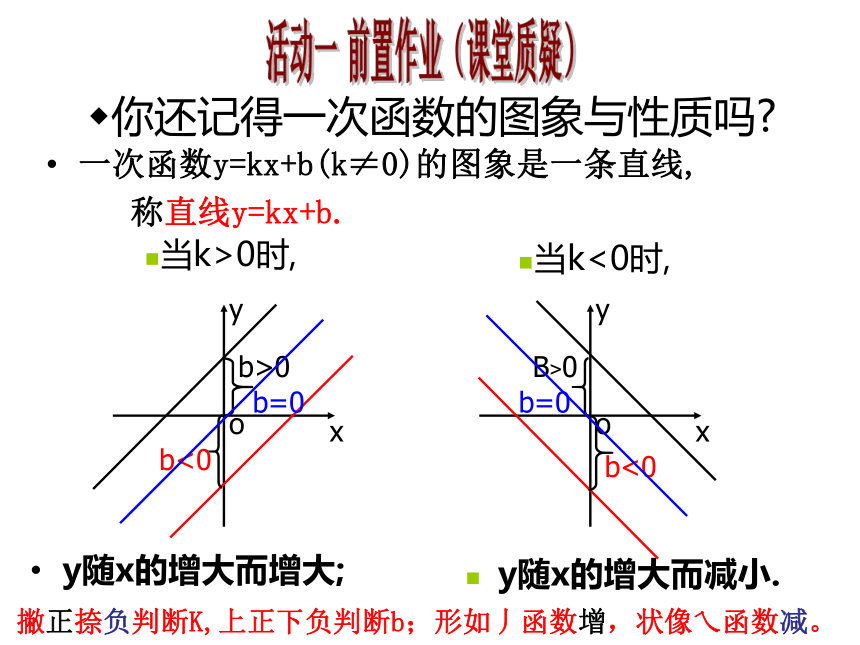
b决定:你还记得一次函数的图象与性质吗?一次函数y=kx+b(k≠0)的图象是一条直线,
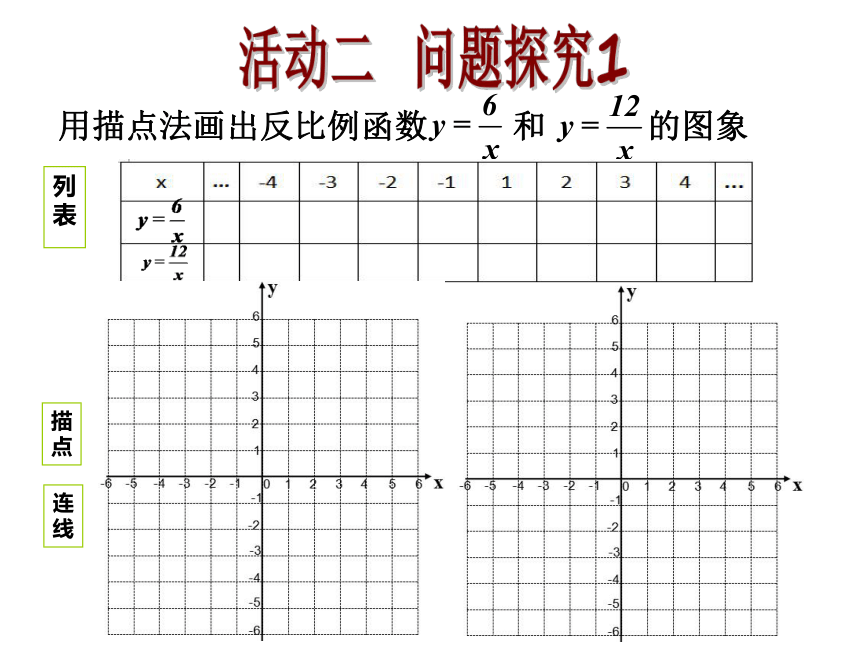
称直线y=kx+b.y随x的增大而增大;y随x的增大而减小.当k>0时,当k<0时,活动一 前置作业(课堂质疑)撇正捺负判断K,上正下负判断b;形如丿函数增,状像乀函数减。活动二 问题探究1用描点法画出反比例函数 和 的图象列
表描
点连
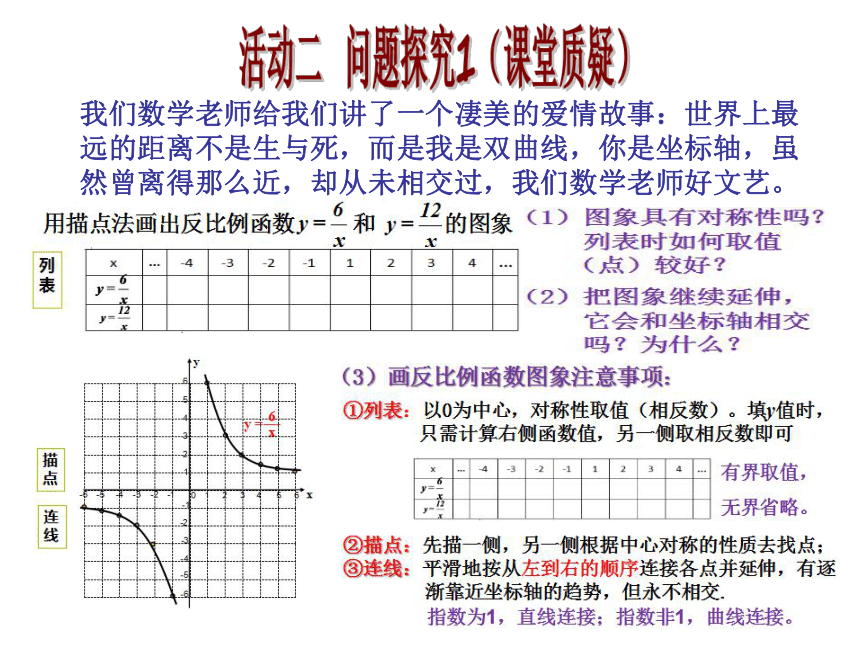
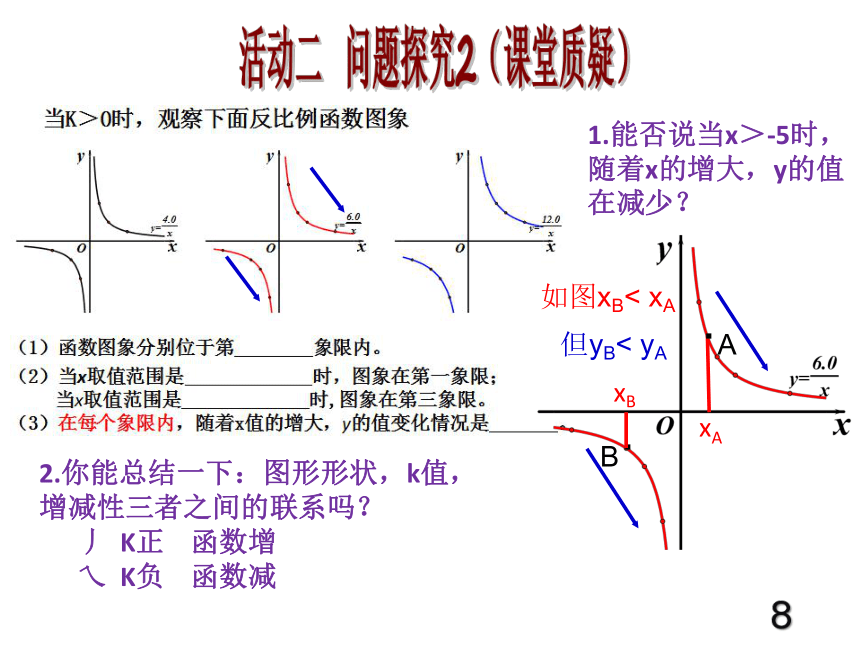
线活动二 问题探究1(课堂质疑)我们数学老师给我们讲了一个凄美的爱情故事:世界上最远的距离不是生与死,而是我是双曲线,你是坐标轴,虽然曾离得那么近,却从未相交过,我们数学老师好文艺。当K>0时,观察下面反比例函数图象(1)函数图象的两个分支分别位于第 象限内。(2)当x取值范围是 时,图象在第一象限;当x取值范围是 时,图象在第三象限。(3)在每个象限内,随着x值的增大,y的值变化情况是 。活动二 问题探究27B·如图xB< xA但yB< yAxA·AxB活动二 问题探究2(课堂质疑)1.能否说当x>-5时,随着x的增大,y的值在减少?2.你能总结一下:图形形状,k值,
增减性三者之间的联系吗?
丿 K正 函数增
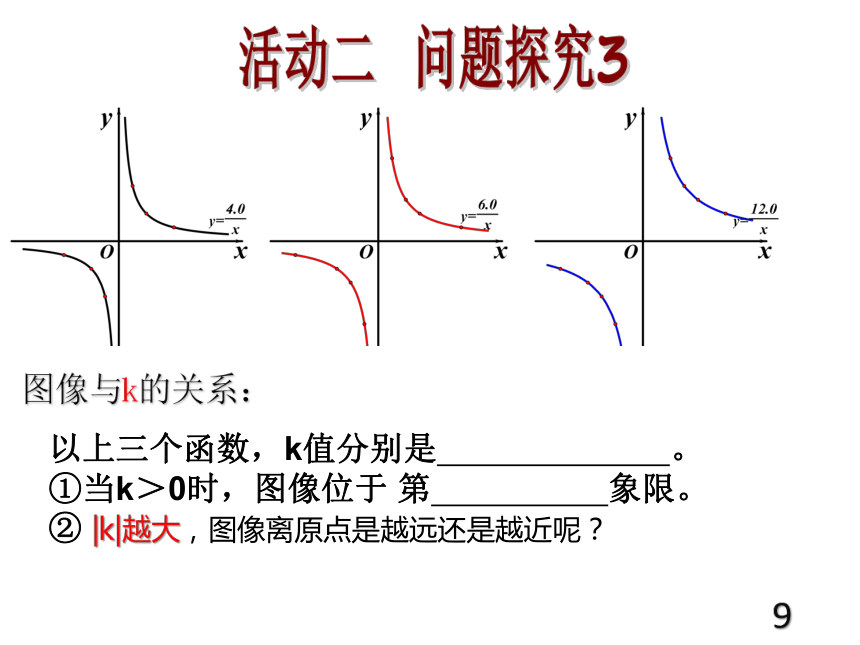
乀 K负 函数减8活动二 问题探究3图像与k的关系:以上三个函数,k值分别是 。
①当k>0时,图像位于 第 象限。
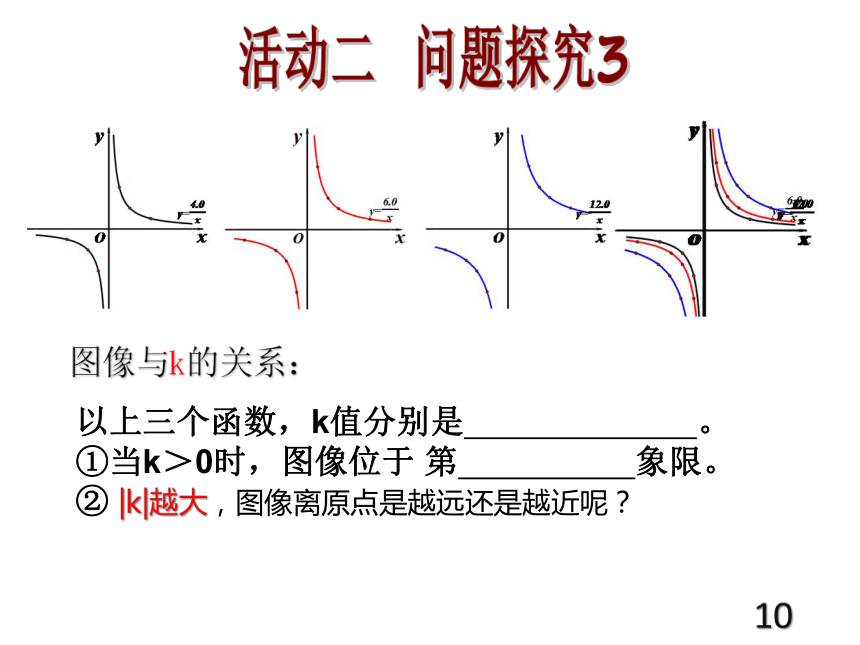
② |k|越大,图像离原点是越远还是越近呢?9活动二 问题探究3图像与k的关系:以上三个函数,k值分别是 。
①当k>0时,图像位于 第 象限。
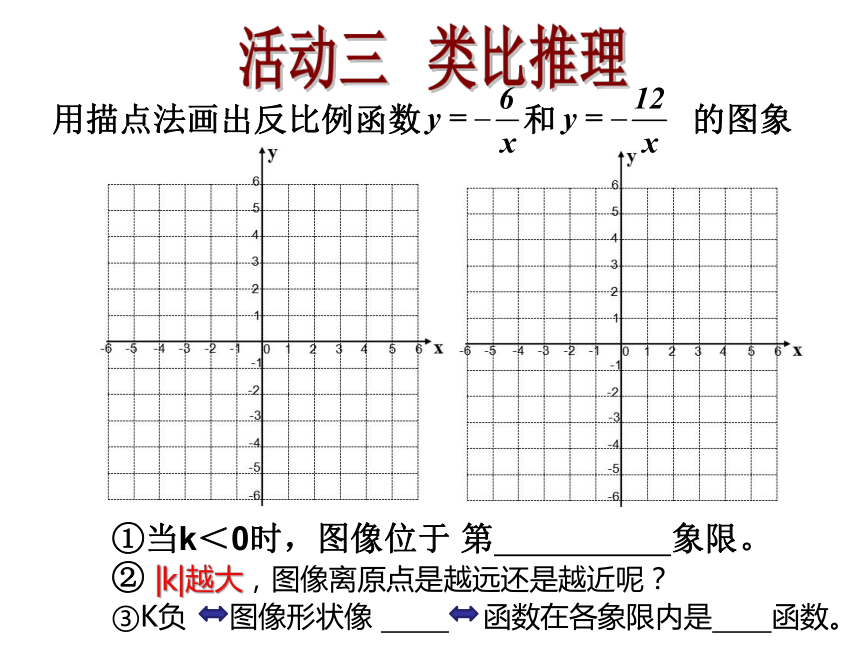
② |k|越大,图像离原点是越远还是越近呢?10活动三 类比推理用描点法画出反比例函数 和 的图象①当k<0时,图像位于 第 象限。
② |k|越大,图像离原点是越远还是越近呢?
③K负 图像形状像 函数在各象限内是 函数。
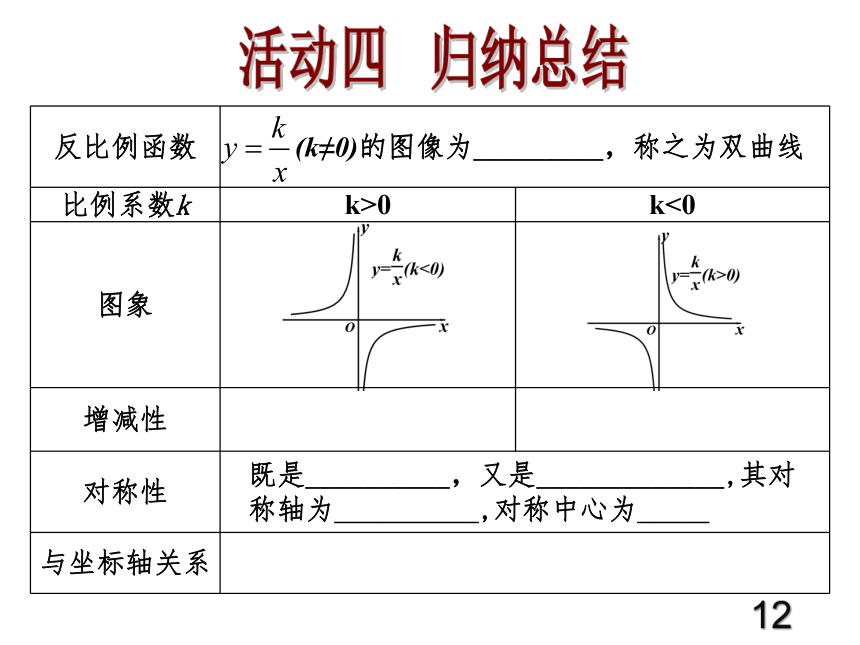
12活动四 归纳总结活动五 巩固练习1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________.2.反比例函数 的图象经过点(-3,-4) ,则点(m,m-2)在第______象限?????3.已知点A(-2,y1),B(-1,y2),C(3,y3) 都在反比例函数
的图象上,比较y1、 y2 、y3的大小关系。134.在同一直角坐标系中,函数y=kx与 (k≠0) 的图象可能是________?(1) (2) (3) (4)145.如图是三个反比例函数在x轴
上方的图像,由此观察得到k1、
k2、k3的大小关系为( )
A.k1>k2>k3 B. k3>k2>k1
C.k2>k3>k1 D. k3>k1>k21k2k326.1.2 反比例函数的
图像和性质(2)反比例函数与几何图形面积学习内容和目标1.学习内容:中考题型总结
2.学习目标:
(1)掌握反比例函数与正比例函数的区别与联系
(2)掌握反比例函数中k 的几何意义
3.学习重点: 重点:反比例函数的图像的面积定理
活动一 面积性质1(2)点P位置变化了,△OAP的面积会
变化吗?为什么?
(3)若将此题改为过P点作y轴的垂线
段,其结论成立吗?写出推理过程:
活动一 课堂质疑活动二 面积性质2(2)点P位置变化了,四边形OAPB
的面积会变化吗?为什么?活动二 课堂质疑活动三 面积性质3活动三 课堂质疑1.如图,点P是反比例函数 图象上的
一点,PD⊥x轴于D.则△POD的面积为 .活动四 巩固练习A.S = 1 B.124.如图:A、C是函数 的图象上任意两点,
过A作X轴的垂线,垂足为B;过C作y轴
的垂线,垂足为D,记Rt△AOB的面积为S1
Rt△OCB的面积为S2,则 A.S1>S2 B.S1 S2 >S3 26.1.2 反比例函数的
图像和性质(3)反比例函数交点问题学习内容和目标1.学习内容:中考题型总结
2.学习目标:
(1)掌握反比例函数与正比例函数的区别与联系
(2)掌握反比例函数与一次函数的区别与联系
3.学习重点: 重点:掌握反比例函数与一次函数的区别与联系
活动一 前置作业1.①在左图中任意做一条直线y=kx(k>0)
②在图中找出直线与双曲线的交点坐标
是 。
③你从正比例函数的图像和反比例函数
图像的交点坐标中发现什么规律了吗?
2.如图所示,你能求出直线 与双曲
线 的交点坐标吗?活动一 课堂质疑1、与坐标轴的交点问题:
无限趋近于x、y轴, 与x、y轴无交点。
2、与正比例函数的交点问题:
可以利用反比例函数的中心对称性。
3、与一次函数的交点问题:
列方程组,求公共解,即交点坐标。活动二 题型讲练活动三 题型巩固1.5.如图所示,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2= (k<0)分别交于点C、D,且C点坐标为(-1,2). (3)利用图象直接写出当x在什么范围内取何值时,y1>y2.(2)求出点D的坐标;(1)分别求直线AB与双曲线的解析式;(4)试着在坐标轴上找点D,使△AOD≌△BOC。(1)分别写出这两个函数的表达式。(2)你能求出点B的坐标吗?你是怎样求的?(3)若点C坐标是(–4,0).请求△BOC的面积。6、如图所示,正比例函数y=k1x的图象与反比例函数y= 的图象交于A、B两点,其中点A的坐标为 。 (4,0)画图象①列表:以0为中心,对称性取值(相反数)。填y值时,只需计算右侧函数值,另一侧取相反数即可②描点:先描一侧,另一侧根据中心对称的性质去找点;
③连线:平滑地按从左到右的顺序连接各点并延伸,有逐渐靠近坐标轴的趋势,但永不相交.(3)画反比例函数图象注意事项:37有界取值,
无界省略。指数为1,直线连接;指数非1,曲线连接。
图像和性质(1)学习内容和目标1.学习内容:书4页至6页
2.学习目标:
(1)会画反比例函数的图像,会正确辨析反比例函数的增减性
(2)能根据图像,确定反比例函数的解析式
3.学习重点: 重点:会画反比例函数的图像,会正确辨析反比例函数的增减性
你还记得一次函数的图象与性质吗?①一次函数y=kx+b(k≠0)的图象是 ,也叫 。
当k>0时,当k<0时,活动一 前置作业②按要求作出一次函数y=kx+b(k≠0)的图象:
撇正捺负判断K,上正下负判断b;
形如丿函数增,状像乀函数减。③K决定:
b决定:你还记得一次函数的图象与性质吗?一次函数y=kx+b(k≠0)的图象是一条直线,
称直线y=kx+b.y随x的增大而增大;y随x的增大而减小.当k>0时,当k<0时,活动一 前置作业(课堂质疑)撇正捺负判断K,上正下负判断b;形如丿函数增,状像乀函数减。活动二 问题探究1用描点法画出反比例函数 和 的图象列
表描
点连
线活动二 问题探究1(课堂质疑)我们数学老师给我们讲了一个凄美的爱情故事:世界上最远的距离不是生与死,而是我是双曲线,你是坐标轴,虽然曾离得那么近,却从未相交过,我们数学老师好文艺。当K>0时,观察下面反比例函数图象(1)函数图象的两个分支分别位于第 象限内。(2)当x取值范围是 时,图象在第一象限;当x取值范围是 时,图象在第三象限。(3)在每个象限内,随着x值的增大,y的值变化情况是 。活动二 问题探究27B·如图xB< xA但yB< yAxA·AxB活动二 问题探究2(课堂质疑)1.能否说当x>-5时,随着x的增大,y的值在减少?2.你能总结一下:图形形状,k值,
增减性三者之间的联系吗?
丿 K正 函数增
乀 K负 函数减8活动二 问题探究3图像与k的关系:以上三个函数,k值分别是 。
①当k>0时,图像位于 第 象限。
② |k|越大,图像离原点是越远还是越近呢?9活动二 问题探究3图像与k的关系:以上三个函数,k值分别是 。
①当k>0时,图像位于 第 象限。
② |k|越大,图像离原点是越远还是越近呢?10活动三 类比推理用描点法画出反比例函数 和 的图象①当k<0时,图像位于 第 象限。
② |k|越大,图像离原点是越远还是越近呢?
③K负 图像形状像 函数在各象限内是 函数。
12活动四 归纳总结活动五 巩固练习1.下列函数中,其图象位于第一、三象限的有____________;
在其所在的象限内,y随x的增大而增大的有___________.2.反比例函数 的图象经过点(-3,-4) ,则点(m,m-2)在第______象限?????3.已知点A(-2,y1),B(-1,y2),C(3,y3) 都在反比例函数
的图象上,比较y1、 y2 、y3的大小关系。134.在同一直角坐标系中,函数y=kx与 (k≠0) 的图象可能是________?(1) (2) (3) (4)145.如图是三个反比例函数在x轴
上方的图像,由此观察得到k1、
k2、k3的大小关系为( )
A.k1>k2>k3 B. k3>k2>k1
C.k2>k3>k1 D. k3>k1>k21k2k326.1.2 反比例函数的
图像和性质(2)反比例函数与几何图形面积学习内容和目标1.学习内容:中考题型总结
2.学习目标:
(1)掌握反比例函数与正比例函数的区别与联系
(2)掌握反比例函数中k 的几何意义
3.学习重点: 重点:反比例函数的图像的面积定理
活动一 面积性质1(2)点P位置变化了,△OAP的面积会
变化吗?为什么?
(3)若将此题改为过P点作y轴的垂线
段,其结论成立吗?写出推理过程:
活动一 课堂质疑活动二 面积性质2(2)点P位置变化了,四边形OAPB
的面积会变化吗?为什么?活动二 课堂质疑活动三 面积性质3活动三 课堂质疑1.如图,点P是反比例函数 图象上的
一点,PD⊥x轴于D.则△POD的面积为 .活动四 巩固练习A.S = 1 B.1
过A作X轴的垂线,垂足为B;过C作y轴
的垂线,垂足为D,记Rt△AOB的面积为S1
Rt△OCB的面积为S2,则 A.S1>S2 B.S1
图像和性质(3)反比例函数交点问题学习内容和目标1.学习内容:中考题型总结
2.学习目标:
(1)掌握反比例函数与正比例函数的区别与联系
(2)掌握反比例函数与一次函数的区别与联系
3.学习重点: 重点:掌握反比例函数与一次函数的区别与联系
活动一 前置作业1.①在左图中任意做一条直线y=kx(k>0)
②在图中找出直线与双曲线的交点坐标
是 。
③你从正比例函数的图像和反比例函数
图像的交点坐标中发现什么规律了吗?
2.如图所示,你能求出直线 与双曲
线 的交点坐标吗?活动一 课堂质疑1、与坐标轴的交点问题:
无限趋近于x、y轴, 与x、y轴无交点。
2、与正比例函数的交点问题:
可以利用反比例函数的中心对称性。
3、与一次函数的交点问题:
列方程组,求公共解,即交点坐标。活动二 题型讲练活动三 题型巩固1.5.如图所示,已知直线y1=x+m与x轴、y轴分别交于点A、B,与双曲线y2= (k<0)分别交于点C、D,且C点坐标为(-1,2). (3)利用图象直接写出当x在什么范围内取何值时,y1>y2.(2)求出点D的坐标;(1)分别求直线AB与双曲线的解析式;(4)试着在坐标轴上找点D,使△AOD≌△BOC。(1)分别写出这两个函数的表达式。(2)你能求出点B的坐标吗?你是怎样求的?(3)若点C坐标是(–4,0).请求△BOC的面积。6、如图所示,正比例函数y=k1x的图象与反比例函数y= 的图象交于A、B两点,其中点A的坐标为 。 (4,0)画图象①列表:以0为中心,对称性取值(相反数)。填y值时,只需计算右侧函数值,另一侧取相反数即可②描点:先描一侧,另一侧根据中心对称的性质去找点;
③连线:平滑地按从左到右的顺序连接各点并延伸,有逐渐靠近坐标轴的趋势,但永不相交.(3)画反比例函数图象注意事项:37有界取值,
无界省略。指数为1,直线连接;指数非1,曲线连接。
