2023-2024学年浙江省杭州市临平区五年级(下)期中数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年浙江省杭州市临平区五年级(下)期中数学试卷(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 707.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 00:00:00 | ||
图片预览


文档简介
2023-2024学年浙江省杭州市临平区五年级(下)期中数学试卷
一、填空题(28分)
1.(4分)第24届冬奥会2月4日20:04在北京开幕,开幕式以24节气开启倒计时,再辅之以诗词民谚,24秒,24种惊艳展现中国文化。24的因数有 ,这些数中 是质数, 是合数。今年是2024年,2024这个数至少加上 就是2和5的倍数。
2.(5分)(1)7050mL= L
(2)0.09m3= dm3= cm3
(3)360m2= dm2
(4)15分=小时
3.(4分)在下面横线上填上合适的单位和分数。
我们教室的占地面积约50 ,讲台上放着一瓶容积约60 的红墨水,墨水边上有一盒体积约1 的粉笔。如图所示,粉笔已经用去了全部的。
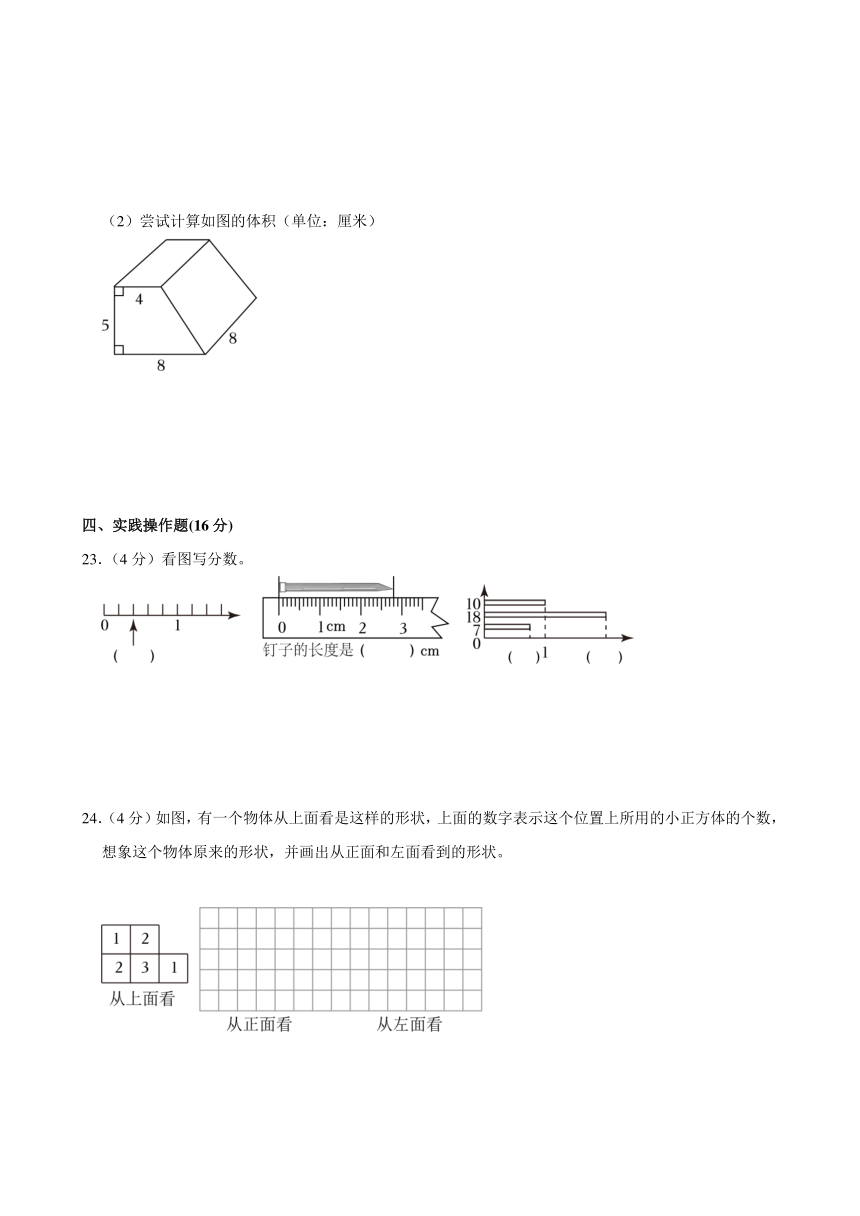
4.(2分)一根2米长的绳子,平均截成7段,每段是这根绳子的 ,每段长 米.
5.(3分)分数单位是的最大真分数是 ,最小假分数是 ,最小带分数是 。
6.(2分)要搭成一个正方体框架,还需要 个磁力珠和 根磁力棒。
7.(2分)多多有6根长3厘米,2根4厘米,9根5厘米的小棒,选取12根搭成一个长方体,这个长方体的表面积是 cm2;体积是 cm3。
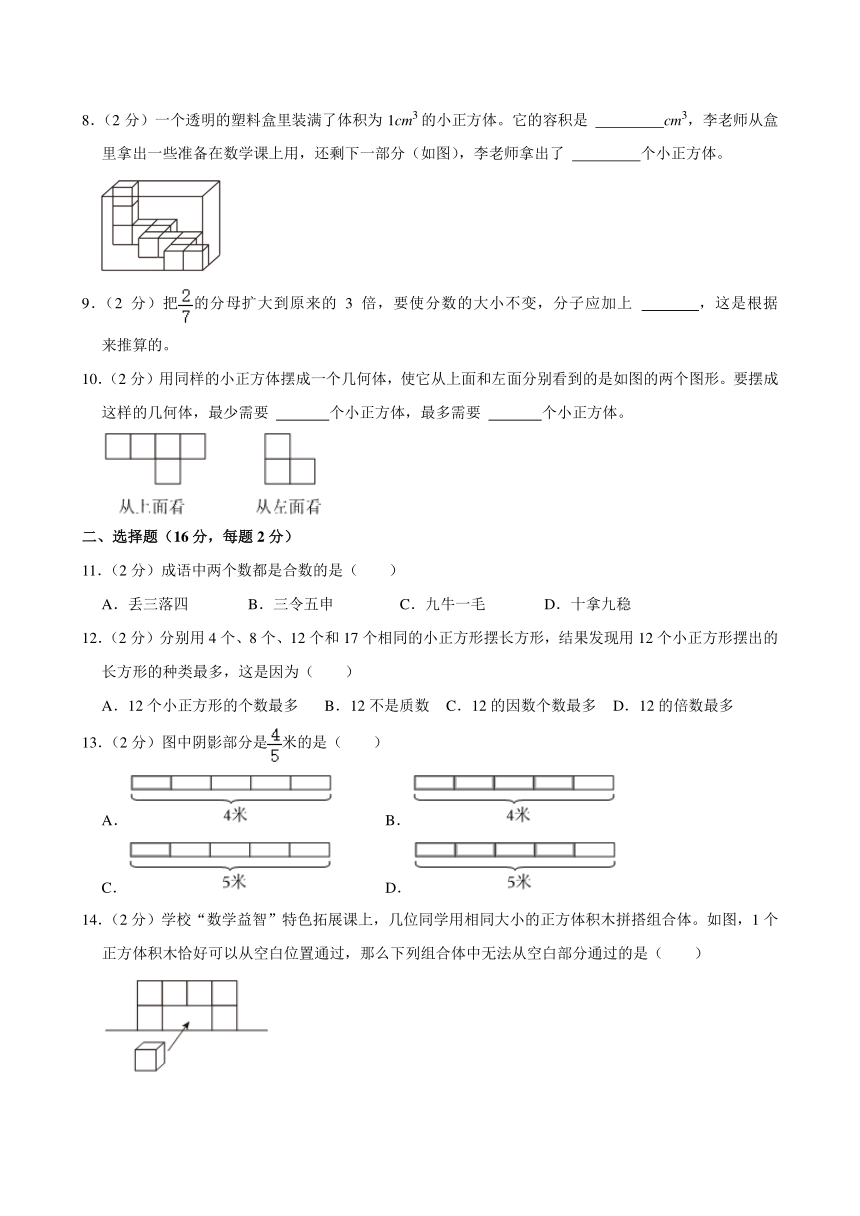
8.(2分)一个透明的塑料盒里装满了体积为1cm3的小正方体。它的容积是 cm3,李老师从盒里拿出一些准备在数学课上用,还剩下一部分(如图),李老师拿出了 个小正方体。
9.(2分)把的分母扩大到原来的3倍,要使分数的大小不变,分子应加上 ,这是根据 来推算的。
10.(2分)用同样的小正方体摆成一个几何体,使它从上面和左面分别看到的是如图的两个图形。要摆成这样的几何体,最少需要 个小正方体,最多需要 个小正方体。
二、选择题(16分,每题2分)
11.(2分)成语中两个数都是合数的是( )
A.丢三落四 B.三令五申 C.九牛一毛 D.十拿九稳
12.(2分)分别用4个、8个、12个和17个相同的小正方形摆长方形,结果发现用12个小正方形摆出的长方形的种类最多,这是因为( )
A.12个小正方形的个数最多 B.12不是质数 C.12的因数个数最多 D.12的倍数最多
13.(2分)图中阴影部分是米的是( )
A. B.
C. D.
14.(2分)学校“数学益智”特色拓展课上,几位同学用相同大小的正方体积木拼搭组合体。如图,1个正方体积木恰好可以从空白位置通过,那么下列组合体中无法从空白部分通过的是( )
A. B. C. D.
15.(2分)某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际,想象一下,这个产品最有可能是( )
A.一部手机 B.一台微波炉 C.一台冰箱 D.一台笔记本电脑
16.(2分)如图是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
17.(2分)下面说法中,错误的有( )个。
①两个质数的积一定是合数。
②一个非零自然数,它的最大因数和最小倍数都是它本身。
③一个长方体,可能有8条长度相等的棱。
④如果一个长方体的长、宽、高都扩大到原来的3倍,那么体积扩大到原来的9倍。
A.1 B.2 C.3 D.4
18.(2分)一个长方体用三种方法(如图)分割成两个小长方体,表面积分别增加了16平方厘米、24平方厘米、12平方厘米。原来的长方体的表面积是( )平方厘米。
A.24 B.32 C.48 D.52
三、计算题(20分)
19.(6分)直接写出得数。
20.24÷0.01= 11÷7= 0.63=
7÷15= =
20.(4分)下面算式的计算结果是“奇数”或“偶数”?请在算式后面的横线上填上“奇数”或“偶数”。
3+20004=
1001×12a(a是非零自然数)=
1+3+5+7+…+17+19=
1×2+3×4+5×6+…+199×200+5=
21.(4分)计算下面长方体或正方体的表面积。
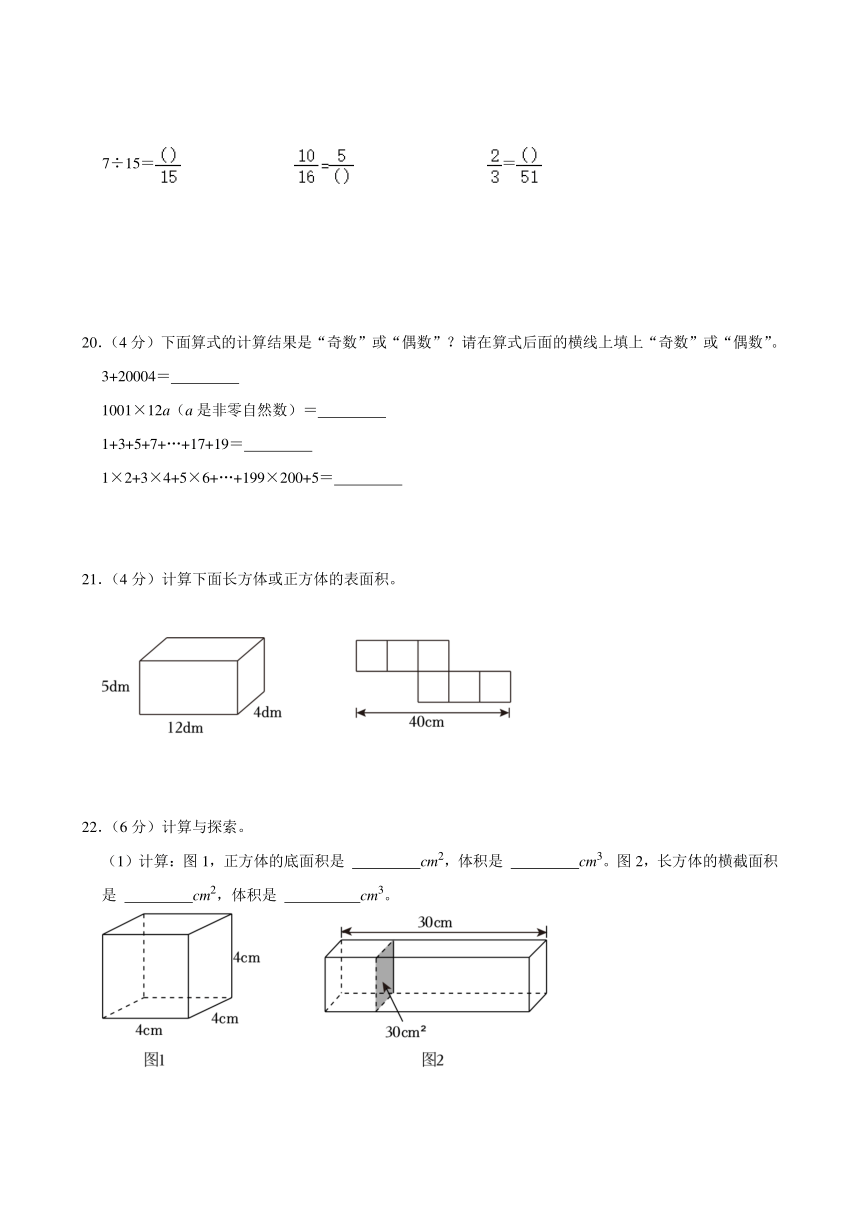
22.(6分)计算与探索。
(1)计算:图1,正方体的底面积是 cm2,体积是 cm3。图2,长方体的横截面积是 cm2,体积是 cm3。
(2)尝试计算如图的体积(单位:厘米)
四、实践操作题(16分)
23.(4分)看图写分数。
24.(4分)如图,有一个物体从上面看是这样的形状,上面的数字表示这个位置上所用的小正方体的个数,想象这个物体原来的形状,并画出从正面和左面看到的形状。
25.(4分)如图为一个长方体无盖木箱的底面和左面的示意图。(每个小方格的边长为1dm)
(1)在方格纸上画出木箱前面的示意图。
(2)做这样一个木箱至少需要多少平方分米的木板?
26.(4分)商店里有237枚鸡蛋,选择下面哪一种包装能正好把这些鸡蛋装完?请你用“因数和倍数”单元的知识解答。
五、解决问题(20分)
27.(2分)智能快递柜进小区,解决了社区居民取快递“最后100米”的烦恼。这天,居民李阿姨收到一条带有取件码的信息,根据下面的描述,请你猜一猜,李阿姨收到的取件码是 。
28.(3分)一本书,小江看了23页,还剩37页没有看,小江看了这本书总页数的几分之几?
29.(4分)小宝宝刚学会走路,为了安全,张阿姨打算给长方体的茶几各边装上防撞条(地面的四边不装),如图所示,张阿姨至少需要买多长的防撞条?
30.(5分)希望小学有一间教室,长是9m、宽6m、高3m。
(1)这间教室的占地面积是多少平方米?
(2)现在要粉刷教室的四周墙壁和天花板,墙上门窗所占的面积是12m2,门窗不用粉刷,那么至少需要多少平方米的涂料?
31.(6分)数学活动课上,五(1)班四名同学打算测量一块鹅卵石的体积,操作如下。
A.小红把鹅卵石慢慢放进杯中,使得杯中的水完全浸没鹅卵石,水溢出30mL。
B.小刚取出鹅卵石,量得水面到杯口的距离变为0.8cm。
C.小花准备了长方体塑料杯,从里面测,底面是边长为10cm的正方形,高20cm。
D.小华往杯里慢慢地倒入一些水,量得水面到杯口的距离是0.5cm。
▲阅读与理解:请将试验操作过程按顺序排列。(将字母填在横线上)
→ → →
▲分析与解答:请计算鹅卵石的体积。
2023-2024学年浙江省杭州市临平区五年级(下)期中数学试卷
参考答案与试题解析
一、填空题(28分)
1.(4分)第24届冬奥会2月4日20:04在北京开幕,开幕式以24节气开启倒计时,再辅之以诗词民谚,24秒,24种惊艳展现中国文化。24的因数有 1、2、3、4、6、8、12、24 ,这些数中 2、3 是质数, 4、6、12、24 是合数。今年是2024年,2024这个数至少加上 6 就是2和5的倍数。
【解答】24的因数有1、2、3、4、6、8、12、24,这些数中2、3是质数,4、6、12、24是合数。今年是2024年,2024这个数至少加上6就是2和5的倍数。
故答案为:1、2、3、4、6、8、12、24,2、3,4、6、12、24,6。
2.(5分)(1)7050mL= 7.05 L
(2)0.09m3= 90 dm3= 90000 cm3
(3)360m2= 36000 dm2
(4)15分=小时
【解答】解:(1)7050mL=7.05L
(2)0.09m3=90dm3=90000cm3
(3)360m2=36000dm2
(4)15分=小时
故答案为:(1)7.05;(2)90;90000;(3)36000;(4)。
3.(4分)在下面横线上填上合适的单位和分数。
我们教室的占地面积约50 平方米 ,讲台上放着一瓶容积约60 毫升 的红墨水,墨水边上有一盒体积约1 立方分米 的粉笔。如图所示,粉笔已经用去了全部的。
【解答】解:我们教室的占地面积约50平方米,讲台上放着一瓶容积约60毫升的红墨水,墨水边上有一盒体积约1立方分米的粉笔。如图所示,粉笔已经用去了全部的。
故答案为:平方米;毫升;立方分米;。
4.(2分)一根2米长的绳子,平均截成7段,每段是这根绳子的 ,每段长 米.
【解答】解:每段占全长的分率:1÷7=
每段长的米数:2÷7=(米)
答:每段是这根绳子的,每段长米.
故答案为:,.
5.(3分)分数单位是的最大真分数是 ,最小假分数是 ,最小带分数是 1 。
【解答】解:分数单位是的最大真分数是,最小假分数是,最小带分数是1。
故答案为:;;1。
6.(2分)要搭成一个正方体框架,还需要 2 个磁力珠和 7 根磁力棒。
【解答】解:8﹣6=2(个)
12﹣5=7(根)
因此要搭成一个正方体框架,还需要2个磁力珠和7根磁力棒。
故答案为:2,7。
7.(2分)多多有6根长3厘米,2根4厘米,9根5厘米的小棒,选取12根搭成一个长方体,这个长方体的表面积是 110 cm2;体积是 75 cm3。
【解答】解:(3×5+3×5+5×5)×2
=55×2
=110(平方厘米)
3×5×5
=15×5
=75(立方厘米)
答:这个长方体的表面积是110cm2,体积是75cm3。
故答案为:110,75。
8.(2分)一个透明的塑料盒里装满了体积为1cm3的小正方体。它的容积是 90 cm3,李老师从盒里拿出一些准备在数学课上用,还剩下一部分(如图),李老师拿出了 78 个小正方体。
【解答】解:6×5×3
=30×3
=90(立方厘米)
90﹣12=78(立方厘米)
答:它的容积是90cm3,李老师拿出了78个小正方体。
故答案为:90;78。
9.(2分)把的分母扩大到原来的3倍,要使分数的大小不变,分子应加上 4 ,这是根据 分数的基本性质 来推算的。
【解答】解:把的分母扩大到原来的3倍,要使分数的大小不变,分子应加上4,这是根据分数的基本性质来推算的。
故答案为:4;分数的基本性质。
10.(2分)用同样的小正方体摆成一个几何体,使它从上面和左面分别看到的是如图的两个图形。要摆成这样的几何体,最少需要 6 个小正方体,最多需要 9 个小正方体。
【解答】解:要摆成这样的几何体,最少需要6个小正方体,最多需要9个小正方体。
故答案为:6,9。
二、选择题(16分,每题2分)
11.(2分)成语中两个数都是合数的是( )
A.丢三落四 B.三令五申 C.九牛一毛 D.十拿九稳
【解答】解:成语中两个数都是合数的是十拿九稳;丢三落四,3和4不都是合数;三令五申,3和5都是质数,不是合数;九牛一毛,9和1不都是合数。
故选:D。
12.(2分)分别用4个、8个、12个和17个相同的小正方形摆长方形,结果发现用12个小正方形摆出的长方形的种类最多,这是因为( )
A.12个小正方形的个数最多
B.12不是质数
C.12的因数个数最多
D.12的倍数最多
【解答】解:4=4×1=2×2
用4个小正方形拼成的长方形有长4、宽1,长2、宽2,2种;
8=8×1=4×2
用8个小正方形拼成的长方形有长8、宽1,长4、宽2,2种;
12=12×1=6×2=4×3
用12个小正方形拼成的长方形有长12、宽1,长6、宽2,长4、宽3,3种;
17=17×1
用17个小正方形拼成的长方形有长17、宽1,1种。
分别用4个、8个、12个和17个相同的小正方形摆长方形,结果发现用12个小正方形摆出的长方形的种类最多,这是因为12的因数个数最多。
故选:C。
13.(2分)图中阴影部分是米的是( )
A.
B.
C.
D.
【解答】解:A、
4÷5=(米)
B、
4÷5×4=(米)
C、
5÷5×1=1(米)
D、
5÷5×4=4(米)
故选:A。
14.(2分)学校“数学益智”特色拓展课上,几位同学用相同大小的正方体积木拼搭组合体。如图,1个正方体积木恰好可以从空白位置通过,那么下列组合体中无法从空白部分通过的是( )
A. B. C. D.
【解答】解:A、D从上面观察可以看到两并排个正方形,所以可以通过;
C从侧面观察可以看到两并排个正方形,所以可以通过;
B从上面、前面和左面观察到的都是3个正方形,所以无法通过。
故选:B。
15.(2分)某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际,想象一下,这个产品最有可能是( )
A.一部手机 B.一台微波炉
C.一台冰箱 D.一台笔记本电脑
【解答】解:某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际,想象一下,这个产品最有可能是一台微波炉。
故选:B。
16.(2分)如图是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
【解答】解:如图:
是一个正方体展开图的其中5个面,再在③的位置添一个面,就可补全这个正方体的展开图。
故选:C。
17.(2分)下面说法中,错误的有( )个。
①两个质数的积一定是合数。
②一个非零自然数,它的最大因数和最小倍数都是它本身。
③一个长方体,可能有8条长度相等的棱。
④如果一个长方体的长、宽、高都扩大到原来的3倍,那么体积扩大到原来的9倍。
A.1 B.2 C.3 D.4
【解答】解:①根据合数的意义可知,两个质数的积一定是合数,原题说法正确;
②一个非零自然数,它的最大因数和最小倍数都是它本身,原题说法正确;
③一个长方体,可能有8条长度相等的棱,原题说法正确;
④如果一个长方体的长、宽、高都扩大到原来的3倍,那么体积扩大到原来的3×3×3=27倍,原题说法错误。
故选:A。
18.(2分)一个长方体用三种方法(如图)分割成两个小长方体,表面积分别增加了16平方厘米、24平方厘米、12平方厘米。原来的长方体的表面积是( )平方厘米。
A.24 B.32 C.48 D.52
【解答】解:16+24+12
=40+12
=52(平方厘米)
答:原来的长方体的表面积是52平方厘米。
故选:D。
三、计算题(20分)
19.(6分)直接写出得数。
20.24÷0.01= 11÷7= 0.63=
7÷15= =
【解答】解:
20.24÷0.01=2024 11÷7= 0.63=0.216
7÷15= =
故答案为:2024;;0.216;7;8;34。
20.(4分)下面算式的计算结果是“奇数”或“偶数”?请在算式后面的横线上填上“奇数”或“偶数”。
3+20004= 奇数
1001×12a(a是非零自然数)= 偶数
1+3+5+7+…+17+19= 偶数
1×2+3×4+5×6+…+199×200+5= 奇数
【解答】解:3+20004=奇数;
1001×12a(a是非零自然数)=偶数;
1+3+5+7+…+17+19=偶数;
1×2+3×4+5×6+…+199×200+5=奇数。
故答案为:奇数;偶数;偶数;奇数。
21.(4分)计算下面长方体或正方体的表面积。
【解答】解:(12×4+12×5+4×5)×2
=(48+60+20)×2
=128×2
=256(平方分米)
40÷5=8(厘米)
8×8×6
=64×6
=384(平方厘米)
答:长方体的表面积是256平方分米,正方体的表面积是384平方厘米。
22.(6分)计算与探索。
(1)计算:图1,正方体的底面积是 16 cm2,体积是 64 cm3。图2,长方体的横截面积是 30 cm2,体积是 900 cm3。
(2)尝试计算如图的体积(单位:厘米)
【解答】解:(1)4×4=16(平方厘米)
4×4×4=64(立方厘米)
30×30=900(立方厘米)
答:正方体的底面积是16cm2,体积是64cm3。图2,长方体的横截面积是30cm2,体积是900cm3。
(2)(4+8)×5÷2×8
=12×5÷2×8
=60÷2×8
=30×8
=240(立方厘米)
答:图形的体积是240立方厘米。
故答案为:(1)16;64;30;900。
四、实践操作题(16分)
23.(4分)看图写分数。
【解答】解:。
24.(4分)如图,有一个物体从上面看是这样的形状,上面的数字表示这个位置上所用的小正方体的个数,想象这个物体原来的形状,并画出从正面和左面看到的形状。
【解答】解:
25.(4分)如图为一个长方体无盖木箱的底面和左面的示意图。(每个小方格的边长为1dm)
(1)在方格纸上画出木箱前面的示意图。
(2)做这样一个木箱至少需要多少平方分米的木板?
【解答】解:(1)前面的长是4分米,宽是3分米,作图如下:
(2)4×2+4×3×2+2×3×2
=8+24+12
=44(平方分米)
答:做这样一个木箱至少需要44平方分米的木板。
26.(4分)商店里有237枚鸡蛋,选择下面哪一种包装能正好把这些鸡蛋装完?请你用“因数和倍数”单元的知识解答。
【解答】解:237÷3=79
237÷4=59.....1
237÷5=47....2
因此选择第一种包装能正好把这些鸡蛋装完。
五、解决问题(20分)
27.(2分)智能快递柜进小区,解决了社区居民取快递“最后100米”的烦恼。这天,居民李阿姨收到一条带有取件码的信息,根据下面的描述,请你猜一猜,李阿姨收到的取件码是 8362 。
【解答】解:居民李阿姨收到一条带有取件码的信息,李阿姨收到的取件码是8362。
故答案为:8362。
28.(3分)一本书,小江看了23页,还剩37页没有看,小江看了这本书总页数的几分之几?
【解答】解:23÷(23+37)
=23÷60
=
答:小江看了这本书总页数的。
29.(4分)小宝宝刚学会走路,为了安全,张阿姨打算给长方体的茶几各边装上防撞条(地面的四边不装),如图所示,张阿姨至少需要买多长的防撞条?
【解答】解:(18+6+5)×4﹣(18+6)×2
=29×4﹣24×2
=116﹣48
=68(分米)
答:张阿姨至少需要买68分米的防撞条。
30.(5分)希望小学有一间教室,长是9m、宽6m、高3m。
(1)这间教室的占地面积是多少平方米?
(2)现在要粉刷教室的四周墙壁和天花板,墙上门窗所占的面积是12m2,门窗不用粉刷,那么至少需要多少平方米的涂料?
【解答】解:(1)9×6=54(平方米)
答:这间教室的占地面积是54平方米。
(2)9×6+9×3×2+6×3×2﹣12
=54+54+36﹣12
=144﹣12
=132(平方米)
答:至少需要132平方米的涂料。
31.(6分)数学活动课上,五(1)班四名同学打算测量一块鹅卵石的体积,操作如下。
A.小红把鹅卵石慢慢放进杯中,使得杯中的水完全浸没鹅卵石,水溢出30mL。
B.小刚取出鹅卵石,量得水面到杯口的距离变为0.8cm。
C.小花准备了长方体塑料杯,从里面测,底面是边长为10cm的正方形,高20cm。
D.小华往杯里慢慢地倒入一些水,量得水面到杯口的距离是0.5cm。
▲阅读与理解:请将试验操作过程按顺序排列。(将字母填在横线上)
C → D → A → B
▲分析与解答:请计算鹅卵石的体积。
【解答】解:请将试验操作过程按顺序排列。
C→D→A→B
10×10×0.5+30
=50+30
=80(立方厘米)
答:鹅卵石的体积是80立方厘米。
故答案为:C,D,A,B。
一、填空题(28分)
1.(4分)第24届冬奥会2月4日20:04在北京开幕,开幕式以24节气开启倒计时,再辅之以诗词民谚,24秒,24种惊艳展现中国文化。24的因数有 ,这些数中 是质数, 是合数。今年是2024年,2024这个数至少加上 就是2和5的倍数。
2.(5分)(1)7050mL= L
(2)0.09m3= dm3= cm3
(3)360m2= dm2
(4)15分=小时
3.(4分)在下面横线上填上合适的单位和分数。
我们教室的占地面积约50 ,讲台上放着一瓶容积约60 的红墨水,墨水边上有一盒体积约1 的粉笔。如图所示,粉笔已经用去了全部的。
4.(2分)一根2米长的绳子,平均截成7段,每段是这根绳子的 ,每段长 米.
5.(3分)分数单位是的最大真分数是 ,最小假分数是 ,最小带分数是 。
6.(2分)要搭成一个正方体框架,还需要 个磁力珠和 根磁力棒。
7.(2分)多多有6根长3厘米,2根4厘米,9根5厘米的小棒,选取12根搭成一个长方体,这个长方体的表面积是 cm2;体积是 cm3。
8.(2分)一个透明的塑料盒里装满了体积为1cm3的小正方体。它的容积是 cm3,李老师从盒里拿出一些准备在数学课上用,还剩下一部分(如图),李老师拿出了 个小正方体。
9.(2分)把的分母扩大到原来的3倍,要使分数的大小不变,分子应加上 ,这是根据 来推算的。
10.(2分)用同样的小正方体摆成一个几何体,使它从上面和左面分别看到的是如图的两个图形。要摆成这样的几何体,最少需要 个小正方体,最多需要 个小正方体。
二、选择题(16分,每题2分)
11.(2分)成语中两个数都是合数的是( )
A.丢三落四 B.三令五申 C.九牛一毛 D.十拿九稳
12.(2分)分别用4个、8个、12个和17个相同的小正方形摆长方形,结果发现用12个小正方形摆出的长方形的种类最多,这是因为( )
A.12个小正方形的个数最多 B.12不是质数 C.12的因数个数最多 D.12的倍数最多
13.(2分)图中阴影部分是米的是( )
A. B.
C. D.
14.(2分)学校“数学益智”特色拓展课上,几位同学用相同大小的正方体积木拼搭组合体。如图,1个正方体积木恰好可以从空白位置通过,那么下列组合体中无法从空白部分通过的是( )
A. B. C. D.
15.(2分)某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际,想象一下,这个产品最有可能是( )
A.一部手机 B.一台微波炉 C.一台冰箱 D.一台笔记本电脑
16.(2分)如图是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
17.(2分)下面说法中,错误的有( )个。
①两个质数的积一定是合数。
②一个非零自然数,它的最大因数和最小倍数都是它本身。
③一个长方体,可能有8条长度相等的棱。
④如果一个长方体的长、宽、高都扩大到原来的3倍,那么体积扩大到原来的9倍。
A.1 B.2 C.3 D.4
18.(2分)一个长方体用三种方法(如图)分割成两个小长方体,表面积分别增加了16平方厘米、24平方厘米、12平方厘米。原来的长方体的表面积是( )平方厘米。
A.24 B.32 C.48 D.52
三、计算题(20分)
19.(6分)直接写出得数。
20.24÷0.01= 11÷7= 0.63=
7÷15= =
20.(4分)下面算式的计算结果是“奇数”或“偶数”?请在算式后面的横线上填上“奇数”或“偶数”。
3+20004=
1001×12a(a是非零自然数)=
1+3+5+7+…+17+19=
1×2+3×4+5×6+…+199×200+5=
21.(4分)计算下面长方体或正方体的表面积。
22.(6分)计算与探索。
(1)计算:图1,正方体的底面积是 cm2,体积是 cm3。图2,长方体的横截面积是 cm2,体积是 cm3。
(2)尝试计算如图的体积(单位:厘米)
四、实践操作题(16分)
23.(4分)看图写分数。
24.(4分)如图,有一个物体从上面看是这样的形状,上面的数字表示这个位置上所用的小正方体的个数,想象这个物体原来的形状,并画出从正面和左面看到的形状。
25.(4分)如图为一个长方体无盖木箱的底面和左面的示意图。(每个小方格的边长为1dm)
(1)在方格纸上画出木箱前面的示意图。
(2)做这样一个木箱至少需要多少平方分米的木板?
26.(4分)商店里有237枚鸡蛋,选择下面哪一种包装能正好把这些鸡蛋装完?请你用“因数和倍数”单元的知识解答。
五、解决问题(20分)
27.(2分)智能快递柜进小区,解决了社区居民取快递“最后100米”的烦恼。这天,居民李阿姨收到一条带有取件码的信息,根据下面的描述,请你猜一猜,李阿姨收到的取件码是 。
28.(3分)一本书,小江看了23页,还剩37页没有看,小江看了这本书总页数的几分之几?
29.(4分)小宝宝刚学会走路,为了安全,张阿姨打算给长方体的茶几各边装上防撞条(地面的四边不装),如图所示,张阿姨至少需要买多长的防撞条?
30.(5分)希望小学有一间教室,长是9m、宽6m、高3m。
(1)这间教室的占地面积是多少平方米?
(2)现在要粉刷教室的四周墙壁和天花板,墙上门窗所占的面积是12m2,门窗不用粉刷,那么至少需要多少平方米的涂料?
31.(6分)数学活动课上,五(1)班四名同学打算测量一块鹅卵石的体积,操作如下。
A.小红把鹅卵石慢慢放进杯中,使得杯中的水完全浸没鹅卵石,水溢出30mL。
B.小刚取出鹅卵石,量得水面到杯口的距离变为0.8cm。
C.小花准备了长方体塑料杯,从里面测,底面是边长为10cm的正方形,高20cm。
D.小华往杯里慢慢地倒入一些水,量得水面到杯口的距离是0.5cm。
▲阅读与理解:请将试验操作过程按顺序排列。(将字母填在横线上)
→ → →
▲分析与解答:请计算鹅卵石的体积。
2023-2024学年浙江省杭州市临平区五年级(下)期中数学试卷
参考答案与试题解析
一、填空题(28分)
1.(4分)第24届冬奥会2月4日20:04在北京开幕,开幕式以24节气开启倒计时,再辅之以诗词民谚,24秒,24种惊艳展现中国文化。24的因数有 1、2、3、4、6、8、12、24 ,这些数中 2、3 是质数, 4、6、12、24 是合数。今年是2024年,2024这个数至少加上 6 就是2和5的倍数。
【解答】24的因数有1、2、3、4、6、8、12、24,这些数中2、3是质数,4、6、12、24是合数。今年是2024年,2024这个数至少加上6就是2和5的倍数。
故答案为:1、2、3、4、6、8、12、24,2、3,4、6、12、24,6。
2.(5分)(1)7050mL= 7.05 L
(2)0.09m3= 90 dm3= 90000 cm3
(3)360m2= 36000 dm2
(4)15分=小时
【解答】解:(1)7050mL=7.05L
(2)0.09m3=90dm3=90000cm3
(3)360m2=36000dm2
(4)15分=小时
故答案为:(1)7.05;(2)90;90000;(3)36000;(4)。
3.(4分)在下面横线上填上合适的单位和分数。
我们教室的占地面积约50 平方米 ,讲台上放着一瓶容积约60 毫升 的红墨水,墨水边上有一盒体积约1 立方分米 的粉笔。如图所示,粉笔已经用去了全部的。
【解答】解:我们教室的占地面积约50平方米,讲台上放着一瓶容积约60毫升的红墨水,墨水边上有一盒体积约1立方分米的粉笔。如图所示,粉笔已经用去了全部的。
故答案为:平方米;毫升;立方分米;。
4.(2分)一根2米长的绳子,平均截成7段,每段是这根绳子的 ,每段长 米.
【解答】解:每段占全长的分率:1÷7=
每段长的米数:2÷7=(米)
答:每段是这根绳子的,每段长米.
故答案为:,.
5.(3分)分数单位是的最大真分数是 ,最小假分数是 ,最小带分数是 1 。
【解答】解:分数单位是的最大真分数是,最小假分数是,最小带分数是1。
故答案为:;;1。
6.(2分)要搭成一个正方体框架,还需要 2 个磁力珠和 7 根磁力棒。
【解答】解:8﹣6=2(个)
12﹣5=7(根)
因此要搭成一个正方体框架,还需要2个磁力珠和7根磁力棒。
故答案为:2,7。
7.(2分)多多有6根长3厘米,2根4厘米,9根5厘米的小棒,选取12根搭成一个长方体,这个长方体的表面积是 110 cm2;体积是 75 cm3。
【解答】解:(3×5+3×5+5×5)×2
=55×2
=110(平方厘米)
3×5×5
=15×5
=75(立方厘米)
答:这个长方体的表面积是110cm2,体积是75cm3。
故答案为:110,75。
8.(2分)一个透明的塑料盒里装满了体积为1cm3的小正方体。它的容积是 90 cm3,李老师从盒里拿出一些准备在数学课上用,还剩下一部分(如图),李老师拿出了 78 个小正方体。
【解答】解:6×5×3
=30×3
=90(立方厘米)
90﹣12=78(立方厘米)
答:它的容积是90cm3,李老师拿出了78个小正方体。
故答案为:90;78。
9.(2分)把的分母扩大到原来的3倍,要使分数的大小不变,分子应加上 4 ,这是根据 分数的基本性质 来推算的。
【解答】解:把的分母扩大到原来的3倍,要使分数的大小不变,分子应加上4,这是根据分数的基本性质来推算的。
故答案为:4;分数的基本性质。
10.(2分)用同样的小正方体摆成一个几何体,使它从上面和左面分别看到的是如图的两个图形。要摆成这样的几何体,最少需要 6 个小正方体,最多需要 9 个小正方体。
【解答】解:要摆成这样的几何体,最少需要6个小正方体,最多需要9个小正方体。
故答案为:6,9。
二、选择题(16分,每题2分)
11.(2分)成语中两个数都是合数的是( )
A.丢三落四 B.三令五申 C.九牛一毛 D.十拿九稳
【解答】解:成语中两个数都是合数的是十拿九稳;丢三落四,3和4不都是合数;三令五申,3和5都是质数,不是合数;九牛一毛,9和1不都是合数。
故选:D。
12.(2分)分别用4个、8个、12个和17个相同的小正方形摆长方形,结果发现用12个小正方形摆出的长方形的种类最多,这是因为( )
A.12个小正方形的个数最多
B.12不是质数
C.12的因数个数最多
D.12的倍数最多
【解答】解:4=4×1=2×2
用4个小正方形拼成的长方形有长4、宽1,长2、宽2,2种;
8=8×1=4×2
用8个小正方形拼成的长方形有长8、宽1,长4、宽2,2种;
12=12×1=6×2=4×3
用12个小正方形拼成的长方形有长12、宽1,长6、宽2,长4、宽3,3种;
17=17×1
用17个小正方形拼成的长方形有长17、宽1,1种。
分别用4个、8个、12个和17个相同的小正方形摆长方形,结果发现用12个小正方形摆出的长方形的种类最多,这是因为12的因数个数最多。
故选:C。
13.(2分)图中阴影部分是米的是( )
A.
B.
C.
D.
【解答】解:A、
4÷5=(米)
B、
4÷5×4=(米)
C、
5÷5×1=1(米)
D、
5÷5×4=4(米)
故选:A。
14.(2分)学校“数学益智”特色拓展课上,几位同学用相同大小的正方体积木拼搭组合体。如图,1个正方体积木恰好可以从空白位置通过,那么下列组合体中无法从空白部分通过的是( )
A. B. C. D.
【解答】解:A、D从上面观察可以看到两并排个正方形,所以可以通过;
C从侧面观察可以看到两并排个正方形,所以可以通过;
B从上面、前面和左面观察到的都是3个正方形,所以无法通过。
故选:B。
15.(2分)某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际,想象一下,这个产品最有可能是( )
A.一部手机 B.一台微波炉
C.一台冰箱 D.一台笔记本电脑
【解答】解:某产品说明书上标注的包装尺寸为457mm×395mm×271mm。根据这组数据,联系生活实际,想象一下,这个产品最有可能是一台微波炉。
故选:B。
16.(2分)如图是一个正方体展开图的其中5个面,再在( )的位置添一个面,就可补全这个正方体的展开图。
A.① B.② C.③ D.④
【解答】解:如图:
是一个正方体展开图的其中5个面,再在③的位置添一个面,就可补全这个正方体的展开图。
故选:C。
17.(2分)下面说法中,错误的有( )个。
①两个质数的积一定是合数。
②一个非零自然数,它的最大因数和最小倍数都是它本身。
③一个长方体,可能有8条长度相等的棱。
④如果一个长方体的长、宽、高都扩大到原来的3倍,那么体积扩大到原来的9倍。
A.1 B.2 C.3 D.4
【解答】解:①根据合数的意义可知,两个质数的积一定是合数,原题说法正确;
②一个非零自然数,它的最大因数和最小倍数都是它本身,原题说法正确;
③一个长方体,可能有8条长度相等的棱,原题说法正确;
④如果一个长方体的长、宽、高都扩大到原来的3倍,那么体积扩大到原来的3×3×3=27倍,原题说法错误。
故选:A。
18.(2分)一个长方体用三种方法(如图)分割成两个小长方体,表面积分别增加了16平方厘米、24平方厘米、12平方厘米。原来的长方体的表面积是( )平方厘米。
A.24 B.32 C.48 D.52
【解答】解:16+24+12
=40+12
=52(平方厘米)
答:原来的长方体的表面积是52平方厘米。
故选:D。
三、计算题(20分)
19.(6分)直接写出得数。
20.24÷0.01= 11÷7= 0.63=
7÷15= =
【解答】解:
20.24÷0.01=2024 11÷7= 0.63=0.216
7÷15= =
故答案为:2024;;0.216;7;8;34。
20.(4分)下面算式的计算结果是“奇数”或“偶数”?请在算式后面的横线上填上“奇数”或“偶数”。
3+20004= 奇数
1001×12a(a是非零自然数)= 偶数
1+3+5+7+…+17+19= 偶数
1×2+3×4+5×6+…+199×200+5= 奇数
【解答】解:3+20004=奇数;
1001×12a(a是非零自然数)=偶数;
1+3+5+7+…+17+19=偶数;
1×2+3×4+5×6+…+199×200+5=奇数。
故答案为:奇数;偶数;偶数;奇数。
21.(4分)计算下面长方体或正方体的表面积。
【解答】解:(12×4+12×5+4×5)×2
=(48+60+20)×2
=128×2
=256(平方分米)
40÷5=8(厘米)
8×8×6
=64×6
=384(平方厘米)
答:长方体的表面积是256平方分米,正方体的表面积是384平方厘米。
22.(6分)计算与探索。
(1)计算:图1,正方体的底面积是 16 cm2,体积是 64 cm3。图2,长方体的横截面积是 30 cm2,体积是 900 cm3。
(2)尝试计算如图的体积(单位:厘米)
【解答】解:(1)4×4=16(平方厘米)
4×4×4=64(立方厘米)
30×30=900(立方厘米)
答:正方体的底面积是16cm2,体积是64cm3。图2,长方体的横截面积是30cm2,体积是900cm3。
(2)(4+8)×5÷2×8
=12×5÷2×8
=60÷2×8
=30×8
=240(立方厘米)
答:图形的体积是240立方厘米。
故答案为:(1)16;64;30;900。
四、实践操作题(16分)
23.(4分)看图写分数。
【解答】解:。
24.(4分)如图,有一个物体从上面看是这样的形状,上面的数字表示这个位置上所用的小正方体的个数,想象这个物体原来的形状,并画出从正面和左面看到的形状。
【解答】解:
25.(4分)如图为一个长方体无盖木箱的底面和左面的示意图。(每个小方格的边长为1dm)
(1)在方格纸上画出木箱前面的示意图。
(2)做这样一个木箱至少需要多少平方分米的木板?
【解答】解:(1)前面的长是4分米,宽是3分米,作图如下:
(2)4×2+4×3×2+2×3×2
=8+24+12
=44(平方分米)
答:做这样一个木箱至少需要44平方分米的木板。
26.(4分)商店里有237枚鸡蛋,选择下面哪一种包装能正好把这些鸡蛋装完?请你用“因数和倍数”单元的知识解答。
【解答】解:237÷3=79
237÷4=59.....1
237÷5=47....2
因此选择第一种包装能正好把这些鸡蛋装完。
五、解决问题(20分)
27.(2分)智能快递柜进小区,解决了社区居民取快递“最后100米”的烦恼。这天,居民李阿姨收到一条带有取件码的信息,根据下面的描述,请你猜一猜,李阿姨收到的取件码是 8362 。
【解答】解:居民李阿姨收到一条带有取件码的信息,李阿姨收到的取件码是8362。
故答案为:8362。
28.(3分)一本书,小江看了23页,还剩37页没有看,小江看了这本书总页数的几分之几?
【解答】解:23÷(23+37)
=23÷60
=
答:小江看了这本书总页数的。
29.(4分)小宝宝刚学会走路,为了安全,张阿姨打算给长方体的茶几各边装上防撞条(地面的四边不装),如图所示,张阿姨至少需要买多长的防撞条?
【解答】解:(18+6+5)×4﹣(18+6)×2
=29×4﹣24×2
=116﹣48
=68(分米)
答:张阿姨至少需要买68分米的防撞条。
30.(5分)希望小学有一间教室,长是9m、宽6m、高3m。
(1)这间教室的占地面积是多少平方米?
(2)现在要粉刷教室的四周墙壁和天花板,墙上门窗所占的面积是12m2,门窗不用粉刷,那么至少需要多少平方米的涂料?
【解答】解:(1)9×6=54(平方米)
答:这间教室的占地面积是54平方米。
(2)9×6+9×3×2+6×3×2﹣12
=54+54+36﹣12
=144﹣12
=132(平方米)
答:至少需要132平方米的涂料。
31.(6分)数学活动课上,五(1)班四名同学打算测量一块鹅卵石的体积,操作如下。
A.小红把鹅卵石慢慢放进杯中,使得杯中的水完全浸没鹅卵石,水溢出30mL。
B.小刚取出鹅卵石,量得水面到杯口的距离变为0.8cm。
C.小花准备了长方体塑料杯,从里面测,底面是边长为10cm的正方形,高20cm。
D.小华往杯里慢慢地倒入一些水,量得水面到杯口的距离是0.5cm。
▲阅读与理解:请将试验操作过程按顺序排列。(将字母填在横线上)
C → D → A → B
▲分析与解答:请计算鹅卵石的体积。
【解答】解:请将试验操作过程按顺序排列。
C→D→A→B
10×10×0.5+30
=50+30
=80(立方厘米)
答:鹅卵石的体积是80立方厘米。
故答案为:C,D,A,B。
同课章节目录
