浙江省温州市十校联合体2023-2024学年高二下学期5月期中联考数学试题(含答案)
文档属性
| 名称 | 浙江省温州市十校联合体2023-2024学年高二下学期5月期中联考数学试题(含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 705.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 06:12:31 | ||
图片预览



文档简介
2023学年第二学期温州十校联合体期中联考
高二年级数学学科试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、设集合,若,则( )
A. B. C. D.
2、若函数是指数函数,则的值为( )
A.2 B.-2 C. D.
3、设复数,则复数的共轭复数的虚部是( )
A. B. C.1 D.-1
4、已知非负实数满足,则的最小值为( )
A. B.2 C. D.
5、已知,则( )
A. B. C. D.
6、已知正方形的边长为2,若将正方形沿对角线折叠为三棱锥,则在折叠过程中,不能出现( )
A. B.面面
C. D.
7、一个袋子中装有大小相同的5个小球,其中有3个白球,2个黑球,从中无放回地取出3个小球,摸到一个白球记2分,摸到一个黑球记1分,则总得分的数学期望等于( )
A.5分 B.4.8分 C.4.6分 D.4.4分
8、已知,则( )
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9、已知向量,则下列命题正确的是( )
A. B.向量在向量上的投影向量为
C. D.
10、下列命题中正确的是( )
A.已知随机变量,则
B.已知随机变量,若函数为偶函数,则
C.数据第80百分位数是8
D.样本甲中有件样品,其方差为,样本乙中有件样品,其方差为,则由甲乙组成的总体样本的方差为
11、定义在上的函数,满足,且当时,,则使得在上恒成立的可以是( )
A.1 B.2 C. D.
非选择题部分
三、填空题:本大题共3小题,每小题5分,共15分.把答案填在题中的横线上.
12、______.
13、一位射击运动员向一个目标射击二次,记事件“第次命中目标”,,则______.
14、已知在三棱锥中,,点为三棱锥外接球上一点,则三棱锥的体积最大为______.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15、(本题13分)在中,内角所对的边分别为,且
(1)若,求的值;
(2)若,且的面积为,求和的值.
16、(本题15分)已知四棱锥面,底面为正方形,,为的中点.
(1)求证:面;
(2)求直线与面所成的角.
17、(本题15分)已知的最小正周期为,
(1)求的值;
(2)若在上恰2个极值点和2个零点,求实数的取值范围.
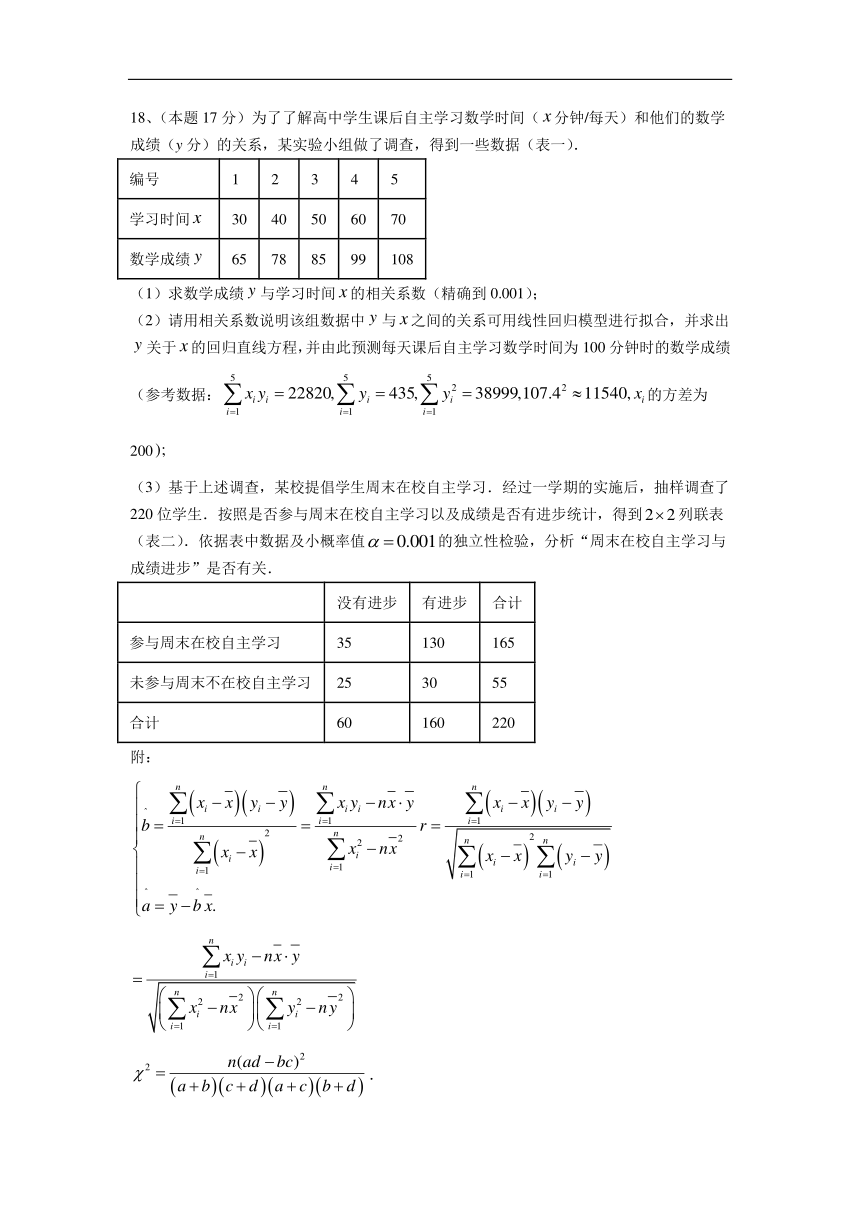
18、(本题17分)为了了解高中学生课后自主学习数学时间(分钟/每天)和他们的数学成绩(y分)的关系,某实验小组做了调查,得到一些数据(表一).
编号 1 2 3 4 5
学习时间 30 40 50 60 70
数学成绩 65 78 85 99 108
(1)求数学成绩与学习时间的相关系数(精确到0.001);
(2)请用相关系数说明该组数据中与之间的关系可用线性回归模型进行拟合,并求出关于的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据:的方差为200
(3)基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到列联表(表二).依据表中数据及小概率值的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.
没有进步 有进步 合计
参与周末在校自主学习 35 130 165
未参与周末不在校自主学习 25 30 55
合计 60 160 220
附:
.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
19、(本题17分)已知
(1)当时,解关于的不等式;
(2)若有两个零点,求的值;
(3)当时,的最大值,最小值为,若,求的取值范围.
2023学年第二学期温州十校联合体期中联考
高二年级数学学科参考答案
一、选择题:本大题共8小题,每小题5分,共40分
题号 1 2 3 4 5 6 7 8
答案 A D C B C D B A
二、选择题:本大题共8小题,每小题5分,共40分
题号 9 10 11
答案 AB ABC ABC
二、填空题:本大题共3小题,每小题5分,共15分
12、152 13、 14、40
15、(本题13分)
(1),所以,于是
(2)由,正弦定理得:.
又,所以又,所以.于是
16、(本题15分)
(1)证明:面面
又面
(2)方法1:面点B到面的距离就是点到面距离
由(1)得点到面距离为.记线面角为
方法2:设,则,,线面角记为,
方法3:设,
以为轴,为轴,为轴建立直角坐标系,
设面的法向量为则
.令线面角记为,.
方法4:将四棱锥还原为立方体,面为直线与面所成的角.
记为,
17、(本题15分)
解析:(1)因为,
由函数的最小正周期为,即,得,.
(2),因为,
要使在上恰有2个极值点和2个零点,则需,得
18、(本题17分)
(1),,又的方差为,
(2)由(1)知r=0.996接近1,故与之间具有极强的线性相关关系,可用线性回归直线方程模型进行拟合:,
,故当时,,
故预测每天课后自主学习数学时间达到100分钟时的数学成绩为140.5分.
(3)零假设为学生周末在校自主学习与成绩进步无关.
根据数据,计算得到:
因为,所以依据的独立性检验,可以认为“周末自主学习与成绩进步”有关.
19、(本题17分)
(1)当时,
或所以或
所以不等式的解集为
(2)
因为,所以当时,必有一零点记为),
所以当时,有且仅有一零点(记为),
由得,故,
当时,令,解得,所以.
(3)由知在上单调递增,
在上单调递减,在上单调递增.当时,,
解得,所以,当即时,
,
要使,分析可知需满足:,解得:;
当即时,分析可知需满足:
,解得:,
又,综上可得,.故的取值范围为.
高二年级数学学科试题
考生须知:
1.本卷共4页满分150分,考试时间120分钟.
2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字.
3.所有答案必须写在答题纸上,写在试卷上无效.
4.考试结束后,只需上交答题纸.
选择题部分
一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1、设集合,若,则( )
A. B. C. D.
2、若函数是指数函数,则的值为( )
A.2 B.-2 C. D.
3、设复数,则复数的共轭复数的虚部是( )
A. B. C.1 D.-1
4、已知非负实数满足,则的最小值为( )
A. B.2 C. D.
5、已知,则( )
A. B. C. D.
6、已知正方形的边长为2,若将正方形沿对角线折叠为三棱锥,则在折叠过程中,不能出现( )
A. B.面面
C. D.
7、一个袋子中装有大小相同的5个小球,其中有3个白球,2个黑球,从中无放回地取出3个小球,摸到一个白球记2分,摸到一个黑球记1分,则总得分的数学期望等于( )
A.5分 B.4.8分 C.4.6分 D.4.4分
8、已知,则( )
A. B. C. D.
二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9、已知向量,则下列命题正确的是( )
A. B.向量在向量上的投影向量为
C. D.
10、下列命题中正确的是( )
A.已知随机变量,则
B.已知随机变量,若函数为偶函数,则
C.数据第80百分位数是8
D.样本甲中有件样品,其方差为,样本乙中有件样品,其方差为,则由甲乙组成的总体样本的方差为
11、定义在上的函数,满足,且当时,,则使得在上恒成立的可以是( )
A.1 B.2 C. D.
非选择题部分
三、填空题:本大题共3小题,每小题5分,共15分.把答案填在题中的横线上.
12、______.
13、一位射击运动员向一个目标射击二次,记事件“第次命中目标”,,则______.
14、已知在三棱锥中,,点为三棱锥外接球上一点,则三棱锥的体积最大为______.
四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.
15、(本题13分)在中,内角所对的边分别为,且
(1)若,求的值;
(2)若,且的面积为,求和的值.
16、(本题15分)已知四棱锥面,底面为正方形,,为的中点.
(1)求证:面;
(2)求直线与面所成的角.
17、(本题15分)已知的最小正周期为,
(1)求的值;
(2)若在上恰2个极值点和2个零点,求实数的取值范围.
18、(本题17分)为了了解高中学生课后自主学习数学时间(分钟/每天)和他们的数学成绩(y分)的关系,某实验小组做了调查,得到一些数据(表一).
编号 1 2 3 4 5
学习时间 30 40 50 60 70
数学成绩 65 78 85 99 108
(1)求数学成绩与学习时间的相关系数(精确到0.001);
(2)请用相关系数说明该组数据中与之间的关系可用线性回归模型进行拟合,并求出关于的回归直线方程,并由此预测每天课后自主学习数学时间为100分钟时的数学成绩(参考数据:的方差为200
(3)基于上述调查,某校提倡学生周末在校自主学习.经过一学期的实施后,抽样调查了220位学生.按照是否参与周末在校自主学习以及成绩是否有进步统计,得到列联表(表二).依据表中数据及小概率值的独立性检验,分析“周末在校自主学习与成绩进步”是否有关.
没有进步 有进步 合计
参与周末在校自主学习 35 130 165
未参与周末不在校自主学习 25 30 55
合计 60 160 220
附:
.
0.10 0.05 0.010 0.005 0.001
2.706 3.841 6.635 7.879 10.828
19、(本题17分)已知
(1)当时,解关于的不等式;
(2)若有两个零点,求的值;
(3)当时,的最大值,最小值为,若,求的取值范围.
2023学年第二学期温州十校联合体期中联考
高二年级数学学科参考答案
一、选择题:本大题共8小题,每小题5分,共40分
题号 1 2 3 4 5 6 7 8
答案 A D C B C D B A
二、选择题:本大题共8小题,每小题5分,共40分
题号 9 10 11
答案 AB ABC ABC
二、填空题:本大题共3小题,每小题5分,共15分
12、152 13、 14、40
15、(本题13分)
(1),所以,于是
(2)由,正弦定理得:.
又,所以又,所以.于是
16、(本题15分)
(1)证明:面面
又面
(2)方法1:面点B到面的距离就是点到面距离
由(1)得点到面距离为.记线面角为
方法2:设,则,,线面角记为,
方法3:设,
以为轴,为轴,为轴建立直角坐标系,
设面的法向量为则
.令线面角记为,.
方法4:将四棱锥还原为立方体,面为直线与面所成的角.
记为,
17、(本题15分)
解析:(1)因为,
由函数的最小正周期为,即,得,.
(2),因为,
要使在上恰有2个极值点和2个零点,则需,得
18、(本题17分)
(1),,又的方差为,
(2)由(1)知r=0.996接近1,故与之间具有极强的线性相关关系,可用线性回归直线方程模型进行拟合:,
,故当时,,
故预测每天课后自主学习数学时间达到100分钟时的数学成绩为140.5分.
(3)零假设为学生周末在校自主学习与成绩进步无关.
根据数据,计算得到:
因为,所以依据的独立性检验,可以认为“周末自主学习与成绩进步”有关.
19、(本题17分)
(1)当时,
或所以或
所以不等式的解集为
(2)
因为,所以当时,必有一零点记为),
所以当时,有且仅有一零点(记为),
由得,故,
当时,令,解得,所以.
(3)由知在上单调递增,
在上单调递减,在上单调递增.当时,,
解得,所以,当即时,
,
要使,分析可知需满足:,解得:;
当即时,分析可知需满足:
,解得:,
又,综上可得,.故的取值范围为.
同课章节目录
