九年级数学上册试题 24.4相似三角形的判定-沪教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 24.4相似三角形的判定-沪教版(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 503.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 00:00:00 | ||
图片预览




文档简介
24.4相似三角形的判定
一、单选题
1.如图,AD、BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( )
A.AB∥CD B.
C. D.
2.在△ABC中,直线DE分别与AB、AC相交于点D、E,下列条件不能推出△ABC与△ADE相似的是( )
A. B.∠ADE=∠ACB
C.AE﹒AC=AB﹒AD D.
3.下列各组图形中,不一定相似的是( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
4.如图,已知则添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
5.下列说法中,正确的是( )
①有两边成比例且一对内角相等的两个三角形相似;②有一对锐角相等的两个直角三角形相似;③有两边对应成比例且夹角相等的两个三角形相似;④一条直线截三角形两边所得的三角形与原三角形相似.
A.①,② B.②,③ C.③,④ D.①,④.
6.如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图,下列选项中不能判定的是( )
A. B.
C. D.
8.在△ABC中,D为AB上一点,过点D作一条直线截△ABC,使截得的三角形与△ABC相似,这样的直线可以作( )
A.2条 B.3条 C.4条 D.5条
9.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,由下列条件判定△ABC∽△DEF的是( )
①∠A=55°,∠D=35°;②AC=3,BC=4,DF=6,DE=8;③AC=9,BC=12,DF=6,EF=8;④AB=10,AC=8,EF=9,DE=15.
A.1个 B.2个 C.3个 D.4个
10.如图,在正三角形ABC中,点D、E分别在AC、AB上,且,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
11.下列条件,能使和相似的是( )
A.
B.
C.
D.
12.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1 B.2 C.3 D.4
二、填空题
13.如图,在△ABC中,DE∥BC,则=______.
14.如图,在△ABC中,DE∥BC,,则△ABC∽______,其相似比为______.
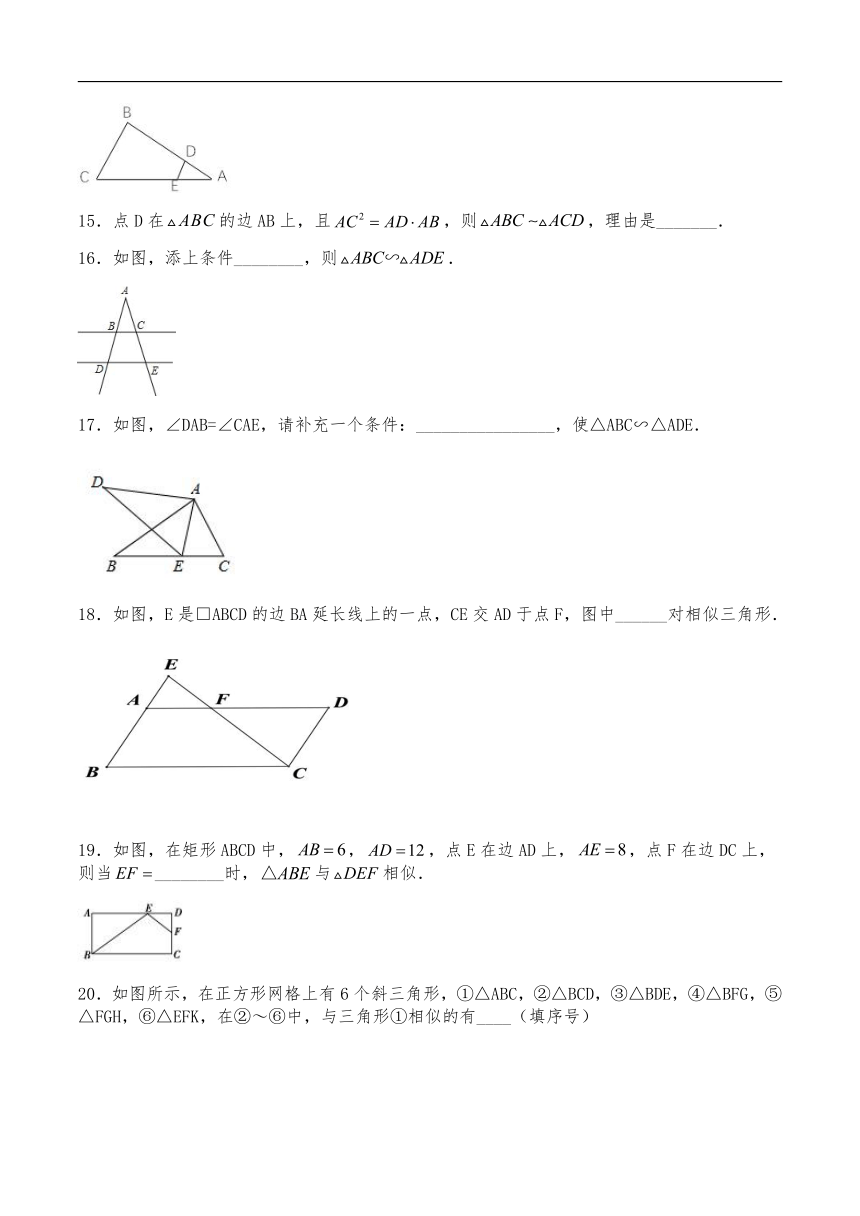
15.点D在的边AB上,且,则,理由是_______.
16.如图,添上条件________,则.
17.如图,∠DAB=∠CAE,请补充一个条件:________________,使△ABC∽△ADE.
18.如图,E是□ABCD的边BA延长线上的一点,CE交AD于点F,图中______对相似三角形.
19.如图,在矩形ABCD中,,,点E在边AD上,,点F在边DC上,则当________时,与相似.
20.如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有____(填序号)
21.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
三、解答题
22.如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,求证:△ADP∽△BCP.
23.如图,在正方形ABCD中,E是CD上的一点,F是BC的延长线上的一点,且CE=CF,BE的延长线交DF于点G,求证:△BGF∽△DCF.
24.如图,∠C=90°,AC=CD=DE=BE,试找出图中的一对相似三角形,并加以证明.
25.如图,在中,,于.
(1)写出图中的两对相似三角形;
(2)选择其中的一对相似三角形说明它们相似的理由.
26.如图,已知.求证:.
27.如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E.
求证:△DME∽△BCA.
28.如图,和的顶点都在正方形网格的格点上,则与相似吗?请说明理由.
29.已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.
30.如图,在中,E是DC上一点,连接AE、F为AE上一点,且.
求证:.
31.如图1,在正方形ABCD中,对角线AC、BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
(3)如图2,若PE=BE,PC=,求CF的值.
答案
一、单选题
1.D
【解析】
本题中已知∠AOB=∠DOC是对顶角,应用两三角形相似的判定定理,即可作出判断.
解:A、由AB∥CD能判定△AOB∽△DOC,故本选项不符合题意.
B、由∠AOB=∠DOC、∠A=∠D能判定△AOB∽△DOC,故本选项不符合题意.
C、由、∠AOB=∠DOC能判定△AOB∽△DOC,故本选项不符合题意.
D、已知两组对应边的比相等:,但其夹角不一定对应相等,不能判定△AOB与△DOC相似,故本选项符合题意.
故选:D
2.D
【解析】
由题意可得一组对角相等,根据相似三角形的判定:(1)两角对应相等,两三角形相似;(2)两边对应成比例且夹角相等,两三角形相似添加条件即可.
【详解】
解:有两边对应成比例且夹角相等的两个三角形相似,故选项A不符合题意;
两角对应相等,两三角形相似,故选项B不符合题意;
由AE﹒AC=AB﹒AD得,且∠A=∠A,故可得△ABC与△ADE相似,所以选项C不符合题意;
而D不是夹角相等,故选项D符合题意;
故选:D
3.D
【解析】
根据相似图形的定义,以及等边三角形的性质对各选项分析判断求解.
【详解】
A、各有一个角是100°的两个等腰三角形,100°的角只能是顶角,夹顶角的两边成比例,所以一定相似;
B、两个等腰直角三角形,对应边的比相等,锐角都是45°,相等,所以一定相似;
C、各有一个角是60°的两个等腰三角形,是等边三角形,有两对对应角相等,所以一定相似;
D、各有一个角是50°的两个等腰三角形,可能是顶角为50°,也可能底角为50°,所以对应角不一定相等,所以不一定不相似;
故选:D.
4.A
【解析】
先根据∠1=∠2得出∠BAC=∠DAE,再由相似三角形的判定定理对各选项进行逐一判定即可.
【详解】
解:∵∠1=∠2,
∴∠BAC=∠DAE.
A. ,∠B与∠D的大小无法判定,∴无法判定△ABC∽△ADE,故本选项符合题意;
B. ,∴△ABC∽△ADE,故本选项不符合题意;
C. ∴△ABC∽△ADE,故本选项不符合题意;
D. ∴△ABC∽△ADE,故本选项不符合题意;
故选:A
5.B
【解析】
根据三角形相似的判定判定即可;
【详解】
①必须是夹角,故错误;②有一对锐角相等的两个直角三角形相似,正确;③有两边对应成比例且夹角相等的两个三角形相似,正确;④必须是第三边的平行线,故错误;
故答案选D.
6.D
【解析】
试题分析:∵∠ADE=∠ACD=∠ABC,∴DE∥BC,∴△ADE∽△ABC,∵DE∥BC,∴∠EDC=∠DCB,∵∠ACD=∠ABC,∴△EDC∽△DCB,同理:∠ACD=∠ABC,∠A=∠A,∴△ABC∽△ACD,∵△ADE∽△ABC,△ABC∽△ACD,∴△ADE∽△ACD,∴共4对,故选D.
7.B
【解析】
根据相似三角形的判定定理逐个判断即可.
【详解】
解:A、∵AC2=AD AB,
∴,
∵∠A=∠A,
∴△ACD∽△ABC,
故本选项不符合题意;
B、∵BC2=BD AB,
∴,
∵∠B=∠B,
∴△BCD∽△ABC,
不能推出△ACD∽△ABC,故本选项符合题意;
C、∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,
故本选项不符合题意;
D、∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故本选项不符合题意;
故选:B.
8.C
【解析】
根据相似三角形的判定方法分析,即可做出判断.
【详解】
满足条件的直线有4条,如图所示:
如图1,过D作DE∥AC,则有△BDE∽△BAC;
如图2,过D作DE∥BC,则有△ADE∽△ABC;
如图3,过D作∠AED=∠B,又∠A=∠A,则有△ADE∽△ACB;
如图4,过D作∠BED=∠A,又∠B=∠B,则有△BED∽△BAC,
故选:C.
9.B
10.B
【解析】
本题可以采用排除法,即根据已知中正三角形ABC中,D、E分别在AC、AB上,,AE=BE,我们可以分别得到:△AED、△BCD为锐角三角形,△BED、△ABD为钝角三角形,然后根据锐角三角形不可能与钝角三角形相似排除错误答案,得到正确答案.
【详解】
由已知中正三角形ABC中,D、E分别在AC、AB上,,AE=BE,
易判断出:△AED为一个锐角三角形,△BED为一个钝角三角形,故A错误;
△ABD也是一个钝角三角形,故C也错误;
但△BCD为一个锐角三角形,故D也错误;
故选:B.
11.B
【解析】
【解析】
根据相似三角形的判定定理进行判断.
【详解】
解:A、,不能使和△相似,错误;
B、,能使和△相似,正确;
C、,不能使和△相似,错误;
D、,不能使和△相似,错误;
故选B.
12.D
【详解】
试题解析:如图①,∠OAB=∠,∠AOB=∠时,△AOB∽△.
如图②,AO∥BC,BA⊥,则∠=∠OAB,故△AOB∽△;
如图③,∥OB,∠ABC3=,则∠ABO=∠CAB,故△AOB∽△;
如图④,∠AOB=∠=,∠ABO=∠,则△AOB∽△.
故选D.
二、填空题
13.
【解析】
根据平行线的性质得∠ADE=∠B,∠AED=∠C,利用“有两个角对应相等的两个三角形相似”证得△ADE∽△ABC,根据相似三角形的性质即可得出结论.
【详解】
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴,
故答案为:.
14.△ADE
【解析】
根据已知条件判定相似三角形即可;
【详解】
∵DE∥BC,
∴,
∵,
∴,
∴;
故答案是△ADE和.
15.有两边对应成比例且夹角相等的两个三角形相似
【解析】
先依题意画出图形,再根据相似三角形的判定即可得.
【详解】
依题意,画图如下:
,即,
又,
(有两边对应成比例且夹角相等的两个三角形相似),
故答案为:有两边对应成比例且夹角相等的两个三角形相似.
16.∠ABC=∠ADE(答案不唯一)
【解析】
根据相似三角形的判定定理添加即可.
【详解】
添上∠ABC=∠ADE条件,则△ABC∽△ACD.
理由:∵∠ABC=∠ADE,∠A=∠A,
∴△ABC∽△ACD.
故答案为∠ACD=∠B(答案不唯一)
17.解:∠D=∠B或∠AED=∠C.
【解析】
根据相似三角形的判定定理再补充一个相等的角即可.
【详解】
解:∵∠DAB=∠CAE
∴∠DAE=∠BAC
∴当∠D=∠B或∠AED=∠C或AD:AB=AE:AC或AD AC=AB AE时两三角形相似.
故答案为∠D=∠B(答案不唯一).
18.3
【解析】
由□ABCD可得,,再由平行线性质推导而证明△AFE∽△CFD∽△BCE,从而完成求解.
【详解】
∵□ABCD
∴,
∴,
∵
∴
∵,
∴
△CFD∽△BCE
∴△AFE∽△CFD∽△BCE
故答案为:3.
19.5或
【解析】
若要与相似,则需要对应直角边成比例,代入数值计算即可.
【详解】
由题意,知与都是直角三角形,
所以当或时,与相似,
由,,,得,,
∴或,
∴5或.
故答案为: 5或.
20.③④⑤
【解析】
两三角形三条边对应成比例,两三角形相似,据此即可解答.
【详解】
解:设每个小正方形的边长为1,则△ABC的各边长分别为1、、.则
②△BCD的各边长分别为1、、2;
③△BDE的各边长分别为2、2、2(为△ABC各边长的2倍);
④△BFG的各边长分别为5、、(为△ABC各边长的倍);
⑤△FGH的各边长分别为2、、(为△ABC各边长的倍);
⑥△EFK的各边长分别为3、、.
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤.
故答案为③④⑤.
21.145
【解析】
先画出示意图,由相似三角形的判定可知,在△ABD和△DBC中,已知∠ABD=∠CBD,所以需另一组对应角相等,若∠A=∠C,则△ABD与△DBC全等不符合题意,所以必定有∠A=∠BDC,再根据四边形的内角和为360°列式求解.
【详解】
解:根据题意画出示意图,已知∠ABD=∠CBD,
△ABD与△DBC相似,但不全等,
∴∠A=∠BDC,∠ADB=∠C.
又∠A+∠ABC+∠C+∠ADC=360°,
∴2∠ADB+2∠BDC+∠ABC=360°,
∴∠ADB+∠BDC=145°,
即∠ADC=145°.
三、解答题
22.证明:∵∠1=∠2,∠DPA=∠CPB,∴△ADP∽△BCP.
23.∵正方形ABCD
∴∠DCB=∠DCF=90,DC=BC
∵CE=CF
∴△DCF≌△ECB
∴∠CDF =∠CBE
∵∠CDF+∠F=90
∴∠CBE+∠F=90
∴∠BGF=90=∠DCF
∴△BGF∽△DCF
24.∵∠C=90°,AC=CD=DE=BE,
∴AD=,BD=2,
∴,
∵∠ADB=∠ADB,
∴△ADE∽△BDA.
25.解:根据相似三角形的判定定理可知:
图中的两对相似三角形为:和;
(2)∵,,
∴,
又∵,
∴.
26.解:.
.
.
∴,
∴.
27.证明:∵∠C=90°,DM⊥AB于点M,DN⊥BC于点N,
∴∠C=∠ENB=∠DME=90°,
∴AC∥DN,
∴∠BEN=∠A,
∵∠BEN=∠DEM,
∴∠DEM=∠A.
在与中,
,
∴∽.
28.解:相似,理由如下:
设网格中小正方形的边长均为1.
根据勾股定理,得,
∴,
∴.
29.∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠2+∠ADE+∠3=180°,∠ADE=45°,
∴∠2+∠3=180°﹣∠ADE=135°,
∴∠1=∠3,
∴△ABD∽△DCE.
30.证明∵四边形ABCD是平行四边形,
∴,,,
∴
∵,且,
∴.
∵,
∴,
∴.
31.(1)∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠BCD=∠DCF=90°,
∵AE=CF,
∴△ADE≌△CDF(SAS);
(2)如图1,作FH∥AB交AC的延长线于H.
∵四边形ABCD是正方形,
∴∠ACB=∠FCH=45°,
∵AB∥FH,
∴∠HFC=∠ABC=90°,
∴∠FCH=∠H=45°,
∴CF=FH=AE,
∵∠PAE=∠H=45°,∠APE=∠FPH,
∴△APE≌△HPF(AAS),
∴PE=PF,
∵△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF,
∴∠EDF=∠ADC=90°,
∴△DEF是等腰直角三角形,
∵EP=PF,
∴∠EDP=∠FDP=45°,
∵ADP=∠ADE+∠PDE=∠ADE+45°,∠BDF=∠CDF+∠BDC=∠CDF+45°,
∴∠ADP=∠BDF,
∵∠DAP=∠DBF=45°,
∴△ADP∽△BDF;
(3)如图2中,作PH⊥BC于H.
∵∠ACB=45°,PC=,
∴PH=CH=1.
由(2)得:BE=PE=PF,
∴BE=EF,
∴∠BFE=30°,
∴PF=2,
∴HF=,
∴CF=﹣1,
一、单选题
1.如图,AD、BC相交于点O,由下列条件不能判定△AOB与△DOC相似的是( )
A.AB∥CD B.
C. D.
2.在△ABC中,直线DE分别与AB、AC相交于点D、E,下列条件不能推出△ABC与△ADE相似的是( )
A. B.∠ADE=∠ACB
C.AE﹒AC=AB﹒AD D.
3.下列各组图形中,不一定相似的是( )
A.各有一个角是100°的两个等腰三角形
B.各有一个角是90°的两个等腰三角形
C.各有一个角是60°的两个等腰三角形
D.各有一个角是50°的两个等腰三角形
4.如图,已知则添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
5.下列说法中,正确的是( )
①有两边成比例且一对内角相等的两个三角形相似;②有一对锐角相等的两个直角三角形相似;③有两边对应成比例且夹角相等的两个三角形相似;④一条直线截三角形两边所得的三角形与原三角形相似.
A.①,② B.②,③ C.③,④ D.①,④.
6.如图,∠ADE=∠ACD=∠ABC,图中相似三角形共有( )
A.1对 B.2对 C.3对 D.4对
7.如图,下列选项中不能判定的是( )
A. B.
C. D.
8.在△ABC中,D为AB上一点,过点D作一条直线截△ABC,使截得的三角形与△ABC相似,这样的直线可以作( )
A.2条 B.3条 C.4条 D.5条
9.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,由下列条件判定△ABC∽△DEF的是( )
①∠A=55°,∠D=35°;②AC=3,BC=4,DF=6,DE=8;③AC=9,BC=12,DF=6,EF=8;④AB=10,AC=8,EF=9,DE=15.
A.1个 B.2个 C.3个 D.4个
10.如图,在正三角形ABC中,点D、E分别在AC、AB上,且,AE=BE,则有( )
A.△AED∽△BED B.△AED∽△CBD
C.△AED∽△ABD D.△BAD∽△BCD
11.下列条件,能使和相似的是( )
A.
B.
C.
D.
12.如图,在平面直角坐标系中,A(0,4),B(2,0),点C在第一象限,若以A、B、C为顶点的三角形与△AOB相似(不包括全等),则点C的个数是( )
A.1 B.2 C.3 D.4
二、填空题
13.如图,在△ABC中,DE∥BC,则=______.
14.如图,在△ABC中,DE∥BC,,则△ABC∽______,其相似比为______.
15.点D在的边AB上,且,则,理由是_______.
16.如图,添上条件________,则.
17.如图,∠DAB=∠CAE,请补充一个条件:________________,使△ABC∽△ADE.
18.如图,E是□ABCD的边BA延长线上的一点,CE交AD于点F,图中______对相似三角形.
19.如图,在矩形ABCD中,,,点E在边AD上,,点F在边DC上,则当________时,与相似.
20.如图所示,在正方形网格上有6个斜三角形,①△ABC,②△BCD,③△BDE,④△BFG,⑤△FGH,⑥△EFK,在②~⑥中,与三角形①相似的有____(填序号)
21.定义:我们知道,四边形的一条对角线把这个四边形分成两个三角形,如果这两个三角形相似但不全等,我们就把这条对角线叫做这个四边形的相似对角线,在四边形ABCD中,对角线BD是它的相似对角线,∠ABC=70°,BD平分∠ABC,那么∠ADC=____________度
三、解答题
22.如图,BD、AC相交于点P,连接BC、AD,且∠1=∠2,求证:△ADP∽△BCP.
23.如图,在正方形ABCD中,E是CD上的一点,F是BC的延长线上的一点,且CE=CF,BE的延长线交DF于点G,求证:△BGF∽△DCF.
24.如图,∠C=90°,AC=CD=DE=BE,试找出图中的一对相似三角形,并加以证明.
25.如图,在中,,于.
(1)写出图中的两对相似三角形;
(2)选择其中的一对相似三角形说明它们相似的理由.
26.如图,已知.求证:.
27.如图,在△ABC中,∠C=90°,DM⊥AB于点M,DN⊥BC于点N,交AB于点E.
求证:△DME∽△BCA.
28.如图,和的顶点都在正方形网格的格点上,则与相似吗?请说明理由.
29.已知:如图,△ABC中,∠BAC=90°,AB=AC,点D是BC边上的一个动点(不与B,C重合),∠ADE=45°.求证:△ABD∽△DCE.
30.如图,在中,E是DC上一点,连接AE、F为AE上一点,且.
求证:.
31.如图1,在正方形ABCD中,对角线AC、BD交于点O,点E在AB上,点F在BC的延长线上,且AE=CF,连接EF交AC于点P,分别连接DE,DF,DP
(1)求证:△ADE≌△CDF;
(2)求证:△ADP∽△BDF;
(3)如图2,若PE=BE,PC=,求CF的值.
答案
一、单选题
1.D
【解析】
本题中已知∠AOB=∠DOC是对顶角,应用两三角形相似的判定定理,即可作出判断.
解:A、由AB∥CD能判定△AOB∽△DOC,故本选项不符合题意.
B、由∠AOB=∠DOC、∠A=∠D能判定△AOB∽△DOC,故本选项不符合题意.
C、由、∠AOB=∠DOC能判定△AOB∽△DOC,故本选项不符合题意.
D、已知两组对应边的比相等:,但其夹角不一定对应相等,不能判定△AOB与△DOC相似,故本选项符合题意.
故选:D
2.D
【解析】
由题意可得一组对角相等,根据相似三角形的判定:(1)两角对应相等,两三角形相似;(2)两边对应成比例且夹角相等,两三角形相似添加条件即可.
【详解】
解:有两边对应成比例且夹角相等的两个三角形相似,故选项A不符合题意;
两角对应相等,两三角形相似,故选项B不符合题意;
由AE﹒AC=AB﹒AD得,且∠A=∠A,故可得△ABC与△ADE相似,所以选项C不符合题意;
而D不是夹角相等,故选项D符合题意;
故选:D
3.D
【解析】
根据相似图形的定义,以及等边三角形的性质对各选项分析判断求解.
【详解】
A、各有一个角是100°的两个等腰三角形,100°的角只能是顶角,夹顶角的两边成比例,所以一定相似;
B、两个等腰直角三角形,对应边的比相等,锐角都是45°,相等,所以一定相似;
C、各有一个角是60°的两个等腰三角形,是等边三角形,有两对对应角相等,所以一定相似;
D、各有一个角是50°的两个等腰三角形,可能是顶角为50°,也可能底角为50°,所以对应角不一定相等,所以不一定不相似;
故选:D.
4.A
【解析】
先根据∠1=∠2得出∠BAC=∠DAE,再由相似三角形的判定定理对各选项进行逐一判定即可.
【详解】
解:∵∠1=∠2,
∴∠BAC=∠DAE.
A. ,∠B与∠D的大小无法判定,∴无法判定△ABC∽△ADE,故本选项符合题意;
B. ,∴△ABC∽△ADE,故本选项不符合题意;
C. ∴△ABC∽△ADE,故本选项不符合题意;
D. ∴△ABC∽△ADE,故本选项不符合题意;
故选:A
5.B
【解析】
根据三角形相似的判定判定即可;
【详解】
①必须是夹角,故错误;②有一对锐角相等的两个直角三角形相似,正确;③有两边对应成比例且夹角相等的两个三角形相似,正确;④必须是第三边的平行线,故错误;
故答案选D.
6.D
【解析】
试题分析:∵∠ADE=∠ACD=∠ABC,∴DE∥BC,∴△ADE∽△ABC,∵DE∥BC,∴∠EDC=∠DCB,∵∠ACD=∠ABC,∴△EDC∽△DCB,同理:∠ACD=∠ABC,∠A=∠A,∴△ABC∽△ACD,∵△ADE∽△ABC,△ABC∽△ACD,∴△ADE∽△ACD,∴共4对,故选D.
7.B
【解析】
根据相似三角形的判定定理逐个判断即可.
【详解】
解:A、∵AC2=AD AB,
∴,
∵∠A=∠A,
∴△ACD∽△ABC,
故本选项不符合题意;
B、∵BC2=BD AB,
∴,
∵∠B=∠B,
∴△BCD∽△ABC,
不能推出△ACD∽△ABC,故本选项符合题意;
C、∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,
故本选项不符合题意;
D、∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故本选项不符合题意;
故选:B.
8.C
【解析】
根据相似三角形的判定方法分析,即可做出判断.
【详解】
满足条件的直线有4条,如图所示:
如图1,过D作DE∥AC,则有△BDE∽△BAC;
如图2,过D作DE∥BC,则有△ADE∽△ABC;
如图3,过D作∠AED=∠B,又∠A=∠A,则有△ADE∽△ACB;
如图4,过D作∠BED=∠A,又∠B=∠B,则有△BED∽△BAC,
故选:C.
9.B
10.B
【解析】
本题可以采用排除法,即根据已知中正三角形ABC中,D、E分别在AC、AB上,,AE=BE,我们可以分别得到:△AED、△BCD为锐角三角形,△BED、△ABD为钝角三角形,然后根据锐角三角形不可能与钝角三角形相似排除错误答案,得到正确答案.
【详解】
由已知中正三角形ABC中,D、E分别在AC、AB上,,AE=BE,
易判断出:△AED为一个锐角三角形,△BED为一个钝角三角形,故A错误;
△ABD也是一个钝角三角形,故C也错误;
但△BCD为一个锐角三角形,故D也错误;
故选:B.
11.B
【解析】
【解析】
根据相似三角形的判定定理进行判断.
【详解】
解:A、,不能使和△相似,错误;
B、,能使和△相似,正确;
C、,不能使和△相似,错误;
D、,不能使和△相似,错误;
故选B.
12.D
【详解】
试题解析:如图①,∠OAB=∠,∠AOB=∠时,△AOB∽△.
如图②,AO∥BC,BA⊥,则∠=∠OAB,故△AOB∽△;
如图③,∥OB,∠ABC3=,则∠ABO=∠CAB,故△AOB∽△;
如图④,∠AOB=∠=,∠ABO=∠,则△AOB∽△.
故选D.
二、填空题
13.
【解析】
根据平行线的性质得∠ADE=∠B,∠AED=∠C,利用“有两个角对应相等的两个三角形相似”证得△ADE∽△ABC,根据相似三角形的性质即可得出结论.
【详解】
∵DE∥BC,
∴∠ADE=∠B,∠AED=∠C,
∴△ADE∽△ABC,
∴,
故答案为:.
14.△ADE
【解析】
根据已知条件判定相似三角形即可;
【详解】
∵DE∥BC,
∴,
∵,
∴,
∴;
故答案是△ADE和.
15.有两边对应成比例且夹角相等的两个三角形相似
【解析】
先依题意画出图形,再根据相似三角形的判定即可得.
【详解】
依题意,画图如下:
,即,
又,
(有两边对应成比例且夹角相等的两个三角形相似),
故答案为:有两边对应成比例且夹角相等的两个三角形相似.
16.∠ABC=∠ADE(答案不唯一)
【解析】
根据相似三角形的判定定理添加即可.
【详解】
添上∠ABC=∠ADE条件,则△ABC∽△ACD.
理由:∵∠ABC=∠ADE,∠A=∠A,
∴△ABC∽△ACD.
故答案为∠ACD=∠B(答案不唯一)
17.解:∠D=∠B或∠AED=∠C.
【解析】
根据相似三角形的判定定理再补充一个相等的角即可.
【详解】
解:∵∠DAB=∠CAE
∴∠DAE=∠BAC
∴当∠D=∠B或∠AED=∠C或AD:AB=AE:AC或AD AC=AB AE时两三角形相似.
故答案为∠D=∠B(答案不唯一).
18.3
【解析】
由□ABCD可得,,再由平行线性质推导而证明△AFE∽△CFD∽△BCE,从而完成求解.
【详解】
∵□ABCD
∴,
∴,
∵
∴
∵,
∴
△CFD∽△BCE
∴△AFE∽△CFD∽△BCE
故答案为:3.
19.5或
【解析】
若要与相似,则需要对应直角边成比例,代入数值计算即可.
【详解】
由题意,知与都是直角三角形,
所以当或时,与相似,
由,,,得,,
∴或,
∴5或.
故答案为: 5或.
20.③④⑤
【解析】
两三角形三条边对应成比例,两三角形相似,据此即可解答.
【详解】
解:设每个小正方形的边长为1,则△ABC的各边长分别为1、、.则
②△BCD的各边长分别为1、、2;
③△BDE的各边长分别为2、2、2(为△ABC各边长的2倍);
④△BFG的各边长分别为5、、(为△ABC各边长的倍);
⑤△FGH的各边长分别为2、、(为△ABC各边长的倍);
⑥△EFK的各边长分别为3、、.
根据三组对应边的比相等的两个三角形相似得到与三角形①相似的是③④⑤.
故答案为③④⑤.
21.145
【解析】
先画出示意图,由相似三角形的判定可知,在△ABD和△DBC中,已知∠ABD=∠CBD,所以需另一组对应角相等,若∠A=∠C,则△ABD与△DBC全等不符合题意,所以必定有∠A=∠BDC,再根据四边形的内角和为360°列式求解.
【详解】
解:根据题意画出示意图,已知∠ABD=∠CBD,
△ABD与△DBC相似,但不全等,
∴∠A=∠BDC,∠ADB=∠C.
又∠A+∠ABC+∠C+∠ADC=360°,
∴2∠ADB+2∠BDC+∠ABC=360°,
∴∠ADB+∠BDC=145°,
即∠ADC=145°.
三、解答题
22.证明:∵∠1=∠2,∠DPA=∠CPB,∴△ADP∽△BCP.
23.∵正方形ABCD
∴∠DCB=∠DCF=90,DC=BC
∵CE=CF
∴△DCF≌△ECB
∴∠CDF =∠CBE
∵∠CDF+∠F=90
∴∠CBE+∠F=90
∴∠BGF=90=∠DCF
∴△BGF∽△DCF
24.∵∠C=90°,AC=CD=DE=BE,
∴AD=,BD=2,
∴,
∵∠ADB=∠ADB,
∴△ADE∽△BDA.
25.解:根据相似三角形的判定定理可知:
图中的两对相似三角形为:和;
(2)∵,,
∴,
又∵,
∴.
26.解:.
.
.
∴,
∴.
27.证明:∵∠C=90°,DM⊥AB于点M,DN⊥BC于点N,
∴∠C=∠ENB=∠DME=90°,
∴AC∥DN,
∴∠BEN=∠A,
∵∠BEN=∠DEM,
∴∠DEM=∠A.
在与中,
,
∴∽.
28.解:相似,理由如下:
设网格中小正方形的边长均为1.
根据勾股定理,得,
∴,
∴.
29.∵∠BAC=90°,AB=AC,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠2+∠ADE+∠3=180°,∠ADE=45°,
∴∠2+∠3=180°﹣∠ADE=135°,
∴∠1=∠3,
∴△ABD∽△DCE.
30.证明∵四边形ABCD是平行四边形,
∴,,,
∴
∵,且,
∴.
∵,
∴,
∴.
31.(1)∵四边形ABCD是正方形,
∴DA=DC,∠DAE=∠BCD=∠DCF=90°,
∵AE=CF,
∴△ADE≌△CDF(SAS);
(2)如图1,作FH∥AB交AC的延长线于H.
∵四边形ABCD是正方形,
∴∠ACB=∠FCH=45°,
∵AB∥FH,
∴∠HFC=∠ABC=90°,
∴∠FCH=∠H=45°,
∴CF=FH=AE,
∵∠PAE=∠H=45°,∠APE=∠FPH,
∴△APE≌△HPF(AAS),
∴PE=PF,
∵△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF,
∴∠EDF=∠ADC=90°,
∴△DEF是等腰直角三角形,
∵EP=PF,
∴∠EDP=∠FDP=45°,
∵ADP=∠ADE+∠PDE=∠ADE+45°,∠BDF=∠CDF+∠BDC=∠CDF+45°,
∴∠ADP=∠BDF,
∵∠DAP=∠DBF=45°,
∴△ADP∽△BDF;
(3)如图2中,作PH⊥BC于H.
∵∠ACB=45°,PC=,
∴PH=CH=1.
由(2)得:BE=PE=PF,
∴BE=EF,
∴∠BFE=30°,
∴PF=2,
∴HF=,
∴CF=﹣1,
