沪教版九年级数学上册试题 24.5相似三角形的性质(含答案)
文档属性
| 名称 | 沪教版九年级数学上册试题 24.5相似三角形的性质(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 739.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 08:15:49 | ||
图片预览




文档简介
24.5相似三角形的性质
一、单选题
1.如果两个相似三角形的对应高之比是,那么它们的周长比是( )
A. B.
C. D.
2.已知两个三角形相似,其中一个三角形的两个内角分别为,则另一个三角形的最小内角为( )
A. B. C. D.不能确定
3.如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
4.下列命题中,不正确的是:( )
A.两个全等三角形一定相似; B.两个等边三角形一定相似;
C.两个直角三角形一定相似; D.两个正方形一定相似.
5.已知与相似,且,那么下列结论中,一定成立的是( )
A. B. C.相似比为 D.相似比为
6.直角梯形ABCD中,AD//BC,∠A=90°,AD=2,BC=3,AB=7,点P是线段AB上一个动点,要使以A、P、D为顶点的三角形与△BPC相似,P的位置有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在△中,,垂足为,那么下列结论错误的是( )
A. B.
C. D.
8.已知△ABC和△ADC均为直角三角形,点B、D位于AC的两侧,∠ACB=∠ACD=90°,BC=a,AC=b,AB=c,要使△ADC和△ABC相似,CD可以等于( ).
A. B. C. D.
9.如图,中,是中点,是中点,的延长线交于,则的值为( )
A. B. C. D.
10.如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
① ; ② ; ③;④CE2=CD×BC; ⑤BE2=AE×BC
A.2个 B.3个 C.4个 D.5个
11.如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则的值为( )
A. B. C. D.1
12.如图,在正方形ABCD中,是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
A.AE=2DE B. C. D.
二、填空题
13.相似三角形对应高的比为4:3,那么它们的对应中线的比为______.
14.若两个相似多边形的对应边之比为5:2,则它们的周长比是______,面积比是______.
15.一个三角形三边长度之比为2:5:6,另一个与它相似的三角形最长边为24,则三角形的最短边为_________.
16.在△ABC中,D、E分别在边AB、AC上,且DE∥BC,又,则S△ADE:S四边形BCED=_____.
17.如图,已知点O是△ABC的重心,过点O作EF∥BC,分别交AB、AC于点E、F,若BC=6,则EF=________.
18.如图,小杰同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是6米(即OD=6米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是_____米.
19.如图,在ABC中,点D是边BC的中点,直线DF交边AC于点F,交AB的延长线于点E,如果CF∶CA=a∶b,那么BE∶AE的值为______.(用含a、b的式子表示)
20.如图,已知在平行四边形中,点E在边上,,联结交对角线于点O,那么的值为_____.
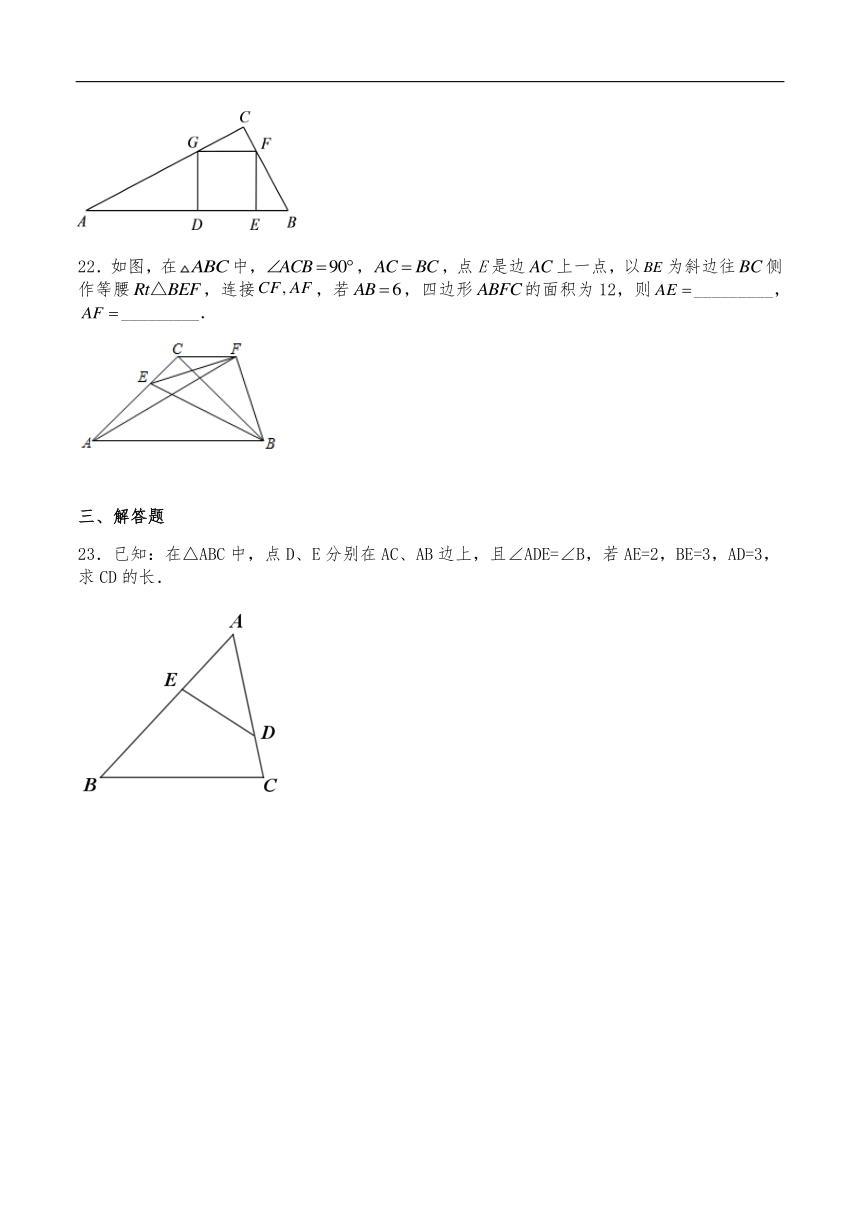
21.如图,已知在中,,,,正方形的顶点G、F分别在边、上,点D、E在斜边上,那么正方形的边长为_____.
22.如图,在中,,,点E是边上一点,以为斜边往侧作等腰,连接,若,四边形的面积为12,则_________,_________.
三、解答题
23.已知:在△ABC中,点D、E分别在AC、AB边上,且∠ADE=∠B,若AE=2,BE=3,AD=3,求CD的长.
24.如图所示,梯形ABCD中,AB∥CD,对角线AC,BD交于O点,若S△AOD:S△DOC=2:3,求S△AOB:S△COD.
25.如图,四边形ABCD中,∠A=∠BCD=90°.过C作对角线BD的垂线交BD、AD于点E、F,求证:CD是DF和DA的比例中项.
26.已知:如图,E、M是AB边的三等分点,EF∥MN∥BC.求:△AEF的面积:四边形EMNF的面积:四边形MBCN的面积.
27.如图,已知,在平行四边形ABCD中,E为射线CB上一点,联结DE交对角线AC于点F,∠ADE=∠BAC.
(1)求证:CF CA=CB CE;
(2)如果AC=DE,求证:四边形ABCD是菱形.
28.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且.
(1)求证:△CDE∽△ACB;
(2)当DA∶EA=时,求△CDE与△ABC的面积比.
29.如图,在平行四边形中,E为边的中点,连接,若的延长线和的延长线相交于点F.
(1)求证:;
(2)连接和相交于点为G,若的面积为2,求平行四边形的面积.
30.如图①,在四边形中,,,于点,作于点.
(1)求证:;
(2)连接,交于点(如图②),
①若,求的值;
②求证:.
答案
一、单选题
1.A
【解析】
根据相似三角形对应高的比等于相似比,周长的比等于相似比解答.
解:∵对应高之比是1:2,
∴相似比=1:2,
∴对应周长之比是1:2.
故选:A.
2.C
【解析】
根据相似三角形的性质、三角形的内角和定理可得出另一个三角形的三个内角度数,由此即可得.
由相似三角形的性质得:另一个三角形的两个内角分别为,
则另一个三角形的第三个内角为,
因此,另一个三角形的最小内角为,
故选:C.
3.A
【解析】
根据相似三角形的性质判断即可.
解:∵△OAB∽△OCD,OA:OC=3:2,
∴,A正确;
∴,B错误;
∴,C错误;
∴OA:OC=3:2,D错误;
故选:A.
4.C
【解析】
根据相似三角形的判定方法对各个选项进行分析解答即可.
解:、全等三角形是特殊的相似三角形,故正确;
、等边三角形的三个角均相等,可根据两角对应相等两三角形相似判定,故正确;
、若一个等腰直角三角形与一个一般直角三角形,则不能判定其相似,故不正确;
、由正方形的性质可判定其相似,故正确.
故选:C.
5.D
【解析】
根据相似三角形的性质对不同的对应角和对应边进行分类讨论.
解:∵B可以与E对应,也可以与F对应,∴∠B=∠E或∠B=∠F,A不一定成立;
同上,AB可以与DE对应,也可以与DF对应,∴或 ,B不一定成立;
同上,AB可以与DE对应,也可以与DF对应,∴相似比可能是,也可能是,C不一定成立;
∵∠A=∠D ,即∠A与∠D是对应角,∴它们的对边一定是对应比,即BC与EF是对应比,
∴相似比为,∴D一定成立,
故选D .
6.C
【解析】
要使两个三角形相似,则可能是△PAD∽△PBC,也可能是△ADP∽△BPC,所以应分两种情况讨论,进而求解.
解:(1)①当△PAD∽△PBC时,
AP:PB=AD:BC,
∵AB=AP+PB=7,AD=2,BC=3,
∴AP=;
②当△ADP∽△BPC时,
AP:BC=AD:BP,
∵AB=AP+PB=7,AD=2,BC=3,
∴PA=1或PA=6;
综合①②P点距离A点有三个位置:PA=;PA=1或PA=6;
故选:C.
7.B
【解析】
【解析】
根据直角三角形的性质与相似三角形的判定可知△ADC∽△CDB∽△ACB,利用相似三角形的对应线段成比例即可求解.
【详解】
∵∠ACB=90°,CD⊥AB,
∴△ADC∽△CDB∽△ACB
∴AC2=AD·AB,BC2=BD·AB,
故,A正确,B错误;
∵△ADC∽△CDB
∴
∴,,C,D选项正确;
故选B.
8.B
【解析】
由△ADC和△ABC相似,可得到,从而完成求解.
【详解】
∵△ADC和△ABC相似,且∠ACB=∠ACD=90°
∴
∴
∴
故选:B.
9.B
【解析】
过G作GF∥AB,交CD于F,得到△CFG∽△CDB,再根据AAS得出△ADE△GFE,然后根据相似三角形和全等三角形的性质即可得出答案
【详解】
解:过G作GF∥AB,交CD于F,
∴△CFG∽△CDB,
∴BG:CG=DF:FC
∵G是BC的中点,
∴BG=CG
∴DF=FC
∵GF∥AB,
∴∠DAG=∠FGA
∵E是AG的中点,
∴AE=GE
∵∠DEA=∠FEG
∴△DAE≌△FEG
∴DE=EF
∴DF=2DE=2EF
∴FC=2DE
∴EC=3DE
∴
故选:B
10.B
【解析】
【解析】
根据角平分线的性质,推出角相等,再得出边相等,判断出①②正确,再利用三角形不相似,排除其它选项,最后得解.
【详解】
解:如图,∵BE平分∠ABC,CE平分∠BCD
∴∠ABE=∠CBE,∠ABE=∠CBE.
∵CD∥BA,
∴∠ABC+∠BCD=180°.
∴∠BEC=∠D=∠A=90°.
则有△CED∽△BEA∽△CBE,
∴① 正确,③ 正确;
无法证明CD=DE,故②不正确;
故④CE 2=CD×BC正确;
故BE2=AE×BC不正确.
因此只有①②④正确.
故选B.
11.C
【解析】
首先证明AG:AB=CH:BC=1:3,推出GH∥AC,推出△BGH∽△BAC,可得,,由此即可解决问题.
【详解】
∵四边形ABCD是平行四边形
∴AD=BC,DC=AB,
∵AC=CA,
∴△ADC≌△CBA,
∴S△ADC=S△ABC,
∵AE=CF=AC,AG∥CD,CH∥AD,
∴AG:DC=AE:CE=1:3,CH:AD=CF:AF=1:3,
∴AG:AB=CH:BC=1:3,
∴GH∥AC,
∴△BGH∽△BAC,
∴,
∵,
∴.
故选C.
12.C
【解析】
A.利用直角三角形30度角的性质即可解决问题.
B.根据两角相等两个三角形相似即可判断.
C.通过计算证明∠DPB≠∠DPF,即可判断.
D.利用相似三角形的性质即可证明.
【详解】
解:∵四边形ABCD是正方形,
∴∠D=∠DAB=90°,
∵△ABP是等边三角形,
∴∠PAB=∠PBA=∠APB=60°,
∴∠DAE=30°,
∴AE=2DE,故A正确;
∵AB∥CD,
∴∠CFP=∠ABP=∠APH=60°,
∵∠PHA=∠PBA+∠BAH=60°+45°=105°,
又∵BC=BP,∠PBC=30°,
∴∠BPC=∠BCP=75°,
∴∠CPF=105°,
∴∠PHA=∠CPF,又易得∠APB=∠CFP=60°,
∴△CFP∽△APH,故B正确;
∵∠CPB=60°+75°=135°≠∠DPF,
∴△PFC与△PCA不相似,故C错误;
∵∠PCH=∠PCB-∠BCH=75°-45°=30°,
∴∠PCH=∠PBC,
∵∠CPH=∠BPC,
∴△PCH∽△PBC,
∴,
∴PC2=PH PB,故D正确,
故选:C.
二、填空题
13.4:3
【解析】
根据相似三角形对应中线的比、对应高的比、对应角平分线的比都等于相似比解答即可.
【详解】
解:相似三角形对应高的比为4:3,那么它们的对应中线的比为4:3.
故答案为:4:3.
14.5:2 25:4
【解析】
根据周长比、面积比与相似比的关系可以解得答案.
【详解】
相似多边形的周长的比等于相似比,相似多边形的面积的比等于相似比的平方.
两个相似多边形的对应边之比为5:2,则它们的周长比是5:2,面积比是25:4.
故答案为5:2;25:4.
15.8
【解析】
首先设与它相似的三角形的最短边的长为x,然后根据相似三角形的对应边成比例,即可得方程,解此方程即可求得答案.
【详解】
解:设与它相似的三角形的最短边的长为x,则
,
∴;
∴三角形的最短边为8.
故答案为:8.
16.4:5
【解析】
由已知条件可证得△ADE∽△ABC,则,再根据已知条件,得出,由相似三角形的面积之比等于相似比的平方即可求解.
【详解】
如图:
∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵AD:DB=2:1,
∴,
∴,
∵S△ADE+S四边形DBCE=S△ABC,
∴S△ADE:S四边形BCED=4:5.
故答案为:4:5.
17.4
【解析】
连接AO并延长交BC于Q,利用重心性质得AO:OQ=2:1,则AO:AQ=2:3,再证明△AEF∽△ABC,△AEO∽△ABQ,然后根据相似三角形的性质求解.
【详解】
解:∵连接AO并延长交BC于Q,
∵O是△ABC的重心,
∴AO:OQ=2:1,
∴AO:AQ=2:3,
∵EF∥BC,
∴△AEO∽△ABQ,△AEF∽△ABC,
∴
∵BC=6,
∴EF=4.
故答案为:4.
18.5.4
【解析】
依据题意可得∠AOC=∠BOD,通过说明△ACO~△BDO,得出比例式可求得结论.
【详解】
解:由题意得:∠AOC=∠BOD.
∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°.
∴△ACO~△BDO.
∴.
即.
∴BD=5.4(米).
故答案为:5.4.
19.a:(b-a)
【解析】
做辅助线构造全等三角形得出BG=CF,再由△BGE∽△AFE得即可.
【详解】
解:如图:
过点B作BG∥AC交EF于点G
∴∠1=∠C
∵点D是边BC的中点
∴BD=CD
在△BDG和△CDF中
∴△BDG≌△CDF
∴BG=CF
又∵BG∥AC
∴△BGE∽△AFE
∴ =
即BE:AE=a:(b-a)
故答案为:a:(b-a) .
20.
【解析】
由题意可以得到△AOE∽△COD,再根据三角形相似的性质和已知条件可以求得AO:OC的值.
【详解】
解:∵四边形ABCD是平行四边形,
∴∠OAE=∠DCO,∠OEA=∠ODC,
∴△AOE∽△COD,
∴,
∵,
∴,
∴,
故答案为.
21.
【解析】
作CM⊥AB于M,交GF于N,由勾股定理可得出AB,由面积法求出CM,证明△CGF∽△CAB,再根据对应边成比例,即可得出答案.
【详解】
作CM⊥AB于M,交GF于N,如图所示:
∵Rt△ABC中,∠C=90°,AB=10,,
∴设BC=k,则AC=2k,AB2=AC2+BC2,即:102=(2k)2+k2,解得:k=2,
∴BC=2,AC=4,
∴CM===4,
∵正方形DEFG内接于△ABC,
∴GF=EF=MN,GF∥AB,
∴△CGF∽△CAB,
∴,即,
解得:EF=;
故答案为:.
22.
【解析】
如图,过点作于,过点作,交的延长线于,由面积和差关系可求,通过证明,可得,可求,由勾股定理可求,,的长,通过证明,可得,可求,,由勾股定理可求解.
【详解】
解:如图,过点作于,过点作,交的延长线于,
,,
,
,
,
四边形的面积为12,
,
,
等腰,
,,,
,,
,
,
,
,
,
,,
,
,,
,,
,
,
,
,且
,且,
,
,
,,
,
,
故答案为:,.
三、解答题
23.
∵∠ADE=∠B,∠A=∠A
∴△ADE∽△ABC
∴
∴
∴AC=
∴CD=.
24.
∵AB∥CD
∴△CDO∽△ABO
∵S△AOD∶S△DOC=2∶3
∴AO:CO=2∶3
∴S△AOB∶S△COD=4:9.
25.
证明:(1)∵∠DEF=∠DAB=90°,∠BDA=∠FDE,
∴△DEF∽△DAB,
∴DE:DA=DF:DB,
∴DE DB=DA DF,
∵∠DCB=∠DEC=90°,∠BDC=∠CDE,
∴△DEC∽△DCB,
∴,
∴DC2=DE DB,
又∵DE DB=DA DF,
∴CD2=DF DA.
∴CD是DF和DA的比例中项
26.
∵EF∥MN∥BC,
∴△AEF∽△AMN∽△ABC,
∵E、M是AB边的三等分点,
∴△AEF,△AMN,△ABC的相似比为1:2:3,
∴△AEF,△AMN,△ABC的面积比为1:4:9,
∴△AEF的面积∶四边形EMNF的面积∶四边形MBCN的面积=1:3:5.
27.
证明:(1)∵四边形ABCD是平行四边形.
∴AD∥BC.
∴∠ADE=∠E.
∵∠ADE=∠BAC.
∴∠BAC=∠E.
∵∠ACB=∠ECF.
∴△ACB∽△ECF.
∴.
∴CF CA=CB CE
(2)由(1)知∠ADE=∠E.
∵∠ADF=∠CFE.
∴△ADF∽△CEF.
∴.
∴.
∵AC=DE.
∴EF=CF.
∵△ACB∽△ECF.
∴AB=BC
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
28.
(1)∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A.
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B-∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B.
∴△CDE∽△ACB.
(2)令EA=k,DA=,CE=x.
由△CDE∽△ACB,
得,即,
解得,(舍).
所以.
29.
(1)证明:∵四边形ABCD是平行四边形,
∴,,
∴,
∵点E为DC的中点,
∴,
在和中
∴,
∴,
∴;
(2)∵四边形ABCD是平行四边形,点E为DC的中点,
∴,,
∴,,
∴,
∵的面积为2,
∴,即,
∵
∴,
∴,
∴,
∴.
30.
(1)证明:∵,∴.
∵,∴,
∴.
又∵,
∴;
(2)①解:如解图①,过点作交的延长线于点.
∵,,
∴是等边三角形,.
∵,
∴,.
∴,.
设的边长为,∵,
∴,,,
∴.
∵,,∴,
∴,
∴,即;
图①
②证明:如解图②,过点作交于点,则.
∵,∴,
∴,
∴.
∵,
∴,
∴,则.
又∵,∴,,
∴,
∴.
图②
一、单选题
1.如果两个相似三角形的对应高之比是,那么它们的周长比是( )
A. B.
C. D.
2.已知两个三角形相似,其中一个三角形的两个内角分别为,则另一个三角形的最小内角为( )
A. B. C. D.不能确定
3.如图,△OAB∽△OCD,OA:OC=3:2,△OAB与△OCD的面积分别是S1与S2,周长分别是C1与C2,则下列说法正确的是( )
A. B. C. D.
4.下列命题中,不正确的是:( )
A.两个全等三角形一定相似; B.两个等边三角形一定相似;
C.两个直角三角形一定相似; D.两个正方形一定相似.
5.已知与相似,且,那么下列结论中,一定成立的是( )
A. B. C.相似比为 D.相似比为
6.直角梯形ABCD中,AD//BC,∠A=90°,AD=2,BC=3,AB=7,点P是线段AB上一个动点,要使以A、P、D为顶点的三角形与△BPC相似,P的位置有( )
A.1个 B.2个 C.3个 D.4个
7.如图,在△中,,垂足为,那么下列结论错误的是( )
A. B.
C. D.
8.已知△ABC和△ADC均为直角三角形,点B、D位于AC的两侧,∠ACB=∠ACD=90°,BC=a,AC=b,AB=c,要使△ADC和△ABC相似,CD可以等于( ).
A. B. C. D.
9.如图,中,是中点,是中点,的延长线交于,则的值为( )
A. B. C. D.
10.如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
① ; ② ; ③;④CE2=CD×BC; ⑤BE2=AE×BC
A.2个 B.3个 C.4个 D.5个
11.如图,E,F是平行四边形ABCD对角线AC上两点,AE=CF=AC.连接DE,DF并延长,分别交AB,BC于点G,H,连接GH,则的值为( )
A. B. C. D.1
12.如图,在正方形ABCD中,是等边三角形,AP、BP的延长线分别交边CD于点E、F,联结AC、CP、AC与BF相交于点H,下列结论中错误的是( )
A.AE=2DE B. C. D.
二、填空题
13.相似三角形对应高的比为4:3,那么它们的对应中线的比为______.
14.若两个相似多边形的对应边之比为5:2,则它们的周长比是______,面积比是______.
15.一个三角形三边长度之比为2:5:6,另一个与它相似的三角形最长边为24,则三角形的最短边为_________.
16.在△ABC中,D、E分别在边AB、AC上,且DE∥BC,又,则S△ADE:S四边形BCED=_____.
17.如图,已知点O是△ABC的重心,过点O作EF∥BC,分别交AB、AC于点E、F,若BC=6,则EF=________.
18.如图,小杰同学跳起来把一个排球打在离他2米(即CO=2米)远的地上,排球反弹碰到墙上,如果他跳起击球时的高度是1.8米(即AC=1.8米),排球落地点离墙的距离是6米(即OD=6米),假设排球一直沿直线运动,那么排球能碰到墙面离地的高度BD的长是_____米.
19.如图,在ABC中,点D是边BC的中点,直线DF交边AC于点F,交AB的延长线于点E,如果CF∶CA=a∶b,那么BE∶AE的值为______.(用含a、b的式子表示)
20.如图,已知在平行四边形中,点E在边上,,联结交对角线于点O,那么的值为_____.
21.如图,已知在中,,,,正方形的顶点G、F分别在边、上,点D、E在斜边上,那么正方形的边长为_____.
22.如图,在中,,,点E是边上一点,以为斜边往侧作等腰,连接,若,四边形的面积为12,则_________,_________.
三、解答题
23.已知:在△ABC中,点D、E分别在AC、AB边上,且∠ADE=∠B,若AE=2,BE=3,AD=3,求CD的长.
24.如图所示,梯形ABCD中,AB∥CD,对角线AC,BD交于O点,若S△AOD:S△DOC=2:3,求S△AOB:S△COD.
25.如图,四边形ABCD中,∠A=∠BCD=90°.过C作对角线BD的垂线交BD、AD于点E、F,求证:CD是DF和DA的比例中项.
26.已知:如图,E、M是AB边的三等分点,EF∥MN∥BC.求:△AEF的面积:四边形EMNF的面积:四边形MBCN的面积.
27.如图,已知,在平行四边形ABCD中,E为射线CB上一点,联结DE交对角线AC于点F,∠ADE=∠BAC.
(1)求证:CF CA=CB CE;
(2)如果AC=DE,求证:四边形ABCD是菱形.
28.如图,CD是直角△ABC斜边AB上的中线,点E位于边AC上,且.
(1)求证:△CDE∽△ACB;
(2)当DA∶EA=时,求△CDE与△ABC的面积比.
29.如图,在平行四边形中,E为边的中点,连接,若的延长线和的延长线相交于点F.
(1)求证:;
(2)连接和相交于点为G,若的面积为2,求平行四边形的面积.
30.如图①,在四边形中,,,于点,作于点.
(1)求证:;
(2)连接,交于点(如图②),
①若,求的值;
②求证:.
答案
一、单选题
1.A
【解析】
根据相似三角形对应高的比等于相似比,周长的比等于相似比解答.
解:∵对应高之比是1:2,
∴相似比=1:2,
∴对应周长之比是1:2.
故选:A.
2.C
【解析】
根据相似三角形的性质、三角形的内角和定理可得出另一个三角形的三个内角度数,由此即可得.
由相似三角形的性质得:另一个三角形的两个内角分别为,
则另一个三角形的第三个内角为,
因此,另一个三角形的最小内角为,
故选:C.
3.A
【解析】
根据相似三角形的性质判断即可.
解:∵△OAB∽△OCD,OA:OC=3:2,
∴,A正确;
∴,B错误;
∴,C错误;
∴OA:OC=3:2,D错误;
故选:A.
4.C
【解析】
根据相似三角形的判定方法对各个选项进行分析解答即可.
解:、全等三角形是特殊的相似三角形,故正确;
、等边三角形的三个角均相等,可根据两角对应相等两三角形相似判定,故正确;
、若一个等腰直角三角形与一个一般直角三角形,则不能判定其相似,故不正确;
、由正方形的性质可判定其相似,故正确.
故选:C.
5.D
【解析】
根据相似三角形的性质对不同的对应角和对应边进行分类讨论.
解:∵B可以与E对应,也可以与F对应,∴∠B=∠E或∠B=∠F,A不一定成立;
同上,AB可以与DE对应,也可以与DF对应,∴或 ,B不一定成立;
同上,AB可以与DE对应,也可以与DF对应,∴相似比可能是,也可能是,C不一定成立;
∵∠A=∠D ,即∠A与∠D是对应角,∴它们的对边一定是对应比,即BC与EF是对应比,
∴相似比为,∴D一定成立,
故选D .
6.C
【解析】
要使两个三角形相似,则可能是△PAD∽△PBC,也可能是△ADP∽△BPC,所以应分两种情况讨论,进而求解.
解:(1)①当△PAD∽△PBC时,
AP:PB=AD:BC,
∵AB=AP+PB=7,AD=2,BC=3,
∴AP=;
②当△ADP∽△BPC时,
AP:BC=AD:BP,
∵AB=AP+PB=7,AD=2,BC=3,
∴PA=1或PA=6;
综合①②P点距离A点有三个位置:PA=;PA=1或PA=6;
故选:C.
7.B
【解析】
【解析】
根据直角三角形的性质与相似三角形的判定可知△ADC∽△CDB∽△ACB,利用相似三角形的对应线段成比例即可求解.
【详解】
∵∠ACB=90°,CD⊥AB,
∴△ADC∽△CDB∽△ACB
∴AC2=AD·AB,BC2=BD·AB,
故,A正确,B错误;
∵△ADC∽△CDB
∴
∴,,C,D选项正确;
故选B.
8.B
【解析】
由△ADC和△ABC相似,可得到,从而完成求解.
【详解】
∵△ADC和△ABC相似,且∠ACB=∠ACD=90°
∴
∴
∴
故选:B.
9.B
【解析】
过G作GF∥AB,交CD于F,得到△CFG∽△CDB,再根据AAS得出△ADE△GFE,然后根据相似三角形和全等三角形的性质即可得出答案
【详解】
解:过G作GF∥AB,交CD于F,
∴△CFG∽△CDB,
∴BG:CG=DF:FC
∵G是BC的中点,
∴BG=CG
∴DF=FC
∵GF∥AB,
∴∠DAG=∠FGA
∵E是AG的中点,
∴AE=GE
∵∠DEA=∠FEG
∴△DAE≌△FEG
∴DE=EF
∴DF=2DE=2EF
∴FC=2DE
∴EC=3DE
∴
故选:B
10.B
【解析】
【解析】
根据角平分线的性质,推出角相等,再得出边相等,判断出①②正确,再利用三角形不相似,排除其它选项,最后得解.
【详解】
解:如图,∵BE平分∠ABC,CE平分∠BCD
∴∠ABE=∠CBE,∠ABE=∠CBE.
∵CD∥BA,
∴∠ABC+∠BCD=180°.
∴∠BEC=∠D=∠A=90°.
则有△CED∽△BEA∽△CBE,
∴① 正确,③ 正确;
无法证明CD=DE,故②不正确;
故④CE 2=CD×BC正确;
故BE2=AE×BC不正确.
因此只有①②④正确.
故选B.
11.C
【解析】
首先证明AG:AB=CH:BC=1:3,推出GH∥AC,推出△BGH∽△BAC,可得,,由此即可解决问题.
【详解】
∵四边形ABCD是平行四边形
∴AD=BC,DC=AB,
∵AC=CA,
∴△ADC≌△CBA,
∴S△ADC=S△ABC,
∵AE=CF=AC,AG∥CD,CH∥AD,
∴AG:DC=AE:CE=1:3,CH:AD=CF:AF=1:3,
∴AG:AB=CH:BC=1:3,
∴GH∥AC,
∴△BGH∽△BAC,
∴,
∵,
∴.
故选C.
12.C
【解析】
A.利用直角三角形30度角的性质即可解决问题.
B.根据两角相等两个三角形相似即可判断.
C.通过计算证明∠DPB≠∠DPF,即可判断.
D.利用相似三角形的性质即可证明.
【详解】
解:∵四边形ABCD是正方形,
∴∠D=∠DAB=90°,
∵△ABP是等边三角形,
∴∠PAB=∠PBA=∠APB=60°,
∴∠DAE=30°,
∴AE=2DE,故A正确;
∵AB∥CD,
∴∠CFP=∠ABP=∠APH=60°,
∵∠PHA=∠PBA+∠BAH=60°+45°=105°,
又∵BC=BP,∠PBC=30°,
∴∠BPC=∠BCP=75°,
∴∠CPF=105°,
∴∠PHA=∠CPF,又易得∠APB=∠CFP=60°,
∴△CFP∽△APH,故B正确;
∵∠CPB=60°+75°=135°≠∠DPF,
∴△PFC与△PCA不相似,故C错误;
∵∠PCH=∠PCB-∠BCH=75°-45°=30°,
∴∠PCH=∠PBC,
∵∠CPH=∠BPC,
∴△PCH∽△PBC,
∴,
∴PC2=PH PB,故D正确,
故选:C.
二、填空题
13.4:3
【解析】
根据相似三角形对应中线的比、对应高的比、对应角平分线的比都等于相似比解答即可.
【详解】
解:相似三角形对应高的比为4:3,那么它们的对应中线的比为4:3.
故答案为:4:3.
14.5:2 25:4
【解析】
根据周长比、面积比与相似比的关系可以解得答案.
【详解】
相似多边形的周长的比等于相似比,相似多边形的面积的比等于相似比的平方.
两个相似多边形的对应边之比为5:2,则它们的周长比是5:2,面积比是25:4.
故答案为5:2;25:4.
15.8
【解析】
首先设与它相似的三角形的最短边的长为x,然后根据相似三角形的对应边成比例,即可得方程,解此方程即可求得答案.
【详解】
解:设与它相似的三角形的最短边的长为x,则
,
∴;
∴三角形的最短边为8.
故答案为:8.
16.4:5
【解析】
由已知条件可证得△ADE∽△ABC,则,再根据已知条件,得出,由相似三角形的面积之比等于相似比的平方即可求解.
【详解】
如图:
∵DE∥BC,
∴△ADE∽△ABC,
∴,
∵AD:DB=2:1,
∴,
∴,
∵S△ADE+S四边形DBCE=S△ABC,
∴S△ADE:S四边形BCED=4:5.
故答案为:4:5.
17.4
【解析】
连接AO并延长交BC于Q,利用重心性质得AO:OQ=2:1,则AO:AQ=2:3,再证明△AEF∽△ABC,△AEO∽△ABQ,然后根据相似三角形的性质求解.
【详解】
解:∵连接AO并延长交BC于Q,
∵O是△ABC的重心,
∴AO:OQ=2:1,
∴AO:AQ=2:3,
∵EF∥BC,
∴△AEO∽△ABQ,△AEF∽△ABC,
∴
∵BC=6,
∴EF=4.
故答案为:4.
18.5.4
【解析】
依据题意可得∠AOC=∠BOD,通过说明△ACO~△BDO,得出比例式可求得结论.
【详解】
解:由题意得:∠AOC=∠BOD.
∵AC⊥CD,BD⊥CD,
∴∠ACO=∠BDO=90°.
∴△ACO~△BDO.
∴.
即.
∴BD=5.4(米).
故答案为:5.4.
19.a:(b-a)
【解析】
做辅助线构造全等三角形得出BG=CF,再由△BGE∽△AFE得即可.
【详解】
解:如图:
过点B作BG∥AC交EF于点G
∴∠1=∠C
∵点D是边BC的中点
∴BD=CD
在△BDG和△CDF中
∴△BDG≌△CDF
∴BG=CF
又∵BG∥AC
∴△BGE∽△AFE
∴ =
即BE:AE=a:(b-a)
故答案为:a:(b-a) .
20.
【解析】
由题意可以得到△AOE∽△COD,再根据三角形相似的性质和已知条件可以求得AO:OC的值.
【详解】
解:∵四边形ABCD是平行四边形,
∴∠OAE=∠DCO,∠OEA=∠ODC,
∴△AOE∽△COD,
∴,
∵,
∴,
∴,
故答案为.
21.
【解析】
作CM⊥AB于M,交GF于N,由勾股定理可得出AB,由面积法求出CM,证明△CGF∽△CAB,再根据对应边成比例,即可得出答案.
【详解】
作CM⊥AB于M,交GF于N,如图所示:
∵Rt△ABC中,∠C=90°,AB=10,,
∴设BC=k,则AC=2k,AB2=AC2+BC2,即:102=(2k)2+k2,解得:k=2,
∴BC=2,AC=4,
∴CM===4,
∵正方形DEFG内接于△ABC,
∴GF=EF=MN,GF∥AB,
∴△CGF∽△CAB,
∴,即,
解得:EF=;
故答案为:.
22.
【解析】
如图,过点作于,过点作,交的延长线于,由面积和差关系可求,通过证明,可得,可求,由勾股定理可求,,的长,通过证明,可得,可求,,由勾股定理可求解.
【详解】
解:如图,过点作于,过点作,交的延长线于,
,,
,
,
,
四边形的面积为12,
,
,
等腰,
,,,
,,
,
,
,
,
,
,,
,
,,
,,
,
,
,
,且
,且,
,
,
,,
,
,
故答案为:,.
三、解答题
23.
∵∠ADE=∠B,∠A=∠A
∴△ADE∽△ABC
∴
∴
∴AC=
∴CD=.
24.
∵AB∥CD
∴△CDO∽△ABO
∵S△AOD∶S△DOC=2∶3
∴AO:CO=2∶3
∴S△AOB∶S△COD=4:9.
25.
证明:(1)∵∠DEF=∠DAB=90°,∠BDA=∠FDE,
∴△DEF∽△DAB,
∴DE:DA=DF:DB,
∴DE DB=DA DF,
∵∠DCB=∠DEC=90°,∠BDC=∠CDE,
∴△DEC∽△DCB,
∴,
∴DC2=DE DB,
又∵DE DB=DA DF,
∴CD2=DF DA.
∴CD是DF和DA的比例中项
26.
∵EF∥MN∥BC,
∴△AEF∽△AMN∽△ABC,
∵E、M是AB边的三等分点,
∴△AEF,△AMN,△ABC的相似比为1:2:3,
∴△AEF,△AMN,△ABC的面积比为1:4:9,
∴△AEF的面积∶四边形EMNF的面积∶四边形MBCN的面积=1:3:5.
27.
证明:(1)∵四边形ABCD是平行四边形.
∴AD∥BC.
∴∠ADE=∠E.
∵∠ADE=∠BAC.
∴∠BAC=∠E.
∵∠ACB=∠ECF.
∴△ACB∽△ECF.
∴.
∴CF CA=CB CE
(2)由(1)知∠ADE=∠E.
∵∠ADF=∠CFE.
∴△ADF∽△CEF.
∴.
∴.
∵AC=DE.
∴EF=CF.
∵△ACB∽△ECF.
∴AB=BC
∵四边形ABCD是平行四边形,
∴四边形ABCD是菱形.
28.
(1)∵CD是直角△ABC斜边上的中线,
∴DC=DA=DB,
∴∠DCA=∠A.
在△ADE中,∠DEC=∠A+∠ADE.
又∠ADE=∠B-∠A,即∠B=∠A+∠ADE,
∴∠DEC=∠B.
∴△CDE∽△ACB.
(2)令EA=k,DA=,CE=x.
由△CDE∽△ACB,
得,即,
解得,(舍).
所以.
29.
(1)证明:∵四边形ABCD是平行四边形,
∴,,
∴,
∵点E为DC的中点,
∴,
在和中
∴,
∴,
∴;
(2)∵四边形ABCD是平行四边形,点E为DC的中点,
∴,,
∴,,
∴,
∵的面积为2,
∴,即,
∵
∴,
∴,
∴,
∴.
30.
(1)证明:∵,∴.
∵,∴,
∴.
又∵,
∴;
(2)①解:如解图①,过点作交的延长线于点.
∵,,
∴是等边三角形,.
∵,
∴,.
∴,.
设的边长为,∵,
∴,,,
∴.
∵,,∴,
∴,
∴,即;
图①
②证明:如解图②,过点作交于点,则.
∵,∴,
∴,
∴.
∵,
∴,
∴,则.
又∵,∴,,
∴,
∴.
图②
