九年级数学上册试题 25.3解直角三角形-沪教版(含解析)
文档属性
| 名称 | 九年级数学上册试题 25.3解直角三角形-沪教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 08:13:33 | ||
图片预览


文档简介
25.3解直角三角形
一、单选题
1.在△ABC中,∠C=90°,以下条件不能解直角三角形的是( )
A.已知a与∠A B.已知a与c
C.已知∠A与∠B D.已知c与∠B
2.如图,中,,则的面积是( )
A. B.12 C.14 D.21
3.在中,,则边长为( )
A.7 B.8 C.7或17 D.8或17
4.如图,在直角中,延长斜边到点C,使,连接,若tanB=,则的值( )
A. B. C. D.
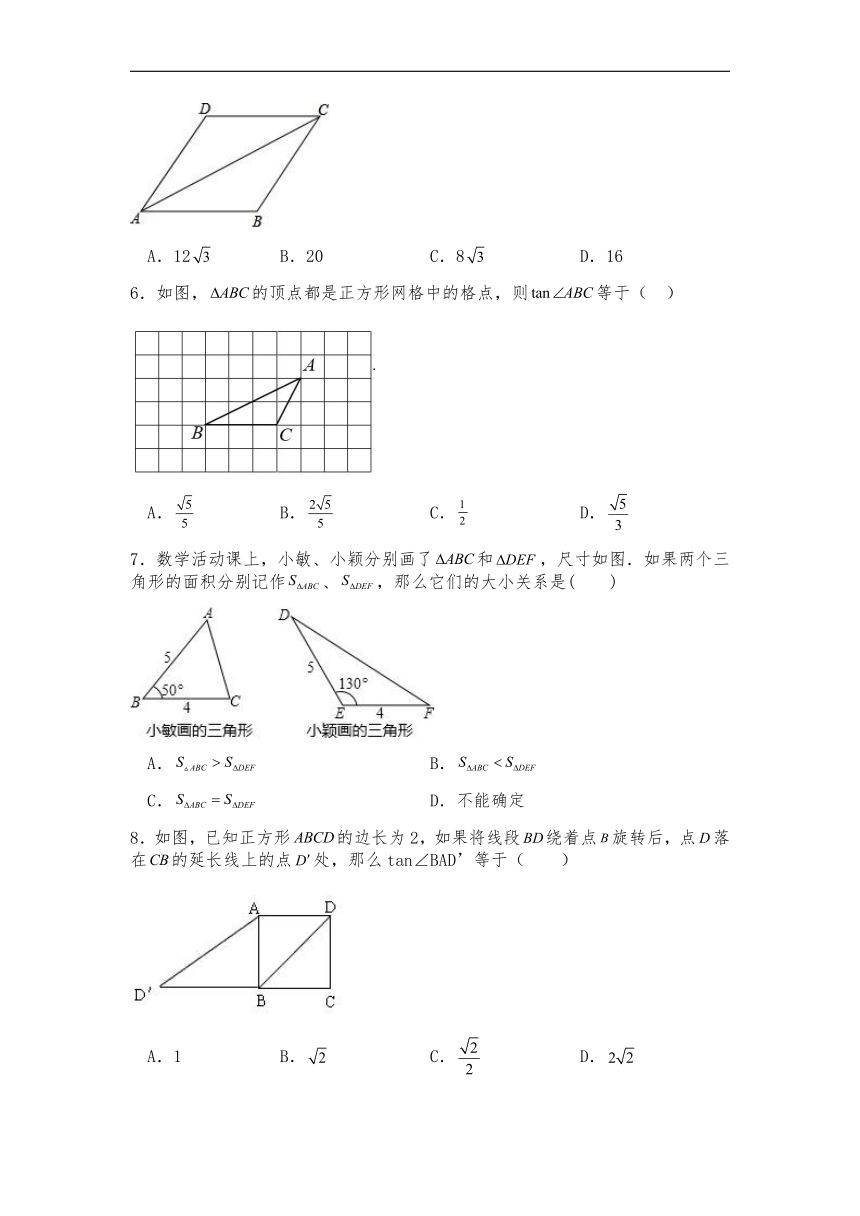
5.如图,在菱形ABCD中,∠ABC=120°,对角线AC=4,则菱形ABCD的周长为( )
A.12 B.20 C.8 D.16
6.如图,的顶点都是正方形网格中的格点,则等于( )
A. B. C. D.
7.数学活动课上,小敏、小颖分别画了和,尺寸如图.如果两个三角形的面积分别记作、,那么它们的大小关系是( )
A. B.
C. D.不能确定
8.如图,已知正方形的边长为2,如果将线段绕着点旋转后,点落在的延长线上的点处,那么tan∠BAD’等于( )
A.1 B. C. D.
9.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°.类比这种方法,计算tan22.5°的值为( )
A. B.﹣1 C. D.
10.如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( )
A. B. C. D.
二、填空题
11.在中,边上的高,则__________.
12.在中,,则边的长为______
13.如图,在四边形中,,,,.则的长的值为__________.
14.如图,在四边形中,,,,,则线段AD的长为___________.
15.如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么的值为_________。
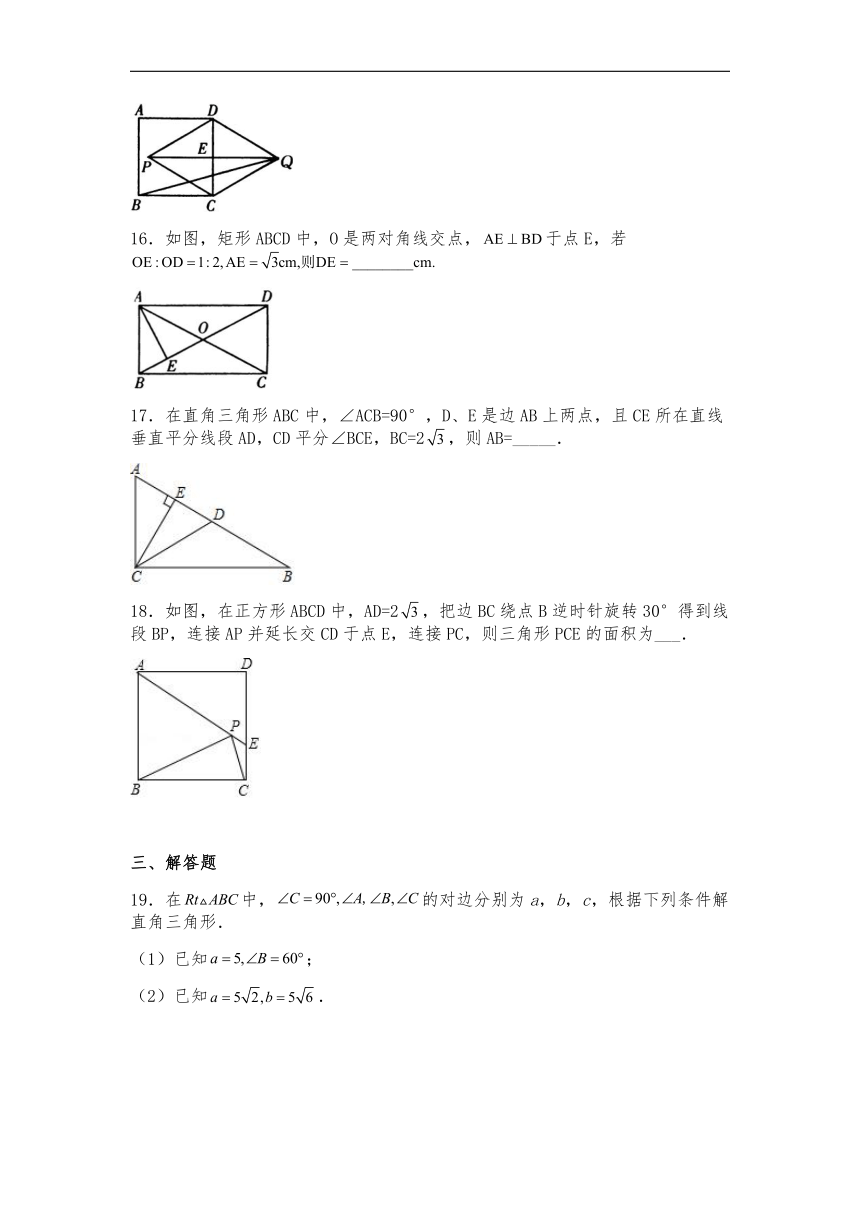
16.如图,矩形ABCD中,O是两对角线交点,于点E,若
17.在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2,则AB=_____.
18.如图,在正方形ABCD中,AD=2,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
三、解答题
19.在中,的对边分别为a,b,c,根据下列条件解直角三角形.
(1)已知;
(2)已知.
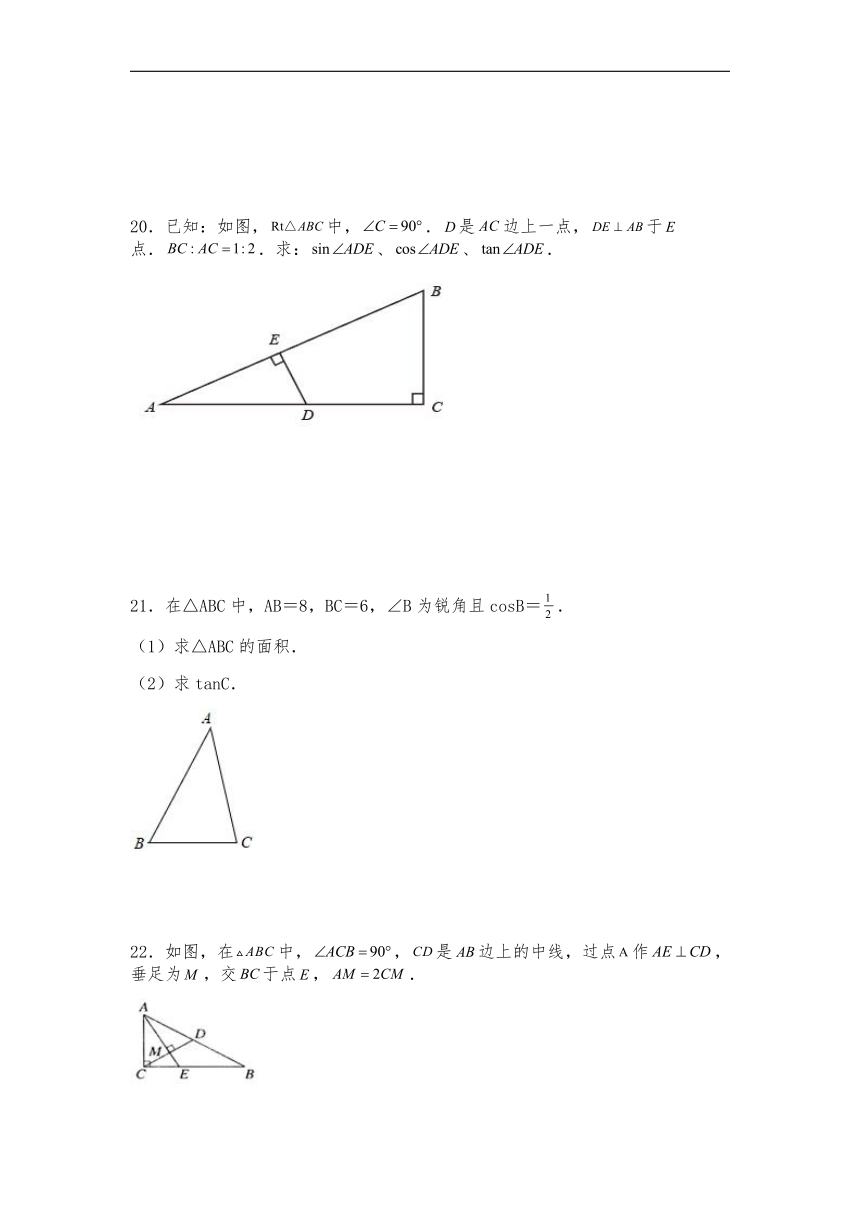
20.已知:如图,中,.是边上一点,于点..求:、、.
21.在△ABC中,AB=8,BC=6,∠B为锐角且cosB=.
(1)求△ABC的面积.
(2)求tanC.
22.如图,在中,,是边上的中线,过点作,垂足为,交于点,.
(1)求的值:
(2)若,求的长.
23.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
24.如图,中,是中点,过点作直线的垂线,垂足为点.
求的值.
连接求四边形的面积.
25.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若,求tan∠EBC的值.
26.如图,平面直角坐标系中直线:分别与x轴,y轴交于点A和点B,过点A的直线与y轴交于点C,.
(1)求直线的解析式;
(2)若D为线段上一点,E为线段上一点,当时,求的最小值,并求出此时点E的坐标.
答案
一、单选题
1.C
【分析】
根据解直角三角形的方法和计算进行判断.
【解析】
解:∵已知a和A,在Rt△ABC中,∠C=90°,
∴∠B=∠C-∠A,c=,b=csinB.
故选项A错误.
∵已知c和a,在Rt△ABC中,∠C=90°,
∴b=,sinA=,sinB=.
故选项B错误.
∵在Rt△ABC中,∠C=90°,已知A和B,∠A+∠B=∠C=90°,
∴只能知道直角三角形的三个角的大小,而三条边无法确定大小.
故选项C正确.
∵已知c和B,在Rt△ABC中,∠C=90°,
∴∠A=∠C-∠B,a=csinA,b=csinB.
故选项D错误.
故选C.
2.A
【分析】
根据已知作出三角形的高线AD,进而得出AD的长,即可得出三角形的面积.
【解析】
解:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,BC=5,
∴cosB==,
∴∠B=45°,
∴AD=BD,
∵sinC==,
∴
∴,
∴,
∵,
∴,
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选A.
3.C
【分析】
由的余弦值得到它的度数,再分情况讨论,画出图象,利用锐角三角函数求出BC的长.
【解析】
解:∵,
∴,
如图,当是钝角三角形时,
∵,,
∴,
∵,
∴,
∴,
如图,当是锐角三角形时,
.
故选:C.
4.D
【分析】
延长,过点作,垂足为,由,即,设,则,然后可证明,然后相似三角形的对应边成比例可得:,进而可得,,从而可求.
【解析】
解:如图,延长,过点作,垂足为,
,即,
设,则,
,,
,
,
,,
,
.
故选:.
5.D
【分析】
连接BD交AC于点O,由菱形的性质得出AB=BC=CD=AD,AC⊥BD,OA=OC=AC=2,∠ABD=∠CBD=∠ABC=60°,求出∠BAO=30°,由直角三角形的性质得OB=OA=2,AB=2OB=4,即可得出答案.
【解析】
解:连接BD交AC于点O,如图:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC=AC=2,∠ABD=∠CBD=∠ABC=60°,
∴∠BAO=30°,
∴OB= OA==2,AB=2OB=4,
∴菱形ABCD的周长=4AB=16;
故选:D.
6.C
【分析】
如图,过点A作AD⊥BC于D.解直角三角形即可解决问题.
【解析】
解:如图,过点A作AD⊥BC于D.
在Rt△ABD中,tan∠ABC=,
故选:C.
7.C
【分析】
在两个图形中分别作BC、EF边上的高,欲比较面积,由于底边相等,所以只需比较两条高即可.
【解析】
如图,过点A、D分别作AG⊥BC,DH⊥EF,垂足分别为G、H,
在Rt△ABG中,AG=ABsinB=5×sin 50°=5sin 50°,
在Rt△DHE中,∠DEH=180° 130°=50°,
DH=DEsin∠DEH=5sin 50°,
∴AG=DH.
∵BC=4,EF=4,
∵等底等高两三角形面积相等
∴.
故选:C.
8.B
【解析】
试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B.
9.B
【分析】
作Rt△ABC,使∠C=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,根据构造的直角三角形,设AC=x,再用x表示出CD,即可求出tan22.5°的值.
【解析】
解:作Rt△ABC,使∠C=90°,∠ABC=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,设AC=x,则:BC=x,AB=,CD=,
故选:B.
10.C
【分析】
根据题意和30°角所对的直角边与斜边的关系,设AB=4a,可以用a分别表示出CE和CB的值,从而可以求得tan∠CBE的值.
【解析】
设AB=4a,
∵在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,
∴BC=2a,AC=2a,AD:AB=1:4,
∵∠C=90°,DE⊥AC,
∴∠AED=90°,
∴∠AED=∠C,
∴DE∥BC,
∴△AED∽△ACB,
∴,
∴,
∴AE=a=,
∴EC=AC-AE=2a =,
∴tan∠CBE=,
故选C.
二、填空题
11.
【分析】
由题意易得,则有,然后根据三角函数可得,,进而问题可求解.
【解析】
解:如图,
∵AD⊥BC,
∴,
∵,
∴,
∵,
∴,,
∴.
故答案为.
12.
【分析】
根据锐角三角函数定义即可解决问题.
【解析】
解:∵△ABC中,,
∴tan20°=,
∴BC=AC tan20°=,
故答案为:
13.
【分析】
如图,延长BC,AD交于E,解直角三角形分别求出AE、DE、CE、BC的长,再运用勾股定理即可求解.
【解析】
解:如图,延长BC,AD交于E,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴BC=BE-CE=,
∴.
故答案为:
14.
【分析】
连结AC,先在Rt△ABC中,根据正切函数的定义求得tan∠ACB,进而求得∠ACB=30,于是AC=2AB=4,由∠BCD=120,得出∠ACD=∠BCD-∠ACB=90.然后在Rt△ADC中,利用勾股定理即可求出AD的长.
【解析】
如图,连接AC,
在中,,, ,
,
∵,
,
,
,
,
在中,,,,
.
故答案为:.
15.
【解析】
【分析】
延长QP交AB于F,根据正方形与等边三角形的性质可得CD=CP=DP=DQ=CQ,DE=CE,QE=PE,再利用=求解即可.
【解析】
如图,延长QP交AB于F,
∵四边形ABCD为正方形,△PCD与△QCD是以CD为边的等边三角形,
∴四边形PCQD为菱形,
设正方形的边长为a,则可得,
PE=QE=a,DE=EC=a,
∴==.
故答案为.
16.3
【分析】
先根据矩形的性质得到AO=OD,再根据特殊角的三角函数值得到∠OAE=30°,进而求得OE的长,然后即可得解.
【解析】
∵四边形ABCD为矩形,
∴OA=OD,
在Rt△AOE中,
∵,
∴sin∠OAE=,
∴∠OAE=30°,
则OE=AE·tan∠OAE=×=1,
OA===2,
故DE=OE+OD=OE+OA=3.
故答案为3.
17.4
【解析】
分析:由CE所在直线垂直平分线段AD可得出CE平分∠ACD,进而可得出∠ACE=∠DCE,由CD平分∠BCE利用角平分线的性质可得出∠DCE=∠DCB,结合∠ACB=90°可求出∠ACE、∠A的度数,再利用余弦的定义结合特殊角的三角函数值,即可求出AB的长度.
详解:∵CE所在直线垂直平分线段AD,
∴CE平分∠ACD,
∴∠ACE=∠DCE.
∵CD平分∠BCE,
∴∠DCE=∠DCB.
∵∠ACB=90°,
∴∠ACE=∠ACB=30°,
∴∠A=60°,
∴AB==4.
18.9﹣5
【分析】
根据旋转的想知道的PB=BC=AB,∠PBC=30°,推出△ABP是等边三角形,得到∠BAP=60°,AP=AB=2,解直角三角形得到CE=2-2,PE=4-2,过P作PF⊥CD于F,于是得到结论.
【解析】
∵四边形ABCD是正方形,∴∠ABC=90°,∵把边BC绕点B逆时针旋转30°得到线段BP,∴PB=BC=AB,∠PBC=30°,∴∠ABP=60°,∴△ABP是等边三角形,∴∠BAP=60°,AP=AB=2,∵AD=2,∴AE=4,DE=2,∴CE=2﹣2,PE=4﹣2,过P作PF⊥CD于F,∴PF=PE=2﹣3,∴三角形PCE的面积=CE PF=×(2﹣2)×(2﹣3)=9-5,故答案为9-5.
三、解答题
19.
(1)∵,
∴,
∴;
(2)∵.
∴,,,
∴.
20.
解:设BC=x,则AC=2x,
在中,
∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠ABC,
∴,
,
.
21.
(1)如图,过点A作AH⊥BC于H.
∵cosB=,
∴∠B=60°,
∴BH=AB cosB=8=4,AH=,
∴S△ABC= BC AH=×6×=;
(2)在Rt△ACH中,
∵∠AHC=90°,AH=,CH=BC﹣BH=7﹣4=2,
∴tanC.
22.
(1)∵,是斜边的中线,
∴,
∴∠B=∠DCB,
∵,
∴.
∵,
∴.
∴.
在中,∵,
∴.
∴.
(2)∵,
∴.
由(1)知,
∴.
∴.
23.
(1)证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)∵tan∠ABD=1,∠ADB=90°
∴=1,
∴AD=BD,
∵△ACD∽△BFD,
∴,
∴BF=AC=3
24.
在中,
而,,
是中点,
;
在中,,
,
是中点,
,
即,
在中, ;
在中,,
是中点,
,
25.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°.
∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°.
∴∠AFB+∠DFE=180°-∠BFE=90°.
又∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,∴△ABF∽△DFE.
(2)在Rt△DEF中,,
∴设DE=a,则EF=3a,
∴.
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,∠EBC=∠EBF,
∴CD=DE+CE=4a,
∴AB=4a.
又由(1)知△ABF∽△DFE,
∴.
∴,即.
26.
解:(1)在中,求当y=0时,
解得:
∴A(,0)
又∵OC=6
∴C(0,6)
设直线AC的解析式为,将A(,0),C(0,6)代入得
,解得
∴直线AC的解析式为;
(2)过点B作BF⊥AC,
在中,x=0时,y=2
∴B(0,2)
在Rt△AOB中,,
在Rt△AOC中,,
∴∠BAO=30°,∠CAO=60°,∠ACO=30°
∴BF=,DF=2
∵
∴
∴,解得AD==BF
∴此时点D与点F重合,即BD⊥AC
∴CD=AC-AD=,
在y轴右侧作∠NCO=30°,过点D作DM⊥NC,交y轴于点E
此时EM=,
∴此时最短
又∵DM⊥NC,∠ACO=∠NCO=30°,
∴在Rt△CDM中,∠CDM=30°
∴CM=,DM=
又∵在Rt△CEM中,∠ECM=30°
∴,CE=2EM=2
∴OE=OC-CE=4
∴的最小值为3,点E的坐标为(0,4).
一、单选题
1.在△ABC中,∠C=90°,以下条件不能解直角三角形的是( )
A.已知a与∠A B.已知a与c
C.已知∠A与∠B D.已知c与∠B
2.如图,中,,则的面积是( )
A. B.12 C.14 D.21
3.在中,,则边长为( )
A.7 B.8 C.7或17 D.8或17
4.如图,在直角中,延长斜边到点C,使,连接,若tanB=,则的值( )
A. B. C. D.
5.如图,在菱形ABCD中,∠ABC=120°,对角线AC=4,则菱形ABCD的周长为( )
A.12 B.20 C.8 D.16
6.如图,的顶点都是正方形网格中的格点,则等于( )
A. B. C. D.
7.数学活动课上,小敏、小颖分别画了和,尺寸如图.如果两个三角形的面积分别记作、,那么它们的大小关系是( )
A. B.
C. D.不能确定
8.如图,已知正方形的边长为2,如果将线段绕着点旋转后,点落在的延长线上的点处,那么tan∠BAD’等于( )
A.1 B. C. D.
9.构建几何图形解决代数问题是“数形结合”思想的重要性,在计算tan15°时,如图.在Rt△ACB中,∠C=90°,∠ABC=30°,延长CB使BD=AB,连接AD,得∠D=15°,所以tan15°.类比这种方法,计算tan22.5°的值为( )
A. B.﹣1 C. D.
10.如图,在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,DE⊥AC于点E,连接BE,则tan∠CBE的值等于( )
A. B. C. D.
二、填空题
11.在中,边上的高,则__________.
12.在中,,则边的长为______
13.如图,在四边形中,,,,.则的长的值为__________.
14.如图,在四边形中,,,,,则线段AD的长为___________.
15.如图,已知ABCD是正方形,以CD为一边向CD两旁作等边三角形PCD和等边三角形QCD,那么的值为_________。
16.如图,矩形ABCD中,O是两对角线交点,于点E,若
17.在直角三角形ABC中,∠ACB=90°,D、E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,BC=2,则AB=_____.
18.如图,在正方形ABCD中,AD=2,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为___.
三、解答题
19.在中,的对边分别为a,b,c,根据下列条件解直角三角形.
(1)已知;
(2)已知.
20.已知:如图,中,.是边上一点,于点..求:、、.
21.在△ABC中,AB=8,BC=6,∠B为锐角且cosB=.
(1)求△ABC的面积.
(2)求tanC.
22.如图,在中,,是边上的中线,过点作,垂足为,交于点,.
(1)求的值:
(2)若,求的长.
23.如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
24.如图,中,是中点,过点作直线的垂线,垂足为点.
求的值.
连接求四边形的面积.
25.如图,点E是矩形ABCD中CD边上一点,△BCE沿BE折叠为△BFE,点F落在AD上.
(1)求证:△ABF∽△DFE;
(2)若,求tan∠EBC的值.
26.如图,平面直角坐标系中直线:分别与x轴,y轴交于点A和点B,过点A的直线与y轴交于点C,.
(1)求直线的解析式;
(2)若D为线段上一点,E为线段上一点,当时,求的最小值,并求出此时点E的坐标.
答案
一、单选题
1.C
【分析】
根据解直角三角形的方法和计算进行判断.
【解析】
解:∵已知a和A,在Rt△ABC中,∠C=90°,
∴∠B=∠C-∠A,c=,b=csinB.
故选项A错误.
∵已知c和a,在Rt△ABC中,∠C=90°,
∴b=,sinA=,sinB=.
故选项B错误.
∵在Rt△ABC中,∠C=90°,已知A和B,∠A+∠B=∠C=90°,
∴只能知道直角三角形的三个角的大小,而三条边无法确定大小.
故选项C正确.
∵已知c和B,在Rt△ABC中,∠C=90°,
∴∠A=∠C-∠B,a=csinA,b=csinB.
故选项D错误.
故选C.
2.A
【分析】
根据已知作出三角形的高线AD,进而得出AD的长,即可得出三角形的面积.
【解析】
解:过点A作AD⊥BC,
∵△ABC中,cosB=,sinC=,BC=5,
∴cosB==,
∴∠B=45°,
∴AD=BD,
∵sinC==,
∴
∴,
∴,
∵,
∴,
则△ABC的面积是:×AD×BC=×3×(3+4)=.
故选A.
3.C
【分析】
由的余弦值得到它的度数,再分情况讨论,画出图象,利用锐角三角函数求出BC的长.
【解析】
解:∵,
∴,
如图,当是钝角三角形时,
∵,,
∴,
∵,
∴,
∴,
如图,当是锐角三角形时,
.
故选:C.
4.D
【分析】
延长,过点作,垂足为,由,即,设,则,然后可证明,然后相似三角形的对应边成比例可得:,进而可得,,从而可求.
【解析】
解:如图,延长,过点作,垂足为,
,即,
设,则,
,,
,
,
,,
,
.
故选:.
5.D
【分析】
连接BD交AC于点O,由菱形的性质得出AB=BC=CD=AD,AC⊥BD,OA=OC=AC=2,∠ABD=∠CBD=∠ABC=60°,求出∠BAO=30°,由直角三角形的性质得OB=OA=2,AB=2OB=4,即可得出答案.
【解析】
解:连接BD交AC于点O,如图:
∵四边形ABCD是菱形,
∴AB=BC=CD=AD,AC⊥BD,OA=OC=AC=2,∠ABD=∠CBD=∠ABC=60°,
∴∠BAO=30°,
∴OB= OA==2,AB=2OB=4,
∴菱形ABCD的周长=4AB=16;
故选:D.
6.C
【分析】
如图,过点A作AD⊥BC于D.解直角三角形即可解决问题.
【解析】
解:如图,过点A作AD⊥BC于D.
在Rt△ABD中,tan∠ABC=,
故选:C.
7.C
【分析】
在两个图形中分别作BC、EF边上的高,欲比较面积,由于底边相等,所以只需比较两条高即可.
【解析】
如图,过点A、D分别作AG⊥BC,DH⊥EF,垂足分别为G、H,
在Rt△ABG中,AG=ABsinB=5×sin 50°=5sin 50°,
在Rt△DHE中,∠DEH=180° 130°=50°,
DH=DEsin∠DEH=5sin 50°,
∴AG=DH.
∵BC=4,EF=4,
∵等底等高两三角形面积相等
∴.
故选:C.
8.B
【解析】
试题解析:正方形ABCD的边长为2,则对角线BD=.
∴BD′=BD=.
∴tan∠BAD’=.
故选B.
9.B
【分析】
作Rt△ABC,使∠C=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,根据构造的直角三角形,设AC=x,再用x表示出CD,即可求出tan22.5°的值.
【解析】
解:作Rt△ABC,使∠C=90°,∠ABC=90°,∠ABC=45°,延长CB到D,使BD=AB,连接AD,设AC=x,则:BC=x,AB=,CD=,
故选:B.
10.C
【分析】
根据题意和30°角所对的直角边与斜边的关系,设AB=4a,可以用a分别表示出CE和CB的值,从而可以求得tan∠CBE的值.
【解析】
设AB=4a,
∵在△ABC中,∠C=90°,∠A=30°,D为AB上一点,且AD:DB=1:3,
∴BC=2a,AC=2a,AD:AB=1:4,
∵∠C=90°,DE⊥AC,
∴∠AED=90°,
∴∠AED=∠C,
∴DE∥BC,
∴△AED∽△ACB,
∴,
∴,
∴AE=a=,
∴EC=AC-AE=2a =,
∴tan∠CBE=,
故选C.
二、填空题
11.
【分析】
由题意易得,则有,然后根据三角函数可得,,进而问题可求解.
【解析】
解:如图,
∵AD⊥BC,
∴,
∵,
∴,
∵,
∴,,
∴.
故答案为.
12.
【分析】
根据锐角三角函数定义即可解决问题.
【解析】
解:∵△ABC中,,
∴tan20°=,
∴BC=AC tan20°=,
故答案为:
13.
【分析】
如图,延长BC,AD交于E,解直角三角形分别求出AE、DE、CE、BC的长,再运用勾股定理即可求解.
【解析】
解:如图,延长BC,AD交于E,
∵,
∴,
∴,
∵,
∴,
∵,
∴,
∴BC=BE-CE=,
∴.
故答案为:
14.
【分析】
连结AC,先在Rt△ABC中,根据正切函数的定义求得tan∠ACB,进而求得∠ACB=30,于是AC=2AB=4,由∠BCD=120,得出∠ACD=∠BCD-∠ACB=90.然后在Rt△ADC中,利用勾股定理即可求出AD的长.
【解析】
如图,连接AC,
在中,,, ,
,
∵,
,
,
,
,
在中,,,,
.
故答案为:.
15.
【解析】
【分析】
延长QP交AB于F,根据正方形与等边三角形的性质可得CD=CP=DP=DQ=CQ,DE=CE,QE=PE,再利用=求解即可.
【解析】
如图,延长QP交AB于F,
∵四边形ABCD为正方形,△PCD与△QCD是以CD为边的等边三角形,
∴四边形PCQD为菱形,
设正方形的边长为a,则可得,
PE=QE=a,DE=EC=a,
∴==.
故答案为.
16.3
【分析】
先根据矩形的性质得到AO=OD,再根据特殊角的三角函数值得到∠OAE=30°,进而求得OE的长,然后即可得解.
【解析】
∵四边形ABCD为矩形,
∴OA=OD,
在Rt△AOE中,
∵,
∴sin∠OAE=,
∴∠OAE=30°,
则OE=AE·tan∠OAE=×=1,
OA===2,
故DE=OE+OD=OE+OA=3.
故答案为3.
17.4
【解析】
分析:由CE所在直线垂直平分线段AD可得出CE平分∠ACD,进而可得出∠ACE=∠DCE,由CD平分∠BCE利用角平分线的性质可得出∠DCE=∠DCB,结合∠ACB=90°可求出∠ACE、∠A的度数,再利用余弦的定义结合特殊角的三角函数值,即可求出AB的长度.
详解:∵CE所在直线垂直平分线段AD,
∴CE平分∠ACD,
∴∠ACE=∠DCE.
∵CD平分∠BCE,
∴∠DCE=∠DCB.
∵∠ACB=90°,
∴∠ACE=∠ACB=30°,
∴∠A=60°,
∴AB==4.
18.9﹣5
【分析】
根据旋转的想知道的PB=BC=AB,∠PBC=30°,推出△ABP是等边三角形,得到∠BAP=60°,AP=AB=2,解直角三角形得到CE=2-2,PE=4-2,过P作PF⊥CD于F,于是得到结论.
【解析】
∵四边形ABCD是正方形,∴∠ABC=90°,∵把边BC绕点B逆时针旋转30°得到线段BP,∴PB=BC=AB,∠PBC=30°,∴∠ABP=60°,∴△ABP是等边三角形,∴∠BAP=60°,AP=AB=2,∵AD=2,∴AE=4,DE=2,∴CE=2﹣2,PE=4﹣2,过P作PF⊥CD于F,∴PF=PE=2﹣3,∴三角形PCE的面积=CE PF=×(2﹣2)×(2﹣3)=9-5,故答案为9-5.
三、解答题
19.
(1)∵,
∴,
∴;
(2)∵.
∴,,,
∴.
20.
解:设BC=x,则AC=2x,
在中,
∵,
∴,
又∵∠A=∠A,
∴△ADE∽△ABC,
∴∠ADE=∠ABC,
∴,
,
.
21.
(1)如图,过点A作AH⊥BC于H.
∵cosB=,
∴∠B=60°,
∴BH=AB cosB=8=4,AH=,
∴S△ABC= BC AH=×6×=;
(2)在Rt△ACH中,
∵∠AHC=90°,AH=,CH=BC﹣BH=7﹣4=2,
∴tanC.
22.
(1)∵,是斜边的中线,
∴,
∴∠B=∠DCB,
∵,
∴.
∵,
∴.
∴.
在中,∵,
∴.
∴.
(2)∵,
∴.
由(1)知,
∴.
∴.
23.
(1)证明:∵AD⊥BC,BE⊥AC,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC,
∴△ACD∽△BFD.
(2)∵tan∠ABD=1,∠ADB=90°
∴=1,
∴AD=BD,
∵△ACD∽△BFD,
∴,
∴BF=AC=3
24.
在中,
而,,
是中点,
;
在中,,
,
是中点,
,
即,
在中, ;
在中,,
是中点,
,
25.
(1)证明:∵四边形ABCD是矩形,
∴∠A=∠D=∠C=90°.
∵△BCE沿BE折叠为△BFE,∴∠BFE=∠C=90°.
∴∠AFB+∠DFE=180°-∠BFE=90°.
又∠AFB+∠ABF=90°,
∴∠ABF=∠DFE,∴△ABF∽△DFE.
(2)在Rt△DEF中,,
∴设DE=a,则EF=3a,
∴.
∵△BCE沿BE折叠为△BFE,
∴CE=EF=3a,∠EBC=∠EBF,
∴CD=DE+CE=4a,
∴AB=4a.
又由(1)知△ABF∽△DFE,
∴.
∴,即.
26.
解:(1)在中,求当y=0时,
解得:
∴A(,0)
又∵OC=6
∴C(0,6)
设直线AC的解析式为,将A(,0),C(0,6)代入得
,解得
∴直线AC的解析式为;
(2)过点B作BF⊥AC,
在中,x=0时,y=2
∴B(0,2)
在Rt△AOB中,,
在Rt△AOC中,,
∴∠BAO=30°,∠CAO=60°,∠ACO=30°
∴BF=,DF=2
∵
∴
∴,解得AD==BF
∴此时点D与点F重合,即BD⊥AC
∴CD=AC-AD=,
在y轴右侧作∠NCO=30°,过点D作DM⊥NC,交y轴于点E
此时EM=,
∴此时最短
又∵DM⊥NC,∠ACO=∠NCO=30°,
∴在Rt△CDM中,∠CDM=30°
∴CM=,DM=
又∵在Rt△CEM中,∠ECM=30°
∴,CE=2EM=2
∴OE=OC-CE=4
∴的最小值为3,点E的坐标为(0,4).
