沪教版九年级数学上册试题 25.4解直角三角形的应用(含答案)
文档属性
| 名称 | 沪教版九年级数学上册试题 25.4解直角三角形的应用(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 00:00:00 | ||
图片预览


文档简介
25.4解直角三角形的应用
一、单选题
1.已知两点,若点对点的仰角为,那么对的俯角是( ).
A. B. C. D.
2.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为( ).
A. B. C. D.
3.从地面上的两处望正西方向山顶,仰角分别为和两处相距,那么山高为( ).
A. B. C. D.
4.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米
A. B. C. D.24
5.小明同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时小明同学离A地 ( )
A.150 m B.50 m C.100 m D.100 m
6.小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆的高度与拉绳的长度相等,小明先将拉到的位置,测得为水平线),测角仪的高度为米,则旗杆的高度为( )
A.米 B.米 C.米 D.米
7.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后公里”问题,电力公司在 改造时把某一输电线铁塔建在了一个坡度为的山坡的平台上(如图),测得米,米,米,则铁塔的高度约为( )(参考数据:)
A. B. C. D.
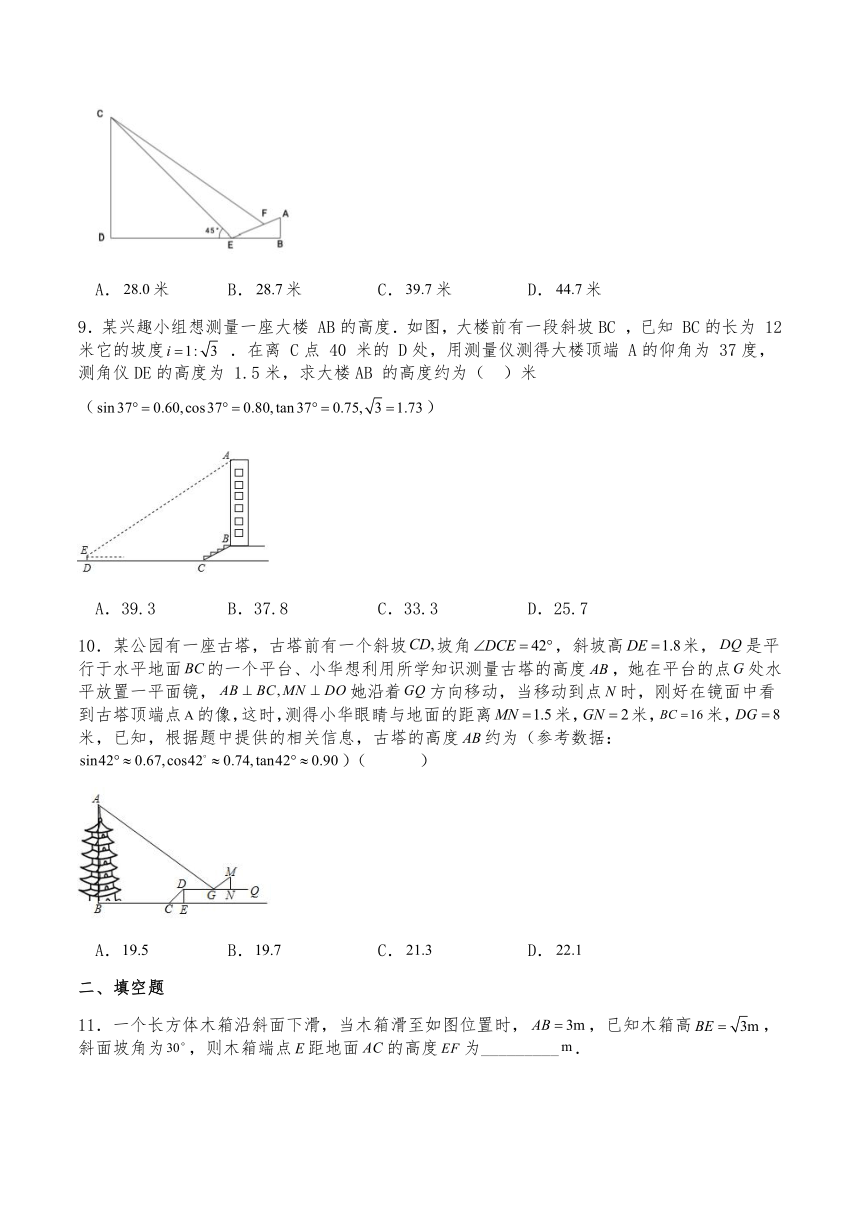
8.数学实践活动课中小明同学测量某建筑物的高度,如图,已知斜坡的坡度为,小明在坡底点处测得建筑物顶端处的仰角为,他沿着斜坡行走米到达点处,在测得建筑 物顶端处的仰角为,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的高度约为( )(参考数据:)
A.米 B.米 C.米 D.米
9.某兴趣小组想测量一座大楼 AB的高度.如图,大楼前有一段斜坡BC ,已知 BC的长为 12 米它的坡度 .在离 C点 40 米的 D处,用测量仪测得大楼顶端 A的仰角为 37度,测角仪DE的高度为 1.5米,求大楼AB 的高度约为( )米()
A.39.3 B.37.8 C.33.3 D.25.7
10.某公园有一座古塔,古塔前有一个斜坡坡角,斜坡高米,是平行于水平地面的一个平台、小华想利用所学知识测量古塔的高度,她在平台的点处水平放置一平面镜,她沿着方向移动,当移动到点时,刚好在镜面中看到古塔顶端点的像,这时,测得小华眼睛与地面的距离米,米,米,米,已知,根据题中提供的相关信息,古塔的高度约为(参考数据:)( )
A. B. C. D.
二、填空题
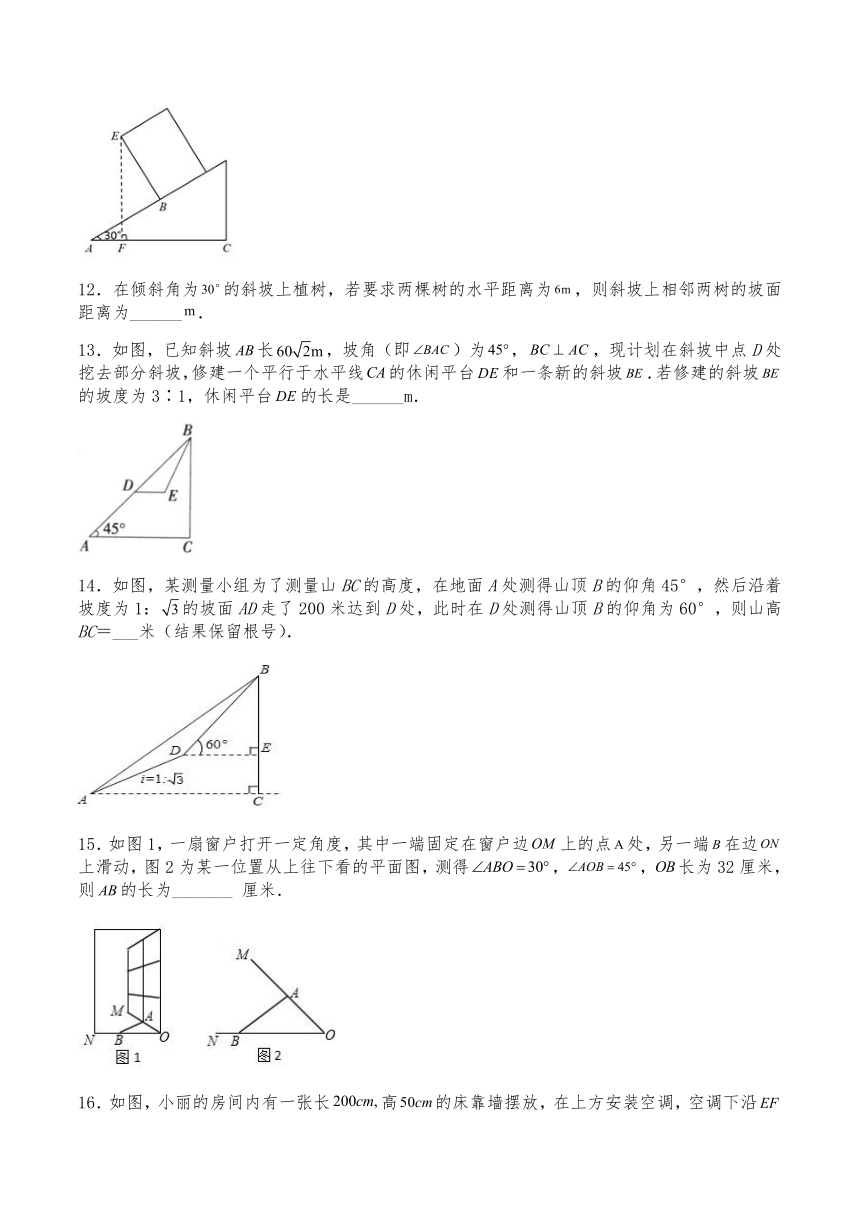
11.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜面坡角为,则木箱端点距地面的高度为_________.
12.在倾斜角为的斜坡上植树,若要求两棵树的水平距离为,则斜坡上相邻两树的坡面距离为______.
13.如图,已知斜坡长,坡角(即)为,,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡.若修建的斜坡的坡度为3∶1,休闲平台的长是______m.
14.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC=___米(结果保留根号).
15.如图1,一扇窗户打开一定角度,其中一端固定在窗户边上的点处,另一端在边上滑动,图2为某一位置从上往下看的平面图,测得,,长为32厘米,则的长为_______ 厘米.
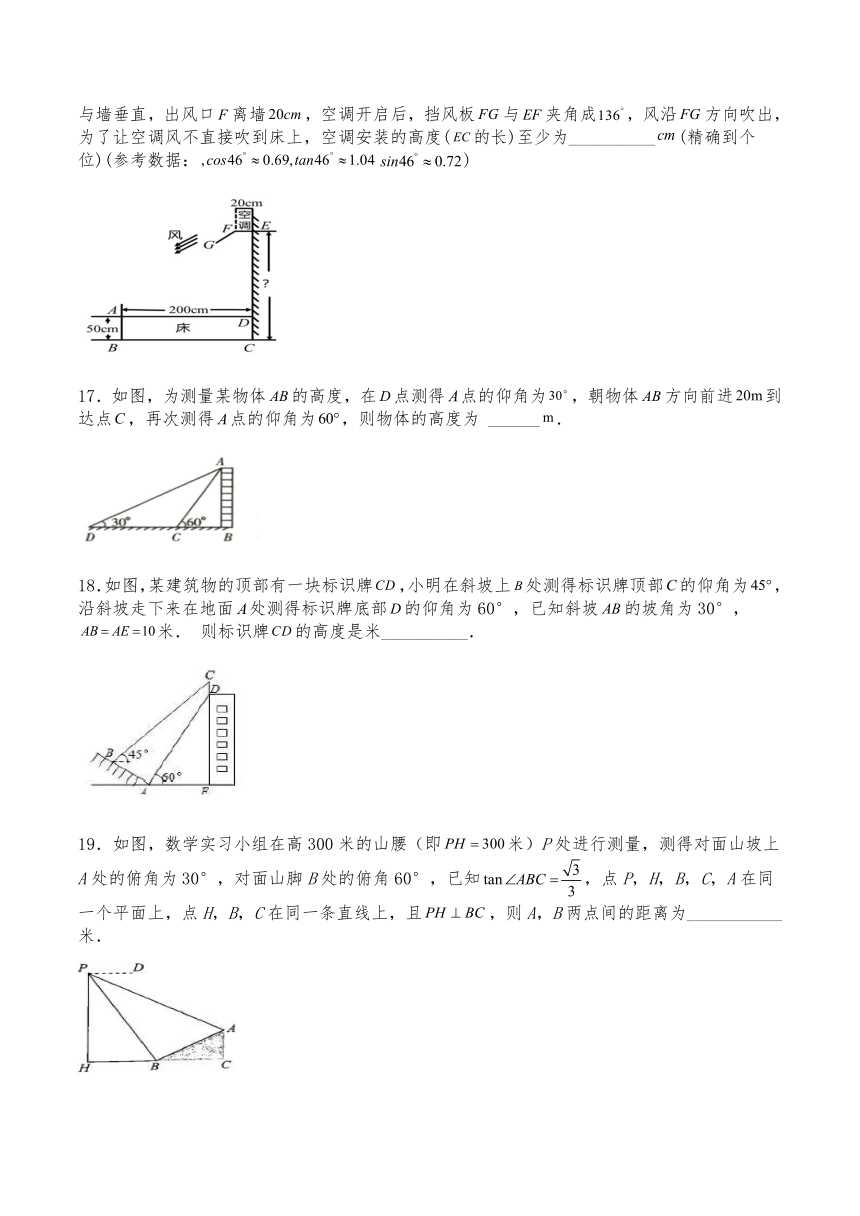
16.如图,小丽的房间内有一张长高的床靠墙摆放,在上方安装空调,空调下沿与墙垂直,出风口离墙,空调开启后,挡风板与夹角成,风沿方向吹出,为了让空调风不直接吹到床上,空调安装的高度(的长)至少为__________(精确到个位)(参考数据:)
17.如图,为测量某物体的高度,在点测得点的仰角为,朝物体方向前进到达点,再次测得点的仰角为,则物体的高度为 ______.
18.如图,某建筑物的顶部有一块标识牌,小明在斜坡上处测得标识牌顶部的仰角为,沿斜坡走下来在地面处测得标识牌底部的仰角为60°,已知斜坡的坡角为30°,米. 则标识牌的高度是米__________.
19.如图,数学实习小组在高300米的山腰(即米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且,则A,B两点间的距离为___________米.
20.有一种双层长方体垃圾桶AB=70cm,BC=25cm,CF=30cm,侧面如图1所示,隔板EG等分上下两层,下方内桶BCHG绕底部轴(CF)旋转开,若点H恰好能卡在原来点G的位置,则内桶边CH的长度应设计为___;现将CH调整为25cm,打开最大角度时,点H卡在隔板上,如图2所示,则可完全放入下方桶内的球体的直径不大于____.
三、解答题
21.北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由降为,已知原斜坡坡面长为200米,点在同一水平地面上,求改善后的斜坡坡角向前推进的距离.(结果保留整数.参考数据: ,)
22.如图,在甲建筑物上从点到点挂一长为的宣传条幅,在乙建筑物的顶部点测得条幅顶端的仰角为,测得条幅底端点的俯角为,求底部不能直接到达的甲、乙两建筑物之间的水平距离.(答案保留根号)
23.某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图.其中,AB⊥BD.∠BAD=18°,C在BD上,BC=0.5m.车库坡道入口上方要张贴限高标志.以便告知驾驶员所驾车辆能否安全驶入.为标明限高,请你根据该图计算CE的长度(即点C到AD的距离).(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.33)(结果精确到0.1m)
24.我市里运河有一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.(参考数据:1.414,1.732)
25.如图,在一条笔直的海岸线上有,两个观测站,在的正东方向.有一艘小船从处沿北偏西方向出发,以每小时20海里速度行驶半小时到达处,从处测得小船在它的北偏东的方向上.
(1)求的距离;
(2)小船沿射线的方向继续航行一段时间后,到达点处,此时,从测得小船在北偏西的方向.求点与点之间的距离.(上述两小题的结果都保留根号)
26.如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
27.如图,河流的两岸、互相平行,河岸上有一排间隔为的电线杆、、某人在河岸的处测得,然后沿河岸走了到达处,测得.求河流的宽度.(结果精确到,参考数据:,,,,,)
28.如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一电缆,共有如下两种铺设方案:
方案一:; 方案二:.
经测量得AB=4千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.
答案
一、单选题
1.A
【分析】
根据俯角和仰角的定义和平行线的性质即可得到B对A的仰角为.
【解析】
解:如图,
∵A对B的俯角为,
∴B对A的仰角为.
故选A.
2.A
【分析】
在中,,由此可以求出之长.
【解析】
解:在中,
,
.
又,,
.
故选:.
3.A
【分析】
设山高为,利用三角函数分别表示和BC的长.根据得方程求解.
【解析】
解:设山高为,
在中,,
∴,
在中,,
∴.
∵,
∴.
解得:.
故选:.
4.B
【分析】
根据斜面坡度为1:2,斜坡AB的水平宽度为12米,可得AE=12,BE=6,然后利用勾股定理求出AB的长度.
【解析】
解:如图,过B作BE⊥AD于点E,
∵斜面坡度为1:2,AE=12,
∴BE=6,
在Rt△ABC中, .
故选:B.
5.D
【分析】
根据在Rt△ABD中利用三角函数分别求AD,BD的长,从而得到CD的长.再利用勾股定理求AC的长即可.
【解析】
解:如图:
由B在A的北偏西60°方向可求得∠B=60°,
在Rt△ABD中,
AD=AB sin60°=,
BD=AB cos60°=50,
∴CD=BC-BD=150.
∴AC==.
故选D.
6.C
【分析】
设PA=PB=PB′=x,在RT△PCB′中,根据,列出方程即可解决问题.
【解析】
解:设PA=PB=PB′=x,
在RT△PCB′中,
∴
∴,
∴(1-)x=1,
∴x=.
故选C.
7.C
【分析】
延长AB交ED于G,过C作CF⊥DE于F,得到GF=BC=5,设DF=3k,CF=4k,解直角三角形得到结论.
【解析】
解:延长AB交ED于G,过C作CF⊥DE于F,
则四边形BGFC是矩形
∴GF=BC=5,
∵山坡CD的坡度为1:0.75,
∴设DF=3k,CF=4k,
∴CD=5k=35,
∴k=7,
∴DF=21,BG=CF=28,
∴EG=GF+DF+DE=5+21+19=45,
∵∠AED=52.5°,
∴AG=EG tan52.5°=45×1.30=58.5,
∴AB=AG-BG=30.5米,
答:铁塔AB的高度约为30.5米.
故选:C.
8.D
【分析】
如图,过F点作FH⊥CD,垂足为H,作FG⊥EB,垂足为G.利用坡度先求出FG与EG,设DE=CD=x,表示出FH,CH,再利用三角函数即可解得.
【解析】
如图,过F点作FH⊥CD,垂足为H,作FG⊥EB,垂足为G.
根据题意易知DC=DE,EF=13m,∠CFH=35°,HF=GD,HD=FG
∵斜坡的坡度为,且EF=13m
故FG=5m,EG=12m
设DE=CD=x,则FH=DE+EG=x+12,CH=CD-HD=CD-FG=x-5
在直角三角形CHF中,
解得x≈44.7
故选D
9.C
【分析】
延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
【解析】
解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,=,
∴设BF=k,则CF=k,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=,
∵DF=DC+CF,
∴DF=40+,
∵在Rt△AEH中,tan∠AEH=,
∴AH=tan37°×(40+)≈37.785(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=37.785-4.5≈33.3.
故选C.
10.C
【分析】
由正切定义求出CE,延长GD交AB于点H,则BH=DE=1.8(米),DH=BE=BC+CE=18(米),HG=DH+DG=26(米),证明△AHG∽△MNG,求出AH的长,则可求出答案.
【解析】
解:在Rt△CDE中,tan∠DCE,
∴0.9,
∴CE=2,
延长GD交AB于点H,
则BH=DE=1.8(米),DH=BE=BC+CE=18(米),HG=DH+DG=26(米),
∵∠AHG=∠MNG=90°,∠AGH=∠MGN,
∴△AHG∽△MNG,
∴,
即,
∴AH=19.5(米),
∴AB=AH+HB=21.3(米).
答:古塔的高度AB为21.3米.
故选:C.
二、填空题
11.3
【分析】
连接AE,在Rt△ABE中,利用勾股定理求得AE的长,利用三角函数即可求得,然后在Rt△AEF中,利用三角函数求得的长.
【解析】
解:连接AE,在Rt△ABE中,已知AB=3m,BE=,
∴根据勾股定理得.
又∵,∴.
在Rt△AEF中,,
∴.
故答案为:3.
12.
【分析】
由题意可知,利用角的余弦即可求出的长.
【解析】
解:,,
,
米,
米,
故答案为:.
13.20
【分析】
由三角函数的定义,即可求得AC与BC的长,又由坡度的定义,即可求得EH的长,继而求得休闲平台DE的长.
【解析】
解:如图,延长交于点H,
在中,,,
∴,
∵点D为中点,
∴,
又∵,
∴,
∵斜坡的坡度为:,
∴,
∴,即休闲平台的长是.
故答案为:20.
14.100.
【分析】
作DF⊥AC于F.解直角三角形分别求出BE、EC即可解决问题.
【解析】
解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米);
故答案为:100.
15.
【分析】
作AC⊥OB于点C,然后根据题意和锐角三角函数可以求得AC和BC的长,再根据直角三角形中的性质即可得到AB的长.
【解析】
解:作AC⊥OB于点C,如右图2所示,
则∠ACO=∠ACB=90°,
∵,
∴,
∴AC=OC,
设AC=x,则OC=x,
∵
由
解得,
∴(厘米),
即AB的长为厘米.
故答案为:.
16.
【分析】
连接AF,作FH⊥AD构造直角三角形运用三角函数解出FH,再将床高加上即可求出EC的值.
【解析】
当A、F在一条直线时,就正好不会吹到床上,连接AF,过点F作FH⊥AD,
∵AD=200,HD=20,
∴AH=180,
∵∠EFA=136°,
∴∠FAD=46°,
∴FH=.
∴ED=FH=187.2,
∴EC=187.2+50=237.2≈237.
故答案为237.
17.
【分析】
首先根据题意分析图形,本题涉及到两个直角三角形,应利用其公共边AB及CD=DC BC=20构造方程关系式,进而可解,即可求出答案.
【解析】
∵在直角三角形ADB中,∠D=30°,
∴=tan30°,
∴BD==AB,
∵在直角三角形ABC中,∠ACB=60°,
∴BC==AB,
∵CD=20,
∴CD=BD BC=AB AB=20,
解得:AB=m.
故答案为:.
18.
【分析】
过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,通过解直角三角形可求出BM,AM,CN,DE的长,再结合CD=CN+EN DE即可求出结论.
【解析】
解:过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,如图所示.
在Rt△ABM中,AB=10米,∠BAM=30°,
∴AM=AB cos30°=5(米),BM=AB sin30°=5(米).
在Rt△ADE中,AE=10(米),∠DAE=60°,
∴DE=AE tan60°=10(米).
在Rt△BCN中,BN=AE+AM=10+5(米),∠CBN=45°,
∴CN=BN tan45°=10+5(米),
∴CD=CN+EN DE=10+5+5 10=15 5(米).
故答案为:15 5.
19.200
【分析】
在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
【解析】
解:由题意得.
∵,
,
,
为直角三角形.
在中,(米).
在中,(米).
A,B两点之间的距离为200米.
故答案为:200.
20. 21
【分析】
① 由题意,EG等分上下两层,,勾股定理直接求解即可
②过点作于点,交于点,过点作于点,分别通过勾股定理和三角函数求出,继而求出,过点作于点,交于点,过作于点,通过证明,继而用勾股定理和锐角三角函数解直角三角形,求出,即为球的直径大小
【解析】
①点恰好能卡在原点的位置
故答案为:
②如图:
根据旋转,,,
过点作于点,交于点
过点作于点,
过点作于点,交于点,过作于点
又
,
球体的直径不大于21
故答案为21.
三、解答题
21.
解:,,,
∴在中,,
米,
∵在中,,
米,
米,
答:改善后的斜坡坡角向前推进的距离为104米.
22.
解:过点作于,
,,
,
是矩形,
,,
∵在中,,
,
∵在中,,
,
∵,
∴,
解得:米
即 米.
23.
解:在Rt△ABD中,∠ABD=90°,∠BAD=18°,AB=9,
∴BD=tan18°×AB≈0.33×9=2.97米,
∵∠DCE+∠ADB=90°,∠BAD+∠ADB=90°,
∴∠DCE=∠BAD=18°,
在Rt△CDE中,∠CED=90°,∠DCE=18°,CD=BD﹣BC=2.97﹣0.5=2.47(米),
∴CE=cos18°×CD≈0.95×2.47≈2.3(米).
24.
解:该文化墙PM不需要拆除,理由:设新坡面坡角为α,新坡面的坡度为1:,
∴tanα,∴α=30°.作CD⊥AB于点D,则CD=6米,
∵新坡面的坡度为1:,∴tan∠CAD,
解得,AD=6,∵坡面BC的坡度为1:1,CD=6米,∴BD=6米,
∴AB=AD﹣BD=(6)米,又∵PB=8米,
∴PA=PB﹣AB=8﹣(6)=14﹣614﹣6×1.732≈3.6米>3米,
∴该文化墙PM不需要拆除.
25.
解:(1)如图,过点作于点,
在中,,,
∵,
∴
在中,,,
∴.
∴海里
(2)如图,过点作于点,
在中,,,
∴
在中,.
在中,,,
∴海里.
∴点与点之间的距离为海里.
26.
过B点作BE⊥l1,交l1于E,CD于F,l2于G.
在Rt△ABE中,BE=AB sin30°=20×=10km,
在Rt△BCF中,BF=BC÷cos30°=10÷km,
CF=BF sin30°=km,
DF=CD﹣CF=(30﹣)km,
在Rt△DFG中,FG=DF sin30°=(30﹣)×=(15﹣)km,
∴EG=BE+BF+FG=(25+5)km.
故两高速公路间的距离为(25+5)km.
27.
过点C作CG∥DA交AB于点G.
∵MN∥PQ,CG∥DA,
∴四边形AGCD是平行四边形.
∴AG=CD=50m,∠CGB=38°.
∴GB=AB-AG=120-50=70(m).
∴,
在Rt△BFC中,
=2.75,
∴BF=,
∴,
解得:CF≈76.2(m).
答:河流的宽是76.2米.
28.
(1)过点B作BF⊥AD,交DA的延长线于点F.
由题意得:∠BAF=∠ABD+∠ADB=15°+45°=60°,
在Rt△BFA中,
BF=ABsin60°=4×=6(千米),
AF=ABcos60°=4×=2(千米).
∵CD⊥AD,∠BDC=45°,
∴∠BDF=45°,
在Rt△BFD中,∵∠BDF=45°,
∴DF=BF=6千米.
∴AD=DF-AF=6-2(千米).
即河宽AD为(6-2)千米;
(2)过点B作BG⊥CD于G,易证四边形BFDG是正方形,
∴BG=BF=6千米.
在Rt△BGC中,CG==8(千米),
∴CD=CG+GD=14千米.
即公路CD的长为14千米;
(3)方案一的铺设电缆费用低.
由(2)得DE=CD-CE=8千米.
∴方案一的铺设费用为:2(DE+AB)+4AD=40万元,
方案二的铺设费用为:2(CE+BC+AB)=(32+8)万元.
∵40<32+8,
∴方案一的铺设电缆费用低.
一、单选题
1.已知两点,若点对点的仰角为,那么对的俯角是( ).
A. B. C. D.
2.如图,为测河两岸相对两抽水泵的距离,在距点的处,测得,则间的距离为( ).
A. B. C. D.
3.从地面上的两处望正西方向山顶,仰角分别为和两处相距,那么山高为( ).
A. B. C. D.
4.如图是拦水坝的横断面,斜坡AB的水平宽度为12米,斜面坡度为1:2,则斜坡AB的长为( )米
A. B. C. D.24
5.小明同学从A地沿北偏西60°方向走100 m到B地,再从B地向正南方向走200 m到C地,此时小明同学离A地 ( )
A.150 m B.50 m C.100 m D.100 m
6.小明在学完《解直角三角形》一章后,利用测角仪和校园旗杆的拉绳测量校园旗杆的高度,如图,旗杆的高度与拉绳的长度相等,小明先将拉到的位置,测得为水平线),测角仪的高度为米,则旗杆的高度为( )
A.米 B.米 C.米 D.米
7.国家电网近来实施了新一轮农村电网改造升级工程,解决了农村供电“最后公里”问题,电力公司在 改造时把某一输电线铁塔建在了一个坡度为的山坡的平台上(如图),测得米,米,米,则铁塔的高度约为( )(参考数据:)
A. B. C. D.
8.数学实践活动课中小明同学测量某建筑物的高度,如图,已知斜坡的坡度为,小明在坡底点处测得建筑物顶端处的仰角为,他沿着斜坡行走米到达点处,在测得建筑 物顶端处的仰角为,小明和建筑物的剖面在同一平面内,小明的身高忽略不计.则建筑物的高度约为( )(参考数据:)
A.米 B.米 C.米 D.米
9.某兴趣小组想测量一座大楼 AB的高度.如图,大楼前有一段斜坡BC ,已知 BC的长为 12 米它的坡度 .在离 C点 40 米的 D处,用测量仪测得大楼顶端 A的仰角为 37度,测角仪DE的高度为 1.5米,求大楼AB 的高度约为( )米()
A.39.3 B.37.8 C.33.3 D.25.7
10.某公园有一座古塔,古塔前有一个斜坡坡角,斜坡高米,是平行于水平地面的一个平台、小华想利用所学知识测量古塔的高度,她在平台的点处水平放置一平面镜,她沿着方向移动,当移动到点时,刚好在镜面中看到古塔顶端点的像,这时,测得小华眼睛与地面的距离米,米,米,米,已知,根据题中提供的相关信息,古塔的高度约为(参考数据:)( )
A. B. C. D.
二、填空题
11.一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,,已知木箱高,斜面坡角为,则木箱端点距地面的高度为_________.
12.在倾斜角为的斜坡上植树,若要求两棵树的水平距离为,则斜坡上相邻两树的坡面距离为______.
13.如图,已知斜坡长,坡角(即)为,,现计划在斜坡中点D处挖去部分斜坡,修建一个平行于水平线的休闲平台和一条新的斜坡.若修建的斜坡的坡度为3∶1,休闲平台的长是______m.
14.如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为1:的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,则山高BC=___米(结果保留根号).
15.如图1,一扇窗户打开一定角度,其中一端固定在窗户边上的点处,另一端在边上滑动,图2为某一位置从上往下看的平面图,测得,,长为32厘米,则的长为_______ 厘米.
16.如图,小丽的房间内有一张长高的床靠墙摆放,在上方安装空调,空调下沿与墙垂直,出风口离墙,空调开启后,挡风板与夹角成,风沿方向吹出,为了让空调风不直接吹到床上,空调安装的高度(的长)至少为__________(精确到个位)(参考数据:)
17.如图,为测量某物体的高度,在点测得点的仰角为,朝物体方向前进到达点,再次测得点的仰角为,则物体的高度为 ______.
18.如图,某建筑物的顶部有一块标识牌,小明在斜坡上处测得标识牌顶部的仰角为,沿斜坡走下来在地面处测得标识牌底部的仰角为60°,已知斜坡的坡角为30°,米. 则标识牌的高度是米__________.
19.如图,数学实习小组在高300米的山腰(即米)P处进行测量,测得对面山坡上A处的俯角为30°,对面山脚B处的俯角60°,已知,点P,H,B,C,A在同一个平面上,点H,B,C在同一条直线上,且,则A,B两点间的距离为___________米.
20.有一种双层长方体垃圾桶AB=70cm,BC=25cm,CF=30cm,侧面如图1所示,隔板EG等分上下两层,下方内桶BCHG绕底部轴(CF)旋转开,若点H恰好能卡在原来点G的位置,则内桶边CH的长度应设计为___;现将CH调整为25cm,打开最大角度时,点H卡在隔板上,如图2所示,则可完全放入下方桶内的球体的直径不大于____.
三、解答题
21.北京联合张家口成功申办2022年冬奥会后,滑雪运动已成为人们喜爱的娱乐健身项目.如图是某滑雪场为初学者练习用的斜坡示意图,出于安全因素考虑,决定将斜坡的倾角由降为,已知原斜坡坡面长为200米,点在同一水平地面上,求改善后的斜坡坡角向前推进的距离.(结果保留整数.参考数据: ,)
22.如图,在甲建筑物上从点到点挂一长为的宣传条幅,在乙建筑物的顶部点测得条幅顶端的仰角为,测得条幅底端点的俯角为,求底部不能直接到达的甲、乙两建筑物之间的水平距离.(答案保留根号)
23.某商场为缓解我市“停车难”问题,拟建造地下停车库,如图是该地下停车库坡道入口的设计示意图.其中,AB⊥BD.∠BAD=18°,C在BD上,BC=0.5m.车库坡道入口上方要张贴限高标志.以便告知驾驶员所驾车辆能否安全驶入.为标明限高,请你根据该图计算CE的长度(即点C到AD的距离).(参考数据:sin18°≈0.31,cos18°≈0.95,tan18°≈0.33)(结果精确到0.1m)
24.我市里运河有一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,文化墙PM在天桥底部正前方8米处(PB的长),为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1:.有关部门规定,文化墙距天桥底部小于3米时应拆除,天桥改造后,该文化墙PM是否需要拆除?请说明理由.(参考数据:1.414,1.732)
25.如图,在一条笔直的海岸线上有,两个观测站,在的正东方向.有一艘小船从处沿北偏西方向出发,以每小时20海里速度行驶半小时到达处,从处测得小船在它的北偏东的方向上.
(1)求的距离;
(2)小船沿射线的方向继续航行一段时间后,到达点处,此时,从测得小船在北偏西的方向.求点与点之间的距离.(上述两小题的结果都保留根号)
26.如图,在同一平面内,两条平行高速公路l1和l2间有一条“Z”型道路连通,其中AB段与高速公路l1成30°角,长为20km;BC段与AB、CD段都垂直,长为10km,CD段长为30km,求两高速公路间的距离(结果保留根号).
27.如图,河流的两岸、互相平行,河岸上有一排间隔为的电线杆、、某人在河岸的处测得,然后沿河岸走了到达处,测得.求河流的宽度.(结果精确到,参考数据:,,,,,)
28.如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为地,AD为河宽,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一电缆,共有如下两种铺设方案:
方案一:; 方案二:.
经测量得AB=4千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15°.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.
答案
一、单选题
1.A
【分析】
根据俯角和仰角的定义和平行线的性质即可得到B对A的仰角为.
【解析】
解:如图,
∵A对B的俯角为,
∴B对A的仰角为.
故选A.
2.A
【分析】
在中,,由此可以求出之长.
【解析】
解:在中,
,
.
又,,
.
故选:.
3.A
【分析】
设山高为,利用三角函数分别表示和BC的长.根据得方程求解.
【解析】
解:设山高为,
在中,,
∴,
在中,,
∴.
∵,
∴.
解得:.
故选:.
4.B
【分析】
根据斜面坡度为1:2,斜坡AB的水平宽度为12米,可得AE=12,BE=6,然后利用勾股定理求出AB的长度.
【解析】
解:如图,过B作BE⊥AD于点E,
∵斜面坡度为1:2,AE=12,
∴BE=6,
在Rt△ABC中, .
故选:B.
5.D
【分析】
根据在Rt△ABD中利用三角函数分别求AD,BD的长,从而得到CD的长.再利用勾股定理求AC的长即可.
【解析】
解:如图:
由B在A的北偏西60°方向可求得∠B=60°,
在Rt△ABD中,
AD=AB sin60°=,
BD=AB cos60°=50,
∴CD=BC-BD=150.
∴AC==.
故选D.
6.C
【分析】
设PA=PB=PB′=x,在RT△PCB′中,根据,列出方程即可解决问题.
【解析】
解:设PA=PB=PB′=x,
在RT△PCB′中,
∴
∴,
∴(1-)x=1,
∴x=.
故选C.
7.C
【分析】
延长AB交ED于G,过C作CF⊥DE于F,得到GF=BC=5,设DF=3k,CF=4k,解直角三角形得到结论.
【解析】
解:延长AB交ED于G,过C作CF⊥DE于F,
则四边形BGFC是矩形
∴GF=BC=5,
∵山坡CD的坡度为1:0.75,
∴设DF=3k,CF=4k,
∴CD=5k=35,
∴k=7,
∴DF=21,BG=CF=28,
∴EG=GF+DF+DE=5+21+19=45,
∵∠AED=52.5°,
∴AG=EG tan52.5°=45×1.30=58.5,
∴AB=AG-BG=30.5米,
答:铁塔AB的高度约为30.5米.
故选:C.
8.D
【分析】
如图,过F点作FH⊥CD,垂足为H,作FG⊥EB,垂足为G.利用坡度先求出FG与EG,设DE=CD=x,表示出FH,CH,再利用三角函数即可解得.
【解析】
如图,过F点作FH⊥CD,垂足为H,作FG⊥EB,垂足为G.
根据题意易知DC=DE,EF=13m,∠CFH=35°,HF=GD,HD=FG
∵斜坡的坡度为,且EF=13m
故FG=5m,EG=12m
设DE=CD=x,则FH=DE+EG=x+12,CH=CD-HD=CD-FG=x-5
在直角三角形CHF中,
解得x≈44.7
故选D
9.C
【分析】
延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H,在Rt△BCF中利用坡度的定义求得CF的长,则DF即可求得,然后在直角△AEH中利用三角函数求得AF的长,进而求得AB的长.
【解析】
解:延长AB交直线DC于点F,过点E作EH⊥AF,垂足为点H.
∵在Rt△BCF中,=,
∴设BF=k,则CF=k,BC=2k.
又∵BC=12,
∴k=6,
∴BF=6,CF=,
∵DF=DC+CF,
∴DF=40+,
∵在Rt△AEH中,tan∠AEH=,
∴AH=tan37°×(40+)≈37.785(米),
∵BH=BF-FH,
∴BH=6-1.5=4.5.
∵AB=AH-HB,
∴AB=37.785-4.5≈33.3.
故选C.
10.C
【分析】
由正切定义求出CE,延长GD交AB于点H,则BH=DE=1.8(米),DH=BE=BC+CE=18(米),HG=DH+DG=26(米),证明△AHG∽△MNG,求出AH的长,则可求出答案.
【解析】
解:在Rt△CDE中,tan∠DCE,
∴0.9,
∴CE=2,
延长GD交AB于点H,
则BH=DE=1.8(米),DH=BE=BC+CE=18(米),HG=DH+DG=26(米),
∵∠AHG=∠MNG=90°,∠AGH=∠MGN,
∴△AHG∽△MNG,
∴,
即,
∴AH=19.5(米),
∴AB=AH+HB=21.3(米).
答:古塔的高度AB为21.3米.
故选:C.
二、填空题
11.3
【分析】
连接AE,在Rt△ABE中,利用勾股定理求得AE的长,利用三角函数即可求得,然后在Rt△AEF中,利用三角函数求得的长.
【解析】
解:连接AE,在Rt△ABE中,已知AB=3m,BE=,
∴根据勾股定理得.
又∵,∴.
在Rt△AEF中,,
∴.
故答案为:3.
12.
【分析】
由题意可知,利用角的余弦即可求出的长.
【解析】
解:,,
,
米,
米,
故答案为:.
13.20
【分析】
由三角函数的定义,即可求得AC与BC的长,又由坡度的定义,即可求得EH的长,继而求得休闲平台DE的长.
【解析】
解:如图,延长交于点H,
在中,,,
∴,
∵点D为中点,
∴,
又∵,
∴,
∵斜坡的坡度为:,
∴,
∴,即休闲平台的长是.
故答案为:20.
14.100.
【分析】
作DF⊥AC于F.解直角三角形分别求出BE、EC即可解决问题.
【解析】
解:作DF⊥AC于F.
∵DF:AF=1:,AD=200米,
∴tan∠DAF=,
∴∠DAF=30°,
∴DF=AD=×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=,
∴BE=BD sin∠BDE=200×=100(米),
∴BC=BE+EC=100+100(米);
故答案为:100.
15.
【分析】
作AC⊥OB于点C,然后根据题意和锐角三角函数可以求得AC和BC的长,再根据直角三角形中的性质即可得到AB的长.
【解析】
解:作AC⊥OB于点C,如右图2所示,
则∠ACO=∠ACB=90°,
∵,
∴,
∴AC=OC,
设AC=x,则OC=x,
∵
由
解得,
∴(厘米),
即AB的长为厘米.
故答案为:.
16.
【分析】
连接AF,作FH⊥AD构造直角三角形运用三角函数解出FH,再将床高加上即可求出EC的值.
【解析】
当A、F在一条直线时,就正好不会吹到床上,连接AF,过点F作FH⊥AD,
∵AD=200,HD=20,
∴AH=180,
∵∠EFA=136°,
∴∠FAD=46°,
∴FH=.
∴ED=FH=187.2,
∴EC=187.2+50=237.2≈237.
故答案为237.
17.
【分析】
首先根据题意分析图形,本题涉及到两个直角三角形,应利用其公共边AB及CD=DC BC=20构造方程关系式,进而可解,即可求出答案.
【解析】
∵在直角三角形ADB中,∠D=30°,
∴=tan30°,
∴BD==AB,
∵在直角三角形ABC中,∠ACB=60°,
∴BC==AB,
∵CD=20,
∴CD=BD BC=AB AB=20,
解得:AB=m.
故答案为:.
18.
【分析】
过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,通过解直角三角形可求出BM,AM,CN,DE的长,再结合CD=CN+EN DE即可求出结论.
【解析】
解:过点B作BM⊥EA的延长线于点M,过点B作BN⊥CE于点N,如图所示.
在Rt△ABM中,AB=10米,∠BAM=30°,
∴AM=AB cos30°=5(米),BM=AB sin30°=5(米).
在Rt△ADE中,AE=10(米),∠DAE=60°,
∴DE=AE tan60°=10(米).
在Rt△BCN中,BN=AE+AM=10+5(米),∠CBN=45°,
∴CN=BN tan45°=10+5(米),
∴CD=CN+EN DE=10+5+5 10=15 5(米).
故答案为:15 5.
19.200
【分析】
在直角△PHB中,根据三角函数即可求得PB的长,然后在直角△PBA中利用三角函数即可求解.
【解析】
解:由题意得.
∵,
,
,
为直角三角形.
在中,(米).
在中,(米).
A,B两点之间的距离为200米.
故答案为:200.
20. 21
【分析】
① 由题意,EG等分上下两层,,勾股定理直接求解即可
②过点作于点,交于点,过点作于点,分别通过勾股定理和三角函数求出,继而求出,过点作于点,交于点,过作于点,通过证明,继而用勾股定理和锐角三角函数解直角三角形,求出,即为球的直径大小
【解析】
①点恰好能卡在原点的位置
故答案为:
②如图:
根据旋转,,,
过点作于点,交于点
过点作于点,
过点作于点,交于点,过作于点
又
,
球体的直径不大于21
故答案为21.
三、解答题
21.
解:,,,
∴在中,,
米,
∵在中,,
米,
米,
答:改善后的斜坡坡角向前推进的距离为104米.
22.
解:过点作于,
,,
,
是矩形,
,,
∵在中,,
,
∵在中,,
,
∵,
∴,
解得:米
即 米.
23.
解:在Rt△ABD中,∠ABD=90°,∠BAD=18°,AB=9,
∴BD=tan18°×AB≈0.33×9=2.97米,
∵∠DCE+∠ADB=90°,∠BAD+∠ADB=90°,
∴∠DCE=∠BAD=18°,
在Rt△CDE中,∠CED=90°,∠DCE=18°,CD=BD﹣BC=2.97﹣0.5=2.47(米),
∴CE=cos18°×CD≈0.95×2.47≈2.3(米).
24.
解:该文化墙PM不需要拆除,理由:设新坡面坡角为α,新坡面的坡度为1:,
∴tanα,∴α=30°.作CD⊥AB于点D,则CD=6米,
∵新坡面的坡度为1:,∴tan∠CAD,
解得,AD=6,∵坡面BC的坡度为1:1,CD=6米,∴BD=6米,
∴AB=AD﹣BD=(6)米,又∵PB=8米,
∴PA=PB﹣AB=8﹣(6)=14﹣614﹣6×1.732≈3.6米>3米,
∴该文化墙PM不需要拆除.
25.
解:(1)如图,过点作于点,
在中,,,
∵,
∴
在中,,,
∴.
∴海里
(2)如图,过点作于点,
在中,,,
∴
在中,.
在中,,,
∴海里.
∴点与点之间的距离为海里.
26.
过B点作BE⊥l1,交l1于E,CD于F,l2于G.
在Rt△ABE中,BE=AB sin30°=20×=10km,
在Rt△BCF中,BF=BC÷cos30°=10÷km,
CF=BF sin30°=km,
DF=CD﹣CF=(30﹣)km,
在Rt△DFG中,FG=DF sin30°=(30﹣)×=(15﹣)km,
∴EG=BE+BF+FG=(25+5)km.
故两高速公路间的距离为(25+5)km.
27.
过点C作CG∥DA交AB于点G.
∵MN∥PQ,CG∥DA,
∴四边形AGCD是平行四边形.
∴AG=CD=50m,∠CGB=38°.
∴GB=AB-AG=120-50=70(m).
∴,
在Rt△BFC中,
=2.75,
∴BF=,
∴,
解得:CF≈76.2(m).
答:河流的宽是76.2米.
28.
(1)过点B作BF⊥AD,交DA的延长线于点F.
由题意得:∠BAF=∠ABD+∠ADB=15°+45°=60°,
在Rt△BFA中,
BF=ABsin60°=4×=6(千米),
AF=ABcos60°=4×=2(千米).
∵CD⊥AD,∠BDC=45°,
∴∠BDF=45°,
在Rt△BFD中,∵∠BDF=45°,
∴DF=BF=6千米.
∴AD=DF-AF=6-2(千米).
即河宽AD为(6-2)千米;
(2)过点B作BG⊥CD于G,易证四边形BFDG是正方形,
∴BG=BF=6千米.
在Rt△BGC中,CG==8(千米),
∴CD=CG+GD=14千米.
即公路CD的长为14千米;
(3)方案一的铺设电缆费用低.
由(2)得DE=CD-CE=8千米.
∴方案一的铺设费用为:2(DE+AB)+4AD=40万元,
方案二的铺设费用为:2(CE+BC+AB)=(32+8)万元.
∵40<32+8,
∴方案一的铺设电缆费用低.
