人教版小学数学六年级下册第三单元《圆柱与圆锥》单元练习题(含答案解析)
文档属性
| 名称 | 人教版小学数学六年级下册第三单元《圆柱与圆锥》单元练习题(含答案解析) |  | |
| 格式 | docx | ||
| 文件大小 | 116.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 08:28:12 | ||
图片预览


文档简介
六年级数学下册第三单元《圆柱与圆锥》单元练习题
一、选择题(共6小题,每小题2分,满分12分)
1.将直角三角形沿一条直角边旋转,得到的立体图形是 ( )。
A. B. C. D.
2.把一个圆柱的侧面沿高展开得到一个边长为分米的正方形,这个圆柱的侧面积是( )分米。
A. B. C. D.
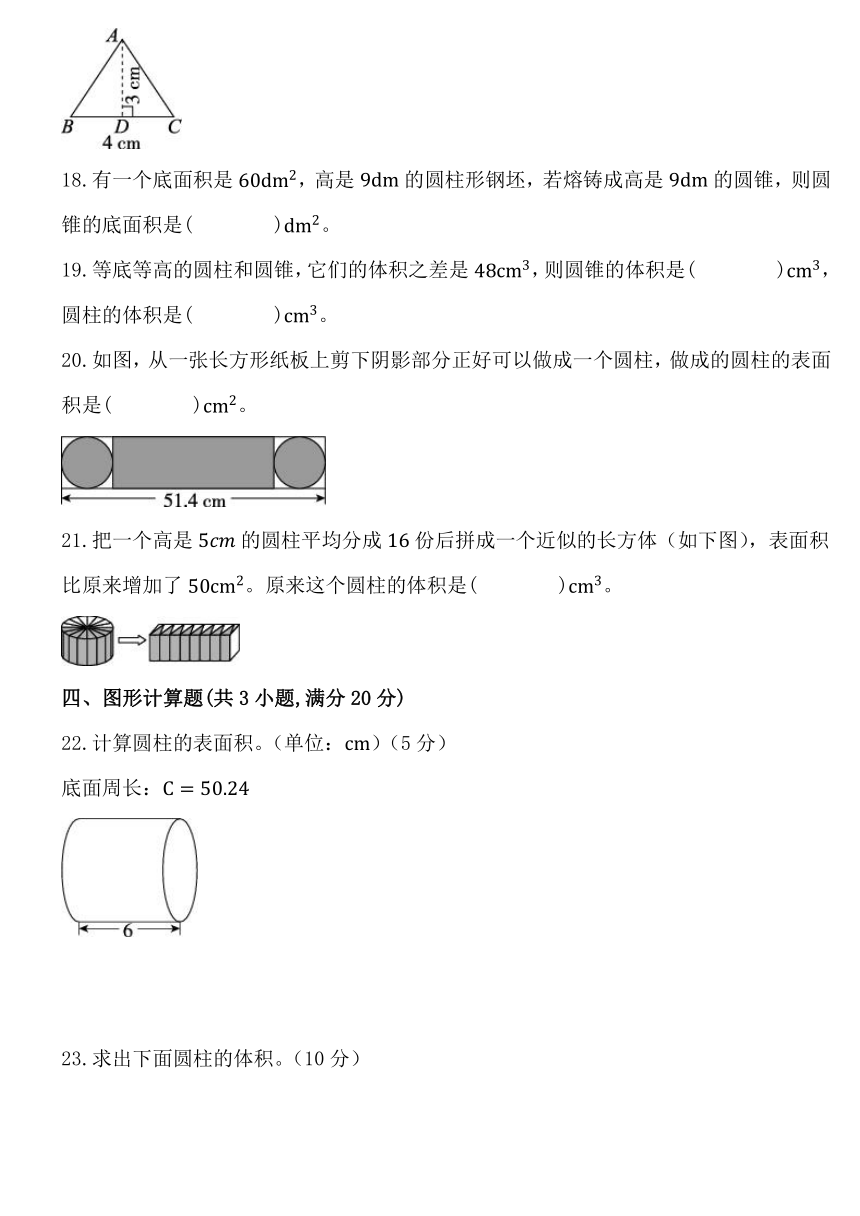
3.下面图( )恰好可以围成一个圆柱。(接头处忽略不计)(单位:)
A. B.
C. D.
4.如图,这两个等底等高的容器内的沙子图中阴影部分相比,( )。
A.甲比乙多 B.乙比甲多 C.同样多 D.无法确定
5.下面圆柱形易拉罐里的饮料如果倒入底面半径厘米、高厘米的杯子里,大约可以倒( )杯。(得数保留整数)
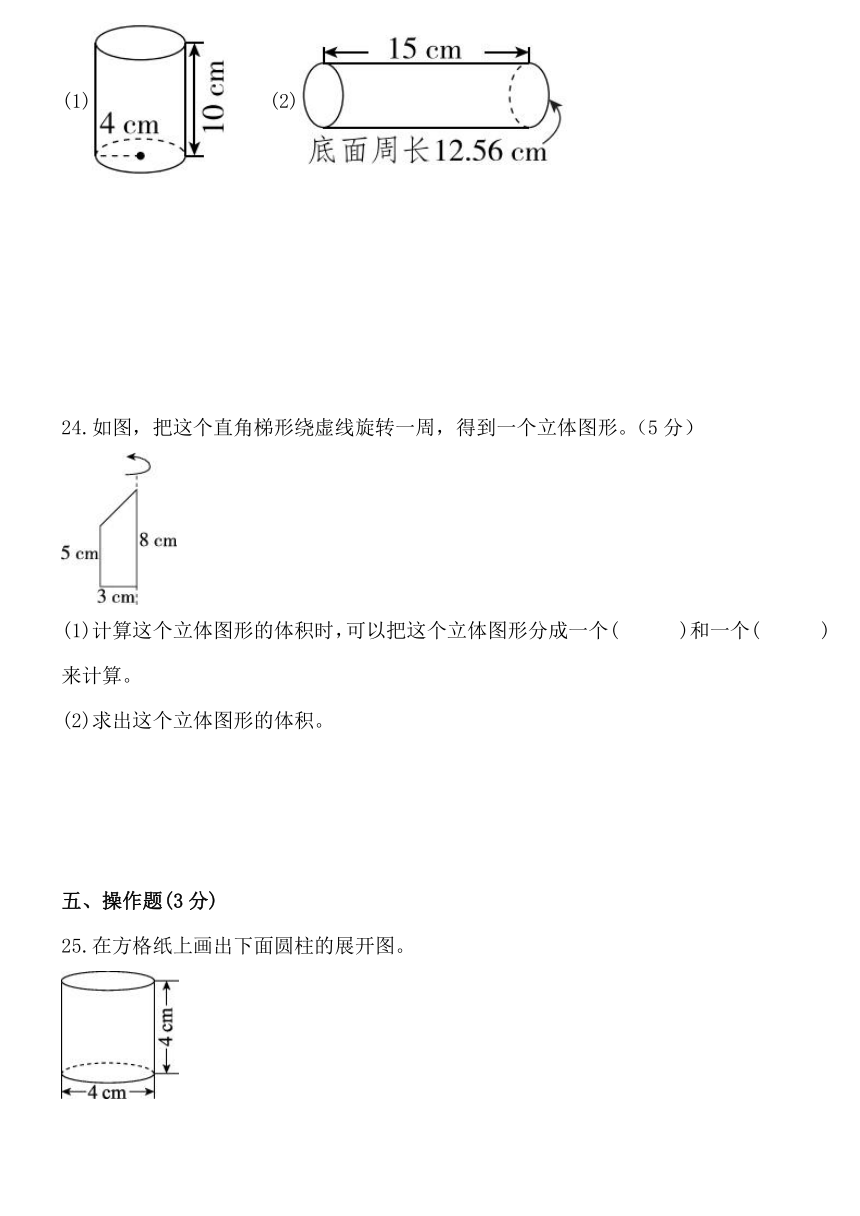
A. B. C. D.
6.下面四个图形的体积之间分别是什么关系?下面的说法中正确的有( )。(单位:
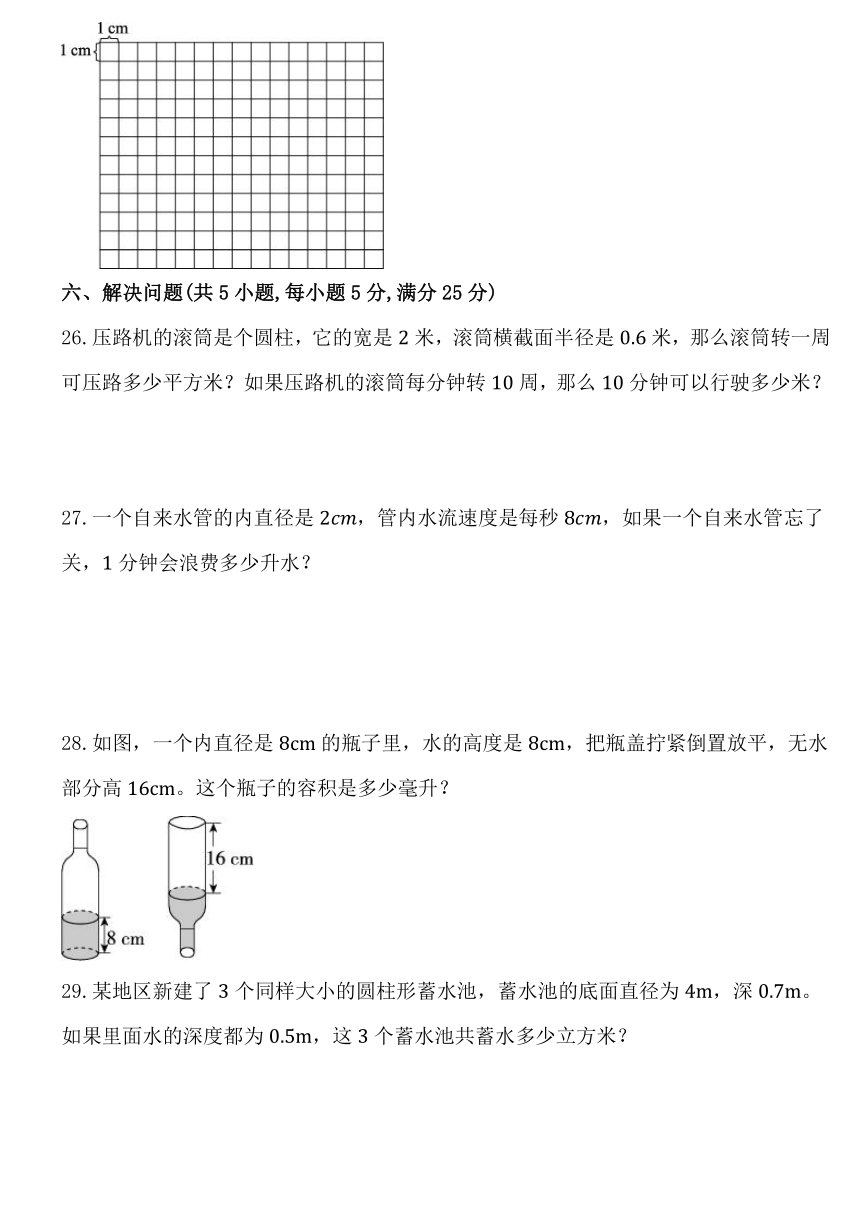
①甲乙 ②乙丙 ③乙丁 ④甲丁
A.①③ B.①②③ C.③④ D.①②④
二、判断题(共5小题,每小题2分,满分10分)
7.圆柱的侧面沿着高展开后会得到一个长方形或者正方形。( )
8.如果两个圆柱的底面积相等,那么它们的表面积也一定相等。( )
9.一个圆柱体的高扩大倍,底面积缩小倍,它的体积不变。( )
10.圆锥的侧面展开后是一个三角形。( )
11.圆柱的底面积越大,体积越大。( )
三、填空题(共10小题,每小题3分,满分30分)
12.做一节底面直径是厘米、长是厘米的烟囱,至少需要( )平方分米的铁皮。
13.把一根长的圆柱形木料截成段小圆柱,表面积增加了,这根木料原来的体积是( )。
14.一个圆柱形水瓶的容积是升,从里面量,底面积是平方分米。用这个水瓶装瓶水,水面高( )分米。
15.一个圆柱的侧面展开图是一个正方形,这个圆柱的高是,那么它的底面周长是( ), 底面直径是( )。
16.一个圆柱和一个圆锥的底面积和体积都相等,圆锥的高是,圆柱的高是()。
17.如图,高是,底是的等腰三角形绕旋转形成一个圆锥,体积为( )。
18.有一个底面积是,高是的圆柱形钢坯,若熔铸成高是的圆锥,则圆锥的底面积是( )。
19.等底等高的圆柱和圆锥,它们的体积之差是,则圆锥的体积是( ),圆柱的体积是( )。
20.如图,从一张长方形纸板上剪下阴影部分正好可以做成一个圆柱,做成的圆柱的表面积是( )。
21.把一个高是的圆柱平均分成份后拼成一个近似的长方体(如下图),表面积比原来增加了。原来这个圆柱的体积是( )。
四、图形计算题(共3小题,满分20分)
22.计算圆柱的表面积。( 单位:)(5分)
底面周长:
23.求出下面圆柱的体积。(10分)
(1) (2)
24.如图,把这个直角梯形绕虚线旋转一周,得到一个立体图形。(5分)
(1)计算这个立体图形的体积时,可以把这个立体图形分成一个( )和一个( )来计算。
(2)求出这个立体图形的体积。
五、操作题(3分)
25.在方格纸上画出下面圆柱的展开图。
六、解决问题(共5小题,每小题5分,满分25分)
26.压路机的滚筒是个圆柱,它的宽是米,滚筒横截面半径是米,那么滚筒转一周可压路多少平方米?如果压路机的滚筒每分钟转周,那么分钟可以行驶多少米?
27.一个自来水管的内直径是,管内水流速度是每秒,如果一个自来水管忘了关,分钟会浪费多少升水?
28.如图,一个内直径是的瓶子里,水的高度是,把瓶盖拧紧倒置放平,无水部分高。这个瓶子的容积是多少毫升?
29.某地区新建了个同样大小的圆柱形蓄水池,蓄水池的底面直径为,深。如果里面水的深度都为,这个蓄水池共蓄水多少立方米?
30.在一个从里面量底面半径为,高为,水深的圆柱形玻璃缸中,放入一个底面直径为的圆锥形铁块,水面淹没铁块并上升了,求放入的圆锥形铁块的高。
参考答案
1.C
2.B
3.A
【解析】根据圆柱的侧面展开图的特点可知,圆柱沿高侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,利用题目中的数据,计算后进行选择。
4.C
5.B
【解析】根据圆柱的体积公式:,求出圆柱形易拉罐的体积和杯子的体积,用易拉罐的体积除以杯子的体积即可。
故选。
6.D
7.对
【解析】沿圆柱高剪开的侧面是以圆柱底面周长为长,以圆柱高为宽的长方形,如果底面周长等于高,则得到一个正方形。
8.错
9.对
【解析】根据圆柱体的体积公式和因数与积的变化规律可知,一个圆柱体的高扩大倍,底面积缩小倍,体积是原来的倍,即它的体积不变。 由此可得答案为:正确
10.错
【解析】圆锥的侧面展开后是一个扇形。
11.错
【解析】因为圆柱的体积底面积高,所以,只说底面积越大,而高不确定,那么体积也就不一定越大。 由此可得答案为:错误
12.
13.
14.
15.;
16.
17.
18.
19.;
20.
【解析】根据图示,长方形的长加上条直径等于,长方形的长是圆柱的底面周长,因此,求得,,根据圆柱的表面积公式即可求解。
21.
22.(平方厘米)
(厘米)
(平方厘米)
(平方厘米)
23.(1)(立方厘米)
(2)(厘米)(立方厘米)
24.(1)圆柱;圆锥
(2)
答:这个立体图形的体积是。
【解析】(1)把这个直角梯形绕虚线旋转一周,旋转后得到的立体图形的上半部分是一个圆锥,下半部分是一个圆柱。
(2)圆柱和圆锥的底面半径都是,圆锥的高是,圆柱的高是。分别计算圆柱和圆锥的体积,再相加即可。
25.画法不唯一,如:
26.(平方米)
(米)
27.分秒
答:分钟会浪费升水。
28.
答:这个瓶子的容积是。
【解析】由题意可知,瓶子正放时无水部分的体积等于倒放时无水部分的体积,所以这个瓶子的容积就等于正放时瓶中水的体积加上倒放时无水部分的体积,也就是这两个圆柱的体积之和。
29.
答:这个蓄水池共蓄水。
【解析】个蓄水池的蓄水量蓄水池的底面积水深。
30.
答:圆锥形铁块的高。
一、选择题(共6小题,每小题2分,满分12分)
1.将直角三角形沿一条直角边旋转,得到的立体图形是 ( )。
A. B. C. D.
2.把一个圆柱的侧面沿高展开得到一个边长为分米的正方形,这个圆柱的侧面积是( )分米。
A. B. C. D.
3.下面图( )恰好可以围成一个圆柱。(接头处忽略不计)(单位:)
A. B.
C. D.
4.如图,这两个等底等高的容器内的沙子图中阴影部分相比,( )。
A.甲比乙多 B.乙比甲多 C.同样多 D.无法确定
5.下面圆柱形易拉罐里的饮料如果倒入底面半径厘米、高厘米的杯子里,大约可以倒( )杯。(得数保留整数)
A. B. C. D.
6.下面四个图形的体积之间分别是什么关系?下面的说法中正确的有( )。(单位:
①甲乙 ②乙丙 ③乙丁 ④甲丁
A.①③ B.①②③ C.③④ D.①②④
二、判断题(共5小题,每小题2分,满分10分)
7.圆柱的侧面沿着高展开后会得到一个长方形或者正方形。( )
8.如果两个圆柱的底面积相等,那么它们的表面积也一定相等。( )
9.一个圆柱体的高扩大倍,底面积缩小倍,它的体积不变。( )
10.圆锥的侧面展开后是一个三角形。( )
11.圆柱的底面积越大,体积越大。( )
三、填空题(共10小题,每小题3分,满分30分)
12.做一节底面直径是厘米、长是厘米的烟囱,至少需要( )平方分米的铁皮。
13.把一根长的圆柱形木料截成段小圆柱,表面积增加了,这根木料原来的体积是( )。
14.一个圆柱形水瓶的容积是升,从里面量,底面积是平方分米。用这个水瓶装瓶水,水面高( )分米。
15.一个圆柱的侧面展开图是一个正方形,这个圆柱的高是,那么它的底面周长是( ), 底面直径是( )。
16.一个圆柱和一个圆锥的底面积和体积都相等,圆锥的高是,圆柱的高是()。
17.如图,高是,底是的等腰三角形绕旋转形成一个圆锥,体积为( )。
18.有一个底面积是,高是的圆柱形钢坯,若熔铸成高是的圆锥,则圆锥的底面积是( )。
19.等底等高的圆柱和圆锥,它们的体积之差是,则圆锥的体积是( ),圆柱的体积是( )。
20.如图,从一张长方形纸板上剪下阴影部分正好可以做成一个圆柱,做成的圆柱的表面积是( )。
21.把一个高是的圆柱平均分成份后拼成一个近似的长方体(如下图),表面积比原来增加了。原来这个圆柱的体积是( )。
四、图形计算题(共3小题,满分20分)
22.计算圆柱的表面积。( 单位:)(5分)
底面周长:
23.求出下面圆柱的体积。(10分)
(1) (2)
24.如图,把这个直角梯形绕虚线旋转一周,得到一个立体图形。(5分)
(1)计算这个立体图形的体积时,可以把这个立体图形分成一个( )和一个( )来计算。
(2)求出这个立体图形的体积。
五、操作题(3分)
25.在方格纸上画出下面圆柱的展开图。
六、解决问题(共5小题,每小题5分,满分25分)
26.压路机的滚筒是个圆柱,它的宽是米,滚筒横截面半径是米,那么滚筒转一周可压路多少平方米?如果压路机的滚筒每分钟转周,那么分钟可以行驶多少米?
27.一个自来水管的内直径是,管内水流速度是每秒,如果一个自来水管忘了关,分钟会浪费多少升水?
28.如图,一个内直径是的瓶子里,水的高度是,把瓶盖拧紧倒置放平,无水部分高。这个瓶子的容积是多少毫升?
29.某地区新建了个同样大小的圆柱形蓄水池,蓄水池的底面直径为,深。如果里面水的深度都为,这个蓄水池共蓄水多少立方米?
30.在一个从里面量底面半径为,高为,水深的圆柱形玻璃缸中,放入一个底面直径为的圆锥形铁块,水面淹没铁块并上升了,求放入的圆锥形铁块的高。
参考答案
1.C
2.B
3.A
【解析】根据圆柱的侧面展开图的特点可知,圆柱沿高侧面展开后是一个长方形,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,利用题目中的数据,计算后进行选择。
4.C
5.B
【解析】根据圆柱的体积公式:,求出圆柱形易拉罐的体积和杯子的体积,用易拉罐的体积除以杯子的体积即可。
故选。
6.D
7.对
【解析】沿圆柱高剪开的侧面是以圆柱底面周长为长,以圆柱高为宽的长方形,如果底面周长等于高,则得到一个正方形。
8.错
9.对
【解析】根据圆柱体的体积公式和因数与积的变化规律可知,一个圆柱体的高扩大倍,底面积缩小倍,体积是原来的倍,即它的体积不变。 由此可得答案为:正确
10.错
【解析】圆锥的侧面展开后是一个扇形。
11.错
【解析】因为圆柱的体积底面积高,所以,只说底面积越大,而高不确定,那么体积也就不一定越大。 由此可得答案为:错误
12.
13.
14.
15.;
16.
17.
18.
19.;
20.
【解析】根据图示,长方形的长加上条直径等于,长方形的长是圆柱的底面周长,因此,求得,,根据圆柱的表面积公式即可求解。
21.
22.(平方厘米)
(厘米)
(平方厘米)
(平方厘米)
23.(1)(立方厘米)
(2)(厘米)(立方厘米)
24.(1)圆柱;圆锥
(2)
答:这个立体图形的体积是。
【解析】(1)把这个直角梯形绕虚线旋转一周,旋转后得到的立体图形的上半部分是一个圆锥,下半部分是一个圆柱。
(2)圆柱和圆锥的底面半径都是,圆锥的高是,圆柱的高是。分别计算圆柱和圆锥的体积,再相加即可。
25.画法不唯一,如:
26.(平方米)
(米)
27.分秒
答:分钟会浪费升水。
28.
答:这个瓶子的容积是。
【解析】由题意可知,瓶子正放时无水部分的体积等于倒放时无水部分的体积,所以这个瓶子的容积就等于正放时瓶中水的体积加上倒放时无水部分的体积,也就是这两个圆柱的体积之和。
29.
答:这个蓄水池共蓄水。
【解析】个蓄水池的蓄水量蓄水池的底面积水深。
30.
答:圆锥形铁块的高。
