第四单元巧手小工匠同步练习(含答案) 青岛版数学四年级下册
文档属性
| 名称 | 第四单元巧手小工匠同步练习(含答案) 青岛版数学四年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 144.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 09:39:28 | ||
图片预览





文档简介
第四单元巧手小工匠
(共27题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意书写整洁
一、选择题
1.能围成三角形的一组线段是( ).
A.3㎝ 4㎝ 5㎝ B.4㎝ 4㎝ 8㎝ C.5㎝ 4㎝ 10㎝
2.在一个等腰直角三角形中,它的一个底角是( )。
A.30° B.45° C.60°
3.把一个梯形剪成两个小梯形,每个小梯形的内角和是( ).
A.90° B.180° C.360°
4.下面说法错误的是( )。
A.平行四边形有无数条高
B.有一组对边平行的四边形是梯形
C.用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形
5.下面每组中的3条线段能围成三角形的是( )。(单位:厘米)
A.2,2,3 B.2,1,3 C.2,5,7
6.下列说法正确的是( )。
A.直角三角形只有一条高
B.三个角都是钝角的三角形是钝角三角形
C.三个角都是锐角的三角形是锐角三角形
7.把正方形沿它的一条对角线对折可以得到两个( )。
A.等腰直角三角形 B.钝角三角形 C.直角三角形
8.一个三角形中,有一个角是75°,另外两个角可能是( )。
A.35°和60° B.45°和60° C.25°和90°
二、填空题
9.一个正五边形的一条边长是6厘米,它的周长是( )厘米,一个内角是( )度。
10.自行车车架一般设计成( )形,这是因为这种图形具有( )性。
11.两底角相等的梯形是( ),它有( )条高.
12.一个等腰三角形的一个底角是35°,它的顶角是( )°。如果它的顶角是40°,它的一个底角是( )°。
13.小红用一根15厘米长的铁丝围成了一个三角形,三角形的边长可能是( )厘米、( )厘米、( )厘米。(取整厘米数)
14.一个三角形的两个角分别是24°和32°,另一个角是( ),它是( )三角形。
15.平面图形镶嵌的条件:每个拼接点处,几个多边形的各内角之和为( ),且将( )的边重合.
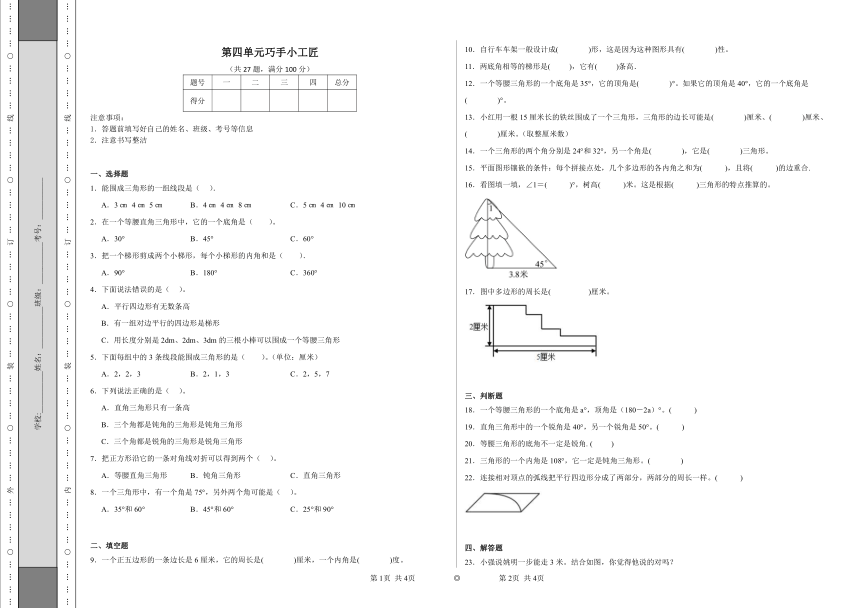
16.看图填一填,∠1=( )°,树高( )米。这是根据( )三角形的特点推算的。
17.图中多边形的周长是( )厘米。
三、判断题
18.一个等腰三角形的一个底角是a°,顶角是(180-2a)°。( )
19.直角三角形中的一个锐角是40°,另一个锐角是50°。( )
20.等腰三角形的底角不一定是锐角. ( )
21.三角形的一个内角是108°,它一定是钝角三角形。( )
22.连接相对顶点的弧线把平行四边形分成了两部分,两部分的周长一样。( )
四、解答题
23.小强说姚明一步能走3米。结合如图,你觉得他说的对吗?
(1)我认为他说的( )。
(2)理由是:( )。
24.周晓梦同学星期天和弟弟在家里打造了一个别具一格的小花园,这个小花园是一个等腰梯形,其周长是98分米,上底和下底长度的和是58分米。这个小花园的一条腰长是多少?
25.(1)求出∠1、∠2的度数。
∠1=( )° ∠2=( )°
(2)分别画出三角形底边上的高,并判断是什么三角形。
( )三角形
( )三角形
26.王爷爷有一块三角形的菜地(如图)
(1)如果从顶点A处,穿过菜地修一条水渠到底边BC,怎样修最省力?请你在图上画出来。
(2)这块菜地有两个角是60°,那么它是一个什么三角形?如果在菜地的外面围上一圈篱笆,篱笆长多少米?
27.一个等腰梯形中,上底是5cm,下底是上底的3倍,腰比下底少8cm,求这个梯形的周长是多少?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【详解】略
2.B
【分析】由题目可知,三角形为等腰直角三角形,所以三角形中一个角为直角,并且另外两个底角要相等,又三角形内角和为180°,减掉直角后的角度由两个底角平分。
【详解】两个底角和:180°-90°=90°
其中一个底角为:90°2=45°
故答案为:B
【点睛】掌握等腰直角三角形的角度特征,还要排除底角是直角的情况。
3.C
【详解】梯形的内角和是360°,将它剪成两个小梯形,每个小梯形的内角和是360°.
4.B
【分析】先对每个选项中的说法进行分析并判断,然后选择正确的一项即可。
A.从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,依此判断;
B.只有一组对边平行的四边形叫做梯形,依此判断;
C.等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此判断即可。
【详解】A.平行四边形有无数条高,即原说法正确;
B.只有一组对边平行的四边形是梯形,即原说法错误;
C.2dm+2dm>3dm,3dm-2dm<2dm,2dm=2dm,即用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形,即原说法正确。
故答案为:B
【点睛】此题考查的是平行四边形的高,梯形的特点,以及三角形3条边的关系,应熟练掌握。
5.A
【分析】判断三角形能否构成,关键是看三条线段是否满足:任意两边之和是否大于第三边。但通常不需一一验证,其简便方法是将较短两边之和与较长边比较。
【详解】A、2+2>4,所以三条线段能围成三角形;
B、2+1=3,所以三条线段不能围成三角形;
C、2+5=7,所以三条线段不能围成三角形。
故答案为:A
【点睛】本题主要考查了三角形三边关系定理:三角形任意两边之和大于第三边。
6.C
【分析】从三角形的一个顶点到它的对边作一条垂线,顶点到垂足之间的线段叫做三角形的高;
有一个角是钝角的三角形就是钝角三角形;
三个角都是锐角的三角形是锐角三角形。
【详解】A.直角三角形只有一条高,不符合,三角形有三条高。
B.三个角都是钝角的三角形是钝角三角形,不符合,一个三角形中只有一个钝角。
C.三个角都是锐角的三角形是锐角三角形,符合。
故答案为:C
【点睛】明确三角形高的定义和三角形的分类是解决本题关键。
7.A
【分析】正方形的四条边都相等,四个角都是直角;等腰直角三角形中有一个角是直角,且两个底角的度数相等,两腰相等;有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,依此画图并选择。
【详解】画图如下:
由此可知,把正方形沿它的一条对角线对折可以得到两个等腰直角三角形。
故答案为:A
8.B
【分析】利用三角形内角和等于180°,即可得解。
【详解】A.75°+35°+60°=170°,不符合条件
B.45°+60°+75°=180°,符合条件
C.25°+90°+75°=190°,不符合条件
故答案为:B。
9. 30 108
【分析】正五边形的5条边相等,5个角相等。正五边形的周长=边长×5,据此求出它的周长。正五边形的内角和是540度,一个内角是(540÷5)度。
【详解】6×5=30(厘米)
540÷5=108(度)
它的周长是30厘米,一个内角是108度。
【点睛】本题考查正五边形的周长和内角和,关键是熟记周长公式以及五边形的内角和为540度。
10. 三角 稳定
【分析】三角形具有稳定性。自行车的车架是三角形形状,自行车的行驶稳定也是由于三角形的稳定性的特征。在生活中,三角形的稳定性有着非常广泛的应用,如:篮球架上篮板的支架是三角形;电线杆的支架是三角形的;上述物体中的三角形都能使物体更加稳固。
【详解】自行车车架一般设计成三角形,这是因为这种图形具有稳定性。
11. 等腰梯形 无数
【详解】略
12. 110 70
【分析】等腰三角形的两个底角相等,则另一个底角是35°。根据三角形的内角和为180°可知,顶角是180°-35°-35°。若顶角是40°,一个底角是(180°-40°)÷2。
【详解】180°-35°-35°=110°
它的顶角是110°。
(180°-40°)÷2
=140°÷2
=70°
它的一个底角是70°。
【点睛】本题考查等腰三角形的特征和三角形的内角和,等腰三角形中,底角+底角+顶角=180°。
13. 7 5 3
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此可知,三角形的周长为15厘米时,最长的边不超过8厘米,最大是7厘米。当最长边为7厘米时,其余两条边的长度和为8厘米,可能是5厘米和3厘米,据此解答。
【详解】5+3>7,5-3<7,则长7厘米、5厘米、3厘米的三根铁丝能围成一个三角形,即三角形的边长可能是7厘米、5厘米、3厘米。(答案不唯一)
【点睛】本题考查三角形的三边关系,关键是根据三角形的三边关系明确最长的边最大是7厘米。
14. 124° 钝角
【分析】根据三角形的内角度数和是180°,已知其他两个角的度数,要求另一个角的度数,用180°减去24°,再减去32°即可;根据计算出来的角的度数发现,有一个角是钝角,再根据有一个角是钝角的三角形是钝角三角形,据此解答。
【详解】
一个三角形的两个角分别是24°和32°,另一个角是(124°),它是(钝角)三角形。
【点睛】本题考查三角形的内角度数和以及钝角三角形的特征,熟练掌握并灵活运用。
15. 360° 相邻
【详解】由多边形镶嵌成平面图形的条件可知:(1)拼接在同一个点的各个角和恰好等于360°;(2)相邻的多边形有公共边.
16. 45 3.8 等腰
【分析】三角形的一个角是45度,树与地面垂直且于三角形一条边重合,根据三角形的内角和是180度即可算出角1度数,再根据三角形特点进行推测即可;
有两个角相等,两条边相等的三角形是等腰三角形。
【详解】180°-90°-45°
=90°-45°
=45°
即∠1=45°,树高3.8米。这是根据等腰三角形的特点推算的。
【点睛】明确等腰三角形的特征和三角形内角和是180度是解决本题关键。
17.14
【详解】(2+5)×2
=7×2
=14(厘米)
18.√
【分析】等腰三角形的两个底角相等,三角形的内角和为180°,所以顶角为180°减去两个底角的度数;据此解答。
【详解】根据分析:一个等腰三角形的一个底角是a°,顶角是(180-2a)°,原题说法正确。
故答案为:√
19.√
【分析】直角三角形中,两个锐角的和是90°,90°-其中一个锐角度数=另一个锐角度数,据此求解。
【详解】由分析可得,直角三角形中,一个锐角为40°,另一个锐角为90°-40°=50°
故答案为:√
【点睛】明确直角三角形三个角的特点以及三角形的内角和都为180°是解决本题的关键。
20.×
【详解】略
21.√
【分析】锐角三角形:三个角都小于90°;直角三角形:其中一个角等于90°;钝角三角形:有一个角大于90°。据此判断即可。
【详解】108°>90°
三角形的一个内角是108°,它一定是钝角三角形。原题说法正确。
故答案为:√
22.√
【分析】根据平行四边形的性质,平行四边形的对边相等,分别看分成的两部分的周长都有哪几部分围成,据此判断。
【详解】平行四边形对边相等,分成两部分的周长分别由平行四边形的一组对边和一条共同的弧围成,所以两部分的周长一样。
故答案为:√
【点睛】解答本题的关键是熟练掌握平行四边形的性质和周长的意义。
23.(1)错误
(2)因为三角形的两边之和大于第三边,而姚明的腿长1.3米,,所以姚明一步不能走3米。
【分析】先求出两条腿的长度之和,根据三角形的第三条边一定小于两边之和可知:姚明走一步的长度一定小于他两条腿的长度之和,据此解答。
【详解】(1)1.3+1.3=2.6(米)<3米
故姚明一步能走3米说法是错误的。
(2)因为三角形的两边之和大于第三边,而姚明的腿长1.3米,,所以姚明一步不能走3米。
【点睛】熟练掌握三角形的三边关系是解答本题的关键。
24.20分米
【分析】等腰梯形,其周长是98分米,上底和下底长度的和是58分米,可先用减法求出两条腰的长度之和。同时,在等腰梯形中,两腰的长度相等,所以用除法即可求出一条腰的长度。
【详解】(98-58)÷2
=40÷2
=20(分米)
答:这个小花园的一条腰长是20分米。
25.(1)59;137
(2)图见详解过程;锐角;钝角
【分析】(1)根据三角形的内角和是180°,用180°减去已知两个内角的和,即可求出∠1、∠2的度数,由此求解。
(2)经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;然后再根据三角形的分类进行解答。
【详解】(1)∠1=180°-82°-39°
=98°-39°
=59°
∠2=180°-17°-26°
=163°-26°
=137°
∠1=(59)° ∠2=(137)°
(2)如图所示:
(锐角)三角形
(钝角)三角形
【点睛】本题主要考查的知识点有:三角形内角和定理、作三角形的高以及三角形的(按角)分类。
26.(1)图见详解过程
(2)等边三角形;45米
【分析】(1)根据“垂线段最短”,过点A画BC边上的垂线段,沿这条垂线段修,可使修水渠最省力;
(2)三角形的内角和是180°,已知这个三角形有两个角是60°,那么另外一个角也是60°,所以这个三角形是等边三角形;等边三角形的三条边都相等,所以这个三角形的三边都是15米,用15乘3,即可求出所需篱笆的长度。
【详解】(1)从点A作BC边上的垂线段,这样修最省力。如图所示:
(2)180°-60°×2
=180°-120°
=60°
这块菜地有两个角是60°,那么它是等边三角形。
15×3=45(米)
答:篱笆长45米。
27.5×3=15 (cm) 15-8=7 (cm)
5+15+7×2=34 (cm)
答:这个梯形的周长是34 cm.
【详解】略
答案第1页,共2页
答案第1页,共2页
(共27题,满分100分)
题号 一 二 三 四 总分
得分
注意事项:
1.答题前填写好自己的姓名、班级、考号等信息
2.注意书写整洁
一、选择题
1.能围成三角形的一组线段是( ).
A.3㎝ 4㎝ 5㎝ B.4㎝ 4㎝ 8㎝ C.5㎝ 4㎝ 10㎝
2.在一个等腰直角三角形中,它的一个底角是( )。
A.30° B.45° C.60°
3.把一个梯形剪成两个小梯形,每个小梯形的内角和是( ).
A.90° B.180° C.360°
4.下面说法错误的是( )。
A.平行四边形有无数条高
B.有一组对边平行的四边形是梯形
C.用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形
5.下面每组中的3条线段能围成三角形的是( )。(单位:厘米)
A.2,2,3 B.2,1,3 C.2,5,7
6.下列说法正确的是( )。
A.直角三角形只有一条高
B.三个角都是钝角的三角形是钝角三角形
C.三个角都是锐角的三角形是锐角三角形
7.把正方形沿它的一条对角线对折可以得到两个( )。
A.等腰直角三角形 B.钝角三角形 C.直角三角形
8.一个三角形中,有一个角是75°,另外两个角可能是( )。
A.35°和60° B.45°和60° C.25°和90°
二、填空题
9.一个正五边形的一条边长是6厘米,它的周长是( )厘米,一个内角是( )度。
10.自行车车架一般设计成( )形,这是因为这种图形具有( )性。
11.两底角相等的梯形是( ),它有( )条高.
12.一个等腰三角形的一个底角是35°,它的顶角是( )°。如果它的顶角是40°,它的一个底角是( )°。
13.小红用一根15厘米长的铁丝围成了一个三角形,三角形的边长可能是( )厘米、( )厘米、( )厘米。(取整厘米数)
14.一个三角形的两个角分别是24°和32°,另一个角是( ),它是( )三角形。
15.平面图形镶嵌的条件:每个拼接点处,几个多边形的各内角之和为( ),且将( )的边重合.
16.看图填一填,∠1=( )°,树高( )米。这是根据( )三角形的特点推算的。
17.图中多边形的周长是( )厘米。
三、判断题
18.一个等腰三角形的一个底角是a°,顶角是(180-2a)°。( )
19.直角三角形中的一个锐角是40°,另一个锐角是50°。( )
20.等腰三角形的底角不一定是锐角. ( )
21.三角形的一个内角是108°,它一定是钝角三角形。( )
22.连接相对顶点的弧线把平行四边形分成了两部分,两部分的周长一样。( )
四、解答题
23.小强说姚明一步能走3米。结合如图,你觉得他说的对吗?
(1)我认为他说的( )。
(2)理由是:( )。
24.周晓梦同学星期天和弟弟在家里打造了一个别具一格的小花园,这个小花园是一个等腰梯形,其周长是98分米,上底和下底长度的和是58分米。这个小花园的一条腰长是多少?
25.(1)求出∠1、∠2的度数。
∠1=( )° ∠2=( )°
(2)分别画出三角形底边上的高,并判断是什么三角形。
( )三角形
( )三角形
26.王爷爷有一块三角形的菜地(如图)
(1)如果从顶点A处,穿过菜地修一条水渠到底边BC,怎样修最省力?请你在图上画出来。
(2)这块菜地有两个角是60°,那么它是一个什么三角形?如果在菜地的外面围上一圈篱笆,篱笆长多少米?
27.一个等腰梯形中,上底是5cm,下底是上底的3倍,腰比下底少8cm,求这个梯形的周长是多少?
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
※※请※※不※※要※※在※※装※※订※※线※※内※※答※※题※※
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
(
…………○…………内…………○…………装…………○…………订…………○…………线…………○…………
) (
学校:___________姓名:___________班级:___________考号:___________
) (
…………○…………外…………○…………装…………○…………订…………○…………线…………○…………
)
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.A
【详解】略
2.B
【分析】由题目可知,三角形为等腰直角三角形,所以三角形中一个角为直角,并且另外两个底角要相等,又三角形内角和为180°,减掉直角后的角度由两个底角平分。
【详解】两个底角和:180°-90°=90°
其中一个底角为:90°2=45°
故答案为:B
【点睛】掌握等腰直角三角形的角度特征,还要排除底角是直角的情况。
3.C
【详解】梯形的内角和是360°,将它剪成两个小梯形,每个小梯形的内角和是360°.
4.B
【分析】先对每个选项中的说法进行分析并判断,然后选择正确的一项即可。
A.从平行四边形一条边上的一点向对边引一条垂线,这点和垂足之间的线段叫做平行四边形的高,依此判断;
B.只有一组对边平行的四边形叫做梯形,依此判断;
C.等腰三角形的两腰相等,三角形3条边的关系是:任意两边的长度之和大于第三边,任意两边的长度之差小于第三边,依此判断即可。
【详解】A.平行四边形有无数条高,即原说法正确;
B.只有一组对边平行的四边形是梯形,即原说法错误;
C.2dm+2dm>3dm,3dm-2dm<2dm,2dm=2dm,即用长度分别是2dm、2dm、3dm的三根小棒可以围成一个等腰三角形,即原说法正确。
故答案为:B
【点睛】此题考查的是平行四边形的高,梯形的特点,以及三角形3条边的关系,应熟练掌握。
5.A
【分析】判断三角形能否构成,关键是看三条线段是否满足:任意两边之和是否大于第三边。但通常不需一一验证,其简便方法是将较短两边之和与较长边比较。
【详解】A、2+2>4,所以三条线段能围成三角形;
B、2+1=3,所以三条线段不能围成三角形;
C、2+5=7,所以三条线段不能围成三角形。
故答案为:A
【点睛】本题主要考查了三角形三边关系定理:三角形任意两边之和大于第三边。
6.C
【分析】从三角形的一个顶点到它的对边作一条垂线,顶点到垂足之间的线段叫做三角形的高;
有一个角是钝角的三角形就是钝角三角形;
三个角都是锐角的三角形是锐角三角形。
【详解】A.直角三角形只有一条高,不符合,三角形有三条高。
B.三个角都是钝角的三角形是钝角三角形,不符合,一个三角形中只有一个钝角。
C.三个角都是锐角的三角形是锐角三角形,符合。
故答案为:C
【点睛】明确三角形高的定义和三角形的分类是解决本题关键。
7.A
【分析】正方形的四条边都相等,四个角都是直角;等腰直角三角形中有一个角是直角,且两个底角的度数相等,两腰相等;有一个角是钝角的三角形是钝角三角形,有一个角是直角的三角形是直角三角形,依此画图并选择。
【详解】画图如下:
由此可知,把正方形沿它的一条对角线对折可以得到两个等腰直角三角形。
故答案为:A
8.B
【分析】利用三角形内角和等于180°,即可得解。
【详解】A.75°+35°+60°=170°,不符合条件
B.45°+60°+75°=180°,符合条件
C.25°+90°+75°=190°,不符合条件
故答案为:B。
9. 30 108
【分析】正五边形的5条边相等,5个角相等。正五边形的周长=边长×5,据此求出它的周长。正五边形的内角和是540度,一个内角是(540÷5)度。
【详解】6×5=30(厘米)
540÷5=108(度)
它的周长是30厘米,一个内角是108度。
【点睛】本题考查正五边形的周长和内角和,关键是熟记周长公式以及五边形的内角和为540度。
10. 三角 稳定
【分析】三角形具有稳定性。自行车的车架是三角形形状,自行车的行驶稳定也是由于三角形的稳定性的特征。在生活中,三角形的稳定性有着非常广泛的应用,如:篮球架上篮板的支架是三角形;电线杆的支架是三角形的;上述物体中的三角形都能使物体更加稳固。
【详解】自行车车架一般设计成三角形,这是因为这种图形具有稳定性。
11. 等腰梯形 无数
【详解】略
12. 110 70
【分析】等腰三角形的两个底角相等,则另一个底角是35°。根据三角形的内角和为180°可知,顶角是180°-35°-35°。若顶角是40°,一个底角是(180°-40°)÷2。
【详解】180°-35°-35°=110°
它的顶角是110°。
(180°-40°)÷2
=140°÷2
=70°
它的一个底角是70°。
【点睛】本题考查等腰三角形的特征和三角形的内角和,等腰三角形中,底角+底角+顶角=180°。
13. 7 5 3
【分析】三角形的三边关系为三角形的两边之和大于第三边,三角形的两边之差一定小于第三边;据此可知,三角形的周长为15厘米时,最长的边不超过8厘米,最大是7厘米。当最长边为7厘米时,其余两条边的长度和为8厘米,可能是5厘米和3厘米,据此解答。
【详解】5+3>7,5-3<7,则长7厘米、5厘米、3厘米的三根铁丝能围成一个三角形,即三角形的边长可能是7厘米、5厘米、3厘米。(答案不唯一)
【点睛】本题考查三角形的三边关系,关键是根据三角形的三边关系明确最长的边最大是7厘米。
14. 124° 钝角
【分析】根据三角形的内角度数和是180°,已知其他两个角的度数,要求另一个角的度数,用180°减去24°,再减去32°即可;根据计算出来的角的度数发现,有一个角是钝角,再根据有一个角是钝角的三角形是钝角三角形,据此解答。
【详解】
一个三角形的两个角分别是24°和32°,另一个角是(124°),它是(钝角)三角形。
【点睛】本题考查三角形的内角度数和以及钝角三角形的特征,熟练掌握并灵活运用。
15. 360° 相邻
【详解】由多边形镶嵌成平面图形的条件可知:(1)拼接在同一个点的各个角和恰好等于360°;(2)相邻的多边形有公共边.
16. 45 3.8 等腰
【分析】三角形的一个角是45度,树与地面垂直且于三角形一条边重合,根据三角形的内角和是180度即可算出角1度数,再根据三角形特点进行推测即可;
有两个角相等,两条边相等的三角形是等腰三角形。
【详解】180°-90°-45°
=90°-45°
=45°
即∠1=45°,树高3.8米。这是根据等腰三角形的特点推算的。
【点睛】明确等腰三角形的特征和三角形内角和是180度是解决本题关键。
17.14
【详解】(2+5)×2
=7×2
=14(厘米)
18.√
【分析】等腰三角形的两个底角相等,三角形的内角和为180°,所以顶角为180°减去两个底角的度数;据此解答。
【详解】根据分析:一个等腰三角形的一个底角是a°,顶角是(180-2a)°,原题说法正确。
故答案为:√
19.√
【分析】直角三角形中,两个锐角的和是90°,90°-其中一个锐角度数=另一个锐角度数,据此求解。
【详解】由分析可得,直角三角形中,一个锐角为40°,另一个锐角为90°-40°=50°
故答案为:√
【点睛】明确直角三角形三个角的特点以及三角形的内角和都为180°是解决本题的关键。
20.×
【详解】略
21.√
【分析】锐角三角形:三个角都小于90°;直角三角形:其中一个角等于90°;钝角三角形:有一个角大于90°。据此判断即可。
【详解】108°>90°
三角形的一个内角是108°,它一定是钝角三角形。原题说法正确。
故答案为:√
22.√
【分析】根据平行四边形的性质,平行四边形的对边相等,分别看分成的两部分的周长都有哪几部分围成,据此判断。
【详解】平行四边形对边相等,分成两部分的周长分别由平行四边形的一组对边和一条共同的弧围成,所以两部分的周长一样。
故答案为:√
【点睛】解答本题的关键是熟练掌握平行四边形的性质和周长的意义。
23.(1)错误
(2)因为三角形的两边之和大于第三边,而姚明的腿长1.3米,,所以姚明一步不能走3米。
【分析】先求出两条腿的长度之和,根据三角形的第三条边一定小于两边之和可知:姚明走一步的长度一定小于他两条腿的长度之和,据此解答。
【详解】(1)1.3+1.3=2.6(米)<3米
故姚明一步能走3米说法是错误的。
(2)因为三角形的两边之和大于第三边,而姚明的腿长1.3米,,所以姚明一步不能走3米。
【点睛】熟练掌握三角形的三边关系是解答本题的关键。
24.20分米
【分析】等腰梯形,其周长是98分米,上底和下底长度的和是58分米,可先用减法求出两条腰的长度之和。同时,在等腰梯形中,两腰的长度相等,所以用除法即可求出一条腰的长度。
【详解】(98-58)÷2
=40÷2
=20(分米)
答:这个小花园的一条腰长是20分米。
25.(1)59;137
(2)图见详解过程;锐角;钝角
【分析】(1)根据三角形的内角和是180°,用180°减去已知两个内角的和,即可求出∠1、∠2的度数,由此求解。
(2)经过三角形的顶点(与底相对的点)向对边(底)作垂线,顶点和垂足之间的线段就是三角形的一条高,用三角板的直角可以画出三角形的高;然后再根据三角形的分类进行解答。
【详解】(1)∠1=180°-82°-39°
=98°-39°
=59°
∠2=180°-17°-26°
=163°-26°
=137°
∠1=(59)° ∠2=(137)°
(2)如图所示:
(锐角)三角形
(钝角)三角形
【点睛】本题主要考查的知识点有:三角形内角和定理、作三角形的高以及三角形的(按角)分类。
26.(1)图见详解过程
(2)等边三角形;45米
【分析】(1)根据“垂线段最短”,过点A画BC边上的垂线段,沿这条垂线段修,可使修水渠最省力;
(2)三角形的内角和是180°,已知这个三角形有两个角是60°,那么另外一个角也是60°,所以这个三角形是等边三角形;等边三角形的三条边都相等,所以这个三角形的三边都是15米,用15乘3,即可求出所需篱笆的长度。
【详解】(1)从点A作BC边上的垂线段,这样修最省力。如图所示:
(2)180°-60°×2
=180°-120°
=60°
这块菜地有两个角是60°,那么它是等边三角形。
15×3=45(米)
答:篱笆长45米。
27.5×3=15 (cm) 15-8=7 (cm)
5+15+7×2=34 (cm)
答:这个梯形的周长是34 cm.
【详解】略
答案第1页,共2页
答案第1页,共2页
