西藏自治区拉萨市2024届高三下学期5月月考试题 数学(文)(PDF版含解析)
文档属性
| 名称 | 西藏自治区拉萨市2024届高三下学期5月月考试题 数学(文)(PDF版含解析) |

|
|
| 格式 | |||
| 文件大小 | 517.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 11:34:39 | ||
图片预览



文档简介
绝密★启用前
2024届高三 5月大联考(全国甲卷)
文科数学
本卷满分 150分,考试时间 120分钟.
注意事项:
1.答卷前,考生务必将自已的姓名 考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
一 选择题:本题共 12小题,每小题 5分,共 60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合M {x∣0 x 1 2},N {x∣ x 2 x 1 0},则M N ( )
A. 0,2 B. 0,3 C. 1,3 D. 1,3
2.已知 z 1 i是方程 z2 2az b 0 a,b R 的根,则 a b ( )
A.-3 B.-1 C.2 D.3
3.空气质量指数(Air Quality Index,简称AQI)等级表:
空气质量等
优 良 轻度污染 中度污染 重度污染 严重污染
级
空气质量指
数 0,50 50,100 100,150 150,200 200,300 300,
(AQI)
以下是某市 2024年 4月 1日至 22日空气质量指数分布的散点图,下列关于这 22天空气质量的描述,不正
确的是( )
A.空气质量为“良”的天数最多
B.空气质量为“优”和“良”的天数超过一半
C.17日空气质量为“重度污染”
D.该市这 22天空气质量越来越差
4.已知平面向量 a 1, 3 ,b 3,1 ,且 a b a ,则实数 的值为( )
2 3 3 1A. B. C. D. 3
3 2 2 3
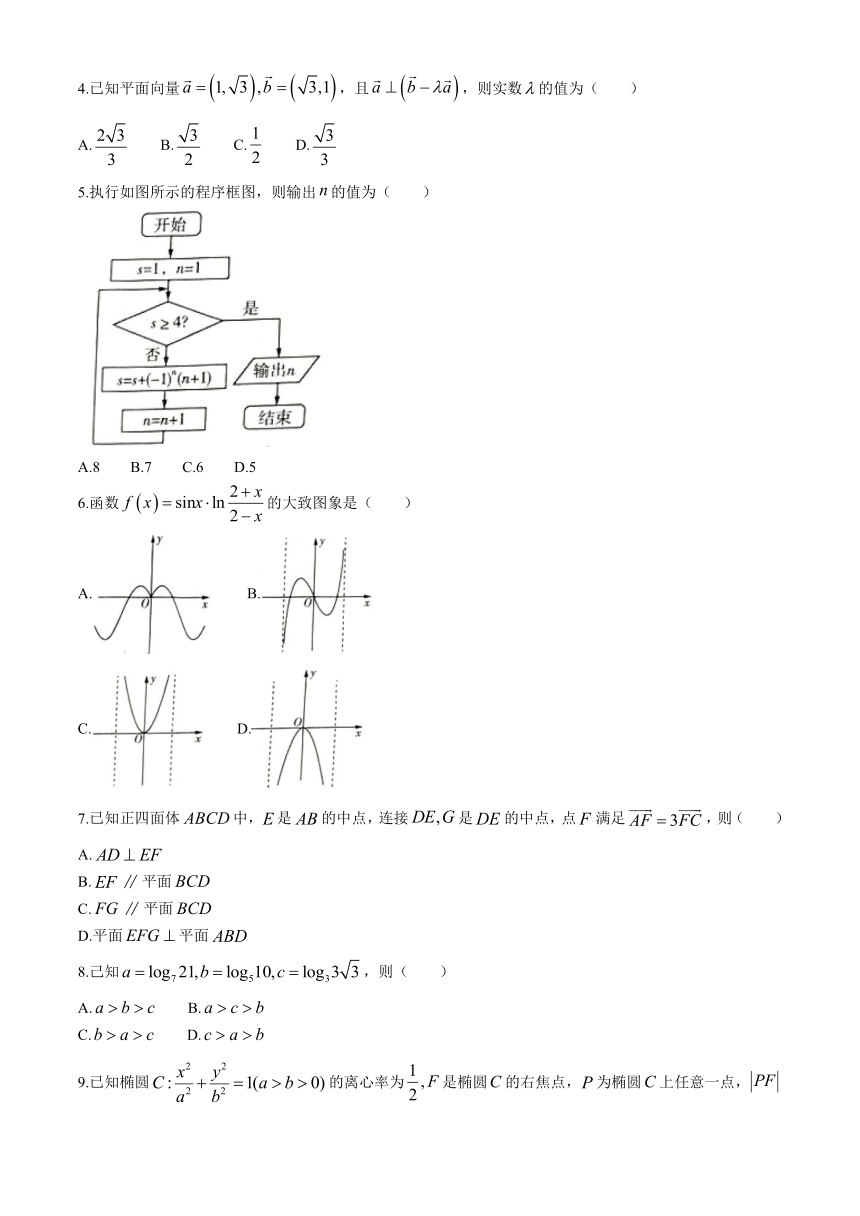
5.执行如图所示的程序框图,则输出 n的值为( )
A.8 B.7 C.6 D.5
6.函数 f x sinx ln 2 x 的大致图象是( )
2 x
A. B.
C. D.
7.已知正四面体 ABCD中,E是 AB的中点,连接DE,G是DE的中点,点F 满足 AF 3FC ,则( )
A. AD EF
B. EF∥平面 BCD
C. FG∥平面 BCD
D.平面 EFG 平面 ABD
8.己知 a log721,b log510,c log33 3,则( )
A. a b c B. a c b
C.b a c D. c a b
2
9. C : x y
2 1
已知椭圆 1(a b 0)的离心率为 ,F是椭圆C的右焦点,P为椭圆2 2 C上任意一点, PFa b 2
的最大值为3 2 .设点 A 2,1 ,则 PA PF 的最小值为( )
A. 4 2 3 B. 4 2 1 C. 4 2 3 D.6
10.已知等差数列 an 的公差为 d ,前 n项和为 Sn ,a1 5 .若 S1 4, S2 4, S3 4成等差数列,且
d 1,10 ,则 S4 ( )
A.12 B.21 C.32 D.56
11.已知函数 f x 2 sinx cosx,下列关于 f x 的描述,不正确的是( )
f 25 2A. π
8 2
B. f x 的最小正周期为 2π
C. f x 的图象关于直线 x 3π对称
D. f x 6π,13 π 在 上单调递增
2
12.已知圆锥 SO的母线长为6, AB是底面圆的直径,C为底面圆周上一点, AOC 120 ,当圆锥 SO的
体积最大时,直线 AC和 SB所成角的余弦值为( )
A. 2 B. 2 C. 5 D. 3
2 3 5 4
二 填空题:本题共 4小题,每小题 5分,共 20分.
13.已知函数 f x aex x,若曲线 y f x 在点 1, f 1 处的切线与直线 1 2e x y 1 0平行,
则实数a __________.
1
14.已知等比数列 an 的前 n项和为 Sn ,a2 ,a5 4 ,则 S3 __________.2
15.某企业钳工 车工和焊工三个车间分别推荐了 1名男员工和 1名女员工,供该企业工会从中选出 2名员工
参加全国技能比赛.若这 6名员工每人被选上的机会相等,则选出的 2人恰好是 1名男员工和 1名女员工,
且他们来自不同车间的概率为__________.
x2 y2
16.设双曲线C : 1(a 0,b 0)的左 右焦点分别为 F1,F2 , A为左顶点,过点 F1的直线与双曲线2 2 Ca b
的左 右两支分别交于点 N ,M(点M 在第一象限).若MF2 4NA,则双曲线C的离心率 e __________,
cos F1MF2 __________.(第一空 2分,第二空 3分)
三 解答题:共 0分.解答应写出文字说明 证明过程或演算步骤.第 17~21题为必考题,每个试
题考生都必须作答.第 22 23题为选考题,考生根据要求作答.
(一)必考题:共 60分.
17.(12分)
已知 ABC的内角 A,B,C a,b,c,C π的对边分别为 ,ab 4b 4ccosA .
6
(1)求b;
(2)若 c 3,求 ABC的面积.
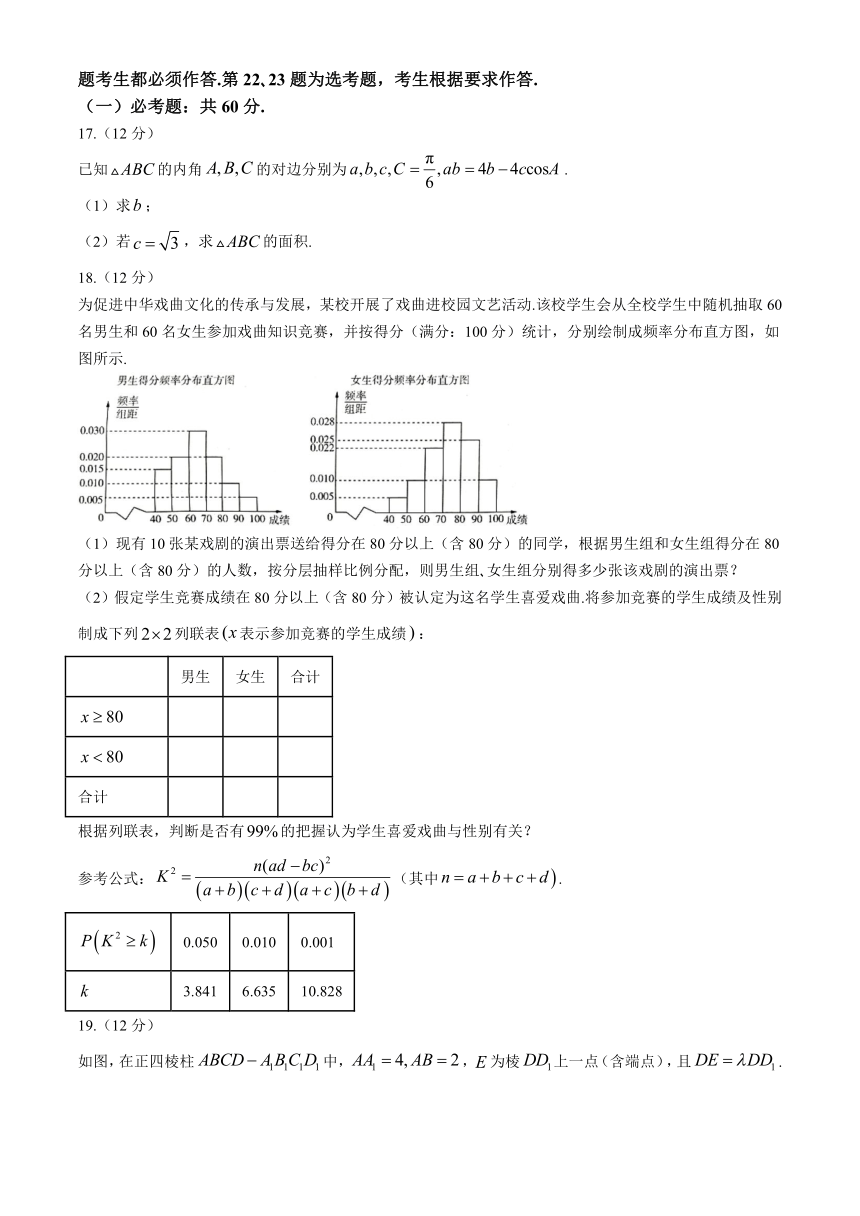
18.(12分)
为促进中华戏曲文化的传承与发展,某校开展了戏曲进校园文艺活动.该校学生会从全校学生中随机抽取 60
名男生和 60名女生参加戏曲知识竞赛,并按得分(满分:100分)统计,分别绘制成频率分布直方图,如
图所示.
(1)现有 10张某戏剧的演出票送给得分在 80分以上(含 80分)的同学,根据男生组和女生组得分在 80
分以上(含 80分)的人数,按分层抽样比例分配,则男生组 女生组分别得多少张该戏剧的演出票?
(2)假定学生竞赛成绩在 80分以上(含 80分)被认定为这名学生喜爱戏曲.将参加竞赛的学生成绩及性别
制成下列 2 2列联表 (x表示参加竞赛的学生成绩 ):
男生 女生 合计
x 80
x 80
合计
根据列联表,判断是否有99%的把握认为学生喜爱戏曲与性别有关?
2 n(ad bc)2
参考公式:K n a b c d a b c d (其中 .a c b d
P K 2 k 0.050 0.010 0.001
k 3.841 6.635 10.828
19.(12分)
如图,在正四棱柱 ABCD A1B1C1D1中,AA1 4, AB 2,E为棱DD1上一点(含端点),且DE DD1 .
(1)证明: AC B1E;
1(2)当 时,证明: B E 平面 ACE;
2 1
(3)设几何体 B1ACE的体积为V ,若V 3,5 ,求 的取值范围.
20.(12分)
己知函数 f x 1 x2 2lnx ax a R .
2
(1)讨论 f x 的单调性:
(2)若 f x 有两个极值点 x1, x2,求证: f x1 x2 3ln2 4 .
21.(12分)
已知抛物线C : y2 2px(p 0),准线 l与 x轴交于点M , A x0 , y0 为抛物线C上一点,AD l交 y轴于
点D .当 y0 4 2时,MA MD MF .
(1)求抛物线C的方程;
(2)设直线 AM 与抛物线C的另一交点为 B(点B在点 A,M 之间),过点 F 且垂直于 x轴的直线交 AM
于点 N .是否存在实数 ,使得 AM BN BM AN ?若存在,求出 的值;若不存在,请说明理由.
(二)选考题:共 10分.请考生在第 22 23题中任选一题作答.如果多做,则按所做的第一题计
分.
22.[选修 4-4:坐标系与参数方程](10分)
x a tcos
π
已知直线 l 4的参数方程为 ( t为参数,a R).以坐标原点O为极点, x轴正半轴为极轴建
y tsin π
4
立极坐标系,曲线C的极坐标方程为 2cos 2sin .
(1)写出直线 l的普通方程和曲线C的直角坐标方程;
π
(2)设 A,B是曲线C上的两点,且 AB 2 .若直线 l上存在点 P,使得 APB ,求 a的取值范围.
2
23.[选修 4-5:不等式选讲](10分)
设函数 f x 2 x 1 x a b a,b R .
(1)若 f 3 f 1 ,求实数 a的取值范围;
(2)当 a 5时,函数 f x 有两个零点 x1, x2 x1 x2 ,且满足 x1 x2 4,求实数b的值.
2024届高三 5月大联考(全国甲卷)
文科数学·全解全析及评分标准阅卷
注意事项:
1阅卷前请各学科教研组长,组织本学科改卷老师开会,强调改卷纪律,统一标准.
2请老师改卷前务必先做一遍试题,了解自己所改试题的答案 评分细则 答题角度后,再开始
改卷.
3.请老师认真批阅,不可出现漏改 错改现象,如果不小心漏改或错改了,可以点击回评按钮
重评.
4.成绩发布后,如果有学校反馈错评乱评,平台定位阅卷老师,进行通报批评.
5解答题要在学生的答案中找寻有用的文字说明 证明过程或演算步骤,合理即可给分.
6解答题不要只看结果,结果正确,但中间的文字说明 证明过程或演算步骤无法建立有效衔
接的,不能给满分;同样,结果错误,但正确写出相应的文字说明 证明过程或演算步骤应给
分,因第(1)问中结果算错,使后面最终结果出错(过程列式正确),不宜重复扣分.
7阅卷平台出现的相关问题,如果刷新页面重新登录未能解决,请将问题反馈给学校负责技术
的老师(或考试负责人),由其统一在技术 QQ群里反馈问题并协助解决.
一 选择题:本题共 12小题,每小题 5分,共 60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1 2 3 4 5 6 7 8 9 10 11 12
C A D B B C C B A C D A
1.C 【解析】由题意,知M {x∣1 x 3},N {x∣ 1 x 2},所以M N 1,3 .故选 C.
2.A 2【解析】由题意,得 (1 i) 2a 1 i b 0 ,即 2a b 2 2a i 0,所以 2a b 0,且
2 2a 0,解得a 1,b 2,所以 a b 3 .故选 A.
3.D 【解析】从该市 4月 1日至 22日空气质量指数分布的散点图可以看出,空气质量为“优”和“良”的天数
超过一半,且为“良”的天数最多;17日的空气质量指数位于 200,300 之间,属于“重度污染”,所以 A,B,
C都正确,而这 22天的空气质量有变化,不完全是越来越差,所以 D错误.故选 D.
4.B 【解析】由已知,得 a 2,a b 2 3,又 a b a ,所以 a b a 0,即 a b a2 0,
3
所以 2 3 4 0,解得 .故选 B.
2
5.B 【解析】执行程序框图,初始值 s 1,n 1,判断“否”,
第一次执行循环体: s 1,n 2,判断“否”;
第二次执行循环体: s 2,n 3,判断“否”;
第三次执行循环体: s 2,n 4,判断“否”;
第四次执行循环体: s 3,n 5,判断“否”;
第五次执行循环体: s 3,n 6,判断“否”;
第六次执行循环体: s 4,n 7,判断“是”,输出 n 7 .故选 B.
2 x
6.C 【解析】由 0,得 x 2,2 ,所以 f x 的定义域为 2,2 .又
2 x
f x sin x ln 2 x sinx ln 2 x sinx ln 2 x f x ,所以函数 f x 为偶函数,图2 x 2 x 2 x
2 x 4 2 x
象关于 y轴对称,故 B错误;因为 ln ln 1 ,所以当 x 0,2 时, ln 0,sinx 0,2 x 2 x 2 x
所以 f x 0,故 A,D错误.故选 C.
7.C 【解析】如图,连接DF,平面 EFG即平面DEF .由E是 AB的中点和 AF 3FC ,知EF与 BC相
交.对于A,因为四面体 ABCD为正四面体,所以 AD BC, DAB 60 .若 AD EF ,又 BC,EF 平
面 ABC,且 BC,EF 相交,所以 AD 平面 ABC .又 AB 平面 ABC,所以 AD AB,与 DAB 60
矛盾,所以A错误;
对于B,若 EF∥平面 BCD,由 EF 平面 ABC,平面 ABC 平面 BCD BC,得 BC∥ EF,与
BC,EF 相交矛盾,所以B错误;
对于C,由 AF 3FC ,知 A,F ,C三点共线,且 AF 3FC .取BE的中点M ,连接 FM ,GM ,所以
AM 3MB,所以MF∥ BC .又MF 平面 BCD,BC 平面 BCD,所以MF∥平面 BCD .又G 是
DE的中点,所以MG∥ BD .又MG 平面 BCD,BD 平面 BCD,所以MG∥平面 BCD .因为
MG,MF 平面MFG,且MG MF M ,所以平面MFG∥平面 BCD .因为 FG 平面MFG,所以
FG∥平面 BCD,所以C正确;
对于D,连接CE,因为 E是 AB的中点,所以DE AB .若平面EFG 平面 ABD,又平面 EFG 平
面 ABD DE,所以 AB 平面 EFG .又EF 平面 EFG,所以 AB EF,与CE AB矛盾,所以D
错误.故选 C.
8.B 【解析】由已知,得
3
c log33 3 log 32
3
3 ,a log721 log7 3 7 1 log73 1
1 3
log7 7 1 ,2 2 2
b log 1 3510 log5 2 5 1 log52 1 log5 5 1 ,所以a c b .故选 B.2 2
c 1
9.A 【解析】设椭圆C的半焦距为c,由题意,得 ,a c 3 2 ,所以 c 2,a 2 2 .设椭圆C的
a 2
左焦点为 F ,则 F 2,0 ,
所以 PA PF PA 2a PF 2a PA PF 2a AF 4 2 3 .故选 A.
10.C 【解析】因为数列 an 的公差为 d(1 d 10),S1 5,S2 10 d ,S3 15 3d,所以 S1 4 3,
S2 4 14 d , S3 4 19 3d .由题意,知 2 S2 4 S1 4 S3 4 ,即
2 14 d 3 19 3d ,整理,得 d 2 52d 100 0,解得 d 2或 d 50(舍去).当 d 2时,
4 3 4 4 1S4 4a1 d 4 5
2 32 .故选 C.
2 2
f 25 π 2 sin 3π 1 1 π π π 211.D 【解析】 π
cos
3π π
2sin cos sin ,所以 A正
8 8 8 8 8 4 2
sin2x sinx 0确; f x 2 sinx cosx ,画出函数 f x 的部分简图,如图:
sin2x(sinx 0)
由图象,知 f x 的最小正周期为 2π,所以B正确;
又 f x 的图象关于直线 x π对称,由周期性,知 f x 的图象关于直线 x 3π对称,所以 C正确;
因为 f x 在 0,
π π π
上单调递增,在 , 上单调递减,由 f x
13
的周期性,知当 x
4 4 2
6π, π 时,f x
2
在 6π,
25 π 25 13
4
上单调递增,在 π, π 上单调递减,所以 D错误.故选 D.
4 2
12.A 【解析】如图,圆锥 SO的母线长 l 6 .设圆锥 SO的底面半径为 r,高为 h,则 r2 h2 36,圆锥
V 1 1SO的体积 πr 2h πh 36 h2 1 π 36h h33 3 3 .
令 f h 36h h3(h 0) 2,则 f h 36 3h 3 h 2 3 h 2 3 .令 f h 0,得 h 2 3或
h 2 3 .因为 h 0,所以 f h 在 0,2 3 上单调递增,在 2 3, 上单调递减,
所以当h 2 3时, f h 取得最大值,此时 r 2 24, r 2 6 .
因为 AOC 120 ,所以 AC 3r 6 2 .
延长CO交 O于点D,连接 AD,BD,SD,则四边形 ACBD是平行四边形,所以
BD∥ AC,BD AC 6 2 ,
所以直线 AC与 SB所成的角为 SBD或其补角.
在等腰三角形 SBD中, SB SD 6,BD 6 2 ,所以 cos SBD 2 ,
2
2
所以直线 AC与 SB所成角的余弦值为 .故选 A.
2
二 填空题:本题共 4小题,每小题 5分,共 20分.
13.2 【解析】因为 f x aex 1,所以 f 1 ae 1 2e 1,所以 a 2 .故填 2.
7 1 1
14. 【解析】设等比数列 an 的公比为 q 3,由 a2 ,a5 4 a2q ,得 q3 8,所以 q 2,所以 a1 ,4 2 4
a 1 q3 7
S 73
1 .故填 .
1 q 4 4
2
15. 【解析】设 3名男员工分别为 A,B,C,3名女员工分别为 X ,Y ,Z,其情况如下表:
5
钳工 车工 焊工
男员工 A B C
女员工 X Y Z
则从 6人中选出 2人的基本事件有 A,B , A,C , A, X , A,Y , A,Z , B,C , B, X , B,Y ,
B,Z , C, X , C,Y , C,Z , X ,Y , X ,Z , Y ,Z ,共 15个,其中满足条件的基本事件有 A,Y ,
A,Z , B, X , B,Z , C, X , C,Y ,共 6个,所以选出的 2人恰好是 1名男员工和 1名女员工,且他
6 2 2
们来自不同车间的概率 P .故填 .
15 5 5
7
16.2; 【解析】由题意,知 A a,0 ,设双曲线C的焦距为 2c,则 F1 c,0 ,F2 c,0 .15
由MF2 4NA,得MF2∥ NA,且 MF2 4 NA ,所以 F2A 3 AF1 , MN 3 NF1 ,所以
c a 3 c a ,即 c 2a,所以双曲线C的离心率 e 2 .
如图,连接NF2,设 MF2 m,则
MF 2a 11 m, NF1 2a m , NF 2a
1
2 2a
1
m 10a m .在 F1NF2和 F1MF2中,由余4 4 4
弦定理的推论,得
1 (2a m)2 16a2 1 (10a m)2 2 2 2
cos NFF 16 16 (2a m) 16a m 51 2 1 ,化简整理,得m a,2 (2a m) 4a 2 (2a m) 4a 2
4
所以在 F1MF2中,由余弦定理的推论,得
5 2 2 5 2
(2a m)2 m2
2a a
(4a)2 2
a (4a)
cos F 2 71MF2 .2 2a m m 2 2a 5 5 a a
15
2 2
故填 2; 7 .
15
三 解答题:共 70分.解答应写出文字说明 证明过程或演算步骤.第 17~21题为必考题,每个试
题考生都必须作答.第 22 23题为选考题,考生根据要求作答.
(一)必考题:共 60分.
17.(12分)
【解析】(1)由 ab 4b 4ccosA和正弦定理,
得bsinA 4sinB 4sinCcosA
4sin A C 4sinCcosA
4sinAcosC .
因为 sinA 0,所以b 4cosC .
π
因为C ,所以
6 b 2 3
.
(2 2 2 2)由余弦定理,得 c b a 2abcos
π
,
6
所以12 a2 6a 3,
即 (a 3)2 0,解得 a 3
S 1 absinC 1所以 ABC的面积 3 2 3 sin
π
2 2 6
3 3
.
2
18.(12分)
【解析】(1)由频率分布直方图,
知男生组得分在 80分以上(含 80分)的有 0.010 0.005 10 60 9(人),
女生组得分在 80分以上(含 80分)的有 0.025 0.010 10 60 21(人),
9 21
男生占比为 ,女生占比为 ,
9 21 9 21
9
所以男生组分得票数为 10 3,
9 21
21
女生组分得票数为 10 7,
9 21
所以男生组 女生组分别得 3张和 7张该戏剧的演出票.
(2)由(1),知男生组得分在 80分以上(含 80分)的有 9人,80分以下的有 51人;女生组得分在 80
分以上(含 80分)的有 21人,80分以下的有 39人,
所以得如下2 2列联表:
男生 女生 合计
x 80 9 21 30
x 80 51 39 90
合计 60 60 120
K 2 120 (9 39 21 51)
2
根据列联表中数据计算,得
60 60 30 90
32
6.4
5
6.635,
根据临界值表,知没有99%的把握认为学生喜爱戏曲与性别有关.
19.(12分)
【解析】(1)如图,连接 BD,B1D1 .因为 ABCD A1B1C1D1是正四棱柱,所以底面 ABCD为正方形,
且BB1 平面 ABCD,所以 AC BD .又 AC 平面 ABCD,所以 AC BB1 .
又BD,BB1 平面 BDD1B1,BD BB1 B,所以 AC 平面 BDD1B1 .
又B1E 平面 BDD1B1,所以 AC B1E .
(2)当
1
时, E为DD
1 1
1的中点,所以D1E DE DD1 AA1 2,2 2 2
所以 AE 2 2,B1E D1E
2 D1B
2
1 2 3 .
又 AB1 2 5,所以 AE
2 B1E
2 AB21 ,所以 AE B1E .
由(1)知, AC B1E .
因为 AC, AE 平面 ACE, AC AE A,所以B1E 平面 ACE .
(3)因为 E为棱DD1上一点(含端点),且DE DD1,所以 0,1 .
又 AC 2 2,
所以
V V V V 16 8 8 8 A BDEB 1 C BDEB 1 E ACD VB ABC 2VA BDEB V V 1 1 .1 1 E ACD B1 ABC 3 3 3 3
因为V 3,5 ,所以3 8 1 5 ,
3
1 7 1 7
解得 ,即 的取值范围是 , .
8 8 8 8
20.(12分)
2
【解析】(1) f x 的定义域为 0, , f x x 2 x ax 2 a .
x x
①若 a 0,则 f x 0,所以 f x 在 0, 上单调递增;
②若 a 0,令 x2 ax 2 0,此时Δ a2 8,
i)当Δ a2 8 0,即0 a 2 2 时, f x 0,所以 f x 在 0, 上单调递增;
ii)当Δ a2 8 0,即 a 2 2时,
2 2
方程 x2 ax 2 0 x a a 8 , x a a 8的两个实数根为 ,且0 x3 x3 4,2 4 2
当 x 0, x3 或 x x4 , 时, f x 0;当 x x3 , x4 时, f x 0,
所以 f x 在 x3, x4 上单调递减,在 0, x3 , x4 , 上单调递增.
综上,当 a 2 2时, f x 在 0, 上单调递增;
f x 0, a a
2 8 a a2 8
当 a 2 2时, 在 , , 上单调递增,
2 2
a a2 8 a a2 8
在 , 2 2
上单调递减.
(2) f x 有两个极值点 x1, x2,结合(1),知 a 2 2,且 x1, x2是方程 x2 ax 2 0的两个实数根,
所以 x1 x2 a, x1x2 2,
所以 f x1 x2 f a 2lna
1
a 2 .
2
1 2
令 g a 2lna a 2(a 2 2) a 2 a 2 ,则
2 g a
2 a 2 a .
a a a
因为 a 2 2,所以 g a 0,所以 g a 在 2 2, 上单调递减,
所以 g a g 2 2 3ln2 4,即 f x1 x2 3ln2 4 .
21.(12分)
【解析】(1)因为当 y0 4 2时,MA MD MF ,所以四边形MFAD为平行四边形,
所以 AD MF p,即 x0 p,所以 A p, 4 2 ,
将 A p, 4 2 代入 y2 2px,得32 2p2,
解得 p 4,(4分 )
所以抛物线C的方程为 y2 8x .
(2)如图,由题意,得M 2,0 .设直线 AM 的方程为 x my 2 m 4 0 ,B x1, y
1 ,则 N 2,m
.
y2 8x
由 ,得 y2 8my 16 0,Δ 64m2 64 0,所以 y y
x my 2 0 1
8m, y0 y1 16 .
AM BN
假设存在实数 ,使得 AM BN BM AN ,即 .
BM AN
| AM | y0 , | BN |
2 x
1
my1 4
由题意,知 ,
| BM | y1 | AN | x0 2 my0 4
| AM | | BN | y my
0 1
4 my y
0 1
4y0
所以 .
| BM | | AN | y1 my0 4 my0y1 4y1
又 y0 y1 8m, y0 y1 16,
| AM | | BN | my0 y1 4y0 16m 4y0 16m 4y
所以
0 1
| BM | | AN | my0y1 4y1 16m 4 8m y0 4y
,
0 16m
即存在实数 1,使得 AM BN BM AN 成立.
(二)选考题:共 10分.请考生在第 22 23题中任选一题作答.如果多做,则按所做的第一题计
分.
22.[选修 4-4:坐标系与参数方程](10分)
x a
π
tcos
4
【解析】(1)由 ( t为参数, a R ,消去参数 t,得直线 l的普通方程为 x y a 0 .
y π tsin
4
由 2cos 2sin ,得 2 2 cos 2 sin .
将 x cos , y sin 代入 2 2 cos 2 sin ,
得曲线C的直角坐标方程为 x2 y2 2x 2y 0,即 (x 1)2 (y 1)2 2 .
(2)由(1),知曲线C表示圆心为 1,1 ,半径为 2 的圆, l为一条直线.
设弦 AB的中点为M ,
因为 AB 2,所以 CM 1,
所以点M 在以C 1,1 为圆心,1为半径的圆上.
又 APB π ,所以 PM 1,所以点 P在以M 为圆心,1为半径的圆上.
2
依题意,直线 l上存在点 P,使得 PC 2,
a
所以点C到直线 l的距离 d 2,即 d 2,
2
所以 2 2 a 2 2 ,
所以 a的取值范围为 2 2,2 2 .
23.[选修 4-5:不等式选讲](10分)
【解析】(1)若 f 3 f 1 ,则 2 3 1 3 a b 2 1 1 1 a b,
即 3 a 1 a ,
两边平方,得9 6a a2 a2 2a 1,即8a 8,
解得 a 1,所以实数 a的取值范围是 , 1 .
x 7 b x 1
(2)因为 a 5,所以函数 f x 2 x 1 x 5 b 3x 3 b( 1 x 5) .
x 7 b x 5
观察图象(图略),知函数 f x 2 x 1 x 5 b在 , 1 上单调递减,在 1,5 和 5, 上单
调递增,且 f 1 6 b, f 5 12 b,
所以①当 12 b 6时, x 7 b, x
3 b 18 2b
1 2 .由 x1 x2 4,解得b 3;3 3
②当b 12时, x1 7 b, x2 7 b,此时 x1 x2 14,与 x1 x2 4矛盾,舍去.
综上,实数b的值为 3.
2024届高三 5月大联考(全国甲卷)
文科数学
本卷满分 150分,考试时间 120分钟.
注意事项:
1.答卷前,考生务必将自已的姓名 考生号等填写在答题卡和试卷指定位置上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,
用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上
无效.
3.考试结束后,将本试卷和答题卡一并交回.
一 选择题:本题共 12小题,每小题 5分,共 60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知集合M {x∣0 x 1 2},N {x∣ x 2 x 1 0},则M N ( )
A. 0,2 B. 0,3 C. 1,3 D. 1,3
2.已知 z 1 i是方程 z2 2az b 0 a,b R 的根,则 a b ( )
A.-3 B.-1 C.2 D.3
3.空气质量指数(Air Quality Index,简称AQI)等级表:
空气质量等
优 良 轻度污染 中度污染 重度污染 严重污染
级
空气质量指
数 0,50 50,100 100,150 150,200 200,300 300,
(AQI)
以下是某市 2024年 4月 1日至 22日空气质量指数分布的散点图,下列关于这 22天空气质量的描述,不正
确的是( )
A.空气质量为“良”的天数最多
B.空气质量为“优”和“良”的天数超过一半
C.17日空气质量为“重度污染”
D.该市这 22天空气质量越来越差
4.已知平面向量 a 1, 3 ,b 3,1 ,且 a b a ,则实数 的值为( )
2 3 3 1A. B. C. D. 3
3 2 2 3
5.执行如图所示的程序框图,则输出 n的值为( )
A.8 B.7 C.6 D.5
6.函数 f x sinx ln 2 x 的大致图象是( )
2 x
A. B.
C. D.
7.已知正四面体 ABCD中,E是 AB的中点,连接DE,G是DE的中点,点F 满足 AF 3FC ,则( )
A. AD EF
B. EF∥平面 BCD
C. FG∥平面 BCD
D.平面 EFG 平面 ABD
8.己知 a log721,b log510,c log33 3,则( )
A. a b c B. a c b
C.b a c D. c a b
2
9. C : x y
2 1
已知椭圆 1(a b 0)的离心率为 ,F是椭圆C的右焦点,P为椭圆2 2 C上任意一点, PFa b 2
的最大值为3 2 .设点 A 2,1 ,则 PA PF 的最小值为( )
A. 4 2 3 B. 4 2 1 C. 4 2 3 D.6
10.已知等差数列 an 的公差为 d ,前 n项和为 Sn ,a1 5 .若 S1 4, S2 4, S3 4成等差数列,且
d 1,10 ,则 S4 ( )
A.12 B.21 C.32 D.56
11.已知函数 f x 2 sinx cosx,下列关于 f x 的描述,不正确的是( )
f 25 2A. π
8 2
B. f x 的最小正周期为 2π
C. f x 的图象关于直线 x 3π对称
D. f x 6π,13 π 在 上单调递增
2
12.已知圆锥 SO的母线长为6, AB是底面圆的直径,C为底面圆周上一点, AOC 120 ,当圆锥 SO的
体积最大时,直线 AC和 SB所成角的余弦值为( )
A. 2 B. 2 C. 5 D. 3
2 3 5 4
二 填空题:本题共 4小题,每小题 5分,共 20分.
13.已知函数 f x aex x,若曲线 y f x 在点 1, f 1 处的切线与直线 1 2e x y 1 0平行,
则实数a __________.
1
14.已知等比数列 an 的前 n项和为 Sn ,a2 ,a5 4 ,则 S3 __________.2
15.某企业钳工 车工和焊工三个车间分别推荐了 1名男员工和 1名女员工,供该企业工会从中选出 2名员工
参加全国技能比赛.若这 6名员工每人被选上的机会相等,则选出的 2人恰好是 1名男员工和 1名女员工,
且他们来自不同车间的概率为__________.
x2 y2
16.设双曲线C : 1(a 0,b 0)的左 右焦点分别为 F1,F2 , A为左顶点,过点 F1的直线与双曲线2 2 Ca b
的左 右两支分别交于点 N ,M(点M 在第一象限).若MF2 4NA,则双曲线C的离心率 e __________,
cos F1MF2 __________.(第一空 2分,第二空 3分)
三 解答题:共 0分.解答应写出文字说明 证明过程或演算步骤.第 17~21题为必考题,每个试
题考生都必须作答.第 22 23题为选考题,考生根据要求作答.
(一)必考题:共 60分.
17.(12分)
已知 ABC的内角 A,B,C a,b,c,C π的对边分别为 ,ab 4b 4ccosA .
6
(1)求b;
(2)若 c 3,求 ABC的面积.
18.(12分)
为促进中华戏曲文化的传承与发展,某校开展了戏曲进校园文艺活动.该校学生会从全校学生中随机抽取 60
名男生和 60名女生参加戏曲知识竞赛,并按得分(满分:100分)统计,分别绘制成频率分布直方图,如
图所示.
(1)现有 10张某戏剧的演出票送给得分在 80分以上(含 80分)的同学,根据男生组和女生组得分在 80
分以上(含 80分)的人数,按分层抽样比例分配,则男生组 女生组分别得多少张该戏剧的演出票?
(2)假定学生竞赛成绩在 80分以上(含 80分)被认定为这名学生喜爱戏曲.将参加竞赛的学生成绩及性别
制成下列 2 2列联表 (x表示参加竞赛的学生成绩 ):
男生 女生 合计
x 80
x 80
合计
根据列联表,判断是否有99%的把握认为学生喜爱戏曲与性别有关?
2 n(ad bc)2
参考公式:K n a b c d a b c d (其中 .a c b d
P K 2 k 0.050 0.010 0.001
k 3.841 6.635 10.828
19.(12分)
如图,在正四棱柱 ABCD A1B1C1D1中,AA1 4, AB 2,E为棱DD1上一点(含端点),且DE DD1 .
(1)证明: AC B1E;
1(2)当 时,证明: B E 平面 ACE;
2 1
(3)设几何体 B1ACE的体积为V ,若V 3,5 ,求 的取值范围.
20.(12分)
己知函数 f x 1 x2 2lnx ax a R .
2
(1)讨论 f x 的单调性:
(2)若 f x 有两个极值点 x1, x2,求证: f x1 x2 3ln2 4 .
21.(12分)
已知抛物线C : y2 2px(p 0),准线 l与 x轴交于点M , A x0 , y0 为抛物线C上一点,AD l交 y轴于
点D .当 y0 4 2时,MA MD MF .
(1)求抛物线C的方程;
(2)设直线 AM 与抛物线C的另一交点为 B(点B在点 A,M 之间),过点 F 且垂直于 x轴的直线交 AM
于点 N .是否存在实数 ,使得 AM BN BM AN ?若存在,求出 的值;若不存在,请说明理由.
(二)选考题:共 10分.请考生在第 22 23题中任选一题作答.如果多做,则按所做的第一题计
分.
22.[选修 4-4:坐标系与参数方程](10分)
x a tcos
π
已知直线 l 4的参数方程为 ( t为参数,a R).以坐标原点O为极点, x轴正半轴为极轴建
y tsin π
4
立极坐标系,曲线C的极坐标方程为 2cos 2sin .
(1)写出直线 l的普通方程和曲线C的直角坐标方程;
π
(2)设 A,B是曲线C上的两点,且 AB 2 .若直线 l上存在点 P,使得 APB ,求 a的取值范围.
2
23.[选修 4-5:不等式选讲](10分)
设函数 f x 2 x 1 x a b a,b R .
(1)若 f 3 f 1 ,求实数 a的取值范围;
(2)当 a 5时,函数 f x 有两个零点 x1, x2 x1 x2 ,且满足 x1 x2 4,求实数b的值.
2024届高三 5月大联考(全国甲卷)
文科数学·全解全析及评分标准阅卷
注意事项:
1阅卷前请各学科教研组长,组织本学科改卷老师开会,强调改卷纪律,统一标准.
2请老师改卷前务必先做一遍试题,了解自己所改试题的答案 评分细则 答题角度后,再开始
改卷.
3.请老师认真批阅,不可出现漏改 错改现象,如果不小心漏改或错改了,可以点击回评按钮
重评.
4.成绩发布后,如果有学校反馈错评乱评,平台定位阅卷老师,进行通报批评.
5解答题要在学生的答案中找寻有用的文字说明 证明过程或演算步骤,合理即可给分.
6解答题不要只看结果,结果正确,但中间的文字说明 证明过程或演算步骤无法建立有效衔
接的,不能给满分;同样,结果错误,但正确写出相应的文字说明 证明过程或演算步骤应给
分,因第(1)问中结果算错,使后面最终结果出错(过程列式正确),不宜重复扣分.
7阅卷平台出现的相关问题,如果刷新页面重新登录未能解决,请将问题反馈给学校负责技术
的老师(或考试负责人),由其统一在技术 QQ群里反馈问题并协助解决.
一 选择题:本题共 12小题,每小题 5分,共 60分.在每小题给出的四个选项中,只有一项是
符合题目要求的.
1 2 3 4 5 6 7 8 9 10 11 12
C A D B B C C B A C D A
1.C 【解析】由题意,知M {x∣1 x 3},N {x∣ 1 x 2},所以M N 1,3 .故选 C.
2.A 2【解析】由题意,得 (1 i) 2a 1 i b 0 ,即 2a b 2 2a i 0,所以 2a b 0,且
2 2a 0,解得a 1,b 2,所以 a b 3 .故选 A.
3.D 【解析】从该市 4月 1日至 22日空气质量指数分布的散点图可以看出,空气质量为“优”和“良”的天数
超过一半,且为“良”的天数最多;17日的空气质量指数位于 200,300 之间,属于“重度污染”,所以 A,B,
C都正确,而这 22天的空气质量有变化,不完全是越来越差,所以 D错误.故选 D.
4.B 【解析】由已知,得 a 2,a b 2 3,又 a b a ,所以 a b a 0,即 a b a2 0,
3
所以 2 3 4 0,解得 .故选 B.
2
5.B 【解析】执行程序框图,初始值 s 1,n 1,判断“否”,
第一次执行循环体: s 1,n 2,判断“否”;
第二次执行循环体: s 2,n 3,判断“否”;
第三次执行循环体: s 2,n 4,判断“否”;
第四次执行循环体: s 3,n 5,判断“否”;
第五次执行循环体: s 3,n 6,判断“否”;
第六次执行循环体: s 4,n 7,判断“是”,输出 n 7 .故选 B.
2 x
6.C 【解析】由 0,得 x 2,2 ,所以 f x 的定义域为 2,2 .又
2 x
f x sin x ln 2 x sinx ln 2 x sinx ln 2 x f x ,所以函数 f x 为偶函数,图2 x 2 x 2 x
2 x 4 2 x
象关于 y轴对称,故 B错误;因为 ln ln 1 ,所以当 x 0,2 时, ln 0,sinx 0,2 x 2 x 2 x
所以 f x 0,故 A,D错误.故选 C.
7.C 【解析】如图,连接DF,平面 EFG即平面DEF .由E是 AB的中点和 AF 3FC ,知EF与 BC相
交.对于A,因为四面体 ABCD为正四面体,所以 AD BC, DAB 60 .若 AD EF ,又 BC,EF 平
面 ABC,且 BC,EF 相交,所以 AD 平面 ABC .又 AB 平面 ABC,所以 AD AB,与 DAB 60
矛盾,所以A错误;
对于B,若 EF∥平面 BCD,由 EF 平面 ABC,平面 ABC 平面 BCD BC,得 BC∥ EF,与
BC,EF 相交矛盾,所以B错误;
对于C,由 AF 3FC ,知 A,F ,C三点共线,且 AF 3FC .取BE的中点M ,连接 FM ,GM ,所以
AM 3MB,所以MF∥ BC .又MF 平面 BCD,BC 平面 BCD,所以MF∥平面 BCD .又G 是
DE的中点,所以MG∥ BD .又MG 平面 BCD,BD 平面 BCD,所以MG∥平面 BCD .因为
MG,MF 平面MFG,且MG MF M ,所以平面MFG∥平面 BCD .因为 FG 平面MFG,所以
FG∥平面 BCD,所以C正确;
对于D,连接CE,因为 E是 AB的中点,所以DE AB .若平面EFG 平面 ABD,又平面 EFG 平
面 ABD DE,所以 AB 平面 EFG .又EF 平面 EFG,所以 AB EF,与CE AB矛盾,所以D
错误.故选 C.
8.B 【解析】由已知,得
3
c log33 3 log 32
3
3 ,a log721 log7 3 7 1 log73 1
1 3
log7 7 1 ,2 2 2
b log 1 3510 log5 2 5 1 log52 1 log5 5 1 ,所以a c b .故选 B.2 2
c 1
9.A 【解析】设椭圆C的半焦距为c,由题意,得 ,a c 3 2 ,所以 c 2,a 2 2 .设椭圆C的
a 2
左焦点为 F ,则 F 2,0 ,
所以 PA PF PA 2a PF 2a PA PF 2a AF 4 2 3 .故选 A.
10.C 【解析】因为数列 an 的公差为 d(1 d 10),S1 5,S2 10 d ,S3 15 3d,所以 S1 4 3,
S2 4 14 d , S3 4 19 3d .由题意,知 2 S2 4 S1 4 S3 4 ,即
2 14 d 3 19 3d ,整理,得 d 2 52d 100 0,解得 d 2或 d 50(舍去).当 d 2时,
4 3 4 4 1S4 4a1 d 4 5
2 32 .故选 C.
2 2
f 25 π 2 sin 3π 1 1 π π π 211.D 【解析】 π
cos
3π π
2sin cos sin ,所以 A正
8 8 8 8 8 4 2
sin2x sinx 0确; f x 2 sinx cosx ,画出函数 f x 的部分简图,如图:
sin2x(sinx 0)
由图象,知 f x 的最小正周期为 2π,所以B正确;
又 f x 的图象关于直线 x π对称,由周期性,知 f x 的图象关于直线 x 3π对称,所以 C正确;
因为 f x 在 0,
π π π
上单调递增,在 , 上单调递减,由 f x
13
的周期性,知当 x
4 4 2
6π, π 时,f x
2
在 6π,
25 π 25 13
4
上单调递增,在 π, π 上单调递减,所以 D错误.故选 D.
4 2
12.A 【解析】如图,圆锥 SO的母线长 l 6 .设圆锥 SO的底面半径为 r,高为 h,则 r2 h2 36,圆锥
V 1 1SO的体积 πr 2h πh 36 h2 1 π 36h h33 3 3 .
令 f h 36h h3(h 0) 2,则 f h 36 3h 3 h 2 3 h 2 3 .令 f h 0,得 h 2 3或
h 2 3 .因为 h 0,所以 f h 在 0,2 3 上单调递增,在 2 3, 上单调递减,
所以当h 2 3时, f h 取得最大值,此时 r 2 24, r 2 6 .
因为 AOC 120 ,所以 AC 3r 6 2 .
延长CO交 O于点D,连接 AD,BD,SD,则四边形 ACBD是平行四边形,所以
BD∥ AC,BD AC 6 2 ,
所以直线 AC与 SB所成的角为 SBD或其补角.
在等腰三角形 SBD中, SB SD 6,BD 6 2 ,所以 cos SBD 2 ,
2
2
所以直线 AC与 SB所成角的余弦值为 .故选 A.
2
二 填空题:本题共 4小题,每小题 5分,共 20分.
13.2 【解析】因为 f x aex 1,所以 f 1 ae 1 2e 1,所以 a 2 .故填 2.
7 1 1
14. 【解析】设等比数列 an 的公比为 q 3,由 a2 ,a5 4 a2q ,得 q3 8,所以 q 2,所以 a1 ,4 2 4
a 1 q3 7
S 73
1 .故填 .
1 q 4 4
2
15. 【解析】设 3名男员工分别为 A,B,C,3名女员工分别为 X ,Y ,Z,其情况如下表:
5
钳工 车工 焊工
男员工 A B C
女员工 X Y Z
则从 6人中选出 2人的基本事件有 A,B , A,C , A, X , A,Y , A,Z , B,C , B, X , B,Y ,
B,Z , C, X , C,Y , C,Z , X ,Y , X ,Z , Y ,Z ,共 15个,其中满足条件的基本事件有 A,Y ,
A,Z , B, X , B,Z , C, X , C,Y ,共 6个,所以选出的 2人恰好是 1名男员工和 1名女员工,且他
6 2 2
们来自不同车间的概率 P .故填 .
15 5 5
7
16.2; 【解析】由题意,知 A a,0 ,设双曲线C的焦距为 2c,则 F1 c,0 ,F2 c,0 .15
由MF2 4NA,得MF2∥ NA,且 MF2 4 NA ,所以 F2A 3 AF1 , MN 3 NF1 ,所以
c a 3 c a ,即 c 2a,所以双曲线C的离心率 e 2 .
如图,连接NF2,设 MF2 m,则
MF 2a 11 m, NF1 2a m , NF 2a
1
2 2a
1
m 10a m .在 F1NF2和 F1MF2中,由余4 4 4
弦定理的推论,得
1 (2a m)2 16a2 1 (10a m)2 2 2 2
cos NFF 16 16 (2a m) 16a m 51 2 1 ,化简整理,得m a,2 (2a m) 4a 2 (2a m) 4a 2
4
所以在 F1MF2中,由余弦定理的推论,得
5 2 2 5 2
(2a m)2 m2
2a a
(4a)2 2
a (4a)
cos F 2 71MF2 .2 2a m m 2 2a 5 5 a a
15
2 2
故填 2; 7 .
15
三 解答题:共 70分.解答应写出文字说明 证明过程或演算步骤.第 17~21题为必考题,每个试
题考生都必须作答.第 22 23题为选考题,考生根据要求作答.
(一)必考题:共 60分.
17.(12分)
【解析】(1)由 ab 4b 4ccosA和正弦定理,
得bsinA 4sinB 4sinCcosA
4sin A C 4sinCcosA
4sinAcosC .
因为 sinA 0,所以b 4cosC .
π
因为C ,所以
6 b 2 3
.
(2 2 2 2)由余弦定理,得 c b a 2abcos
π
,
6
所以12 a2 6a 3,
即 (a 3)2 0,解得 a 3
S 1 absinC 1所以 ABC的面积 3 2 3 sin
π
2 2 6
3 3
.
2
18.(12分)
【解析】(1)由频率分布直方图,
知男生组得分在 80分以上(含 80分)的有 0.010 0.005 10 60 9(人),
女生组得分在 80分以上(含 80分)的有 0.025 0.010 10 60 21(人),
9 21
男生占比为 ,女生占比为 ,
9 21 9 21
9
所以男生组分得票数为 10 3,
9 21
21
女生组分得票数为 10 7,
9 21
所以男生组 女生组分别得 3张和 7张该戏剧的演出票.
(2)由(1),知男生组得分在 80分以上(含 80分)的有 9人,80分以下的有 51人;女生组得分在 80
分以上(含 80分)的有 21人,80分以下的有 39人,
所以得如下2 2列联表:
男生 女生 合计
x 80 9 21 30
x 80 51 39 90
合计 60 60 120
K 2 120 (9 39 21 51)
2
根据列联表中数据计算,得
60 60 30 90
32
6.4
5
6.635,
根据临界值表,知没有99%的把握认为学生喜爱戏曲与性别有关.
19.(12分)
【解析】(1)如图,连接 BD,B1D1 .因为 ABCD A1B1C1D1是正四棱柱,所以底面 ABCD为正方形,
且BB1 平面 ABCD,所以 AC BD .又 AC 平面 ABCD,所以 AC BB1 .
又BD,BB1 平面 BDD1B1,BD BB1 B,所以 AC 平面 BDD1B1 .
又B1E 平面 BDD1B1,所以 AC B1E .
(2)当
1
时, E为DD
1 1
1的中点,所以D1E DE DD1 AA1 2,2 2 2
所以 AE 2 2,B1E D1E
2 D1B
2
1 2 3 .
又 AB1 2 5,所以 AE
2 B1E
2 AB21 ,所以 AE B1E .
由(1)知, AC B1E .
因为 AC, AE 平面 ACE, AC AE A,所以B1E 平面 ACE .
(3)因为 E为棱DD1上一点(含端点),且DE DD1,所以 0,1 .
又 AC 2 2,
所以
V V V V 16 8 8 8 A BDEB 1 C BDEB 1 E ACD VB ABC 2VA BDEB V V 1 1 .1 1 E ACD B1 ABC 3 3 3 3
因为V 3,5 ,所以3 8 1 5 ,
3
1 7 1 7
解得 ,即 的取值范围是 , .
8 8 8 8
20.(12分)
2
【解析】(1) f x 的定义域为 0, , f x x 2 x ax 2 a .
x x
①若 a 0,则 f x 0,所以 f x 在 0, 上单调递增;
②若 a 0,令 x2 ax 2 0,此时Δ a2 8,
i)当Δ a2 8 0,即0 a 2 2 时, f x 0,所以 f x 在 0, 上单调递增;
ii)当Δ a2 8 0,即 a 2 2时,
2 2
方程 x2 ax 2 0 x a a 8 , x a a 8的两个实数根为 ,且0 x3 x3 4,2 4 2
当 x 0, x3 或 x x4 , 时, f x 0;当 x x3 , x4 时, f x 0,
所以 f x 在 x3, x4 上单调递减,在 0, x3 , x4 , 上单调递增.
综上,当 a 2 2时, f x 在 0, 上单调递增;
f x 0, a a
2 8 a a2 8
当 a 2 2时, 在 , , 上单调递增,
2 2
a a2 8 a a2 8
在 , 2 2
上单调递减.
(2) f x 有两个极值点 x1, x2,结合(1),知 a 2 2,且 x1, x2是方程 x2 ax 2 0的两个实数根,
所以 x1 x2 a, x1x2 2,
所以 f x1 x2 f a 2lna
1
a 2 .
2
1 2
令 g a 2lna a 2(a 2 2) a 2 a 2 ,则
2 g a
2 a 2 a .
a a a
因为 a 2 2,所以 g a 0,所以 g a 在 2 2, 上单调递减,
所以 g a g 2 2 3ln2 4,即 f x1 x2 3ln2 4 .
21.(12分)
【解析】(1)因为当 y0 4 2时,MA MD MF ,所以四边形MFAD为平行四边形,
所以 AD MF p,即 x0 p,所以 A p, 4 2 ,
将 A p, 4 2 代入 y2 2px,得32 2p2,
解得 p 4,(4分 )
所以抛物线C的方程为 y2 8x .
(2)如图,由题意,得M 2,0 .设直线 AM 的方程为 x my 2 m 4 0 ,B x1, y
1 ,则 N 2,m
.
y2 8x
由 ,得 y2 8my 16 0,Δ 64m2 64 0,所以 y y
x my 2 0 1
8m, y0 y1 16 .
AM BN
假设存在实数 ,使得 AM BN BM AN ,即 .
BM AN
| AM | y0 , | BN |
2 x
1
my1 4
由题意,知 ,
| BM | y1 | AN | x0 2 my0 4
| AM | | BN | y my
0 1
4 my y
0 1
4y0
所以 .
| BM | | AN | y1 my0 4 my0y1 4y1
又 y0 y1 8m, y0 y1 16,
| AM | | BN | my0 y1 4y0 16m 4y0 16m 4y
所以
0 1
| BM | | AN | my0y1 4y1 16m 4 8m y0 4y
,
0 16m
即存在实数 1,使得 AM BN BM AN 成立.
(二)选考题:共 10分.请考生在第 22 23题中任选一题作答.如果多做,则按所做的第一题计
分.
22.[选修 4-4:坐标系与参数方程](10分)
x a
π
tcos
4
【解析】(1)由 ( t为参数, a R ,消去参数 t,得直线 l的普通方程为 x y a 0 .
y π tsin
4
由 2cos 2sin ,得 2 2 cos 2 sin .
将 x cos , y sin 代入 2 2 cos 2 sin ,
得曲线C的直角坐标方程为 x2 y2 2x 2y 0,即 (x 1)2 (y 1)2 2 .
(2)由(1),知曲线C表示圆心为 1,1 ,半径为 2 的圆, l为一条直线.
设弦 AB的中点为M ,
因为 AB 2,所以 CM 1,
所以点M 在以C 1,1 为圆心,1为半径的圆上.
又 APB π ,所以 PM 1,所以点 P在以M 为圆心,1为半径的圆上.
2
依题意,直线 l上存在点 P,使得 PC 2,
a
所以点C到直线 l的距离 d 2,即 d 2,
2
所以 2 2 a 2 2 ,
所以 a的取值范围为 2 2,2 2 .
23.[选修 4-5:不等式选讲](10分)
【解析】(1)若 f 3 f 1 ,则 2 3 1 3 a b 2 1 1 1 a b,
即 3 a 1 a ,
两边平方,得9 6a a2 a2 2a 1,即8a 8,
解得 a 1,所以实数 a的取值范围是 , 1 .
x 7 b x 1
(2)因为 a 5,所以函数 f x 2 x 1 x 5 b 3x 3 b( 1 x 5) .
x 7 b x 5
观察图象(图略),知函数 f x 2 x 1 x 5 b在 , 1 上单调递减,在 1,5 和 5, 上单
调递增,且 f 1 6 b, f 5 12 b,
所以①当 12 b 6时, x 7 b, x
3 b 18 2b
1 2 .由 x1 x2 4,解得b 3;3 3
②当b 12时, x1 7 b, x2 7 b,此时 x1 x2 14,与 x1 x2 4矛盾,舍去.
综上,实数b的值为 3.
同课章节目录
