天津市武清区杨村第一中学2024届高考数学热身训练卷(无答案)
文档属性
| 名称 | 天津市武清区杨村第一中学2024届高考数学热身训练卷(无答案) | 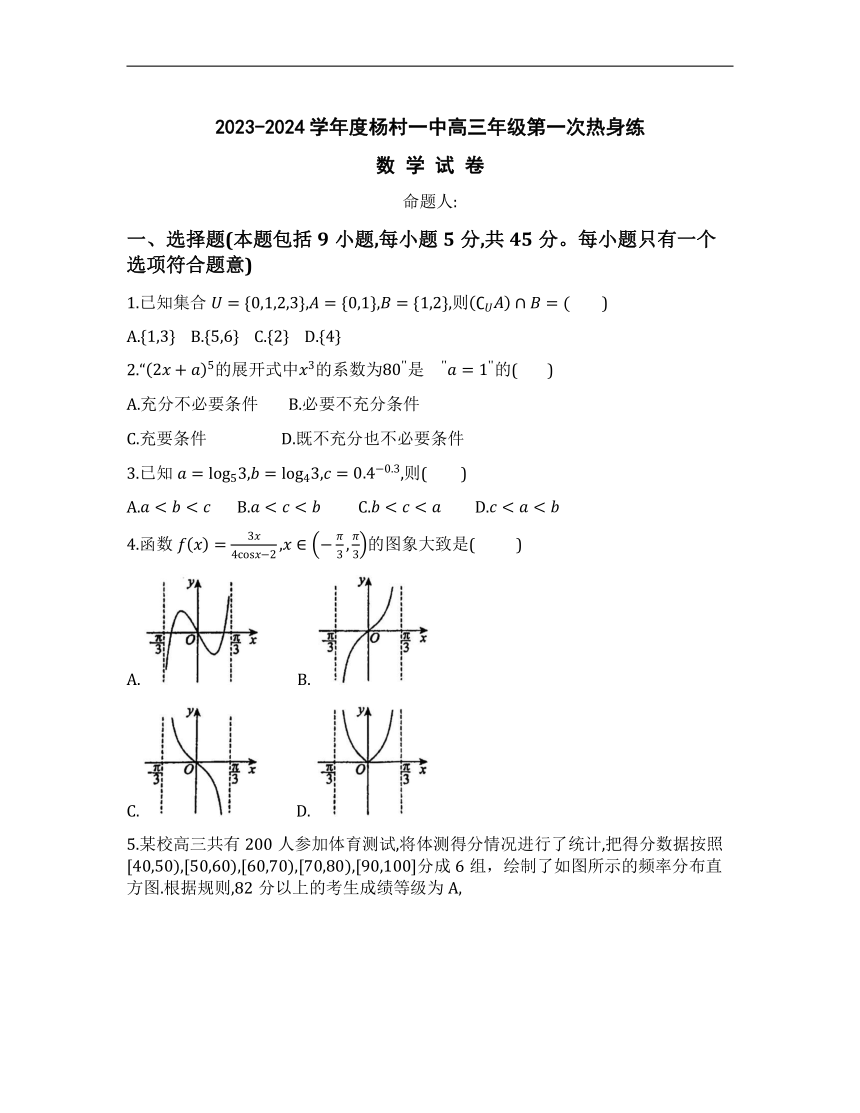 | |
| 格式 | docx | ||
| 文件大小 | 92.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 15:56:20 | ||
图片预览


文档简介
2023-2024学年度杨村一中高三年级第一次热身练
数 学 试 卷
命题人:
一、选择题(本题包括9小题,每小题5分,共45分。每小题只有一个选项符合题意)
1.已知集合,则)
A. B. C. D.
2.“的展开式中的系数为是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知,则( )
A. B.C. D.
4.函数的图象大致是( )
A. B.
C. D.
5.某校高三共有200人参加体育测试,将体测得分情况进行了统计,把得分数据按照分成6组,绘制了如图所示的频率分布直方图.根据规则,82分以上的考生成绩等级为A,
则估计获得的考生人数约为( )
A.25 B.50 C.75 D.100
6.在等差数列中,公差,若,则
A.12 B.13 C.14 D.15
7.四棱雉的底面为正方形,,动点在线段上,则下列结论正确的是( )
A.四棱雉的体积为
B.四棱雉的表面积为
C.在中,当时,
D.四棱雉的外接球表面积为
8.函数的图象经过点和点,则的单调递增区间是( )
A. B.
C. D.
9.双曲线的左顶点为,右焦点为,过点且倾斜角为的直线顺次交两条渐近线和的右支于,且,下列结论不正确的是( )
A.高心率为2 B. C. D.
二、填空题(本题共6小题,共30分)
10.已知,且,则________.
11.已知圆,直线的便斜角为且与圆相切,则的方程为________.
12.已知,若,则的值为________.
13.某学校为普及垃圾分类知识,增强学生的垃圾分类意识,在全校范围内举办垃圾分类知识竞赛.通过选拔,仅有甲、乙两名选手进入决赛.决赛采用积分制,规则为:抢答3道题,每题10分,答对得10分,答错自己不得分,对方得10分.选手是否抢到试题是等可能的,且回答对错互不影响,得分高的获胜.已知甲、乙两名选手答对每道题的概率分别为,记事件为“答第一道题,甲选手得分”,则记甲选手的得分为(单位,分),________.
14.在边长为1的正三角形中,分别为边上的动点,满足,,且,则的最小值为________;
,若,则________.
15.已知函数若关于的方程恰有三个实数解,则实数的取值范围是________.
三、解答题(本题共5小题,共75分)
16.(本小题满分14分)
在中,内角所对的边分别为,已知
(I)求角的大小:
(II)已知的面积为6,求:
(i)边长的值;
(ii)的值.
17.(本小题满分15分)
三棱台中,若平面A,
分别是中点.
(I)求证:平面;
(II)求二面角的正弦值;
(III)求点到平面的距离.
18.(本小题满分15分)
已知椭圆经过点和,椭圆上三点与原点构成平行四边形.
(I)求椭圆的方程:
(II)若四点共圆,求直线的斜率.
19.(本小题满分15分)
已知数列是正项等比数列,是等差数列,且,
(I)求数列和的通项公式;
(II),求数列的前项和.
(III)表示不超过的最大整数,表示数列的前项和,集合共有4个元素,求范围;
20.(本小题满分16分)
帕德近似是法国数学家亨利帕德发明的用有理多项式近似特定函数的方法.给定两个正整数,函数在处的阶帕德近似定义为:,且
满足:,
注:
已知函数.
(I)求函数在处的阶帕德近似,并求的近似数(精确到;
(II)在(1)的条件下:
(i)求证:;
(ii)若恒成立,求实数的取值范围.
数 学 试 卷
命题人:
一、选择题(本题包括9小题,每小题5分,共45分。每小题只有一个选项符合题意)
1.已知集合,则)
A. B. C. D.
2.“的展开式中的系数为是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.已知,则( )
A. B.C. D.
4.函数的图象大致是( )
A. B.
C. D.
5.某校高三共有200人参加体育测试,将体测得分情况进行了统计,把得分数据按照分成6组,绘制了如图所示的频率分布直方图.根据规则,82分以上的考生成绩等级为A,
则估计获得的考生人数约为( )
A.25 B.50 C.75 D.100
6.在等差数列中,公差,若,则
A.12 B.13 C.14 D.15
7.四棱雉的底面为正方形,,动点在线段上,则下列结论正确的是( )
A.四棱雉的体积为
B.四棱雉的表面积为
C.在中,当时,
D.四棱雉的外接球表面积为
8.函数的图象经过点和点,则的单调递增区间是( )
A. B.
C. D.
9.双曲线的左顶点为,右焦点为,过点且倾斜角为的直线顺次交两条渐近线和的右支于,且,下列结论不正确的是( )
A.高心率为2 B. C. D.
二、填空题(本题共6小题,共30分)
10.已知,且,则________.
11.已知圆,直线的便斜角为且与圆相切,则的方程为________.
12.已知,若,则的值为________.
13.某学校为普及垃圾分类知识,增强学生的垃圾分类意识,在全校范围内举办垃圾分类知识竞赛.通过选拔,仅有甲、乙两名选手进入决赛.决赛采用积分制,规则为:抢答3道题,每题10分,答对得10分,答错自己不得分,对方得10分.选手是否抢到试题是等可能的,且回答对错互不影响,得分高的获胜.已知甲、乙两名选手答对每道题的概率分别为,记事件为“答第一道题,甲选手得分”,则记甲选手的得分为(单位,分),________.
14.在边长为1的正三角形中,分别为边上的动点,满足,,且,则的最小值为________;
,若,则________.
15.已知函数若关于的方程恰有三个实数解,则实数的取值范围是________.
三、解答题(本题共5小题,共75分)
16.(本小题满分14分)
在中,内角所对的边分别为,已知
(I)求角的大小:
(II)已知的面积为6,求:
(i)边长的值;
(ii)的值.
17.(本小题满分15分)
三棱台中,若平面A,
分别是中点.
(I)求证:平面;
(II)求二面角的正弦值;
(III)求点到平面的距离.
18.(本小题满分15分)
已知椭圆经过点和,椭圆上三点与原点构成平行四边形.
(I)求椭圆的方程:
(II)若四点共圆,求直线的斜率.
19.(本小题满分15分)
已知数列是正项等比数列,是等差数列,且,
(I)求数列和的通项公式;
(II),求数列的前项和.
(III)表示不超过的最大整数,表示数列的前项和,集合共有4个元素,求范围;
20.(本小题满分16分)
帕德近似是法国数学家亨利帕德发明的用有理多项式近似特定函数的方法.给定两个正整数,函数在处的阶帕德近似定义为:,且
满足:,
注:
已知函数.
(I)求函数在处的阶帕德近似,并求的近似数(精确到;
(II)在(1)的条件下:
(i)求证:;
(ii)若恒成立,求实数的取值范围.
同课章节目录
