六年级下数学-数的运算_青岛版课件
文档属性
| 名称 | 六年级下数学-数的运算_青岛版课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 245.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-25 00:00:00 | ||
图片预览


文档简介
课件16张PPT。百分数的综合运用(一)一、回顾与梳理怎样进行整数、小数、分数加减运算?它们的计算方法有什么共同之处?●相同数位上的数要对齐;●从低位算起;●加法中满几十就向前一位 进几;减法中不够减时,就从前一位退一,退一当 十。 ●相同数位上的数要对齐;●从低位算起;●按整数加减法的法则
进行计算。●异分母分数相加减,
先通分,再计算;●结果能约分的要约
分。 ●同分母分数相加减,
分母不变,分子相
加减;●相同数位上的数要对齐;●相同数位上的数要对齐;●异分母分数相加减,
先通分,再计算;●同分母分数相加减,
分母不变,分子相
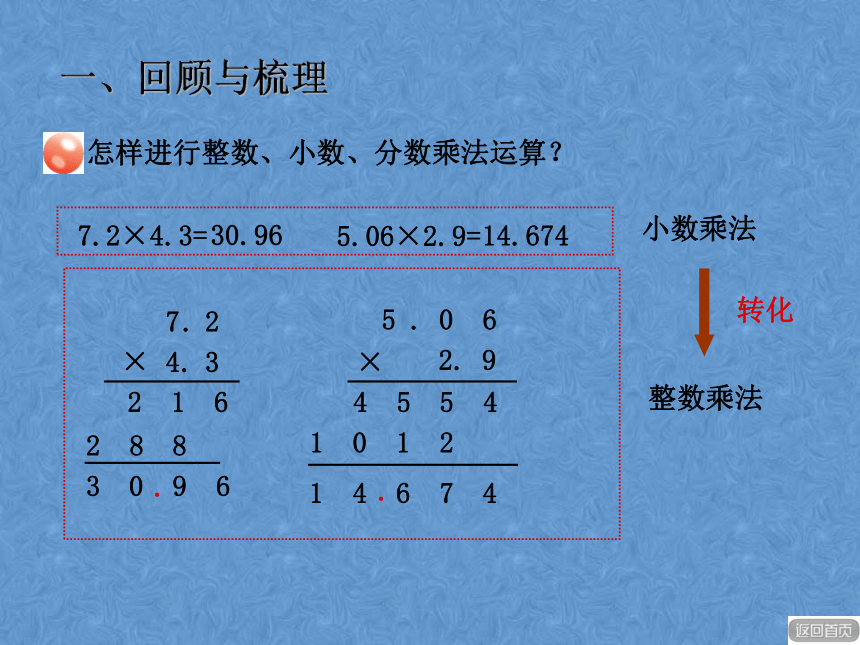
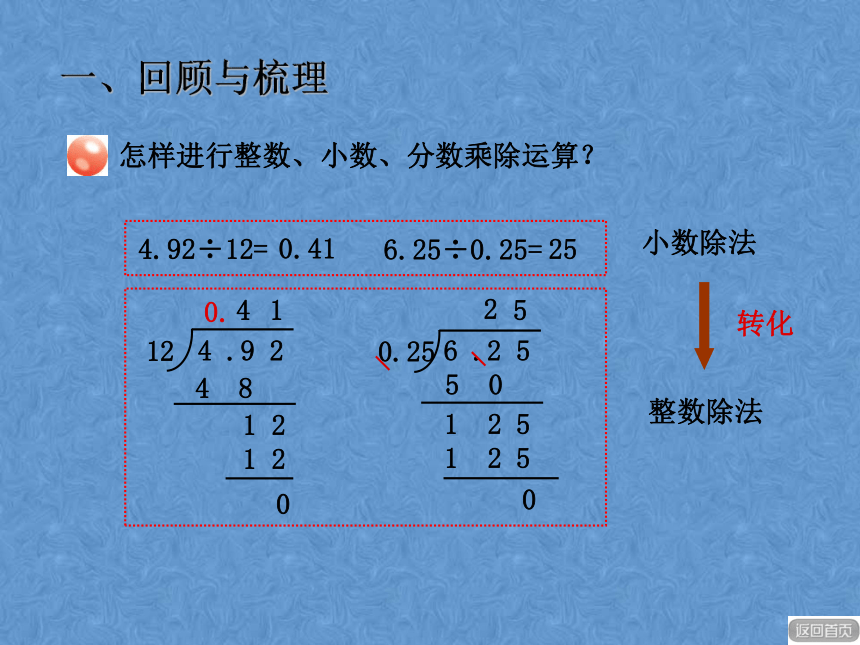
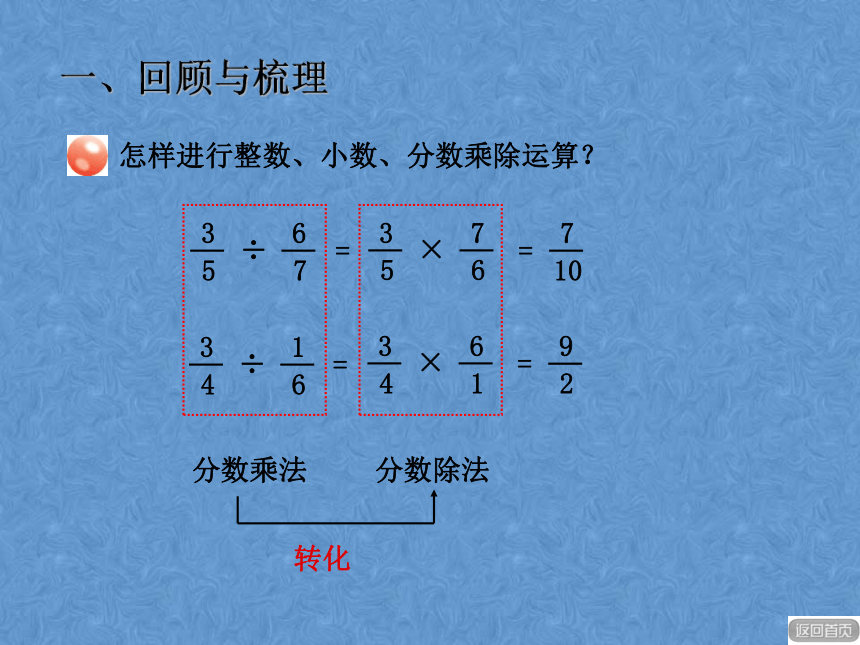
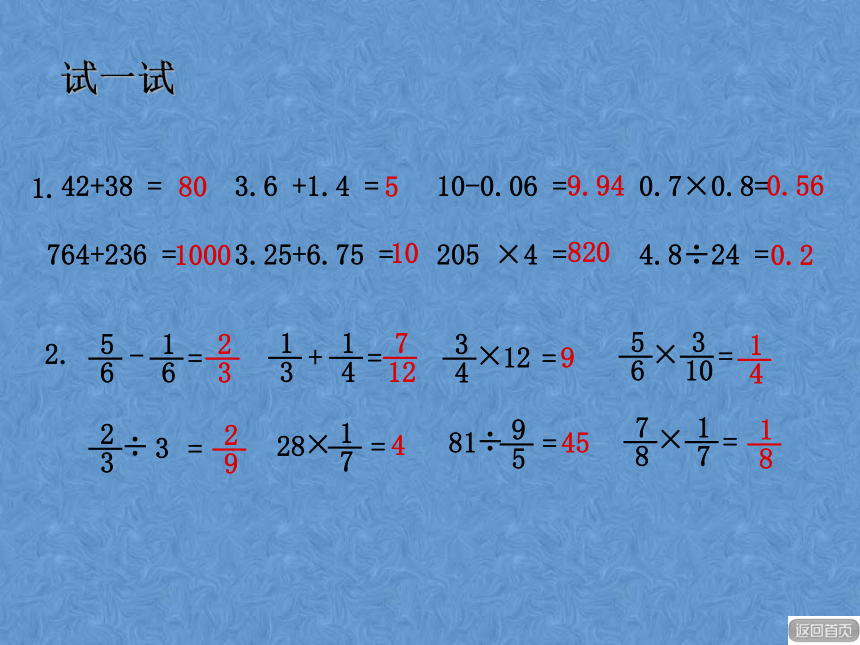
加减;把相同计数单位的数相加或相减。2 1 67.2×4.3=7.×24.32 8 83 0 9 6.30.964 5 5 45.06×2.9=×5 . 0 62. 91 0 1 21 4 6 7 4.14.674小数乘法整数乘法转化一、回顾与梳理怎样进行整数、小数、分数乘法运算?4.92÷12=0.416.25÷0.25=25小数除法整数除法转化44 81 211 200.25 01 2 551 2 50一、回顾与梳理怎样进行整数、小数、分数乘除运算?转化÷÷==分数乘法分数除法怎样进行整数、小数、分数乘除运算?一、回顾与梳理 42+38 = 3.6 +1.4 = 10-0.06 = 0.7×0.8=
764+236 = 3.25+6.75 = 205 ×4 = 4.8÷24 =试一试8059.940.561000108200.22.94451.我们学过哪些运算律?加法运算律乘法运算律运
算
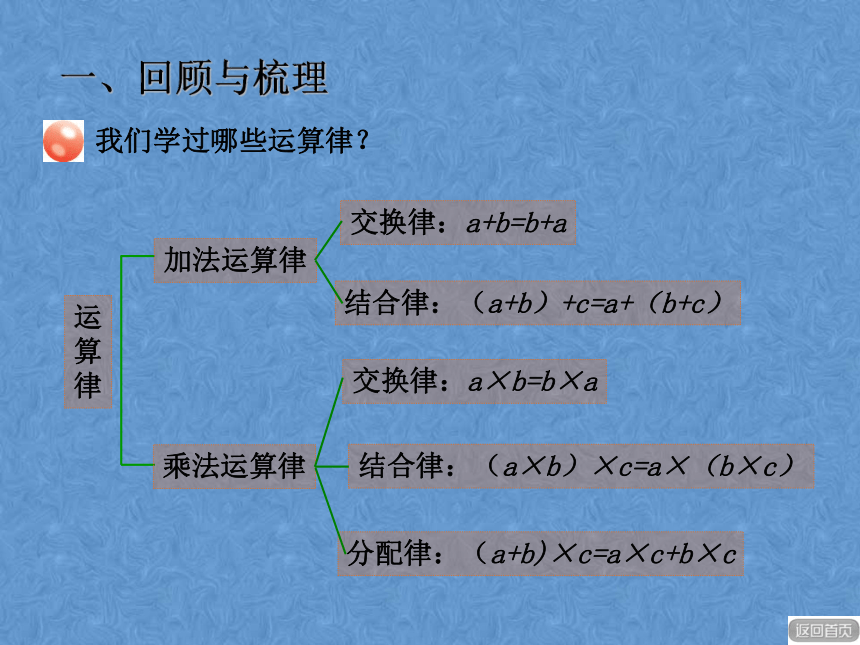
律交换律:a+b=b+a交换律:a×b=b×a结合律:(a+b)+c=a+(b+c)结合律:(a×b)×c=a×(b×c)分配律:(a+b)×c=a×c+b×c一、回顾与梳理56+89+4426×11+89×266.75+8.8+3.250.7×4.5-0.7×0.5=(56+44)+89×-()24=189=(6.75+3.25)+8.8=18.8=(11+89)×26=100×26=2600=(4.5-0.5)×0.8=4×0.8=3.2=4-3=1应用运算律可以使计算简便。这些运算律在整数、小数、分数范围内都适用。一、回顾与梳理试一试7.35-(1.9+2.35)=7.35-2.35 -1.9 10+×10×--=5 -1.9 =3.1=1×10 =10 二、讨论与交流●四则运算之间有什么关系?10+5=1515-5=10a + =b cc- =b a8×12=9696÷12=8a × =bcc÷ =b a9+9+9+9+9+9=9×6=54n个a相加a ×n=二、讨论与交流●四则运算之间有什么关系?a+b=cc-b=a减法是加法的逆运算a×b=cc÷b=a除法是乘法的逆运算n个乘法是加法的简便运算a+a+a+……+a=a×n1.竖式计算。三、应用与反思 699-402=498÷12=197+301=203×98=6 9 9-4 0 27922974 9 81244 81811 26.0056 00.41.51 9 7+3 0 18944982 0 3×9 84221 67221 849891198942.根据53×74=3922,直接写出下列各题的得数。三、应用与反思 53×0.74 = 5.3×0.074 =
39.22÷0.74 = 3922÷7.4 =39.220.3922535303.计算下列各题,能简算的要简算。三、应用与反思 2000-1978.8-6.75+9.2-0.2541×1020.8×3.6-0.8×0.6 =2000-200+3=1800+3=1803=(8.8+9.2)-(6.75+0.25)=18-7=11=41×(100+2)=41×100+41×2=4100+82=4182=0.8×(3.6-0.6)=0.8×3=2.43.计算下列各题,能简算的要简算。三、应用与反思 ======1511161-14+9-230-=3.计算下列各题,能简算的要简算。三、应用与反思 1042-384÷16×134.86×[1÷(2.1-2.09)]=1042-24×13=1042-312=730=4.86×[1÷0.01]=4.86×100=486
进行计算。●异分母分数相加减,
先通分,再计算;●结果能约分的要约
分。 ●同分母分数相加减,
分母不变,分子相
加减;●相同数位上的数要对齐;●相同数位上的数要对齐;●异分母分数相加减,
先通分,再计算;●同分母分数相加减,
分母不变,分子相
加减;把相同计数单位的数相加或相减。2 1 67.2×4.3=7.×24.32 8 83 0 9 6.30.964 5 5 45.06×2.9=×5 . 0 62. 91 0 1 21 4 6 7 4.14.674小数乘法整数乘法转化一、回顾与梳理怎样进行整数、小数、分数乘法运算?4.92÷12=0.416.25÷0.25=25小数除法整数除法转化44 81 211 200.25 01 2 551 2 50一、回顾与梳理怎样进行整数、小数、分数乘除运算?转化÷÷==分数乘法分数除法怎样进行整数、小数、分数乘除运算?一、回顾与梳理 42+38 = 3.6 +1.4 = 10-0.06 = 0.7×0.8=
764+236 = 3.25+6.75 = 205 ×4 = 4.8÷24 =试一试8059.940.561000108200.22.94451.我们学过哪些运算律?加法运算律乘法运算律运
算
律交换律:a+b=b+a交换律:a×b=b×a结合律:(a+b)+c=a+(b+c)结合律:(a×b)×c=a×(b×c)分配律:(a+b)×c=a×c+b×c一、回顾与梳理56+89+4426×11+89×266.75+8.8+3.250.7×4.5-0.7×0.5=(56+44)+89×-()24=189=(6.75+3.25)+8.8=18.8=(11+89)×26=100×26=2600=(4.5-0.5)×0.8=4×0.8=3.2=4-3=1应用运算律可以使计算简便。这些运算律在整数、小数、分数范围内都适用。一、回顾与梳理试一试7.35-(1.9+2.35)=7.35-2.35 -1.9 10+×10×--=5 -1.9 =3.1=1×10 =10 二、讨论与交流●四则运算之间有什么关系?10+5=1515-5=10a + =b cc- =b a8×12=9696÷12=8a × =bcc÷ =b a9+9+9+9+9+9=9×6=54n个a相加a ×n=二、讨论与交流●四则运算之间有什么关系?a+b=cc-b=a减法是加法的逆运算a×b=cc÷b=a除法是乘法的逆运算n个乘法是加法的简便运算a+a+a+……+a=a×n1.竖式计算。三、应用与反思 699-402=498÷12=197+301=203×98=6 9 9-4 0 27922974 9 81244 81811 26.0056 00.41.51 9 7+3 0 18944982 0 3×9 84221 67221 849891198942.根据53×74=3922,直接写出下列各题的得数。三、应用与反思 53×0.74 = 5.3×0.074 =
39.22÷0.74 = 3922÷7.4 =39.220.3922535303.计算下列各题,能简算的要简算。三、应用与反思 2000-1978.8-6.75+9.2-0.2541×1020.8×3.6-0.8×0.6 =2000-200+3=1800+3=1803=(8.8+9.2)-(6.75+0.25)=18-7=11=41×(100+2)=41×100+41×2=4100+82=4182=0.8×(3.6-0.6)=0.8×3=2.43.计算下列各题,能简算的要简算。三、应用与反思 ======1511161-14+9-230-=3.计算下列各题,能简算的要简算。三、应用与反思 1042-384÷16×134.86×[1÷(2.1-2.09)]=1042-24×13=1042-312=730=4.86×[1÷0.01]=4.86×100=486
