探索勾股定理
图片预览





文档简介
课件45张PPT。复习提问 任意三角形三边满足怎样的关系?对于直角三角形,三边之间
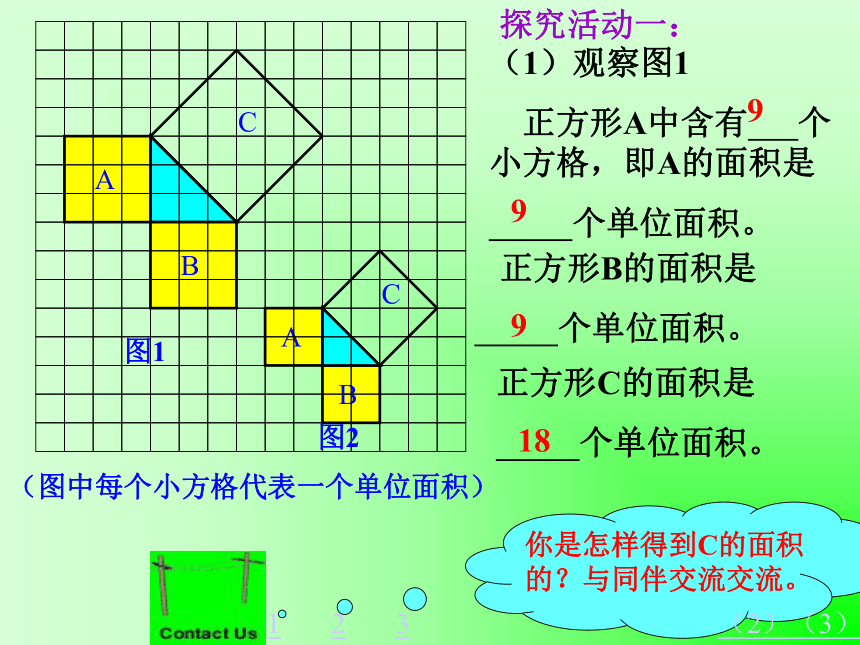
存在怎样的特殊关系?探索勾股定理做一做 书P2 (1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
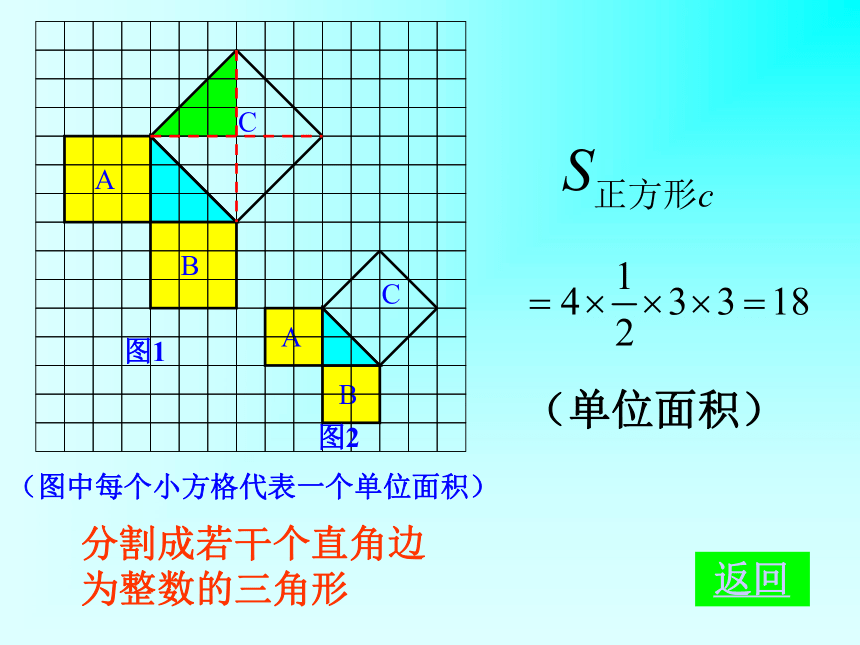
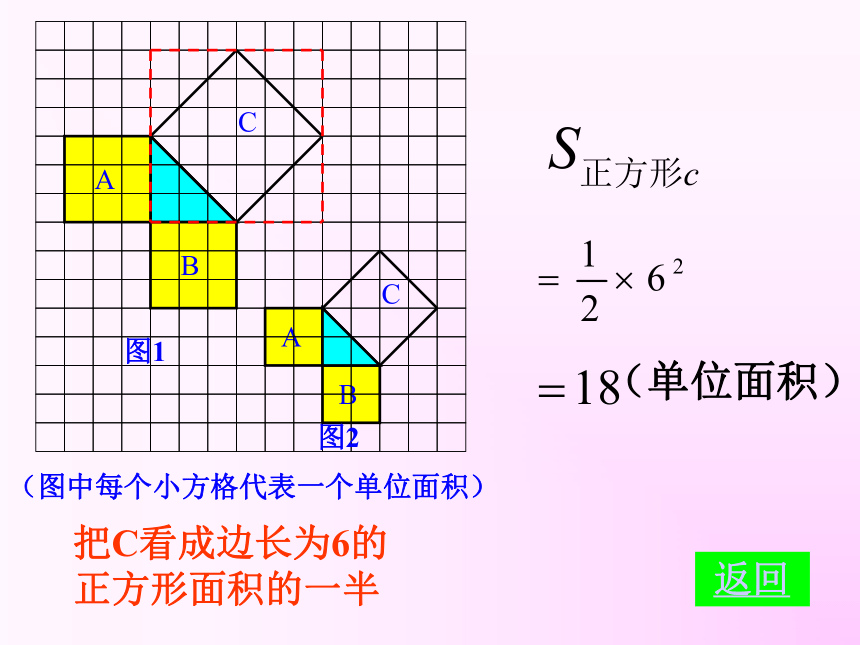
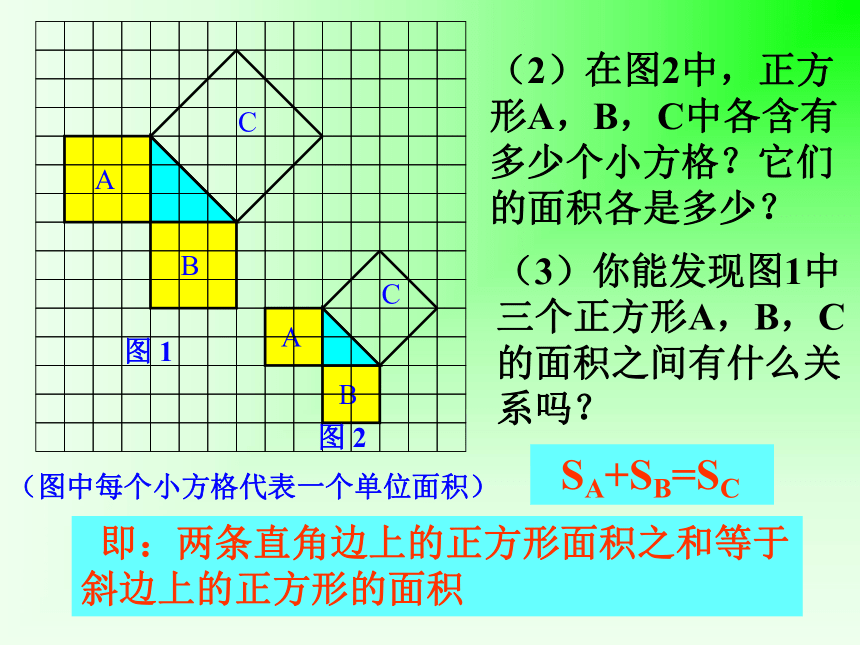
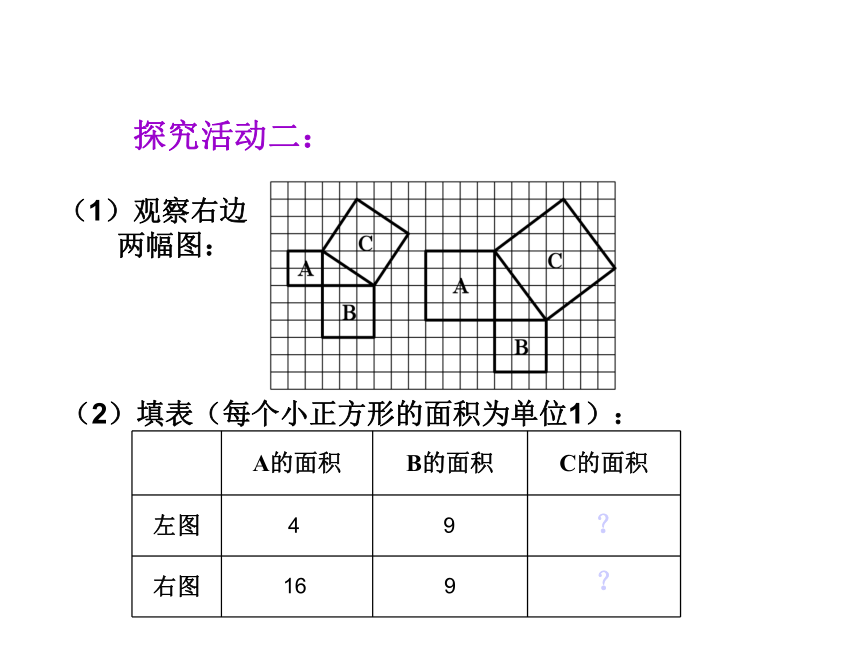
个单位面积。99918123(2)(3)探究活动一:分割成若干个直角边为整数的三角形(单位面积) 返回(单位面积)把C看成边长为6的正方形面积的一半 返回(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积 结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.探究活动二:(1)观察右边
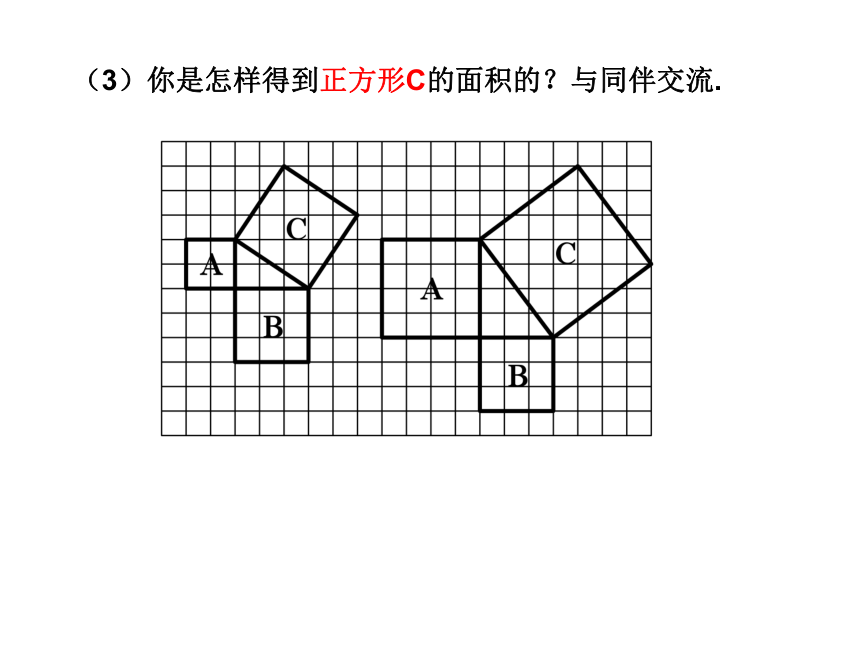
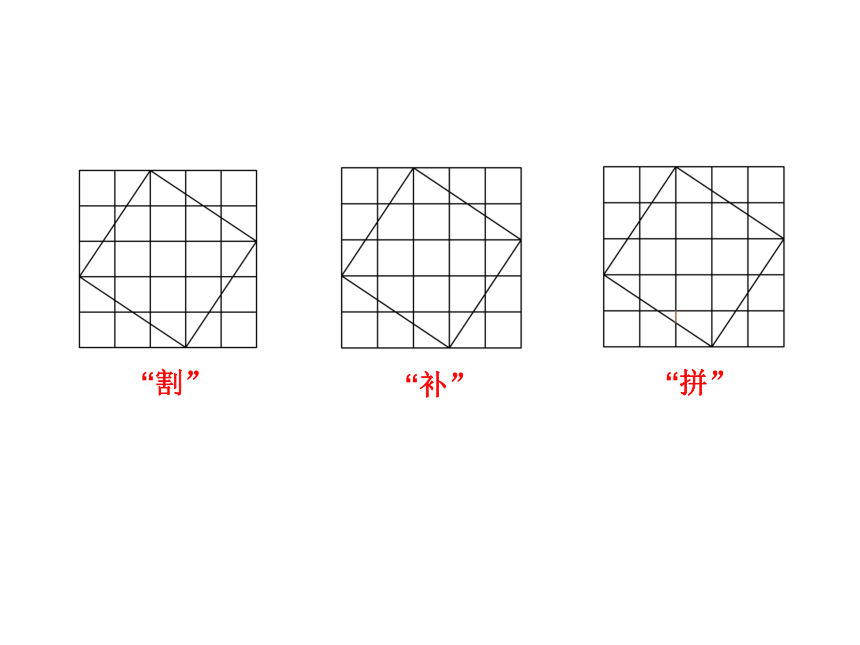
两幅图: (2)填表(每个小正方形的面积为单位1):4 916 9??(3)你是怎样得到正方形C的面积的?与同伴交流. “割”“补”“拼”(4)分析填表数据,你发现了什么? 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.议一议: (1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗? (2)你能发现直角三角形三边长度之间存在什么
关系吗? 结论3 如果直角三角形两直角边长分别为a、b,斜边长为 c ,那么
即直角三角形两直角边的平方和等于斜边的平方. abc表示为:Rt△ABC中,∠C=90° 则 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。 在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾股定理的由来 毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为"毕达哥拉斯定理",以后就流传开了。这个定理在中国又称为“商高定理”,商高是公元
前十一世纪的中国人。当时中国的朝代是西周,
是奴隶社会时期。在中国古代大约是战国时期西汉
的数学著作《周髀算经》中记录着商高同周公的
一段对话。商高说:“…故折矩,勾广三,股修四,
经隅五。商高那段话的意思就是说:当直角三角形
的两条直角边分别为3(短边)和4(长边)时,
径隅(就是弦)则为5。以后人们就简单地把这个
事实说成“勾三股四弦五”。由于勾股定理的内容
最早见于商高的话中,所以人们就把这个定理叫
作"商高定理"。议一议:判断下列说法是否正确,并说明理由:
(1)在Rt△ABC中,∠C=90° , 如果a=3,b=4,则c=5.
(2)在Rt△ABC中,如果a=3,b=4,则c=5.
(3)在△ABC中,若a=3,b=4,则c=5探究活动 分成四人小组,按下列步骤进行拼图实验并探究. 每个小组课前准备好4个全等的直角三角形和以直角三角形各边为边长的3个正方形(如右图). 运用这些材料(不一定全用),你能另外拼出一些正方形吗?试试看,你能拼几种. 图1图3图2方法一:而所以即,,..因为,方法二:,化简得:方法三:,化简得:我国古代两种证法: 1、公元3世纪我国汉代数学家赵爽在为《周髀算经》作注时给出的“弦图”: 我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的。每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图。2002年的国际数学家大会将此图作为大会会徽. 2、我国数学家刘徽在他的《九章算术注》中给出的“青朱出入图” :证法四:(伽菲尔德证法1876年) 如图,Rt△ABE≌Rt△ECD,
可知∠AED=90°;梯形ABCD的面积=梯形ABCD的面积=∴∴证法五:(欧几里得证法公元前3世纪)“新娘的轿椅”或“修士的头巾” 如图,Rt△ ABC中,∠ACB=90°,四边形ACHK、BCGF、ABED都是正方形,CN⊥DE,连接BK、CD。同理:S 正方形BCGF = S 四边形BENM ∴某楼房在20米高处的楼层失火,消防员取来25米长的云梯救火,已知梯子的底部离墙的距离是15米。问消防队员能否进入该楼层灭火? 已知两直角边求斜边?????求下列图形中未知正方形的面积或未知边的长度:求下图中的A或x:直角三角形ABC的斜边c=10,直角边a=6,
则三角形的面积为 ,斜边上的高为 . 做一做:在△ABC中,∠C=90°,
(1)若a=7,c=25,则b=_______.
(3) 若CD⊥AB,a=10,b=24,则CD=______.(2)若a:b=3:4,c=20,则a=_____, b=______.练一练 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米4658如图,将长为2.5米的梯子AC斜靠在墙上,
BC长为0.7米,
求:(1)梯子上端A到墙的底端B的距离AB。
ACB(梯子长度不变2)如果梯子上端A向下滑动0.4米到A′处,则
梯子的底端C向C′是否也滑动了0.4米,如果是,
请说明理由;如果不是,请说出滑动了多少米? 本节课学习了什么内容?你对学习本节课知识有什么体会?谈一谈试一试: 请大家利用作图工具在纸上作图
(1)作一个直角边分别为5和12的直角三角形,并测量斜边的长度。
(2)作一个一条直角边为6,斜边为10的直角三角形,并测量另一条直角边的长度。问:这两个直角三角形的三边关系是否满足刚才的猜想? 1. 如图,根据以下数学情境,你可以提出多少个数学问题?你能解决所提出的问题吗?2. 若正方形的面积为2cm2,则它的对角线长 .
3. 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .练一练受台风影响,一棵树在离地面4米处断裂,树的
顶部落在离树跟底部3米处,这棵树折断前有多高?
受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米3米如右图,某同学将一直角三角形纸片折叠,
A与B重合,折痕为DE,若已知AC=10cm,
BC=6cm,你能求CE的长吗? 古代问题:
在我国古代数学著作《九章算术》中
记载了一道有趣的问题,这个问题的意
思是:有一个水池,水面是一个边长为10尺的正方形. 在水池正中央有一根新生的芦苇,它高出水面1尺. 如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面. 请问这个水池的深度和这根芦苇的长度各是多少?
存在怎样的特殊关系?探索勾股定理做一做 书P2 (1)观察图1
正方形A中含有 个小方格,即A的面积是
个单位面积。 正方形B的面积是
个单位面积。正方形C的面积是
个单位面积。99918123(2)(3)探究活动一:分割成若干个直角边为整数的三角形(单位面积) 返回(单位面积)把C看成边长为6的正方形面积的一半 返回(2)在图2中,正方形A,B,C中各含有多少个小方格?它们的面积各是多少?(3)你能发现图1中三个正方形A,B,C的面积之间有什么关系吗? SA+SB=SC 即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积 结论1 以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.探究活动二:(1)观察右边
两幅图: (2)填表(每个小正方形的面积为单位1):4 916 9??(3)你是怎样得到正方形C的面积的?与同伴交流. “割”“补”“拼”(4)分析填表数据,你发现了什么? 结论2 以直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.议一议: (1)你能用直角三角形的两直角边的长a、b和斜边长c来表示图中正方形的面积吗? (2)你能发现直角三角形三边长度之间存在什么
关系吗? 结论3 如果直角三角形两直角边长分别为a、b,斜边长为 c ,那么
即直角三角形两直角边的平方和等于斜边的平方. abc表示为:Rt△ABC中,∠C=90° 则 勾股定理(gou-gu theorem)如果直角三角形两直角边分别为a、b,斜边为c,那么即 直角三角形两直角边的平方和等于斜边的平方。 在中国古代,人们把弯曲成直角的手臂的上半部分称为"勾",下半部分称为"股"。我国古代学者把直角三角形较短的直角边称为“勾”,较长的直角边称为“股”,斜边称为“弦”.勾股定理的由来 毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。希腊另一位数学家欧几里德(Euclid,是公元前三百年左右的人)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为"毕达哥拉斯定理",以后就流传开了。这个定理在中国又称为“商高定理”,商高是公元
前十一世纪的中国人。当时中国的朝代是西周,
是奴隶社会时期。在中国古代大约是战国时期西汉
的数学著作《周髀算经》中记录着商高同周公的
一段对话。商高说:“…故折矩,勾广三,股修四,
经隅五。商高那段话的意思就是说:当直角三角形
的两条直角边分别为3(短边)和4(长边)时,
径隅(就是弦)则为5。以后人们就简单地把这个
事实说成“勾三股四弦五”。由于勾股定理的内容
最早见于商高的话中,所以人们就把这个定理叫
作"商高定理"。议一议:判断下列说法是否正确,并说明理由:
(1)在Rt△ABC中,∠C=90° , 如果a=3,b=4,则c=5.
(2)在Rt△ABC中,如果a=3,b=4,则c=5.
(3)在△ABC中,若a=3,b=4,则c=5探究活动 分成四人小组,按下列步骤进行拼图实验并探究. 每个小组课前准备好4个全等的直角三角形和以直角三角形各边为边长的3个正方形(如右图). 运用这些材料(不一定全用),你能另外拼出一些正方形吗?试试看,你能拼几种. 图1图3图2方法一:而所以即,,..因为,方法二:,化简得:方法三:,化简得:我国古代两种证法: 1、公元3世纪我国汉代数学家赵爽在为《周髀算经》作注时给出的“弦图”: 我国有记载的最早勾股定理的证明,是三国时,我国古代数学家赵爽在他所著的《勾股方圆图注》中,用四个全等的直角三角形拼成一个中空的正方形来证明的。每个直角三角形的面积叫朱实,中间的正方形面积叫黄实,大正方形面积叫弦实,这个图也叫弦图。2002年的国际数学家大会将此图作为大会会徽. 2、我国数学家刘徽在他的《九章算术注》中给出的“青朱出入图” :证法四:(伽菲尔德证法1876年) 如图,Rt△ABE≌Rt△ECD,
可知∠AED=90°;梯形ABCD的面积=梯形ABCD的面积=∴∴证法五:(欧几里得证法公元前3世纪)“新娘的轿椅”或“修士的头巾” 如图,Rt△ ABC中,∠ACB=90°,四边形ACHK、BCGF、ABED都是正方形,CN⊥DE,连接BK、CD。同理:S 正方形BCGF = S 四边形BENM ∴某楼房在20米高处的楼层失火,消防员取来25米长的云梯救火,已知梯子的底部离墙的距离是15米。问消防队员能否进入该楼层灭火? 已知两直角边求斜边?????求下列图形中未知正方形的面积或未知边的长度:求下图中的A或x:直角三角形ABC的斜边c=10,直角边a=6,
则三角形的面积为 ,斜边上的高为 . 做一做:在△ABC中,∠C=90°,
(1)若a=7,c=25,则b=_______.
(3) 若CD⊥AB,a=10,b=24,则CD=______.(2)若a:b=3:4,c=20,则a=_____, b=______.练一练 小明的妈妈买了一部29英寸(74厘米)的电视机。小明量了电视机的屏幕后,发现屏幕只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你能解释这是为什么吗?∴售货员没搞错∵想一想荧屏对角线大约为74厘米4658如图,将长为2.5米的梯子AC斜靠在墙上,
BC长为0.7米,
求:(1)梯子上端A到墙的底端B的距离AB。
ACB(梯子长度不变2)如果梯子上端A向下滑动0.4米到A′处,则
梯子的底端C向C′是否也滑动了0.4米,如果是,
请说明理由;如果不是,请说出滑动了多少米? 本节课学习了什么内容?你对学习本节课知识有什么体会?谈一谈试一试: 请大家利用作图工具在纸上作图
(1)作一个直角边分别为5和12的直角三角形,并测量斜边的长度。
(2)作一个一条直角边为6,斜边为10的直角三角形,并测量另一条直角边的长度。问:这两个直角三角形的三边关系是否满足刚才的猜想? 1. 如图,根据以下数学情境,你可以提出多少个数学问题?你能解决所提出的问题吗?2. 若正方形的面积为2cm2,则它的对角线长 .
3. 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .练一练受台风影响,一棵树在离地面4米处断裂,树的
顶部落在离树跟底部3米处,这棵树折断前有多高?
受台风影响,一棵树在离地面4米处断裂,树的顶部落在离树跟底部3米处,这棵树折断前有多高?
4米3米如右图,某同学将一直角三角形纸片折叠,
A与B重合,折痕为DE,若已知AC=10cm,
BC=6cm,你能求CE的长吗? 古代问题:
在我国古代数学著作《九章算术》中
记载了一道有趣的问题,这个问题的意
思是:有一个水池,水面是一个边长为10尺的正方形. 在水池正中央有一根新生的芦苇,它高出水面1尺. 如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面. 请问这个水池的深度和这根芦苇的长度各是多少?
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
