2024年北京中考数学二轮专题复习 专题七 二次函数综合题 课件(共92张PPT)
文档属性
| 名称 | 2024年北京中考数学二轮专题复习 专题七 二次函数综合题 课件(共92张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 15:11:01 | ||
图片预览




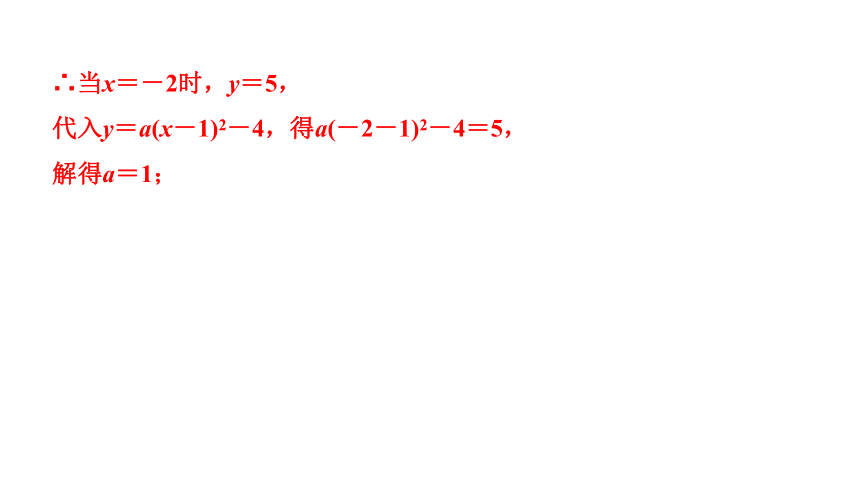







文档简介
(共92张PPT)
专题七 二次函数综合题
类型一 对称性、增减性问题
1
类型二 公共点问题
2
类型三 整点问题
3
类型一 对称性、增减性问题
1.(2021朝阳区一模)在平面直角坐标系xOy中,抛物线
y=ax2+bx+a-4(a≠0)的对称轴是直线x=1.
(1)求抛物线y=ax2+bx+a-4(a≠0)的顶点坐标;
综合提升
三阶
解:(1)∵对称轴是直线x=1,
∴ =1,
∴b=-2a,
∴y=ax2-2ax+a-4=a(x-1)2-4,
∴顶点坐标为(1,-4);
(2)当-2≤x≤3时,y的最大值是5,求a的值;
(2)若a<0,则抛物线开口向下,y的最大值在对称轴处取得,从而y有最大值为-4,
∵当-2≤x≤3时,y的最大值是5,且抛物线的对称轴为直线x=1,
∴函数此时在x=1时取得最大值5,
这与y有最大值-4矛盾,从而a>0,
∴抛物线的顶点为图象的最低点.
∵1-(-2)>3-1,
∴当x=-2时,y=5,
代入y=a(x-1)2-4,得a(-2-1)2-4=5,
解得a=1;
(3)在(2)的条件下,当t≤x≤t+1时,y的最大值是m,最小值是n,且
m-n=3.求t的值.
(3)由(2)得,a=1,
∴y=(x-1)2-4.
①当t ≤ 1 ≤ t+1时,此时0 ≤ t ≤ 1,
∴n=-4,函数的最大值在t+1或t处取得,即m=t2-4或
m=(t-1)2-4,
∴m的最大值为-3,
此时m-n=1,
不符合题意,舍去;
②当t+1<1,即t<0时,
m=(t-1)2-4,n=(t+1-1)2-4=t2-4,
∵m-n=3,
∴(t-1)2-4-(t2-4)=3,
∴t=-1;
③当t>1时,
同理可得t=2,
综上所述,t的值为-1或2.
2. (2023北京)在平面直角坐标系xOy中,抛物线y=x2-4x+3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
解:(1)∵抛物线y=x2-4x+3与x轴交于点A,B(点A在点B左侧),
∴令y=0,则有x2-4x+3=(x-3)(x-1)=0,
解得x1=1,x2=3,
∴A(1,0),B(3,0).
∵抛物线y=x2-4x+3与y轴交于点C,
∴令x=0,得y=3,
∴C(0,3).
设直线BC的表达式为y=kx+b(k≠0),
将B(3,0),C(0,3)代入y=kx+b,得 解得
∴直线BC的表达式为y=-x+3;
(2)垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC交于点N(x3,y3).若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,-1).
由题意可知,点P(x1,y1),Q(x2,y2)(x1∴x1+x2=4.
如解图①,当x1<x2且x2=x3时,
此时N、B、Q三点重合,x3=3,
此时x1+x2+x3=1+3+3=7;
第2题解图①
如解图②,当x1=x2<x3时,
此时点P、Q重合且在抛物线顶点处,
此时点P纵坐标为-1,
将y=-1代入直线BC的表达式,则x3=4,
此时x1+x2+x3=2+2+4=8;
第2题解图②
结合解图①,解图②,
当x1<x2<x3时,则3<x3<4,
当直线l位于x轴上方或抛物线顶点下方时,
均不满足x1∴7<x1+x2+x3<8.
第2题解图①
第2题解图②
3.(2021海淀区二模)在平面直角坐标系xOy中,抛物线y=x2-2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.
(1)求抛物线的对称轴(用含m的式子表示);
解:(1)抛物线y=x2-2mx+m2的对称轴为直线x= =m;
(2)将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
①当m=0时,若x1<x2,判断y1与y2的大小关系,并说明理由;
(2)①y1>y2,理由如下:
当m=0时,二次函数解析式是y=x2,对称轴为y轴;
∴图形G如解图①.
第3题解图①
∴图形G上的点的横纵坐标x和y,满足y随x的增大而减小.
∵x1y2;
②若对于x1=m-2,x2=m+2,都有y1>y2,求m的取值范围.
②通过计算可知,抛物线翻折之前M、N对应点的坐标分别为
P(m-2,4),Q(m+2,4)为抛物线上关于对称轴x=m对称的两点,
下面讨论当m变化时,y轴与点P,Q的相对位置:
(ⅰ)如解图②,当y轴在点P左侧时(含点P),
第3题解图②
经翻折后,得到点M,N的纵坐标相同,
即y1=y2,不符合题意;
(ⅱ)如解图③,当y轴在点Q右侧时(含点Q),
第3题解图③
第3题解图④
(ⅲ)如解图④,当y轴在点P,Q之间时(不含点P,Q),
点M,N分别和点P,Q重合,
y1=y2,不符合题意;
经翻折后,点N在l下方,点M,P重合,在l上方,
y1>y2,符合题意.
此时有m-2<0综上所述,m的取值范围为-24.(2021朝阳区二模)在平面直角坐标系xOy中,点P(x1,y1),Q(x2,y2)为抛物线y=ax2-2ahx+ah2+1(a<0)上的两点.
(1)当h=1时,求抛物线的对称轴;
解:(1)当h=1时,抛物线的表达式为y=ax2-2ax+a+1,
∴y=a(x-1)2+1,
∴抛物线的对称轴为直线x=1;
(2)若对于0≤x1≤2,4-h≤x2≤5-h,都有y1≥y2,求h的取值范围.
(2)设抛物线上四个点的坐标为A(0,yA),B(2,yB),C(4-h,yC),D(5-h,yD).
∵a<0,
∴y1的最小值必为yA或yB.
抛物线的对称轴为直线x= =h.
①由a<0可知,当2≤h≤时,存在y2≥y1,不符合题意;
②当h<2时,总有4-h>2.
∵当x>h时,y随x的增大而减小,
∴yB>yC>yD.
当h≤ 时,4-h-h≥ .
∴yA≥yC>yD,符合题意.
当∴yA③当h> 时,
∵当x∴yC当h≥5时,5-h≤0.
∴yD≤yA,符合题意.
当0.
∴yD>yA,不符合题意.
综上所述,h的取值范围是h≤ 或h≥5.
5. (2021房山区一模)在平面直角坐标系xOy中,抛物线y=ax2-2ax+c(a≠0)被x轴截得的线段长度为4.
(1)求抛物线的对称轴;
解:(1)由抛物线y=ax2-2ax+c(a≠0)可得,
抛物线的对称轴为直线x= =1;
(2)求c的值(用含a的式子表示);
(2)设抛物线与x轴的交点横坐标分别为x1,x2,且x1在x2的右侧,由题意可得x1-x2=4,
∴ax2-2ax+c=0,
∴x1+x2=2,x1·x2= ,
∴(x1-x2)2=(x1+x2)2-4x1x2=16,∴4- =16,
解得c=-3a;
(3)若点M(x1,3),N(x2,3)为抛物线上不重合的两点(其中x1(3)由(2)及点M(x1,3),N(x2,3)为抛物线上不重合的两点(其中x1∴b2-4ac=4a2+4a(3a+3)>0,
解得a>0或a< ,
∴根据一元二次方程的公式法可得x=1± ,
则x1·x2=-3- ,
①当a>0时,由x1∵x1(x2-5)≤0,即x1x2-5x1≤0,
∴-3- -5(1- )≤0,化简得 ≤8,
解得-1≤a≤ ,
∵a>0,
∴0②当a< 时,由x1由①可得-3- -5(1+ )≤0,化简得- ≤8,
解得-1≤a≤ ,
∵a<- ,
∴-1≤a<- .
综上所述,a的取值范围为06. (2021大兴区一模)在平面直角坐标系xOy中,抛物线y=x2-2bx+b2-2(b>0)经过点A(m,n).
(1)用含b的代数式表示抛物线顶点的坐标;
解:(1)∵y=x2-2bx+b2-2=(x-b)2-2,
∴顶点坐标为(b,-2);
(2)若抛物线经过点B(0,2),且满足0(2)把(0,2)代入y=x2-2bx+b2-2(b>0),
得b=2或b=-2(舍去),
∴b=2,
∴抛物线解析式为y=x2-4x+2,对称轴为直线x=2,
∴顶点坐标为(2,-2).
如解图①,结合函数图象可得,
第6题解图①
在顶点处n取得最小值-2;
当x=0时,y=2,∴当0<m<3时,-2≤n<2;
(3)若3≤m≤5时,n≤2,结合函数图象,直接写出b的取值范围.
①当3≤m≤5≤b时,ymax=(3-b)2-2≤2,
∴1≤b≤5,矛盾,不成立.
②当3≤b≤5时,
则当x=3时,y=(3-b)2-2≤2,得1≤b≤5,
且当x=5时,y=(5-b)2-2≤2,得3≤b≤7,
∴3≤b≤5;
第6题解图②
(3)如解图②,
③当b≤3≤m≤5时,
ymax=(5-b)2-2≤2,得3≤b≤7,矛盾,不成立.
综上所述,b的取值范围为3≤b≤5.
第6题解图②
类型二 公共点问题
1.在平面直角坐标系xOy中,抛物线
y=mx2-2mx+n(m≠0)与x轴交于点A(-2,0),B.
(1)求出抛物线的对称轴;
综合提升
三阶
考向一 定抛物线与动线段
第1题图
解:(1)∵抛物线y=mx2-2mx+n,
∴抛物线的对称轴为直线x=- =1;
(2)直线y= x-4m-n过点B,且与抛物线的另一个交点为C.
①分别求直线和抛物线所对应的函数表达式;
(2)①∵抛物线是轴对称图形,
∴点A、B关于直线x=1对称.
∵点A的坐标为(-2,0),∴点B的坐标为(4,0).
∵抛物线y=mx2-2mx+n过点B,
直线y= x-4m-n过点B,
∴ 16m-8m+n=0,
2-4m-n=0,
解得 m= ,
n=4,
∴直线所对应的函数表达式为y= x-2,抛物线所对应的函数表达式为y= x2+x+4;
②点P为抛物线对称轴上的动点,过点P的两条直线l1:y=x+a和
l2:y=-x+b组成图形G.当图形G与线段BC有公共点时,直接写出点P的纵坐标t的取值范围.
联立 ,解得
∵点B的坐标为(4,0),∴点C的坐标为(-3, ).
当直线l2:y=-x+b1过点B时,
0=-4+b1,解得b1=4,
∴此时直线l2所对应的函数表达式为y=-x+4,
第1题解图
【解法提示】如解图,
当x=1时,y=-x+4=3,
∴点P1的坐标为(1,3);
第1题解图
当直线l2:y=-x+b2过点C时,
=3+b2,解得b2= ,
∴此时直线l2所对应的函数表达式为y=-x ,
当x=1时,y=-x = ,∴点P2的坐标为(1, ),
∴当图形G与线段BC有公共点时,
点P的纵坐标t的取值范围为 ≤ t ≤3.
②点P的纵坐标t的取值范围为 ≤t≤3.
2. 抛物线M:y=ax2-4ax+a-1(a≠0)与x轴交于A,B两点(点A在点B左侧),抛物线的顶点为D.
(1)抛物线M的对称轴是直线________;
x=2
第2题图
【解法提示】∵抛物线M:y=ax2-4ax+a-1(a≠0),
∴抛物线的对称轴为直线x= =2.
(2)当AB=2时,求抛物线M的函数表达式以及顶点D的坐标;
(2)∵抛物线M:y=ax2-4ax+a-1(a≠0)的对称轴为直线x=2,抛物线M与x轴的交点为点A,点B(点A在点B的左侧),AB=2,
∴点A,B的坐标分别为(1,0),(3,0).
∵点A在抛物线M上,
∴将点A的坐标代入抛物线的函数表达式,得a-4a+a-1=0,
解得a=-12,
∴抛物线M的函数表达式为y=- x2+2x-32=- (x-2)2+12,
∴顶点D的坐标为(2, );
(3)在(2)的条件下,直线l:y=kx+b(k≠0)经过抛物线的顶点D,直线y=n与抛物线M有两个公共点,它们的横坐标分别记为x1,x2,直线y=n与直线l的交点的横坐标记为x3(x3<4),若当-2≤n≤-1时,总有x1-x3<x3-x2<0,请结合函数的图象,直接写出k的取值范围.
第2题解图
由(2)知点D的坐标为(2, ).
当y=-1时,- (-2)2+ =-2,解得x=2± ,
当y=-2时,- (x-2)2+ =-2,解得x=2± .
∵直线y=n与直线l的交点横坐标记为x3(x3<4),
且当-2≤n≤-1时,总有x1-x3<x3-x2<0,
∴可以得出
【解法提示】如解图,
∵x3<4,∴2<x3<4,k<0,当直线l:y=kx+b(k≠0)经过抛物线的顶点D(2, )和(4,-2)时, 解得k= ,
∴k的取值范围为k< .
(3)k的取值范围为k< .
第2题解图
3. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,-3).
(1)求抛物线的解析式;
解:(1)由题意可得,m-4=-3,
∴m=1,
∴抛物线的解析式为y=x2-2x-3;
第3题图
(2)当a-3≤x≤a时,函数有最小值为5,求a的值;
(2)∵抛物线的解析式为y=x2-2x-3=(x-1)2-4,
∴抛物线的对称轴为直线x=1,当x=1时,函数有最小值,最小值为-4.
∵当a-3≤x≤a时,函数有最小值为5,
∴x的取值范围一定在对称轴的左侧或右侧,
①当a≤1时,函数在x=a处取得最小值,最小值为5,
∴(a-1)2-4=5,
解得a1=4,a2=-2.
∵a≤1,
∴a=-2;
②当a-3≥1,即a≥4时,函数在x=a-3处取得最小值,最小值为5,
∴(a-3-1)2-4=5,
解得a1=7,a2=1.
∵a≥4,
∴a=7,
综上所述,a的值为-2或7;
(3)将抛物线在B,C之间的部分记为图象G(包含B,C两点),若直线
y=5x+b与图象G有公共点,请直接写出b的取值范围.
【解法提示】当x=0时,直线y=5x+b≤-3,解得b≤-3;
当直线y=5x+b与抛物线相切时,得x2-7x-(3+b)=0,49-4(-3-b)=0,解得b=- ,此时x= >3,切点在点B的右侧,不符合题意,把(3,0)代入y=5x+b中,得到b=-15,
∴符合题意的b的取值范围是-15≤b≤-3.
(3)b的取值范围是-15≤b≤-3.
1. 已知:二次函数C1:y1=ax2+2ax+a-1(a≠0).
(1)把二次函数C1的表达式化成y=a(x-h)2+b(a≠0)的形式,并写出顶点坐标;
综合提升
三阶
考向二 动抛物线与定线(线段、射线、直线)
第1题图
解:(1)y1=ax2+2ax+a-1=a(x+1)2-1,
∴二次函数C1的顶点坐标为(-1,-1);
(2)已知二次函数C1的图象经过点A(-3,1).
①求a的值;
(2)①∵二次函数C1的图象经过点A(-3,1),
∴a(-3+1)2-1=1,
∴a= ;
②点B在二次函数C1的图象上,点A,B关于对称轴对称,连接AB.二次函数C2:y2=kx2+kx(k≠0)的图象,与线段AB只有一个交点,求k的取值范围.
②∵A(-3,1),对称轴为直线x=-1,点A,B关于对称轴对称,
∴B(1,1),
当k>0时,
二次函数C2:y2=kx2+kx(k≠0)的图象经过A(-3,1)时,
1=9k-3k,解得k= ,
二次函数C2:y2=kx2+kx(k≠0)的图象经过B(1,1)时,
1=k+k,解得k= ,
∴ ≤ k< .
当k<0时,∵二次函数C2:y2=kx2+kx=k(x+ )2- k,若使二次函数C2与线段AB仅有一个交点,
∴- k=1,
∴k=-4,
综上所述,k的取值范围是 ≤k< 或k=-4.
2. (2021燕山区二模)在平面直角坐标系xOy中,抛物线
y=ax2-2ax-3a(a≠0).
(1)求抛物线的对称轴及抛物线与y轴交点坐标;
第1题图
解:(1)∵抛物线y=ax2-2ax-3a(a≠0),
∴抛物线的对称轴是直线x=- =1,
令x=0,则y=-3a,
∴抛物线与y轴的交点坐标为(0,-3a) ;
(2)已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.
(2)y=ax2-2ax-3a=a(x2-2x-3)=a(x+1)(x-3),
∴抛物线与x轴交于点A(-1,0),D(3,0),与y轴交于点E(0,-3a),顶点坐标是(1,-4a).
由题意得点C(0,4),B(3,4),
第2题解图①
当a>0时,如解图①,显然抛物线与线段BC无公共点.
第2题解图②
当a<0时,
如解图②,若抛物线的顶点在线段BC上,则顶点坐标为(1,4),
∴-4a=4,∴a=-1.
如解图③,若抛物线的顶点不在线段BC上,由抛物线与线段BC恰有一个公共点,得-3a>4,
∴a < .
综上所述,a的取值范围是a <- 或a=-1.
第2题解图③
综合提升
三阶
考向三 动抛物线与动线段
1. (2021东城区二模)在平面直角坐标系xOy中,抛物线y=ax2-3ax+1与y轴交于点A.
(1)求抛物线的对称轴;
解:(1)由抛物线y=ax2-3ax+1,可知x= = ,
∴抛物线的对称轴为直线x= ;
(2)点B是点A关于对称轴的对称点,求点B的坐标;
(2)∵抛物线y=ax2-3ax+1与y轴交于点A,
令x=0,y=1,
∴点A的坐标为(0,1).
∵点B是点A关于直线x= 的对称点,
∴点B的坐标为(3,1);
(3)已知点P(0,2),Q(a+1,1).若线段PQ与抛物线恰有一个公共点,结合函数图象,求a的取值范围.
(3)∵点A (0,1),点B (3,1),点 P(0,2),点
Q(a+1,1),
∴点 P在点A 的上方,点Q在直线y=1上.
①当a>0时,a+1>1,点Q在点A的右侧,
第1题解图①
(i)如解图①,当a+1<3,即a<2时,点Q在点B的左侧,
结合函数图象,可知线段PQ与抛物线没有公共点;
(ii)如解图②,当a+1≥3,即a≥2时,点Q在点B的右侧,或与点B重合,
结合函数图象,可知线段PQ与抛物线恰有一个公共点;
第1题解图②
②当a<0时,a+1<1,点Q在点B的左侧,
(i)如解图③,当0≤a+1<1,即-1≤a<0时,点Q在点A的右侧,或与点A重合,
结合函数图象,可知线段PQ与抛物线恰有一个公共点;
第1题解图③
(ii)如解图④,当a+1<0,即a<-1时,点Q在点A的左侧,结合函数图象,可知线段PQ与抛物线没有公共点.
综上所述,a的取值范围是-1≤a<0或a≥2.
第1题解图④
2. (2022朝阳区期末)在平面直角坐标系xOy中,抛物线y=ax2+bx经过点(3,3).
(1)用含a的式子表示b;
解:(1)将点(3,3)代入y=ax2+bx中,得9a+3b=3.
∴b=-3a+1;
(2)直线y=x+4a+4与直线y=4交于点B,求点B的坐标(用含a的式子表示);
(2)令x+4a+4=4,得x=-4a.
∴B(-4a,4);
(3)在(2)的条件下,已知点A(1,4).若抛物线与线段AB恰有一个公共点,直接写出a(a<0)的取值范围.
【解法提示】∵a<0,∴抛物线开口向下.∵A(1,4),B(-4a,4),∴点A、B所在的直线为y=4,由(1)得b=1-3a,则抛物线可化为
y=ax2+(1-3a)x,分两种情况讨论:①当抛物线y=ax2+(1-3a)x的顶点在线段AB上时,则1≤ ≤-4a或-4a≤ ≤1,方程
ax2+(1-3a)x=4的根的判别式b2-4ac=0,即(1-3a)2+16a=0,解得a1= ,a2=-1,当a1= 时, =6(不符合题意),
当a2=-1时, =2,则1≤ ≤-4a成立;②当抛物线经过点A时,即当x=1,y=4时,a+1-3a=4,解得a= ;∴a< 时,抛物线与线段AB恰有一个公共点,综上所述,a的取值范围为a=-1或a< 时,抛物线与线段AB恰有一个公共点.
(3)a的取值范围为a=-1或a< .
3. (2021北师大附中期中改编)在平面直角坐标系xOy中,抛物线F1:y=ax2+bx-1(a>1)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,已知点A的坐标为( ,0),
(1)求b的值(用含a的代数式表示);
解:(1)点A的坐标为( ,0),
将点A的坐标代入抛物线表达式并整理得b=1-a;
第3题图
(2)求点B的坐标;
(2)抛物线的表达式为y=ax2+(1-a)x-1,
令y=0,则x=1或x= ,
故点B的坐标为(1,0);
(3)设抛物线F1的顶点为P1,将该抛物线平移后得到抛物线F2,抛物线F2的顶点P2满足P1P2∥BC,并且抛物线F2过点B,
①设抛物线F2与直线BC的另一个交点为D,判断线段BC与CD的数量关系(不需证明),并直接写出点D的坐标;
【解法提示】如解图,根据平移的性质可得BC=P1P2=BD,∴CD=2BC;对于y=ax2+bx-1,令x=0,则y=-1;则点C(0,-1),因为点B是C、D的中点,点B坐标(1,0),由中点公式得D(2,1).
第3题解图
(3)①CD=2BC,D(2,1);
②求出抛物线F2与y轴的交点纵坐标的取值范围.
②设平移后抛物线表达式为y=ax2+b′x+c,图象过B(1,0),D(2,1),
将点B、D的坐标代入抛物线表达式y=ax2b′x+c得
解得c=2a-1,
∵a>1,∴c=2a-1>1,
抛物线F2与y轴的交点纵坐标的取值范围为c>1.
4. 在平面直角坐标系xOy中,抛物线y=-x2+2mx-m2+m的顶点为A.
(1)求抛物线的顶点坐标(用含m的式子表示);
解:(1)∵y=-x2+2mx-m2+m=-(x-m)2+m,
故点A的坐标为(m,m);
第4题图
(2)若点A在第一象限,且OA= ,求抛物线的解析式;
(2)∵点A在第一象限,且点A的坐标为(m,m),
则OA= m= ,解得m=1,
故抛物线的解析式为y=-x2+2x;
(3)已知点B(m-1,m-2),点C(2,2).若该抛物线与线段BC有公共点,结合函数图象,求出m的取值范围.
(3)将点B的坐标代入抛物线表达式得
m-2=-(m-1)2+2m(m-1)-m2+m,此方程无解;
将点C的坐标代入抛物线表达式得
2=-22+2m×2-m2+m,
解得m=2或3,
如解图①,当m≤2时,抛物线和线段BC有公共点;
第4题解图①
如解图②,当2第4题解图②
如解图③,当m≥3时,抛物线和线段BC有公共点;
第4题解图③
综上所述,m的取值范围为m≤2或m≥3.
考向拓展 动抛物线与动线段
1. (2022海淀区二模)在平面直角坐标系xOy中,已知二次函数y=mx2+2mx+3的图象与x轴交于点A(-3,0),与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
(1)求点B的坐标及该函数的表达式;
解:(1)∵二次函数y=mx2+2mx+3的图象与x轴交于点A(-3,0),与y轴交于点B,∴B(0,3),
把A(-3,0)代入y=mx2+2mx+3,得m=-1,
∴函数的表达式为y=-x2-2x+3;
第1题图
(2)若二次函数y=x2+2x+a的图象与F只有一个公共点,结合函数图象,求a的取值范围.
由题意知F的端点为A,B,
且经过抛物线y=-x2-2x+3的顶点C(-1,4),
∵二次函数y=x2+2x+a的图象对称轴为x=-1,且与F只有一个公共点,
∴分别把A、B、C三点坐标代入y=x2+2x+a中,可得a的值分别为-3、3、5.
第1题解图
(2)如解图,
结合函数图象可知,二次函数y=x2+2x+a的图象与F只有一个公共点时,
a的取值范围为-3≤a<3或a=5.
第1题解图
2. 在平面直角坐标系xOy中,抛物线y=mx2+4mx+4m-3(m>0)与x轴分别交于A、B两点(点A在点B的左侧).
(1)求抛物线的对称轴和顶点的坐标;
第2题图
解:(1)由题意得,抛物线y=mx2+4mx+4m-3=m(x+2)2-3,
∴抛物线的对称轴为直线x= =-2,
顶点坐标为(-2,-3);
(2)对于该抛物线上的两点 P(a,y1 ),Q(a+3,y2 ),若 y1>y2,求a的取值范围;
(2)∵m>0,
∴该函数图象开口向上,
∴抛物线上的点距离对称轴越远,y值越大.
∵点P(a,y1),Q(a+3,y2)在该抛物线上,且y1>y2,
∴点P到对称轴的距离大于点Q到对称轴的距离,
分三种情况讨论:
①当P、Q两点均在对称轴左侧(点Q可以在对称轴上)时,a+3≤-2,即a≤-5,
此时点P到对称轴的距离大于点Q到对称轴的距离,
∴a≤-5;
②当点P在对称轴左侧,点Q在对称轴右侧时,a<-2∵点P到对称轴的距离大于点Q到对称轴的距离,
∴-2-a>a+3-(-2),
解得a< ,∴-5③当P、Q两点均在对称轴右侧(点P可以在对称轴上)时,a≥-2,
此时点P到对称轴的距离小于点Q到对称轴的距离,不符合题意.
综上所述,a的取值范围为a< ;
(3)记抛物线y=-x2-2x+3在第二象限的部分为图形W.若抛物线y=mx2+4mx+4m-3与图形W有且只有一个交点,结合函数图象,求m的取值范围.
(3)设抛物线y=-x2-2x+3与x轴负半轴交于点C,与y轴交于点D,
则令y=0,解得x1=-3,x2=1(舍去),∴C(-3,0).
令x=0,得y=3,∴D(0,3).
当抛物线y=mx2+4mx+4m-3过点C时,
将C(-3,0)代入得,0=9m-12m+4m-3,
解得m=3;
第2题解图①
当抛物线y=mx2+4mx+4m-3过点D时,
将D(0,3)代入得,3=4m-3,
解得m= ;
第2题解图②
如解图①,
如解图②,
结合函数图象可得,若抛物线y=mx2+4mx+4m-3与图形W有且只有一个交点,则m的取值范围为图①
图②
第2题解图
类型三 整点问题
综合提升
三阶
1. (2022石景山区一模)在平面直角坐标系xOy中,抛物线
y=ax2+4ax+b(a>0)的顶点A在x轴上,与y轴交于点B.
(1)用含a的代数式表示b;
解:(1)∵y=ax2+4ax+b=a(x+2)2+(b-4a),
∴该抛物线顶点A的坐标为(-2,b-4a),
∵顶点A在x轴上,
∴b-4a=0,即b=4a;
(2)若∠BAO=45°,求a的值;
(2)∵b=4a,
∴抛物线的解析式为y=ax2+4ax+4a(a>0).
∵抛物线的顶点为A(-2,0),与y轴的交点B(0,4a)在y轴的正半轴,∠BAO=45°,
∴OB=OA=2,
∴4a=2,
∴a= ;
(3)横、纵坐标都是整数的点叫做整点.若抛物线在点A,B之间的部分与线段AB所围成的区域(不含边界)内恰好没有整点,结合函数的图象,直接写出a的取值范围.
【解法提示】∵点A(-2,0),点B(0,4a),
设直线AB的函数解析式为y=mx+n,
代入A(-2,0),B(0,4a),
得 ,解得
即直线AB的解析式为y=2ax+4a,
如解图①,当直线AB过点(-1,1)时,1=-2a+4a,解得a= ;
第1题解图①
当直线AB过点(-1,2)时,2=-2a+4a,解得a=1;
抛物线的顶点固定,a越大,开口越小,点B的纵坐标越大.
结合函数图象可得,a的取值范围为0<a≤ 或a=1.
第1题解图②
如解图②,
(3)0<a≤ 或a=1.
2. 在平面直角坐标系xOy中,抛物线C1:y=mx2+2mx+m-1沿x轴翻折得到抛物线C2.
(1)求抛物线C2的顶点坐标;
解:(1)顶点坐标为(-1,1);
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求抛物线C1和C2围成的封闭区域内(包括边界)整点的个数;
(2)①当m=1时,C1:y=x2+2x,C2:y=-x2-2x.
如解图,C1和C2围成的区域内(包括边界)整点有5个;
第2题解图
②如果抛物线C1和C2围成的封闭区域内(包括边界)恰有7个整点,求出m的取值范围.
②抛物线在C1和C2围成的区域内 (包括边界) 恰有7个整点,结合函数图象,可得抛物线与x轴的一个交点的横坐标的取值范围为 1≤x<2,
将(1,0)代入y=mx2+2mx+m-1,得到 m= ,
将(2,0)代入y=mx2+2mx+m-1,得到 m= ,
结合图象可得 <m≤ .
第2题解图
3. (2022门头沟区二模)在平面直角坐标系xOy中,抛物线
y=x2-2ax+a2的顶点为A,直线y=x+3与抛物线交于点B,C(点B在点C的左侧).
(1)求点A坐标;
第3题图
解:(1)∵y=x2-2ax+a2=(x-a)2,
∴顶点A(a,0);
(2)横、纵坐标都是整数的点叫做整点.线段BC及抛物线在B,C两点之间的部分围成的封闭区域(不含边界)记为W.
①当a=0时,结合函数图象,直接写出区域W内的整点个数;
由函数图象可知,区域W内的整点个数是4;
(2)①当a=0时,则抛物线y=x2,
如解图①所示,
第3题解图①
②如果区域W内有2个整点,请求出a的取值范围.
第3题解图②
②如解图②所示:
当抛物线经过(0,2),区域W内有1个整点,
此时a=- ;
当抛物线经过(0,1),区域W内有2个整点,
此时a=-1;
由函数图象可知,如果区域W内有2个整点,
a的取值范围为- <a≤-1.
专题七 二次函数综合题
类型一 对称性、增减性问题
1
类型二 公共点问题
2
类型三 整点问题
3
类型一 对称性、增减性问题
1.(2021朝阳区一模)在平面直角坐标系xOy中,抛物线
y=ax2+bx+a-4(a≠0)的对称轴是直线x=1.
(1)求抛物线y=ax2+bx+a-4(a≠0)的顶点坐标;
综合提升
三阶
解:(1)∵对称轴是直线x=1,
∴ =1,
∴b=-2a,
∴y=ax2-2ax+a-4=a(x-1)2-4,
∴顶点坐标为(1,-4);
(2)当-2≤x≤3时,y的最大值是5,求a的值;
(2)若a<0,则抛物线开口向下,y的最大值在对称轴处取得,从而y有最大值为-4,
∵当-2≤x≤3时,y的最大值是5,且抛物线的对称轴为直线x=1,
∴函数此时在x=1时取得最大值5,
这与y有最大值-4矛盾,从而a>0,
∴抛物线的顶点为图象的最低点.
∵1-(-2)>3-1,
∴当x=-2时,y=5,
代入y=a(x-1)2-4,得a(-2-1)2-4=5,
解得a=1;
(3)在(2)的条件下,当t≤x≤t+1时,y的最大值是m,最小值是n,且
m-n=3.求t的值.
(3)由(2)得,a=1,
∴y=(x-1)2-4.
①当t ≤ 1 ≤ t+1时,此时0 ≤ t ≤ 1,
∴n=-4,函数的最大值在t+1或t处取得,即m=t2-4或
m=(t-1)2-4,
∴m的最大值为-3,
此时m-n=1,
不符合题意,舍去;
②当t+1<1,即t<0时,
m=(t-1)2-4,n=(t+1-1)2-4=t2-4,
∵m-n=3,
∴(t-1)2-4-(t2-4)=3,
∴t=-1;
③当t>1时,
同理可得t=2,
综上所述,t的值为-1或2.
2. (2023北京)在平面直角坐标系xOy中,抛物线y=x2-4x+3与x轴交于点A,B(点A在点B的左侧),与y轴交于点C.
(1)求直线BC的表达式;
解:(1)∵抛物线y=x2-4x+3与x轴交于点A,B(点A在点B左侧),
∴令y=0,则有x2-4x+3=(x-3)(x-1)=0,
解得x1=1,x2=3,
∴A(1,0),B(3,0).
∵抛物线y=x2-4x+3与y轴交于点C,
∴令x=0,得y=3,
∴C(0,3).
设直线BC的表达式为y=kx+b(k≠0),
将B(3,0),C(0,3)代入y=kx+b,得 解得
∴直线BC的表达式为y=-x+3;
(2)垂直于y轴的直线l与抛物线交于点P(x1,y1),Q(x2,y2),与直线BC交于点N(x3,y3).若x1<x2<x3,结合函数的图象,求x1+x2+x3的取值范围.
(2)∵y=x2-4x+3=(x-2)2-1,
∴抛物线的对称轴为直线x=2,顶点坐标为(2,-1).
由题意可知,点P(x1,y1),Q(x2,y2)(x1
如解图①,当x1<x2且x2=x3时,
此时N、B、Q三点重合,x3=3,
此时x1+x2+x3=1+3+3=7;
第2题解图①
如解图②,当x1=x2<x3时,
此时点P、Q重合且在抛物线顶点处,
此时点P纵坐标为-1,
将y=-1代入直线BC的表达式,则x3=4,
此时x1+x2+x3=2+2+4=8;
第2题解图②
结合解图①,解图②,
当x1<x2<x3时,则3<x3<4,
当直线l位于x轴上方或抛物线顶点下方时,
均不满足x1
第2题解图①
第2题解图②
3.(2021海淀区二模)在平面直角坐标系xOy中,抛物线y=x2-2mx+m2与y轴的交点为A,过点A作直线l垂直于y轴.
(1)求抛物线的对称轴(用含m的式子表示);
解:(1)抛物线y=x2-2mx+m2的对称轴为直线x= =m;
(2)将抛物线在y轴右侧的部分沿直线l翻折,其余部分保持不变,组成图形G.点M(x1,y1),N(x2,y2)为图形G上任意两点.
①当m=0时,若x1<x2,判断y1与y2的大小关系,并说明理由;
(2)①y1>y2,理由如下:
当m=0时,二次函数解析式是y=x2,对称轴为y轴;
∴图形G如解图①.
第3题解图①
∴图形G上的点的横纵坐标x和y,满足y随x的增大而减小.
∵x1
②若对于x1=m-2,x2=m+2,都有y1>y2,求m的取值范围.
②通过计算可知,抛物线翻折之前M、N对应点的坐标分别为
P(m-2,4),Q(m+2,4)为抛物线上关于对称轴x=m对称的两点,
下面讨论当m变化时,y轴与点P,Q的相对位置:
(ⅰ)如解图②,当y轴在点P左侧时(含点P),
第3题解图②
经翻折后,得到点M,N的纵坐标相同,
即y1=y2,不符合题意;
(ⅱ)如解图③,当y轴在点Q右侧时(含点Q),
第3题解图③
第3题解图④
(ⅲ)如解图④,当y轴在点P,Q之间时(不含点P,Q),
点M,N分别和点P,Q重合,
y1=y2,不符合题意;
经翻折后,点N在l下方,点M,P重合,在l上方,
y1>y2,符合题意.
此时有m-2<0
(1)当h=1时,求抛物线的对称轴;
解:(1)当h=1时,抛物线的表达式为y=ax2-2ax+a+1,
∴y=a(x-1)2+1,
∴抛物线的对称轴为直线x=1;
(2)若对于0≤x1≤2,4-h≤x2≤5-h,都有y1≥y2,求h的取值范围.
(2)设抛物线上四个点的坐标为A(0,yA),B(2,yB),C(4-h,yC),D(5-h,yD).
∵a<0,
∴y1的最小值必为yA或yB.
抛物线的对称轴为直线x= =h.
①由a<0可知,当2≤h≤时,存在y2≥y1,不符合题意;
②当h<2时,总有4-h>2.
∵当x>h时,y随x的增大而减小,
∴yB>yC>yD.
当h≤ 时,4-h-h≥ .
∴yA≥yC>yD,符合题意.
当
∵当x
∴yD≤yA,符合题意.
当
∴yD>yA,不符合题意.
综上所述,h的取值范围是h≤ 或h≥5.
5. (2021房山区一模)在平面直角坐标系xOy中,抛物线y=ax2-2ax+c(a≠0)被x轴截得的线段长度为4.
(1)求抛物线的对称轴;
解:(1)由抛物线y=ax2-2ax+c(a≠0)可得,
抛物线的对称轴为直线x= =1;
(2)求c的值(用含a的式子表示);
(2)设抛物线与x轴的交点横坐标分别为x1,x2,且x1在x2的右侧,由题意可得x1-x2=4,
∴ax2-2ax+c=0,
∴x1+x2=2,x1·x2= ,
∴(x1-x2)2=(x1+x2)2-4x1x2=16,∴4- =16,
解得c=-3a;
(3)若点M(x1,3),N(x2,3)为抛物线上不重合的两点(其中x1
解得a>0或a< ,
∴根据一元二次方程的公式法可得x=1± ,
则x1·x2=-3- ,
①当a>0时,由x1
∴-3- -5(1- )≤0,化简得 ≤8,
解得-1≤a≤ ,
∵a>0,
∴0
解得-1≤a≤ ,
∵a<- ,
∴-1≤a<- .
综上所述,a的取值范围为0
(1)用含b的代数式表示抛物线顶点的坐标;
解:(1)∵y=x2-2bx+b2-2=(x-b)2-2,
∴顶点坐标为(b,-2);
(2)若抛物线经过点B(0,2),且满足0
得b=2或b=-2(舍去),
∴b=2,
∴抛物线解析式为y=x2-4x+2,对称轴为直线x=2,
∴顶点坐标为(2,-2).
如解图①,结合函数图象可得,
第6题解图①
在顶点处n取得最小值-2;
当x=0时,y=2,∴当0<m<3时,-2≤n<2;
(3)若3≤m≤5时,n≤2,结合函数图象,直接写出b的取值范围.
①当3≤m≤5≤b时,ymax=(3-b)2-2≤2,
∴1≤b≤5,矛盾,不成立.
②当3≤b≤5时,
则当x=3时,y=(3-b)2-2≤2,得1≤b≤5,
且当x=5时,y=(5-b)2-2≤2,得3≤b≤7,
∴3≤b≤5;
第6题解图②
(3)如解图②,
③当b≤3≤m≤5时,
ymax=(5-b)2-2≤2,得3≤b≤7,矛盾,不成立.
综上所述,b的取值范围为3≤b≤5.
第6题解图②
类型二 公共点问题
1.在平面直角坐标系xOy中,抛物线
y=mx2-2mx+n(m≠0)与x轴交于点A(-2,0),B.
(1)求出抛物线的对称轴;
综合提升
三阶
考向一 定抛物线与动线段
第1题图
解:(1)∵抛物线y=mx2-2mx+n,
∴抛物线的对称轴为直线x=- =1;
(2)直线y= x-4m-n过点B,且与抛物线的另一个交点为C.
①分别求直线和抛物线所对应的函数表达式;
(2)①∵抛物线是轴对称图形,
∴点A、B关于直线x=1对称.
∵点A的坐标为(-2,0),∴点B的坐标为(4,0).
∵抛物线y=mx2-2mx+n过点B,
直线y= x-4m-n过点B,
∴ 16m-8m+n=0,
2-4m-n=0,
解得 m= ,
n=4,
∴直线所对应的函数表达式为y= x-2,抛物线所对应的函数表达式为y= x2+x+4;
②点P为抛物线对称轴上的动点,过点P的两条直线l1:y=x+a和
l2:y=-x+b组成图形G.当图形G与线段BC有公共点时,直接写出点P的纵坐标t的取值范围.
联立 ,解得
∵点B的坐标为(4,0),∴点C的坐标为(-3, ).
当直线l2:y=-x+b1过点B时,
0=-4+b1,解得b1=4,
∴此时直线l2所对应的函数表达式为y=-x+4,
第1题解图
【解法提示】如解图,
当x=1时,y=-x+4=3,
∴点P1的坐标为(1,3);
第1题解图
当直线l2:y=-x+b2过点C时,
=3+b2,解得b2= ,
∴此时直线l2所对应的函数表达式为y=-x ,
当x=1时,y=-x = ,∴点P2的坐标为(1, ),
∴当图形G与线段BC有公共点时,
点P的纵坐标t的取值范围为 ≤ t ≤3.
②点P的纵坐标t的取值范围为 ≤t≤3.
2. 抛物线M:y=ax2-4ax+a-1(a≠0)与x轴交于A,B两点(点A在点B左侧),抛物线的顶点为D.
(1)抛物线M的对称轴是直线________;
x=2
第2题图
【解法提示】∵抛物线M:y=ax2-4ax+a-1(a≠0),
∴抛物线的对称轴为直线x= =2.
(2)当AB=2时,求抛物线M的函数表达式以及顶点D的坐标;
(2)∵抛物线M:y=ax2-4ax+a-1(a≠0)的对称轴为直线x=2,抛物线M与x轴的交点为点A,点B(点A在点B的左侧),AB=2,
∴点A,B的坐标分别为(1,0),(3,0).
∵点A在抛物线M上,
∴将点A的坐标代入抛物线的函数表达式,得a-4a+a-1=0,
解得a=-12,
∴抛物线M的函数表达式为y=- x2+2x-32=- (x-2)2+12,
∴顶点D的坐标为(2, );
(3)在(2)的条件下,直线l:y=kx+b(k≠0)经过抛物线的顶点D,直线y=n与抛物线M有两个公共点,它们的横坐标分别记为x1,x2,直线y=n与直线l的交点的横坐标记为x3(x3<4),若当-2≤n≤-1时,总有x1-x3<x3-x2<0,请结合函数的图象,直接写出k的取值范围.
第2题解图
由(2)知点D的坐标为(2, ).
当y=-1时,- (-2)2+ =-2,解得x=2± ,
当y=-2时,- (x-2)2+ =-2,解得x=2± .
∵直线y=n与直线l的交点横坐标记为x3(x3<4),
且当-2≤n≤-1时,总有x1-x3<x3-x2<0,
∴可以得出
【解法提示】如解图,
∵x3<4,∴2<x3<4,k<0,当直线l:y=kx+b(k≠0)经过抛物线的顶点D(2, )和(4,-2)时, 解得k= ,
∴k的取值范围为k< .
(3)k的取值范围为k< .
第2题解图
3. 在平面直角坐标系xOy中,抛物线y=mx2-2mx+m-4(m≠0)与x轴交于A,B两点(点A在点B左侧),与y轴交于点C(0,-3).
(1)求抛物线的解析式;
解:(1)由题意可得,m-4=-3,
∴m=1,
∴抛物线的解析式为y=x2-2x-3;
第3题图
(2)当a-3≤x≤a时,函数有最小值为5,求a的值;
(2)∵抛物线的解析式为y=x2-2x-3=(x-1)2-4,
∴抛物线的对称轴为直线x=1,当x=1时,函数有最小值,最小值为-4.
∵当a-3≤x≤a时,函数有最小值为5,
∴x的取值范围一定在对称轴的左侧或右侧,
①当a≤1时,函数在x=a处取得最小值,最小值为5,
∴(a-1)2-4=5,
解得a1=4,a2=-2.
∵a≤1,
∴a=-2;
②当a-3≥1,即a≥4时,函数在x=a-3处取得最小值,最小值为5,
∴(a-3-1)2-4=5,
解得a1=7,a2=1.
∵a≥4,
∴a=7,
综上所述,a的值为-2或7;
(3)将抛物线在B,C之间的部分记为图象G(包含B,C两点),若直线
y=5x+b与图象G有公共点,请直接写出b的取值范围.
【解法提示】当x=0时,直线y=5x+b≤-3,解得b≤-3;
当直线y=5x+b与抛物线相切时,得x2-7x-(3+b)=0,49-4(-3-b)=0,解得b=- ,此时x= >3,切点在点B的右侧,不符合题意,把(3,0)代入y=5x+b中,得到b=-15,
∴符合题意的b的取值范围是-15≤b≤-3.
(3)b的取值范围是-15≤b≤-3.
1. 已知:二次函数C1:y1=ax2+2ax+a-1(a≠0).
(1)把二次函数C1的表达式化成y=a(x-h)2+b(a≠0)的形式,并写出顶点坐标;
综合提升
三阶
考向二 动抛物线与定线(线段、射线、直线)
第1题图
解:(1)y1=ax2+2ax+a-1=a(x+1)2-1,
∴二次函数C1的顶点坐标为(-1,-1);
(2)已知二次函数C1的图象经过点A(-3,1).
①求a的值;
(2)①∵二次函数C1的图象经过点A(-3,1),
∴a(-3+1)2-1=1,
∴a= ;
②点B在二次函数C1的图象上,点A,B关于对称轴对称,连接AB.二次函数C2:y2=kx2+kx(k≠0)的图象,与线段AB只有一个交点,求k的取值范围.
②∵A(-3,1),对称轴为直线x=-1,点A,B关于对称轴对称,
∴B(1,1),
当k>0时,
二次函数C2:y2=kx2+kx(k≠0)的图象经过A(-3,1)时,
1=9k-3k,解得k= ,
二次函数C2:y2=kx2+kx(k≠0)的图象经过B(1,1)时,
1=k+k,解得k= ,
∴ ≤ k< .
当k<0时,∵二次函数C2:y2=kx2+kx=k(x+ )2- k,若使二次函数C2与线段AB仅有一个交点,
∴- k=1,
∴k=-4,
综上所述,k的取值范围是 ≤k< 或k=-4.
2. (2021燕山区二模)在平面直角坐标系xOy中,抛物线
y=ax2-2ax-3a(a≠0).
(1)求抛物线的对称轴及抛物线与y轴交点坐标;
第1题图
解:(1)∵抛物线y=ax2-2ax-3a(a≠0),
∴抛物线的对称轴是直线x=- =1,
令x=0,则y=-3a,
∴抛物线与y轴的交点坐标为(0,-3a) ;
(2)已知点B(3,4),将点B向左平移3个单位长度,得到点C.若抛物线与线段BC恰有一个公共点,结合函数的图象,求a的取值范围.
(2)y=ax2-2ax-3a=a(x2-2x-3)=a(x+1)(x-3),
∴抛物线与x轴交于点A(-1,0),D(3,0),与y轴交于点E(0,-3a),顶点坐标是(1,-4a).
由题意得点C(0,4),B(3,4),
第2题解图①
当a>0时,如解图①,显然抛物线与线段BC无公共点.
第2题解图②
当a<0时,
如解图②,若抛物线的顶点在线段BC上,则顶点坐标为(1,4),
∴-4a=4,∴a=-1.
如解图③,若抛物线的顶点不在线段BC上,由抛物线与线段BC恰有一个公共点,得-3a>4,
∴a < .
综上所述,a的取值范围是a <- 或a=-1.
第2题解图③
综合提升
三阶
考向三 动抛物线与动线段
1. (2021东城区二模)在平面直角坐标系xOy中,抛物线y=ax2-3ax+1与y轴交于点A.
(1)求抛物线的对称轴;
解:(1)由抛物线y=ax2-3ax+1,可知x= = ,
∴抛物线的对称轴为直线x= ;
(2)点B是点A关于对称轴的对称点,求点B的坐标;
(2)∵抛物线y=ax2-3ax+1与y轴交于点A,
令x=0,y=1,
∴点A的坐标为(0,1).
∵点B是点A关于直线x= 的对称点,
∴点B的坐标为(3,1);
(3)已知点P(0,2),Q(a+1,1).若线段PQ与抛物线恰有一个公共点,结合函数图象,求a的取值范围.
(3)∵点A (0,1),点B (3,1),点 P(0,2),点
Q(a+1,1),
∴点 P在点A 的上方,点Q在直线y=1上.
①当a>0时,a+1>1,点Q在点A的右侧,
第1题解图①
(i)如解图①,当a+1<3,即a<2时,点Q在点B的左侧,
结合函数图象,可知线段PQ与抛物线没有公共点;
(ii)如解图②,当a+1≥3,即a≥2时,点Q在点B的右侧,或与点B重合,
结合函数图象,可知线段PQ与抛物线恰有一个公共点;
第1题解图②
②当a<0时,a+1<1,点Q在点B的左侧,
(i)如解图③,当0≤a+1<1,即-1≤a<0时,点Q在点A的右侧,或与点A重合,
结合函数图象,可知线段PQ与抛物线恰有一个公共点;
第1题解图③
(ii)如解图④,当a+1<0,即a<-1时,点Q在点A的左侧,结合函数图象,可知线段PQ与抛物线没有公共点.
综上所述,a的取值范围是-1≤a<0或a≥2.
第1题解图④
2. (2022朝阳区期末)在平面直角坐标系xOy中,抛物线y=ax2+bx经过点(3,3).
(1)用含a的式子表示b;
解:(1)将点(3,3)代入y=ax2+bx中,得9a+3b=3.
∴b=-3a+1;
(2)直线y=x+4a+4与直线y=4交于点B,求点B的坐标(用含a的式子表示);
(2)令x+4a+4=4,得x=-4a.
∴B(-4a,4);
(3)在(2)的条件下,已知点A(1,4).若抛物线与线段AB恰有一个公共点,直接写出a(a<0)的取值范围.
【解法提示】∵a<0,∴抛物线开口向下.∵A(1,4),B(-4a,4),∴点A、B所在的直线为y=4,由(1)得b=1-3a,则抛物线可化为
y=ax2+(1-3a)x,分两种情况讨论:①当抛物线y=ax2+(1-3a)x的顶点在线段AB上时,则1≤ ≤-4a或-4a≤ ≤1,方程
ax2+(1-3a)x=4的根的判别式b2-4ac=0,即(1-3a)2+16a=0,解得a1= ,a2=-1,当a1= 时, =6(不符合题意),
当a2=-1时, =2,则1≤ ≤-4a成立;②当抛物线经过点A时,即当x=1,y=4时,a+1-3a=4,解得a= ;∴a< 时,抛物线与线段AB恰有一个公共点,综上所述,a的取值范围为a=-1或a< 时,抛物线与线段AB恰有一个公共点.
(3)a的取值范围为a=-1或a< .
3. (2021北师大附中期中改编)在平面直角坐标系xOy中,抛物线F1:y=ax2+bx-1(a>1)与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,已知点A的坐标为( ,0),
(1)求b的值(用含a的代数式表示);
解:(1)点A的坐标为( ,0),
将点A的坐标代入抛物线表达式并整理得b=1-a;
第3题图
(2)求点B的坐标;
(2)抛物线的表达式为y=ax2+(1-a)x-1,
令y=0,则x=1或x= ,
故点B的坐标为(1,0);
(3)设抛物线F1的顶点为P1,将该抛物线平移后得到抛物线F2,抛物线F2的顶点P2满足P1P2∥BC,并且抛物线F2过点B,
①设抛物线F2与直线BC的另一个交点为D,判断线段BC与CD的数量关系(不需证明),并直接写出点D的坐标;
【解法提示】如解图,根据平移的性质可得BC=P1P2=BD,∴CD=2BC;对于y=ax2+bx-1,令x=0,则y=-1;则点C(0,-1),因为点B是C、D的中点,点B坐标(1,0),由中点公式得D(2,1).
第3题解图
(3)①CD=2BC,D(2,1);
②求出抛物线F2与y轴的交点纵坐标的取值范围.
②设平移后抛物线表达式为y=ax2+b′x+c,图象过B(1,0),D(2,1),
将点B、D的坐标代入抛物线表达式y=ax2b′x+c得
解得c=2a-1,
∵a>1,∴c=2a-1>1,
抛物线F2与y轴的交点纵坐标的取值范围为c>1.
4. 在平面直角坐标系xOy中,抛物线y=-x2+2mx-m2+m的顶点为A.
(1)求抛物线的顶点坐标(用含m的式子表示);
解:(1)∵y=-x2+2mx-m2+m=-(x-m)2+m,
故点A的坐标为(m,m);
第4题图
(2)若点A在第一象限,且OA= ,求抛物线的解析式;
(2)∵点A在第一象限,且点A的坐标为(m,m),
则OA= m= ,解得m=1,
故抛物线的解析式为y=-x2+2x;
(3)已知点B(m-1,m-2),点C(2,2).若该抛物线与线段BC有公共点,结合函数图象,求出m的取值范围.
(3)将点B的坐标代入抛物线表达式得
m-2=-(m-1)2+2m(m-1)-m2+m,此方程无解;
将点C的坐标代入抛物线表达式得
2=-22+2m×2-m2+m,
解得m=2或3,
如解图①,当m≤2时,抛物线和线段BC有公共点;
第4题解图①
如解图②,当2
如解图③,当m≥3时,抛物线和线段BC有公共点;
第4题解图③
综上所述,m的取值范围为m≤2或m≥3.
考向拓展 动抛物线与动线段
1. (2022海淀区二模)在平面直角坐标系xOy中,已知二次函数y=mx2+2mx+3的图象与x轴交于点A(-3,0),与y轴交于点B,将其图象在点A,B之间的部分(含A,B两点)记为F.
(1)求点B的坐标及该函数的表达式;
解:(1)∵二次函数y=mx2+2mx+3的图象与x轴交于点A(-3,0),与y轴交于点B,∴B(0,3),
把A(-3,0)代入y=mx2+2mx+3,得m=-1,
∴函数的表达式为y=-x2-2x+3;
第1题图
(2)若二次函数y=x2+2x+a的图象与F只有一个公共点,结合函数图象,求a的取值范围.
由题意知F的端点为A,B,
且经过抛物线y=-x2-2x+3的顶点C(-1,4),
∵二次函数y=x2+2x+a的图象对称轴为x=-1,且与F只有一个公共点,
∴分别把A、B、C三点坐标代入y=x2+2x+a中,可得a的值分别为-3、3、5.
第1题解图
(2)如解图,
结合函数图象可知,二次函数y=x2+2x+a的图象与F只有一个公共点时,
a的取值范围为-3≤a<3或a=5.
第1题解图
2. 在平面直角坐标系xOy中,抛物线y=mx2+4mx+4m-3(m>0)与x轴分别交于A、B两点(点A在点B的左侧).
(1)求抛物线的对称轴和顶点的坐标;
第2题图
解:(1)由题意得,抛物线y=mx2+4mx+4m-3=m(x+2)2-3,
∴抛物线的对称轴为直线x= =-2,
顶点坐标为(-2,-3);
(2)对于该抛物线上的两点 P(a,y1 ),Q(a+3,y2 ),若 y1>y2,求a的取值范围;
(2)∵m>0,
∴该函数图象开口向上,
∴抛物线上的点距离对称轴越远,y值越大.
∵点P(a,y1),Q(a+3,y2)在该抛物线上,且y1>y2,
∴点P到对称轴的距离大于点Q到对称轴的距离,
分三种情况讨论:
①当P、Q两点均在对称轴左侧(点Q可以在对称轴上)时,a+3≤-2,即a≤-5,
此时点P到对称轴的距离大于点Q到对称轴的距离,
∴a≤-5;
②当点P在对称轴左侧,点Q在对称轴右侧时,a<-2
∴-2-a>a+3-(-2),
解得a< ,∴-5
此时点P到对称轴的距离小于点Q到对称轴的距离,不符合题意.
综上所述,a的取值范围为a< ;
(3)记抛物线y=-x2-2x+3在第二象限的部分为图形W.若抛物线y=mx2+4mx+4m-3与图形W有且只有一个交点,结合函数图象,求m的取值范围.
(3)设抛物线y=-x2-2x+3与x轴负半轴交于点C,与y轴交于点D,
则令y=0,解得x1=-3,x2=1(舍去),∴C(-3,0).
令x=0,得y=3,∴D(0,3).
当抛物线y=mx2+4mx+4m-3过点C时,
将C(-3,0)代入得,0=9m-12m+4m-3,
解得m=3;
第2题解图①
当抛物线y=mx2+4mx+4m-3过点D时,
将D(0,3)代入得,3=4m-3,
解得m= ;
第2题解图②
如解图①,
如解图②,
结合函数图象可得,若抛物线y=mx2+4mx+4m-3与图形W有且只有一个交点,则m的取值范围为
图②
第2题解图
类型三 整点问题
综合提升
三阶
1. (2022石景山区一模)在平面直角坐标系xOy中,抛物线
y=ax2+4ax+b(a>0)的顶点A在x轴上,与y轴交于点B.
(1)用含a的代数式表示b;
解:(1)∵y=ax2+4ax+b=a(x+2)2+(b-4a),
∴该抛物线顶点A的坐标为(-2,b-4a),
∵顶点A在x轴上,
∴b-4a=0,即b=4a;
(2)若∠BAO=45°,求a的值;
(2)∵b=4a,
∴抛物线的解析式为y=ax2+4ax+4a(a>0).
∵抛物线的顶点为A(-2,0),与y轴的交点B(0,4a)在y轴的正半轴,∠BAO=45°,
∴OB=OA=2,
∴4a=2,
∴a= ;
(3)横、纵坐标都是整数的点叫做整点.若抛物线在点A,B之间的部分与线段AB所围成的区域(不含边界)内恰好没有整点,结合函数的图象,直接写出a的取值范围.
【解法提示】∵点A(-2,0),点B(0,4a),
设直线AB的函数解析式为y=mx+n,
代入A(-2,0),B(0,4a),
得 ,解得
即直线AB的解析式为y=2ax+4a,
如解图①,当直线AB过点(-1,1)时,1=-2a+4a,解得a= ;
第1题解图①
当直线AB过点(-1,2)时,2=-2a+4a,解得a=1;
抛物线的顶点固定,a越大,开口越小,点B的纵坐标越大.
结合函数图象可得,a的取值范围为0<a≤ 或a=1.
第1题解图②
如解图②,
(3)0<a≤ 或a=1.
2. 在平面直角坐标系xOy中,抛物线C1:y=mx2+2mx+m-1沿x轴翻折得到抛物线C2.
(1)求抛物线C2的顶点坐标;
解:(1)顶点坐标为(-1,1);
(2)横、纵坐标都是整数的点叫做整点.
①当m=1时,求抛物线C1和C2围成的封闭区域内(包括边界)整点的个数;
(2)①当m=1时,C1:y=x2+2x,C2:y=-x2-2x.
如解图,C1和C2围成的区域内(包括边界)整点有5个;
第2题解图
②如果抛物线C1和C2围成的封闭区域内(包括边界)恰有7个整点,求出m的取值范围.
②抛物线在C1和C2围成的区域内 (包括边界) 恰有7个整点,结合函数图象,可得抛物线与x轴的一个交点的横坐标的取值范围为 1≤x<2,
将(1,0)代入y=mx2+2mx+m-1,得到 m= ,
将(2,0)代入y=mx2+2mx+m-1,得到 m= ,
结合图象可得 <m≤ .
第2题解图
3. (2022门头沟区二模)在平面直角坐标系xOy中,抛物线
y=x2-2ax+a2的顶点为A,直线y=x+3与抛物线交于点B,C(点B在点C的左侧).
(1)求点A坐标;
第3题图
解:(1)∵y=x2-2ax+a2=(x-a)2,
∴顶点A(a,0);
(2)横、纵坐标都是整数的点叫做整点.线段BC及抛物线在B,C两点之间的部分围成的封闭区域(不含边界)记为W.
①当a=0时,结合函数图象,直接写出区域W内的整点个数;
由函数图象可知,区域W内的整点个数是4;
(2)①当a=0时,则抛物线y=x2,
如解图①所示,
第3题解图①
②如果区域W内有2个整点,请求出a的取值范围.
第3题解图②
②如解图②所示:
当抛物线经过(0,2),区域W内有1个整点,
此时a=- ;
当抛物线经过(0,1),区域W内有2个整点,
此时a=-1;
由函数图象可知,如果区域W内有2个整点,
a的取值范围为- <a≤-1.
同课章节目录
