人教版数学八下 16.3 二次根式的加减(希沃课件+图片版PPT)仅适用希沃白板
文档属性
| 名称 | 人教版数学八下 16.3 二次根式的加减(希沃课件+图片版PPT)仅适用希沃白板 |

|
|
| 格式 | zip | ||
| 文件大小 | 21.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览








文档简介
(共56张PPT)
16.3 二次根式的加减/
16.3二次根式的加减
第一课时
第二课时
人教版 数学 八年级 下册
16.3 二次根式的加减/
二次根式的加减运算
第一课时
返回
16.3 二次根式的加减/
有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
导入新知
16.3 二次根式的加减/
1. 理解二次根式可以合并的条件.
3. 能熟练地进行二次根式的加减法运算.
素养目标
2. 类比整式的合并同类项,掌握二次根式的加减运算法则.
16.3 二次根式的加减/
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;......
知识点 1
二次根式可以合并的条件
探究新知
你发现了什么?
16.3 二次根式的加减/
因为 ,由前面知两者可以合并.
当a= ,b= 时,得2a+3b= .
a
2a+3b
b
=
+
b
b
a
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
探究新知
这两个二次根式可以合并吗?
你又有什么发现吗
16.3 二次根式的加减/
探究新知
归纳总结
将二次根式化成最简二次根式,如果被开方数相同,则这样的二次根式可以合并.
注意:1.判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
2.合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
16.3 二次根式的加减/
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2.下列二次根式,不能与 合并的是________(填 序号).
②
巩固练习
⑤
16.3 二次根式的加减/
例1 若最简二次根式 与 可以合并,求 的值.
解:由题意得
即
探究新知
素养考点 1
利用二次根式可以合并的条件求字母的值
提示:可以合并的二次根式中字母取值的方法:利用被开方数相同,根指数都为2列关于字母的方程(组)求解即可.
解得
16.3 二次根式的加减/
1
(1) 与最简二次根式 能合并,则m =_____.
1
巩固练习
(2)若两个最简二次根式 与 可
以合并,则a=_____,b=_______.
3.完成下列各题:
1
16.3 二次根式的加减/
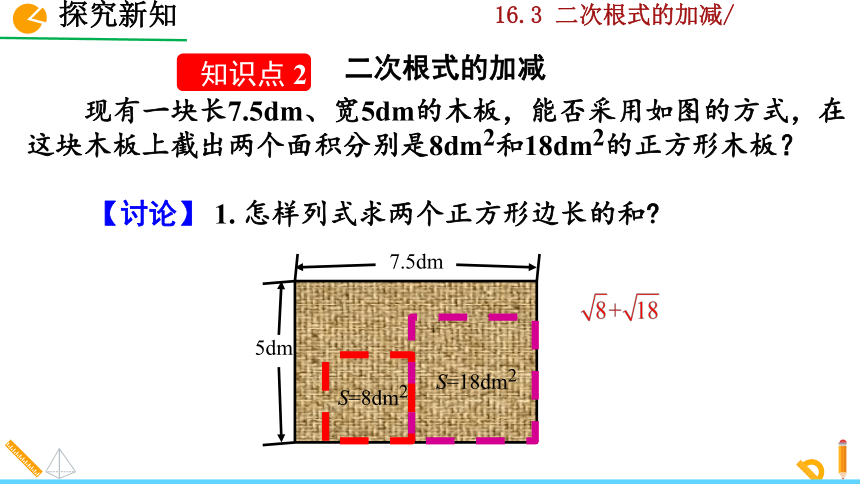
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
【讨论】 1. 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
知识点 2
二次根式的加减
探究新知
16.3 二次根式的加减/
【讨论】2.所列算式能直接进行加减运算吗 如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
探究新知
16.3 二次根式的加减/
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
探究新知
16.3 二次根式的加减/
探究新知
归纳总结
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
16.3 二次根式的加减/
解:
例2 计算:
素养考点 1
二次根式的加减计算
(3)
(4)
(1)
(1)
(2)
(2)
(3)
(4)
探究新知
16.3 二次根式的加减/
4.下列计算正确的是 ( )
A. B.
C. D.
C
5.已知一个矩形的长为 ,宽为 ,则其周长为______.
巩固练习
16.3 二次根式的加减/
例3 计算:
解:
探究新知
素养考点 2
二次根式的加减混合运算
(1)
(2)
(1)
(2)
计算时,有括号,一定要先去括号!
16.3 二次根式的加减/
6.计算
(1) ;
解:原式
解:原式
(2) .
巩固练习
16.3 二次根式的加减/
例4 有一个等腰三角形的两边长分别为 ,求其周长.
解:①当腰长为 时,
∵
∴此时能构成三角形,周长为
②当腰长为 时,
∵
∴此时能构成三角形,周长为
素养考点 3
二次根式的综合性题目
探究新知
16.3 二次根式的加减/
7. 如图,两个圆的圆心相同,它们的面积分别是8cm2和18cm2,求圆环的宽度d(两圆半径之差).
巩固练习
解:
答:圆环的宽度d为 cm.
R-r
16.3 二次根式的加减/
1.(2018 曲靖)下列二次根式中能与 合并的是( )
A. B. C. D.
巩固练习
连接中考
B
2.(2019 兰州)计算: =( )
A. B. C.3 D.
A
16.3 二次根式的加减/
D
基础巩固题
1. 与 能合并的二次根式是( )
A. B. C. D.
2.下列计算正确的是 ( )
A. B. C. D.
C
课堂检测
16.3 二次根式的加减/
3.三角形的三边长分别为 则这个三角形的周长为__________.
4.计算:
(1) =___
(2) =___
(3) =___
(4) =_________
基础巩固题
课堂检测
16.3 二次根式的加减/
解:
5.计算:
(1)
(2)
(1)
(2)
基础巩固题
课堂检测
16.3 二次根式的加减/
6.如果最简二次根式 与 可以合并,那么要使式子 有意义,求x的取值范围.
解:由题意得3a-8=17-2a,
∴a=5,
∴
∴20-2x≥0,x-5>0,
∴5<x≤10.
基础巩固题
课堂检测
16.3 二次根式的加减/
已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成三角形,求出
其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:
课堂检测
能力提升题
∵ 即a<c<b,
又∵ ∴a+c>b,
∴能够成三角形,周长为
16.3 二次根式的加减/
已知a,b都是有理数,现定义新运算:a*b= ,求(2*3)-(27*32)的值.
解:∵a*b= ,
∴(2*3)-(27*32)
=
=
=
拓广探索题
课堂检测
16.3 二次根式的加减/
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
课堂小结
16.3 二次根式的加减/
二次根式的混合运算
第二课时
返回
16.3 二次根式的加减/
如何进行单项式与多项式相乘的运算?
你能用字母表示这一结论吗?
思路:
单×多
转 化
分配律
单×单
m(a+b+c)
=
ma+mb+mc
导入新知
【讨论】若把字母a,b,c,m都用二次根式代替(每个同学任选一组),然后对比归纳,你们发现了什么?
16.3 二次根式的加减/
2. 掌握二次根式的运算方法,明确数的运算顺序、运算律及乘法公式在二次根式运算中仍然适用.
1. 正确运用二次根式的性质及运算法则进行二次根式的混合运算.
素养目标
16.3 二次根式的加减/
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
例1 计算:
解:
探究新知
知识点 1
二次根式的混合运算
素养考点 1
考查二次根式的多项式与单项式乘除运算能力
(1)
(2)
(1)
(2)
16.3 二次根式的加减/
巩固练习
1.计算:(1) (2)
(1)原式
解:
(2)原式
16.3 二次根式的加减/
例2 计算:
解:
(1)原式
【思考】(1)中,每一步的依据是什么?
第一步的依据是:多项式乘多项式法则;
第二步的依据是:二次根式化简,合并被开方数
相同的二次根式;
第三步的依据是:合并同类项.
(1)
探究新知
素养考点 2
考查二次根式的多项式乘法运算能力
16.3 二次根式的加减/
2.计算:
巩固练习
(1)
(2)
解:
(1)
(2)
16.3 二次根式的加减/
回顾提问1 整式乘法运算中的乘法公式有哪些
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
回顾提问2 整式的乘法公式对于二次根式的运算也适用吗
探究新知
知识点 2
利用乘法公式计算二次根式
前面我们已经知道二次根式运算类比整式运算,所以适用.
16.3 二次根式的加减/
例3 计算:
解:
探究新知
素养考点 1
考查利用乘法公式计算二次根式的能力
(1)
(2)
(1)
(2)
16.3 二次根式的加减/
拓展计算:
解:(1)原式
(2)原式
探究新知
(1)
(2)
16.3 二次根式的加减/
3. 计算:
巩固练习
(1)
解:
(1)
(2)
(2)
16.3 二次根式的加减/
例3 已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
探究新知
有关代数式的二次根式运算
素养考点 2
16.3 二次根式的加减/
解:∵ ,
巩固练习
∴
4. 已知 ,求x3y+xy3.
x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
∴
16.3 二次根式的加减/
在前面我们学习二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
【思考】 如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
知识点 3
分母有理化
探究新知
根据整式的乘法公式在二次根式中也适用,你能想到什么好方法吗?
16.3 二次根式的加减/
例4 计算:
解:
探究新知
素养考点 1
分母有理化的应用
提示:分母形如 的式子,分子、分母同乘以 的式子,构成平方差公式,可以使分母不含根号.
(1)
(2)
(1)
(2)
16.3 二次根式的加减/
5. 已知 ,求 .
解:∵
巩固练习
16.3 二次根式的加减/
巩固练习
连接中考
3
1.(2018 天津)计算 的结果
等于______.
2.(2019 常州)下列各数中与 的积是有理数
的是( )
A. B.2 C. D.
D
16.3 二次根式的加减/
1.下列计算中正确的是( )
B
2.计算:
5
3.设 则a b(填“>”“ < ”或
“= ”).
=
基础巩固题
课堂检测
16.3 二次根式的加减/
4.计算:
解:
(1)
(2)
基础巩固题
课堂检测
(1)
(2)
16.3 二次根式的加减/
(4)
(3)
解:原式=
=9-3
=6
解:原式=
(5)
基础巩固题
课堂检测
解:原式
16.3 二次根式的加减/
解:(1)原式
(2)原式
5.计算:
(1)
(2)
基础巩固题
课堂检测
16.3 二次根式的加减/
甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 m ,下底宽 m,高 m 的梯形,这段路基长 500 m,那么这段路基的土石方 (即路基的体积,其中路基的体积=路基横断面面积×路基的长度)为多少立方米呢?
能力提升题
课堂检测
16.3 二次根式的加减/
解:路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
答:这段路基的土石方为
能力提升题
课堂检测
16.3 二次根式的加减/
1.已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
拓广探索题
课堂检测
16.3 二次根式的加减/
2.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
拓广探索题
课堂检测
16.3 二次根式的加减/
解:(1)
(1)请用两种不同的方法化简:
(2)化简:
课堂检测
拓广探索题
(2)
16.3 二次根式的加减/
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
课堂小结
16.3 二次根式的加减/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
16.3 二次根式的加减/
16.3二次根式的加减
第一课时
第二课时
人教版 数学 八年级 下册
16.3 二次根式的加减/
二次根式的加减运算
第一课时
返回
16.3 二次根式的加减/
有八只小白兔,每只身上都标有一个最简二次根式,你能根据被开方数的特征将这些小白兔分到四个不同的栅栏里吗?
导入新知
16.3 二次根式的加减/
1. 理解二次根式可以合并的条件.
3. 能熟练地进行二次根式的加减法运算.
素养目标
2. 类比整式的合并同类项,掌握二次根式的加减运算法则.
16.3 二次根式的加减/
a
a
a
a
a
a
a
a
a
a
=
+
在七年级我们就已经学过单项式加单项式的法则.观察下图并思考.
由上图,易得2a+3a=5a.
当a= 时,分别代入左右得 ;
当a= 时,分别代入左右得 ;......
知识点 1
二次根式可以合并的条件
探究新知
你发现了什么?
16.3 二次根式的加减/
因为 ,由前面知两者可以合并.
当a= ,b= 时,得2a+3b= .
a
2a+3b
b
=
+
b
b
a
前面依次往下推导,由特殊到一般易知二次根式的被开方数相同可以合并.继续观察下面的过程:
探究新知
这两个二次根式可以合并吗?
你又有什么发现吗
16.3 二次根式的加减/
探究新知
归纳总结
将二次根式化成最简二次根式,如果被开方数相同,则这样的二次根式可以合并.
注意:1.判断几个二次根式是否可以合并,一定都要化为最简二次根式再判断.
2.合并的方法与合并同类项类似,把根号外的因数(式)相加,根指数和被开方数(式)不变.如:
16.3 二次根式的加减/
1.下列各式中,与 是同类二次根式的是( )
A. B. C. D.
D
2.下列二次根式,不能与 合并的是________(填 序号).
②
巩固练习
⑤
16.3 二次根式的加减/
例1 若最简二次根式 与 可以合并,求 的值.
解:由题意得
即
探究新知
素养考点 1
利用二次根式可以合并的条件求字母的值
提示:可以合并的二次根式中字母取值的方法:利用被开方数相同,根指数都为2列关于字母的方程(组)求解即可.
解得
16.3 二次根式的加减/
1
(1) 与最简二次根式 能合并,则m =_____.
1
巩固练习
(2)若两个最简二次根式 与 可
以合并,则a=_____,b=_______.
3.完成下列各题:
1
16.3 二次根式的加减/
现有一块长7.5dm、宽5dm的木板,能否采用如图的方式,在这块木板上截出两个面积分别是8dm2和18dm2的正方形木板?
7.5dm
5dm
【讨论】 1. 怎样列式求两个正方形边长的和
S=8dm2
S=18dm2
知识点 2
二次根式的加减
探究新知
16.3 二次根式的加减/
【讨论】2.所列算式能直接进行加减运算吗 如果不能,把式中各个二次根式化成最简二次根式后,再试一试(说出每步运算的依据).
(化成最简二次根式)
(逆用分配律)
∴在这块木板上可以截出两个分别是8dm2和18dm2的正方形木板.
解:列式如下:
在有理数范围内成立的运算律,在实数范围内仍然成立.
探究新知
16.3 二次根式的加减/
化为最简
二次根式
用分配
律合并
整式
加减
二次根
式性质
分配律
整式加
减法则
依据:二次根式的性质、分配律和整式加减法则.
基本思想:把二次根式加减问题转化为整式加减问题.
探究新知
16.3 二次根式的加减/
探究新知
归纳总结
二次根式的加减法法则:
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
(1)化——将非最简二次根式的二次根式化简;
加减法的运算步骤:
(2)找——找出被开方数相同的二次根式;
(3)并——把被开方数相同的二次根式合并.
“一化简二判断三合并”
16.3 二次根式的加减/
解:
例2 计算:
素养考点 1
二次根式的加减计算
(3)
(4)
(1)
(1)
(2)
(2)
(3)
(4)
探究新知
16.3 二次根式的加减/
4.下列计算正确的是 ( )
A. B.
C. D.
C
5.已知一个矩形的长为 ,宽为 ,则其周长为______.
巩固练习
16.3 二次根式的加减/
例3 计算:
解:
探究新知
素养考点 2
二次根式的加减混合运算
(1)
(2)
(1)
(2)
计算时,有括号,一定要先去括号!
16.3 二次根式的加减/
6.计算
(1) ;
解:原式
解:原式
(2) .
巩固练习
16.3 二次根式的加减/
例4 有一个等腰三角形的两边长分别为 ,求其周长.
解:①当腰长为 时,
∵
∴此时能构成三角形,周长为
②当腰长为 时,
∵
∴此时能构成三角形,周长为
素养考点 3
二次根式的综合性题目
探究新知
16.3 二次根式的加减/
7. 如图,两个圆的圆心相同,它们的面积分别是8cm2和18cm2,求圆环的宽度d(两圆半径之差).
巩固练习
解:
答:圆环的宽度d为 cm.
R-r
16.3 二次根式的加减/
1.(2018 曲靖)下列二次根式中能与 合并的是( )
A. B. C. D.
巩固练习
连接中考
B
2.(2019 兰州)计算: =( )
A. B. C.3 D.
A
16.3 二次根式的加减/
D
基础巩固题
1. 与 能合并的二次根式是( )
A. B. C. D.
2.下列计算正确的是 ( )
A. B. C. D.
C
课堂检测
16.3 二次根式的加减/
3.三角形的三边长分别为 则这个三角形的周长为__________.
4.计算:
(1) =___
(2) =___
(3) =___
(4) =_________
基础巩固题
课堂检测
16.3 二次根式的加减/
解:
5.计算:
(1)
(2)
(1)
(2)
基础巩固题
课堂检测
16.3 二次根式的加减/
6.如果最简二次根式 与 可以合并,那么要使式子 有意义,求x的取值范围.
解:由题意得3a-8=17-2a,
∴a=5,
∴
∴20-2x≥0,x-5>0,
∴5<x≤10.
基础巩固题
课堂检测
16.3 二次根式的加减/
已知a,b,c满足 .
(1)求a,b,c的值;
(2)以a,b,c为三边长能否构成三角形?若能构成三角形,求出
其周长;若不能,请说明理由.
解:(1)由题意得 ;
(2)能.理由如下:
课堂检测
能力提升题
∵ 即a<c<b,
又∵ ∴a+c>b,
∴能够成三角形,周长为
16.3 二次根式的加减/
已知a,b都是有理数,现定义新运算:a*b= ,求(2*3)-(27*32)的值.
解:∵a*b= ,
∴(2*3)-(27*32)
=
=
=
拓广探索题
课堂检测
16.3 二次根式的加减/
二次根式加减
法则
注意
运算顺序
运算原理
一般地,二次根式加减时,可以先将二次根式化成最简二次根式,再将被开方数相同的二次根式进行合并.
运算律仍然适用
与实数的运算顺序一样
课堂小结
16.3 二次根式的加减/
二次根式的混合运算
第二课时
返回
16.3 二次根式的加减/
如何进行单项式与多项式相乘的运算?
你能用字母表示这一结论吗?
思路:
单×多
转 化
分配律
单×单
m(a+b+c)
=
ma+mb+mc
导入新知
【讨论】若把字母a,b,c,m都用二次根式代替(每个同学任选一组),然后对比归纳,你们发现了什么?
16.3 二次根式的加减/
2. 掌握二次根式的运算方法,明确数的运算顺序、运算律及乘法公式在二次根式运算中仍然适用.
1. 正确运用二次根式的性质及运算法则进行二次根式的混合运算.
素养目标
16.3 二次根式的加减/
二次根式的加、减、乘、除混合运算与整式运算一样,体现在:运算律、运算顺序、乘法法则仍然适用.
例1 计算:
解:
探究新知
知识点 1
二次根式的混合运算
素养考点 1
考查二次根式的多项式与单项式乘除运算能力
(1)
(2)
(1)
(2)
16.3 二次根式的加减/
巩固练习
1.计算:(1) (2)
(1)原式
解:
(2)原式
16.3 二次根式的加减/
例2 计算:
解:
(1)原式
【思考】(1)中,每一步的依据是什么?
第一步的依据是:多项式乘多项式法则;
第二步的依据是:二次根式化简,合并被开方数
相同的二次根式;
第三步的依据是:合并同类项.
(1)
探究新知
素养考点 2
考查二次根式的多项式乘法运算能力
16.3 二次根式的加减/
2.计算:
巩固练习
(1)
(2)
解:
(1)
(2)
16.3 二次根式的加减/
回顾提问1 整式乘法运算中的乘法公式有哪些
平方差公式:(a+b)(a-b)=a2-b2;
完全平方公式:(a+b)2=a2+2ab+b2;
(a-b)2=a2-2ab+b2.
回顾提问2 整式的乘法公式对于二次根式的运算也适用吗
探究新知
知识点 2
利用乘法公式计算二次根式
前面我们已经知道二次根式运算类比整式运算,所以适用.
16.3 二次根式的加减/
例3 计算:
解:
探究新知
素养考点 1
考查利用乘法公式计算二次根式的能力
(1)
(2)
(1)
(2)
16.3 二次根式的加减/
拓展计算:
解:(1)原式
(2)原式
探究新知
(1)
(2)
16.3 二次根式的加减/
3. 计算:
巩固练习
(1)
解:
(1)
(2)
(2)
16.3 二次根式的加减/
例3 已知 试求x2+2xy+y2的值.
解: x2+2xy+y2=(x+y)2
把 代入上式得
原式=
探究新知
有关代数式的二次根式运算
素养考点 2
16.3 二次根式的加减/
解:∵ ,
巩固练习
∴
4. 已知 ,求x3y+xy3.
x3y+xy3=xy(x2+y2)=xy[(x+y)2-2xy]
∴
16.3 二次根式的加减/
在前面我们学习二次根式的除法法则时,学会了怎样去掉分母的二次根式的方法,比如:
【思考】 如果分母不是单个的二次根式,而是含二次根式的式子,如: 等,该怎样去掉分母中的二次根式呢?
知识点 3
分母有理化
探究新知
根据整式的乘法公式在二次根式中也适用,你能想到什么好方法吗?
16.3 二次根式的加减/
例4 计算:
解:
探究新知
素养考点 1
分母有理化的应用
提示:分母形如 的式子,分子、分母同乘以 的式子,构成平方差公式,可以使分母不含根号.
(1)
(2)
(1)
(2)
16.3 二次根式的加减/
5. 已知 ,求 .
解:∵
巩固练习
16.3 二次根式的加减/
巩固练习
连接中考
3
1.(2018 天津)计算 的结果
等于______.
2.(2019 常州)下列各数中与 的积是有理数
的是( )
A. B.2 C. D.
D
16.3 二次根式的加减/
1.下列计算中正确的是( )
B
2.计算:
5
3.设 则a b(填“>”“ < ”或
“= ”).
=
基础巩固题
课堂检测
16.3 二次根式的加减/
4.计算:
解:
(1)
(2)
基础巩固题
课堂检测
(1)
(2)
16.3 二次根式的加减/
(4)
(3)
解:原式=
=9-3
=6
解:原式=
(5)
基础巩固题
课堂检测
解:原式
16.3 二次根式的加减/
解:(1)原式
(2)原式
5.计算:
(1)
(2)
基础巩固题
课堂检测
16.3 二次根式的加减/
甲、乙两个城市间计划修建一条城际铁路, 其中有一段路基的横断面设计为上底宽 m ,下底宽 m,高 m 的梯形,这段路基长 500 m,那么这段路基的土石方 (即路基的体积,其中路基的体积=路基横断面面积×路基的长度)为多少立方米呢?
能力提升题
课堂检测
16.3 二次根式的加减/
解:路基的土石方等于路基横断面面积乘以路基的长度,所以这段路基的土石方为:
答:这段路基的土石方为
能力提升题
课堂检测
16.3 二次根式的加减/
1.已知 的整数部分是a,小数部分是b,求a2-b2的值.
解:
拓广探索题
课堂检测
16.3 二次根式的加减/
2.阅读下列材料,然后回答问题:
在进行类似于二次根式 的运算时,通常有如下两种方法将其进一步化简:
方法一:
方法二:
拓广探索题
课堂检测
16.3 二次根式的加减/
解:(1)
(1)请用两种不同的方法化简:
(2)化简:
课堂检测
拓广探索题
(2)
16.3 二次根式的加减/
二次根式混合运算
乘法公式
化简求值
分母有理化
化简已知条件和所求代数式
(a+b)(a-b)=a2-b2
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
(x+a)(x+b)=x2+(a+b)x+ab
课堂小结
16.3 二次根式的加减/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
