人教版数学八下 17.2 勾股定理的逆定理(希沃课件+图片版PPT)仅适用希沃白板
文档属性
| 名称 | 人教版数学八下 17.2 勾股定理的逆定理(希沃课件+图片版PPT)仅适用希沃白板 |
|
|
| 格式 | zip | ||
| 文件大小 | 10.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览








文档简介
(共53张PPT)
17.2 勾股定理的逆定理/
17.2勾股定理的逆定理
第一课时
第二课时
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
人教版 数学 八年级 下册
17.2 勾股定理的逆定理/
勾股定理的逆定理
第一课时
返回
17.2 勾股定理的逆定理/
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
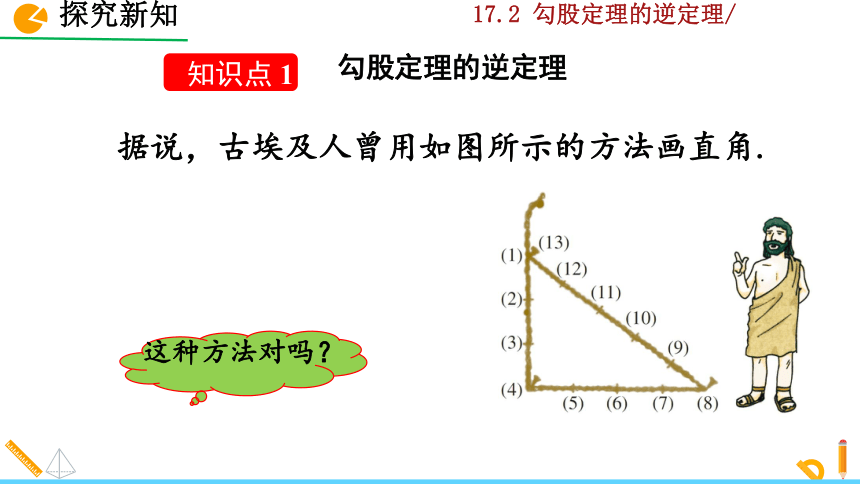
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
导入新知
17.2 勾股定理的逆定理/
1. 掌握勾股定理逆定理的概念并理解互逆命题、互逆定理的概念、关系及勾股数.
2. 能证明勾股定理的逆定理,能利用勾股定理的逆定理判断一个三角形是直角三角形.
素养目标
17.2 勾股定理的逆定理/
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?
探究新知
知识点 1
勾股定理的逆定理
17.2 勾股定理的逆定理/
3
4
5
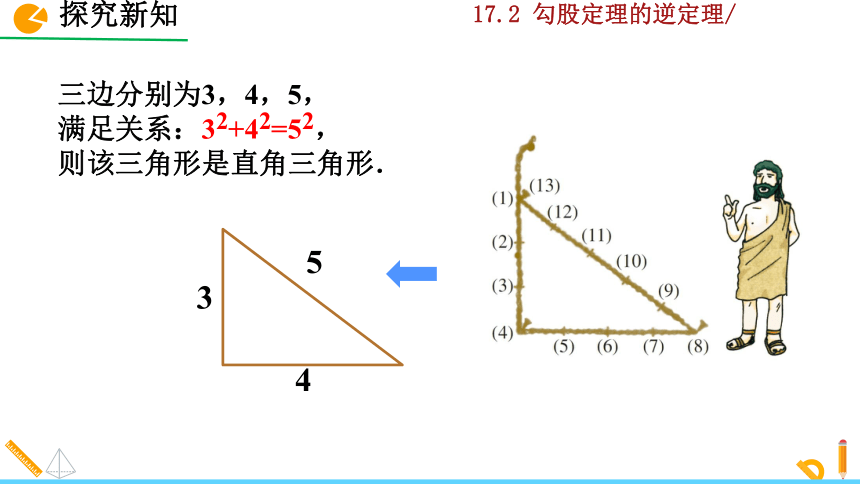
三边分别为3,4,5,
满足关系:32+42=52,
则该三角形是直角三角形.
探究新知
17.2 勾股定理的逆定理/
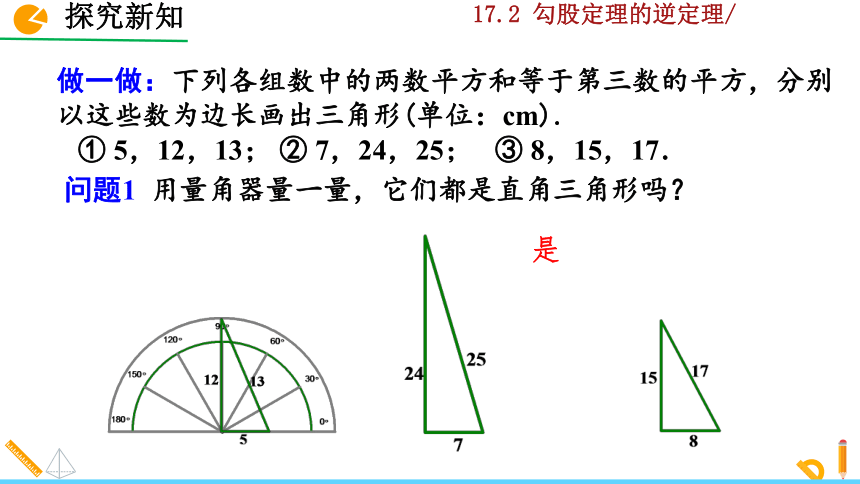
问题1 用量角器量一量,它们都是直角三角形吗?
是
做一做:下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17.
探究新知
17.2 勾股定理的逆定理/
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题2 这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
问题3 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
探究新知
17.2 勾股定理的逆定理/
问题4 据此你有什么猜想呢
由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
探究新知
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
17.2 勾股定理的逆定理/
已知:如图,在△ABC中,AB=c,BC=a,CA=b,
并且
A
B
b
c
a
b
证明:作 A1B1C1
在△ABC和△A1B1C 1中,
C
a
求证:∠C=90°
使∠C1=90°
根据勾股定理,则有
∠C=∠
=90°
探究新知
B
A
B1C1=a,C1A1=b
A1B1 2=B1C1 2+C1A1 2=a2+b2
∵a2+b2=c2
∴A1B1 =c,
∴AB=A1B1
≌
∴ ABC
A1B1C1
17.2 勾股定理的逆定理/
符号语言:
在△ABC中,
若a2 + b2 = c2
则△ABC是直角三角形
探究新知
如果三角形的三边长a、b、c满足 a2 + b2 = c2,那么这个三角形是直角三角形.
勾股定理的逆定理:
b
c
C
a
B
A
17.2 勾股定理的逆定理/
探究新知
方法点拨
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
17.2 勾股定理的逆定理/
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=15 , b=8 ,c=17;
解:(1)∵152+82=289,172=289,
(2) a=13 ,b=14 ,c=15.
(2)∵132+142=365,152=225,
总结:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
探究新知
素养考点 1
利用勾股定理的逆定理判断直角三角形
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
∴132+142≠152,
不符合勾股定理的逆定理,∴这个三角形不是直角三角形.
17.2 勾股定理的逆定理/
1.下列各组线段中,能够组成直角三角形的一组是( )
A. 1,2,3 B. 2,3,4
C. 4,5,6 D.
2.满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1:2:1 B. 三边之比为1:2:
C.三边之比为 D. 三个内角比为1:2:3
D
C
D
C
巩固练习
17.2 勾股定理的逆定理/
例2 若△ABC的三边a,b,c,且a+b=4,ab=1,c= ,
试说明△ABC是直角三角形.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
探究新知
素养考点 2
勾股定理的逆定理和乘法公式判断三角形
17.2 勾股定理的逆定理/
3.若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c.
试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴△ABC是直角三角形.
巩固练习
17.2 勾股定理的逆定理/
探究新知
知识点 2
勾股数
如果三角形的三边长a,b,c满足a2+b2=c2那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
17.2 勾股定理的逆定理/
4.下列各组数是勾股数的是 ( )
A.3,4,6 B.6,7,8
C.0.3,0.4,0.5 D.5,12,13
D
巩固练习
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
17.2 勾股定理的逆定理/
命题1 如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
命题2 如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
看下边的两个命题:
探究新知
知识点 3
互逆命题和互逆定理
你发现了什么?
17.2 勾股定理的逆定理/
命题1:
直角三角形
a2+b2=c2
命题2:
直角三角形
a2+b2=c2
题设
结论
它们是题设和结论正好相反的两个命题.
发现1 两个命题的条件和结论如下所示:
发现2 两个命题的条件和结论有如下联系:
探究新知
17.2 勾股定理的逆定理/
归纳总结:一般地,原命题成立时,它的逆命题可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
探究新知
17.2 勾股定理的逆定理/
5.说出下列命题的逆命题.这些命题的逆命题是真命题吗?
(1)两条直线平行,内错角相等;
逆命题:内错角相等,两直线平行.真命题.
(2)对顶角相等;
逆命题:相等的角是对顶角.假命题.
(3)线段垂直平分线上的点到线段两端点的距离相等.
逆命题:到线段两端点的距离相等的点在线段的垂直平
分线上.真命题.
任何一个命题都有逆
命题;原命题是真命题,其
逆命题不一定是真命题.
巩固练习
17.2 勾股定理的逆定理/
1. (2019 威海模拟)已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
巩固练习
连接中考
B
17.2 勾股定理的逆定理/
1.下列各组数是勾股数的是 ( )
A.3,4,7 B.5,12,13
C.1.5,2,2.5 D.1,3,5
2.将直角三角形的三边长扩大同样的倍数,则得到的三角形 ( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
B
A
课堂检测
基础巩固题
17.2 勾股定理的逆定理/
3.写出下列命题的逆命题,并判断其逆命题的真假性.
(1)如果两个角是直角,那么它们相等.
(2)在角的内部,到角的两边距离相等的点在角的平分线上.
(3)如果 ,那么a≥0.
解:(1)如果两个角相等,那么这两个角是直角.假命题.
(2)在角的内部,角的平分线上的点到两边的距离相等.真命题.
(3)如果a≥0,那么 .真命题.
课堂检测
基础巩固题
17.2 勾股定理的逆定理/
4.若△ABC的三边a,b,c满足 a:b: c=3:4:5,试判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
课堂检测
基础巩固题
17.2 勾股定理的逆定理/
A,B,C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
解:∵AB2+BC2=122+52
=144+25=169,
AC2=132=169,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,且∠B=90°,
由于A地在B地的正东方向,所以C地在B地的正北方向.
课堂检测
能力提升题
17.2 勾股定理的逆定理/
如图,在正方形ABCD中,F是CD的中点,E为BC上一点,
且CE= CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,∴△AEF为直角三角形,且AE为斜边.∴∠AFE=90°,即AF⊥EF.
课堂检测
拓广探索题
17.2 勾股定理的逆定理/
勾股定理
的逆定理
内容
作用
从三边数量关系判定一个三角形是否是直角形三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
注意
最长边不一定是c, ∠C也不一定是直角.
勾股数一定是正整数
课堂小结
勾股数
互逆命题和互逆定理
17.2 勾股定理的逆定理/
勾股定理的逆定理的应用
第二课时
返回
N
E
P
Q
R
1
2
17.2 勾股定理的逆定理/
工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定。你能测出这个零件是否合格呢?(身边只有刻度尺)
A
B
C
导入新知
17.2 勾股定理的逆定理/
在军事和航海上经常要确定方向和位置,从而常需要使用一些数学知识和方法,其中勾股定理的逆定理经常会被用到,这节课让我们一起来学习吧.
导入新知
17.2 勾股定理的逆定理/
2. 进一步加深对勾股定理与其逆定理之间关系的认识.
1. 应用勾股定理的逆定理解决实际问题.
素养目标
3. 将实际问题转化成用勾股定理的逆定理解决的数学问题.
17.2 勾股定理的逆定理/
1
2
如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
N
E
P
Q
R
探究新知
知识点 1
利用勾股定理的逆定理解答角度问题
【思考】1.认真读题,找已知是什么?
“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如下图.
17.2 勾股定理的逆定理/
1
2
N
E
P
Q
R
16×1.5=24
12×1.5=18
30
3.由于我们现在所能得到的都是线段长,要求角,由此我们想到利用什么思想?
要解决的问题是求出两艘船航向所成角.
勾股定理逆定理
探究新知
【思考】2.需要解决的问题是什么?
转化的思想
4.知道线段长度,通过线段长度来求角的度数,我们可以利用什么转化呢?
17.2 勾股定理的逆定理/
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
探究新知
方法点拨:解决实际问题的步骤:①标注有用信息,明确已知和所求;②构建几何模型(从整体到局部);③应用数学知识求解.
17.2 勾股定理的逆定理/
1.在寻找马航MH370航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标A、B. 接到消息后,一艘舰艇以16海里/时的速度离开港口O(如图所示)向北偏东40°方向航行,另一艘舰艇在同时以12海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距30海里,问另一艘舰艇的航行方向是北偏西多少度?
巩固练习
17.2 勾股定理的逆定理/
解:由题意得,OB=12×1.5=18海里,
OA=16×1.5=24海里,
又∵AB=30海里,
∴182+242=302,即OB2+OA2=AB2,
∴∠AOB=90°.
∵∠DOA=40°,
∴∠BOD=50°.
则另一艘舰艇的航行方向是北偏西50°.
巩固练习
17.2 勾股定理的逆定理/
如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.
在Rt△ABD中,由勾股定理得 BD2=AB2+AD2,
∴BD=5cm.又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD = ×(5×12-3×4)=24 (cm2).
C
B
A
D
探究新知
知识点 2
利用勾股定理的逆定理解答面积问题
17.2 勾股定理的逆定理/
2.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
巩固练习
17.2 勾股定理的逆定理/
如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,∴∠ABC≠90°,
∴该农民挖的不合格.
知识点 3
探究新知
利用勾股定理的逆定理解答检测问题
17.2 勾股定理的逆定理/
3. 一个零件的形状如图 所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图
图
巩固练习
17.2 勾股定理的逆定理/
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
D
A
B
C
4
3
5
13
12
图
巩固练习
AB2+AD2=32+42=25=52=BD2
BD2+BC2=52+122=169=132=CD2
17.2 勾股定理的逆定理/
(2018 长沙)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五
里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的
是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米
C.75平方千米 D.750平方千米
巩固练习
连接中考
A
17.2 勾股定理的逆定理/
B
B
课堂检测
基础巩固题
1.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中摆放方法正确的是 ( )
D
A. B.
C. D.
17.2 勾股定理的逆定理/
2.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300 m,公园到医院的距离为400 m,若公园到超市的距离为500 m,则公园在医院的 ( )
A.北偏东75°的方向上 B.北偏东65°的方向上
C.北偏东55°的方向上 D.无法确定
B
基础巩固题
课堂检测
17.2 勾股定理的逆定理/
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行了12×2=24(km),
B组行了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
基础巩固题
课堂检测
A
O
B
17.2 勾股定理的逆定理/
4.在城市街路上速度不得超过70千米/时,一辆小汽车某一时刻行驶在路边车速检测仪的北偏东30°距离30米处,过了2秒后行驶了50米,此时小汽车与车速检测仪间的距离为40米. 问:2秒后小汽车在车速检测仪的哪个方向 这辆小汽车超速了吗
车速检测仪
小汽车
30米
30°
北
60°
解:小汽车在车速检测仪的南偏东60°方向或北偏西60°方向.
25米/秒=90千米/时>70千米/时
∴小汽车超速了.
2秒后
50米
40米
基础巩固题
课堂检测
17.2 勾股定理的逆定理/
如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
分析:连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
能力提升题
课堂检测
17.2 勾股定理的逆定理/
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
能力提升题
课堂检测
A
D
B
C
3
4
13
12
17.2 勾股定理的逆定理/
如图,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3s时,求PQ的长.
解:设AB为3xcm,BC为4xcm,AC为5xcm,∵周长为36cm,即AB+BC+AC=36cm,
∴AB=9cm,BC=12cm,AC=15cm.
∵AB2+BC2=AC2,∴△ABC是直角三角形,过3秒时,
BP=9-3×2=3(cm),BQ=12-1×3=9(cm),
在Rt△PBQ中,由勾股定理得
课堂检测
拓广探索题
∴3x+4x+5x=36,
解得x=3.
P
C
B
A
Q
17.2 勾股定理的逆定理/
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题
与勾股定理结合解决不规则图形等问题
课堂小结
17.2 勾股定理的逆定理/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
17.2 勾股定理的逆定理/
17.2勾股定理的逆定理
第一课时
第二课时
(1)
(2)
(3)
(4)
(5)
(6)
(7)
(8)
(13)
(12)
(11)
(10)
(9)
人教版 数学 八年级 下册
17.2 勾股定理的逆定理/
勾股定理的逆定理
第一课时
返回
17.2 勾股定理的逆定理/
按照这种做法真能得到一个直角三角形吗?
古埃及人曾用下面的方法得到直角:
用13个等距的结,把一根绳子分成等长的12段,然后以3个结,4个结,5个结的长度为边长,用木桩钉成一个三角形,其中一个角便是直角.
导入新知
17.2 勾股定理的逆定理/
1. 掌握勾股定理逆定理的概念并理解互逆命题、互逆定理的概念、关系及勾股数.
2. 能证明勾股定理的逆定理,能利用勾股定理的逆定理判断一个三角形是直角三角形.
素养目标
17.2 勾股定理的逆定理/
据说,古埃及人曾用如图所示的方法画直角.
这种方法对吗?
探究新知
知识点 1
勾股定理的逆定理
17.2 勾股定理的逆定理/
3
4
5
三边分别为3,4,5,
满足关系:32+42=52,
则该三角形是直角三角形.
探究新知
17.2 勾股定理的逆定理/
问题1 用量角器量一量,它们都是直角三角形吗?
是
做一做:下列各组数中的两数平方和等于第三数的平方,分别以这些数为边长画出三角形(单位:cm).
① 5,12,13; ② 7,24,25; ③ 8,15,17.
探究新知
17.2 勾股定理的逆定理/
下面有三组数分别是一个三角形的三边长a, b, c:
①5,12,13; ②7,24,25; ③8,15,17.
问题2 这三组数在数量关系上有什么相同点?
① 5,12,13满足52+122=132,
② 7,24,25满足72+242=252,
③ 8,15,17满足82+152=172.
问题3 古埃及人用来画直角的三边满足这个等式吗?
∵32+42=52,∴满足.
a2+b2=c2
探究新知
17.2 勾股定理的逆定理/
问题4 据此你有什么猜想呢
由上面几个例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
探究新知
我觉得这个猜想不准确,因为测量结果可能有误差.
我也觉得猜想不严谨,前面我们只取了几组数据,不能由部分代表整体.
17.2 勾股定理的逆定理/
已知:如图,在△ABC中,AB=c,BC=a,CA=b,
并且
A
B
b
c
a
b
证明:作 A1B1C1
在△ABC和△A1B1C 1中,
C
a
求证:∠C=90°
使∠C1=90°
根据勾股定理,则有
∠C=∠
=90°
探究新知
B
A
B1C1=a,C1A1=b
A1B1 2=B1C1 2+C1A1 2=a2+b2
∵a2+b2=c2
∴A1B1 =c,
∴AB=A1B1
≌
∴ ABC
A1B1C1
17.2 勾股定理的逆定理/
符号语言:
在△ABC中,
若a2 + b2 = c2
则△ABC是直角三角形
探究新知
如果三角形的三边长a、b、c满足 a2 + b2 = c2,那么这个三角形是直角三角形.
勾股定理的逆定理:
b
c
C
a
B
A
17.2 勾股定理的逆定理/
探究新知
方法点拨
勾股定理的逆定理是直角三角形的判定定理,即已知三角形的三边长,且满足两条较小边的平方和等于最长边的平方,即可判断此三角形为直角三角形 ,最长边所对应的角为直角.
17.2 勾股定理的逆定理/
例1 下面以a,b,c为边长的三角形是不是直角三角形?如果是,那么哪一个角是直角?
(1) a=15 , b=8 ,c=17;
解:(1)∵152+82=289,172=289,
(2) a=13 ,b=14 ,c=15.
(2)∵132+142=365,152=225,
总结:根据勾股定理的逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
探究新知
素养考点 1
利用勾股定理的逆定理判断直角三角形
∴152+82=172,
根据勾股定理的逆定理,这个三角形是直角三角形,且∠C是直角.
∴132+142≠152,
不符合勾股定理的逆定理,∴这个三角形不是直角三角形.
17.2 勾股定理的逆定理/
1.下列各组线段中,能够组成直角三角形的一组是( )
A. 1,2,3 B. 2,3,4
C. 4,5,6 D.
2.满足下列条件的三角形中,不是直角三角形的是( )
A.三个内角比为1:2:1 B. 三边之比为1:2:
C.三边之比为 D. 三个内角比为1:2:3
D
C
D
C
巩固练习
17.2 勾股定理的逆定理/
例2 若△ABC的三边a,b,c,且a+b=4,ab=1,c= ,
试说明△ABC是直角三角形.
解:∵a+b=4,ab=1,
∴a2+b2=(a+b)2-2ab=16-2=14.
又∵c2=14,
∴a2+b2=c2,
∴△ABC是直角三角形.
探究新知
素养考点 2
勾股定理的逆定理和乘法公式判断三角形
17.2 勾股定理的逆定理/
3.若△ABC的三边 a,b,c 满足a2+b2+c2+50=6a+8b+10c.
试判断△ABC的形状.
解:∵ a2+b2+c2+50=6a+8b+10c,
∴ a2-6a+9+b2-8b+16+c2-10c+25=0.
即 (a-3) + (b-4) + (c-5) =0.
∴ a=3, b=4, c=5,
即 a2+b2=c2.
∴△ABC是直角三角形.
巩固练习
17.2 勾股定理的逆定理/
探究新知
知识点 2
勾股数
如果三角形的三边长a,b,c满足a2+b2=c2那么这个三角形是直角三角形.满足a2+b2=c2的三个正整数,称为勾股数.
常见勾股数:
3,4,5;5,12,13;6,8,10;7,24,25;8,15,17;9,40,41;10,24,26等等.
勾股数拓展性质:
一组勾股数,都扩大相同倍数k(k为正整数),得到一组新数,这组数同样是勾股数.
17.2 勾股定理的逆定理/
4.下列各组数是勾股数的是 ( )
A.3,4,6 B.6,7,8
C.0.3,0.4,0.5 D.5,12,13
D
巩固练习
方法点拨:根据勾股数的定义,勾股数必须为正整数,先排除小数,再计算最长边的平方是否等于其他两边的平方和即可.
17.2 勾股定理的逆定理/
命题1 如果直角三角形的两条直角边长分别为a,b,斜边为c,那么a2+b2=c2.
命题2 如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
看下边的两个命题:
探究新知
知识点 3
互逆命题和互逆定理
你发现了什么?
17.2 勾股定理的逆定理/
命题1:
直角三角形
a2+b2=c2
命题2:
直角三角形
a2+b2=c2
题设
结论
它们是题设和结论正好相反的两个命题.
发现1 两个命题的条件和结论如下所示:
发现2 两个命题的条件和结论有如下联系:
探究新知
17.2 勾股定理的逆定理/
归纳总结:一般地,原命题成立时,它的逆命题可能成立,也可能不成立.如果一个定理的逆命题经过证明是正确的,那么它也是一个定理,我们称这两个定理互为逆定理.勾股定理与勾股定理的逆定理为互逆定理.
题设和结论正好相反的两个命题,叫做互逆命题,其中一个叫做原命题,另一个叫做原命题的逆命题.
探究新知
17.2 勾股定理的逆定理/
5.说出下列命题的逆命题.这些命题的逆命题是真命题吗?
(1)两条直线平行,内错角相等;
逆命题:内错角相等,两直线平行.真命题.
(2)对顶角相等;
逆命题:相等的角是对顶角.假命题.
(3)线段垂直平分线上的点到线段两端点的距离相等.
逆命题:到线段两端点的距离相等的点在线段的垂直平
分线上.真命题.
任何一个命题都有逆
命题;原命题是真命题,其
逆命题不一定是真命题.
巩固练习
17.2 勾股定理的逆定理/
1. (2019 威海模拟)已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
巩固练习
连接中考
B
17.2 勾股定理的逆定理/
1.下列各组数是勾股数的是 ( )
A.3,4,7 B.5,12,13
C.1.5,2,2.5 D.1,3,5
2.将直角三角形的三边长扩大同样的倍数,则得到的三角形 ( )
A.是直角三角形 B.可能是锐角三角形
C.可能是钝角三角形 D.不可能是直角三角形
B
A
课堂检测
基础巩固题
17.2 勾股定理的逆定理/
3.写出下列命题的逆命题,并判断其逆命题的真假性.
(1)如果两个角是直角,那么它们相等.
(2)在角的内部,到角的两边距离相等的点在角的平分线上.
(3)如果 ,那么a≥0.
解:(1)如果两个角相等,那么这两个角是直角.假命题.
(2)在角的内部,角的平分线上的点到两边的距离相等.真命题.
(3)如果a≥0,那么 .真命题.
课堂检测
基础巩固题
17.2 勾股定理的逆定理/
4.若△ABC的三边a,b,c满足 a:b: c=3:4:5,试判断△ABC的形状.
解:设a=3k,b=4k,c=5k(k>0),
∵(3k)2+(4k)2=25k2,(5k)2=25k2,
∴(3k)2+(4k)2=(5k)2,
∴△ABC是直角三角形,且∠C是直角.
课堂检测
基础巩固题
17.2 勾股定理的逆定理/
A,B,C三地的两两距离如图所示,A地在B地的正东方向,C地在B地的什么方向?
解:∵AB2+BC2=122+52
=144+25=169,
AC2=132=169,
∴AB2+BC2=AC2,
∴△ABC为直角三角形,且∠B=90°,
由于A地在B地的正东方向,所以C地在B地的正北方向.
课堂检测
能力提升题
17.2 勾股定理的逆定理/
如图,在正方形ABCD中,F是CD的中点,E为BC上一点,
且CE= CB,试判断AF与EF的位置关系,并说明理由.
解:AF⊥EF.理由如下:
设正方形的边长为4a, 则EC=a,BE=3a,CF=DF=2a.
在Rt△ABE中,得AE2=AB2+BE2=16a2+9a2=25a2.
在Rt△CEF中,得EF2=CE2+CF2=a2+4a2=5a2.
在Rt△ADF中,得AF2=AD2+DF2=16a2+4a2=20a2.
在△AEF中,AE2=EF2+AF2,∴△AEF为直角三角形,且AE为斜边.∴∠AFE=90°,即AF⊥EF.
课堂检测
拓广探索题
17.2 勾股定理的逆定理/
勾股定理
的逆定理
内容
作用
从三边数量关系判定一个三角形是否是直角形三角形.
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
注意
最长边不一定是c, ∠C也不一定是直角.
勾股数一定是正整数
课堂小结
勾股数
互逆命题和互逆定理
17.2 勾股定理的逆定理/
勾股定理的逆定理的应用
第二课时
返回
N
E
P
Q
R
1
2
17.2 勾股定理的逆定理/
工厂生产的产品都有一定的规格要求,如图所示:该模板中的AB、BC 相交成直角才符合规定。你能测出这个零件是否合格呢?(身边只有刻度尺)
A
B
C
导入新知
17.2 勾股定理的逆定理/
在军事和航海上经常要确定方向和位置,从而常需要使用一些数学知识和方法,其中勾股定理的逆定理经常会被用到,这节课让我们一起来学习吧.
导入新知
17.2 勾股定理的逆定理/
2. 进一步加深对勾股定理与其逆定理之间关系的认识.
1. 应用勾股定理的逆定理解决实际问题.
素养目标
3. 将实际问题转化成用勾股定理的逆定理解决的数学问题.
17.2 勾股定理的逆定理/
1
2
如图,某港口P位于东西方向的海岸线上. “远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.它们离开港口一个半小时后分别位于点Q,R处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
N
E
P
Q
R
探究新知
知识点 1
利用勾股定理的逆定理解答角度问题
【思考】1.认真读题,找已知是什么?
“远航”号的航向、两艘船的一个半小时后的航程及距离已知,如下图.
17.2 勾股定理的逆定理/
1
2
N
E
P
Q
R
16×1.5=24
12×1.5=18
30
3.由于我们现在所能得到的都是线段长,要求角,由此我们想到利用什么思想?
要解决的问题是求出两艘船航向所成角.
勾股定理逆定理
探究新知
【思考】2.需要解决的问题是什么?
转化的思想
4.知道线段长度,通过线段长度来求角的度数,我们可以利用什么转化呢?
17.2 勾股定理的逆定理/
解:根据题意得
PQ=16×1.5=24(海里),
PR=12×1.5=18(海里),
QR=30海里.
∵242+182=302,即PQ2+PR2=QR2,∴∠QPR=90°.
由“远航”号沿东北方向航行可知∠1=45°.
∴∠2=45°,即“海天”号沿西北方向航行.
N
E
P
Q
R
1
2
探究新知
方法点拨:解决实际问题的步骤:①标注有用信息,明确已知和所求;②构建几何模型(从整体到局部);③应用数学知识求解.
17.2 勾股定理的逆定理/
1.在寻找马航MH370航班过程中,两艘搜救舰艇接到消息,在海面上有疑似漂浮目标A、B. 接到消息后,一艘舰艇以16海里/时的速度离开港口O(如图所示)向北偏东40°方向航行,另一艘舰艇在同时以12海里/时的速度向北偏西一定角度的航向行驶,已知它们离港口一个半小时后相距30海里,问另一艘舰艇的航行方向是北偏西多少度?
巩固练习
17.2 勾股定理的逆定理/
解:由题意得,OB=12×1.5=18海里,
OA=16×1.5=24海里,
又∵AB=30海里,
∴182+242=302,即OB2+OA2=AB2,
∴∠AOB=90°.
∵∠DOA=40°,
∴∠BOD=50°.
则另一艘舰艇的航行方向是北偏西50°.
巩固练习
17.2 勾股定理的逆定理/
如图,四边形ABCD中,AB⊥AD,已知AD=3cm,AB=4cm,CD=12cm,BC=13cm,求四边形ABCD 的面积.
解:连接BD.
在Rt△ABD中,由勾股定理得 BD2=AB2+AD2,
∴BD=5cm.又∵ CD=12cm,BC=13cm,
∴ BC2=CD2+BD2,∴△BDC是直角三角形.
∴S四边形ABCD=SRt△BCD-SRt△ABD= BD CD- AB AD = ×(5×12-3×4)=24 (cm2).
C
B
A
D
探究新知
知识点 2
利用勾股定理的逆定理解答面积问题
17.2 勾股定理的逆定理/
2.如图,在四边形ABCD中,AC⊥DC,△ADC的面积为30 cm2,DC=12 cm,AB=3cm,BC=4cm,求△ABC的面积.
解: ∵ S△ACD=30 cm2,DC=12 cm.
∴ AC=5 cm.
又∵
∴△ABC是直角三角形, ∠B是直角.
∴
D
C
B
A
巩固练习
17.2 勾股定理的逆定理/
如图,是一农民建房时挖地基的平面图,按标准应为长方形,他在挖完后测量了一下,发现AB=DC=8m,AD=BC=6m,AC=9m,请你运用所学知识帮他检验一下挖的是否合格?
解:∵AB=DC=8m,AD=BC=6m,
∴AB2+BC2=82+62=64+36=100.
又∵AC2=92=81,
∴AB2+BC2≠AC2,∴∠ABC≠90°,
∴该农民挖的不合格.
知识点 3
探究新知
利用勾股定理的逆定理解答检测问题
17.2 勾股定理的逆定理/
3. 一个零件的形状如图 所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图 所示,这个零件符合要求吗
D
A
B
C
4
3
5
13
12
D
A
B
C
图
图
巩固练习
17.2 勾股定理的逆定理/
在△BCD中,
∴△BCD 是直角三角形,∠DBC是直角.
因此,这个零件符合要求.
解:在△ABD中,
∴△ABD 是直角三角形,∠A是直角.
D
A
B
C
4
3
5
13
12
图
巩固练习
AB2+AD2=32+42=25=52=BD2
BD2+BC2=52+122=169=132=CD2
17.2 勾股定理的逆定理/
(2018 长沙)我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题:“问有沙田一块,有三斜,其中小斜五
里,中斜十二里,大斜十三里,欲知为田几何?”这道题讲的
是:有一块三角形沙田,三条边长分别为5里,12里,13里,问这块沙田面积有多大?题中“里”是我国市制长度单位,1里=500米,则该沙田的面积为( )
A.7.5平方千米 B.15平方千米
C.75平方千米 D.750平方千米
巩固练习
连接中考
A
17.2 勾股定理的逆定理/
B
B
课堂检测
基础巩固题
1.五根小木棒,其长度分别为7,15,20,24,25,现将他们摆成两个直角三角形,其中摆放方法正确的是 ( )
D
A. B.
C. D.
17.2 勾股定理的逆定理/
2.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300 m,公园到医院的距离为400 m,若公园到超市的距离为500 m,则公园在医院的 ( )
A.北偏东75°的方向上 B.北偏东65°的方向上
C.北偏东55°的方向上 D.无法确定
B
基础巩固题
课堂检测
17.2 勾股定理的逆定理/
3.如图,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.此时,A,B两组行进的方向成直角吗?请说明理由.
解:∵出发2小时,A组行了12×2=24(km),
B组行了9×2=18(km),
又∵A,B两组相距30km,
且有242+182=302,
∴A,B两组行进的方向成直角.
基础巩固题
课堂检测
A
O
B
17.2 勾股定理的逆定理/
4.在城市街路上速度不得超过70千米/时,一辆小汽车某一时刻行驶在路边车速检测仪的北偏东30°距离30米处,过了2秒后行驶了50米,此时小汽车与车速检测仪间的距离为40米. 问:2秒后小汽车在车速检测仪的哪个方向 这辆小汽车超速了吗
车速检测仪
小汽车
30米
30°
北
60°
解:小汽车在车速检测仪的南偏东60°方向或北偏西60°方向.
25米/秒=90千米/时>70千米/时
∴小汽车超速了.
2秒后
50米
40米
基础巩固题
课堂检测
17.2 勾股定理的逆定理/
如图,四边形ABCD中,∠B=90°,AB=3,BC=4,CD=12,AD=13,求四边形ABCD的面积.
分析:连接AC,把四边形分成两个三角形.先用勾股定理求出AC的长度,再利用勾股定理的逆定理判断△ACD是直角三角形.
A
D
B
C
3
4
13
12
能力提升题
课堂检测
17.2 勾股定理的逆定理/
解:连接AC.
在Rt△ABC中,
在△ACD中,
AC2+CD2=52+122=169=AD2,
∴△ACD是直角三角形,
且∠ACD=90°.
∴S四边形ABCD=SRt△ABC+SRt△ACD=6+30=36.
能力提升题
课堂检测
A
D
B
C
3
4
13
12
17.2 勾股定理的逆定理/
如图,在△ABC中,AB:BC:CA=3:4:5且周长为36cm,点P从点A开始沿AB边向B点以每秒2cm的速度移动,点Q从点C沿CB边向点B以每秒1cm的速度移动,如果同时出发,则过3s时,求PQ的长.
解:设AB为3xcm,BC为4xcm,AC为5xcm,∵周长为36cm,即AB+BC+AC=36cm,
∴AB=9cm,BC=12cm,AC=15cm.
∵AB2+BC2=AC2,∴△ABC是直角三角形,过3秒时,
BP=9-3×2=3(cm),BQ=12-1×3=9(cm),
在Rt△PBQ中,由勾股定理得
课堂检测
拓广探索题
∴3x+4x+5x=36,
解得x=3.
P
C
B
A
Q
17.2 勾股定理的逆定理/
勾股定理的逆定理的应用
应用
航海问题
方法
认真审题,画出符合题意的图形,熟练运用勾股定理及其逆定理来解决问题
与勾股定理结合解决不规则图形等问题
课堂小结
17.2 勾股定理的逆定理/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
