第19章《 一次函数 》单元同步检测试题(含答案)
文档属性
| 名称 | 第19章《 一次函数 》单元同步检测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 20:00:14 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.下面各点中,在函数y=﹣x+3图象上的点是( )
A.(3,0) B.(﹣2,2) C.(2,﹣2) D.(4,1)
2.若直线y=2x﹣1经过点A(﹣2,m),B(1,n),则m,n的大小关系正确的
是( )
A.m<n B.m>n C.m=n D.无法确定
3.函数y=﹣3x+1的图象一定经过点( )
A.(﹣1,﹣2) B.(﹣2,7) C.(3,﹣10) D.(4,﹣1)
4.已知在平面直角坐标系xOy中,直线y=2x+2和直线y=x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2 B.y=x+2 C.y=4x+2 D.y=x+2
5.根据如图所示的计算程序计算函数y的值,若输入m=﹣1,n=2时,则输出y的值是3,若输入m=4,n=3时,则输出y的值是( )
A.﹣5 B.﹣1 C.1 D.13
6.在平面直角坐标系中,若一个正比例函数的图象经过A(m,6),B(5,n)
两点,则m,n一定满足的关系式为( )
A.m﹣n=1 B.m+n=11 C.= D.mn=30
7.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
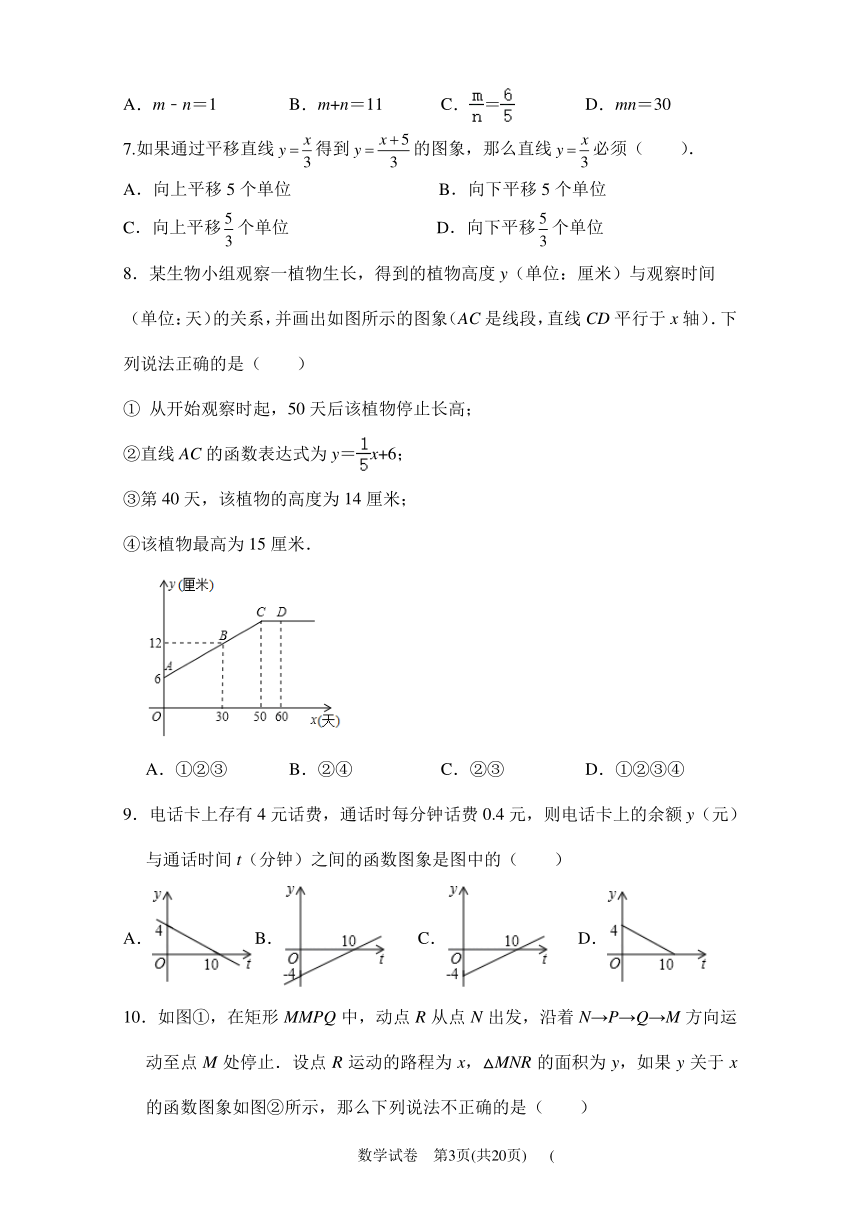
8.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间
(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下
列说法正确的是( )
1 从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③ B.②④ C.②③ D.①②③④
9.电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A.B. C. D.
10.如图①,在矩形MMPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,那么下列说法不正确的是( )
A.当x=2时,y=5 B.矩形MNPQ的周长是18
C.当x=6时,y=10 D.当y=8时,x=10
二、填空题(每题3分,共30分)
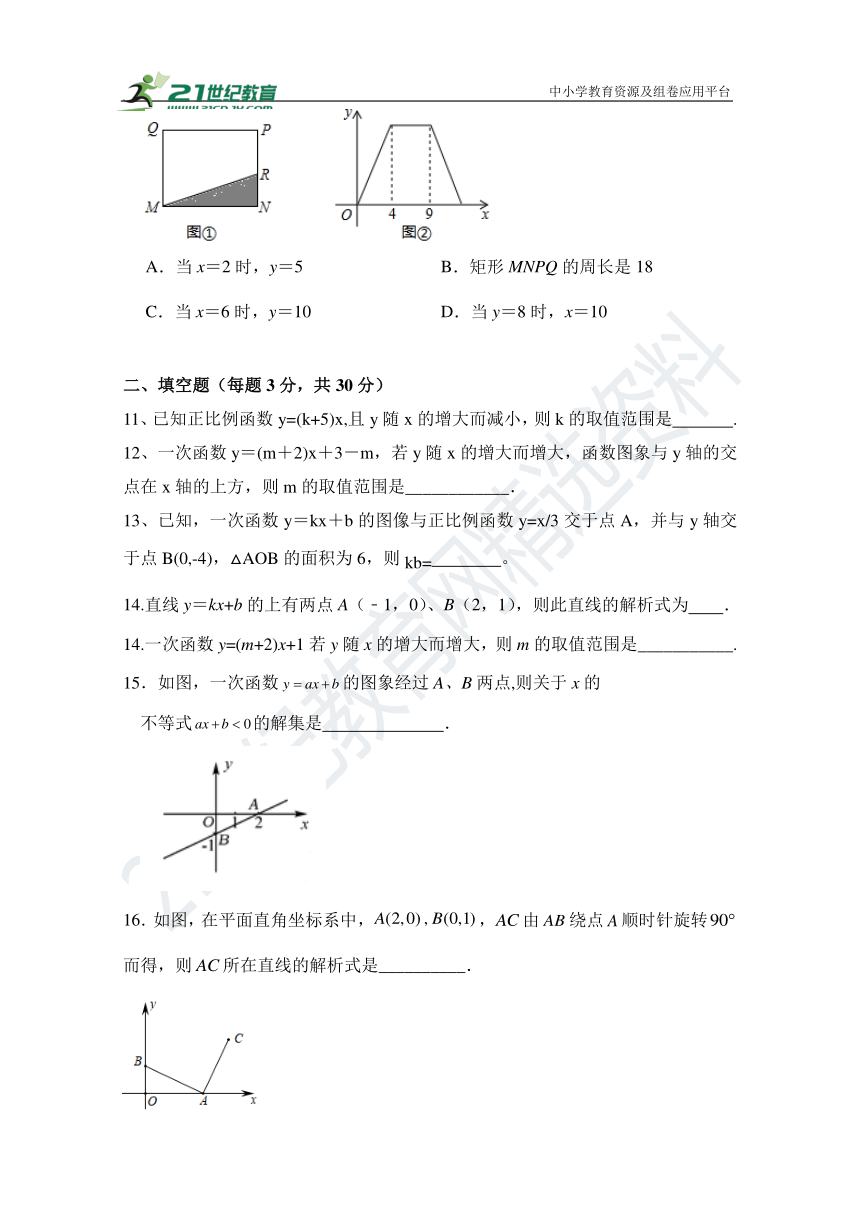
11、已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是 .
12、一次函数y=(m+2)x+3-m,若y随x的增大而增大,函数图象与y轴的交点在x轴的上方,则m的取值范围是____________.
13、已知,一次函数y=kx+b的图像与正比例函数y=x/3交于点A,并与y轴交于点B(0,-4),△AOB的面积为6,则kb= 。
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,已知直线l:y=x,过点A(1,)作直线l的垂线交x轴于点B,过点B作x轴的垂线交直线l于点A1;再过点A1作直线l的垂线交x轴于点B1,过点B1作x轴的垂线交直线l于点A2;…;按此作法继续下去,则点A3的坐标是 .
18.探究与发现:
在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,…点A1,A2,A3,A4,…在直线l上,点C1,C2,C3,C4,…在x轴正半轴上,则:
(1)An的坐标是 ;
(2)前n个正方形对角线长的和是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.在平面直角坐标系中,点P(m+7,2m)是一次函数y=﹣2x+2图象上一点.
(1)求点P的坐标.
(2)当﹣2<x≤3时,求y的取值范围.
20.设一次函数y=mx+n(m,n是常数,m≠0).
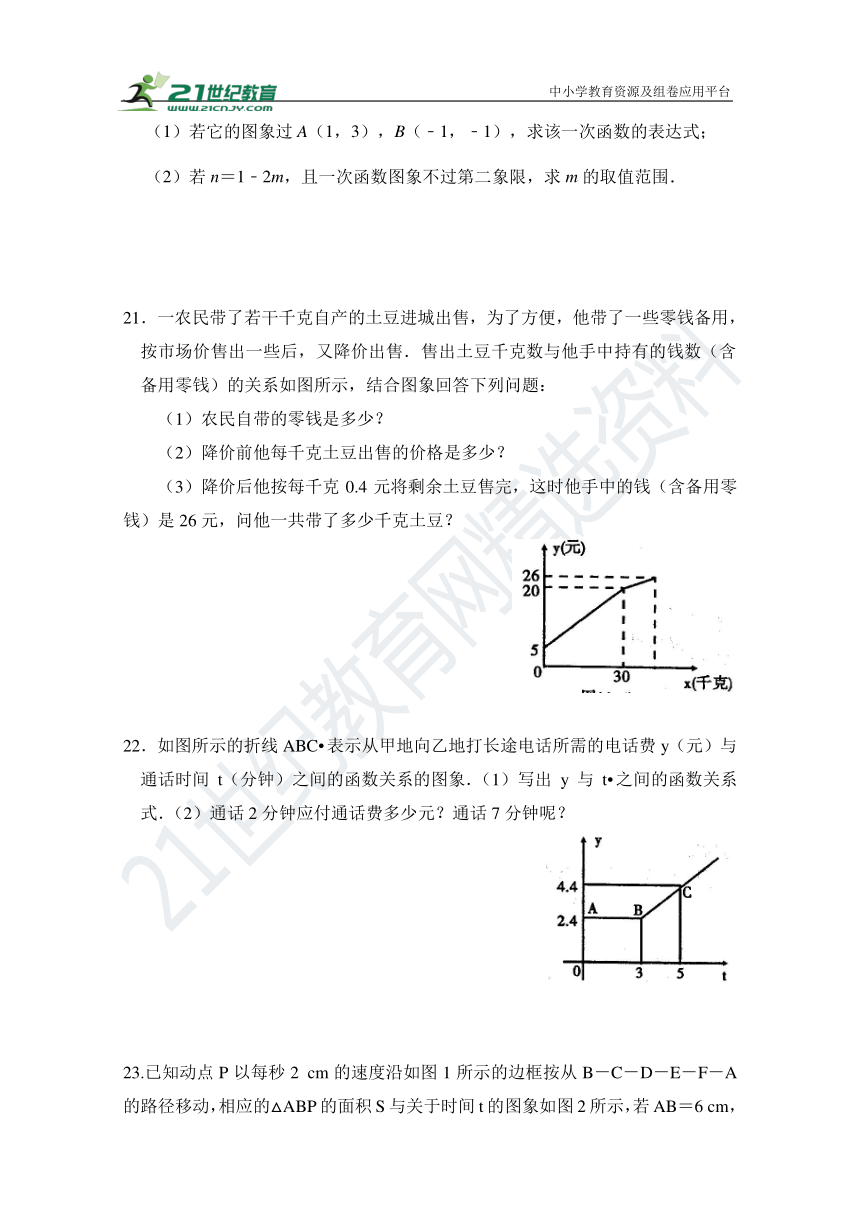
(1)若它的图象过A(1,3),B(﹣1,﹣1),求该一次函数的表达式;
(2)若n=1﹣2m,且一次函数图象不过第二象限,求m的取值范围.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.已知动点P以每秒2 cm的速度沿如图1所示的边框按从B-C-D-E-F-A的路径移动,相应的△ABP的面积S与关于时间t的图象如图2所示,若AB=6 cm,求:
(1)BC长为多少 cm
(2)图2中a为多少
(3)图1的面积为多少 cm2
(4)图2中b为多少?
24.五一假期过后,小明到校后发现忘记带数学课本;一看手表,离上课还有20分钟,他立刻步行返回家中取书,同时,他的父亲也发现小明忘记带数学课本,带上课本立刻以小明步行速度的2倍骑车赶往学校;父子在途中相遇,小明拿到课本后马上按原速步行返回学校,到校后发现迟到了4分钟.下图是父子俩离学校的路程s(米)与所用时间t(分钟)之间的函数关系,请结合图象,回答下列问题:
(1)两人相遇处离学校的距离是多少米?
(2)试求小明的父亲在赶往学校的过程中,路程s与时间t之间的函数解析式;
(3)假如小明父子相遇拿到课本后,改由他的父亲骑车搭他到学校,他会迟到吗?如果会,迟到几分钟;如果不会,能提前几分钟到校?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B D D A C A D D
二、填空题(每题3分,共24分)
11、k<-5
12、-2<m<3
13、-20/3或4
14.y=x+.
15. X<2
16.
17.【解答】解:∵直线l:y=x,
∴∠AOB=60°,
∵A(1,),
∴OA==2,
∵AB⊥直线l,
∴OB=2OA=4,
又∵A1B⊥x轴,
∴A1B=4,
∴A1(4,4),
∴OA1==8,
∴OB1=2OA1=16,
∴A2B1=16,
∴A2(16,16),
……
∴An(22n,22n),
由此可得,点A3的坐标为(26,26)即(64,64),
故答案为(64,64).
18.【解答】解:(1)由题意可得正方形OA1B1C1边长为1,正方形A2B2C2C1的边长为2,正方形A3B3C3C2的边长为4,…正方形AnBn nCn﹣1的边长为2n﹣1,
∴A1(0,1),A2(1,2),A3(3,4),A4(7,8)…An(2n﹣1﹣1,2n﹣1),
故答案为:(2n﹣1﹣1,2n﹣1);
(2)∵点A1的坐标为(0,1),点A2的坐标为(1,2),点A3的坐标为(3,4),点A4的坐标为(7,8),……,
∴OA1=1,C1A2=2,C2A3=4,C3A4=8,……,
∴前n个正方形对角线长的和是:(OA1+C1A2+C2A3+C3A4+…+Cn﹣1An)=(1+2+4+8+…+2n﹣1),
设S=1+2+4+8+…+2n﹣1,则2S=2+4+8+…+2n﹣1+2n,
则2S﹣S=2n﹣1,
∴S=2n﹣1,
∴1+2+4+8+…+2n﹣1=2n﹣1,
∴前n个正方形对角线长的和是:×(2n﹣1),
故答案为:(2n﹣1),
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:(1)∵点P(m+7,2m)是一次函数y=﹣2x+2图象上一点,
∴2m=﹣2(m+7)+2,解得m=﹣3,
故点P的坐标为(4,﹣6);
(2)∵y=﹣2x+2,
∴当x=﹣2时,y=﹣2×(﹣2)+2=6,
当x=3时,y=﹣2×3+2=﹣4,
∴当﹣2<x≤3时,y的取值范围是﹣4≤y<6.
20.解:(1)∵一次函数y=mx+n的图象经过两点A(1,3)、B(﹣1,﹣1),
∴,
解得,
∴函数解析式为:y=2x+1;
(2)把n=1﹣2m代入得y=mx+1﹣2m,
∵y=m(x﹣2)+1,
∴图象一定经过点(2,1),
∵一次函数图象不过第二象限,
∴m>0,1﹣2m≤0,
∴m≥.
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23、(1)由图可知:点P从点B到点C运动的时间是4 s,运动的速度是每秒2 cm,故BC的长度是4×2=8(cm),即BC长是8 cm.
(2)∵BC=8 cm,AB=6 cm,∴a=AB·BC=×6×8=24.
(3)由图可知:BC=8 cm,CD=(6-4)×2=4(cm),DE=(9-6)×2=6(cm),AB=6 cm,∴AF=BC+DE=14 cm.∴图1的面积是:AB·AF-CD·DE=6×14-4×6=60(cm2).
(4)由题意可得:
b===17.
24、(1)在图象中可以看出,从出发到父子相遇花费了12分钟.设小明步行速度为x米/分,则小明父亲骑车速度为2x米/分,根据题意,得12x+12×2x=2 880.解得x=80.∴两人相遇处离学校的距离是80×12=960(米).
(2)设小明的父亲在赶往学校的过程中,路程s与时间t之间的函数关系式为s=kt+b.
把(0,2 880)和(12,960)分别代入,得解得∴s=-160t+2 880.
(3)在s=-160t+2 880中,令s=0,得0=-160t+2 880.解得t=18.∴20-18=2(分钟).
答:如果由他的父亲骑车搭他到学校,他不会迟到,且能提前2分钟到校.
数学试卷 第19页(共22页) ( 数学试卷 第20页(共22页)
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.下面各点中,在函数y=﹣x+3图象上的点是( )
A.(3,0) B.(﹣2,2) C.(2,﹣2) D.(4,1)
2.若直线y=2x﹣1经过点A(﹣2,m),B(1,n),则m,n的大小关系正确的
是( )
A.m<n B.m>n C.m=n D.无法确定
3.函数y=﹣3x+1的图象一定经过点( )
A.(﹣1,﹣2) B.(﹣2,7) C.(3,﹣10) D.(4,﹣1)
4.已知在平面直角坐标系xOy中,直线y=2x+2和直线y=x+2分别交x轴于点A和点B.则下列直线中,与x轴的交点不在线段AB上的直线是( )
A.y=x+2 B.y=x+2 C.y=4x+2 D.y=x+2
5.根据如图所示的计算程序计算函数y的值,若输入m=﹣1,n=2时,则输出y的值是3,若输入m=4,n=3时,则输出y的值是( )
A.﹣5 B.﹣1 C.1 D.13
6.在平面直角坐标系中,若一个正比例函数的图象经过A(m,6),B(5,n)
两点,则m,n一定满足的关系式为( )
A.m﹣n=1 B.m+n=11 C.= D.mn=30
7.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.某生物小组观察一植物生长,得到的植物高度y(单位:厘米)与观察时间
(单位:天)的关系,并画出如图所示的图象(AC是线段,直线CD平行于x轴).下
列说法正确的是( )
1 从开始观察时起,50天后该植物停止长高;
②直线AC的函数表达式为y=x+6;
③第40天,该植物的高度为14厘米;
④该植物最高为15厘米.
A.①②③ B.②④ C.②③ D.①②③④
9.电话卡上存有4元话费,通话时每分钟话费0.4元,则电话卡上的余额y(元)与通话时间t(分钟)之间的函数图象是图中的( )
A.B. C. D.
10.如图①,在矩形MMPQ中,动点R从点N出发,沿着N→P→Q→M方向运动至点M处停止.设点R运动的路程为x,△MNR的面积为y,如果y关于x的函数图象如图②所示,那么下列说法不正确的是( )
A.当x=2时,y=5 B.矩形MNPQ的周长是18
C.当x=6时,y=10 D.当y=8时,x=10
二、填空题(每题3分,共30分)
11、已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是 .
12、一次函数y=(m+2)x+3-m,若y随x的增大而增大,函数图象与y轴的交点在x轴的上方,则m的取值范围是____________.
13、已知,一次函数y=kx+b的图像与正比例函数y=x/3交于点A,并与y轴交于点B(0,-4),△AOB的面积为6,则kb= 。
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.如图,已知直线l:y=x,过点A(1,)作直线l的垂线交x轴于点B,过点B作x轴的垂线交直线l于点A1;再过点A1作直线l的垂线交x轴于点B1,过点B1作x轴的垂线交直线l于点A2;…;按此作法继续下去,则点A3的坐标是 .
18.探究与发现:
在平面直角坐标系中,直线l:y=x+1与y轴交于点A1,如图所示,依次作正方形OA1B1C1,正方形C1A2B2C2,正方形C2A3B3C3,正方形C3A4B4C4,…点A1,A2,A3,A4,…在直线l上,点C1,C2,C3,C4,…在x轴正半轴上,则:
(1)An的坐标是 ;
(2)前n个正方形对角线长的和是 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.在平面直角坐标系中,点P(m+7,2m)是一次函数y=﹣2x+2图象上一点.
(1)求点P的坐标.
(2)当﹣2<x≤3时,求y的取值范围.
20.设一次函数y=mx+n(m,n是常数,m≠0).
(1)若它的图象过A(1,3),B(﹣1,﹣1),求该一次函数的表达式;
(2)若n=1﹣2m,且一次函数图象不过第二象限,求m的取值范围.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.已知动点P以每秒2 cm的速度沿如图1所示的边框按从B-C-D-E-F-A的路径移动,相应的△ABP的面积S与关于时间t的图象如图2所示,若AB=6 cm,求:
(1)BC长为多少 cm
(2)图2中a为多少
(3)图1的面积为多少 cm2
(4)图2中b为多少?
24.五一假期过后,小明到校后发现忘记带数学课本;一看手表,离上课还有20分钟,他立刻步行返回家中取书,同时,他的父亲也发现小明忘记带数学课本,带上课本立刻以小明步行速度的2倍骑车赶往学校;父子在途中相遇,小明拿到课本后马上按原速步行返回学校,到校后发现迟到了4分钟.下图是父子俩离学校的路程s(米)与所用时间t(分钟)之间的函数关系,请结合图象,回答下列问题:
(1)两人相遇处离学校的距离是多少米?
(2)试求小明的父亲在赶往学校的过程中,路程s与时间t之间的函数解析式;
(3)假如小明父子相遇拿到课本后,改由他的父亲骑车搭他到学校,他会迟到吗?如果会,迟到几分钟;如果不会,能提前几分钟到校?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D A B D D A C A D D
二、填空题(每题3分,共24分)
11、k<-5
12、-2<m<3
13、-20/3或4
14.y=x+.
15. X<2
16.
17.【解答】解:∵直线l:y=x,
∴∠AOB=60°,
∵A(1,),
∴OA==2,
∵AB⊥直线l,
∴OB=2OA=4,
又∵A1B⊥x轴,
∴A1B=4,
∴A1(4,4),
∴OA1==8,
∴OB1=2OA1=16,
∴A2B1=16,
∴A2(16,16),
……
∴An(22n,22n),
由此可得,点A3的坐标为(26,26)即(64,64),
故答案为(64,64).
18.【解答】解:(1)由题意可得正方形OA1B1C1边长为1,正方形A2B2C2C1的边长为2,正方形A3B3C3C2的边长为4,…正方形AnBn nCn﹣1的边长为2n﹣1,
∴A1(0,1),A2(1,2),A3(3,4),A4(7,8)…An(2n﹣1﹣1,2n﹣1),
故答案为:(2n﹣1﹣1,2n﹣1);
(2)∵点A1的坐标为(0,1),点A2的坐标为(1,2),点A3的坐标为(3,4),点A4的坐标为(7,8),……,
∴OA1=1,C1A2=2,C2A3=4,C3A4=8,……,
∴前n个正方形对角线长的和是:(OA1+C1A2+C2A3+C3A4+…+Cn﹣1An)=(1+2+4+8+…+2n﹣1),
设S=1+2+4+8+…+2n﹣1,则2S=2+4+8+…+2n﹣1+2n,
则2S﹣S=2n﹣1,
∴S=2n﹣1,
∴1+2+4+8+…+2n﹣1=2n﹣1,
∴前n个正方形对角线长的和是:×(2n﹣1),
故答案为:(2n﹣1),
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:(1)∵点P(m+7,2m)是一次函数y=﹣2x+2图象上一点,
∴2m=﹣2(m+7)+2,解得m=﹣3,
故点P的坐标为(4,﹣6);
(2)∵y=﹣2x+2,
∴当x=﹣2时,y=﹣2×(﹣2)+2=6,
当x=3时,y=﹣2×3+2=﹣4,
∴当﹣2<x≤3时,y的取值范围是﹣4≤y<6.
20.解:(1)∵一次函数y=mx+n的图象经过两点A(1,3)、B(﹣1,﹣1),
∴,
解得,
∴函数解析式为:y=2x+1;
(2)把n=1﹣2m代入得y=mx+1﹣2m,
∵y=m(x﹣2)+1,
∴图象一定经过点(2,1),
∵一次函数图象不过第二象限,
∴m>0,1﹣2m≤0,
∴m≥.
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23、(1)由图可知:点P从点B到点C运动的时间是4 s,运动的速度是每秒2 cm,故BC的长度是4×2=8(cm),即BC长是8 cm.
(2)∵BC=8 cm,AB=6 cm,∴a=AB·BC=×6×8=24.
(3)由图可知:BC=8 cm,CD=(6-4)×2=4(cm),DE=(9-6)×2=6(cm),AB=6 cm,∴AF=BC+DE=14 cm.∴图1的面积是:AB·AF-CD·DE=6×14-4×6=60(cm2).
(4)由题意可得:
b===17.
24、(1)在图象中可以看出,从出发到父子相遇花费了12分钟.设小明步行速度为x米/分,则小明父亲骑车速度为2x米/分,根据题意,得12x+12×2x=2 880.解得x=80.∴两人相遇处离学校的距离是80×12=960(米).
(2)设小明的父亲在赶往学校的过程中,路程s与时间t之间的函数关系式为s=kt+b.
把(0,2 880)和(12,960)分别代入,得解得∴s=-160t+2 880.
(3)在s=-160t+2 880中,令s=0,得0=-160t+2 880.解得t=18.∴20-18=2(分钟).
答:如果由他的父亲骑车搭他到学校,他不会迟到,且能提前2分钟到校.
数学试卷 第19页(共22页) ( 数学试卷 第20页(共22页)
