第19章《 一次函数 》单元同步检测试题(含答案)
文档属性
| 名称 | 第19章《 一次函数 》单元同步检测试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 20:01:41 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.已知正比例函数y=kx(k是不为零的常数)过点(﹣1,2),则k的值为( )
A.2 B.1 C.﹣1 D.﹣2
2.将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式
( )
A.y=﹣2x﹣5 B.y=﹣2x﹣3 C.y=﹣2x+1 D.y=﹣2x+3
3.函数y=的自变量x的取值范围是( )
A.x≠5 B.x>2且x≠5 C.x≥2 D.x≥2且x≠5
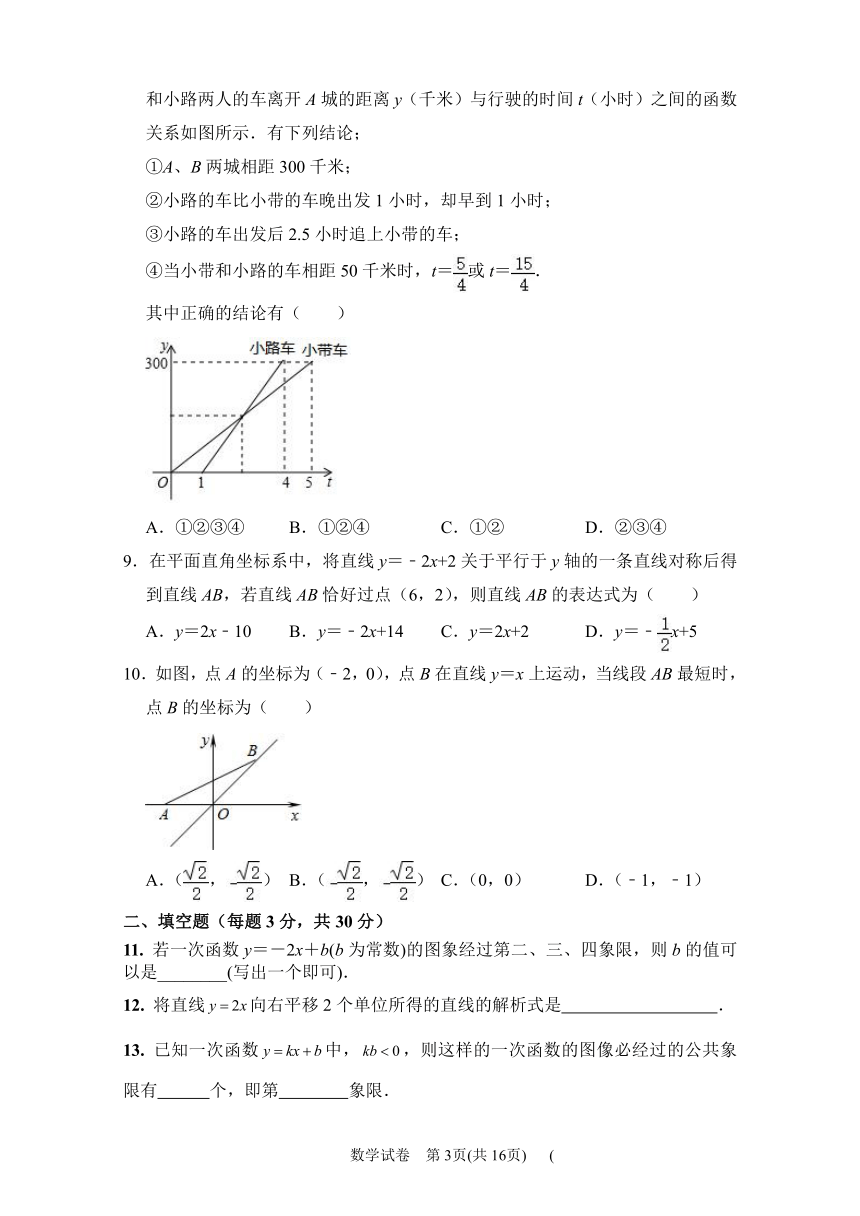
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.函数y=kx+b与函数y=﹣bx在同一坐标系中的图象可能是( )
A. B. C. D.
6.若一次函数y=2x﹣3的图象平移后经过点(3,1),则下列叙述正确的是( )
A.沿x轴向右平移3个单位长度 B.沿x轴向右平移1个单位长度
C.沿x轴向左平移3个单位长度 D.沿x轴向左平移1个单位长度
7.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人的车离开A城的距离y(千米)与行驶的时间t(小时)之间的函数关系如图所示.有下列结论;
①A、B两城相距300千米;
②小路的车比小带的车晚出发1小时,却早到1小时;
③小路的车出发后2.5小时追上小带的车;
④当小带和小路的车相距50千米时,t=或t=.
其中正确的结论有( )
A.①②③④ B.①②④ C.①② D.②③④
9.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB恰好过点(6,2),则直线AB的表达式为( )
A.y=2x﹣10 B.y=﹣2x+14 C.y=2x+2 D.y=﹣x+5
10.如图,点A的坐标为(﹣2,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(,) B.(,) C.(0,0) D.(﹣1,﹣1)
二、填空题(每题3分,共30分)
11. 若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是________(写出一个即可).
12. 将直线向右平移2个单位所得的直线的解析式是 .
13. 已知一次函数中,,则这样的一次函数的图像必经过的公共象限有 个,即第 象限.
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.黑龙江省某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程y(km)与行驶时间x(h)的函数关系如图所示,2小时后货车的速度是 km/h.
18.如图,在平面直角坐标系中,函数y=x和y=﹣x的图象分别为直线l1,l2,过l1上的点A1(1,)作x轴的垂线交l2于点A2,过点A2作y轴的垂线交l1于点A3,过点A3作x轴的垂线交l2于点A4,…依次进行下去,则点A2020的横坐标为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知y=y1+y2,y1与x成正比例,y2与x﹣2成正比例,当x=1时,y=﹣3;当x=﹣2时,y=0.
(1)求y与x的函数关系式;
(2)当x=3时,求y的值.
20.已知直线y=kx+b经过点(3,3)和(﹣1,1),求该直线的解析式.
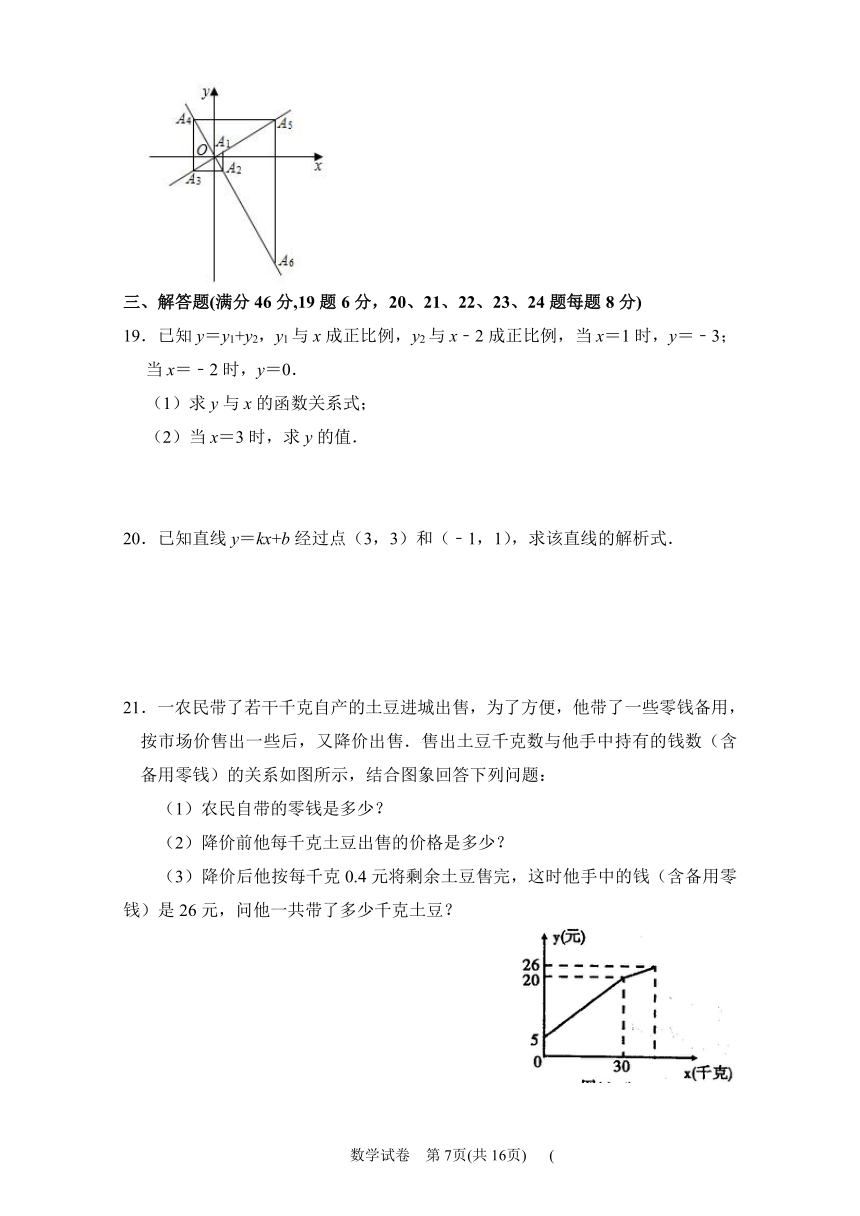
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23. 某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程;加工过程中,当油箱中油量为10升时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185分钟才能将这批工件加工完.下图是油箱中油量(升)与机器运行时间(分)之间的函数图象.根据图象回答问题:
⑴求在第一个加工过程中,油箱中油量(升)与机器运行时间(分)之间的函数关系式(不必写出自变量的取值范围);
⑵机器运行多少分钟时,第一个加工过程停止?
⑶加工完这批工件,机器耗油多少升?
24. 北京某厂和上海某厂同时制成电子计算机若干台,北京厂可支援外地10台,上海厂可支援外地4台,现在决定给重庆8台,汉口6台.如果从北京运往汉口、重庆的运费分别是4百元/台、8百元/台,从上海运往汉口、重庆的运费分别是3百元/台、5百元/台.求:
⑴若总运费为8400元,上海运往汉口应是多少台?
⑵若要求总运费不超过8200元,共有几种调运方案?
⑶求出总运费最低的调运方案,最低总运费是多少元?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:(1)设y1=ax,y2=b(x﹣2),
所以y=ax+b(x﹣2),
把x=1时,y=﹣3;当x=﹣2时,y=0分别代入得,
解得,
所以y与x的函数关系式为y=﹣2x+(x﹣2),即y=﹣x﹣2;
(2)当x=3时,y=﹣3﹣2=﹣5,即y=﹣5.
20.解:设该直线的解析式为y=kx+b,
把(3,3),(﹣1,1)代入得:,
解得
∴该直线的解析式为.
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23. 【答案】
⑴;⑵100;⑶166
【解析】⑴设所求函数关系式为.
由图象可知过(10,100),(30,80)两点,
得 解得
∴
⑵当时,
机器运行100分钟时,第一个加工过程停止
⑶第一个加工过程停止后再加满油只需9分钟
加工完这批工件,机器耗油166升.
24. 【答案】
⑴4;⑵四种;⑶上海运往重庆有4台,北京厂运往汉口6台,北京厂运往重庆4台,最低总运费是7600元.
【解析】设上海厂运往汉口台,那么上海运往重庆有台,北京厂运往汉口台,北京厂运往重
庆台,则总运费W关于的一次函数关系式:
.
⑴当 (百元)时,则有,解得.
若总运费为8400元,上海厂应运往汉口4台.
⑵当 (元),则
解得,因为只能取整数,所以只有四种可的能值:0、1、2、3.
答:若要求总运费不超过8200元,共有4种调运方案.
⑶因为一次函数随着的增大而增大,又因为,所以当时,函数有最小值,最小值是 (百元),即最低总运费是7600元.
数学试卷 第15页(共16页) ( 数学试卷 第16页(共16页)
第19章《一次函数》单元测试
.
一.选择题(每题3分,共30分)
1.已知正比例函数y=kx(k是不为零的常数)过点(﹣1,2),则k的值为( )
A.2 B.1 C.﹣1 D.﹣2
2.将直线y=﹣2x﹣1向上平移两个单位,平移后的直线所对应的函数关系式
( )
A.y=﹣2x﹣5 B.y=﹣2x﹣3 C.y=﹣2x+1 D.y=﹣2x+3
3.函数y=的自变量x的取值范围是( )
A.x≠5 B.x>2且x≠5 C.x≥2 D.x≥2且x≠5
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.函数y=kx+b与函数y=﹣bx在同一坐标系中的图象可能是( )
A. B. C. D.
6.若一次函数y=2x﹣3的图象平移后经过点(3,1),则下列叙述正确的是( )
A.沿x轴向右平移3个单位长度 B.沿x轴向右平移1个单位长度
C.沿x轴向左平移3个单位长度 D.沿x轴向左平移1个单位长度
7.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.小带和小路两个人开车从A城出发匀速行驶至B城.在整个行驶过程中,小带和小路两人的车离开A城的距离y(千米)与行驶的时间t(小时)之间的函数关系如图所示.有下列结论;
①A、B两城相距300千米;
②小路的车比小带的车晚出发1小时,却早到1小时;
③小路的车出发后2.5小时追上小带的车;
④当小带和小路的车相距50千米时,t=或t=.
其中正确的结论有( )
A.①②③④ B.①②④ C.①② D.②③④
9.在平面直角坐标系中,将直线y=﹣2x+2关于平行于y轴的一条直线对称后得到直线AB,若直线AB恰好过点(6,2),则直线AB的表达式为( )
A.y=2x﹣10 B.y=﹣2x+14 C.y=2x+2 D.y=﹣x+5
10.如图,点A的坐标为(﹣2,0),点B在直线y=x上运动,当线段AB最短时,点B的坐标为( )
A.(,) B.(,) C.(0,0) D.(﹣1,﹣1)
二、填空题(每题3分,共30分)
11. 若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是________(写出一个即可).
12. 将直线向右平移2个单位所得的直线的解析式是 .
13. 已知一次函数中,,则这样的一次函数的图像必经过的公共象限有 个,即第 象限.
14.直线y=kx+b的上有两点A(﹣1,0)、B(2,1),则此直线的解析式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转而得,则所在直线的解析式是__________.
17.黑龙江省某企业用货车向乡镇运送农用物资,行驶2小时后,天空突然下起大雨,影响车辆行驶速度,货车行驶的路程y(km)与行驶时间x(h)的函数关系如图所示,2小时后货车的速度是 km/h.
18.如图,在平面直角坐标系中,函数y=x和y=﹣x的图象分别为直线l1,l2,过l1上的点A1(1,)作x轴的垂线交l2于点A2,过点A2作y轴的垂线交l1于点A3,过点A3作x轴的垂线交l2于点A4,…依次进行下去,则点A2020的横坐标为 .
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知y=y1+y2,y1与x成正比例,y2与x﹣2成正比例,当x=1时,y=﹣3;当x=﹣2时,y=0.
(1)求y与x的函数关系式;
(2)当x=3时,求y的值.
20.已知直线y=kx+b经过点(3,3)和(﹣1,1),求该直线的解析式.
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23. 某工厂用一种自动控制加工机制作一批工件,该机器运行过程分为加油过程和加工过程;加工过程中,当油箱中油量为10升时,机器自动停止加工进入加油过程,将油箱加满后继续加工,如此往复.已知机器需运行185分钟才能将这批工件加工完.下图是油箱中油量(升)与机器运行时间(分)之间的函数图象.根据图象回答问题:
⑴求在第一个加工过程中,油箱中油量(升)与机器运行时间(分)之间的函数关系式(不必写出自变量的取值范围);
⑵机器运行多少分钟时,第一个加工过程停止?
⑶加工完这批工件,机器耗油多少升?
24. 北京某厂和上海某厂同时制成电子计算机若干台,北京厂可支援外地10台,上海厂可支援外地4台,现在决定给重庆8台,汉口6台.如果从北京运往汉口、重庆的运费分别是4百元/台、8百元/台,从上海运往汉口、重庆的运费分别是3百元/台、5百元/台.求:
⑴若总运费为8400元,上海运往汉口应是多少台?
⑵若要求总运费不超过8200元,共有几种调运方案?
⑶求出总运费最低的调运方案,最低总运费是多少元?
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 D C D D D A C B C A
二、填空题(每题3分,共24分)
11.
12.平行
13. y=3x
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.解:(1)设y1=ax,y2=b(x﹣2),
所以y=ax+b(x﹣2),
把x=1时,y=﹣3;当x=﹣2时,y=0分别代入得,
解得,
所以y与x的函数关系式为y=﹣2x+(x﹣2),即y=﹣x﹣2;
(2)当x=3时,y=﹣3﹣2=﹣5,即y=﹣5.
20.解:设该直线的解析式为y=kx+b,
把(3,3),(﹣1,1)代入得:,
解得
∴该直线的解析式为.
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23. 【答案】
⑴;⑵100;⑶166
【解析】⑴设所求函数关系式为.
由图象可知过(10,100),(30,80)两点,
得 解得
∴
⑵当时,
机器运行100分钟时,第一个加工过程停止
⑶第一个加工过程停止后再加满油只需9分钟
加工完这批工件,机器耗油166升.
24. 【答案】
⑴4;⑵四种;⑶上海运往重庆有4台,北京厂运往汉口6台,北京厂运往重庆4台,最低总运费是7600元.
【解析】设上海厂运往汉口台,那么上海运往重庆有台,北京厂运往汉口台,北京厂运往重
庆台,则总运费W关于的一次函数关系式:
.
⑴当 (百元)时,则有,解得.
若总运费为8400元,上海厂应运往汉口4台.
⑵当 (元),则
解得,因为只能取整数,所以只有四种可的能值:0、1、2、3.
答:若要求总运费不超过8200元,共有4种调运方案.
⑶因为一次函数随着的增大而增大,又因为,所以当时,函数有最小值,最小值是 (百元),即最低总运费是7600元.
数学试卷 第15页(共16页) ( 数学试卷 第16页(共16页)
