人教版数学八下 19.1.2函数的图像(希沃课件+图片版PPT)仅适用希沃白板
文档属性
| 名称 | 人教版数学八下 19.1.2函数的图像(希沃课件+图片版PPT)仅适用希沃白板 |

|
|
| 格式 | zip | ||
| 文件大小 | 10.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 09:31:35 | ||
图片预览






文档简介
(共58张PPT)
19.1 函数/
19.1 函数
19.1.2 函数的图象
人教版 数学 八年级 下册
19.1 函数/
1. 了解函数图象的意义.了解函数的三种表示法及其优缺点 .
2. 会观察函数图象获取信息,根据图象初步分析函数的对应关系和变化规律.
素养目标
3. 经历画函数图象的过程,体会函数图象建立数形联系的关键是分别用点的横、纵坐标表示自变量和对应的函数值.
一般地,在一个变化过程中,如果有两个变量 x和 y,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应 ,那么我们就说 x 是自变量,y 是 x 的函数.
函数的定义:
函数的三种表示方法:
解析式法、图象法、列表法
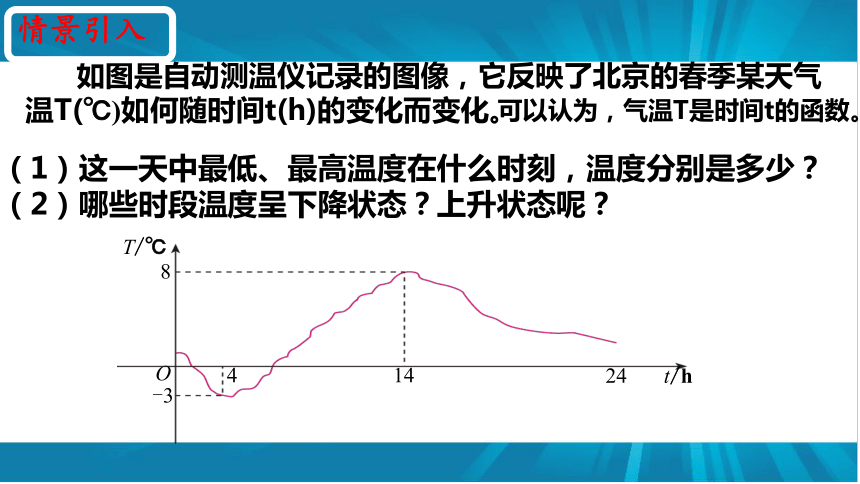
如图是自动测温仪记录的图像,它反映了北京的春季某天气温T(℃)如何随时间t(h)的变化而变化。
-3
O
4
14
24
8
T/℃
t/h
情景引入
(1)这一天中最低、最高温度在什么时刻,温度分别是多少?
(2)哪些时段温度呈下降状态?上升状态呢?
可以认为,气温T是时间t的函数。
问题: 正方形面积 S 与边长 x 之间的函数解析式为 _________.
(1)这个函数的自变量取值范围是什么?
(2)如果想和上题那样,直观的看出S和x之间的
对应关系,需要具备哪些条件?
平面直角坐标系和所对应的曲线
>
S=x2
怎样用画图的方法来表示S与x的关系呢?
(3)怎样获得曲线上的点?
取一个自变量的值,计算出相应的函数值,当作一个点的横坐标与纵坐标。
19.1 函数/
S=x2
(x>0)
0
0.25
1
2.25
4
6.25
9
12.25
16
探究新知
19.1 函数/
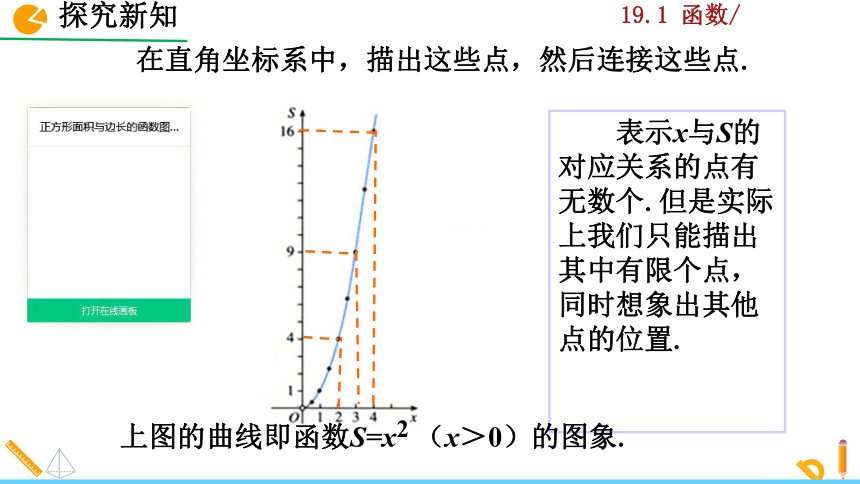
在直角坐标系中,描出这些点,然后连接这些点.
表示x与S的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.
探究新知
上图的曲线即函数S=x2 (x>0)的图象.
19.1 函数/
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
探究新知
函数图象是典型的数形结合,
自变量-----横坐标
函数(因变量)-----纵坐标
数(两个变量的值)---对应---形(图象上的每一个点)
19.1 函数/
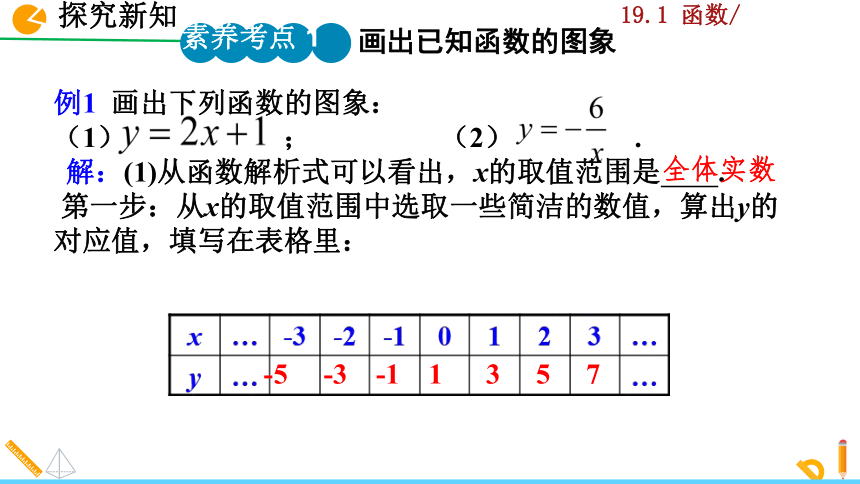
例1 画出下列函数的图象:
(1) ; (2) .
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值,算出y的
对应值,填写在表格里:
-5 -3 -1 1 3 5 7
全体实数
探究新知
素养考点 1
画出已知函数的图象
19.1 函数/
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
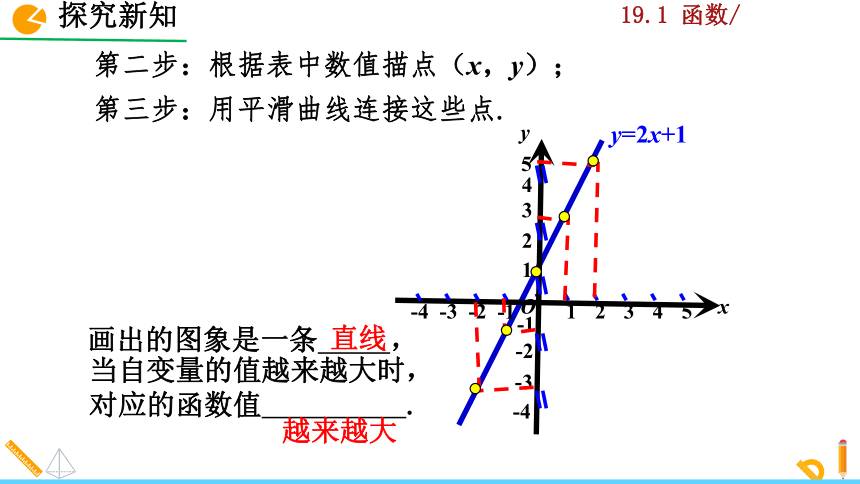
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,
对应的函数值 .
画出的图象是一条 ,
直线
越来越大
探究新知
19.1 函数/
-6
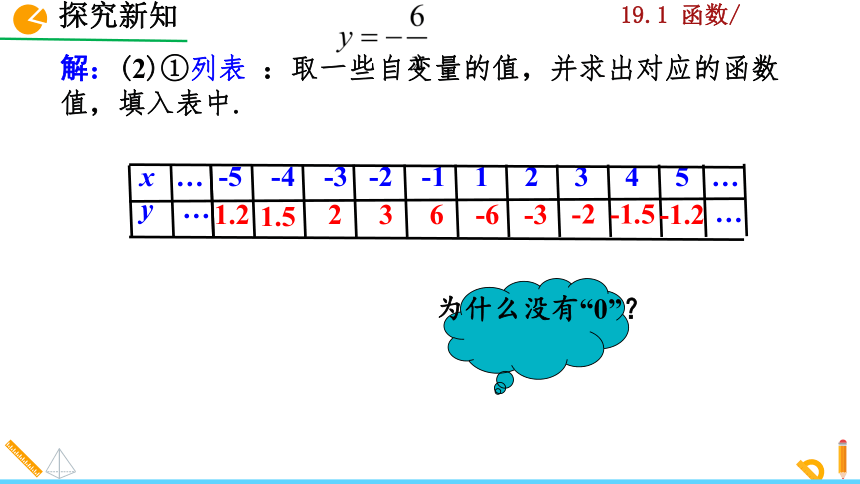
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
解:(2)①列表 :取一些自变量的值,并求出对应的函数值,填入表中.
探究新知
为什么没有“0”?
19.1 函数/
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
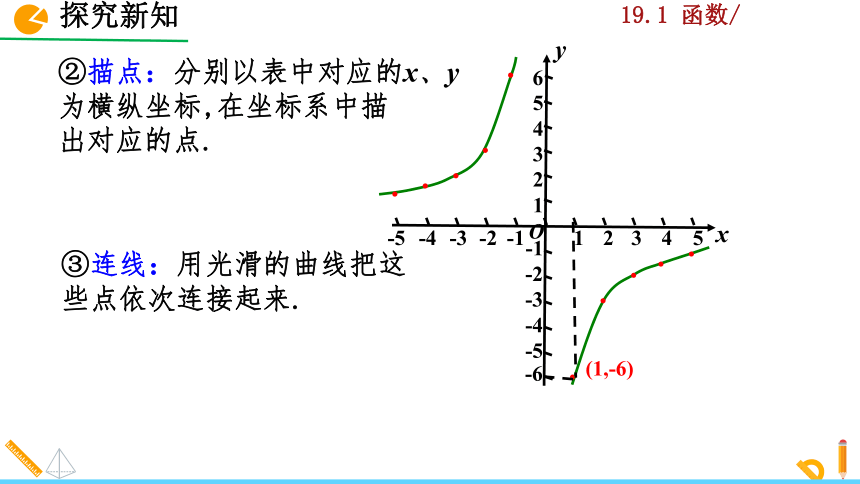
②描点:分别以表中对应的x、y为横纵坐标,在坐标系中描
出对应的点.
③连线:用光滑的曲线把这些点依次连接起来.
(1,-6)
探究新知
(1)列表--表中列出部分自变量的值及其对应的函数值;
(2)描点:--在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
(3)连线:--按照横坐标由小到大的顺序,把所描的各点用平滑的曲线连接起来。
1.画函数图象的一般步骤:
注意:列表时自变量由小到大,5到7个,有代表性,注意自变量的取值范围.
归纳总结
1.判断下列各点是否在函数y=2x+1的图象上?
①(-0.5,1) ②(1.5,4)
做一做
2.判断下列各点是否在函数 的图象上?
①(2,3) ②(4,2)
19.1 函数/
函数的三种表示法:
y = 2.88x
图象法、
列表法、
解析式法.
1 4 9 16 25 36 49
探究新知
19.1 函数/
探究新知
归纳总结
函数的三种表示方法:
(1)列表法:用_______列出自变量与函数的对应值,表示函数两个变量之间的关系,这种表示函数的方法叫做列表法.
(2)图象法:用_______表示两个变量之间的函数关系,这种表示函数的方法叫做图象法.
(3)解析式法:用__________表示函数的方法叫做解析式法.
表格
图象
数学式
19.1 函数/
请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点,填写下表:
提示:从所填表中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.
√
×
×
×
×
×
√
√
√
√
√
探究新知
×
例2.下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
家
食堂
图书馆
答:食堂离小明家0.6km,小明从家到食堂用了8min.
从实际问题的图象中读取信息
(2)小明吃早餐用了多少时间?
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(4)小明读报用了多长时间?
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
分析函数图象时要注意:
①横、纵坐标表示的意义;
②每条线段表示的意义;
③端点、转折点表示的意义;
④与坐标轴平行的线段.
课堂总结
例:
19.1 函数/
(1)这一天内,上海与北京何时气温相同?
(2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?
答:7时 和 12时.
答:上海在0时— 7时和12时— 24时比北京气温高;
在7时—12时比北京气温低.
2.如图是某一天北京与上海的气温随时间变化的图象.
根据图像回答下列问题.
巩固练习
19.1 函数/
1.最近中旗连降雨雪,德岭山水库水位上涨.如图表示某一天水位变化情况,0时的水位为警戒水位.结合图象判断下列叙述不正确的是( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
C
课堂检测
2.放学后小刚骑车回家,他离学校的距离S(m)与时间t(min)的函数关系如图,则小刚家距离学校____m,小刚回家需要___min,小刚的骑车速度是______m/min。
t
S
O
10
2000
(m)
(min)
2000
10
200
B
C
A
思考:线段BC的含义是什么?
课堂练习
3.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )
h
t
O
A
h
t
O
B
h
t
O
C
h
t
O
D
19.1 函数/
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
答:体育场离张强家2.5千米.
张强从家到体育场用15分钟.
4.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,图中x表示时间,y表示张强离家的距离.
课堂检测
19.1 函数/
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)张强从文具店回家的平均速度是多少?
答:2.5-1.5=1(千米)
答:65-45=20(分)
课堂检测
解:依题意可得
1.5÷[(100-65)÷60]
19.1 函数/
给出下列说法:①学校到景点的路程为55 km;②甲组在途中停留了5 min;③甲、乙两组同时到达景点;④相遇后,乙组的速度小于甲组的速度.根据图象信息,以上说法正确的有 .
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
课堂检测
①
②
19.1 函数/
3.小明同学骑自行车去郊外春游,
如图表示他离家的距离y(km)与所
用的时间x(h)之间关系的函数图象.
(1)根据图象回答:小明到达离
家最远的地方需______h;
(2)小明出发2.5 h后离家_______km;
(3)小明出发__________h后离家12 km.
3
22.5
0.8或5.2
课堂检测
例1 一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
19.1 函数/
探究新知
素养考点 1
函数表示方法的相互转化
19.1 函数/
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每小时水位 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
5
探究新知
3
O
5
19.1 函数/
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
解:由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: . 变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
探究新知
19.1 函数/
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
探究新知
3
O
5
其函数的图象如下:
5
A
B
19.1 函数/
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
解:如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
探究新知
19.1 函数/
1.已知火车站托运行李的费用C(元)和托运行李的重量P(千克)(P为整数)的对应关系如表:
(1)已知小周的所要托运的行李重12千克,请问小周托运行李的费用为多少元?
(2)写出C与P之间的函数解析式.
(3)小李托运行李花了15元钱,请问小李的行李重多少千克?
7.5元
C=0.5P+1.5
27千克
巩固练习
19.1 函数/
例2 如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
x
解:(1)y 是 x 的函数,自变量 x 的取
值范围是x>0.
(2)y =2(x + )
素养考点 2
利用函数表达式解答实际问题
探究新知
19.1 函数/
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出函数的图象吗?
40
35
30
25
20
15
10
5
5
10
O
x
y
(3)
探究新知
解:
(4)
19.1 函数/
2.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为:l=3a(a>0).
描点、连线:
用描点法画函数l=3a的图象.
O
2
x
y
1
2
3
4
5
8
6
4
10
12
巩固练习
19.1 函数/
2.(2019 上海)在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是____________.
巩固练习
y=﹣6x+2
连接中考
19.1 函数/
A. A比B先出发;
B. A、B两人的速度相同;
C. A先到达终点;
D. B比A跑的路程多.
C
1.如果A、B两人在一次百米赛跑中,路程(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
课堂检测
19.1 函数/
2.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
下列说法错误的是 ( )
A. 当h=50 cm时,t=1.89 s B. 随着h逐渐升高,t逐渐变小
C. h每增加10 cm,t减小1.23 s D. 随着h逐渐升高,小车的速度逐渐加快
C
C
课堂检测
19.1 函数/
3.已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少cm
解:
(x>0)
(2)当x=10时,y=60÷10=6,
课堂检测
即当底边长为10cm时,底边上的高是6cm.
(1)
4.测得一弹簧的长度L/cm与悬挂物的质量x/kg有下面一组对应值:
试根据表中各对应值解答下列问题.
(1)用代数式表示悬挂质量为x kg的物体时的弹簧长度L;
(2)求所挂物体质量为10 kg时,弹簧长度是多少?
(3)若测得弹簧长度为19 cm,判断所挂物体质量是多少千克?
19.1 函数/
课堂检测
19.1 函数/
解:(1)L与x之间的关系式为L=0.5x+12;
(2)当x=10时,L=0.5×10+12=17.
∴当挂物体的质量为10千克时,弹簧的长度是17厘米.
(3)当L=19 cm,则19=0.5x+12,
∴所挂物体质量是14千克.
课堂检测
解得:x=14.
19.1 函数/
某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,则按每吨1.9元收费,如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)某户3月份用水18吨,应收水费________元.某户4月份用水25吨,应收水费_______元.(2)分别写出每月所收水费y元与用水量x的关系式.(3)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
52
34.2
课堂检测
19.1 函数/
解:(2)当0≤x≤20时,y=1.9x;
当x>20时,y=1.9×20+(x-20)×2.8=2.8x-18.
(3)∵5月份水费平均为每吨2.2元,用水量如果未超过20吨,
按每吨1.9元收费.∴用水量超过了20吨.
1.9×20+(x-20)×2.8=2.2x,
2.8x-18=2.2x,
解得x=30.
答:该户5月份用水30吨.
课堂检测
19.1 函数/
一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离s是时间t的函数吗?
是
课堂检测
19.1 函数/
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:
s = 200-25t
课堂检测
拓广探索题
船速度为
(200-150)÷2=25m/min,
19.1 函数/
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
课堂检测
拓广探索题
0
200
50
1
6
2
3
4
5
100
150
3.某列高铁从起点站出发,加速一段时间后开始匀速行驶,在快到下一站时减速并停下,等乘客上车后开始加速,一段时间后开始匀速行驶.下面的图中哪一个能近似地刻画这一段时间内高铁的速度随时间变化情况( )
4.小风在1000米中长跑训练时,已跑路程s(米)与所用时间t(秒)之间的函数图象如图所示,下列说法错误的是( )
A.小风的成绩是220秒
B.小风最后冲刺阶段的速度是5米/秒
C.小风第一阶段与最后冲刺阶段速度相等
D.小风的平均速度是4米/秒
5.如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A
B
C
D
P
4
8
12
16
4
8
O
x
y
4
8
12
16
4
8
O
x
y
4
8
12
16
4
8
O
x
y
4
8
12
16
4
8
O
x
y
A
B
C
D
6.如图表示甲骑电动自行车和乙驾驶汽车均行驶90千米的过程中,行驶的路程y与经过的时间x之间的函数关系.请根据图象填空:
出发的早,早了 小时, 先到达,先到 小时,电动自行车的速度为 千米/时,汽车的速度为 千米/时.
O
1
2
3
4
5
20
40
60
80
90
x(小时)
y(千米)
乙
甲
8.小明在游乐场坐过山车,某一分钟内过山车的高度h(米)与时间t(秒)之间的函数图象如图7所示.
请结合图象回答下列问题:
(1)当t=41时,h的值是多少?过山车所达到的最大高度是多少?
(2)请描述30秒后,高度h(米)随时间t(秒)的变化情况.
9.某机动车出发前油箱内有油42升,行驶若干小时后,在加油站加油若干升(加油时间忽略不计).油箱中余油量Q(升)与行驶时间t(小时)之间的函数关系如图所示.根据图象回答问题:
(1)机动车行驶5小时后加油,途中加油__________升.
(2)根据图象计算机动车在加油前的
行驶中每小时耗油多少升?
(3)如果加油站距目的地400千米,
车速为60千米/小时,要到达目的地,
油箱中的油是否够用?请说明理由.
10.现甲、乙两工程队共同承包A,B两地之间的道路,两队分别从A,B两地相向修建.已知甲队先施工3天,乙队才开始施工,乙队施工几天后因另有紧急任务暂停施工,因考虑工期,由甲队以原速的2倍修建,乙队完成紧急任务后又以原速恢复施工,直到道路修通.甲、乙两队各自修路长度与时间之间的关系如图所示.
请结合图中信息解答下列问题:
(1)在施工的过程中,甲队在提速
前每天修路多少米?
(2)乙队中途暂停施工多少天?
(3)求A,B两地之间的道路长度.
19.1 函数/
函数的图象
图象的画法
图象表达的实际意义
描点
列表
连线
课堂小结
19.1 函数/
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
课堂小结
19.1 函数/
19.1 函数
19.1.2 函数的图象
人教版 数学 八年级 下册
19.1 函数/
1. 了解函数图象的意义.了解函数的三种表示法及其优缺点 .
2. 会观察函数图象获取信息,根据图象初步分析函数的对应关系和变化规律.
素养目标
3. 经历画函数图象的过程,体会函数图象建立数形联系的关键是分别用点的横、纵坐标表示自变量和对应的函数值.
一般地,在一个变化过程中,如果有两个变量 x和 y,并且对于x 的每一个确定的值,y 都有唯一确定的值与其对应 ,那么我们就说 x 是自变量,y 是 x 的函数.
函数的定义:
函数的三种表示方法:
解析式法、图象法、列表法
如图是自动测温仪记录的图像,它反映了北京的春季某天气温T(℃)如何随时间t(h)的变化而变化。
-3
O
4
14
24
8
T/℃
t/h
情景引入
(1)这一天中最低、最高温度在什么时刻,温度分别是多少?
(2)哪些时段温度呈下降状态?上升状态呢?
可以认为,气温T是时间t的函数。
问题: 正方形面积 S 与边长 x 之间的函数解析式为 _________.
(1)这个函数的自变量取值范围是什么?
(2)如果想和上题那样,直观的看出S和x之间的
对应关系,需要具备哪些条件?
平面直角坐标系和所对应的曲线
>
S=x2
怎样用画图的方法来表示S与x的关系呢?
(3)怎样获得曲线上的点?
取一个自变量的值,计算出相应的函数值,当作一个点的横坐标与纵坐标。
19.1 函数/
S=x2
(x>0)
0
0.25
1
2.25
4
6.25
9
12.25
16
探究新知
19.1 函数/
在直角坐标系中,描出这些点,然后连接这些点.
表示x与S的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.
探究新知
上图的曲线即函数S=x2 (x>0)的图象.
19.1 函数/
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
探究新知
函数图象是典型的数形结合,
自变量-----横坐标
函数(因变量)-----纵坐标
数(两个变量的值)---对应---形(图象上的每一个点)
19.1 函数/
例1 画出下列函数的图象:
(1) ; (2) .
解:(1)从函数解析式可以看出,x的取值范围是 .
第一步:从x的取值范围中选取一些简洁的数值,算出y的
对应值,填写在表格里:
-5 -3 -1 1 3 5 7
全体实数
探究新知
素养考点 1
画出已知函数的图象
19.1 函数/
O
x
y
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y=2x+1
第二步:根据表中数值描点(x,y);
第三步:用平滑曲线连接这些点.
当自变量的值越来越大时,
对应的函数值 .
画出的图象是一条 ,
直线
越来越大
探究新知
19.1 函数/
-6
x … -5 -4 -3 -2 -1 1 2 3 4 5 …
y …
…
6
-3
-2
-1.2
-1.5
3
2
1.5
1.2
解:(2)①列表 :取一些自变量的值,并求出对应的函数值,填入表中.
探究新知
为什么没有“0”?
19.1 函数/
y
5
x
O
-4
-3
-2
-1
1
2
3
4
5
-5
1
2
3
4
-1
-2
-3
-4
-5
6
-6
②描点:分别以表中对应的x、y为横纵坐标,在坐标系中描
出对应的点.
③连线:用光滑的曲线把这些点依次连接起来.
(1,-6)
探究新知
(1)列表--表中列出部分自变量的值及其对应的函数值;
(2)描点:--在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中数值对应的各点;
(3)连线:--按照横坐标由小到大的顺序,把所描的各点用平滑的曲线连接起来。
1.画函数图象的一般步骤:
注意:列表时自变量由小到大,5到7个,有代表性,注意自变量的取值范围.
归纳总结
1.判断下列各点是否在函数y=2x+1的图象上?
①(-0.5,1) ②(1.5,4)
做一做
2.判断下列各点是否在函数 的图象上?
①(2,3) ②(4,2)
19.1 函数/
函数的三种表示法:
y = 2.88x
图象法、
列表法、
解析式法.
1 4 9 16 25 36 49
探究新知
19.1 函数/
探究新知
归纳总结
函数的三种表示方法:
(1)列表法:用_______列出自变量与函数的对应值,表示函数两个变量之间的关系,这种表示函数的方法叫做列表法.
(2)图象法:用_______表示两个变量之间的函数关系,这种表示函数的方法叫做图象法.
(3)解析式法:用__________表示函数的方法叫做解析式法.
表格
图象
数学式
19.1 函数/
请从全面性、直观性、准确性及形象性四个方面来总结归纳函数三种表示方法的优缺点,填写下表:
提示:从所填表中可以清楚看到三种表示方法各有优缺点.在遇到实际问题时,就要根据具体情况选择适当的方法,有时为全面地认识问题,需要几种方法同时使用.
√
×
×
×
×
×
√
√
√
√
√
探究新知
×
例2.下图反映的过程是小明从家去食堂吃早餐,接着去图书馆读报,然后回家.其中x表示时间,y表示小明离家的距离,小明家、食堂、图书馆在同一直线上.根据图象回答下列问题:
(1)食堂离小明家多远?小明从家到食堂用了多少时间?
家
食堂
图书馆
答:食堂离小明家0.6km,小明从家到食堂用了8min.
从实际问题的图象中读取信息
(2)小明吃早餐用了多少时间?
(3)食堂离图书馆多远?小明从食堂到图书馆用了多少时间?
(4)小明读报用了多长时间?
(5)图书馆离小明家多远?小明从图书馆回家的平均速度是多少?
分析函数图象时要注意:
①横、纵坐标表示的意义;
②每条线段表示的意义;
③端点、转折点表示的意义;
④与坐标轴平行的线段.
课堂总结
例:
19.1 函数/
(1)这一天内,上海与北京何时气温相同?
(2)这一天内,上海在哪段时间比北京气温高?在哪段时间比北京气温低?
答:7时 和 12时.
答:上海在0时— 7时和12时— 24时比北京气温高;
在7时—12时比北京气温低.
2.如图是某一天北京与上海的气温随时间变化的图象.
根据图像回答下列问题.
巩固练习
19.1 函数/
1.最近中旗连降雨雪,德岭山水库水位上涨.如图表示某一天水位变化情况,0时的水位为警戒水位.结合图象判断下列叙述不正确的是( )
A.8时水位最高
B.P点表示12时水位为0.6米
C.8时到16时水位都在下降
D.这一天水位均高于警戒水位
C
课堂检测
2.放学后小刚骑车回家,他离学校的距离S(m)与时间t(min)的函数关系如图,则小刚家距离学校____m,小刚回家需要___min,小刚的骑车速度是______m/min。
t
S
O
10
2000
(m)
(min)
2000
10
200
B
C
A
思考:线段BC的含义是什么?
课堂练习
3.某人早上进行登山活动,从山脚到山顶休息一会儿又沿原路返回,若用横轴表示时间t,纵轴表示与山脚距离h,那么下列四个图中反映全程h与t的关系图是( )
h
t
O
A
h
t
O
B
h
t
O
C
h
t
O
D
19.1 函数/
(1)体育场离张强家多远?张强从家到体育场用了多少时间?
答:体育场离张强家2.5千米.
张强从家到体育场用15分钟.
4.下面的图象反映的过程是:张强从家跑步去体育场,在那里锻炼了一阵后又走到文具店去买笔,然后散步走回家,图中x表示时间,y表示张强离家的距离.
课堂检测
19.1 函数/
(2)体育场离文具店多远?
(3)张强在文具店停留了多少时间?
(4)张强从文具店回家的平均速度是多少?
答:2.5-1.5=1(千米)
答:65-45=20(分)
课堂检测
解:依题意可得
1.5÷[(100-65)÷60]
19.1 函数/
给出下列说法:①学校到景点的路程为55 km;②甲组在途中停留了5 min;③甲、乙两组同时到达景点;④相遇后,乙组的速度小于甲组的速度.根据图象信息,以上说法正确的有 .
10
20
30
40
50
60
70
55
s/km
t/min
O
乙
甲
课堂检测
①
②
19.1 函数/
3.小明同学骑自行车去郊外春游,
如图表示他离家的距离y(km)与所
用的时间x(h)之间关系的函数图象.
(1)根据图象回答:小明到达离
家最远的地方需______h;
(2)小明出发2.5 h后离家_______km;
(3)小明出发__________h后离家12 km.
3
22.5
0.8或5.2
课堂检测
例1 一水库的水位在最近5 h内持续上涨,下表记录了这5 h内6 个时间点的水位高度,其中 t 表示时间,y表示水位高度.
(1)在平面直角坐标系中描出表中数据对应的点,这些点是否在一条直线上?由此你发现水位变化有什么规律?
19.1 函数/
探究新知
素养考点 1
函数表示方法的相互转化
19.1 函数/
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
解:可以看出,这6个点 ,且每小时水位 .
由此猜想,在这个时间段中水位可能是以同一速度均匀上升的.
在同一直线上
上升0.3m
5
探究新知
3
O
5
19.1 函数/
(2)水位高度 y 是否为时间 t 的函数?如果是,试写出一个符合表中数据的函数解析式,并画出这个函数的图象.这个函数能表示水位的变化规律吗?
解:由于水位在最近5小时内持续上涨,对于时间t的每一个确定的值,水位高度y 都有 的值与其对应,所以,y t 的函数.
函数解析式为: . 变量的取值范围是: . 它表示在这 小时内,水位匀速上升的速度为 ,这个函数可以近似地表示水位的变化规律.
唯一
是
y=0.3t+3
0≤t≤5
5
0.3m/h
探究新知
19.1 函数/
t/h
y/m
O
1
2
3
4
5
6
7
8
1
2
3
4
5
探究新知
3
O
5
其函数的图象如下:
5
A
B
19.1 函数/
(3)据估计这种上涨规律还会持续2 h,预测再过2 h水位高度将达到多少m.
解:如果水位的变化规律不变,按上述函数预测,再持续2小时,水位的高度: .
此时函数图象(线段AB)向 延伸到对应的位置,这时水位高度约为 m.
5.1m
右
5.1
探究新知
19.1 函数/
1.已知火车站托运行李的费用C(元)和托运行李的重量P(千克)(P为整数)的对应关系如表:
(1)已知小周的所要托运的行李重12千克,请问小周托运行李的费用为多少元?
(2)写出C与P之间的函数解析式.
(3)小李托运行李花了15元钱,请问小李的行李重多少千克?
7.5元
C=0.5P+1.5
27千克
巩固练习
19.1 函数/
例2 如图,要做一个面积为12 m2的小花坛,该花坛的一边长为 x m,周长为 y m.
(1)变量 y 是变量 x 的函数吗?如果是,写出自变量的取值范围;
(2)能求出这个问题的函数解析式吗?
x
解:(1)y 是 x 的函数,自变量 x 的取
值范围是x>0.
(2)y =2(x + )
素养考点 2
利用函数表达式解答实际问题
探究新知
19.1 函数/
(3)当 x 的值分别为1,2,3,4,5,6 时,请列表表示变量之间的对应关系;
(4)能画出函数的图象吗?
40
35
30
25
20
15
10
5
5
10
O
x
y
(3)
探究新知
解:
(4)
19.1 函数/
2.用解析式法与图象法表示等边三角形的周长l是边长a的函数.
解:因为等边三角形的周长l是边长a的3倍,所以周长l与边长a的函数关系可表示为:l=3a(a>0).
描点、连线:
用描点法画函数l=3a的图象.
O
2
x
y
1
2
3
4
5
8
6
4
10
12
巩固练习
19.1 函数/
2.(2019 上海)在登山过程中,海拔每升高1千米,气温下降6℃,已知某登山大本营所在的位置的气温是2℃,登山队员从大本营出发登山,当海拔升高x千米时,所在位置的气温是y℃,那么y关于x的函数解析式是____________.
巩固练习
y=﹣6x+2
连接中考
19.1 函数/
A. A比B先出发;
B. A、B两人的速度相同;
C. A先到达终点;
D. B比A跑的路程多.
C
1.如果A、B两人在一次百米赛跑中,路程(米)与赛跑的时间t(秒)的关系如图所示,则下列说法正确的是( )
课堂检测
19.1 函数/
2.一个学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如下数据:
下列说法错误的是 ( )
A. 当h=50 cm时,t=1.89 s B. 随着h逐渐升高,t逐渐变小
C. h每增加10 cm,t减小1.23 s D. 随着h逐渐升高,小车的速度逐渐加快
C
C
课堂检测
19.1 函数/
3.已知等腰三角形的面积为30cm2,设它的底边长为xcm,底边上的高为ycm
(1)求底边上的高y随底边长x变化的函数解析式.并求自变量的取值范围.
(2)当底边长为10cm时,底边上的高是多少cm
解:
(x>0)
(2)当x=10时,y=60÷10=6,
课堂检测
即当底边长为10cm时,底边上的高是6cm.
(1)
4.测得一弹簧的长度L/cm与悬挂物的质量x/kg有下面一组对应值:
试根据表中各对应值解答下列问题.
(1)用代数式表示悬挂质量为x kg的物体时的弹簧长度L;
(2)求所挂物体质量为10 kg时,弹簧长度是多少?
(3)若测得弹簧长度为19 cm,判断所挂物体质量是多少千克?
19.1 函数/
课堂检测
19.1 函数/
解:(1)L与x之间的关系式为L=0.5x+12;
(2)当x=10时,L=0.5×10+12=17.
∴当挂物体的质量为10千克时,弹簧的长度是17厘米.
(3)当L=19 cm,则19=0.5x+12,
∴所挂物体质量是14千克.
课堂检测
解得:x=14.
19.1 函数/
某城市居民用水实行阶梯收费,每户每月用水量如果未超过20吨,则按每吨1.9元收费,如果超过20吨,未超过的部分按每吨1.9元收费,超过的部分按每吨2.8元收费.设某户每月用水量为x吨,应收水费为y元.
(1)某户3月份用水18吨,应收水费________元.某户4月份用水25吨,应收水费_______元.(2)分别写出每月所收水费y元与用水量x的关系式.(3)若该城市某户5月份水费平均为每吨2.2元,求该户5月份用水多少吨?
52
34.2
课堂检测
19.1 函数/
解:(2)当0≤x≤20时,y=1.9x;
当x>20时,y=1.9×20+(x-20)×2.8=2.8x-18.
(3)∵5月份水费平均为每吨2.2元,用水量如果未超过20吨,
按每吨1.9元收费.∴用水量超过了20吨.
1.9×20+(x-20)×2.8=2.2x,
2.8x-18=2.2x,
解得x=30.
答:该户5月份用水30吨.
课堂检测
19.1 函数/
一条小船沿直线向码头匀速前进.在0min ,2min,4min,6min时,测得小船与码头的距离分别为200m,150m,100m,50m.
(1)小船与码头的距离s是时间t的函数吗?
是
课堂检测
19.1 函数/
(2)如果是,写出函数的解析式,并画出函数图象.
函数解析式为: .
列表:
s = 200-25t
课堂检测
拓广探索题
船速度为
(200-150)÷2=25m/min,
19.1 函数/
t/min
s/m
O
1
2
3
4
5
6
7
50
100
150
200
画图:
课堂检测
拓广探索题
0
200
50
1
6
2
3
4
5
100
150
3.某列高铁从起点站出发,加速一段时间后开始匀速行驶,在快到下一站时减速并停下,等乘客上车后开始加速,一段时间后开始匀速行驶.下面的图中哪一个能近似地刻画这一段时间内高铁的速度随时间变化情况( )
4.小风在1000米中长跑训练时,已跑路程s(米)与所用时间t(秒)之间的函数图象如图所示,下列说法错误的是( )
A.小风的成绩是220秒
B.小风最后冲刺阶段的速度是5米/秒
C.小风第一阶段与最后冲刺阶段速度相等
D.小风的平均速度是4米/秒
5.如图,正方形ABCD的边长为4,P为正方形边上一动点,沿A→D→C→B→A的路径匀速移动,设P点经过的路径长为x,△APD的面积是y,则下列图象能大致反映y与x的函数关系的是( )
A
B
C
D
P
4
8
12
16
4
8
O
x
y
4
8
12
16
4
8
O
x
y
4
8
12
16
4
8
O
x
y
4
8
12
16
4
8
O
x
y
A
B
C
D
6.如图表示甲骑电动自行车和乙驾驶汽车均行驶90千米的过程中,行驶的路程y与经过的时间x之间的函数关系.请根据图象填空:
出发的早,早了 小时, 先到达,先到 小时,电动自行车的速度为 千米/时,汽车的速度为 千米/时.
O
1
2
3
4
5
20
40
60
80
90
x(小时)
y(千米)
乙
甲
8.小明在游乐场坐过山车,某一分钟内过山车的高度h(米)与时间t(秒)之间的函数图象如图7所示.
请结合图象回答下列问题:
(1)当t=41时,h的值是多少?过山车所达到的最大高度是多少?
(2)请描述30秒后,高度h(米)随时间t(秒)的变化情况.
9.某机动车出发前油箱内有油42升,行驶若干小时后,在加油站加油若干升(加油时间忽略不计).油箱中余油量Q(升)与行驶时间t(小时)之间的函数关系如图所示.根据图象回答问题:
(1)机动车行驶5小时后加油,途中加油__________升.
(2)根据图象计算机动车在加油前的
行驶中每小时耗油多少升?
(3)如果加油站距目的地400千米,
车速为60千米/小时,要到达目的地,
油箱中的油是否够用?请说明理由.
10.现甲、乙两工程队共同承包A,B两地之间的道路,两队分别从A,B两地相向修建.已知甲队先施工3天,乙队才开始施工,乙队施工几天后因另有紧急任务暂停施工,因考虑工期,由甲队以原速的2倍修建,乙队完成紧急任务后又以原速恢复施工,直到道路修通.甲、乙两队各自修路长度与时间之间的关系如图所示.
请结合图中信息解答下列问题:
(1)在施工的过程中,甲队在提速
前每天修路多少米?
(2)乙队中途暂停施工多少天?
(3)求A,B两地之间的道路长度.
19.1 函数/
函数的图象
图象的画法
图象表达的实际意义
描点
列表
连线
课堂小结
19.1 函数/
函数的表示方法
解析式法:反映了函数与自变量之间的数量关系
列表法:反映了函数与自变量的数值对应关系
图象法:反映了函数随自变量的变化而变化的规律
课堂小结
