人教版数学八下 19.2.2一次函数(希沃课件+图片版PPT)仅适用希沃白板
文档属性
| 名称 | 人教版数学八下 19.2.2一次函数(希沃课件+图片版PPT)仅适用希沃白板 |  | |
| 格式 | zip | ||
| 文件大小 | 15.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 09:31:35 | ||
图片预览










文档简介
(共101张PPT)
19.2 一次函数/
19.2 一次函数
19.2.2 一次函数
第一课时
第二课时
人教版 数学 八年级 下册
第三课时
第四课时
19.2 一次函数/
一次函数的概念及解析式
第一课时
返回
O
x
y
6
-12
y=2x-12
19.2 一次函数/
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃.登山队员由大本营向上登高x km时,他们所在位置的气温是y℃.试用函数解析式表示y与x的关系.
这个函数是正比例函数吗?它与正比例函数有什么不同?这种形式的函数还会有吗?
y=5-6x
导入新知
19.2 一次函数/
1. 结合具体情境理解一次函数的意义,能结合实际问题中的数量关系写出一次函数的解析式.
2. 能辨别正比例函数与一次函数的区别与联系.
素养目标
3. 能利用一次函数解决简单的实际问题.
19.2 一次函数/
(1)有人发现,在20~25℃时蟋蟀每分鸣叫次数c与温度t(单位:℃)有关,即c的值约是t的7倍与35的差.
(2)一种计算成年人标准体重G(单位:千克)的方法是:以厘米为单位量出身高值h,再减常数105,所得的差是G的值.
解:是函数关系,函数解析式为c=7t-35 (20≤t≤25)
解:是函数关系,函数解析式为G=h-105
探究新知
知识点 1
一次函数的概念
19.2 一次函数/
(3)某城市的市内电话的月收费额y(单位:元)包括月租费22元和拨打电话x分钟的计时费(按0.1元/分钟收取).
(4) 把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的变化而变化.
解:是函数关系,函数解析式为y=0.1x+22
解:是函数关系,函数解析式为y=-5x+50 (0≤x≤10)
探究新知
19.2 一次函数/
【讨论】分别说出这些函数的常数、自变量,这些函数解析式有哪些共同特征?
解:
(1)c=7t-35的常数为7、-35,自变量为t;
发现:它们都是常数k与自变量的______与常数b的____ 的形式.
和
乘积
(2)G=h-105的常数为1、-105,自变量为h;
(4)y=-5x+50的常数为-5、50,自变量为x.
(3)y=0.1x+22的常数为0.1、22,自变量为x;
探究新知
19.2 一次函数/
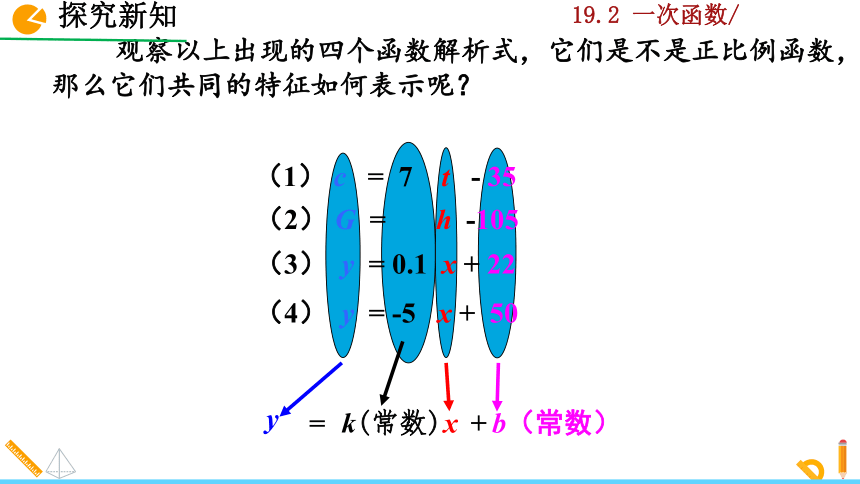
观察以上出现的四个函数解析式,它们是不是正比例函数,那么它们共同的特征如何表示呢?
y
k(常数)
x
=
b(常数)
+
(1) c = 7 t - 35
(2) G = h -105
(3) y = 0.1 x + 22
(4) y = -5 x + 50
探究新知
19.2 一次函数/
一般地,形如y=kx+b (k, b 是常数,k≠0)的函数,叫做一次函数.
一次函数的特点如下:
(1)解析式中自变量x的次数是 次;
(2)比例系数 ;
(3)常数项:通常不为0,但也可以等于0.
1
k≠0
探究新知
19.2 一次函数/
【讨论】一次函数与正比例函数有什么关系?
(2)正比例函数是一种特殊的一次函数.
(1)当b=0时,y=kx+b 即y=kx(k≠0),此时该一次函数是正比例函数.
探究新知
19.2 一次函数/
1.下列函数中哪些是一次函数,哪些又是正比例函数?
(1) ; (2) ;
(3) ; (4)
答:(1)是一次函数,又是正比例函数;
(4)是一次函数.
巩固练习
19.2 一次函数/
解: 因为当x=1时,y=5;当x=-1时,y=1
所以
解得k=2,b=3.
例1 一次函数 ,当x=1时,y=5;当x=-1时,y=1.求k和b的值.
探究新知
素养考点 1
利用一次函数函数一般式求字母的值
19.2 一次函数/
2.已知一次函数 y=kx-b,当 x=3时,y=8;当x=-3时,y=-10.
求 k 和 b 的值.
解:∵当x=3时,y=8;当x=-3时,y=-10
∴
解得k=3,b=1.
巩固练习
19.2 一次函数/
例2 已知函数y=(m-2)x+4-m2
(1)当m为何值时,这个函数是一次函数
解:(1)由题意可得m-2≠0,
解得m≠2.
即m≠2时,这个函数是一次函数.
探究新知
素养考点 2
利用一次函数的概念求字母的值
注意:利用定义求一次函数
解析式时,必须保证:
(1)k ≠ 0;
(2)自变量x的指数是“1”
(2)当m为何值时,这个函数是正比例函数
(2)由题意可得m-2≠0,4-m2=0,
解得m=-2.
即m=-2时,这个函数是正比例函数.
19.2 一次函数/
3.已知函数y=2x|m|+(m+1).
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是正比例函数,求m的值.
解:(1)由题意得: 因此 m=±1.
(2)由题意得:m+1=0 ,
解得m= -1.
巩固练习
19.2 一次函数/
汽车油箱中原有油50升,如果汽车每行驶50千米耗油9升, 求油箱的油量y(单位:升)随行驶路程x(单位:千米)变化的函数关系式,并写出自变量的取值范围,y 是 x 的一次函数吗?
解:油量y与行驶时间x的函数关系式为:
知识点 2
探究新知
利用一次函数解答实际问题
自变量x的取值范围是0≤x≤ .
函数
,是x的一次函数.
19.2 一次函数/
4.如果长方形的周长是30cm,长是xcm,宽是ycm.
(1)写出y与x之间的函数解析式,它是一次函数吗?
(2)若长是宽的2倍,求长方形的面积.
解:(1)y=15-x,是一次函数.
(2)由题意可得x=2(15-x).
解得x=10,所以y=15-x=5.
∴长方形的面积为10×5=50(cm2).
巩固练习
19.2 一次函数/
(2019 陕西)根据记录,从地面向上11km以内,每升高1km,气温降低6℃;又知在距离地面11km以上高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃)
(1)写出距地面的高度在11km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为﹣26℃时,飞机距离地面的高度为7km,求当时这架飞机下方地面的气温;
巩固练习
连接中考
19.2 一次函数/
小敏想,假如飞机当时在距离地面12km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12km时,飞机外的气温.
巩固练习
连接中考
解:(1)根据题意得:y=m﹣6x;
(2)将x=7,y=﹣26代入y=m﹣6x,得﹣26=m﹣42,
∴m=16∴当时地面气温为16℃
∵x=12>11,
∴y=16﹣6×11=﹣50(℃)
假如当时飞机距地面12km时,飞机外的气温为﹣50℃.
19.2 一次函数/
1. 下列函数中,y是x的一次函数的是( )
① ② ③ ④
A. ①②③ B. ①③④
C. ①④ D. ②③④
C
基础巩固题
课堂检测
19.2 一次函数/
2.下列说法正确的是( )
A.一次函数是正比例函数
B.正比例函数不是一次函数
C.不是正比例函数就不是一次函数
D.正比例函数是一次函数
D
3. 要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
n=2
m≠2
基础巩固题
课堂检测
19.2 一次函数/
4.已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式,并指出它是什么函数;
(2)求x=2.5时,y的值.
∴ y=3x-9,
y是x的一次函数.
y=3×2.5 - 9= -1.5.
解 :(1)设y=k(x-3)
把 x=4,y=3 代入上式,得 3= k(4-3)
解得 k=3,
(2)当x=2.5时,
∴y=3(x-3)
课堂检测
基础巩固题
19.2 一次函数/
我国现行个人工资、薪金所得税征收办法规定:月收入低于3500元的部分不收税;月收入超过3500元但低于5000元的部分征收3%的所得税……如某人月收入3860元,他应缴个人工资、薪金所得税为:(3860-3500)×3%=10.8元.
(1)当月收入大于3500元而又小于5000元时,写出应缴所得税y(元)与收入x(元)之间的函数解析式.
解:y=0.03×(x-3500) (3500课堂检测
能力提升题
19.2 一次函数/
(2)某人月收入为4160元,他应缴所得税多少元?
解:当x=4160时,y=0.03×(4160-3500)=19.8(元).
解:设此人本月工资是x元,则 19.2=0.03×(x-3500),
解得 x=4140.
答:此人本月工资是4140元.
(3)如果某人本月应缴所得税19.2元,那么此人本月工资是多少元?
课堂检测
能力提升题
19.2 一次函数/
如图,△ABC是边长为x的等边三角形.
(1)求BC边上的高h与x之间的函数解析式.h是x的一次函数吗?如果是,请指出相应的k与b的值.
解: (1)∵BC边上的高AD也是BC边上的中线, ∴BD= .
即
∴h是x的一次函数,且
课堂检测
拓广探索题
在Rt△ABD中,由勾股定理,得
A
B
C
D
19.2 一次函数/
(2)当 时,求x的值.
(3)求△ABC的面积S与x的函数解析式.S是x的一次函数吗?
解:
(2)当 ,有 .
解得x=2.
(3)∵
即 ∴S不是x的一次函数.
课堂检测
拓广探索题
19.2 一次函数/
一次函数的概念
形式:y=kx+b(k≠0)
特别地,当b=0时,y=kx(k≠0)是正比例函数
一次函数的简单应用
课堂小结
19.2 一次函数/
一次函数的图像和性质
第二课时
返回
6
-2
-5
5
x
y
O
2
4
A
B
C
D
E
y =x+1
y =3x+1
y =-x+1
y =-3x+1
19.2 一次函数/
我们最快捷、最正确地画出正比例函数的图象时,通常在直角坐标系中选取哪两个点?
【思考】能用这种方法作出一次函数的图象吗?
答:画正比例函数y=kx(k≠0)的图像,一般地,过原点和点(1,k).
导入新知
19.2 一次函数/
2.能从图象角度理解正比例函数与一次函数的关系.
1. 会画一次函数的图象,能根据一次函数的图象理解一次函数的增减性 .
素养目标
3. 能灵活运用一次函数的图象与性质解答有关问题.
19.2 一次函数/
1.画出函数y=-6x与y=-6x+5的图象.
12
6
0
-6
-12
17
11
5
-1
-7
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
列表
描点
连线
知识点 1
一次函数的图象
探究新知
19.2 一次函数/
观察与比较:
这两个函数的图象形状都是 ,并且倾斜程度 .函数y=-6x的图象经过原点,函数
y=-6x+5的图象与y轴交于点 ,即它可以看作由直线y=-6x向 平移 个单位长度得到.
比较上面两个函数图象的相同点与不同点.填出你的观察结果并与同伴交流.
一条直线
(0,5)
相同
上
5
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
探究新知
19.2 一次函数/
2
-2
-4
-6
-2
2
x
y
O
描点
连线
列表
2.(1)画一次函数 y =2x-3 的图象.
(2)画正比例函数 y =2x的图象.
y =2x-3
y =2x
4
探究新知
19.2 一次函数/
比较上面两个函数的图象回答下列问题:
(2)函数 y=2x 的图象经过 ,函数
y= 2x-3的图像与y轴交于点( ),即它可以看作由直线 y=2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
原点
0 ,-3
下
3
一条直线
相同
(3)在同一直角坐标系中,直线 y =2x -3与 y =2x的位置关系是 .
平行
探究新知
19.2 一次函数/
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
怎样画一次函数的图象最简单?为什么?
答:y=kx+b与x轴的交点坐标是
由于两点确定一条直线,画一次函数图象时我们只需描点(0,b)和点 或 (1,k+b),连线即可.
探究新知
【思考】一次函数y=kx+b(k≠0)与x轴的交点坐标是什么?
19.2 一次函数/
O
例1 用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1
-1
-3
1
y=-2x-1
1.5
y=0.5x+1
也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1.
素养考点 1
画一次函数的图象
探究新知
19.2 一次函数/
1.在同一直角坐标系中画出下列函数的图象,并指出三个函数的图象有什么关系.
y=x-1 y=x y=x+1
解:列表:
描点并连线:
x
0
1
y=x-1
y=x
y=x+1
-1
0
0
1
1
2
巩固练习
-3
y=x-1
y=x+1
4
2
-2
-4
4
x
y
O
y = x
-3
-2
2
1
1
-1
3
3
-1
19.2 一次函数/
画出函数y=x+1, y=-x+1, y=2x+1,
y=-2x+1的图象.
1
2
1
0
1
3
1
-1
O
1
x
y
1
-1
-1
y=x+1
y=-x+1
y=2x+1
y=-2x+1
探究新知
知识点 2
一次函数的性质
19.2 一次函数/
观察函数y=x+1, y=-x+1, y=2x+1,y=-2x+1的图象.
一次函数y=kx+b(k、b是常数,k≠0)中,k的正、负对函数图象有什么影响?
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
O
1
x
y
1
-1
-1
y=x+1
y=-x+1
y=2x+1
y=-2x+1
探究新知
19.2 一次函数/
例2 P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
提示:反过来也成立:y越大,x就越小.
素养考点 1
利用一次函数的性质比较大小
探究新知
19.2 一次函数/
2.在直线y=3x+6上,对于点A(x1,y1)和B(x2,y2)若x1>x2,则y1 y2.(填写大小关系)
3.下列一次函数中,y随x的增大而减小的是( )
>
B
巩固练习
19.2 一次函数/
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
知识点 3
一次函数经过象限与字母k,b的关系
探究新知
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
19.2 一次函数/
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
① b>0时,直线经过第 一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
探究新知
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
19.2 一次函数/
例3 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
素养考点 1
利用一次函数的性质求字母的值
探究新知
19.2 一次函数/
4.已知一次函数y=(2m+2)x+(3-n),根据下列条件,请你求出m,n的取值范围.
(1)y随x的增大而增大;
(2)直线与y轴交点在x轴下方;
(3)图象经过第二、三、四象限.
巩固练习
19.2 一次函数/
巩固练习
解:(1)由y随x的增大而增大可知2m+2>0,所以当m>-1时,y随x的增大而增大;
(2)由直线与y轴交点在x轴下方可知3-n<0,所以当n>3时,直线与y轴交点在x轴下方,且有2m+2≠0,即m≠-1,所以m≠-1,n>3.
(3)图象经过第二、三、四象限,由一次函数图象分布情况可知 解得
∴当m<-1,n>3时图象经过第二、三、四象限.
19.2 一次函数/
1.(2018 常德)若一次函数y=(k﹣2)x+1的函数值y随x的增大而增大,则( )
A.k<2 B.k>2 C.k>0 D.k<0
巩固练习
连接中考
2.(2019 广安)一次函数y=2x﹣3的图象经过的象限是
( )
A.一、二、三 B.二、三、四
C.一、三、四 D.一、二、四
B
C
19.2 一次函数/
1. 一次函数y=x-2的大致图象为( )
C
A B C D
2.下列函数中,y的值随x值的增大而增大的函数是( )
A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2
C
基础巩固题
课堂检测
19.2 一次函数/
4.直线y =2x-3 与x 轴交点的坐标为________;与y 轴交点的坐标为_______;图象经过第___________象限, y 随x 的增大而________.
3.若直线y=kx+2与y=3x-1平行,则k= .
3
5.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,
则y1-y2 0(填“>”或“<”).
>
(0,-3)
一、三、四
增大
(1.5,0)
课堂检测
基础巩固题
19.2 一次函数/
D
y
x
O
B
已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
B
x
O
C
y
x
O
y
y
x
O
A
分析:由函数 y = kx的图象在二、四象限,可知k<0,所以
-k>0,所以函数y = kx-k的图象经过第一、二、四象限,故选B.
能力提升题
课堂检测
19.2 一次函数/
已知一次函数y=(3m-8)x+1-m图象与 y轴交点在x轴下方,且y随x的增大而减小,其中m为整数,求m的值 .
解: 由题意得 ,解得
又∵m为整数,
∴m=2.
拓广探索题
课堂检测
19.2 一次函数/
一次函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
课堂小结
19.2 一次函数/
待定系数法求一次函数的解析式
第三课时
返回
19.2 一次函数/
【思考】你在作一次函数图象时,分别描了几个点?
在上节课中我们学习了在给定一次函数解析式的前提下,我们可以说出它的图象特征及有关性质;反之,如果给你信息,你能否求出函数的解析式呢?这将是本节课我们要研究的问题.
你为何选取这几个点?
可以有不同取法吗?
导入新知
19.2 一次函数/
1.理解待定系数法的意义.
2. 学会运用待定系数法和数形结合思想求一次函数解析式.
素养目标
19.2 一次函数/
已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
∴这个一次函数的解析式为 .
解方程组得
把点(3,5)与(-4,-9)分别代入,
得:
y=2x-1
探究新知
知识点 1
待定系数法求一次函数的解析式
一次函数的图象过点
(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b.
19.2 一次函数/
像这样先设出____________ ,再根据条件确定____________________ ,从而具体写出这个式子的方法,叫做待定系数法.
你能归纳出待定系数法求函数解析式的基本步骤吗?
函数解析式
解析式中未知的系数
探究新知
19.2 一次函数/
解:设这个一次函数的解析式为
y=kx+b
把x=3,y=5;x=-4,y=-9
分别代入上式得
解得
一次函数的解析式为
y=2x-1
设
代
解
还原
探究新知
19.2 一次函数/
探究新知
归纳总结
求一次函数解析式的步骤:
(1)设:设一次函数的一般形式
y=kx+b(k≠0)
(2)列:把图象上的点 , 代入一次
函数的解析式,组成_________方程组;
二元一次
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
19.2 一次函数/
函数解析式y=kx+b
满足条件的两定点
一次函数的图象直线l
画出
选取
解出
选取
从数到形
从形到数
数学的基本思想方法:
数形结合
整理归纳:从两方面说明:
探究新知
19.2 一次函数/
例1 一次函数图像经过点(9,0)和点(24,20),写出函数解析式.
解方程组得:
这个一次函数的解析式为
解:设这个一次函数的解析式为y=kx+b.
把点(9,0)与(24,20)分别代入y=kx+b,得:
探究新知
素养考点 1
已知两点利用待定系数法求一次函数的解析式
19.2 一次函数/
1.已知一次函数的图象过点(3,5)与(-3,-13),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
解方程组得:
把点(3,5)与(-3,-13)分别代入,得:
∴这个一次函数的解析式为
y=3x-4.
巩固练习
19.2 一次函数/
例2 若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴y=-x+2.
探究新知
素养考点 2
已知一点利用待定系数法求一次函数的解析式
19.2 一次函数/
解:设直线l为y=kx+b,
∵l与直线y=-2x平行,∴k= -2.
又∵直线过点(0,2),
∴2=-2×0+b,
∴直线l的解析式为y=-2x+2.
2. 已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的解析式.
巩固练习
∴b=2,
19.2 一次函数/
例3 已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是( ,0).由题意可列出关于k,b的方程.
y
x
O
2
注意:此题有两种情况.
素养考点 3
探究新知
几何面积和待定系数法求一次函数的解析式
19.2 一次函数/
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是( ,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
探究新知
19.2 一次函数/
3.正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
分析:由OB=5可知点B的坐标为(0,-5).y=k1x的图象过点A(3,4),y=k2x+b的图象过点
A(3,4),B(0,-5),代入解方程(组)即可.
巩固练习
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
19.2 一次函数/
巩固练习
解:(1)由题意可知,B点的坐标是(0,-5)
∵一次函数y=k2x+b的图象过点(0,-5),(3,4)
∴ ,解得
∵正比例函数y=k1x的图象过点(3,4),
∴ 因此
(2)S△AOB=5×3÷2=7.5
因此y=3x-5.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
19.2 一次函数/
(2019 枣庄)如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是( )
A.y=﹣x+4 B.y=x+4
C.y=x+8 D.y=﹣x+8
巩固练习
连接中考
A
x
y
B
O
P
A
19.2 一次函数/
课堂检测
基础巩固题
1.一次函数的图象经过点(2,1)和点(1,5),则这个一次函数是( )
A.y=4x+9 B. y=4x-9 C. y=-4x+9 D. y=-4x-9
2.已知点P的横坐标与纵坐标之和为1,且这点在直线y=x+3上,则该点是( )
A.(-7,8) B. (-5,6) C. (-4,5) D. (-1,2)
C
D
19.2 一次函数/
课堂检测
基础巩固题
3.若点A(-4,0)、B(0,5)、C(m,-5)在同一条直线上,则m的值是( )
A.8 B.4 C.-6 D.-8
4.一次函数的图象如图所示,则k、b的值分别为( )
A.k=-2,b=1 B.k=2,b=1
C.k=-2,b=-1 D.k=2,b=-1
A
D
1
1
x
y
o
19.2 一次函数/
5. 如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
l
y
x
课堂检测
基础巩固题
19.2 一次函数/
若一直线与另一直线y=-3x+2交于y轴同一点,且过(2,-6),
你能求出这条直线的解析式吗?
答案:y=-4x+2
分析:直线y=-3x+2与y轴的交点为(0,2),于是得知该直线过点(0,2),(2,-6),再用待定系数法求解即可.
课堂检测
能力提升题
19.2 一次函数/
已知一次函数y=kx+b(k≠0)的自变量的取值范围是- 3≤x≤ 6,相应函数值的范围是- 5≤y≤ - 2 ,求这个函数的解析式.
分析:(1)当- 3≤x≤ 6时,- 5≤y≤ - 2,实质是给出了两组自变量及对应的函数值;
(2)由于不知道函数的增减性,此题需分两种情况讨论.
答案:
课堂检测
拓广探索题
19.2 一次函数/
用待定系数法求一次函数的解析式
2. 根据已知条件列出关于k,b的方程(组);
1. 设所求的一次函数解析式为y=kx+b;
3. 解方程,求出k,b;
4. 把求出的k,b代回解析式即可.
课堂小结
19.2 一次函数/
一次函数解决实际问题
第四课时
返回
19.2 一次函数/
乌鸦喝水,是《伊索寓言》中一个有趣的寓言故事.故事梗概为:"一只口渴的乌鸦看到窄口瓶内有半瓶水,于是将小石子投入瓶中,使水面升高,从而喝到了水."告诉人们遇到困难要积极想解决办法,认真思考才能让问题迎刃而解的道理.数学问题也一样哦.
导入新知
19.2 一次函数/
10 cm
9 cm
如果将乌鸦喝水的故事进行量化,你能判断乌鸦丢进多少颗石子,水能刚好在瓶口?说说你的做法!
导入新知
19.2 一次函数/
1. 巩固一次函数知识,灵活运用变量关系解决相关实际问题.
2. 有机地把各种数学模型通过函数统一起来使用,提高解决实际问题的能力.
素养目标
19.2 一次函数/
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?
探究新知
知识点 1
一次函数解答实际问题
19.2 一次函数/
解:(1)设h与d之间的函数关系式为:
h=kd+b.
把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169.
解得k=9,b=-20,
即h=9d-20.
(2)当h=196时,196=9d-20,解得d=24(cm).
探究新知
19.2 一次函数/
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
巩固练习
19.2 一次函数/
解: (1)设函数解析式为y=kx+b,
由图可知图象过(0,40),(4,120)
∴这个函数的解析式为y=20x+40.
(2)当y=200时,20x+40=200, 解得x=8
∴小明经过8个月才能存够200元.
解得
∴
巩固练习
40
80
120
y/元
x/月
1
2
3
4
5
o
19.2 一次函数/
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买
2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
探究新知
19.2 一次函数/
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
探究新知
19.2 一次函数/
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
探究新知
19.2 一次函数/
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
的函数图象为:
探究新知
19.2 一次函数/
2.一个试验室在0:00—2:00保持20℃的恒温,在2:00—
4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
解:(1)由题意得
当0≤t≤2时,T=20;
当2函数解析式为:
T=20(0≤t≤2)
T=5t+10(220
10
40
T
t
0
1
2
30
4
3
巩固练习
(2)函数图像为:
19.2 一次函数/
(2019 聊城)某快递公司每天上午9:00﹣10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15 B.9:20
C.9:25 D.9:30
巩固练习
连接中考
B
x/分
y/件
400
240
40
60
O
甲
乙
19.2 一次函数/
1.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过( )
A.(-1,1) B.(2,2) C.(-2,2) D.(2,-2)
2.老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
B
y=-2x+6(答案不唯一)
基础巩固题
课堂检测
19.2 一次函数/
3.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱.
(2)服药5时,血液中含药量为
每毫升____毫克.
x/时
y/毫克
6
3
2
5
O
2
6
3
课堂检测
基础巩固题
19.2 一次函数/
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______小时.
y=3x
y=-x+8
4
x/时
y/毫克
6
3
2
5
O
课堂检测
基础巩固题
19.2 一次函数/
4.某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作几小时?
解:(1)y = -5x + 40.
(2)8 h
课堂检测
基础巩固题
19.2 一次函数/
5.温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
课堂检测
基础巩固题
19.2 一次函数/
用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
解:
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
由已知条件,得
课堂检测
基础巩固题
19.2 一次函数/
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过8立方米部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
能力提升题
课堂检测
19.2 一次函数/
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
课堂检测
能力提升题
解:
19.2 一次函数/
春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害.
某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.右图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.请你
根据图中信息,针对这种植物判断次日是否
需要采取防霜冻措施,并说明理由.
x/时
y/ oC
拓广探索题
课堂检测
19.2 一次函数/
解:根据图象可知:设0时~5时的一次函数关系式为y1=k1x+b1,经过点(0,3),(5,-3),b1=3, 5k1+b1=-3.
解得k1=-1.2, b1=3.
当y1、y2分别为0时,
而|x2-x1|= >3,
∴应采取防霜冻措施.
设5时~8时的一次函数关系式为y2=k2x+b2,
经过点(5,-3),(8,5),5k2+b2=-3 ,
8k2+b2=5.
课堂检测
拓广探索题
∴y1=-1.2x+3.
∴ .
解得 , .
x/时
y/ oC
A
M
E
Q
B
N
C
F
19.2 一次函数/
一次函数与实际问题
一次函数与实际问题
分段函数的解析式与图象
课堂小结
19.2 一次函数/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
19.2 一次函数/
19.2 一次函数
19.2.2 一次函数
第一课时
第二课时
人教版 数学 八年级 下册
第三课时
第四课时
19.2 一次函数/
一次函数的概念及解析式
第一课时
返回
O
x
y
6
-12
y=2x-12
19.2 一次函数/
某登山队大本营所在地的气温为5℃,海拔每升高1km气温下降6℃.登山队员由大本营向上登高x km时,他们所在位置的气温是y℃.试用函数解析式表示y与x的关系.
这个函数是正比例函数吗?它与正比例函数有什么不同?这种形式的函数还会有吗?
y=5-6x
导入新知
19.2 一次函数/
1. 结合具体情境理解一次函数的意义,能结合实际问题中的数量关系写出一次函数的解析式.
2. 能辨别正比例函数与一次函数的区别与联系.
素养目标
3. 能利用一次函数解决简单的实际问题.
19.2 一次函数/
(1)有人发现,在20~25℃时蟋蟀每分鸣叫次数c与温度t(单位:℃)有关,即c的值约是t的7倍与35的差.
(2)一种计算成年人标准体重G(单位:千克)的方法是:以厘米为单位量出身高值h,再减常数105,所得的差是G的值.
解:是函数关系,函数解析式为c=7t-35 (20≤t≤25)
解:是函数关系,函数解析式为G=h-105
探究新知
知识点 1
一次函数的概念
19.2 一次函数/
(3)某城市的市内电话的月收费额y(单位:元)包括月租费22元和拨打电话x分钟的计时费(按0.1元/分钟收取).
(4) 把一个长10cm、宽5cm的长方形的长减少xcm,宽不变,长方形的面积y(单位:cm2)随x的变化而变化.
解:是函数关系,函数解析式为y=0.1x+22
解:是函数关系,函数解析式为y=-5x+50 (0≤x≤10)
探究新知
19.2 一次函数/
【讨论】分别说出这些函数的常数、自变量,这些函数解析式有哪些共同特征?
解:
(1)c=7t-35的常数为7、-35,自变量为t;
发现:它们都是常数k与自变量的______与常数b的____ 的形式.
和
乘积
(2)G=h-105的常数为1、-105,自变量为h;
(4)y=-5x+50的常数为-5、50,自变量为x.
(3)y=0.1x+22的常数为0.1、22,自变量为x;
探究新知
19.2 一次函数/
观察以上出现的四个函数解析式,它们是不是正比例函数,那么它们共同的特征如何表示呢?
y
k(常数)
x
=
b(常数)
+
(1) c = 7 t - 35
(2) G = h -105
(3) y = 0.1 x + 22
(4) y = -5 x + 50
探究新知
19.2 一次函数/
一般地,形如y=kx+b (k, b 是常数,k≠0)的函数,叫做一次函数.
一次函数的特点如下:
(1)解析式中自变量x的次数是 次;
(2)比例系数 ;
(3)常数项:通常不为0,但也可以等于0.
1
k≠0
探究新知
19.2 一次函数/
【讨论】一次函数与正比例函数有什么关系?
(2)正比例函数是一种特殊的一次函数.
(1)当b=0时,y=kx+b 即y=kx(k≠0),此时该一次函数是正比例函数.
探究新知
19.2 一次函数/
1.下列函数中哪些是一次函数,哪些又是正比例函数?
(1) ; (2) ;
(3) ; (4)
答:(1)是一次函数,又是正比例函数;
(4)是一次函数.
巩固练习
19.2 一次函数/
解: 因为当x=1时,y=5;当x=-1时,y=1
所以
解得k=2,b=3.
例1 一次函数 ,当x=1时,y=5;当x=-1时,y=1.求k和b的值.
探究新知
素养考点 1
利用一次函数函数一般式求字母的值
19.2 一次函数/
2.已知一次函数 y=kx-b,当 x=3时,y=8;当x=-3时,y=-10.
求 k 和 b 的值.
解:∵当x=3时,y=8;当x=-3时,y=-10
∴
解得k=3,b=1.
巩固练习
19.2 一次函数/
例2 已知函数y=(m-2)x+4-m2
(1)当m为何值时,这个函数是一次函数
解:(1)由题意可得m-2≠0,
解得m≠2.
即m≠2时,这个函数是一次函数.
探究新知
素养考点 2
利用一次函数的概念求字母的值
注意:利用定义求一次函数
解析式时,必须保证:
(1)k ≠ 0;
(2)自变量x的指数是“1”
(2)当m为何值时,这个函数是正比例函数
(2)由题意可得m-2≠0,4-m2=0,
解得m=-2.
即m=-2时,这个函数是正比例函数.
19.2 一次函数/
3.已知函数y=2x|m|+(m+1).
(1)若这个函数是一次函数,求m的值;
(2)若这个函数是正比例函数,求m的值.
解:(1)由题意得: 因此 m=±1.
(2)由题意得:m+1=0 ,
解得m= -1.
巩固练习
19.2 一次函数/
汽车油箱中原有油50升,如果汽车每行驶50千米耗油9升, 求油箱的油量y(单位:升)随行驶路程x(单位:千米)变化的函数关系式,并写出自变量的取值范围,y 是 x 的一次函数吗?
解:油量y与行驶时间x的函数关系式为:
知识点 2
探究新知
利用一次函数解答实际问题
自变量x的取值范围是0≤x≤ .
函数
,是x的一次函数.
19.2 一次函数/
4.如果长方形的周长是30cm,长是xcm,宽是ycm.
(1)写出y与x之间的函数解析式,它是一次函数吗?
(2)若长是宽的2倍,求长方形的面积.
解:(1)y=15-x,是一次函数.
(2)由题意可得x=2(15-x).
解得x=10,所以y=15-x=5.
∴长方形的面积为10×5=50(cm2).
巩固练习
19.2 一次函数/
(2019 陕西)根据记录,从地面向上11km以内,每升高1km,气温降低6℃;又知在距离地面11km以上高空,气温几乎不变.若地面气温为m(℃),设距地面的高度为x(km)处的气温为y(℃)
(1)写出距地面的高度在11km以内的y与x之间的函数表达式;
(2)上周日,小敏在乘飞机从上海飞回西安途中,某一时刻,她从机舱内屏幕显示的相关数据得知,飞机外气温为﹣26℃时,飞机距离地面的高度为7km,求当时这架飞机下方地面的气温;
巩固练习
连接中考
19.2 一次函数/
小敏想,假如飞机当时在距离地面12km的高空,飞机外的气温是多少度呢?请求出假如当时飞机距离地面12km时,飞机外的气温.
巩固练习
连接中考
解:(1)根据题意得:y=m﹣6x;
(2)将x=7,y=﹣26代入y=m﹣6x,得﹣26=m﹣42,
∴m=16∴当时地面气温为16℃
∵x=12>11,
∴y=16﹣6×11=﹣50(℃)
假如当时飞机距地面12km时,飞机外的气温为﹣50℃.
19.2 一次函数/
1. 下列函数中,y是x的一次函数的是( )
① ② ③ ④
A. ①②③ B. ①③④
C. ①④ D. ②③④
C
基础巩固题
课堂检测
19.2 一次函数/
2.下列说法正确的是( )
A.一次函数是正比例函数
B.正比例函数不是一次函数
C.不是正比例函数就不是一次函数
D.正比例函数是一次函数
D
3. 要使y=(m-2)xn-1+n是关于x的一次函数,n,m应满足 , .
n=2
m≠2
基础巩固题
课堂检测
19.2 一次函数/
4.已知y与x-3成正比例,当x=4时,y=3.
(1)写出y与x之间的函数关系式,并指出它是什么函数;
(2)求x=2.5时,y的值.
∴ y=3x-9,
y是x的一次函数.
y=3×2.5 - 9= -1.5.
解 :(1)设y=k(x-3)
把 x=4,y=3 代入上式,得 3= k(4-3)
解得 k=3,
(2)当x=2.5时,
∴y=3(x-3)
课堂检测
基础巩固题
19.2 一次函数/
我国现行个人工资、薪金所得税征收办法规定:月收入低于3500元的部分不收税;月收入超过3500元但低于5000元的部分征收3%的所得税……如某人月收入3860元,他应缴个人工资、薪金所得税为:(3860-3500)×3%=10.8元.
(1)当月收入大于3500元而又小于5000元时,写出应缴所得税y(元)与收入x(元)之间的函数解析式.
解:y=0.03×(x-3500) (3500
能力提升题
19.2 一次函数/
(2)某人月收入为4160元,他应缴所得税多少元?
解:当x=4160时,y=0.03×(4160-3500)=19.8(元).
解:设此人本月工资是x元,则 19.2=0.03×(x-3500),
解得 x=4140.
答:此人本月工资是4140元.
(3)如果某人本月应缴所得税19.2元,那么此人本月工资是多少元?
课堂检测
能力提升题
19.2 一次函数/
如图,△ABC是边长为x的等边三角形.
(1)求BC边上的高h与x之间的函数解析式.h是x的一次函数吗?如果是,请指出相应的k与b的值.
解: (1)∵BC边上的高AD也是BC边上的中线, ∴BD= .
即
∴h是x的一次函数,且
课堂检测
拓广探索题
在Rt△ABD中,由勾股定理,得
A
B
C
D
19.2 一次函数/
(2)当 时,求x的值.
(3)求△ABC的面积S与x的函数解析式.S是x的一次函数吗?
解:
(2)当 ,有 .
解得x=2.
(3)∵
即 ∴S不是x的一次函数.
课堂检测
拓广探索题
19.2 一次函数/
一次函数的概念
形式:y=kx+b(k≠0)
特别地,当b=0时,y=kx(k≠0)是正比例函数
一次函数的简单应用
课堂小结
19.2 一次函数/
一次函数的图像和性质
第二课时
返回
6
-2
-5
5
x
y
O
2
4
A
B
C
D
E
y =x+1
y =3x+1
y =-x+1
y =-3x+1
19.2 一次函数/
我们最快捷、最正确地画出正比例函数的图象时,通常在直角坐标系中选取哪两个点?
【思考】能用这种方法作出一次函数的图象吗?
答:画正比例函数y=kx(k≠0)的图像,一般地,过原点和点(1,k).
导入新知
19.2 一次函数/
2.能从图象角度理解正比例函数与一次函数的关系.
1. 会画一次函数的图象,能根据一次函数的图象理解一次函数的增减性 .
素养目标
3. 能灵活运用一次函数的图象与性质解答有关问题.
19.2 一次函数/
1.画出函数y=-6x与y=-6x+5的图象.
12
6
0
-6
-12
17
11
5
-1
-7
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
列表
描点
连线
知识点 1
一次函数的图象
探究新知
19.2 一次函数/
观察与比较:
这两个函数的图象形状都是 ,并且倾斜程度 .函数y=-6x的图象经过原点,函数
y=-6x+5的图象与y轴交于点 ,即它可以看作由直线y=-6x向 平移 个单位长度得到.
比较上面两个函数图象的相同点与不同点.填出你的观察结果并与同伴交流.
一条直线
(0,5)
相同
上
5
O
2
x
y
1
2
3
-2
-1
8
6
4
10
12
探究新知
19.2 一次函数/
2
-2
-4
-6
-2
2
x
y
O
描点
连线
列表
2.(1)画一次函数 y =2x-3 的图象.
(2)画正比例函数 y =2x的图象.
y =2x-3
y =2x
4
探究新知
19.2 一次函数/
比较上面两个函数的图象回答下列问题:
(2)函数 y=2x 的图象经过 ,函数
y= 2x-3的图像与y轴交于点( ),即它可以看作由直线 y=2x向 平移 个单位长度而得到.
(1)这两个函数的图象形状都是 ,并且倾斜程度 .
原点
0 ,-3
下
3
一条直线
相同
(3)在同一直角坐标系中,直线 y =2x -3与 y =2x的位置关系是 .
平行
探究新知
19.2 一次函数/
一次函数y=kx+b(k≠0)的图象经过点(0,b),可以由正比例函数y=kx的图象平移 个单位长度得到(当b>0时,向 平移;当b<0时,向 平移).
下
上
怎样画一次函数的图象最简单?为什么?
答:y=kx+b与x轴的交点坐标是
由于两点确定一条直线,画一次函数图象时我们只需描点(0,b)和点 或 (1,k+b),连线即可.
探究新知
【思考】一次函数y=kx+b(k≠0)与x轴的交点坐标是什么?
19.2 一次函数/
O
例1 用你认为最简单的方法画出下列函数的图象:
(1) y=-2x-1;(2) y=0.5x+1
-1
-3
1
y=-2x-1
1.5
y=0.5x+1
也可以先画直线 y=-2x与 y=0.5x,再分别平移它们,也能得到直线y=-2x-1与 y=0.5x+1.
素养考点 1
画一次函数的图象
探究新知
19.2 一次函数/
1.在同一直角坐标系中画出下列函数的图象,并指出三个函数的图象有什么关系.
y=x-1 y=x y=x+1
解:列表:
描点并连线:
x
0
1
y=x-1
y=x
y=x+1
-1
0
0
1
1
2
巩固练习
-3
y=x-1
y=x+1
4
2
-2
-4
4
x
y
O
y = x
-3
-2
2
1
1
-1
3
3
-1
19.2 一次函数/
画出函数y=x+1, y=-x+1, y=2x+1,
y=-2x+1的图象.
1
2
1
0
1
3
1
-1
O
1
x
y
1
-1
-1
y=x+1
y=-x+1
y=2x+1
y=-2x+1
探究新知
知识点 2
一次函数的性质
19.2 一次函数/
观察函数y=x+1, y=-x+1, y=2x+1,y=-2x+1的图象.
一次函数y=kx+b(k、b是常数,k≠0)中,k的正、负对函数图象有什么影响?
当k>0时,y随x的增大而增大;当k<0时,y随x的增大而减小.
O
1
x
y
1
-1
-1
y=x+1
y=-x+1
y=2x+1
y=-2x+1
探究新知
19.2 一次函数/
例2 P1(x1,y1),P2(x2,y2)是一次函数y=-0.5x+3图象上的两点,下列判断中,正确的是( )
A.y1>y2 C.当x1<x2时,y1<y2
B. y1<y2 D.当x1<x2时,y1>y2
D
提示:反过来也成立:y越大,x就越小.
素养考点 1
利用一次函数的性质比较大小
探究新知
19.2 一次函数/
2.在直线y=3x+6上,对于点A(x1,y1)和B(x2,y2)若x1>x2,则y1 y2.(填写大小关系)
3.下列一次函数中,y随x的增大而减小的是( )
>
B
巩固练习
19.2 一次函数/
k 0,b 0
>
>
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
k 0,b 0
>
>
>
<
<
<
<
<
=
=
根据一次函数的图象判断k,b的正负,并说出直线经过的象限:
知识点 3
一次函数经过象限与字母k,b的关系
探究新知
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
x
y
O
19.2 一次函数/
一次函数y=kx+b中,k,b的正负对函数图象及性质有什么影响?
当k>0时,直线y=kx+b由左到右逐渐上升,y随x的增大而增大.
① b>0时,直线经过第 一、二、四象限;
② b<0时,直线经过第二、三、四象限.
① b>0时,直线经过第一、二、三象限;
② b<0时,直线经过第一、三、四象限.
探究新知
当k<0时,直线y=kx+b由左到右逐渐下降,y随x的增大而减小.
19.2 一次函数/
例3 已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
解:(1)由题意得1-2m>0,解得
(2)由题意得1-2m≠0且m-1<0,即
(3)由题意得1-2m<0且m-1<0,解得
素养考点 1
利用一次函数的性质求字母的值
探究新知
19.2 一次函数/
4.已知一次函数y=(2m+2)x+(3-n),根据下列条件,请你求出m,n的取值范围.
(1)y随x的增大而增大;
(2)直线与y轴交点在x轴下方;
(3)图象经过第二、三、四象限.
巩固练习
19.2 一次函数/
巩固练习
解:(1)由y随x的增大而增大可知2m+2>0,所以当m>-1时,y随x的增大而增大;
(2)由直线与y轴交点在x轴下方可知3-n<0,所以当n>3时,直线与y轴交点在x轴下方,且有2m+2≠0,即m≠-1,所以m≠-1,n>3.
(3)图象经过第二、三、四象限,由一次函数图象分布情况可知 解得
∴当m<-1,n>3时图象经过第二、三、四象限.
19.2 一次函数/
1.(2018 常德)若一次函数y=(k﹣2)x+1的函数值y随x的增大而增大,则( )
A.k<2 B.k>2 C.k>0 D.k<0
巩固练习
连接中考
2.(2019 广安)一次函数y=2x﹣3的图象经过的象限是
( )
A.一、二、三 B.二、三、四
C.一、三、四 D.一、二、四
B
C
19.2 一次函数/
1. 一次函数y=x-2的大致图象为( )
C
A B C D
2.下列函数中,y的值随x值的增大而增大的函数是( )
A.y=-2x B.y=-2x+1 C.y=x-2 D.y=-x-2
C
基础巩固题
课堂检测
19.2 一次函数/
4.直线y =2x-3 与x 轴交点的坐标为________;与y 轴交点的坐标为_______;图象经过第___________象限, y 随x 的增大而________.
3.若直线y=kx+2与y=3x-1平行,则k= .
3
5.点A(-1,y1),B(3,y2)是直线y=kx+b(k<0)上的两点,
则y1-y2 0(填“>”或“<”).
>
(0,-3)
一、三、四
增大
(1.5,0)
课堂检测
基础巩固题
19.2 一次函数/
D
y
x
O
B
已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )
B
x
O
C
y
x
O
y
y
x
O
A
分析:由函数 y = kx的图象在二、四象限,可知k<0,所以
-k>0,所以函数y = kx-k的图象经过第一、二、四象限,故选B.
能力提升题
课堂检测
19.2 一次函数/
已知一次函数y=(3m-8)x+1-m图象与 y轴交点在x轴下方,且y随x的增大而减小,其中m为整数,求m的值 .
解: 由题意得 ,解得
又∵m为整数,
∴m=2.
拓广探索题
课堂检测
19.2 一次函数/
一次函数的图象和性质
当k>0时,y的值随x值的增大而增大;
当k<0时,y的值随x值的增大而减小.
与y轴的交点是(0,b),
与x轴的交点是( ,0),
当k>0, b>0时,经过一、二、三象限;
当k>0 ,b<0时,经过一、三、四象限;
当k<0 ,b>0时,经过 一、二、四象限;
当k<0 ,b<0时,经过二、三、四象限.
图象
性质
课堂小结
19.2 一次函数/
待定系数法求一次函数的解析式
第三课时
返回
19.2 一次函数/
【思考】你在作一次函数图象时,分别描了几个点?
在上节课中我们学习了在给定一次函数解析式的前提下,我们可以说出它的图象特征及有关性质;反之,如果给你信息,你能否求出函数的解析式呢?这将是本节课我们要研究的问题.
你为何选取这几个点?
可以有不同取法吗?
导入新知
19.2 一次函数/
1.理解待定系数法的意义.
2. 学会运用待定系数法和数形结合思想求一次函数解析式.
素养目标
19.2 一次函数/
已知一次函数的图象经过点(3,5)与(-4,-9).求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
∴这个一次函数的解析式为 .
解方程组得
把点(3,5)与(-4,-9)分别代入,
得:
y=2x-1
探究新知
知识点 1
待定系数法求一次函数的解析式
一次函数的图象过点
(3,5)与(-4,-9),因此这两点的坐标适合一次函数y=kx+b.
19.2 一次函数/
像这样先设出____________ ,再根据条件确定____________________ ,从而具体写出这个式子的方法,叫做待定系数法.
你能归纳出待定系数法求函数解析式的基本步骤吗?
函数解析式
解析式中未知的系数
探究新知
19.2 一次函数/
解:设这个一次函数的解析式为
y=kx+b
把x=3,y=5;x=-4,y=-9
分别代入上式得
解得
一次函数的解析式为
y=2x-1
设
代
解
还原
探究新知
19.2 一次函数/
探究新知
归纳总结
求一次函数解析式的步骤:
(1)设:设一次函数的一般形式
y=kx+b(k≠0)
(2)列:把图象上的点 , 代入一次
函数的解析式,组成_________方程组;
二元一次
(3)解:解二元一次方程组得k,b;
(4)还原:把k,b的值代入一次函数的解析式.
19.2 一次函数/
函数解析式y=kx+b
满足条件的两定点
一次函数的图象直线l
画出
选取
解出
选取
从数到形
从形到数
数学的基本思想方法:
数形结合
整理归纳:从两方面说明:
探究新知
19.2 一次函数/
例1 一次函数图像经过点(9,0)和点(24,20),写出函数解析式.
解方程组得:
这个一次函数的解析式为
解:设这个一次函数的解析式为y=kx+b.
把点(9,0)与(24,20)分别代入y=kx+b,得:
探究新知
素养考点 1
已知两点利用待定系数法求一次函数的解析式
19.2 一次函数/
1.已知一次函数的图象过点(3,5)与(-3,-13),求这个一次函数的解析式.
解:设这个一次函数的解析式为y=kx+b.
解方程组得:
把点(3,5)与(-3,-13)分别代入,得:
∴这个一次函数的解析式为
y=3x-4.
巩固练习
19.2 一次函数/
例2 若一次函数的图象经过点 A(2,0)且与直线y=-x+3平行,求其解析式.
解:设这个一次函数的解析式为y=kx+b.
k = -1,
2k + b = 0,
{
由题意得
k = -1,
b = 2.
{
解得
∴y=-x+2.
探究新知
素养考点 2
已知一点利用待定系数法求一次函数的解析式
19.2 一次函数/
解:设直线l为y=kx+b,
∵l与直线y=-2x平行,∴k= -2.
又∵直线过点(0,2),
∴2=-2×0+b,
∴直线l的解析式为y=-2x+2.
2. 已知直线l与直线y=-2x平行,且与y轴交于点(0,2),求直线l的解析式.
巩固练习
∴b=2,
19.2 一次函数/
例3 已知一次函数的图象过点(0,2),且与两坐标轴围成的三角形的面积为2,求此一次函数的解析式.
分析:一次函数y=kx+b与y轴的交点是(0,b),与x轴的交点是( ,0).由题意可列出关于k,b的方程.
y
x
O
2
注意:此题有两种情况.
素养考点 3
探究新知
几何面积和待定系数法求一次函数的解析式
19.2 一次函数/
解:设一次函数的解析式为y=kx+b(k≠0)
∵一次函数y=kx+b的图象过点(0,2),
∴b=2
∵一次函数的图象与x轴的交点是( ,0),则
解得k=1或-1.
故此一次函数的解析式为y=x+2或y=-x+2.
探究新知
19.2 一次函数/
3.正比例函数y=k1x与一次函数y=k2x+b的图象如图所示,它们的交点A的坐标为(3,4),并且OB=5.
(1)你能求出这两个函数的解析式吗?
(2)△AOB的面积是多少呢?
分析:由OB=5可知点B的坐标为(0,-5).y=k1x的图象过点A(3,4),y=k2x+b的图象过点
A(3,4),B(0,-5),代入解方程(组)即可.
巩固练习
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
19.2 一次函数/
巩固练习
解:(1)由题意可知,B点的坐标是(0,-5)
∵一次函数y=k2x+b的图象过点(0,-5),(3,4)
∴ ,解得
∵正比例函数y=k1x的图象过点(3,4),
∴ 因此
(2)S△AOB=5×3÷2=7.5
因此y=3x-5.
4
2
-2
-4
4
x
y
O
-4
-2
2
A
(3,4)
B
19.2 一次函数/
(2019 枣庄)如图,一直线与两坐标轴的正半轴分别交于A,B两点,P是线段AB上任意一点(不包括端点),过点P分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8,则该直线的函数表达式是( )
A.y=﹣x+4 B.y=x+4
C.y=x+8 D.y=﹣x+8
巩固练习
连接中考
A
x
y
B
O
P
A
19.2 一次函数/
课堂检测
基础巩固题
1.一次函数的图象经过点(2,1)和点(1,5),则这个一次函数是( )
A.y=4x+9 B. y=4x-9 C. y=-4x+9 D. y=-4x-9
2.已知点P的横坐标与纵坐标之和为1,且这点在直线y=x+3上,则该点是( )
A.(-7,8) B. (-5,6) C. (-4,5) D. (-1,2)
C
D
19.2 一次函数/
课堂检测
基础巩固题
3.若点A(-4,0)、B(0,5)、C(m,-5)在同一条直线上,则m的值是( )
A.8 B.4 C.-6 D.-8
4.一次函数的图象如图所示,则k、b的值分别为( )
A.k=-2,b=1 B.k=2,b=1
C.k=-2,b=-1 D.k=2,b=-1
A
D
1
1
x
y
o
19.2 一次函数/
5. 如图,直线l是一次函数y=kx+b的图象,填空:
(1)b=______,k=______;
(2)当x=30时,y=______;
(3)当y=30时,x=______.
2
-18
-42
l
y
x
课堂检测
基础巩固题
19.2 一次函数/
若一直线与另一直线y=-3x+2交于y轴同一点,且过(2,-6),
你能求出这条直线的解析式吗?
答案:y=-4x+2
分析:直线y=-3x+2与y轴的交点为(0,2),于是得知该直线过点(0,2),(2,-6),再用待定系数法求解即可.
课堂检测
能力提升题
19.2 一次函数/
已知一次函数y=kx+b(k≠0)的自变量的取值范围是- 3≤x≤ 6,相应函数值的范围是- 5≤y≤ - 2 ,求这个函数的解析式.
分析:(1)当- 3≤x≤ 6时,- 5≤y≤ - 2,实质是给出了两组自变量及对应的函数值;
(2)由于不知道函数的增减性,此题需分两种情况讨论.
答案:
课堂检测
拓广探索题
19.2 一次函数/
用待定系数法求一次函数的解析式
2. 根据已知条件列出关于k,b的方程(组);
1. 设所求的一次函数解析式为y=kx+b;
3. 解方程,求出k,b;
4. 把求出的k,b代回解析式即可.
课堂小结
19.2 一次函数/
一次函数解决实际问题
第四课时
返回
19.2 一次函数/
乌鸦喝水,是《伊索寓言》中一个有趣的寓言故事.故事梗概为:"一只口渴的乌鸦看到窄口瓶内有半瓶水,于是将小石子投入瓶中,使水面升高,从而喝到了水."告诉人们遇到困难要积极想解决办法,认真思考才能让问题迎刃而解的道理.数学问题也一样哦.
导入新知
19.2 一次函数/
10 cm
9 cm
如果将乌鸦喝水的故事进行量化,你能判断乌鸦丢进多少颗石子,水能刚好在瓶口?说说你的做法!
导入新知
19.2 一次函数/
1. 巩固一次函数知识,灵活运用变量关系解决相关实际问题.
2. 有机地把各种数学模型通过函数统一起来使用,提高解决实际问题的能力.
素养目标
19.2 一次函数/
如图,大拇指与小拇指尽量张开时,两指间的距离称为指距.某项研究表明,一般情况下人的身高h是指距d的一次函数.下表是测得的指距与身高的一组数据:
①求出h与d之间的函数解析式(不要求写出自变量d的取值范围).
②某人身高为196 cm,一般情况下他的指距应是多少?
探究新知
知识点 1
一次函数解答实际问题
19.2 一次函数/
解:(1)设h与d之间的函数关系式为:
h=kd+b.
把d=20,h=160,d=21,h=169,
分别代入得,
20k+b=160,
21k+b=169.
解得k=9,b=-20,
即h=9d-20.
(2)当h=196时,196=9d-20,解得d=24(cm).
探究新知
19.2 一次函数/
1.小明将父母给的零用钱按每月相等的数额存在储蓄盒内,准备捐给希望工程,盒内钱数y(元)与存钱月数 x(月)之间的关系如图所示,根据下图回答下列问题:
(1)求出y关于x的函数解析式.
(2)根据关系式计算,小明经过几个月才能存够200元?
40
80
120
y/元
x/月
1
2
3
4
5
o
巩固练习
19.2 一次函数/
解: (1)设函数解析式为y=kx+b,
由图可知图象过(0,40),(4,120)
∴这个函数的解析式为y=20x+40.
(2)当y=200时,20x+40=200, 解得x=8
∴小明经过8个月才能存够200元.
解得
∴
巩固练习
40
80
120
y/元
x/月
1
2
3
4
5
o
19.2 一次函数/
“黄金1号”玉米种子的价格为5 元/kg,如果一次购买
2 kg 以上的种子,超过2 kg 部分的种子的价格打8 折.
(1)填写下表:
2.5
5
7.5
10
12
14
16
18
探究新知
19.2 一次函数/
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
分析:从题目可知,种子的价格与 有关.
若购买种子量为x>2时,种子价格y为:
.
若购买种子量为0≤x≤2时,种子价格y为: .
购买种子量
y=5x
y=4(x-2)+10=4x+2
探究新知
19.2 一次函数/
解:设购买量为x千克,付款金额为y元.
当x>2时,y=4(x-2)+10=4x+2.
当0≤x≤2时,y=5x;
(2)写出购买量关于付款金额的函数解析式,并画出函数图象.
叫做分段函数.
注意:1.它是一个函数;
2.要写明自变量取值范围.
探究新知
19.2 一次函数/
y=5x(0≤x≤2)
y=4x+2(x>2)
y
x
O
1
2
10
3
14
的函数图象为:
探究新知
19.2 一次函数/
2.一个试验室在0:00—2:00保持20℃的恒温,在2:00—
4:00匀速升温,每小时升高5℃.写出试验室温度T(单位:℃)关于时间t(单位:h)的函数解析式,并画出函数图象.
解:(1)由题意得
当0≤t≤2时,T=20;
当2
T=20(0≤t≤2)
T=5t+10(2
10
40
T
t
0
1
2
30
4
3
巩固练习
(2)函数图像为:
19.2 一次函数/
(2019 聊城)某快递公司每天上午9:00﹣10:00为集中揽件和派件时段,甲仓库用来揽收快件,乙仓库用来派发快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,那么当两仓库快递件数相同时,此刻的时间为( )
A.9:15 B.9:20
C.9:25 D.9:30
巩固练习
连接中考
B
x/分
y/件
400
240
40
60
O
甲
乙
19.2 一次函数/
1.若一次函数y=3x-b的图象经过点P(1,-1),则该函数图象必经过( )
A.(-1,1) B.(2,2) C.(-2,2) D.(2,-2)
2.老师给出一个函数,甲、乙、丙各正确地指出了这个函数的一个性质:
甲:函数的图象经过第一象限;
乙:函数的图象经过第二象限;
丙:在每个象限内,y随x的增大而减小.
请你根据他们的叙述构造满足上述性质的一个函数,并写出它的函数解析式: .
B
y=-2x+6(答案不唯一)
基础巩固题
课堂检测
19.2 一次函数/
3.某医药研究所开发了一种新药,在实际验药时发现,如果成人按规定剂量服用,那么每毫升血液中含药量y(毫克)随时间x(时)的变化情况如图所示,当成年人按规定剂量服药后.
(1)服药后______时,血液中含药量最高,达到每毫升_______毫克,接着逐步衰弱.
(2)服药5时,血液中含药量为
每毫升____毫克.
x/时
y/毫克
6
3
2
5
O
2
6
3
课堂检测
基础巩固题
19.2 一次函数/
(3)当x≤2时y与x之间的函数解析式是___________.
(4)当x≥2时y与x之间的函数解析式是___________.
(5)如果每毫升血液中含药量3毫克或3毫克以上时,治疗疾病最有效,那么这个有效时间是______小时.
y=3x
y=-x+8
4
x/时
y/毫克
6
3
2
5
O
课堂检测
基础巩固题
19.2 一次函数/
4.某种拖拉机的油箱可储油40L,加满油并开始工作后,油箱中的剩余油量y(L)与工作时间x(h) 之间为一次函数关系,函数图象如图所示.
(1)求y关于x的函数解析式;
(2)一箱油可供拖拉机工作几小时?
解:(1)y = -5x + 40.
(2)8 h
课堂检测
基础巩固题
19.2 一次函数/
5.温度的度量有两种:摄氏温度和华氏温度.
水的沸点温度是100℃,用华氏温度度量为212℉;水的冰点温度是0℃,用华氏温度度量为32 ℉.已知摄氏温度与华氏温度的关近似地为一次函数关系,你能不能想出一个办法方便地把华氏温度换算成摄氏温度?
课堂检测
基础巩固题
19.2 一次函数/
用C,F分别表示摄氏温度与华氏温度,由于摄氏温度与华氏温度的关系近似地为一次函数关系,因此可以设
C = kF + b,
解:
解这个方程组,得
因此摄氏温度与华氏温度的函数关系式为
由已知条件,得
课堂检测
基础巩固题
19.2 一次函数/
为节约用水,某市制定以下用水收费标准,每户每月用水不超过8立方米,每立方米收取1元外加0.3元的污水处理费;超过时,超过8立方米部分每立方米收取1.5元外加1.2元污水处理费,现设一户每月用水x立方米,应缴水费y元.
(1)求出y关于x的函数解析式;
解:y关于x的函数解析式为:
(1+0.3)x =1.3x, (0≤x≤8)
(1.5+1.2)(x-8)+1.3×8=2.7x-11.2. (x>8)
y=
能力提升题
课堂检测
19.2 一次函数/
(2)当x=10时,y=2.7×10-11.2=15.8.
(3)∵1.3×8=10.4<26.6,∴该用户用水量超过8立方米.
∴2.7x-11.2=26.6,解得x=14.
答:应缴水费为15.8元.
答:该户这月用水量为14立方米.
(2)该市一户某月若用水x=10立方米时,求应缴水费;
(3)该市一户某月缴水费26.6元,求该户这月用水量.
课堂检测
能力提升题
解:
19.2 一次函数/
春、秋季节,由于冷空气的入侵,地面气温急剧下降到0℃以下的天气现象称为“霜冻”.由霜冻导致植物生长受到影响或破坏的现象称为霜冻灾害.
某种植物在气温是0℃以下持续时间超过3小时,即遭受霜冻灾害,需采取预防措施.右图是气象台某天发布的该地区气象信息,预报了次日0时~8时气温随时间变化情况,其中0时~5时,5时~8时的图象分别满足一次函数关系.请你
根据图中信息,针对这种植物判断次日是否
需要采取防霜冻措施,并说明理由.
x/时
y/ oC
拓广探索题
课堂检测
19.2 一次函数/
解:根据图象可知:设0时~5时的一次函数关系式为y1=k1x+b1,经过点(0,3),(5,-3),b1=3, 5k1+b1=-3.
解得k1=-1.2, b1=3.
当y1、y2分别为0时,
而|x2-x1|= >3,
∴应采取防霜冻措施.
设5时~8时的一次函数关系式为y2=k2x+b2,
经过点(5,-3),(8,5),5k2+b2=-3 ,
8k2+b2=5.
课堂检测
拓广探索题
∴y1=-1.2x+3.
∴ .
解得 , .
x/时
y/ oC
A
M
E
Q
B
N
C
F
19.2 一次函数/
一次函数与实际问题
一次函数与实际问题
分段函数的解析式与图象
课堂小结
19.2 一次函数/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
