人教版数学八下 20.1.1平均数(希沃课件+图片版PPT)仅适用希沃白板
文档属性
| 名称 | 人教版数学八下 20.1.1平均数(希沃课件+图片版PPT)仅适用希沃白板 |  | |
| 格式 | zip | ||
| 文件大小 | 27.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 09:31:35 | ||
图片预览








文档简介
(共61张PPT)
20.1 数据的集中趋势/
20.1 数据的集中趋势
20.1.1 平均数
第一课时
第二课时
人教版 数学 八年级 下册
20.1 数据的集中趋势/
平均数和加权平均数
第一课时
返回
20.1 数据的集中趋势/
765
4
3
2
1
A B C D
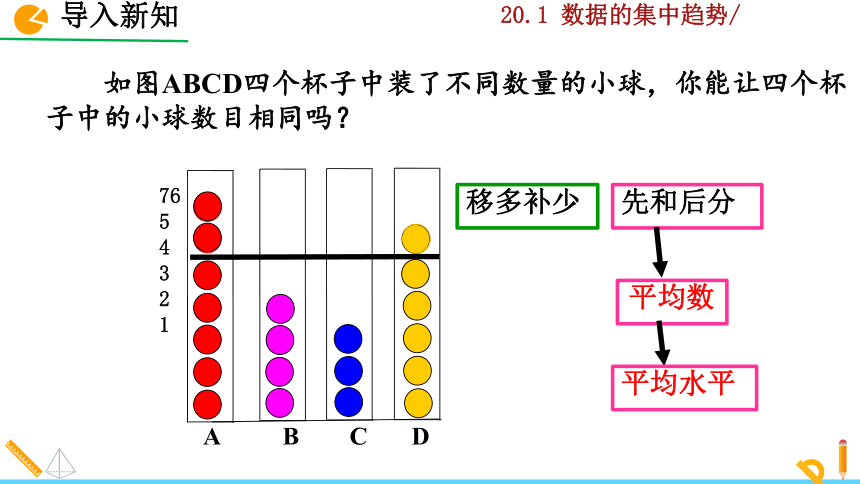
平均数
先和后分
移多补少
如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?
平均水平
导入新知
20.1 数据的集中趋势/
1. 理解数据的权和加权平均数的概念,体会权的作用.
2. 明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法.
素养目标
3. 会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念.
20.1 数据的集中趋势/
重庆7月中旬一周的最高气温如下:
1.你能快速计算这一周的平均最高吗?
2.你还能回忆、归纳出算术平均数的概念吗?
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,对于n个数x1, x2, …, xn,我们把
叫做这n个数的算术平均数,简称平均数.
探究新知
知识点 1
平均数与加权平均数
20.1 数据的集中趋势/
计算某篮球队10个队员的平均年龄:
解法一:平均年龄
解法二:平均年龄
请问,在年龄确定的时候,影响平均数的因素是什么?
在年龄确定的情况下,队员人数1、3、1、4、1是影响平均数的因素.
探究新知
20.1 数据的集中趋势/
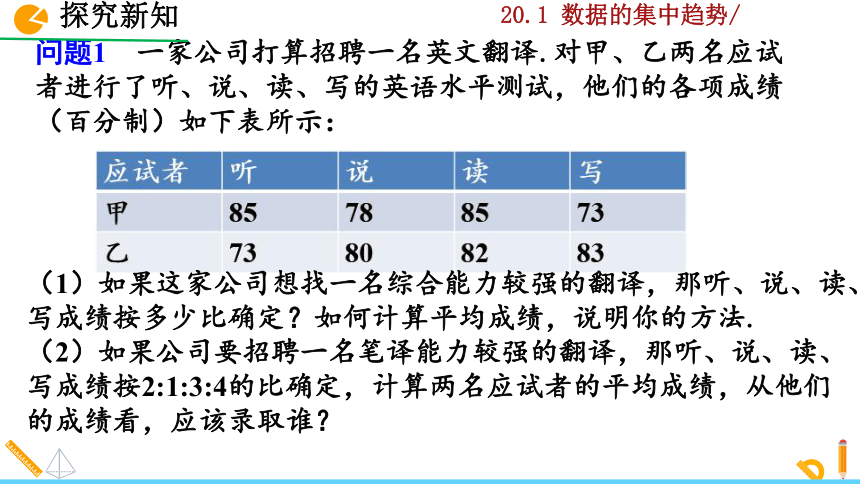
(1)如果这家公司想找一名综合能力较强的翻译,那听、说、读、写成绩按多少比确定?如何计算平均成绩,说明你的方法.
(2)如果公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2:1:3:4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
问题1 一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示:
探究新知
20.1 数据的集中趋势/
解:(1)甲的平均成绩
乙的平均成绩
权
加权平均数
(2)甲的平均成绩
乙的平均成绩
探究新知
20.1 数据的集中趋势/
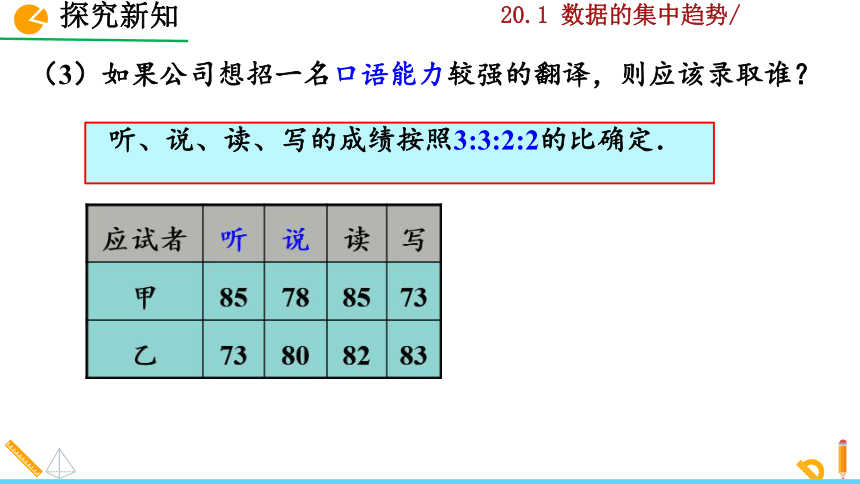
(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?
听、说、读、写的成绩按照3:3:2:2的比确定.
探究新知
20.1 数据的集中趋势/
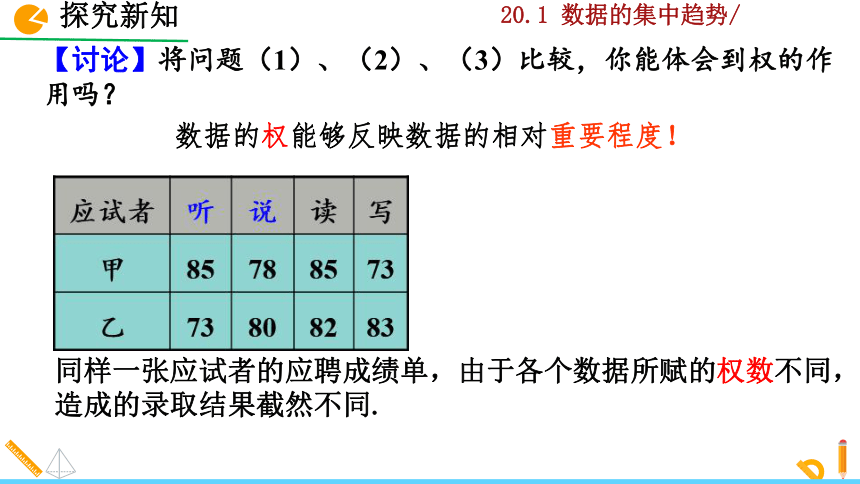
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
【讨论】将问题(1)、(2)、(3)比较,你能体会到权的作用吗?
数据的权能够反映数据的相对重要程度!
探究新知
20.1 数据的集中趋势/
一般地,若n个数x1, x2, …, xn的权分别是w1,w2,…,wn ,则
叫做这n个数的加权平均数.
如上题解(2)中平均数79.5称为甲选手的加权平均数;其中2、1、3、4就是甲选手听、说、读、写各项得分的权!
探究新知
权的意义:(1)数据的重要程度
(2)权衡轻重或份量大小
20.1 数据的集中趋势/
例1 一次演讲比赛中,评委将从演讲内容,演讲能力,演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次.
探究新知
素养考点 1
利用加权平均数解答实际问题
20.1 数据的集中趋势/
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
探究新知
20.1 数据的集中趋势/
你能说说算术平均数与加权平均数的区别和联系吗?
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数.
1.算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);
探究新知
20.1 数据的集中趋势/
1.万载县百合食品公司欲从我县女青年中招聘一名百合天使,作为该公司百合产品的形象代言人。对甲、乙候选人进行了面试和笔试,他们的成绩如下表所示:
巩固练习
20.1 数据的集中趋势/
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为形象代言人面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
巩固练习
解:
解:
所以甲将被录取.
所以乙将被录取.
20.1 数据的集中趋势/
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
知识点 2
探究新知
加权平均数的其他形式
20.1 数据的集中趋势/
例2 某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
=
≈______(岁).
答:这个跳水队运动员的平均年龄约为___岁.
8
16
24
2
14
探究新知
素养考点 1
加权平均数的应用
14
20.1 数据的集中趋势/
2.某校八年级一班有学生50人,八年级二班有学生45人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:(81.5×50 +83.4×45)÷95
=7828÷95
=82.4
答:这两个班95名学生的平均分是82.4分.
巩固练习
20.1 数据的集中趋势/
(2019 遂宁)某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为_________分.
巩固练习
连接中考
88.8
20.1 数据的集中趋势/
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B. 86 C. 88 D. 90
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A. (x+y)/2 B. (mx+ny)/(m+n)
C. (x+y)/(m+n) D. (mx+ny)/(x+y)
D
B
课堂检测
基础巩固题
20.1 数据的集中趋势/
3.已知:x1,x2,x3… x10的平均数是a, x11,x12,x13… x30的平均数
是b,则x1,x2,x3… x30的平均数是( )
D
(10a+30b)
A.
(a+b)
B.
(a+b)
C.
(10a+20b)
D.
课堂检测
基础巩固题
20.1 数据的集中趋势/
4.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元)如下表:
该公司每人所创年利润的平均数是_____万元.
30
课堂检测
基础巩固题
20.1 数据的集中趋势/
5.下表是校女子排球队队员的年龄分布:
求校女子排球队队员的平均年龄.
答:校女子排球队队员的平均年龄为14.7岁.
解:
课堂检测
基础巩固题
20.1 数据的集中趋势/
6.万载三中规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%。小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
基础巩固题
课堂检测
解:
答:小桐这学期的体育成绩是88.5分.
20.1 数据的集中趋势/
某次歌唱比赛,两名选手的成绩如下:
(1)若按三项平均值取第一名,则__________是第一名.
选手B
能力提升题
课堂检测
20.1 数据的集中趋势/
所以,此时第一名是选手A.
(2)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁?
课堂检测
能力提升题
解:
20.1 数据的集中趋势/
某公司欲招聘公关人员,对甲、乙候选人进行了面试和笔试,他们的成绩如下表所示
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
拓广探索题
课堂检测
解:
所以甲将被录取.
20.1 数据的集中趋势/
(2)如果公司认为,作为公关人员面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁将被录取.
课堂检测
拓广探索题
解:
所以乙将被录取.
20.1 数据的集中趋势/
平均数与加权平均数
算术平均数:
加权平均数:
课堂小结
20.1 数据的集中趋势/
用样本平均数估计总体平均数
第二课时
返回
20.1 数据的集中趋势/
某汽车厂为了了解2000辆汽车的安全可靠性能,你认为下列方法是否可行,
1、从中抽出15辆做碰撞试验;
2、用抽取的15辆汽车的安全可靠性可以作为一个样本;
3、用抽取的样本的安全可靠性来估计整批2000辆汽车的安全可靠性能。
你认为这样做是否可行?为什么?
导入新知
20.1 数据的集中趋势/
2. 会用计算器求一组数据的加权平均数.
1. 理解组中值的意义,能利用组中值计算一组数据的加权平均数 .
素养目标
3. 会根据样本平均数估计数据总体的集中趋势,进一步体会用样本估计总体的思想.
20.1 数据的集中趋势/
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
探究新知
知识点 1
一组数据中的平均数和组中值
20.1 数据的集中趋势/
【思考】表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
探究新知
20.1 数据的集中趋势/
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
探究新知
2.根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
20.1 数据的集中趋势/
探究新知
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
解:这天5路公共汽车平均每班的载客量是
答:这天5路公共汽车平均每班的载客量是73人.
20.1 数据的集中趋势/
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f1, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器的方法:
探究新知
20.1 数据的集中趋势/
例1 种菜能手李大叔种植了一批新品种黄瓜.为了考察这种黄瓜的生产情况,他随机抽查了部分黄瓜藤上长出的黄瓜根数,得到如图所示的条形图.请计算这个新品种黄瓜平均每株结多少根黄瓜.
分析:读图,从图中可以得到哪些信息?如何计算平均数?条件是否足够?
探究新知
素养考点 1
在一组数据中求平均数
20.1 数据的集中趋势/
解:条形图中样本的平均数为
(10×10+13×15+14×20+15×18) ÷ (10+15+18+20)≈13(根)
故这个新品种黄瓜平均每株结13根黄瓜.
探究新知
20.1 数据的集中趋势/
1.为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
0
2
4
6
8
10
12
14
40
50
60
70
80
90
频数
周长/cm
巩固练习
20.1 数据的集中趋势/
答:这批梧桐树干的平均周长是64cm.
解:
巩固练习
20.1 数据的集中趋势/
果园里有100 棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?
每个梨的质量?
探究新知
知识点 2
利用样本估计平均数
20.1 数据的集中趋势/
所以平均每棵梨树上梨的个数为154.
(1)果农从100 棵梨树中任意选出10 棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
探究新知
20.1 数据的集中趋势/
梨的质量 x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
12
16
8
(2)果农从这10 棵梨树的每一棵树上分别随机摘4个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以平均每个梨的质量约为0.42 kg.
探究新知
(kg)
20.1 数据的集中趋势/
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
【思考】这个生活中的问题是如何解决的,体现了怎
样的统计思想?
所以该果园中梨的总产量约为6468 kg.
探究新知
(kg)
20.1 数据的集中趋势/
例2 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
探究新知
素养考点 1
利用样本估计求平均数
20.1 数据的集中趋势/
答:即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是1 672 h.
样本估计总体
探究新知
解:据上表得各小组的组中值,于是
(h)
20.1 数据的集中趋势/
2.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
巩固练习
20.1 数据的集中趋势/
(2019 青岛)射击比赛中,某队员10次射击成绩如图所示,则该队员的平均成绩是_________环.
巩固练习
连接中考
8.5
20.1 数据的集中趋势/
1.为了估计某矿区铁矿石的含铁量,抽取了15块矿石,测得它们的含铁量如下:(单位:%)
则样本的平均数是多少 估计这个矿区铁矿石的平均含铁量约为多少
基础巩固题
课堂检测
解:
答:样本的平均数是24.8,估计这个矿区铁矿石的平均含铁量约24.8.
20.1 数据的集中趋势/
2. 某养鱼户搞池塘养鱼,头一年放养鱼20 000尾,其成活率约为70%,在秋季捕捞时,捞出10尾鱼,称得每尾鱼的重量如下:(单位:千克)0.8;0.9;1.2;1.3;0.8;0.9;1.1;1.0;1.2;0.8.
根据样本平均数估计这塘鱼的产量是多少千克?
课堂检测
1×20000×70%=14000(千克)
答:这塘鱼的产量是14000千克.
解:
基础巩固题
20.1 数据的集中趋势/
问班级平均分约是多少?
3.某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
课堂检测
基础巩固题
20.1 数据的集中趋势/
下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
能力提升题
课堂检测
20.1 数据的集中趋势/
解:(1)∵点D,O,E在同一条直线上,∴∠DOE=180°,
∴60≤x<80所占百分比为180/360 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为36/360 ×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%=60(分)
课堂检测
能力提升题
20.1 数据的集中趋势/
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
课堂检测
能力提升题
20.1 数据的集中趋势/
为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况
扇形统计图
拓广探索题
课堂检测
20.1 数据的集中趋势/
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
课堂检测
拓广探索题
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况
扇形统计图
解:
20.1 数据的集中趋势/
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
男生身高情况直方图
女生身高情况
扇形统计图
课堂检测
拓广探索题
身高情况分组表(单位:cm)
解:
20.1 数据的集中趋势/
用样本平均数估计总体平均数
组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
用计算器求平均数
用样本平均数估计总体平均数
课堂小结
20.1 数据的集中趋势/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
20.1 数据的集中趋势/
20.1 数据的集中趋势
20.1.1 平均数
第一课时
第二课时
人教版 数学 八年级 下册
20.1 数据的集中趋势/
平均数和加权平均数
第一课时
返回
20.1 数据的集中趋势/
765
4
3
2
1
A B C D
平均数
先和后分
移多补少
如图ABCD四个杯子中装了不同数量的小球,你能让四个杯子中的小球数目相同吗?
平均水平
导入新知
20.1 数据的集中趋势/
1. 理解数据的权和加权平均数的概念,体会权的作用.
2. 明确加权平均数与算术平均数的关系,掌握加权平均数的计算方法.
素养目标
3. 会用加权平均数分析一组数据的集中趋势,发展数据分析能力,逐步形成数据分析观念.
20.1 数据的集中趋势/
重庆7月中旬一周的最高气温如下:
1.你能快速计算这一周的平均最高吗?
2.你还能回忆、归纳出算术平均数的概念吗?
日常生活中,我们常用平均数表示一组数据的“平均水平”.
一般地,对于n个数x1, x2, …, xn,我们把
叫做这n个数的算术平均数,简称平均数.
探究新知
知识点 1
平均数与加权平均数
20.1 数据的集中趋势/
计算某篮球队10个队员的平均年龄:
解法一:平均年龄
解法二:平均年龄
请问,在年龄确定的时候,影响平均数的因素是什么?
在年龄确定的情况下,队员人数1、3、1、4、1是影响平均数的因素.
探究新知
20.1 数据的集中趋势/
(1)如果这家公司想找一名综合能力较强的翻译,那听、说、读、写成绩按多少比确定?如何计算平均成绩,说明你的方法.
(2)如果公司要招聘一名笔译能力较强的翻译,那听、说、读、写成绩按2:1:3:4的比确定,计算两名应试者的平均成绩,从他们的成绩看,应该录取谁?
问题1 一家公司打算招聘一名英文翻译.对甲、乙两名应试者进行了听、说、读、写的英语水平测试,他们的各项成绩(百分制)如下表所示:
探究新知
20.1 数据的集中趋势/
解:(1)甲的平均成绩
乙的平均成绩
权
加权平均数
(2)甲的平均成绩
乙的平均成绩
探究新知
20.1 数据的集中趋势/
(3)如果公司想招一名口语能力较强的翻译,则应该录取谁?
听、说、读、写的成绩按照3:3:2:2的比确定.
探究新知
20.1 数据的集中趋势/
同样一张应试者的应聘成绩单,由于各个数据所赋的权数不同,造成的录取结果截然不同.
【讨论】将问题(1)、(2)、(3)比较,你能体会到权的作用吗?
数据的权能够反映数据的相对重要程度!
探究新知
20.1 数据的集中趋势/
一般地,若n个数x1, x2, …, xn的权分别是w1,w2,…,wn ,则
叫做这n个数的加权平均数.
如上题解(2)中平均数79.5称为甲选手的加权平均数;其中2、1、3、4就是甲选手听、说、读、写各项得分的权!
探究新知
权的意义:(1)数据的重要程度
(2)权衡轻重或份量大小
20.1 数据的集中趋势/
例1 一次演讲比赛中,评委将从演讲内容,演讲能力,演讲效果三个方面为选手打分,各项成绩均按百分制,然后再按演讲内容占50%,演讲能力占40%,演讲效果占10%的比例,计算选手的综合成绩(百分制).进入决赛的前两名选手的单项成绩如下表所示:
请决出两人的名次.
探究新知
素养考点 1
利用加权平均数解答实际问题
20.1 数据的集中趋势/
解:选手A的最后得分是
选手B的最后得分是
由上可知选手B获得第一名,选手A获得第二名.
探究新知
20.1 数据的集中趋势/
你能说说算术平均数与加权平均数的区别和联系吗?
2.在实际问题中,各项权不相等时,计算平均数时就要采用加权平均数,当各项权相等时,计算平均数就要采用算术平均数.
1.算术平均数是加权平均数的一种特殊情况(它特殊在各项的权相等);
探究新知
20.1 数据的集中趋势/
1.万载县百合食品公司欲从我县女青年中招聘一名百合天使,作为该公司百合产品的形象代言人。对甲、乙候选人进行了面试和笔试,他们的成绩如下表所示:
巩固练习
20.1 数据的集中趋势/
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
(2)如果公司认为,作为形象代言人面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、两人各自的平均成绩,看看谁将被录取。
巩固练习
解:
解:
所以甲将被录取.
所以乙将被录取.
20.1 数据的集中趋势/
在求n个数的算术平均数时,如果x1出现f1次,x2出现f2次,…,xk出现fk次(这里f1+f2+…+fk=n)那么这n个数的算术平均数
也叫做x1,x2,…,xk这k个数的加权平均数,其中f1,f2,…,fk分别叫做x1,x2,…,xk的权.
知识点 2
探究新知
加权平均数的其他形式
20.1 数据的集中趋势/
例2 某跳水队为了解运动员的年龄情况,作了一次年龄调查,结果如下:13岁8人,14岁16人,15岁24人,16岁2人.求这个跳水队运动员的平均年龄(结果取整数).
解:这个跳水队运动员的平均年龄为:
=
≈______(岁).
答:这个跳水队运动员的平均年龄约为___岁.
8
16
24
2
14
探究新知
素养考点 1
加权平均数的应用
14
20.1 数据的集中趋势/
2.某校八年级一班有学生50人,八年级二班有学生45人,期末数学测试中,一班学生的平均分为81.5分,二班学生的平均分为83.4分,这两个班95名学生的平均分是多少?
解:(81.5×50 +83.4×45)÷95
=7828÷95
=82.4
答:这两个班95名学生的平均分是82.4分.
巩固练习
20.1 数据的集中趋势/
(2019 遂宁)某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为_________分.
巩固练习
连接中考
88.8
20.1 数据的集中趋势/
1.某次考试,5名学生的平均分是82,除甲外,其余4名学生的平均分是80,那么甲的得分是( )
A.84 B. 86 C. 88 D. 90
2.若m个数的平均数为x,n个数的平均数为y,则这(m+n)个数的平均数是( )
A. (x+y)/2 B. (mx+ny)/(m+n)
C. (x+y)/(m+n) D. (mx+ny)/(x+y)
D
B
课堂检测
基础巩固题
20.1 数据的集中趋势/
3.已知:x1,x2,x3… x10的平均数是a, x11,x12,x13… x30的平均数
是b,则x1,x2,x3… x30的平均数是( )
D
(10a+30b)
A.
(a+b)
B.
(a+b)
C.
(10a+20b)
D.
课堂检测
基础巩固题
20.1 数据的集中趋势/
4.某公司有15名员工,他们所在的部门及相应每人所创的年利润(万元)如下表:
该公司每人所创年利润的平均数是_____万元.
30
课堂检测
基础巩固题
20.1 数据的集中趋势/
5.下表是校女子排球队队员的年龄分布:
求校女子排球队队员的平均年龄.
答:校女子排球队队员的平均年龄为14.7岁.
解:
课堂检测
基础巩固题
20.1 数据的集中趋势/
6.万载三中规定学生的学期体育成绩满分为100分,其中早锻炼及体育课外活动占20%,期中考试成绩占30%,期末成绩占50%。小桐的三项成绩(百分制)依次是95分、90分、85分,小桐这学期的体育成绩是多少?
基础巩固题
课堂检测
解:
答:小桐这学期的体育成绩是88.5分.
20.1 数据的集中趋势/
某次歌唱比赛,两名选手的成绩如下:
(1)若按三项平均值取第一名,则__________是第一名.
选手B
能力提升题
课堂检测
20.1 数据的集中趋势/
所以,此时第一名是选手A.
(2)若三项测试得分按3:6:1的比例确定个人的测试成绩,此时第一名是谁?
课堂检测
能力提升题
解:
20.1 数据的集中趋势/
某公司欲招聘公关人员,对甲、乙候选人进行了面试和笔试,他们的成绩如下表所示
(1)如果公司认为面试和笔试同等重要,从他们的成绩看,谁将被录取?
拓广探索题
课堂检测
解:
所以甲将被录取.
20.1 数据的集中趋势/
(2)如果公司认为,作为公关人员面试的成绩应该比笔试更重要,并分别赋予它们6和4的权,计算甲、乙两人各自的平均成绩,看看谁将被录取.
课堂检测
拓广探索题
解:
所以乙将被录取.
20.1 数据的集中趋势/
平均数与加权平均数
算术平均数:
加权平均数:
课堂小结
20.1 数据的集中趋势/
用样本平均数估计总体平均数
第二课时
返回
20.1 数据的集中趋势/
某汽车厂为了了解2000辆汽车的安全可靠性能,你认为下列方法是否可行,
1、从中抽出15辆做碰撞试验;
2、用抽取的15辆汽车的安全可靠性可以作为一个样本;
3、用抽取的样本的安全可靠性来估计整批2000辆汽车的安全可靠性能。
你认为这样做是否可行?为什么?
导入新知
20.1 数据的集中趋势/
2. 会用计算器求一组数据的加权平均数.
1. 理解组中值的意义,能利用组中值计算一组数据的加权平均数 .
素养目标
3. 会根据样本平均数估计数据总体的集中趋势,进一步体会用样本估计总体的思想.
20.1 数据的集中趋势/
为了解5路公共汽车的运营情况,公交部门统计了某天5路公共汽车每个运行班次的载客量,得到下表,这天5路公共汽车平均每班的载客量是多少?
探究新知
知识点 1
一组数据中的平均数和组中值
20.1 数据的集中趋势/
【思考】表格中载客量是六个数据组,而不是一个具体的数,各组的实际数据应该选谁呢?
探究新知
20.1 数据的集中趋势/
1.数据分组后,一个小组的组中值是指:这个小组的两个端点的数的平均数.
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
探究新知
2.根据频数分布表求加权平均数时,统计中常用各组的组中值代表各组的实际数据,把各组的频数看作相应组中值的权.
20.1 数据的集中趋势/
探究新知
载客量/人
组中值
频数(班次)
1≤x<21
3
21≤x<41
5
41≤x<61
20
61≤x<81
22
81≤x<101
18
101≤x<121
15
11
31
51
71
91
111
解:这天5路公共汽车平均每班的载客量是
答:这天5路公共汽车平均每班的载客量是73人.
20.1 数据的集中趋势/
1.不同品牌的计算器的操作步骤有所不同,
操作时需要参阅计算器的使用说明书.
2.通常需要先按动有关键,使计算器进入统计状态;然后依次输入数据x1,x2,…,xn ,以及它们的权f1, f2,…,fn ;
最后按动求平均数的功能键(例如 键),计算器便会求出平均数 的值.
使用计算器的方法:
探究新知
20.1 数据的集中趋势/
例1 种菜能手李大叔种植了一批新品种黄瓜.为了考察这种黄瓜的生产情况,他随机抽查了部分黄瓜藤上长出的黄瓜根数,得到如图所示的条形图.请计算这个新品种黄瓜平均每株结多少根黄瓜.
分析:读图,从图中可以得到哪些信息?如何计算平均数?条件是否足够?
探究新知
素养考点 1
在一组数据中求平均数
20.1 数据的集中趋势/
解:条形图中样本的平均数为
(10×10+13×15+14×20+15×18) ÷ (10+15+18+20)≈13(根)
故这个新品种黄瓜平均每株结13根黄瓜.
探究新知
20.1 数据的集中趋势/
1.为了绿化环境,柳荫街引进一批法国梧桐.三年后这些树的树干的周长情况如图所示.计算这批法国梧桐树干的平均周长(结果取整数).
0
2
4
6
8
10
12
14
40
50
60
70
80
90
频数
周长/cm
巩固练习
20.1 数据的集中趋势/
答:这批梧桐树干的平均周长是64cm.
解:
巩固练习
20.1 数据的集中趋势/
果园里有100 棵梨树,在收获前,果农常会先估计果园里梨的产量.你认为该怎样估计呢?
梨的个数?
每个梨的质量?
探究新知
知识点 2
利用样本估计平均数
20.1 数据的集中趋势/
所以平均每棵梨树上梨的个数为154.
(1)果农从100 棵梨树中任意选出10 棵,数出这10棵梨树上梨的个数,得到以下数据:154,150,155,155,159,150,152,155,153,157.你能估计出平均每棵树的梨的个数吗?
探究新知
20.1 数据的集中趋势/
梨的质量 x/kg
0.2≤x<0.3
0.3≤x<0.4
0.4≤x<0.5
0.5≤x<0.6
频数
4
12
16
8
(2)果农从这10 棵梨树的每一棵树上分别随机摘4个梨,这些梨的质量分布如下表:
能估计出这批梨的平均质量吗?
所以平均每个梨的质量约为0.42 kg.
探究新知
(kg)
20.1 数据的集中趋势/
样本估计总体;
用样本平均数估计总体平均数.
(3)能估计出该果园中梨的总产量吗?
【思考】这个生活中的问题是如何解决的,体现了怎
样的统计思想?
所以该果园中梨的总产量约为6468 kg.
探究新知
(kg)
20.1 数据的集中趋势/
例2 某灯泡厂为了测量一批灯泡的使用寿命,从中随机抽查了50只灯泡,它们的使用寿命如下表所示.这批灯泡的平均使用寿命是多少?
使用寿命 x/h
600≤x
<1 000
1 000≤x
<1 400
1 400≤x
<1 800
1 800≤x
<2 200
2 200≤x
<2 600
灯泡只数
5
10
12
17
6
探究新知
素养考点 1
利用样本估计求平均数
20.1 数据的集中趋势/
答:即样本平均数为1 672.
因此,可以估计这批灯泡的平均使用寿命大约是1 672 h.
样本估计总体
探究新知
解:据上表得各小组的组中值,于是
(h)
20.1 数据的集中趋势/
2.下表是截至到2017年菲尔兹奖得主获奖时的年龄,根据表格中的信息计算获菲尔兹奖得主获奖时的平均年龄(保留一位小数)?
答案:36.1岁.
巩固练习
20.1 数据的集中趋势/
(2019 青岛)射击比赛中,某队员10次射击成绩如图所示,则该队员的平均成绩是_________环.
巩固练习
连接中考
8.5
20.1 数据的集中趋势/
1.为了估计某矿区铁矿石的含铁量,抽取了15块矿石,测得它们的含铁量如下:(单位:%)
则样本的平均数是多少 估计这个矿区铁矿石的平均含铁量约为多少
基础巩固题
课堂检测
解:
答:样本的平均数是24.8,估计这个矿区铁矿石的平均含铁量约24.8.
20.1 数据的集中趋势/
2. 某养鱼户搞池塘养鱼,头一年放养鱼20 000尾,其成活率约为70%,在秋季捕捞时,捞出10尾鱼,称得每尾鱼的重量如下:(单位:千克)0.8;0.9;1.2;1.3;0.8;0.9;1.1;1.0;1.2;0.8.
根据样本平均数估计这塘鱼的产量是多少千克?
课堂检测
1×20000×70%=14000(千克)
答:这塘鱼的产量是14000千克.
解:
基础巩固题
20.1 数据的集中趋势/
问班级平均分约是多少?
3.某班学生期中测试数学成绩各分数段人数统计表如下:
50
70
90
110
解:
课堂检测
基础巩固题
20.1 数据的集中趋势/
下图是某学校的一次健康知识测验的分数段统计图(满分100分,分数均为整数),点O是圆心,点D,O,E在同一条直线上,∠AOE=36°.
(1)本次测验的平均分约是多少?
能力提升题
课堂检测
20.1 数据的集中趋势/
解:(1)∵点D,O,E在同一条直线上,∴∠DOE=180°,
∴60≤x<80所占百分比为180/360 ×100%=50%.
∵∠AOE=36°,
∴80≤x≤100所占百分比为36/360 ×100%=10%,
∴0≤x<20所占百分比为1-50%-25%-10%-10%=5%.
∴本次测验的平均分是
10×5%+30×10%+50×25%+70×50%+90×10%=60(分)
课堂检测
能力提升题
20.1 数据的集中趋势/
(2)已知本次测验及格人数比不及格人数(低于60分为不及格)多240人,求参加本次测验的人数.
解:设参加本次测验的有x人,根据题意得
(50%+10%)x-(5%+10%+25%)x=240,
解得x=1200.
即参加本次测验的有1200人.
课堂检测
能力提升题
20.1 数据的集中趋势/
为了了解某校1800名学生的身高情况,随机抽取该校男生和女生进行抽样调查.利用所得数据绘制如下统计图表:
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况
扇形统计图
拓广探索题
课堂检测
20.1 数据的集中趋势/
(1)根据图表提供的信息,样本中男生的平均身高约是多少?
课堂检测
拓广探索题
身高情况分组表(单位:cm)
男生身高情况直方图
女生身高情况
扇形统计图
解:
20.1 数据的集中趋势/
(2)已知抽取的样本中,女生和男生的人数相同,样本中女生的平均身高约是多少?
男生身高情况直方图
女生身高情况
扇形统计图
课堂检测
拓广探索题
身高情况分组表(单位:cm)
解:
20.1 数据的集中趋势/
用样本平均数估计总体平均数
组中值是指两个端点的数的平均数.
把各组的频数看作相应组中值的权.
用计算器求平均数
用样本平均数估计总体平均数
课堂小结
20.1 数据的集中趋势/
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
