北京市和平街第一中学2023-2024学年高二下学期期中调研数学试卷(PDF版无答案)
文档属性
| 名称 | 北京市和平街第一中学2023-2024学年高二下学期期中调研数学试卷(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 448.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-17 07:04:44 | ||
图片预览


文档简介
和平街一中 2023—2024学年度第二学期高二年级
数学期中调研试卷
班级_________ 姓名_________ 学号_________
第 I 卷(选择题)
一、选择题(本大题共 10小题,每小题 5分,共 50分)
1.函数 y = x + cosx的导数为( )
A. y =1+ sinx B. y =1 sinx C. y = x + sinx D. y = x sinx
2.已知随机变量 X 的分布列为:
X 1 0 1
1 1
P a
2 6
则 X 的数学期望E (X )的值是( )
1 1 2 2
A. B. C. D.
6 3 3 3
3. 从 1,2,3,4,5 中不放回地抽取 2 个数,则在第 1 次抽到奇数的条件下,第 2 次
又抽到奇数的概率是( )
2 3 1 3
A. B. C. D.
5 4 2 5
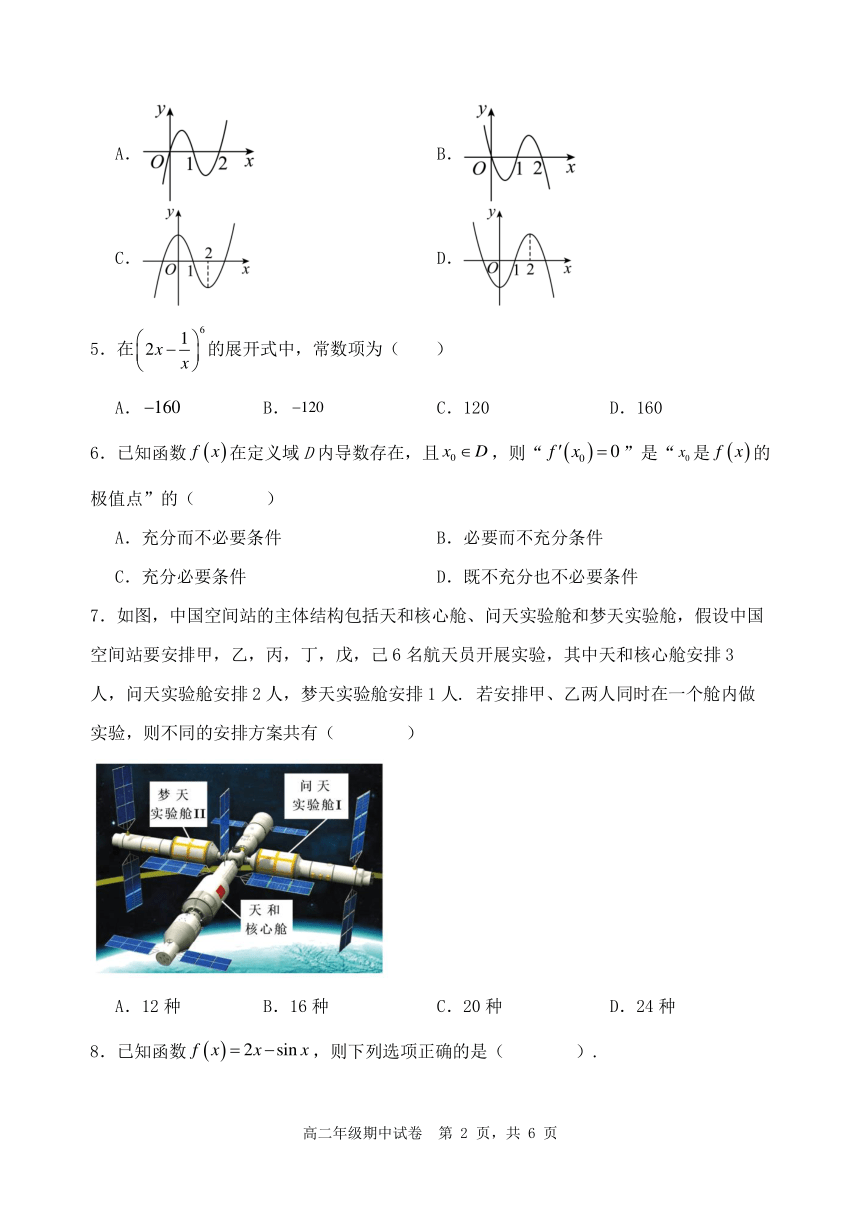
4. f ( x)是函数 f (x)的导函数, y = f (x)的图象如图所示,则 y = f (x)的图象最有可
能是下列选项中的( )
高二年级期中试卷 第 1 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
A. B.
C. D.
6
1
5.在 2x 的展开式中,常数项为( )
x
A. 160 B. 120 C.120 D.160
6.已知函数 f (x)在定义域 D 内导数存在,且 x0 D,则“ f (x0 ) = 0”是“ x0 是 f (x)的
极值点”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.如图,中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱,假设中国
空间站要安排甲,乙,丙,丁,戊,己 6 名航天员开展实验,其中天和核心舱安排 3
人,问天实验舱安排 2 人,梦天实验舱安排 1 人. 若安排甲、乙两人同时在一个舱内做
实验,则不同的安排方案共有( )
A.12 种 B.16 种 C.20 种 D.24 种
8.已知函数 f (x) = 2x sin x,则下列选项正确的是( ).
高二年级期中试卷 第 2 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
A. f (2) f (π) f (e) B. f (π) f (e) f (2)
C. f (e) f (2) f (π) D. f (2) f (e) f (π)
9.放射性元素的特征是不断发生同位素衰变,而衰变的结果是放射性同位素母体的数目
不断减少,但其子体的原子数目将不断增加,假设在某放射性同位素的衰变对程中,其
t
含量 N(单位:贝克)与时间 t(单位:天)满足函数关系N (t ) = N e 24 (e 为自然对数0
的底数),其中N0 为 t = 0时该同位素的含量,已知当 t = 48时,该放射性同位素含量的瞬
时变化率为 1,则N (48) =( )
A.12 贝克 B.12e贝克 C.24 贝克 D.24e贝克
10.已知函数 f (x) = ex e x ,下列命题正确的是( )
① f (x)是奇函数;
② f (x)在 R上是增函数;
③方程 f (x) = x2 + 2x有且仅有 1 个实数根;
④如果对任意 x (0,+ ),都有 f (x) kx,那么 k 的最大值为 2.
A.①②③ B.①②④ C.②③④ D.①②③④
第 II 卷(非选择题)
二、填空题(本大题共 6 小题,每小题 5分,共 30 分)
11.设函数 f (x) = sin x,则 f = .
4
12.把 5 件不同产品摆成一排,若产品 A 与产品 B不相邻,则不同的摆法有 种.
5
13. (1+ x) 的展开式中 x2 的系数是 ,二项式系数的和是 .
14.已知函数 f (x) = lnx ax在区间 1,3 上单调递减,则实数a 的取值范围为 .
15.已知偶函数 f (x)在区间 ( ,0 上单调递减,且 f ( 2) = 0,则不等式(x 1) f (x) 0
的解集为 .
高二年级期中试卷 第 3 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
16.某制造商制造并出售球形瓶装的某种饮料.每个瓶子的造价 P1(单位:元)、瓶内饮
料的获利 P2(单位:元)分别与瓶子的半径 r(单位:cm, r 5)之间的关系如图甲、
乙所示.设制造商的利润为 f (r) = P2 P1 ,给出下列四个结论:
①当 r (0,r1)时, f (r) 0;
② f (r)在区间 (r1,5)上单调递减;
③ f (r)在区间 (0,r1) 上存在极小值;
④ f (r)在区间 (0,r1) 上存在极小值.
其中所有正确结论的序号是 .
三、解答题(本大题共 5小题,共 70分。解答应写出文字说明,演算步骤或证
明过程。)
3 2
17.已知函数 f (x) = x + 2x 4x+1.
(1)求 f (x)的单调区间;
(2)求 f (x)在 3,1 上的最值.
高二年级期中试卷 第 4 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
18.已知箱中装有 2个白球,1个红球和 3个黑球,现从该箱中任取(无放回,且每球取
到的机会均等)3个球,
(1)求取出的三个球的颜色互不相同的概率;
(2)记随机变量 X为取出 3球中白球的个数,求 X的分布列及期望.
19.第24届冬季奥林匹克运动会于2022年2 月 4 日在北京、张家口盛大开幕.为保障本
届冬奥会顺利运行,共招募约 2.7万人参与赛会志愿服务.赛会共设对外联络服务、竞赛
运行服务、媒体运行与转播服务、场馆运行服务、市场开发服务、人力资源服务、技术
运行服务、文化展示服务、赛会综合服务、安保服务、交通服务、其他共12类志愿服
务.
(1)甲、乙两名志愿者被随机分配到不同类志愿服务中,每人只参加一类志愿服务.已知
甲被分配到对外联络服务,求乙被分配到场馆运行服务的概率是多少?
1
(2)已知来自某中学的每名志愿者被分配到文化展示服务类的概率是 ,设来自该中学的
10
2 名志愿者被分配到文化展示服务类的人数为 ,求 的分布列与期望;
(3) 2.7万名志愿者中,18 35岁人群占比达到95%,为了解志愿者对某一活动方案是否支
持,通过分层抽样获得如下数据:
18 35岁人群 其它人群
支持 不支持 支持 不支持
方案 90人 5人 1人 4 人
假设所有志愿者对活动方案是否支持相互独立.将志愿者支持方案的概率估计值记为
p0 ,去掉其它人群志愿者,支持方案的概率估计值记为 p1,试比较 p0 与 p1的大小.(结
论不要求证明)
高二年级期中试卷 第 5 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
20.已知 f (x) = x aex , a R.
(1)求曲线 y = f (x) 在点 (0, f (0))处的切线;
(2)若函数 f (x)在区间 (1,+ )上存在极值,求a 的取值范围;
1
(3)若a 0, ,设 g(x) = f (2 x),试判断函数 g(x)在区间 (1,+ )上的单调性,并说明
e
理由.
21.设函数 f (x) = x2 +m ln (x+1)(m R).
(1)若m = 1,
①求曲线 f (x)在点 (0, f (0))处的切线方程;
②当 x (1,+ )时,求证: f (x) x3 .
(2)若函数 f (x)在区间 (0,1)上存在唯一零点,求实数m 的取值范围.
高二年级期中试卷 第 6 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
数学期中调研试卷
班级_________ 姓名_________ 学号_________
第 I 卷(选择题)
一、选择题(本大题共 10小题,每小题 5分,共 50分)
1.函数 y = x + cosx的导数为( )
A. y =1+ sinx B. y =1 sinx C. y = x + sinx D. y = x sinx
2.已知随机变量 X 的分布列为:
X 1 0 1
1 1
P a
2 6
则 X 的数学期望E (X )的值是( )
1 1 2 2
A. B. C. D.
6 3 3 3
3. 从 1,2,3,4,5 中不放回地抽取 2 个数,则在第 1 次抽到奇数的条件下,第 2 次
又抽到奇数的概率是( )
2 3 1 3
A. B. C. D.
5 4 2 5
4. f ( x)是函数 f (x)的导函数, y = f (x)的图象如图所示,则 y = f (x)的图象最有可
能是下列选项中的( )
高二年级期中试卷 第 1 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
A. B.
C. D.
6
1
5.在 2x 的展开式中,常数项为( )
x
A. 160 B. 120 C.120 D.160
6.已知函数 f (x)在定义域 D 内导数存在,且 x0 D,则“ f (x0 ) = 0”是“ x0 是 f (x)的
极值点”的( )
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分也不必要条件
7.如图,中国空间站的主体结构包括天和核心舱、问天实验舱和梦天实验舱,假设中国
空间站要安排甲,乙,丙,丁,戊,己 6 名航天员开展实验,其中天和核心舱安排 3
人,问天实验舱安排 2 人,梦天实验舱安排 1 人. 若安排甲、乙两人同时在一个舱内做
实验,则不同的安排方案共有( )
A.12 种 B.16 种 C.20 种 D.24 种
8.已知函数 f (x) = 2x sin x,则下列选项正确的是( ).
高二年级期中试卷 第 2 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
A. f (2) f (π) f (e) B. f (π) f (e) f (2)
C. f (e) f (2) f (π) D. f (2) f (e) f (π)
9.放射性元素的特征是不断发生同位素衰变,而衰变的结果是放射性同位素母体的数目
不断减少,但其子体的原子数目将不断增加,假设在某放射性同位素的衰变对程中,其
t
含量 N(单位:贝克)与时间 t(单位:天)满足函数关系N (t ) = N e 24 (e 为自然对数0
的底数),其中N0 为 t = 0时该同位素的含量,已知当 t = 48时,该放射性同位素含量的瞬
时变化率为 1,则N (48) =( )
A.12 贝克 B.12e贝克 C.24 贝克 D.24e贝克
10.已知函数 f (x) = ex e x ,下列命题正确的是( )
① f (x)是奇函数;
② f (x)在 R上是增函数;
③方程 f (x) = x2 + 2x有且仅有 1 个实数根;
④如果对任意 x (0,+ ),都有 f (x) kx,那么 k 的最大值为 2.
A.①②③ B.①②④ C.②③④ D.①②③④
第 II 卷(非选择题)
二、填空题(本大题共 6 小题,每小题 5分,共 30 分)
11.设函数 f (x) = sin x,则 f = .
4
12.把 5 件不同产品摆成一排,若产品 A 与产品 B不相邻,则不同的摆法有 种.
5
13. (1+ x) 的展开式中 x2 的系数是 ,二项式系数的和是 .
14.已知函数 f (x) = lnx ax在区间 1,3 上单调递减,则实数a 的取值范围为 .
15.已知偶函数 f (x)在区间 ( ,0 上单调递减,且 f ( 2) = 0,则不等式(x 1) f (x) 0
的解集为 .
高二年级期中试卷 第 3 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
16.某制造商制造并出售球形瓶装的某种饮料.每个瓶子的造价 P1(单位:元)、瓶内饮
料的获利 P2(单位:元)分别与瓶子的半径 r(单位:cm, r 5)之间的关系如图甲、
乙所示.设制造商的利润为 f (r) = P2 P1 ,给出下列四个结论:
①当 r (0,r1)时, f (r) 0;
② f (r)在区间 (r1,5)上单调递减;
③ f (r)在区间 (0,r1) 上存在极小值;
④ f (r)在区间 (0,r1) 上存在极小值.
其中所有正确结论的序号是 .
三、解答题(本大题共 5小题,共 70分。解答应写出文字说明,演算步骤或证
明过程。)
3 2
17.已知函数 f (x) = x + 2x 4x+1.
(1)求 f (x)的单调区间;
(2)求 f (x)在 3,1 上的最值.
高二年级期中试卷 第 4 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
18.已知箱中装有 2个白球,1个红球和 3个黑球,现从该箱中任取(无放回,且每球取
到的机会均等)3个球,
(1)求取出的三个球的颜色互不相同的概率;
(2)记随机变量 X为取出 3球中白球的个数,求 X的分布列及期望.
19.第24届冬季奥林匹克运动会于2022年2 月 4 日在北京、张家口盛大开幕.为保障本
届冬奥会顺利运行,共招募约 2.7万人参与赛会志愿服务.赛会共设对外联络服务、竞赛
运行服务、媒体运行与转播服务、场馆运行服务、市场开发服务、人力资源服务、技术
运行服务、文化展示服务、赛会综合服务、安保服务、交通服务、其他共12类志愿服
务.
(1)甲、乙两名志愿者被随机分配到不同类志愿服务中,每人只参加一类志愿服务.已知
甲被分配到对外联络服务,求乙被分配到场馆运行服务的概率是多少?
1
(2)已知来自某中学的每名志愿者被分配到文化展示服务类的概率是 ,设来自该中学的
10
2 名志愿者被分配到文化展示服务类的人数为 ,求 的分布列与期望;
(3) 2.7万名志愿者中,18 35岁人群占比达到95%,为了解志愿者对某一活动方案是否支
持,通过分层抽样获得如下数据:
18 35岁人群 其它人群
支持 不支持 支持 不支持
方案 90人 5人 1人 4 人
假设所有志愿者对活动方案是否支持相互独立.将志愿者支持方案的概率估计值记为
p0 ,去掉其它人群志愿者,支持方案的概率估计值记为 p1,试比较 p0 与 p1的大小.(结
论不要求证明)
高二年级期中试卷 第 5 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
20.已知 f (x) = x aex , a R.
(1)求曲线 y = f (x) 在点 (0, f (0))处的切线;
(2)若函数 f (x)在区间 (1,+ )上存在极值,求a 的取值范围;
1
(3)若a 0, ,设 g(x) = f (2 x),试判断函数 g(x)在区间 (1,+ )上的单调性,并说明
e
理由.
21.设函数 f (x) = x2 +m ln (x+1)(m R).
(1)若m = 1,
①求曲线 f (x)在点 (0, f (0))处的切线方程;
②当 x (1,+ )时,求证: f (x) x3 .
(2)若函数 f (x)在区间 (0,1)上存在唯一零点,求实数m 的取值范围.
高二年级期中试卷 第 6 页,共 6 页
{#{QQABDYoEggigQIBAARgCUwEwCAMQkBACCAoORBAEIAIACAFABAA=}#}
同课章节目录
