2024年黑龙江省齐齐哈尔地区中考数学预测卷(四)(含解析)
文档属性
| 名称 | 2024年黑龙江省齐齐哈尔地区中考数学预测卷(四)(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-16 23:21:51 | ||
图片预览


文档简介
2024年齐齐哈尔地区中考数学预测卷(四)
学校:___________姓名:___________班级:___________考号:___________
考生注意:
考试时间120分钟
全卷共三道大题,总分120分
题号 一 二 三 总分 核分人
得分
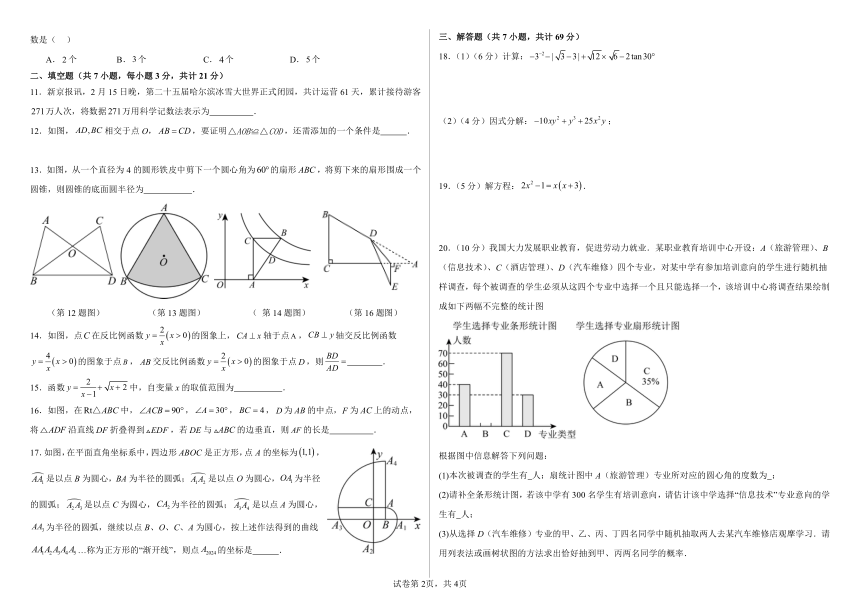
一、单选题(共10小题,每小题3分,共计30分)
1.5的相反数的绝对值是( )
A.﹣5 B.5 C. D.
2.下列2024年巴黎奥运会和残奥会运动项目的图标中,不是中心对称图形的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.下列说法正确的是( )
A.调查中央电视台开学第一课的收视率,应采用全面调查的方式
B.数据,,,,的中位数是
C.一个抽奖活动中,中奖概率为,表示抽奖次就有次中奖
D.甲、乙两名射击运动员次射击成绩单位:环的平均数相等,方差分别为,,则甲的成绩比乙的稳定
5.如图,在中,,,以点为圆心,任意长为半径画弧,分别交、于点和,再分别以、为圆心,大于的长为半径画弧,两弧交于点,连接交于点.若,则的长为( )
A. B. C. D.
6.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要( )个小立方块.
A.36 B.52 C.54 D.55
(第5题图) (第6题图)
7.小李去买套装色水笔和笔记本,若购买袋笔和本笔记本,他身上的钱还差元,若改 成购买袋笔和本笔记本,他身上的钱会剩下元.若他把身上的钱都花掉,购买这两种 物品(两种都买)的方案有( )
A.种 B.种 C.种 D.种
8.如图1,在中,点为的中点,动点从点出发,沿着的路径以每秒1个单位长度的速度运动到点,在此过程中线段的长度随着运动时间的函数关系如图2所示,则的长为( )
A. B. C. D.
(第8题图) (第10题图)
9.若是整数,且关于的方程有整数根,则的值是( )
A.3或5 B.或5 C.或3 D.或
10.如图,拋物线与轴交于点,顶点坐标为,与轴的交点在和两点之间(不包含端点).则下列结论中:①;②;③;④一元二次方程的两个根分别为,;⑤(其中).正确的个数是( )
A.个 B.个 C.个 D.个
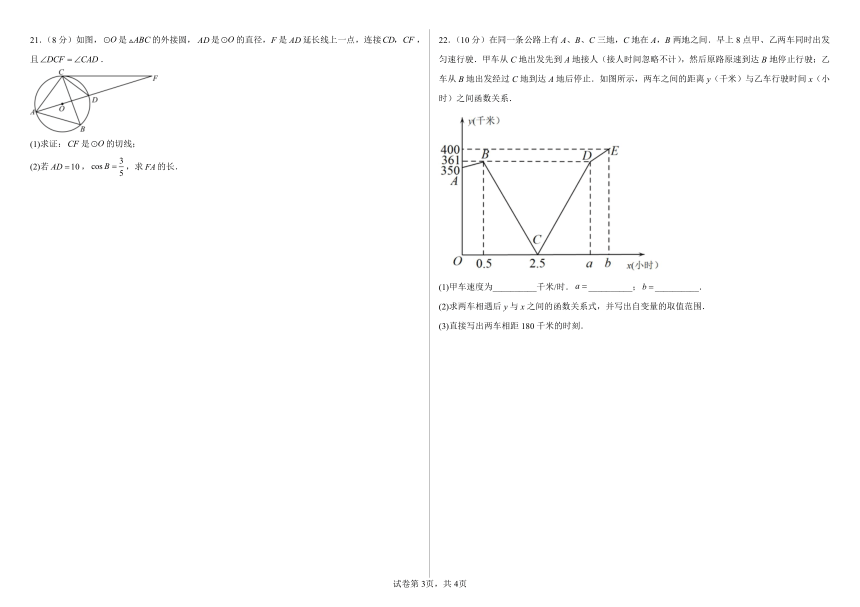
二、填空题(共7小题,每小题3分,共计21分)
11.新京报讯,2月15日晚,第二十五届哈尔滨冰雪大世界正式闭园,共计运营61天,累计接待游客万人次,将数据万用科学记数法表示为 .
12.如图,相交于点O,,要证明,还需添加的一个条件是 .
13.如图,从一个直径为4的圆形铁皮中剪下一个圆心角为的扇形,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为 .
(第12题图) (第13题图) ( 第14题图) (第16题图)
14.如图,点在反比例函数的图象上,轴于点,轴交反比例函数的图象于点,交反比例函数的图象于点,则 .
15.函数中,自变量x的取值范围为 .
16.如图,在中,,,,为的中点,F为上的动点,将沿直线折叠得到,若与的边垂直,则的长是 .
17.如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为,是以点B为圆心,BA为半径的圆弧;是以点O为圆心,为半径的圆弧;是以点C为圆心,为半径的圆弧;是以点A为圆心,为半径的圆弧,继续以点B、O、C、A为圆心,按上述作法得到的曲线…称为正方形的“渐开线”,则点的坐标是 .
三、解答题(共7小题,共计69分)
18.(1)(6分)计算:
(2)(4分)因式分解:;
19.(5分)解方程:.
20.(10分)我国大力发展职业教育,促进劳动力就业.某职业教育培训中心开设:A(旅游管理)、B(信息技术)、C(酒店管理)、D(汽车维修)四个专业,对某中学有参加培训意向的学生进行随机抽样调查,每个被调查的学生必须从这四个专业中选择一个且只能选择一个,该培训中心将调查结果绘制成如下两幅不完整的统计图
根据图中信息解答下列问题:
(1)本次被调查的学生有 人;扇统计图中A(旅游管理)专业所对应的圆心角的度数为 ;
(2)请补全条形统计图,若该中学有300名学生有培训意向,请估计该中学选择“信息技术”专业意向的学生有 人;
(3)从选择D(汽车维修)专业的甲、乙、丙、丁四名同学中随机抽取两人去某汽车维修店观摩学习.请用列表法或画树状图的方法求出恰好抽到甲、丙两名同学的概率.
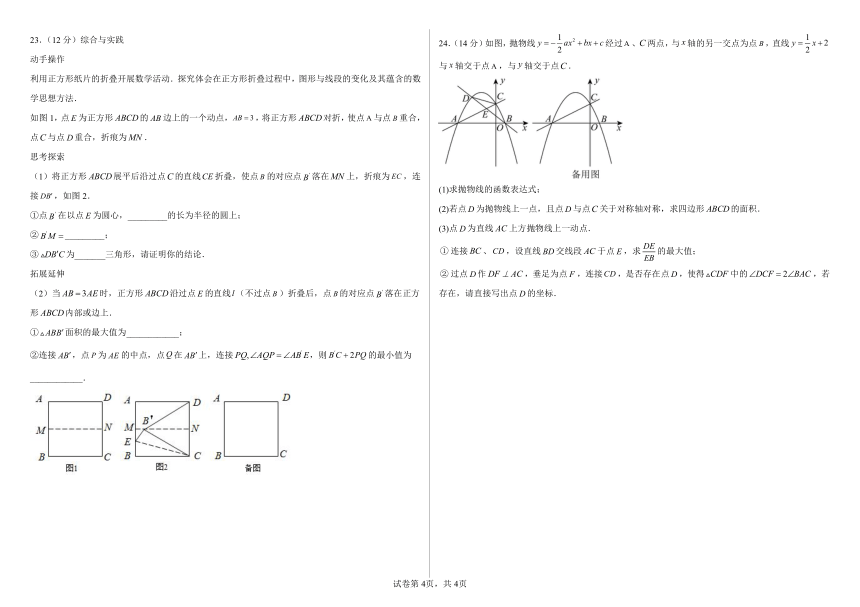
21.(8分)如图,是的外接圆,是的直径,F是延长线上一点,连接,且.
(1)求证:是的切线;
(2)若,,求的长.
22.(10分)在同一条公路上有A、B、C三地,C地在A,B两地之间.早上8点甲、乙两车同时出发匀速行驶.甲车从C地出发先到A地接人(接人时间忽略不计),然后原路原速到达B地停止行驶;乙车从B地出发经过C地到达A地后停止.如图所示,两车之间的距离y(千米)与乙车行驶时间x(小时)之间函数关系.
(1)甲车速度为__________千米/时.__________;__________.
(2)求两车相遇后y与x之间的函数关系式,并写出自变量的取值范围.
(3)直接写出两车相距180千米的时刻.
23.(12分)综合与实践
动手操作
利用正方形纸片的折叠开展数学活动.探究体会在正方形折叠过程中,图形与线段的变化及其蕴含的数学思想方法.
如图1,点为正方形的边上的一个动点,,将正方形对折,使点与点重合,点与点重合,折痕为.
思考探索
(1)将正方形展平后沿过点的直线折叠,使点的对应点落在上,折痕为,连接,如图2.
①点在以点为圆心,_________的长为半径的圆上;
②_________;
③为_______三角形,请证明你的结论.
拓展延伸
(2)当时,正方形沿过点的直线(不过点)折叠后,点的对应点落在正方形内部或边上.
①面积的最大值为____________;
②连接,点为的中点,点在上,连接,则的最小值为____________.
24.(14分)如图,抛物线经过、两点,与轴的另一交点为点,直线与轴交于点,与轴交于点.
(1)求抛物线的函数表达式;
(2)若点为抛物线上一点,且点与点关于对称轴对称,求四边形的面积.
(3)点为直线上方抛物线上一动点.
连接、,设直线交线段于点,求的最大值;
过点作,垂足为点,连接,是否存在点,使得中的,若存在,请直接写出点的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据相反数与绝对值的性质,列出代数式进行化简即可.
【详解】解:5的相反数为:﹣5,
而﹣5的绝对值为:|﹣5|=5,
即5的相反数的绝对值是5,
故选B.
【点睛】本题主要考查了绝对值与相反数的表示,正确用式子表示出:“+5的相反数的绝对值”,是解题关键.
2.D
【分析】本题考查了中心对称图形的识别.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.据此逐一判断即可得到答案.
【详解】解:A、B、C选项中的图形都能找到这样的一个点,使图形绕这个点旋转后与原来的图形重合,所以是中心对称图形;
D选项中的图形不能找到这样的一个点,使图形绕这个点旋转后与原来的图形重合,所以不是中心对称图形.
故选:D.
3.B
【分析】本题考查了整式的混合运算,完全平方公式,准确熟练地进行计算是解题的关键.
利用完全平方公式,同底数 的乘法,幂的乘方与积的乘方法则进行计算,即可解答.
【详解】解:A、,故A不符合题意;
B、,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意;
故选:B.
4.D
【分析】本题考查了概率公式、调查方式的选择、中位数的定义、概率的意义及方差的意义等知识,解题的关键是了解统计的有关知识,难度不大.利用调查方式的选择、中位数的定义、概率的意义及方差的意义分别判断后即可确定正确的选项.
【详解】解:A.调查中央电视台开学第一课的收视率,应采用抽样调查的方式,故错误,不符合题意;
B.数据,,,,的中位数是,故错误,不符合题意;
C.一个抽奖活动中,中奖概率为,抽奖次可能有次中奖,也可能不中奖,故错误,不符合题意;
D.甲、乙两名射击运动员次射击成绩单位:环的平均数相等,方差分别为,,则甲的成绩比乙的稳定,正确,符合题意.
故选:D.
5.C
【分析】本题考查了尺规作图—作角的平分线,含角的直角三角形的性质,等腰直角三角形的判定与性质等知识,正确作出辅助线是解答本题的关键.过点作于点,由作法知平分,从而可得,得到,再证明是等腰直角三角形,根据勾股定理即可求出的长.
【详解】解:如图,过点作于点,
由作法知平分,
,
,
,
,,
是等腰直角三角形,
,
.
故选:C.
6.C
【分析】本题考查了三视图,熟练掌握三视图是解题的关键.根据三视图判断小立方块的数量,再求出搭成一个大正方体需要的最少数量,即可得到答案.
【详解】解:由三视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1个小立方体,那么共有个几何体组成.
若要搭成一个大正方体,共需个小立方体,
所以还需个小立方体,
故选:C.
7.C
【分析】设1袋笔的价格为x元,1本笔记本的价格为y元,根据“若购买4袋笔和6本笔记本,他身上的钱还差22元,若改成购买1袋笔和2本笔记本,他身上的钱会剩下34元”,即可得出关于x,y的二元一次方程,结合x,y均为正整数即可得出结论,再设可购买a袋笔和b本笔记本,根据总价=单价×数量可得出关于a,b的二元一次方程,结合a,b均为正整数即可得出结论.
【详解】设1袋笔的价格为x元,1本笔记本的价格为y元,
依题意,得:4x+6y-22=x+2y+34,
∴3x+4y=56,即y=14-x.
∵x,y均为正整数,
∴,,,.
设可购买a袋笔和b本笔记本.
①当x=4,y=11时,4x+6y-22=60,
∴4a+11b=60,即a=15-b,
∵a,b均为正整数,
∴;
②当x=8,y=8时,4x+6y-22=58,
∴8a+8b=58,即a+b=,
∵a,b均为正整数,
∴方程无解;
③当x=12,y=5时,4x+6y-22=56,
∴12a+5b=56,即b=,
∵a,b均为正整数,
∴;
④当x=16,y=2时,4x+6y-22=54,
∴16a+2b=54,即b=27-8a,
∵a,b均为正整数,
∴,,.
综上所述,共有5种购进方案.
故选:C.
【点睛】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
8.C
【分析】本题考查了动点问题的函数图象、解直角三角形、勾股定理,当时,点在点处,此时,则,当时,,求出,由勾股定理得出,求出,再由计算即可得解.
【详解】解:当时,点在点处,此时,则,
当时,,
,
则,
,
,
,
故选:C.
9.A
【分析】本题主要考查解分式方程,解分式方程,用含m的代数式表示x,根据整数的意义可得m的值.解题的关键是将分式方程转化为整式方程,求出方程的解.
【详解】解:
去分母得:
化简得:
当时,
方程有整数根,的值是整数,
当时,,方程的根;
当时,,方程的根(增根,舍去);
当时,,方程的根;
当时,,方程的根(增根,舍去).
故选:A.
10.C
【分析】根据题干和图像可得,该抛物线的对称轴是,即;点的对称点坐标是;.
将代入该抛物线解析式可判断结论①;
根据和将代入抛物线解析式得到的,联立可求得 、的数量关系,根据可求的范围,以此判断结论②;
将顶点代入抛物线解析式得到,等量替换后得到与的关系再判断范围,以此判断结论③;
综合和、和的数量关系式,解一元二次方程即可判断结论④;
结合二次函数图象中可得,二次函数最小值为,则当时,有,结合、与数量关系式即可判断结论⑤.
【详解】解:依题得:该抛物线的对称轴是,即;
点的对称点坐标是;.
时,有,即,
①错误;
,
,
又将代入抛物线解析式中得,
,即,
又,
,
,
②正确;
将顶点坐标代入抛物线解析式中得,
即,
,
又,
,则,
③正确;
一元二次方程即,
即,
可解得,,
④一元二次方程的两个根分别为,正确;
时,在该抛物线中有,
,
,
,
⑤(其中)正确;
综上,②③④⑤正确,故正确的个数为个.
故选:.
【点睛】本题考查的知识点是二次函数的图象与性质、根据二次函数的图象判断式子符号、解一元二次方程、不等式,解题关键是熟练掌握二次函数的图形与性质,运用数形结合思想分析问题.
11.
【分析】本题考查用科学记数法表示绝对值大于1的数.科学记数法的表示形式为的形式,其中为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正数;当原数的绝对值时,n是负数.熟记相关结论即可.
【详解】解:∵万
故答案为:
12.(答案不唯一)
【分析】本题主要考查了三角形全等的判定方法,添加结合根据即可证明.
【详解】∵
添加结合根据即可证明,
故答案为:(答案不唯一).
13.
【分析】考查圆锥的计算;用的知识点为:圆锥的侧面展开图弧长等于圆锥的底面周长;难点是得到扇形的半径.
圆的半径为2,那么过圆心向引垂线,利用相应的三角函数可得的一半的长度,进而求得的长度,利用弧长公式可求得弧的长度,圆锥的底面圆的半径圆锥的弧长.
【详解】解:作于点,连接,
,,
,
,
圆锥的底面圆的半径.
故答案为:
14.
【分析】本题主要考查了反比例函数的几何应用.相似三角形的判定和性质.过点D作于点E,则,设点C的坐标为,则,可得点A的坐标为,点B的坐标为,再求出直线的解析式,联立可得点D的横坐标为,从而得到,再由,即可求解.
【详解】解:如图,过点D作于点E,则,
设点C的坐标为,则,
∵轴,轴交反比例函数的图象于点,
∴点A的坐标为,点B的坐标为,
∴,
设直线的解析式为,
把点,代入得:
,解得:,
∴直线的解析式为,
联立得:,
整理得:,
解得:,
∴点D的横坐标为,
∴,
∵,
∴,
∴,
∴
∴.
故答案为:
15.且
【分析】本题考查的是函数自变量的取值范围,①当表达式的分母不含有自变量时,自变量取全体实数.②当表达式的分母中含有自变量时,自变量取值要使分母不为零.③当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.
根据分式有意义的条件、二次根式有意义的条件列式计算.
【详解】解:由题意得,,
解得,且,
故答案为:且.
16.4或或
【分析】由直角三角形的性质和勾股定理可得,,,分三种情况:当时,设垂足为;当时,作交于;当时,分别进行计算即可得到答案.
【详解】解:在中,,,
,
,
是的中点,
,
如图1,当时,设垂足为,
,
由折叠可知,,,,
,
,
,
,
,
,,
,
;
如图2,当时,
,
则,
由折叠可知:,
,
,
,
,
,
在中,,,
,
,,
作交于,则,
,
是等腰直角三角形,
,
设,则,
,
,
,即,
解得:,
,
在中,,,
;
如图3,当时,
,
由折叠的性质可得:,,,
,
,
,
,,
,
,
,
综上所述:的长为4或或,
故答案为:4或或.
【点睛】本题主要考查了折叠的性质、相似三角形的判定与性质、直角三角形的性质、勾股定理、等腰三角形的判定与性质等知识,熟练掌握以上知识点,添加适当的辅助线,采用分类讨论的思想解题,是解此题的关键.
17.
【分析】本题考查了规律型中的点的坐标,解题的关键是罗列出部分点的坐标找出坐标规律.本题属于基础题,难度不大,解决该题型题目时,结合画弧的方法以及部分点的坐标寻找出来点的排布规律是关键.根据画弧的方法以及罗列部分点的坐标发现:点Ax的坐标满足“(n为正整数),(n为自然数),(n为自然数),(n为自然数)”,根据这一规律即可得出点的坐标.
【详解】解:观察,找规律∶,,,,,,,,,,,,,,,…,
∴(n为正整数),(n为自然数),(n为自然数),(n为自然数).
∵,
∴的坐标为.
故答案为:.
18.(1);(2)
【详解】(1)解:原式
.
(2)解:
;
19.,.
【分析】本题考查解一元二次方程,熟练掌握一元二次方程的解法是解题的关键,先将所给的一元二次方程整理后,分别找到二次项系数、一次项系数、常数项,利用一元二次方程的求根公式计算即可.
【详解】解:方程整理得:,
则,,,
∵,
∴,
解得:,.
20.(1)200;
(2)见解析;90
(3)
【分析】本题考查的是条形统计图与扇形统计图、用树状图法求概率.
(1)由选择C专业的人数除以所占百分比即可求出总数,由乘以选择A(旅游管理)专业的人数所占的比例即可得出扇形统计图中A(旅游管理)专业所对应的圆心角的度数;
(2)求出B专业的人数,补全条形统计图即可,根据该中学选择“信息技术”专业意向的学生所占比例估计实际人数;
(3)画树状图,共有12种等可能的结果,其中恰好抽到甲、乙两名同学的结果有2种,再由概率公式求解即可.
【详解】(1)本次被调查的学生有:(人),
故答案为:100;
(2)扇形统计图中,A(旅游管理)专业所对应的圆心角的度数为:,
故答案为:200;;
(2)条形统计图中,B(信息技术)专业的人数为:(人),
补全条形统计图如下:
若该中学有300名学生有培训意向,估计该中学选择“信息技术”专业意向的学生有(人),
故答案为:90;
(3)画树状图如下:
共有12种等可能的结果,其中恰好抽到甲、乙两名同学的结果有2种,
∴恰好抽到甲、乙两名同学的概率为.
21.(1)见详解
(2)
【分析】本题考查切线的判定和性质,圆周角定理,直角三角形的边角关系以及相似三角形,掌握切线的判定方法,直角三角形的边角关系以及相似三角形的性质是正确解答的前提.
(1)根据切线的判定,连接,证明出即可,利用直径所得的圆周角为直角,三角形的内角和以及等腰三角形的性质可得答案;
(2)由,根据锐角三角函数的意义和勾股定理可得,再根据相似三角形的性质可求出答案.
【详解】(1)证明:连接,
∵是的直径,
∴,
∴,
又∵,
∴,
又∵.
∴,
即,
∴是的切线;
(2)解:∵,
∴,
在中,
,
,
,
,
,
,
,
设,则,
又,
即,
解得(取正值),
.
22.(1)100;4.5;5
(2)
(3)两车相距180千米的时刻为1.5小时和3.5小时
【分析】(1)根据图形,可知设甲车速度为m千米/时, 乙车速度为n千米/时,可列出方程:m-n=20,m+n=180,可求得m、n,由此即可求出a、b;
(2)利用待定系数法进行求解析式即可,注意取值范围;
(3)分两种情况进行讨论,两车相距180千米时,出现在BC、CD两段,根据题意对两种情况进行分析求解.
【详解】(1)解:设甲车速度为m千米/时, 乙车速度为n千米/时,
由AB段可知:m>n,
则:,
即:m-n=20①,
由BC段可知:,
即:m+n=180②,
联立①、②得:m=100,n=80,
∴甲车速度为100千米/时, 乙车速度为80千米/时,
有CD段可知:,
解得:a=4.5,
由DE可知,此时甲车已到达B地,此段为乙车单独行驶,即:,
解得:b=5,
故答案为:100;4.5;5;
(2)由图可知,两车相遇时,为图中C点,相遇之后分为CD、DE两段,
设CD段函数表达式为:,DE段函数表达式为:,
将(2.5,0),(4.5,360)代入得:
,
解得:,
∴CD段函数表达式为:,
将(4.5,360)、(5,400)代入得:
,
解得:,
∴DE段函数表达式为:,
∴两车相遇后y与x之间的函数关系式为:;
(3)由图可知,两车相距180千米时,出现在BC、CD两段,
在BC段时,两车相距180千米时刻为:2.5-=1.5(小时),
在CD段时,两车相距180千米时刻为:2.5+=3.5(小时),
∴两车相距180千米的时刻为1.5小时和3.5小时.
【点睛】本题主要考查了一次函数的实际应用,解题的关键是理解图象中每段所代表的意义,并结合函数进行解题.
23.(1)①;②;③等边,证明见解析;(2)①3;②.
【分析】(1)①利用圆的基本性质,即可求解;
②根据折叠的性质,利用勾股定理,即可求解;
③利用勾股定理,求得B′D=,即可求解;
(2)①由题意知点B'在以点E为圆心,半径长为2的圆上,△ABB'的面积要最大,只要以AB为底的高最长即可,此时当B'E⊥AB时,△ABB'的面积最大;
②当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,且最小值为EC的长,利用勾股定理即可求解.
【详解】解:(1)根据折叠的性质知:BE=B′E,BC=B′C=3,MA=MB=NC=ND=,
∠B=∠EB′C=90,
①点B′在以点E为圆心,BE的长为半径的圆上;
②B′M=MN- B′N=
=
=;
③B′D=,
∴△DB'C为等边三角形;
故答案为:①BE,②,③等边;
(2)①∵AB=3=3AE,
∴AE=1,BE=2,
故点B'在以点E为圆心,半径长为2的圆上,
∴△ABB'的面积要最大,只要以AB为底的高最长即可,
∴当B'E⊥AB时,△ABB'的面积最大,如图:
△ABB'的面积最大值;
②∵∠AQP=∠AB'E,
∴PQ∥B'E,
∵P为AE的中点,
∴Q为AB'的中点,
∴PQ为△AEB'的中位线,
∴PQ=EB',即EB'=2PQ,
∴B'C+2PQ= B'C+ EB',
当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,
且最小值为EC的长,
∴EC=,
∴B'C+2PQ的最小值为.
故答案为:①;②.
【点睛】本题考查了圆的性质,矩形的性质、图形的折叠、等腰三角形的性质等,有一定的综合性,难度适中,其中(2)①当B'E⊥AB时,△ABB'的面积最大;②当E、B′、C三点共线时,B'C+2PQ取得最小值,是解本题的关键.
24.(1)
(2)
(3)①;②存在,
【分析】(1)用待定系数法即可求解;
(2)证明四边形为梯形,则四边形的面积,即可求解;
(3)①证明,则,即可求解;
证明,则,即,进而求解.
【详解】(1)解:在中,令得,令得,
,,
经过、两点,
,
解得:,
抛物线的函数表达式为;
(2)解:在中,令,得,
解得,,
,
点与点关于对称轴对称,点,抛物线的对称轴为,
点,
则,,
,则四边形为梯形,
则四边形的面积;
(3)解:①过作轴交于点,过作轴交于于,如图:
在中,令得,
,,
设,则,
,
轴,轴,
,
,
,
,
,
,
当时,取最大值,最大值为;
存在点,使得中的,理由如下:
过作轴,交轴于,交直线于,如图:
轴,
,
,
,
,
,
,
,即,
设,
,
,,
,,
,
,
解得,
.
【点睛】本题考查二次函数综合应用,涉及待定系数法,相似三角形的判定与性质,锐角三角函数的应用等知识,解题的关键是用含字母的代数式表示相关点坐标和相关线段的长度.
答案第1页,共2页
答案第1页,共2页
学校:___________姓名:___________班级:___________考号:___________
考生注意:
考试时间120分钟
全卷共三道大题,总分120分
题号 一 二 三 总分 核分人
得分
一、单选题(共10小题,每小题3分,共计30分)
1.5的相反数的绝对值是( )
A.﹣5 B.5 C. D.
2.下列2024年巴黎奥运会和残奥会运动项目的图标中,不是中心对称图形的是( )
A. B. C. D.
3.下列计算正确的是( )
A. B. C. D.
4.下列说法正确的是( )
A.调查中央电视台开学第一课的收视率,应采用全面调查的方式
B.数据,,,,的中位数是
C.一个抽奖活动中,中奖概率为,表示抽奖次就有次中奖
D.甲、乙两名射击运动员次射击成绩单位:环的平均数相等,方差分别为,,则甲的成绩比乙的稳定
5.如图,在中,,,以点为圆心,任意长为半径画弧,分别交、于点和,再分别以、为圆心,大于的长为半径画弧,两弧交于点,连接交于点.若,则的长为( )
A. B. C. D.
6.如图,是由一些小立方块所搭几何体的三种视图,若在所搭几何体的基础上(不改变原几何体中小立方块的位置),继续添加相同的小立方块,以搭成一个大正方体,至少还需要( )个小立方块.
A.36 B.52 C.54 D.55
(第5题图) (第6题图)
7.小李去买套装色水笔和笔记本,若购买袋笔和本笔记本,他身上的钱还差元,若改 成购买袋笔和本笔记本,他身上的钱会剩下元.若他把身上的钱都花掉,购买这两种 物品(两种都买)的方案有( )
A.种 B.种 C.种 D.种
8.如图1,在中,点为的中点,动点从点出发,沿着的路径以每秒1个单位长度的速度运动到点,在此过程中线段的长度随着运动时间的函数关系如图2所示,则的长为( )
A. B. C. D.
(第8题图) (第10题图)
9.若是整数,且关于的方程有整数根,则的值是( )
A.3或5 B.或5 C.或3 D.或
10.如图,拋物线与轴交于点,顶点坐标为,与轴的交点在和两点之间(不包含端点).则下列结论中:①;②;③;④一元二次方程的两个根分别为,;⑤(其中).正确的个数是( )
A.个 B.个 C.个 D.个
二、填空题(共7小题,每小题3分,共计21分)
11.新京报讯,2月15日晚,第二十五届哈尔滨冰雪大世界正式闭园,共计运营61天,累计接待游客万人次,将数据万用科学记数法表示为 .
12.如图,相交于点O,,要证明,还需添加的一个条件是 .
13.如图,从一个直径为4的圆形铁皮中剪下一个圆心角为的扇形,将剪下来的扇形围成一个圆锥,则圆锥的底面圆半径为 .
(第12题图) (第13题图) ( 第14题图) (第16题图)
14.如图,点在反比例函数的图象上,轴于点,轴交反比例函数的图象于点,交反比例函数的图象于点,则 .
15.函数中,自变量x的取值范围为 .
16.如图,在中,,,,为的中点,F为上的动点,将沿直线折叠得到,若与的边垂直,则的长是 .
17.如图,在平面直角坐标系中,四边形ABOC是正方形,点A的坐标为,是以点B为圆心,BA为半径的圆弧;是以点O为圆心,为半径的圆弧;是以点C为圆心,为半径的圆弧;是以点A为圆心,为半径的圆弧,继续以点B、O、C、A为圆心,按上述作法得到的曲线…称为正方形的“渐开线”,则点的坐标是 .
三、解答题(共7小题,共计69分)
18.(1)(6分)计算:
(2)(4分)因式分解:;
19.(5分)解方程:.
20.(10分)我国大力发展职业教育,促进劳动力就业.某职业教育培训中心开设:A(旅游管理)、B(信息技术)、C(酒店管理)、D(汽车维修)四个专业,对某中学有参加培训意向的学生进行随机抽样调查,每个被调查的学生必须从这四个专业中选择一个且只能选择一个,该培训中心将调查结果绘制成如下两幅不完整的统计图
根据图中信息解答下列问题:
(1)本次被调查的学生有 人;扇统计图中A(旅游管理)专业所对应的圆心角的度数为 ;
(2)请补全条形统计图,若该中学有300名学生有培训意向,请估计该中学选择“信息技术”专业意向的学生有 人;
(3)从选择D(汽车维修)专业的甲、乙、丙、丁四名同学中随机抽取两人去某汽车维修店观摩学习.请用列表法或画树状图的方法求出恰好抽到甲、丙两名同学的概率.
21.(8分)如图,是的外接圆,是的直径,F是延长线上一点,连接,且.
(1)求证:是的切线;
(2)若,,求的长.
22.(10分)在同一条公路上有A、B、C三地,C地在A,B两地之间.早上8点甲、乙两车同时出发匀速行驶.甲车从C地出发先到A地接人(接人时间忽略不计),然后原路原速到达B地停止行驶;乙车从B地出发经过C地到达A地后停止.如图所示,两车之间的距离y(千米)与乙车行驶时间x(小时)之间函数关系.
(1)甲车速度为__________千米/时.__________;__________.
(2)求两车相遇后y与x之间的函数关系式,并写出自变量的取值范围.
(3)直接写出两车相距180千米的时刻.
23.(12分)综合与实践
动手操作
利用正方形纸片的折叠开展数学活动.探究体会在正方形折叠过程中,图形与线段的变化及其蕴含的数学思想方法.
如图1,点为正方形的边上的一个动点,,将正方形对折,使点与点重合,点与点重合,折痕为.
思考探索
(1)将正方形展平后沿过点的直线折叠,使点的对应点落在上,折痕为,连接,如图2.
①点在以点为圆心,_________的长为半径的圆上;
②_________;
③为_______三角形,请证明你的结论.
拓展延伸
(2)当时,正方形沿过点的直线(不过点)折叠后,点的对应点落在正方形内部或边上.
①面积的最大值为____________;
②连接,点为的中点,点在上,连接,则的最小值为____________.
24.(14分)如图,抛物线经过、两点,与轴的另一交点为点,直线与轴交于点,与轴交于点.
(1)求抛物线的函数表达式;
(2)若点为抛物线上一点,且点与点关于对称轴对称,求四边形的面积.
(3)点为直线上方抛物线上一动点.
连接、,设直线交线段于点,求的最大值;
过点作,垂足为点,连接,是否存在点,使得中的,若存在,请直接写出点的坐标.
试卷第1页,共3页
试卷第1页,共3页
参考答案:
1.B
【分析】根据相反数与绝对值的性质,列出代数式进行化简即可.
【详解】解:5的相反数为:﹣5,
而﹣5的绝对值为:|﹣5|=5,
即5的相反数的绝对值是5,
故选B.
【点睛】本题主要考查了绝对值与相反数的表示,正确用式子表示出:“+5的相反数的绝对值”,是解题关键.
2.D
【分析】本题考查了中心对称图形的识别.把一个图形绕某一点旋转,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心.据此逐一判断即可得到答案.
【详解】解:A、B、C选项中的图形都能找到这样的一个点,使图形绕这个点旋转后与原来的图形重合,所以是中心对称图形;
D选项中的图形不能找到这样的一个点,使图形绕这个点旋转后与原来的图形重合,所以不是中心对称图形.
故选:D.
3.B
【分析】本题考查了整式的混合运算,完全平方公式,准确熟练地进行计算是解题的关键.
利用完全平方公式,同底数 的乘法,幂的乘方与积的乘方法则进行计算,即可解答.
【详解】解:A、,故A不符合题意;
B、,故B符合题意;
C、,故C不符合题意;
D、,故D不符合题意;
故选:B.
4.D
【分析】本题考查了概率公式、调查方式的选择、中位数的定义、概率的意义及方差的意义等知识,解题的关键是了解统计的有关知识,难度不大.利用调查方式的选择、中位数的定义、概率的意义及方差的意义分别判断后即可确定正确的选项.
【详解】解:A.调查中央电视台开学第一课的收视率,应采用抽样调查的方式,故错误,不符合题意;
B.数据,,,,的中位数是,故错误,不符合题意;
C.一个抽奖活动中,中奖概率为,抽奖次可能有次中奖,也可能不中奖,故错误,不符合题意;
D.甲、乙两名射击运动员次射击成绩单位:环的平均数相等,方差分别为,,则甲的成绩比乙的稳定,正确,符合题意.
故选:D.
5.C
【分析】本题考查了尺规作图—作角的平分线,含角的直角三角形的性质,等腰直角三角形的判定与性质等知识,正确作出辅助线是解答本题的关键.过点作于点,由作法知平分,从而可得,得到,再证明是等腰直角三角形,根据勾股定理即可求出的长.
【详解】解:如图,过点作于点,
由作法知平分,
,
,
,
,,
是等腰直角三角形,
,
.
故选:C.
6.C
【分析】本题考查了三视图,熟练掌握三视图是解题的关键.根据三视图判断小立方块的数量,再求出搭成一个大正方体需要的最少数量,即可得到答案.
【详解】解:由三视图易得最底层有7个小立方体,第二层有2个小立方体,第三层有1个小立方体,那么共有个几何体组成.
若要搭成一个大正方体,共需个小立方体,
所以还需个小立方体,
故选:C.
7.C
【分析】设1袋笔的价格为x元,1本笔记本的价格为y元,根据“若购买4袋笔和6本笔记本,他身上的钱还差22元,若改成购买1袋笔和2本笔记本,他身上的钱会剩下34元”,即可得出关于x,y的二元一次方程,结合x,y均为正整数即可得出结论,再设可购买a袋笔和b本笔记本,根据总价=单价×数量可得出关于a,b的二元一次方程,结合a,b均为正整数即可得出结论.
【详解】设1袋笔的价格为x元,1本笔记本的价格为y元,
依题意,得:4x+6y-22=x+2y+34,
∴3x+4y=56,即y=14-x.
∵x,y均为正整数,
∴,,,.
设可购买a袋笔和b本笔记本.
①当x=4,y=11时,4x+6y-22=60,
∴4a+11b=60,即a=15-b,
∵a,b均为正整数,
∴;
②当x=8,y=8时,4x+6y-22=58,
∴8a+8b=58,即a+b=,
∵a,b均为正整数,
∴方程无解;
③当x=12,y=5时,4x+6y-22=56,
∴12a+5b=56,即b=,
∵a,b均为正整数,
∴;
④当x=16,y=2时,4x+6y-22=54,
∴16a+2b=54,即b=27-8a,
∵a,b均为正整数,
∴,,.
综上所述,共有5种购进方案.
故选:C.
【点睛】本题考查了二元一次方程的应用,找准等量关系,正确列出二元一次方程是解题的关键.
8.C
【分析】本题考查了动点问题的函数图象、解直角三角形、勾股定理,当时,点在点处,此时,则,当时,,求出,由勾股定理得出,求出,再由计算即可得解.
【详解】解:当时,点在点处,此时,则,
当时,,
,
则,
,
,
,
故选:C.
9.A
【分析】本题主要考查解分式方程,解分式方程,用含m的代数式表示x,根据整数的意义可得m的值.解题的关键是将分式方程转化为整式方程,求出方程的解.
【详解】解:
去分母得:
化简得:
当时,
方程有整数根,的值是整数,
当时,,方程的根;
当时,,方程的根(增根,舍去);
当时,,方程的根;
当时,,方程的根(增根,舍去).
故选:A.
10.C
【分析】根据题干和图像可得,该抛物线的对称轴是,即;点的对称点坐标是;.
将代入该抛物线解析式可判断结论①;
根据和将代入抛物线解析式得到的,联立可求得 、的数量关系,根据可求的范围,以此判断结论②;
将顶点代入抛物线解析式得到,等量替换后得到与的关系再判断范围,以此判断结论③;
综合和、和的数量关系式,解一元二次方程即可判断结论④;
结合二次函数图象中可得,二次函数最小值为,则当时,有,结合、与数量关系式即可判断结论⑤.
【详解】解:依题得:该抛物线的对称轴是,即;
点的对称点坐标是;.
时,有,即,
①错误;
,
,
又将代入抛物线解析式中得,
,即,
又,
,
,
②正确;
将顶点坐标代入抛物线解析式中得,
即,
,
又,
,则,
③正确;
一元二次方程即,
即,
可解得,,
④一元二次方程的两个根分别为,正确;
时,在该抛物线中有,
,
,
,
⑤(其中)正确;
综上,②③④⑤正确,故正确的个数为个.
故选:.
【点睛】本题考查的知识点是二次函数的图象与性质、根据二次函数的图象判断式子符号、解一元二次方程、不等式,解题关键是熟练掌握二次函数的图形与性质,运用数形结合思想分析问题.
11.
【分析】本题考查用科学记数法表示绝对值大于1的数.科学记数法的表示形式为的形式,其中为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值时,n是正数;当原数的绝对值时,n是负数.熟记相关结论即可.
【详解】解:∵万
故答案为:
12.(答案不唯一)
【分析】本题主要考查了三角形全等的判定方法,添加结合根据即可证明.
【详解】∵
添加结合根据即可证明,
故答案为:(答案不唯一).
13.
【分析】考查圆锥的计算;用的知识点为:圆锥的侧面展开图弧长等于圆锥的底面周长;难点是得到扇形的半径.
圆的半径为2,那么过圆心向引垂线,利用相应的三角函数可得的一半的长度,进而求得的长度,利用弧长公式可求得弧的长度,圆锥的底面圆的半径圆锥的弧长.
【详解】解:作于点,连接,
,,
,
,
圆锥的底面圆的半径.
故答案为:
14.
【分析】本题主要考查了反比例函数的几何应用.相似三角形的判定和性质.过点D作于点E,则,设点C的坐标为,则,可得点A的坐标为,点B的坐标为,再求出直线的解析式,联立可得点D的横坐标为,从而得到,再由,即可求解.
【详解】解:如图,过点D作于点E,则,
设点C的坐标为,则,
∵轴,轴交反比例函数的图象于点,
∴点A的坐标为,点B的坐标为,
∴,
设直线的解析式为,
把点,代入得:
,解得:,
∴直线的解析式为,
联立得:,
整理得:,
解得:,
∴点D的横坐标为,
∴,
∵,
∴,
∴,
∴
∴.
故答案为:
15.且
【分析】本题考查的是函数自变量的取值范围,①当表达式的分母不含有自变量时,自变量取全体实数.②当表达式的分母中含有自变量时,自变量取值要使分母不为零.③当函数的表达式是偶次根式时,自变量的取值范围必须使被开方数不小于零.
根据分式有意义的条件、二次根式有意义的条件列式计算.
【详解】解:由题意得,,
解得,且,
故答案为:且.
16.4或或
【分析】由直角三角形的性质和勾股定理可得,,,分三种情况:当时,设垂足为;当时,作交于;当时,分别进行计算即可得到答案.
【详解】解:在中,,,
,
,
是的中点,
,
如图1,当时,设垂足为,
,
由折叠可知,,,,
,
,
,
,
,
,,
,
;
如图2,当时,
,
则,
由折叠可知:,
,
,
,
,
,
在中,,,
,
,,
作交于,则,
,
是等腰直角三角形,
,
设,则,
,
,
,即,
解得:,
,
在中,,,
;
如图3,当时,
,
由折叠的性质可得:,,,
,
,
,
,,
,
,
,
综上所述:的长为4或或,
故答案为:4或或.
【点睛】本题主要考查了折叠的性质、相似三角形的判定与性质、直角三角形的性质、勾股定理、等腰三角形的判定与性质等知识,熟练掌握以上知识点,添加适当的辅助线,采用分类讨论的思想解题,是解此题的关键.
17.
【分析】本题考查了规律型中的点的坐标,解题的关键是罗列出部分点的坐标找出坐标规律.本题属于基础题,难度不大,解决该题型题目时,结合画弧的方法以及部分点的坐标寻找出来点的排布规律是关键.根据画弧的方法以及罗列部分点的坐标发现:点Ax的坐标满足“(n为正整数),(n为自然数),(n为自然数),(n为自然数)”,根据这一规律即可得出点的坐标.
【详解】解:观察,找规律∶,,,,,,,,,,,,,,,…,
∴(n为正整数),(n为自然数),(n为自然数),(n为自然数).
∵,
∴的坐标为.
故答案为:.
18.(1);(2)
【详解】(1)解:原式
.
(2)解:
;
19.,.
【分析】本题考查解一元二次方程,熟练掌握一元二次方程的解法是解题的关键,先将所给的一元二次方程整理后,分别找到二次项系数、一次项系数、常数项,利用一元二次方程的求根公式计算即可.
【详解】解:方程整理得:,
则,,,
∵,
∴,
解得:,.
20.(1)200;
(2)见解析;90
(3)
【分析】本题考查的是条形统计图与扇形统计图、用树状图法求概率.
(1)由选择C专业的人数除以所占百分比即可求出总数,由乘以选择A(旅游管理)专业的人数所占的比例即可得出扇形统计图中A(旅游管理)专业所对应的圆心角的度数;
(2)求出B专业的人数,补全条形统计图即可,根据该中学选择“信息技术”专业意向的学生所占比例估计实际人数;
(3)画树状图,共有12种等可能的结果,其中恰好抽到甲、乙两名同学的结果有2种,再由概率公式求解即可.
【详解】(1)本次被调查的学生有:(人),
故答案为:100;
(2)扇形统计图中,A(旅游管理)专业所对应的圆心角的度数为:,
故答案为:200;;
(2)条形统计图中,B(信息技术)专业的人数为:(人),
补全条形统计图如下:
若该中学有300名学生有培训意向,估计该中学选择“信息技术”专业意向的学生有(人),
故答案为:90;
(3)画树状图如下:
共有12种等可能的结果,其中恰好抽到甲、乙两名同学的结果有2种,
∴恰好抽到甲、乙两名同学的概率为.
21.(1)见详解
(2)
【分析】本题考查切线的判定和性质,圆周角定理,直角三角形的边角关系以及相似三角形,掌握切线的判定方法,直角三角形的边角关系以及相似三角形的性质是正确解答的前提.
(1)根据切线的判定,连接,证明出即可,利用直径所得的圆周角为直角,三角形的内角和以及等腰三角形的性质可得答案;
(2)由,根据锐角三角函数的意义和勾股定理可得,再根据相似三角形的性质可求出答案.
【详解】(1)证明:连接,
∵是的直径,
∴,
∴,
又∵,
∴,
又∵.
∴,
即,
∴是的切线;
(2)解:∵,
∴,
在中,
,
,
,
,
,
,
,
设,则,
又,
即,
解得(取正值),
.
22.(1)100;4.5;5
(2)
(3)两车相距180千米的时刻为1.5小时和3.5小时
【分析】(1)根据图形,可知设甲车速度为m千米/时, 乙车速度为n千米/时,可列出方程:m-n=20,m+n=180,可求得m、n,由此即可求出a、b;
(2)利用待定系数法进行求解析式即可,注意取值范围;
(3)分两种情况进行讨论,两车相距180千米时,出现在BC、CD两段,根据题意对两种情况进行分析求解.
【详解】(1)解:设甲车速度为m千米/时, 乙车速度为n千米/时,
由AB段可知:m>n,
则:,
即:m-n=20①,
由BC段可知:,
即:m+n=180②,
联立①、②得:m=100,n=80,
∴甲车速度为100千米/时, 乙车速度为80千米/时,
有CD段可知:,
解得:a=4.5,
由DE可知,此时甲车已到达B地,此段为乙车单独行驶,即:,
解得:b=5,
故答案为:100;4.5;5;
(2)由图可知,两车相遇时,为图中C点,相遇之后分为CD、DE两段,
设CD段函数表达式为:,DE段函数表达式为:,
将(2.5,0),(4.5,360)代入得:
,
解得:,
∴CD段函数表达式为:,
将(4.5,360)、(5,400)代入得:
,
解得:,
∴DE段函数表达式为:,
∴两车相遇后y与x之间的函数关系式为:;
(3)由图可知,两车相距180千米时,出现在BC、CD两段,
在BC段时,两车相距180千米时刻为:2.5-=1.5(小时),
在CD段时,两车相距180千米时刻为:2.5+=3.5(小时),
∴两车相距180千米的时刻为1.5小时和3.5小时.
【点睛】本题主要考查了一次函数的实际应用,解题的关键是理解图象中每段所代表的意义,并结合函数进行解题.
23.(1)①;②;③等边,证明见解析;(2)①3;②.
【分析】(1)①利用圆的基本性质,即可求解;
②根据折叠的性质,利用勾股定理,即可求解;
③利用勾股定理,求得B′D=,即可求解;
(2)①由题意知点B'在以点E为圆心,半径长为2的圆上,△ABB'的面积要最大,只要以AB为底的高最长即可,此时当B'E⊥AB时,△ABB'的面积最大;
②当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,且最小值为EC的长,利用勾股定理即可求解.
【详解】解:(1)根据折叠的性质知:BE=B′E,BC=B′C=3,MA=MB=NC=ND=,
∠B=∠EB′C=90,
①点B′在以点E为圆心,BE的长为半径的圆上;
②B′M=MN- B′N=
=
=;
③B′D=,
∴△DB'C为等边三角形;
故答案为:①BE,②,③等边;
(2)①∵AB=3=3AE,
∴AE=1,BE=2,
故点B'在以点E为圆心,半径长为2的圆上,
∴△ABB'的面积要最大,只要以AB为底的高最长即可,
∴当B'E⊥AB时,△ABB'的面积最大,如图:
△ABB'的面积最大值;
②∵∠AQP=∠AB'E,
∴PQ∥B'E,
∵P为AE的中点,
∴Q为AB'的中点,
∴PQ为△AEB'的中位线,
∴PQ=EB',即EB'=2PQ,
∴B'C+2PQ= B'C+ EB',
当E、B′、C三点共线时,B'C+ EB'取得最小值,即B'C+2PQ取得最小值,
且最小值为EC的长,
∴EC=,
∴B'C+2PQ的最小值为.
故答案为:①;②.
【点睛】本题考查了圆的性质,矩形的性质、图形的折叠、等腰三角形的性质等,有一定的综合性,难度适中,其中(2)①当B'E⊥AB时,△ABB'的面积最大;②当E、B′、C三点共线时,B'C+2PQ取得最小值,是解本题的关键.
24.(1)
(2)
(3)①;②存在,
【分析】(1)用待定系数法即可求解;
(2)证明四边形为梯形,则四边形的面积,即可求解;
(3)①证明,则,即可求解;
证明,则,即,进而求解.
【详解】(1)解:在中,令得,令得,
,,
经过、两点,
,
解得:,
抛物线的函数表达式为;
(2)解:在中,令,得,
解得,,
,
点与点关于对称轴对称,点,抛物线的对称轴为,
点,
则,,
,则四边形为梯形,
则四边形的面积;
(3)解:①过作轴交于点,过作轴交于于,如图:
在中,令得,
,,
设,则,
,
轴,轴,
,
,
,
,
,
,
当时,取最大值,最大值为;
存在点,使得中的,理由如下:
过作轴,交轴于,交直线于,如图:
轴,
,
,
,
,
,
,
,即,
设,
,
,,
,,
,
,
解得,
.
【点睛】本题考查二次函数综合应用,涉及待定系数法,相似三角形的判定与性质,锐角三角函数的应用等知识,解题的关键是用含字母的代数式表示相关点坐标和相关线段的长度.
答案第1页,共2页
答案第1页,共2页
同课章节目录
