苏教版六年级 下册数学 探索规律 面积的变化课件(共16张PPT)
文档属性
| 名称 | 苏教版六年级 下册数学 探索规律 面积的变化课件(共16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-17 09:47:44 | ||
图片预览




文档简介
(共16张PPT)
探索规律:面积的变化
苏教版六年级下册 数学
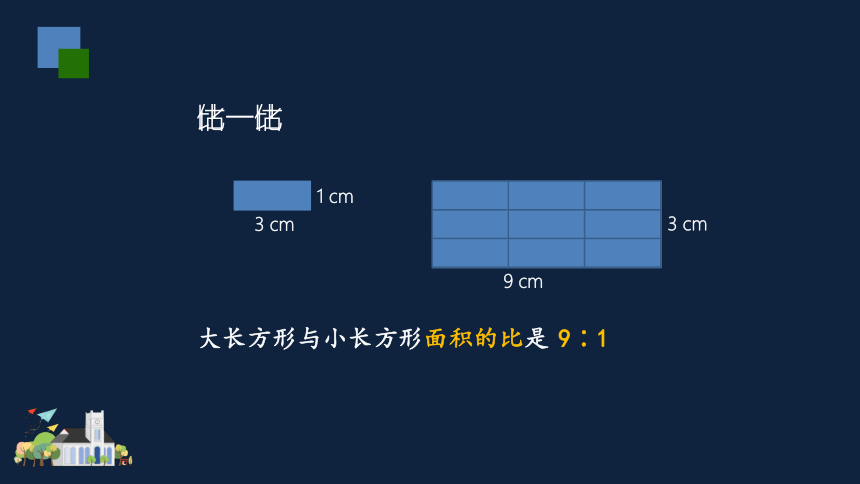
分别量出它们的长和宽,写出对应边长的比。
3 cm
1 cm
9 cm
3 cm
大长方形与小长方形长的比是
9∶3
大长方形与小长方形宽的比是
3∶1
大长方形与小长方形面积的比是?
3∶1 ?
6∶1 ?
9∶1 ?
3∶1
……
3 cm
1 cm
9 cm
3 cm
估一估
比一比
大长方形与小长方形面积的比是
9∶1
3 cm
1 cm
9 cm
3 cm
算一算
3×1=3(cm2)
9×3=27(cm2)
大长方形与小长方形面积的比是
27∶3
9∶1
3 cm
1 cm
9 cm
3 cm
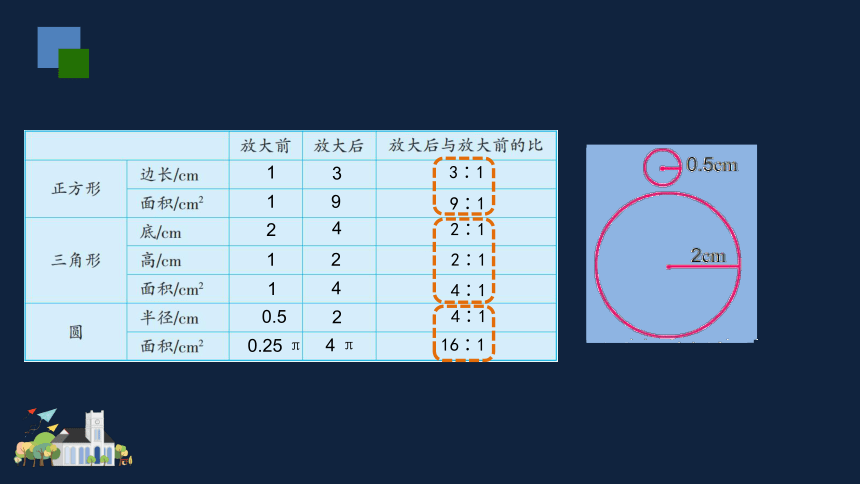
这两个图形对应边的比是
3∶1
它们的面积比是 9∶1 。
3∶1
1
3
9∶1
1
9
2∶1
2
4
2∶1
1
2
4∶1
1
4
4∶1
0.5
2
16∶1
0.25 π
4 π
3 : 1
1
3
9 : 1
1
9
2 : 1
2
4
2 : 1
1
2
4 : 1
1
4
4 : 1
0.5
2
16 : 1
0.25 π
4 π
3 ∶1
3 ∶1
2 ∶1
2 ∶1
2 ∶1
4 ∶1
4 ∶1
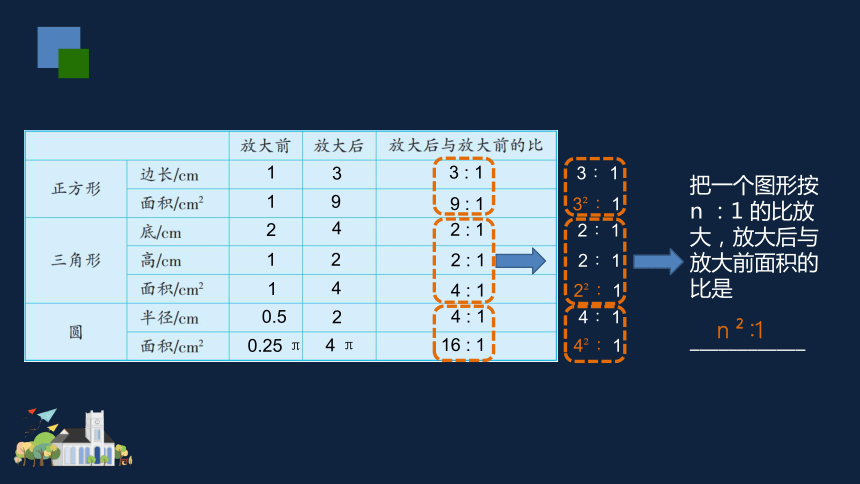
把一个图形按 n :1 的比放大,放大后与放大前面积的比是
____________
n ∶1
3 cm
1 cm
把一个图形按照 n∶1 的比放大,为什么放大后图形的面积是放大前图形面积的n 倍呢?
(3×n)cm
(1×n)cm
(3×n)× (1×n)
= 3×1 × n × n
=(3×1)× n
观察
比较
猜想
验证
把一个图形按照 n ∶ 1 的比放大,
放大后与放大前面积的比是
n ∶1
把一个面积是50平方厘米的三角形按5∶1进行放大,放大后的面积是( )平方厘米。
把一个面积是50平方厘米的三角形
50×(5 ×5)
= 50×25
= 1250(平方厘米)
1250
50÷(5 ×5)
= 50 ÷ 25
= 2(平方厘米)
2
按1∶5进行缩小,
缩小后的
面积是( )平方厘米。
在一幅比例尺是1∶200的平面图上,一个花坛的面积是16平方厘米,求这个花坛的实际占地面积是多少平方米?
图上距离:实际距离
=比例尺
=1∶200
缩小后与缩小前图形对应边长的比
=1∶200
缩小后与缩小前图形面积的比
=1∶200
16×40000=640000(平方厘米)
答:这个花坛的实际占地面积是64平方米。
640000平方厘米=64平方米
=1∶40000
一个零件的横截面积是3平方厘米,把它画在图上,横截面积是300平方厘米。在这幅零件图上量得另一个零件的长是20厘米,这个零件的实际长度是多少厘米?
比例尺
10∶1
300∶3
= 100∶1
= 10 ∶1
解:设这个零件的实际长度是x厘米。
20∶x=10∶1
10x=20
x=2
答:这个零件的实际长度是2厘米。
长方体、正方体等按比例放大后,体积比和长度比会有什么关系?
《面积的变化》(自主练习)
一、判断题:
1、在一幅地图上,用5厘米表示实际距离5分米,这幅地图的比例尺是1∶1。( )
2、一个面积为8平方厘米的长方形,按4∶1的比放大得到大的长方形,这个大长方形面积是32平方厘米。( )
3、一个面积是6平方分米的直角三角形,按一定的比缩小后的面积是1.5平方分米。是按1∶2的比缩小的。( )
4、在一张比例尺为1∶500的地图上,学校一个花坛的面积是16平方厘米,这个花坛的实际面积是80平方米。( )
5、客厅的实际面积是32平方米,画在1:20 的装修图纸上的面积是800平方厘米。( )
二、选择题:
1、一个正方形的边长是3厘米,将其按一定的比放大后,现在的面积是原来的9倍,现在正方形是按( )的比
放大的。
A 、1∶3 B、3∶1 C、9∶1
2、在一张比例尺为1∶200的地图上,测得一块平行四边形的菜地底是8厘米,高5厘米,这块菜地的实际面积是( )平方米。
A、40平方米 B、80平方米 C、160平方米
3、在一张比例尺为1∶2000的地图上,测得正方形花园的边长为2.5厘米,则这个花园的实际面积是( )平方米。
A、2500 B、500 C、2000
4、一个实际面积为100π平方米的圆形花坛,画在地图上的面积是100π平方厘米。这张地图的比例尺是( )。 A、1∶100 B、1∶1000 C、1∶10000
5、一个圆的面积是4平方厘米,如果把它的半径按3∶1的比放大,那么放大后的圆的面积是( )平方厘米。
A、12 B、24 C、36
《面积的变化》(自主练习)
探索规律:面积的变化
苏教版六年级下册 数学
分别量出它们的长和宽,写出对应边长的比。
3 cm
1 cm
9 cm
3 cm
大长方形与小长方形长的比是
9∶3
大长方形与小长方形宽的比是
3∶1
大长方形与小长方形面积的比是?
3∶1 ?
6∶1 ?
9∶1 ?
3∶1
……
3 cm
1 cm
9 cm
3 cm
估一估
比一比
大长方形与小长方形面积的比是
9∶1
3 cm
1 cm
9 cm
3 cm
算一算
3×1=3(cm2)
9×3=27(cm2)
大长方形与小长方形面积的比是
27∶3
9∶1
3 cm
1 cm
9 cm
3 cm
这两个图形对应边的比是
3∶1
它们的面积比是 9∶1 。
3∶1
1
3
9∶1
1
9
2∶1
2
4
2∶1
1
2
4∶1
1
4
4∶1
0.5
2
16∶1
0.25 π
4 π
3 : 1
1
3
9 : 1
1
9
2 : 1
2
4
2 : 1
1
2
4 : 1
1
4
4 : 1
0.5
2
16 : 1
0.25 π
4 π
3 ∶1
3 ∶1
2 ∶1
2 ∶1
2 ∶1
4 ∶1
4 ∶1
把一个图形按 n :1 的比放大,放大后与放大前面积的比是
____________
n ∶1
3 cm
1 cm
把一个图形按照 n∶1 的比放大,为什么放大后图形的面积是放大前图形面积的n 倍呢?
(3×n)cm
(1×n)cm
(3×n)× (1×n)
= 3×1 × n × n
=(3×1)× n
观察
比较
猜想
验证
把一个图形按照 n ∶ 1 的比放大,
放大后与放大前面积的比是
n ∶1
把一个面积是50平方厘米的三角形按5∶1进行放大,放大后的面积是( )平方厘米。
把一个面积是50平方厘米的三角形
50×(5 ×5)
= 50×25
= 1250(平方厘米)
1250
50÷(5 ×5)
= 50 ÷ 25
= 2(平方厘米)
2
按1∶5进行缩小,
缩小后的
面积是( )平方厘米。
在一幅比例尺是1∶200的平面图上,一个花坛的面积是16平方厘米,求这个花坛的实际占地面积是多少平方米?
图上距离:实际距离
=比例尺
=1∶200
缩小后与缩小前图形对应边长的比
=1∶200
缩小后与缩小前图形面积的比
=1∶200
16×40000=640000(平方厘米)
答:这个花坛的实际占地面积是64平方米。
640000平方厘米=64平方米
=1∶40000
一个零件的横截面积是3平方厘米,把它画在图上,横截面积是300平方厘米。在这幅零件图上量得另一个零件的长是20厘米,这个零件的实际长度是多少厘米?
比例尺
10∶1
300∶3
= 100∶1
= 10 ∶1
解:设这个零件的实际长度是x厘米。
20∶x=10∶1
10x=20
x=2
答:这个零件的实际长度是2厘米。
长方体、正方体等按比例放大后,体积比和长度比会有什么关系?
《面积的变化》(自主练习)
一、判断题:
1、在一幅地图上,用5厘米表示实际距离5分米,这幅地图的比例尺是1∶1。( )
2、一个面积为8平方厘米的长方形,按4∶1的比放大得到大的长方形,这个大长方形面积是32平方厘米。( )
3、一个面积是6平方分米的直角三角形,按一定的比缩小后的面积是1.5平方分米。是按1∶2的比缩小的。( )
4、在一张比例尺为1∶500的地图上,学校一个花坛的面积是16平方厘米,这个花坛的实际面积是80平方米。( )
5、客厅的实际面积是32平方米,画在1:20 的装修图纸上的面积是800平方厘米。( )
二、选择题:
1、一个正方形的边长是3厘米,将其按一定的比放大后,现在的面积是原来的9倍,现在正方形是按( )的比
放大的。
A 、1∶3 B、3∶1 C、9∶1
2、在一张比例尺为1∶200的地图上,测得一块平行四边形的菜地底是8厘米,高5厘米,这块菜地的实际面积是( )平方米。
A、40平方米 B、80平方米 C、160平方米
3、在一张比例尺为1∶2000的地图上,测得正方形花园的边长为2.5厘米,则这个花园的实际面积是( )平方米。
A、2500 B、500 C、2000
4、一个实际面积为100π平方米的圆形花坛,画在地图上的面积是100π平方厘米。这张地图的比例尺是( )。 A、1∶100 B、1∶1000 C、1∶10000
5、一个圆的面积是4平方厘米,如果把它的半径按3∶1的比放大,那么放大后的圆的面积是( )平方厘米。
A、12 B、24 C、36
《面积的变化》(自主练习)
