人教版四年级数学下册第五单元《三角形》单元同步练习题(含答案)
文档属性
| 名称 | 人教版四年级数学下册第五单元《三角形》单元同步练习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-17 10:03:17 | ||
图片预览



文档简介
四年级数学下册第五单元《三角形》单元同步练习题
一、选择题(共7小题,每小题3分,满分21分)
1.下面不同长度的四根小棒,( )不能围成三角形。
①厘米 ②厘米 ③厘米 ④厘米
A.①②③ B.①②④ C.①③④ D.②③④
2.下面( )种方法不能增加四边形的稳定性。
A. B. C. D.
3.如图,三角形中,边上的高是( )。
A. B. C. D.无法确定
4.用放大倍的放大镜看一个三角形,看到的三角形的内角和是( )。
A. B. C. D.
5.如图,被纸板遮住的三角形是( )。
A.直角三角形 B.钝角三角形
C.锐角三角形 D.以上三种都有可能
6.将两个完全相同的五边形按照图①和图②的方式裁去一个角,下面的说法正确的是( )。
A.甲和乙的内角和相等 B.甲的内角和比乙的内角和大
C.甲的内角和比乙的内角和大 D.甲的内角和比乙的内角和大
7.如图,为估计池塘岸边、两点之间的距离,在池塘的一侧选取一点测得米米、两点之间的距离不可能是( )米。
A. B. C. D.
二、判断题(共6小题,每小题2分,满分12分)
8.小强用一根和两根长的小棒正好围成一个三角形。( )
9.三角形任意两边长度的和可以等于第三边。( )
10.只要有一个角是锐角的三角形就是锐角三角形。( )
11.三条边都相等的三角形一定是等边三角形。( )
12.如下图,一个四边形可以分成个三角形,所以这个四边形的内角和是。( )
13.将两个完全一样的直角三角形拼成一个大三角形,拼成的大三角形的内角和是。( )
三、填空题(共8小题,每小题3分,满分24分)
14.从三角形的一个顶点到对边的( )线段是三角形的高,这条对边是三角形的( )。任意一个三角形都有( )个底,同时也就有( )条高。
15.如果一个三角形的两条边分别是和,那么第三条边最长是( )。(第三条边的长度为整厘米数)
16.如图,在三角形中,边上的高是线段( ),边上的高是线段( )。
17.下图中一共有( )个三角形。
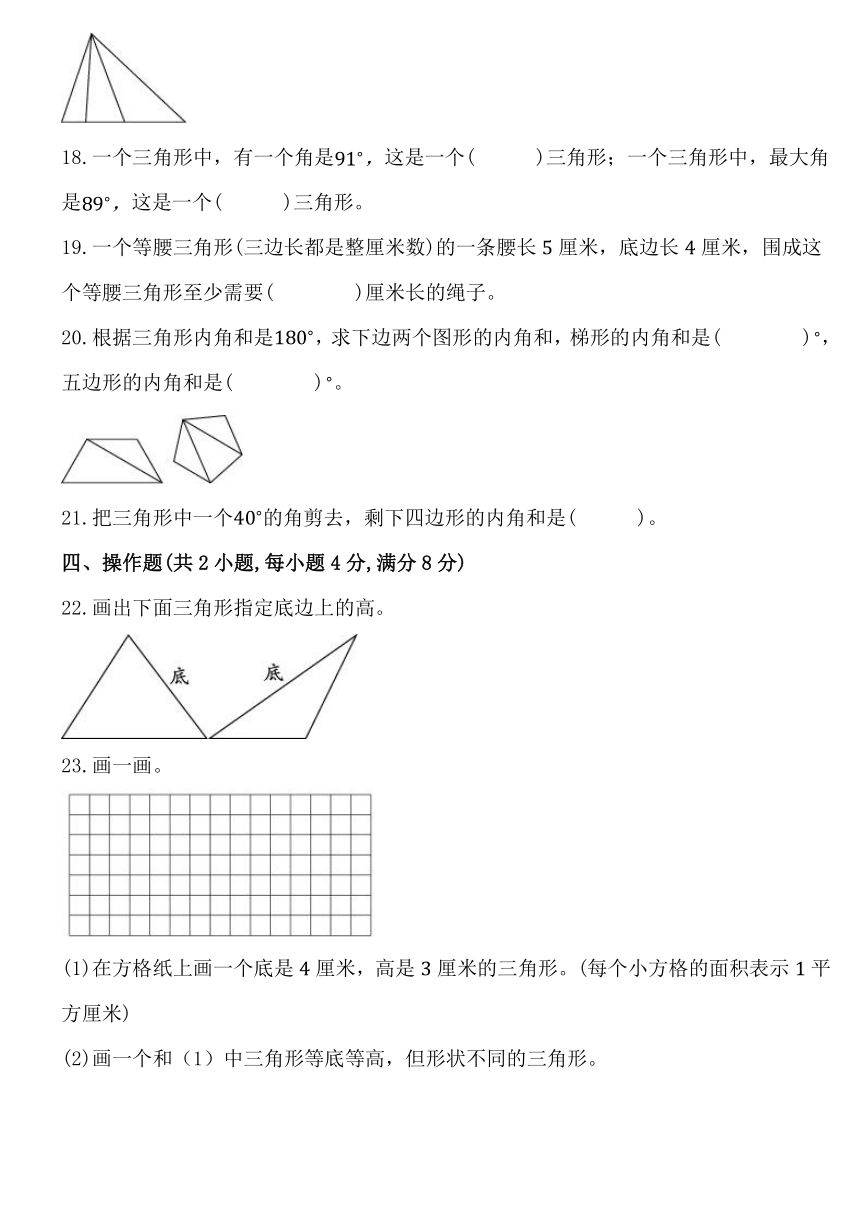
18.一个三角形中,有一个角是这是一个( )三角形;一个三角形中,最大角是这是一个( )三角形。
19.一个等腰三角形(三边长都是整厘米数)的一条腰长厘米,底边长厘米,围成这个等腰三角形至少需要( )厘米长的绳子。
20.根据三角形内角和是,求下边两个图形的内角和,梯形的内角和是( ),五边形的内角和是( )。
21.把三角形中一个的角剪去,剩下四边形的内角和是( )。
四、操作题(共2小题,每小题4分,满分8分)
22.画出下面三角形指定底边上的高。
23.画一画。
(1)在方格纸上画一个底是厘米,高是厘米的三角形。(每个小方格的面积表示平方厘米)
(2)画一个和(1)中三角形等底等高,但形状不同的三角形。
五、连线题(5分)
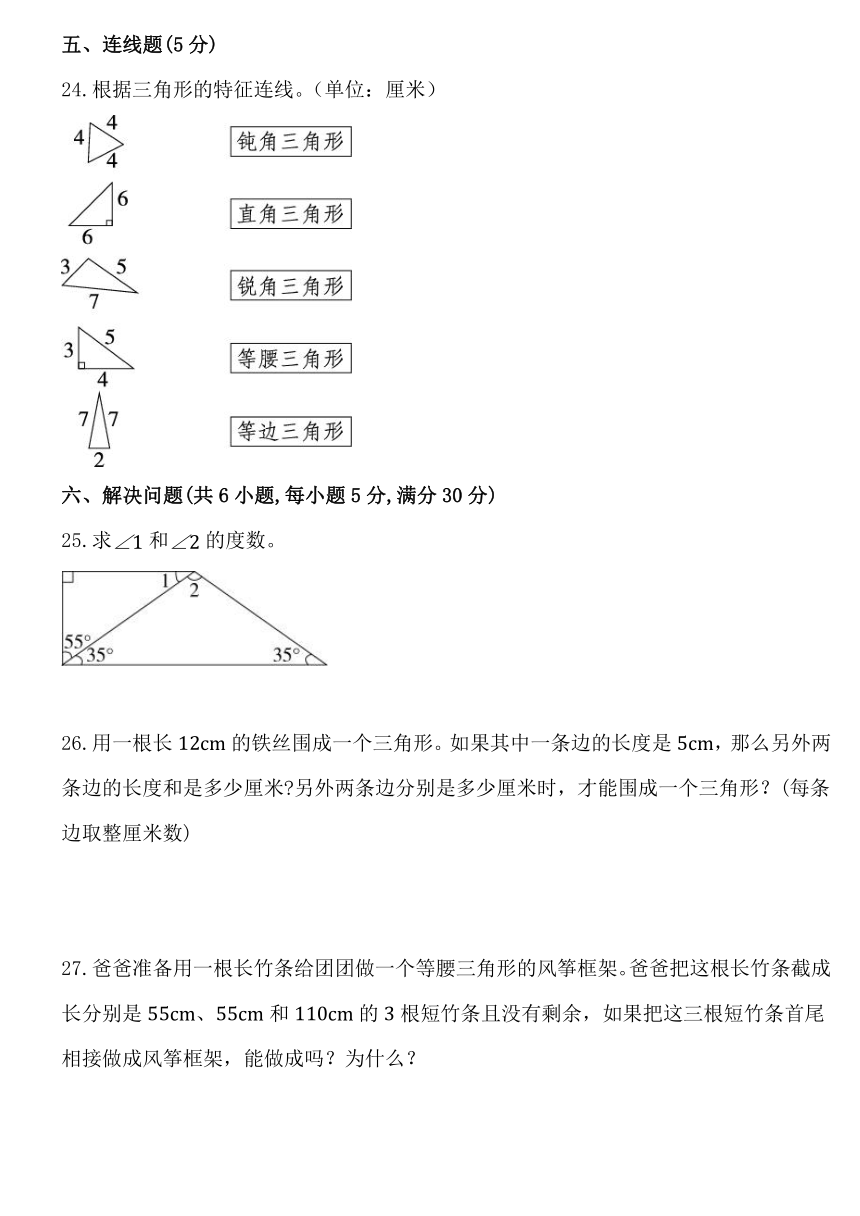
24.根据三角形的特征连线。(单位:厘米)
六、解决问题(共6小题,每小题5分,满分30分)
25.求和的度数。
26.用一根长的铁丝围成一个三角形。如果其中一条边的长度是,那么另外两条边的长度和是多少厘米 另外两条边分别是多少厘米时,才能围成一个三角形?(每条边取整厘米数)
27.爸爸准备用一根长竹条给团团做一个等腰三角形的风筝框架。爸爸把这根长竹条截成长分别是、和的根短竹条且没有剩余,如果把这三根短竹条首尾相接做成风筝框架,能做成吗?为什么?
28.一根铁丝正好能围成一个底是,腰是的等腰三角形,如果改围成一个等边三角形,这个等边三角形一条边的长度是多少厘米?
29.王叔叔为了吃上自己种的绿色蔬菜,他打算开辟一块形状为直角梯形的菜地,梯形中有一个内角是,你知道其他内角的度数吗?
30.乐乐要用纸制作一个直角三角形和一个等腰三角形。但是只知道每个三角形中其中两个角的大小关系,请你帮乐乐算一算每个角的度数。
(1)直角三角形中,其中一个角是另一个角的倍。
(2)等腰三角形中,其中一个角是另一个角的倍。
参考答案
1.C
【解析】选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知可以围成一个三角形;
选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知可以围成一个三角形;
选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知不能围成一个三角形;
选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知可以围成一个三角形。
故选择选项。
2.B
【解析】三角形具有稳定性,下图中只有选项B增加一条边之后,图形中没有出现三角形,因此本题选。
3.C
4.C
5.D
6.D
7.A
8.错
【解析】三角形任意两边之和大于第三边,任意两边之差小于第三边。
,所以这三根小棒不能围成三角形。
故错误。
9.错
10.错
11.对
12.错
13.错
14.垂直;底;;
15.
16.;
17.
18.钝角;锐角
19.
20.;
【解析】连接梯形的对角线,把梯形分成了个三角形,三角形的内角和是所以梯形的内角和是;从五边形的一个顶点引出两条对角线,把五边形分成了个三角形所以五边形的内角和是。
21.
22.
23.(1)
(2)
【解析】(1)每个小方格的面积表示平方厘米,因此每个小方格的边长是厘米。在方格纸的一条横线上数出格,作为底边,从底边上某一点往上(或下)数出格作为顶点,把顶点和底边的两个端点连起来。
(2)在已画的三角形底边所在的横线或其他横线上数出格,作为底边,从底边上某一点(与已画三角形不同)往上(或下)数出格作为顶点,把顶点和底边的两个端点连起来。
24.
25.
26.
另外两条边分别是、或、时才能围成一个三角形。
【解析】已知用的铁丝围成三角形,其中一条边的长度是,则另外两条边的和为,再把分成两个整厘米数,有三种分法:;;。其中可以和组成三角形的另外两条边为或。
27.不能做成。
三角形任意两边之和必须大于第三边,现在是两边之和等于第三边,所以不能做成。
28.
答:这个等边三角形一条边的长度是厘米。
29.
答:其他内角的度数分别是、和。
【解析】梯形是四边形,它的内角和是直角梯形中有两个直角,用减去两个再减去已知的可以求出另外一个角的度数。
30.(1)情况一:这两个角中有一个是直角。三个角的度数分别是、、。情况二:这两个角都不是直角。 三个角的度数分别是、、。答:这个三角形三个角的度数可能是、、或、、。
(2)情况一:底角是顶角的倍。三个角的度数分别是、、。情况二:顶角是底角的倍。三个角的度数分别是、、。答:这个三角形三个角的度数可能是、、或、、。
【解析】(1)①题目中说这个三角形是直角三角形,所以其中一个角就是又说其中一个内角是另一个内角的倍,到底哪个内角是哪个内角的倍,题目中并没有明确给出,所以这里要把每种情况都看一下。②分情况讨论每一种情况。一个角是另一个角的倍,这两个角中,可能有一个角是直角,也可能两个都不是直角。情况一:两个角中有一个是直角,因为直角三角形中最大的角就是直角了,另外两个角都是锐角,所以这两个角中较大的角就是直角,另一个角就是。再根据三角形的内角和求出第三个角的度数:。这种情况下,三个角的度数分别是、、。情况二:两个角都不是直角,那么这两个角的度数之和就是直角,因为两个角是倍关系,较小的角就是较大的角是或。这种情况下,三个角的度数分别是、、。
(2)①题目中说这个三角形是等腰三角形,等腰三角形的两个底角相等。那么题目中说一个角是另一个角的倍,到底哪个角是哪个角的倍呢,题目中并没有明确给出,所以这里要把每种情况都看一下。②分情况讨论每一种情况。一个角是另一个角的倍,可能是顶角是底角的倍,也可能是底角是顶角的倍。情况一:底角是顶角的倍,这样把顶角看作份,那么底角就是份,另一个底角也是份,三个角的和就是(份),根据三角形的内角和是可知份(也就是顶角)是底角就是。这种情况下,三个角的度数分别是、、。情况二:顶角是底角的倍,这样把底角看作份,顶角就是份,三个角一共是(份),根据三角形的内角和是可知份(也就是底角)是顶角就是。这种情况下,三个角的度数分别是、、。
一、选择题(共7小题,每小题3分,满分21分)
1.下面不同长度的四根小棒,( )不能围成三角形。
①厘米 ②厘米 ③厘米 ④厘米
A.①②③ B.①②④ C.①③④ D.②③④
2.下面( )种方法不能增加四边形的稳定性。
A. B. C. D.
3.如图,三角形中,边上的高是( )。
A. B. C. D.无法确定
4.用放大倍的放大镜看一个三角形,看到的三角形的内角和是( )。
A. B. C. D.
5.如图,被纸板遮住的三角形是( )。
A.直角三角形 B.钝角三角形
C.锐角三角形 D.以上三种都有可能
6.将两个完全相同的五边形按照图①和图②的方式裁去一个角,下面的说法正确的是( )。
A.甲和乙的内角和相等 B.甲的内角和比乙的内角和大
C.甲的内角和比乙的内角和大 D.甲的内角和比乙的内角和大
7.如图,为估计池塘岸边、两点之间的距离,在池塘的一侧选取一点测得米米、两点之间的距离不可能是( )米。
A. B. C. D.
二、判断题(共6小题,每小题2分,满分12分)
8.小强用一根和两根长的小棒正好围成一个三角形。( )
9.三角形任意两边长度的和可以等于第三边。( )
10.只要有一个角是锐角的三角形就是锐角三角形。( )
11.三条边都相等的三角形一定是等边三角形。( )
12.如下图,一个四边形可以分成个三角形,所以这个四边形的内角和是。( )
13.将两个完全一样的直角三角形拼成一个大三角形,拼成的大三角形的内角和是。( )
三、填空题(共8小题,每小题3分,满分24分)
14.从三角形的一个顶点到对边的( )线段是三角形的高,这条对边是三角形的( )。任意一个三角形都有( )个底,同时也就有( )条高。
15.如果一个三角形的两条边分别是和,那么第三条边最长是( )。(第三条边的长度为整厘米数)
16.如图,在三角形中,边上的高是线段( ),边上的高是线段( )。
17.下图中一共有( )个三角形。
18.一个三角形中,有一个角是这是一个( )三角形;一个三角形中,最大角是这是一个( )三角形。
19.一个等腰三角形(三边长都是整厘米数)的一条腰长厘米,底边长厘米,围成这个等腰三角形至少需要( )厘米长的绳子。
20.根据三角形内角和是,求下边两个图形的内角和,梯形的内角和是( ),五边形的内角和是( )。
21.把三角形中一个的角剪去,剩下四边形的内角和是( )。
四、操作题(共2小题,每小题4分,满分8分)
22.画出下面三角形指定底边上的高。
23.画一画。
(1)在方格纸上画一个底是厘米,高是厘米的三角形。(每个小方格的面积表示平方厘米)
(2)画一个和(1)中三角形等底等高,但形状不同的三角形。
五、连线题(5分)
24.根据三角形的特征连线。(单位:厘米)
六、解决问题(共6小题,每小题5分,满分30分)
25.求和的度数。
26.用一根长的铁丝围成一个三角形。如果其中一条边的长度是,那么另外两条边的长度和是多少厘米 另外两条边分别是多少厘米时,才能围成一个三角形?(每条边取整厘米数)
27.爸爸准备用一根长竹条给团团做一个等腰三角形的风筝框架。爸爸把这根长竹条截成长分别是、和的根短竹条且没有剩余,如果把这三根短竹条首尾相接做成风筝框架,能做成吗?为什么?
28.一根铁丝正好能围成一个底是,腰是的等腰三角形,如果改围成一个等边三角形,这个等边三角形一条边的长度是多少厘米?
29.王叔叔为了吃上自己种的绿色蔬菜,他打算开辟一块形状为直角梯形的菜地,梯形中有一个内角是,你知道其他内角的度数吗?
30.乐乐要用纸制作一个直角三角形和一个等腰三角形。但是只知道每个三角形中其中两个角的大小关系,请你帮乐乐算一算每个角的度数。
(1)直角三角形中,其中一个角是另一个角的倍。
(2)等腰三角形中,其中一个角是另一个角的倍。
参考答案
1.C
【解析】选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知可以围成一个三角形;
选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知可以围成一个三角形;
选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知不能围成一个三角形;
选项:选择的三根小棒是厘米、厘米和厘米,根据“三角形任意两边的和大于第三边,三角形任意两边的差小于第三边”,可知可以围成一个三角形。
故选择选项。
2.B
【解析】三角形具有稳定性,下图中只有选项B增加一条边之后,图形中没有出现三角形,因此本题选。
3.C
4.C
5.D
6.D
7.A
8.错
【解析】三角形任意两边之和大于第三边,任意两边之差小于第三边。
,所以这三根小棒不能围成三角形。
故错误。
9.错
10.错
11.对
12.错
13.错
14.垂直;底;;
15.
16.;
17.
18.钝角;锐角
19.
20.;
【解析】连接梯形的对角线,把梯形分成了个三角形,三角形的内角和是所以梯形的内角和是;从五边形的一个顶点引出两条对角线,把五边形分成了个三角形所以五边形的内角和是。
21.
22.
23.(1)
(2)
【解析】(1)每个小方格的面积表示平方厘米,因此每个小方格的边长是厘米。在方格纸的一条横线上数出格,作为底边,从底边上某一点往上(或下)数出格作为顶点,把顶点和底边的两个端点连起来。
(2)在已画的三角形底边所在的横线或其他横线上数出格,作为底边,从底边上某一点(与已画三角形不同)往上(或下)数出格作为顶点,把顶点和底边的两个端点连起来。
24.
25.
26.
另外两条边分别是、或、时才能围成一个三角形。
【解析】已知用的铁丝围成三角形,其中一条边的长度是,则另外两条边的和为,再把分成两个整厘米数,有三种分法:;;。其中可以和组成三角形的另外两条边为或。
27.不能做成。
三角形任意两边之和必须大于第三边,现在是两边之和等于第三边,所以不能做成。
28.
答:这个等边三角形一条边的长度是厘米。
29.
答:其他内角的度数分别是、和。
【解析】梯形是四边形,它的内角和是直角梯形中有两个直角,用减去两个再减去已知的可以求出另外一个角的度数。
30.(1)情况一:这两个角中有一个是直角。三个角的度数分别是、、。情况二:这两个角都不是直角。 三个角的度数分别是、、。答:这个三角形三个角的度数可能是、、或、、。
(2)情况一:底角是顶角的倍。三个角的度数分别是、、。情况二:顶角是底角的倍。三个角的度数分别是、、。答:这个三角形三个角的度数可能是、、或、、。
【解析】(1)①题目中说这个三角形是直角三角形,所以其中一个角就是又说其中一个内角是另一个内角的倍,到底哪个内角是哪个内角的倍,题目中并没有明确给出,所以这里要把每种情况都看一下。②分情况讨论每一种情况。一个角是另一个角的倍,这两个角中,可能有一个角是直角,也可能两个都不是直角。情况一:两个角中有一个是直角,因为直角三角形中最大的角就是直角了,另外两个角都是锐角,所以这两个角中较大的角就是直角,另一个角就是。再根据三角形的内角和求出第三个角的度数:。这种情况下,三个角的度数分别是、、。情况二:两个角都不是直角,那么这两个角的度数之和就是直角,因为两个角是倍关系,较小的角就是较大的角是或。这种情况下,三个角的度数分别是、、。
(2)①题目中说这个三角形是等腰三角形,等腰三角形的两个底角相等。那么题目中说一个角是另一个角的倍,到底哪个角是哪个角的倍呢,题目中并没有明确给出,所以这里要把每种情况都看一下。②分情况讨论每一种情况。一个角是另一个角的倍,可能是顶角是底角的倍,也可能是底角是顶角的倍。情况一:底角是顶角的倍,这样把顶角看作份,那么底角就是份,另一个底角也是份,三个角的和就是(份),根据三角形的内角和是可知份(也就是顶角)是底角就是。这种情况下,三个角的度数分别是、、。情况二:顶角是底角的倍,这样把底角看作份,顶角就是份,三个角一共是(份),根据三角形的内角和是可知份(也就是底角)是顶角就是。这种情况下,三个角的度数分别是、、。
