湘教版七年级下学期数学知识总结学案
图片预览
文档简介
第十一章 全等三角形
一、全等三角形
1.能够完全重合的两个图形叫全等形。能够完全重合的两个三角形叫全等三角形。
2.两个全等三角形重合在一起时,重合的顶点叫对应顶点,重合的边叫对应边,
重合的角叫对应角。
3.全等三角形性质定理:全等三角形的对应边相等、全等三角形的对应角相等。
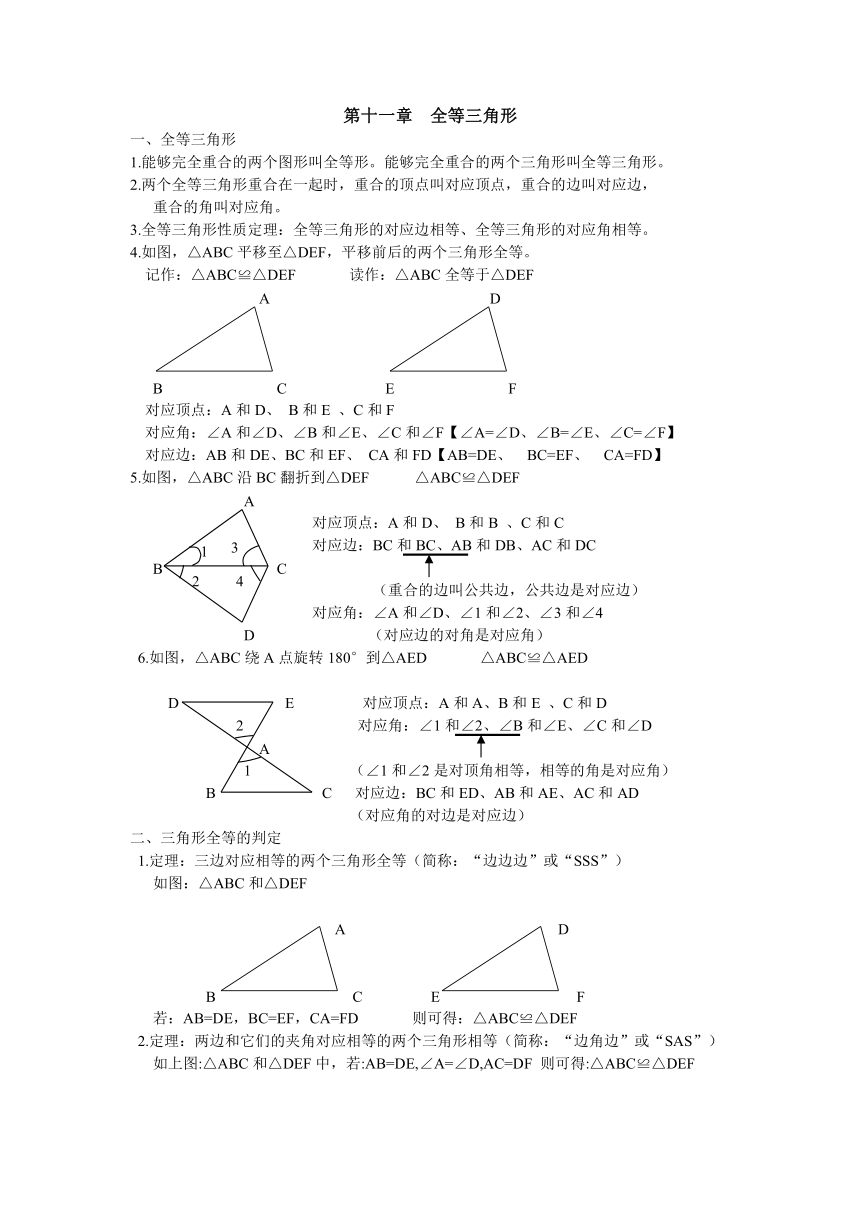
4.如图,△ABC平移至△DEF,平移前后的两个三角形全等。
记作:△ABC≌△DEF 读作:△ABC全等于△DEF
A D
B C E F
对应顶点:A和D、 B和E 、C和F
对应角:∠A和∠D、∠B和∠E、∠C和∠F【∠A=∠D、∠B=∠E、∠C=∠F】
对应边:AB和DE、BC和EF、 CA和FD【AB=DE、 BC=EF、 CA=FD】
5.如图,△ABC沿BC翻折到△DEF △ABC≌△DEF
A
对应顶点:A和D、 B和B 、C和C
对应边:BC和BC、AB和DB、AC和DC
B C
(重合的边叫公共边,公共边是对应边)
对应角:∠A和∠D、∠1和∠2、∠3和∠4
D (对应边的对角是对应角)
6.如图,△ABC绕A点旋转180°到△AED △ABC≌△AED
D E 对应顶点:A和A、B和E 、C和D
2 对应角:∠1和∠2、∠B和∠E、∠C和∠D
A
1 (∠1和∠2是对顶角相等,相等的角是对应角)
B C 对应边:BC和ED、AB和AE、AC和AD
(对应角的对边是对应边)
二、三角形全等的判定
1.定理:三边对应相等的两个三角形全等(简称:“边边边”或“SSS”)
如图:△ABC和△DEF
A D
B C E F
若:AB=DE,BC=EF,CA=FD 则可得:△ABC≌△DEF
2.定理:两边和它们的夹角对应相等的两个三角形相等(简称:“边角边”或“SAS”)
如上图:△ABC和△DEF中,若:AB=DE,∠A=∠D,AC=DF 则可得:△ABC≌△DEF
3.定理:两角和它们的夹边对应相等的两个三角形全等(简称:“角边角”或“ASA”)
如上图:△ABC和△DEF中,若∠B=∠E,BC=EF,∠C=∠F,则可得:△ABC≌△DEF
4.定理:两个角和其中一个角的对边对应相等的两个三角形全等(简称:“角角边”或“AAS”)
如上图:△ABC和△DEF中,若∠A=∠D,∠B=∠E,BC=EF,则可得:△ABC≌△DEF
【三角形具有稳定性,而其它多边形都不具有稳定性】
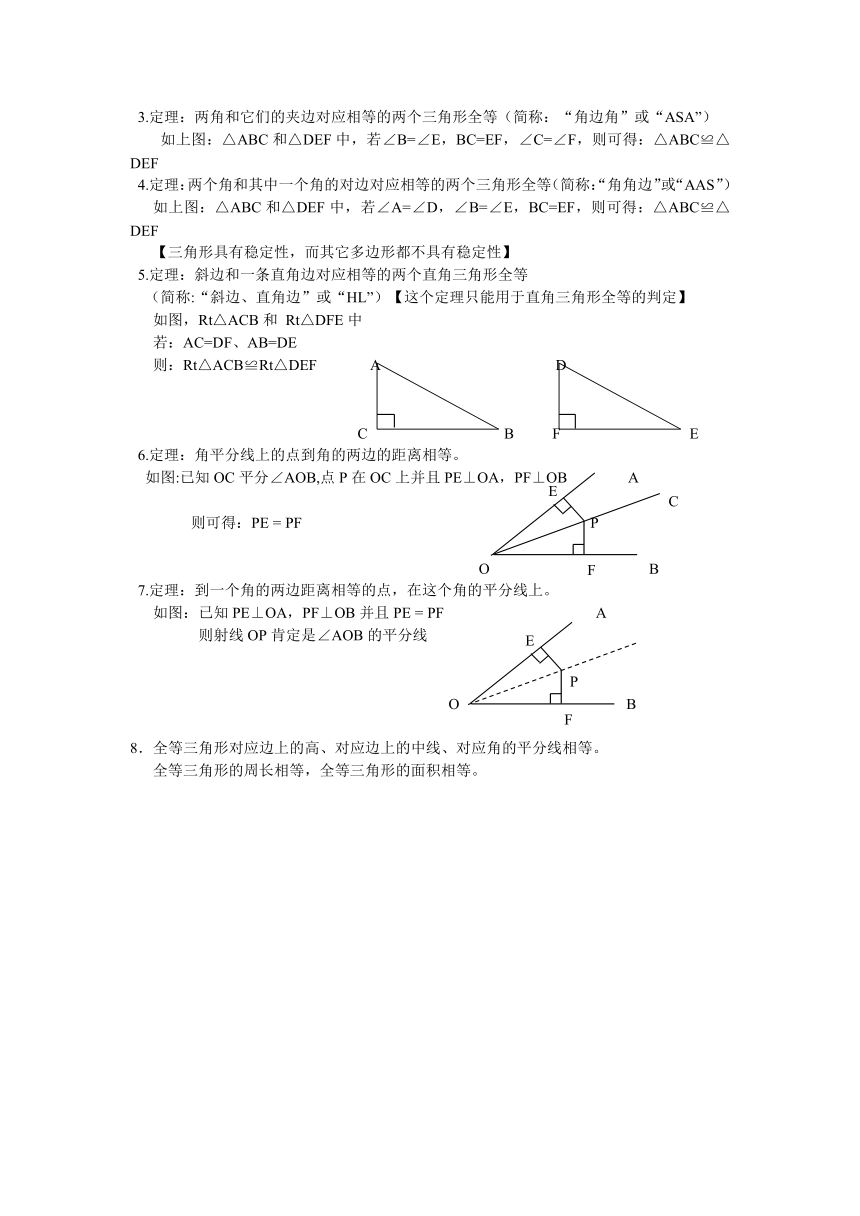
5.定理:斜边和一条直角边对应相等的两个直角三角形全等
(简称:“斜边、直角边”或“HL”)【这个定理只能用于直角三角形全等的判定】
如图,Rt△ACB和 Rt△DFE中
若:AC=DF、AB=DE
则:Rt△ACB≌Rt△DEF A D
C B F E
6.定理:角平分线上的点到角的两边的距离相等。
如图:已知OC平分∠AOB,点P在OC上并且PE⊥OA,PF⊥OB A
C
则可得:PE = PF P
O B
7.定理:到一个角的两边距离相等的点,在这个角的平分线上。
如图:已知PE⊥OA,PF⊥OB并且PE = PF A
则射线OP肯定是∠AOB的平分线
P
O B
8.全等三角形对应边上的高、对应边上的中线、对应角的平分线相等。
全等三角形的周长相等,全等三角形的面积相等。
第十二章 轴对称
一、关于轴对称
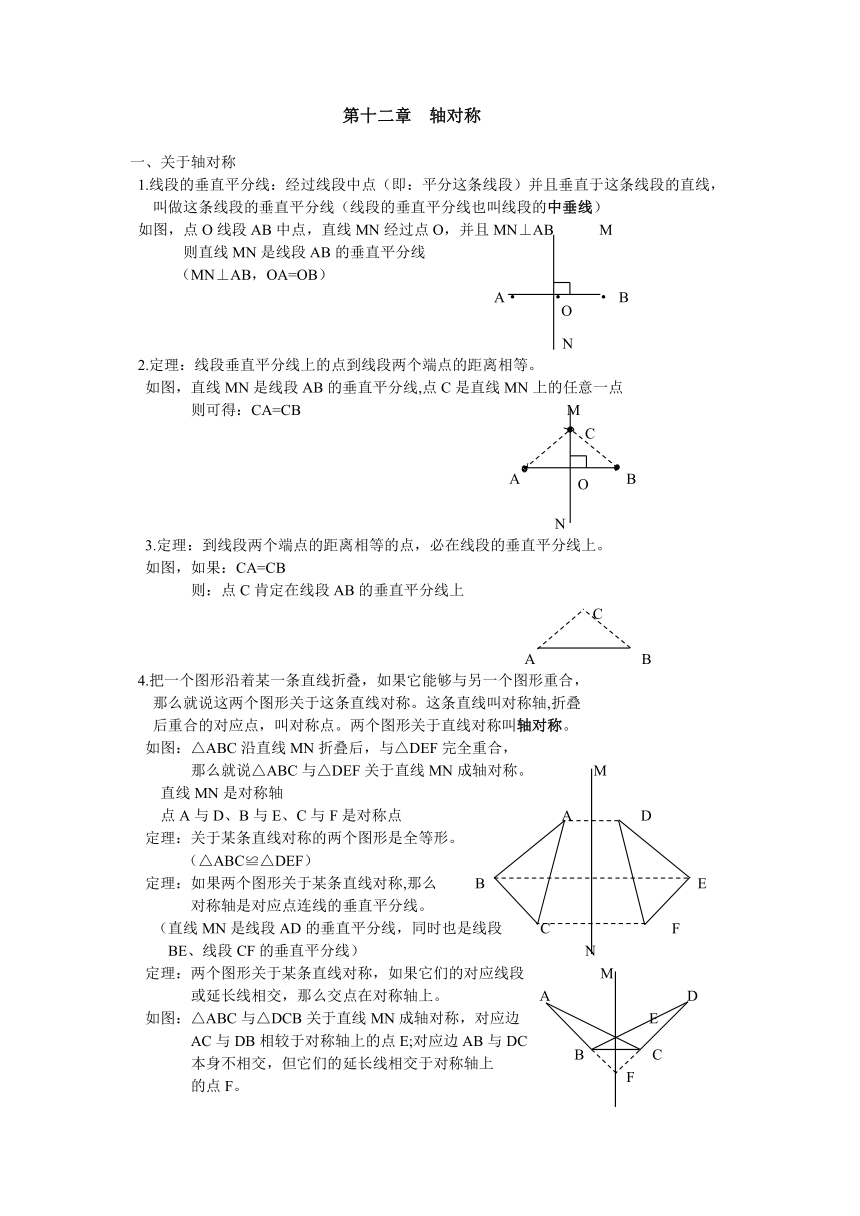
1.线段的垂直平分线:经过线段中点(即:平分这条线段)并且垂直于这条线段的直线,
叫做这条线段的垂直平分线(线段的垂直平分线也叫线段的中垂线)
如图,点O线段AB中点,直线MN经过点O,并且MN⊥AB M
则直线MN是线段AB的垂直平分线
(MN⊥AB,OA=OB)
A· · · B
N
2.定理:线段垂直平分线上的点到线段两个端点的距离相等。
如图,直线MN是线段AB的垂直平分线,点C是直线MN上的任意一点
则可得:CA=CB M
C
A B
N
3.定理:到线段两个端点的距离相等的点,必在线段的垂直平分线上。
如图,如果:CA=CB
则:点C肯定在线段AB的垂直平分线上
C
A B
4.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,
那么就说这两个图形关于这条直线对称。这条直线叫对称轴,折叠
后重合的对应点,叫对称点。两个图形关于直线对称叫轴对称。
如图:△ABC沿直线MN折叠后,与△DEF完全重合,
那么就说△ABC与△DEF关于直线MN成轴对称。 M
直线MN是对称轴
点A与D、B与E、C与F是对称点 A D
定理:关于某条直线对称的两个图形是全等形。
(△ABC≌△DEF)
定理:如果两个图形关于某条直线对称,那么 B E
对称轴是对应点连线的垂直平分线。
(直线MN是线段AD的垂直平分线,同时也是线段 C F
BE、线段CF的垂直平分线) N
定理:两个图形关于某条直线对称,如果它们的对应线段 M
或延长线相交,那么交点在对称轴上。 A D
如图:△ABC与△DCB关于直线MN成轴对称,对应边 E
AC与DB相较于对称轴上的点E;对应边AB与DC
本身不相交,但它们的延长线相交于对称轴上
的点F。
N
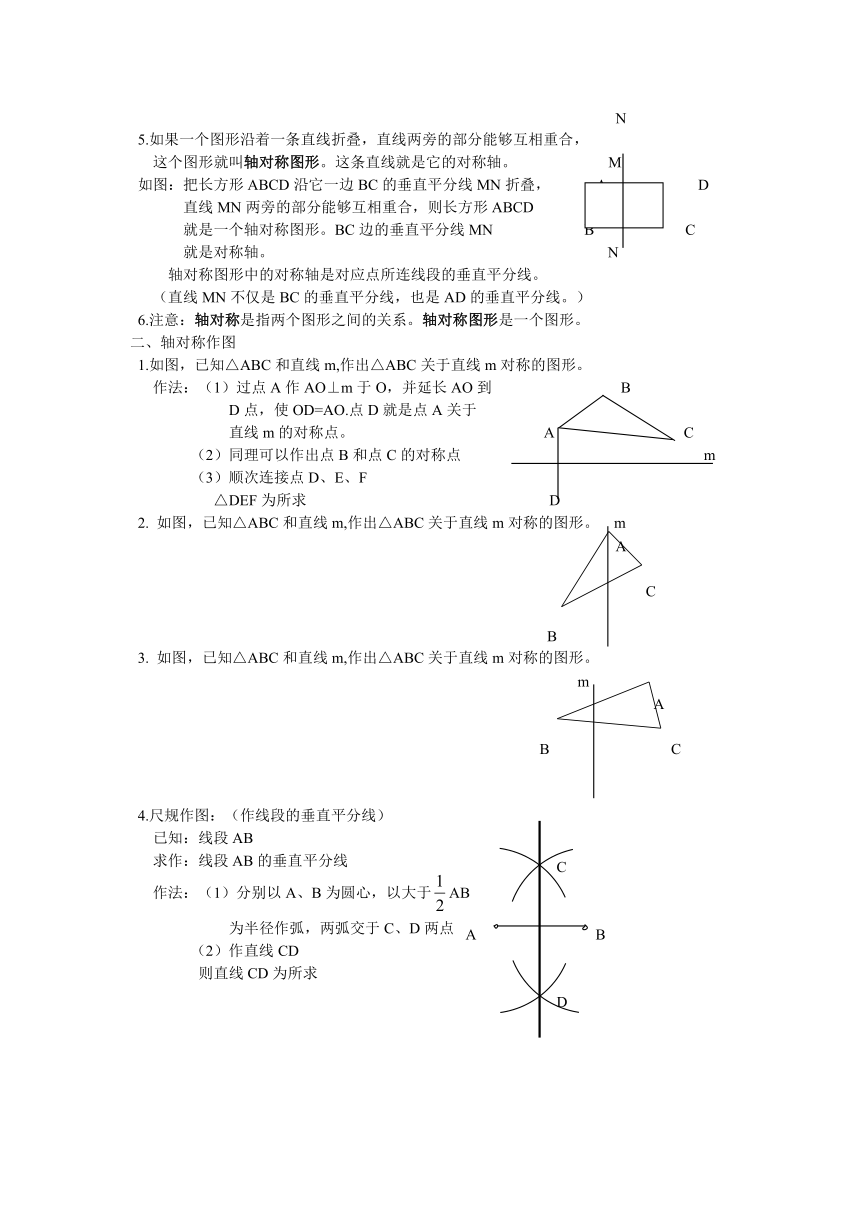
5.如果一个图形沿着一条直线折叠,直线两旁的部分能够互相重合,
这个图形就叫轴对称图形。这条直线就是它的对称轴。 M
如图:把长方形ABCD沿它一边BC的垂直平分线MN折叠, A D
直线MN两旁的部分能够互相重合,则长方形ABCD
就是一个轴对称图形。BC边的垂直平分线MN B C
就是对称轴。 N
轴对称图形中的对称轴是对应点所连线段的垂直平分线。
(直线MN不仅是BC的垂直平分线,也是AD的垂直平分线。)
6.注意:轴对称是指两个图形之间的关系。轴对称图形是一个图形。
二、轴对称作图
1.如图,已知△ABC和直线m,作出△ABC关于直线m对称的图形。
作法:(1)过点A作AO⊥m于O,并延长AO到 B
D点,使OD=AO.点D就是点A关于
直线m的对称点。 A C
(2)同理可以作出点B和点C的对称点 m
(3)顺次连接点D、E、F
△DEF为所求 D
2. 如图,已知△ABC和直线m,作出△ABC关于直线m对称的图形。 m
A
C
B
3. 如图,已知△ABC和直线m,作出△ABC关于直线m对称的图形。
m
A
B C
4.尺规作图:(作线段的垂直平分线)
已知:线段AB
求作:线段AB的垂直平分线
作法:(1)分别以A、B为圆心,以大于AB
为半径作弧,两弧交于C、D两点
(2)作直线CD
则直线CD为所求
三、用坐标表示轴对称
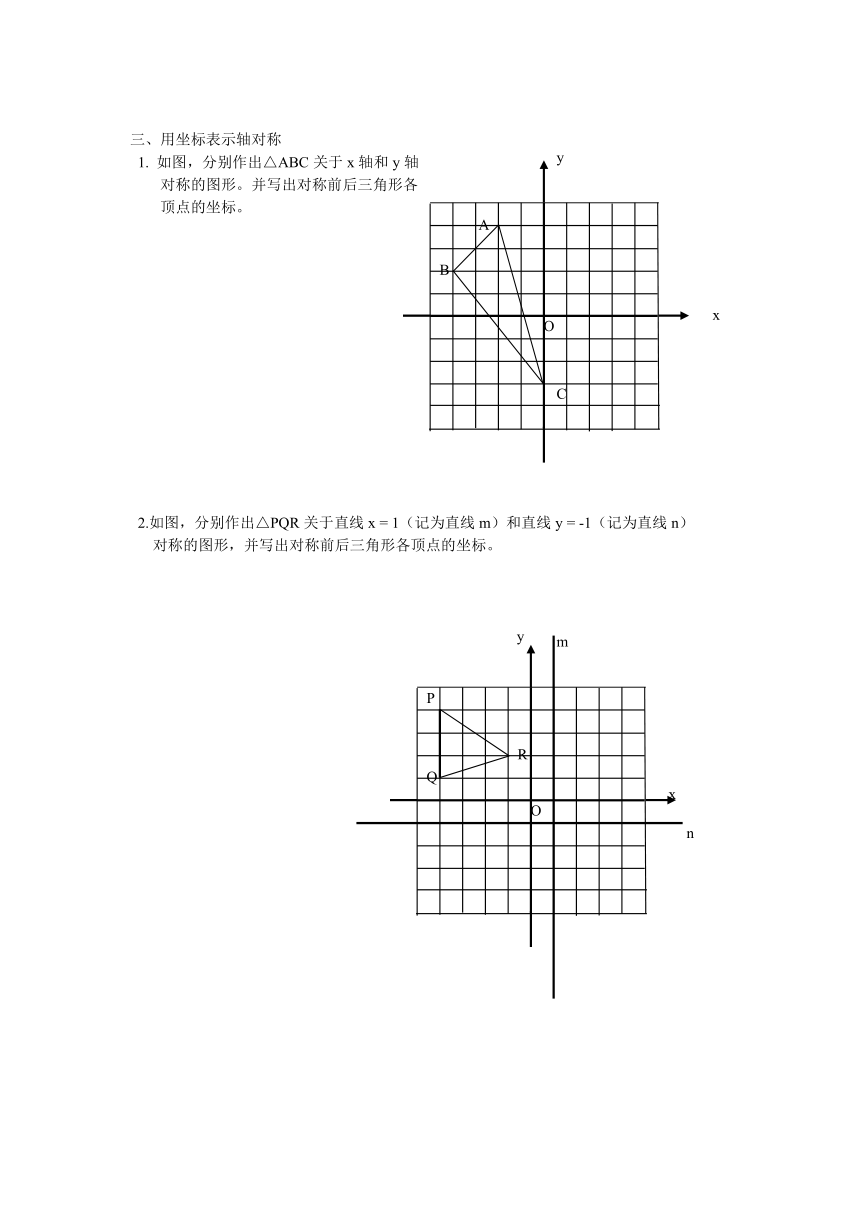
1. 如图,分别作出△ABC关于x轴和y轴
对称的图形。并写出对称前后三角形各
顶点的坐标。
2.如图,分别作出△PQR关于直线x = 1(记为直线m)和直线y = -1(记为直线n)
对称的图形,并写出对称前后三角形各顶点的坐标。
y
x
四、等腰三角形
1.有两条边相等的三角形是等腰三角形。 A
如图,△ABC中,若AB=AC,
则它是一个等腰三角形
B C
2.定理:等腰三角形的两个底角相等。(简称:等边对等角)
如图,△ABC中,若AB=AC A
那么AB边的对角∠C和AC边的对角∠B也相等。
(即:由AB=AC 可得 ∠B=∠C)
B C
3.定理:等腰三角形的顶角平分线、底边上的中线、底边上的高重合。
(简称:等腰三角形“三线合一”) A
如图,等腰△ABC中,AB=AC
线段AD只要具有以下三个身份中的一个
① 顶角∠BAC的平分线,
② 底边BC的中线
③ 底边BC上的高
那么它同时也具备剩下的那两个身份。 B D C
4.定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(简称:等角对等边) (则这个三角形就是一个等腰三角形)
如图,△ABC中,若∠B=∠C A
那么∠B的对边AC和∠C的对边AB也相等。
(即:由∠B=∠C 可得AB=AC)
B C
五、等边三角形
1.三条边都相等的三角形叫等边三角形。 A
如图,△ABC中,若AB=BC=CA
则它就是一个等边三角形,也叫正三角形
B C
2.定理:等边三角形的三个内角都相等,并且每一个角都等于60°
3.定理:有一个角是60°的等腰三角形是等边三角形。 A
4.定理:在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半。
如图,Rt△ACB中,∠C=90°
若∠A=30°,则可得BC=AB B C
第十三章 实数
一、平方根
1.因为3= 9 ,则9是3的平方。而3叫9的平方根。
又有(-3)= 9 ,则 -3也是9的平方根。
也就是说,9的平方根有两个,一个是3,另一个是 -3,它们一正一负,它们互为相反数
2.一般地,如果一个数x的平方等于a ,那么这个数x叫做a的平方根(或二次方根)。
就是说,如果x= a ,那么x叫a的平方根。
3.我们知道:正数有两个平方根。
又:因为:0= 0 所以:0的平方根是0
因为没有任何数的平方等于负数。所以:负数没有平方根
4. 一个正数a的正的平方根用+表示,读作:正的二次根号a (正号通常省略)
其中a叫被开方数,2叫根指数(根指数是2时通常省略)。如: =3
正数a的负的平方根用-表示,读作:负的二次根号a 如:-= -3
合起来:一个正数a的平方根用±表示。
如:9的平方根记为:±=±3 读作:正负根号9等于正负3
5.求一个数的平方根的运算叫做开平方。开平方的运算符号是“±2 ”
如:求16的平方根:±= ±4
6.正数有两个平方根,其中正的那一个平方根叫做这个正数的算术平方根。
如:9的平方根有两个,一个是3,另一个是 -3, 9的算术平方根是3
即:9的算术平方根:= 3 16的算术平方根:= 4
0的算术平方根:= 0
7.正数的算术平方根是正数;0的算术平方根0;负数没有算术平方根
a是非负数时(正数和0叫非负数),表示a的算术平方根。
8.比较大小
(1)因为:= 2 ,= 3 ,= 4 所以:<<
即:等于带根号的数来说,被开方数越大,它的值就越大。如:>
(2)在哪两个整数之间?因为4=,5= 而16<20<25
所以在4和5之间。
二、立方根
1.如果一个数x的立方等于a ,那么这个数x就叫做a的立方根或三次方根。
就是说:如果x= a ,那么x叫a的立方根。
如:2= 8 ,则2是8的立方根。 (-2)= -8 ,则-2是-8的立方根。
2.求一个数的立方根的运算叫做开立方;开立方的运算符号是:读作:三次根号
(根指数3不能省略) 如:8的立方根:= 2 读作:三次根号8等于2
-27的立方根: = 3 读作:三次根号负27等于负3
0的立方根:= 0
3.正数有一个正的立方根,负数有一个负的立方根,0的立方根是0
4.因为 = -2, -= -2 所以 = -
因为 = -3, -= -3 所以 = -
即: = - 如: = -, = -
三、关于逆运算
1.开平方与平方互为逆运算。如:3=9,=3
(1)所以:()= 4(把4开平方再平方,逆运算互相抵消,相当于4没有变化)
同样:()= 9 ,()= 2 ,()= 7 , ()= 11
注意:()是没有意义的【因为负数没有算术平方根,没有意义】
(2)还有:==3 ,=5 ,=6
但是要注意: ≠ - 5 ,而是:==5
2.开立方与立方互为逆运算。如:2= 8 ,= 2
所以:()= 8(把8开立方再立方,逆运算互相抵消,相当于8没有变化)
同样:()= 27 ,()= 5 , ()= -19
== 2 ,=4 ,= -5 ,= -6
四、实数
1.有理数包括整数和分数,而整数和分数都可以写成有限小数或无限循环小数的形式。
如:3=3.0 , -=-0.6 , =0.81
2. 无限不循环小数叫做无理数。如:,-,π,0.12345… ,2.1010010001…
3.有理数和无理数统称实数。
正有理数:2, 0.3,,…
有理数 0
负有理数:-3,-3.1,-…
正无理数:,π,0.12345…
负无理数:-,-π,-0.12345…
正实数:2, 0.1,,,π,0.12345…
实数 0
负实数:-2,-7.3,-,-,-π,-0.12345…
4.当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数。
的相反数是 -, π-3.14的相反数是 -(π-3.14) , |-|=
五、实数运算
1. 3+2=(3+2)= 5 2. 3-2=(3-2)=
3. |- ︳+ 2 = - + 2 = +
4. (+2)= · + 2 =()+ 2 = 2 + 2
5. (+)=· +· =() + = 3 + 1 = 4
第十四章 一次函数
一、常量和变量、自变量与函数
1.汽车以60千米/小时的速度行驶,行驶里程为s千米,行驶时间为t小时,
用式子表达为:s=60t 。在这个变化过程中60是不变的,叫常量;s和t
的值是变化的,叫变量。给定一个t的值,就有唯一的一个s的值与t的
值对应。我们就说t是自变量,s是t的函数。
2.一般地,在一个变化过程中,有两个变量x与y,并且对于x的每一个确定
的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
3.在上例中,我们是用式子s=60t来表达s与t之间的函数关系的。这种用数学式子
表示函数的方法叫做解析式法(或叫关系式法)
4. 在函数s=60t中,当t=3时,s=180,那么180叫做自变量t的值等于3时的函数值。
5. 在上例s=60t中,因为自变量t是表示时间,它不会是负数,所以t≥0
那么t≥0叫做函数s=60t中自变量t的取值范围。
例如:函数y=2x+3 自变量的取值范围是:全体实数
函数y= 自变量的取值范围是:x≠1
函数y= 自变量的取值范围是:x≥2
确定函数自变量的取值范围注意两点:① 使解析式有意义。② 使实际问题有意义。
二、一次函数
1.一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
如:y=2x ,y=-2x(右边是自变量的一次单项式)
2.画出下列正比例函数的图象
(1)y = 2x
解:列表:(在自变量x的取值范围内选取适当的值,算出对应的函数值)
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
描点:(把每组对应值都看成点的坐标,在坐标系中描出这些点)
y y = 2x
连线:(顺次连接各点) 得一条直线, ·
这条直线叫函数y=2x的图象。 ·6
·
·4
·
·2
·
· · · · · · · · · · · · · · ·
· x
·-2
·
·-4
·
·-6
所以函数y=2x的图象也叫直线y=2x
y=-2x y
·6
(2)y=-2x ·
与上面画法一样,可以得到 ·4
函数y = - 2x的图象。 ·
·2
·
· · · · · · · · · · · · · x
·
·-2
·
·-4
·
·-6
3. 正比例函数y=kx(k≠0)的性质
(1)图象是一条经过原点的直线,称为直线y=kx
(2)当k>0时,直线y=kx经过第一、三象限。从左向右上升,即y随x的增大而增大。
当k<0时,直线y=kx经过第二、四象限。从左向右下降,即y随x的增大而减小。
4.一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
当b=0时,就是正比例函数y=kx,即:正比例函数是特殊的一次函数。
5.画函数y = 2x + 1和y = -2x + 1的图像。
列表: x … -2 -1 0 1 2 …
y=2x+1 … -3 -1 1 3 5 …
x … -2 -1 0 1 2 …
y=-2x+1 … 5 3 1 -1 -3 …
描点,连线
y y=2x+1 y=-2x+1 y
· ·
· ·
·4 ·4
· ·
·2 ·2
· ·
· · · · · · · · · x · · · · · · · · · x
· ·
·-2 ·-2
· ·
·-4 ·-4
· ·
· ·
6.一次函数y=kx+b(k≠0)的性质
(1)图像是一条直线。
(2)当k>0时,从左向右上升,即y随x的增大而增大。
当k<0时,从左向右下降,即y随x的增大而减小。
三、正比例函数与一次函数的联系
1.画函数y = 2x , y = 2x + 3 , y = 2x - 3的图象。
列表:
x -2 -1 0 1 2
y=2x -4 -2 0 2 4
y=2x+3 -1 1 3 5 7
y=2x-3
y=2x+3
y=2x
·
·6
·
·4
·
·2
·
· · · · · · · · ·
·
·-2
·
·-4
·
·-6
·
① 对于每一个确定的x的值,函数y=2x+3的值都比函数y=2x的值大3,反映在图象
上就是点的位置高3个单位。
② 即直线y=2x+3上的所有点都比直线y=2x上相应的点高3个单位。(整体来说就是
直线y=2x+3比直线y=2x高3个单位)
③ 把直线y=2x向上平移3个单位就得直线y=2x+3
④ 直线y=2x+3与直线y=2x是平行,平行的原因是k值都等于2
猜想:直线y = 2x - 3在什么地方
(在表中算出y=2x-3的值,画出图象,进行观察、总结)
2. 画函数y = -2x , y = -2x + 3 , y = -2x - 3的图象。
列表:(因为一次函数的图像是直线,所以用两个点就够了)
x 0 1
y = -2x 0 -2
y = -2x + 3 3 1
y = -2x - 3 -3 -5
y=2x+3
y=2x
y=2x-3
2.归纳
(1)对于直线y=kx与直线y=kx+b ,若k= k ,则直线y∥直线y
直线y可以通过平移直线y来得到。b>0时,向上平移b个单位;
b<0时,向下平移∣b∣个单位。
(2)直线y=kx+b与y轴交于点(0,b),b叫直线y=kx+b在y轴上的截距。
(b有正负,即截距有正负)
(3)对于直线y=kx+b
当k>0 ,b>0时,经过第 象限。
当k>0 ,b>0时,经过第 象限。
当k>0 ,b>0时,经过第 象限。
当k>0 ,b>0时,经过第 象限。
四、用待定系数法求函数解析式
1.先设出式子中的未知系数,再根据条件求出未知系数,叫做待定系数法。
2.已知一次函数的图像过点(3,5)与(-4,-9),求这个一次函数的解析式。
解:设这个一次函数的解析式为y=kx+b(k、b这两个系数未知,待定)
得: 3k+b=5 解得: k=2
-4k+b=-9 b=-1
∴ 解析式为 y=2x-1
3.已知正比例函数y=kx ,当x=-2时,y=-1 。求解析式。
4.已知一次函数y=kx+b ,在x=4时,y的值为9 ,在x=6时的值为3 。求解析式。
5.已知y与x成正比例,且x=3时,y=4 ,求关系式。
6.已知y与x-1成正比例,且x=2时,y=-3 ,求y与x的函数关系式。
7.已知y-3与x成正比例,且x=2时,y=7 ,求y与x的函数关系式。
8.直线y=(2m-3)x+m-5与y轴交点的纵坐标为1 ,则m= 。
9.一次函数y=x+m-1的图象与x轴的交点到y轴的距离为4,则此一次函数的解析式为
五、一次函数与一元一次方程和一元一次不等式
1.函数y=2x-4的图象如图所示 y=2x-4
直线y=2x-4与x轴的交点是A(2,0)
(1)点A(2,0)在直线y=2x-4上,意味着
x=2时,可以使y=0 A(2,0)
(2)y=0就是2x-4=0 ,即x=2时,2x-4=0
就是:x=2是方程2x-4=0的解。
总结:函数y=2x-4的图象与x轴的交点A(2,0)
的横坐标x=2就是方程2x-4=0的解。
2.如图,方程mx+2=0的解是 ,m=
y
2 不等式mx+2>0的解集是
x 不等式组0≤mx+2≤2的解集是
y=mx+2
六、用图象法解二元一次方程组
解方程组 x+2y=4 ① y=2x-3
2x-y=3 ② y=-x+2
解:把方程①化为函数形式:y=-x+2
把方程②化为函数形式:y=2x-3
在坐标系中画出直线y=-x+2和直线y=2x-3
两直线交点的坐标为(2,1)
则 x=2 是方程组 x+2y=4 ①
y=1 2x-y=3 ② 的解 (交点坐标为什么就是方程组的解)
不等式mx+2>0的解集是 不等式-x+2>2x-3的解集是
七、一次函数应用题
第十五章 整式的乘除与因式分解
一、幂的运算公式
1.同底数幂相乘:底数不变,指数相加。·=
2.幂的乘方:底数不变,指数相乘。=
3.积的乘方:把积的每一个因式分别乘方,再把所得的幂相乘。=
4.商的乘方:分子、分母分别乘方,再把所得的幂相除。=
二、整式的乘法
1. 单项式乘以单项式:系数乘以系数,相同字母乘以相同字母。对于只在
一个单项式里含有的字母,则连同它的指数保留下来。
如,(2x)·(-5xy)=8x·(-5xy)=[8×(-5)]·(xx)·y=-40xy
2. 单项式乘以多项式:用单项式分别去乘以多项式的每一项。
如,(-4x)·(2x+3x-xy)=(-4x)·(2x)+(-4x)·(3x)+(-4x)·(-xy)
= -8x-12x+4xy
-2a·(ab-b)= -ab + 2ab
3.多项式乘以多项式:用一个多项式的每一项乘以另一个多项式的每一项。
如,(-5m+2)(4m-3) = -20m+ 15m + 8m - 6 = -20m+ 23m - 6
4.乘法公式
平方差公式:(a+b)(a-b)=a-b
如,(3m+2n)(3m-2n)=(3m)-(2n)= 9m-4n
(-4a-1)(4a-1)=(-1-4a)(-1+4a)=(-1)-(4a)=1-16a
完全平方和公式:(a + b)= a + 2ab + b
如,(4x+3y)=(4x)+ 2×4x×3y + (3y)= 16x+ 24xy + 9y
完全平方差公式:(a - b)= a - 2ab + b
如,(-2m-1)=(-2m)- 2×(-2m)×1 + 1= 4m+ 4m + 1
三、整式的除法
1.同底数幂相除:底数不变,指数相减。÷=(a≠0)
2. =1 (≠0) = (≠0 ,p是正整数)
如,(-3)=1 3= =
3.单项式除以单项式:系数除以系数,同底数幂和同底数幂相除。
对于只在被除式里含有的字母,则连同它的指数保留下来。
如,-15abc÷5ab=[(-15)÷5]·(a÷a)·(b÷b)·c =-3ac
4.多项式除以单项式:用多项式的每一项去除以单项式。
如,(25x+ 15xy - 20x)÷(-5x)
=[25x÷(-5x)]+15xy÷(-5x)+(-20x)÷(-5x)
= -5 -3xy + 4x
(-4a + 12ab - 8ab)÷(-4a) = a - 3b + 2ab
四、因式分解
1.把一个多项式化成几个整式的积的形式,叫做因式分解【也叫分解因式】。
2.因式分解的方法
(1)提公因式法:把多项式中各项的公因式提取出来。【提公因式就是做除法】
如,3a- 9ab中,3a和- 9ab这两项共同的因式是3a ,
从3a中提取3a就是做除法:=,即提取后剩下,同理:=-3b
∴3a- 9ab = 3a(a-3b) 【这个因式分解就完成了】
(2)运用公式法:把乘法公式反过来就是因式分解的过程。
乘法公式反过来就成了: a-b = (a+b)(a-b)
a + 2ab + b= (a + b)
a - 2ab + b= (a - b)
这三个公式从左到右就是因式分解的过程。它们可以用来进行因式分解。
如, 1-a=(1=a)(1-a) 8mn-2n=2n(4m-1)=2n(2m+1)(2m-1)
x+6x+9=(x+3) (m+n)-4(m+n)+4=[(m+n)-2]=(m+n-2)
(3)分组分解法:把多项式中能够提取公因式的项,或能够运用公式的项分成一组,
以便用提取公因式法和运用公式法进行因式分解。
如,xy-x+y-1=(xy-x)+(y-1)=x(y-1)+(y-1)=(y-1)(x+1)
-a+ 2ab + ac – bc - b= -( a-2ab+ b)+(ac-bc)
=-(a-b)+c(a-b)
=(a-b)[-(a-b)+c]
=(a-b)(-a+b+c)
(4)十字相乘法
如: 把x+5x+6因式分解:把第一项x和第三项6都分成两个因式的积:
把x分成x和x相乘,6分成2和3相乘,并且竖着写:
x 2
x 3
然后交叉相乘,再把乘得的积相加:3x+2x=5x,相加得到的5x与多项式x+5x+6
的中间项相等,说明算对了。最后横着写 ∴ x+5x+6 =(x+2)(x+3)
因式分解:① y-7y+12=(y -3)(y -4) ② 2x-x-6=(2x+3)(x-2)
y -3 2x 3
y -4 x -2
-4y - 3y = -7y -4x + 3x = - x
注意:第①题中的12不能分成-2乘以-6因为这样乘完后相加得不到-7x
第十六章 分 式
关于分式
1.一般地,如果A、B表示两个整式,并且B中含有字母,那么式子叫分式。
也就是说,分母中含有字母的式子是分式。
2.整式和分式统称为有理式。
3.分母不为0时分式才有意义。
如,当x≠0时,分式有意义。 当x≠2时,分式有意义。
当x≠-时,分式有意义。 当x≠y时,分式有意义。
4.分式的基本性质:分式的分子和分母都乘(或除以)不为0的整式,分式的值不变。
如:=(分子、分母都乘以) =(分子、分母都除以)
5.不改变分式的值,把下列各式的分子与分母中各项的系数都化为整数。
(1) = =
(2)==
6. 不改变分式的值,使下列各式的分子与分母都不含负号。
(1)==【分子、分母都乘以-1】
(2)=(-1)× = -【分式前面乘以-1就是乘到分子上】
(3)===
【总结:分式本身的符号、分子的符号、分母的符号,这三个符号中
任意改变其中两个,分式的值不变】
如:=【同时改变了分子和分母的符号】
=【同时改变了分子的符号和分式本身的符号】
=【同时改变了分子和分母的符号】
二、分式的乘除法
1.约分:把一个分式的分子与分母的公因式约去。【即:分子、分母同时除以公因式】
如: = 【约去公因式5abc】
= = 【约去公因式(x+3)】
= = 2(x-y)【约去公因式3(x-y)】
= = 【约去公因式(x+3)】
注意:分式中出现多项式时,要先因式分解,才容易看出公因式。
【分子、分母没有公因式的分式叫最简分式。约分后的分式应该是最简分式】
2.分式乘法:分子乘分子、分母乘分母。能约分的要约分。
如:(1)· = = 又:· = · =
【先约去公因式,再乘】
(2)· =
=
=
又:· = =
【先约去公因式,再乘】
3.分式的除法:除以一个分式,等于乘以它的倒数。
如:(1)÷ = · = = -
(2)÷ = ·( = -·(
= ·
= -
(3) ÷÷(x-2y)
= ··
= ··
=
4.分式的乘方:分子、分母分别乘方。
如:() = =
÷· = ·· = -
三、分式的加减法
1.同分母的分式相加减:分母不变,分子相加减。
如:+===
-===
2.异分母的分式相加减需要先通分,变成同分母的分式,再加减。
3.通分:把分母不相同的分式化成分母相同的分式。
4.通分需要先找最简公分母。找最简公分母的方法:
(1)最简公分母的的系数取各系数的最小公倍数。
(2)字母取指数大的。
(3)单独的字母参加最简公分母。
5.计算:(1)+=+=+=
(2)=
==
(3)(a+2)- =(a+2)+=+=
四、整数指数幂
1.我们以前学过幂的运算公式:
① 同底数幂相乘:底数不变,指数相加。·=
② 幂的乘方:底数不变,指数相乘。=
③ 积的乘方:把积的每一个因式分别乘方,再把所得的幂相乘。=
④ 商的乘方:分子、分母分别乘方,再把所得的幂相除。=
⑤ 同底数幂相除:底数不变,指数相减。÷=(a≠0)
⑥ =1 (≠0) ⑦ = (≠0 ,p是正整数)
上面公式中的指数m和n是负数时公式仍然成立。如:
( ==
2.科学记数法。
如:2300=2.3×10 420600=4.206×10 2304.23=2.30423×10
(指数=原数的整数位数减1)
又如:0.0023=2.3×10 -0.000205 = -2.05×10 0.01=1×10
0.0001=10
(绝对值小于1的数的科学记数法:指数是负的,到底是负几呢,
是第一个不是0的数前面所有的0的个数。 ( http: / / www.21cnjy.com )包括小数点前面的那个0)
五、分式方程
1.分母中含有未知数的方程叫分式方程。
2.解分式方程:方程两边同时乘以最简公分母,达到去分母的目的,
把分式方程化为整式方程再解方程。
3.最简公分母由各个分母的所有因式组成,相同的因式取指数大的。
4.解方程组:
(1)= (2)=
解:方程两边同时乘以最简公分母x(x-2) 解:=
x=3(x-2) 两边乘以(x+5)(x-5)得
解这个方程 x+5=10
x=3x-6 x=5
x=3 检验:把x=5代入最简公分母(x+5)(x-5)
检验:把x=3代入原方程: 得0
左边==1 ,右边==1 ∴ 原方程无解
左边=右边 【x=5是原方程的增根】
∴ x=3是原方程的解(根)
(3) (4)+=
解:方程两边乘以(x-1)(x+2)得 解:
x(x+2) - (x-1)(x+2)=3 7(x-1)+(x+1)=6x
x+2x-(x+2x-x-2)=3 7x-7+x+1=6x
x+2x-(x+x-2)=3 2x=6
x+2x-x-x+2=3 x=3
x+2=3 经检验x=3是原方程的解
x=1
检验:当x=1时,(x-1)(x+2)=0
∴ 原方程无解
【x=1是原方程的增根】
六、列分式方程解应用题
第十七章 反比例函数
一、反比例函数:一般地,形如(k为不等于0的常数)的函数叫反比例函数。
x是自变量,y是x的函数。自变量x的取值范围是:x≠0
二、反比例函数的图像和性质
1.画反比例函数和的图像
(1)列表
x -6 -4 -3 -2 -1 1 2 3 4 6
y= -1 -1.5 -2 -3 -6 6 3 2 1.5 1
(2)描点、连线
y
·6
·
·4
·
·2
·
· · · · · · · · · · · · · x
·
·-2
·
·-4
·
·
(1)列表:
x -6 -4 -3 -2 -1 1 2 3 4 6
y=- 1 1.5 2 3 6 -6 -3 -2 -1.5 -1
(2)描点、连线
y
·6
·
·4
·
·2
·
· · · · · · · · · · · · · x
·
·-2
·
·-4
·
· ·
2.反比例函数(k为不等于0的常数)的图像的性质:
(1)图像叫双曲线,有两个分支。
(2)当k>0时,图像分别在一、三象限,在每个分支内y随x的增大而减小。
【图像从左向右呈下降趋势】
(3)当k<0时,图像分别在二、四象限,在每个分支内y随x的增大而增大。
【图像从左向右呈上升趋势】
(4)双曲线的两个分支关于原点成中心对称。
(5)双曲线的两个分支无限接近x轴和y轴,但永远不能到达。
三、如图,点P(m,n)在双曲线上, y
过P点作PA⊥x轴,PB⊥y轴。
求长方形OAPB的面积 ( http: / / www.21cnjy.com )
∵ 点P(m,n)在双曲线上 0 x
∴ n= 即 mn=4
∴ S=OA×OB=mn=4 【实际上,在图像上任取一点, (比如H)向两坐标轴作垂线,所围成的长方形面积都等于4】
第十八章 勾股定理
一、勾股定理
1. 勾股定理:直角三角形中,两直角边的平方和等于斜边的平方。
如图,在直角三角形ABC中, A
a和b是直角边,c是斜边
有:
B C
2. 勾股定理公式的变形:
(1) (2) 等等。
3.利用勾股定理画无理数线段
如图,在数轴上画长度为的线段
① 在数轴上从原点向右截取线段OA=3
② 过A点作直线m⊥x轴
③ 在直线m上截取AB=2
④ 连接OB,
则线段OB=为所求。
二、勾股定理的逆定理
1.勾股定理的逆定理:如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形就是直角三角形。【最长的边是斜边,它对的角是直角】
2.如图,在△ABC中, A
如果 AB=5,BC=3,AC=4
那么:
∵ 3
即:BC+AC=AB
则:△ABC是直角三角形,并且AB是斜边,∠C是直角。
3.象3,4,5这样的三个整数,其中两个数的平方和等于第三个数的平方,
则这样的三个整数叫勾股数。如:6,8,10; 5,12,13; 7,24,25;等等。
原命题和逆命题
1.看下面的两个命题:
(1)同位角相等,两直线平行。 (2)两直线平行,同位角相等。
这两个命题的题设和结论互相颠倒,这样的两个命题叫互为逆命题.【简称:互逆命题】
2. (1)同位角相等,两直线平行。(2)两直线平行,同位角相等。
上面的两个互逆命题都是定理,其中一个叫原定理另一个叫逆定理。
3.注意:并不是所有的定理都有逆定理【∵有的定理的逆命题是错误的】
第十九章 平行四边形
一、平行四边形
1.两组对边分别平行的四边形叫平行四边形。
如图,在四边形ABCD中
若,AD∥BC, AB∥DC, 则四边形ABCD是平行四边形 A D
记作:□ ABCD 读作:平行四边形ABCD
对边:AB和DC、AD和BC B C
对角:∠A和∠C、∠B和∠D A D
对角线:AC和BD(如图)
2.平行四边形的性质 B C
(1)平行四边形对边平行。 (2)平行四边形对边相等
(3)平行四边形对角相等。 (4)平行四边形邻角互补。
如图 A D
AB∥DC,AD∥BC(对边平行)
AB=DC,AD=BC(对边相等) B C
∠A=∠C,∠B=∠D(对角相等)
∠A+∠B=180°, ∠A+∠D=180°等(邻角互补)
(5)对角线互相平分
如图, ABCD中, A D
对角线AC和BD相交于O点, O
则有:OA=OC,OB=OD B C
3. 平行四边形的判定定理
(1)两组对边分别平行的四边形是平行四边形。
如图,若AB∥DC,AD∥BC,则四边形ABCD是平行四边形。
(2)两组对边分别相等的四边形是平行四边形。
如图,若AB=DC,AD=BC,则四边形ABCD是平行四边形。
(3)两组对角分别相等的四边形是平行四边形。
如图,若∠A=∠C,∠B=∠D,则四边形ABCD是平行四边形。
(4)对角线互相平分的四边形是平行四边形。
如图,若OA=OC,OB=OD,则四边形ABCD是平行四边形。
O
(5)一组对边平行且相等的四边形是平行四边形。
如图,若AB∥DC并且AB=DC,则四边形ABCD是平行四边形。
如图,若AD∥BC并且AD=BC,则四边形ABCD是平行四边形。
二、三角形的中位线
1.定义:连接三角形两边中点的线段叫三角形的中位线。
如图,△ABC中,点D、E分别是AB、AC的中点
则线段DE叫△ABC的中位线。
2. 三角形的中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半。
如图,线段DE是△ABC的中位线,则DE∥BC,DE=BC
3.如图,点A是直线m外的一点,过A作AE⊥m于E,
则垂线段AE叫点A到直线m的距离。
4.如图,直线a∥b,点A是直线a上的一点,过A作AE⊥b于E,则垂线段AE叫
两条平行线间的距离。
平行线间的距离不只一处,过a上另一点B作BF⊥b于F,则垂线段BF也叫
两条平行线a、b间的距离。
平行线间的距离处处相等。即AE=BF
三、矩形
1.有一个角是直角的平行四边形叫矩形。
如图,若□ ABCD中, 有一个角∠B=90°,则它是矩形。
2.矩形的性质
(1)矩形具有平行四边形的所有性质(因为矩形首先是平行四边形,只不过
它是特殊的平行四边形,特殊在有一个角是直角)
(2)矩形的四个角都是直角,
(3)矩形的对角线相等。
3.定理:直角三角形斜边上的中线等于斜边的一半。
如图,已知,矩形ABCD。
∵ 矩形的对角线相等
∴ AC=BD
又∵ 矩形的对角线互相平分 看Rt△ABC:O为斜边AC的中点,
∴ OA=OC=AC,OB=OD=BD OB为斜边AC上的中线
∴ OA=OC=OB=OD=AC=BD 而OB=AC
4.矩形的判定
(1)有一个角是直角的平行四边形是矩形。
如图,若四边形ABCD是平行四边形,并且有一个角∠B=90°
则它是一个矩形
(2)有三个角是直角的四边形是矩形。
如图,四边形ABCD中,若∠A=∠B=∠C=90°,
则四边形ABCD是矩形。
(3)对角线相等的平行四边形是矩形。
如图,若四边形ABCD是平行四边形,
并且有一组邻边AC=BD,则它是一个矩形。
四、菱形
1.有一组邻边相等的平行四边形叫菱形。
如图,若□ABCD中,有一组邻边AB=BC
则它是一个菱形。
2.菱形的性质
(1)菱形具有平行四边形的所有性质。
(2)菱形的四条边都相等。
如图,若四边形ABCD是菱形,则AB=BC=CD=DA
(3)菱形对角线互相垂直平分,并且每一条对角线平分一组对角。
如图,若四边形ABCD是菱形,则AC⊥BD,OA=OC,OB=OD
并且,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC
(4)菱形的面积等于对角线乘积的一半。
如上图,菱形ABCD的面积=AC·BD
3.菱形的判定
(1)有一组邻边相等的平行四边形是菱形。
如图,若四边形ABCD是平行四边形,
并且有一组邻边AB=BC,则它是一个菱形
(2)四边相等的四边形是菱形。
如图,四边形ABCD中,
若AB=BC=CD=DA,则它是一个菱形
(3)对角线互相垂直的平行四边形是菱形。
如图,若四边形ABCD是平行四边形,并且AC⊥BD
则它是一个菱形
五、正方形
1. 有一个角是直角,并且有一组邻边相等的平行四边形是正方形。
如图,若□ ABCD中, 有一个角∠B=90°,并且有一组邻边AB=BC
则它是一个正方形。
2.正方形的性质(正方形具有平行四边形、矩形、菱形的所有性质)
(1)正方形既是矩形又是菱形。
(2)正方形的对边平行,四边相等。
(3)正方形的四个角都是直角。
如图, AB∥DC,AD∥BC
正方形ABCD AB=BC=CD=DA
∠A=∠B=∠C=∠D=90°
(4)正方形的对角线互相垂直平分,且相等。每一条对角线平分一组对角。
如图,正方形ABCD中,
AC⊥BD,OA=OC=OB=OD=AC=BD,AC=BD
AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC
3.正方形的判定
(1)有一个角是直角,并且有一组邻边相等的平行四边形是正方形。
如图,若□ ABCD中, 有一个角∠B=90°,并且有一组邻边AB=BC
则它是一个正方形。
(2)有一组邻边相等的矩形是正方形。
如图,若四边形ABCD是矩形,并且有一组邻边AB=BC
则它是正方形。
(3)有一个角是直角的菱形是正方形。
如图,若四边形ABCD是菱形,并且有一个角∠B=90°
则它是正方形。
(4)对角线互相垂直的矩形是正方形。
如图,若四边形ABCD是矩形,并且对角线AC⊥BD
则它是正方形。
(5)对角线相等的菱形是正方形。
如图,若四边形ABCD是菱形,并且对角线AC=BD
则它是正方形。
(6)想证明一个四边形是正方形,就要证明它既是矩形又是菱形。
六、梯形
1.有一组对边平行,另一组对边不平行的四边形叫梯形。
如图,四边形ABCD中AD∥BC,AB不平行于DC
则四边形ABCD是一个梯形。
平行的两边叫做底,较短的上底,较长的叫下底。
不平行的两边叫腰。
两底之间的距离叫梯形的高。
2.有一个角是直角的梯形叫直角梯形。
如图,梯形ABCD中,AB⊥BC,
则梯形ABCD就是一个直角梯形。
3. 两腰相等的梯形叫等腰梯形。
如图,梯形ABCD中,AB=DC
则梯形ABCD就是一个等腰梯形。
4.等腰梯形的性质
(1)等腰梯形同一底上的两个角相等。
如图,等腰梯形ABCD中,∠A =∠D,∠B =∠C
(2)等腰梯形的对角线相等。
如图,等腰梯形ABCD中,AC=BD
5.梯形常用辅助线
【作高】
【平移腰,过点D 【平移对角线,过点D
【延长腰】 作DE∥AB,交BC于E】 作DE∥AC,交BC的
延长线于E】
6. 等腰梯形的判定
(1)同一底上的两个角相等梯形是等腰梯形。
如图,梯形ABCD中,AD∥BC
若∠B =∠C,(或∠A =∠D)
则梯形ABCD是等腰梯形。
(2)对角线相等的梯形是等腰梯形。
如图,梯形ABCD中,AD∥BC
若AC=BD,则梯形ABCD是等腰梯形。
7.梯形的中位线:连接梯形两腰中点的线段叫梯形的中位线。
(1)如图,梯形ABCD中,点D、E分别是两腰
AB和DC的中点,则线段DE叫梯形ABCD的中位线。
(2)梯形的中位线平行于两底,并且等于两底和的一半。
如上图,DE是梯形ABCD的中位线,则DE∥BC,并且DE=(AD+BC)
1
2
3
4
E
F
E
F
O
O
B
C
F
D
A
B
C
y
x
A
B
C
O
P
Q
R
O
m
n
实数
无理数
2
4
-2
-4
0
2
4
-2
-4
-2
-4
2
4
0
-2
-4
2
4
0
4
2
-4
-2
x
y
O
-4
-3
-2
-1
1
2
3
4
-4
-3
-2
-1
1
2
3
4
-5
x
y
O
-4
-3
-2
-1
1
2
3
4
-4
-3
-2
-1
1
2
3
4
-2
x
y
O
-4
-3
-2
-1
1
2
3
4
-4
-3
-2
-1
1
2
3
4
3x + 2x = 5x
0
2
4
6
-6
-2
-4
-6
y=
0
2
4
6
-6
-2
-4
-6
y= -
P
H
A
B
a
b
c
m
B
A
O
x
0
1
-5
-4
-3
-2
-1
2
3
4
5
3
4
5
B
C
ABCD
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
D
A
B
C
E
D
A
E
m
B
F
A
E
b
a
A
B
C
D
A
B
C
D
O
A
B
C
D
A
B
C
D
A
B
C
D
O
A
C
B
D
A
C
B
D
A
C
B
D
O
A
C
B
D
A
C
B
D
A
C
B
D
O
A
B
C
D
C
A
D
B
A
B
C
D
O
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
腰
腰
上底
下底
高
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
D
C
E
A
B
D
C
E
A
B
C
D
A
B
C
D
D
A
D
E
C
B
一、全等三角形
1.能够完全重合的两个图形叫全等形。能够完全重合的两个三角形叫全等三角形。
2.两个全等三角形重合在一起时,重合的顶点叫对应顶点,重合的边叫对应边,
重合的角叫对应角。
3.全等三角形性质定理:全等三角形的对应边相等、全等三角形的对应角相等。
4.如图,△ABC平移至△DEF,平移前后的两个三角形全等。
记作:△ABC≌△DEF 读作:△ABC全等于△DEF
A D
B C E F
对应顶点:A和D、 B和E 、C和F
对应角:∠A和∠D、∠B和∠E、∠C和∠F【∠A=∠D、∠B=∠E、∠C=∠F】
对应边:AB和DE、BC和EF、 CA和FD【AB=DE、 BC=EF、 CA=FD】
5.如图,△ABC沿BC翻折到△DEF △ABC≌△DEF
A
对应顶点:A和D、 B和B 、C和C
对应边:BC和BC、AB和DB、AC和DC
B C
(重合的边叫公共边,公共边是对应边)
对应角:∠A和∠D、∠1和∠2、∠3和∠4
D (对应边的对角是对应角)
6.如图,△ABC绕A点旋转180°到△AED △ABC≌△AED
D E 对应顶点:A和A、B和E 、C和D
2 对应角:∠1和∠2、∠B和∠E、∠C和∠D
A
1 (∠1和∠2是对顶角相等,相等的角是对应角)
B C 对应边:BC和ED、AB和AE、AC和AD
(对应角的对边是对应边)
二、三角形全等的判定
1.定理:三边对应相等的两个三角形全等(简称:“边边边”或“SSS”)
如图:△ABC和△DEF
A D
B C E F
若:AB=DE,BC=EF,CA=FD 则可得:△ABC≌△DEF
2.定理:两边和它们的夹角对应相等的两个三角形相等(简称:“边角边”或“SAS”)
如上图:△ABC和△DEF中,若:AB=DE,∠A=∠D,AC=DF 则可得:△ABC≌△DEF
3.定理:两角和它们的夹边对应相等的两个三角形全等(简称:“角边角”或“ASA”)
如上图:△ABC和△DEF中,若∠B=∠E,BC=EF,∠C=∠F,则可得:△ABC≌△DEF
4.定理:两个角和其中一个角的对边对应相等的两个三角形全等(简称:“角角边”或“AAS”)
如上图:△ABC和△DEF中,若∠A=∠D,∠B=∠E,BC=EF,则可得:△ABC≌△DEF
【三角形具有稳定性,而其它多边形都不具有稳定性】
5.定理:斜边和一条直角边对应相等的两个直角三角形全等
(简称:“斜边、直角边”或“HL”)【这个定理只能用于直角三角形全等的判定】
如图,Rt△ACB和 Rt△DFE中
若:AC=DF、AB=DE
则:Rt△ACB≌Rt△DEF A D
C B F E
6.定理:角平分线上的点到角的两边的距离相等。
如图:已知OC平分∠AOB,点P在OC上并且PE⊥OA,PF⊥OB A
C
则可得:PE = PF P
O B
7.定理:到一个角的两边距离相等的点,在这个角的平分线上。
如图:已知PE⊥OA,PF⊥OB并且PE = PF A
则射线OP肯定是∠AOB的平分线
P
O B
8.全等三角形对应边上的高、对应边上的中线、对应角的平分线相等。
全等三角形的周长相等,全等三角形的面积相等。
第十二章 轴对称
一、关于轴对称
1.线段的垂直平分线:经过线段中点(即:平分这条线段)并且垂直于这条线段的直线,
叫做这条线段的垂直平分线(线段的垂直平分线也叫线段的中垂线)
如图,点O线段AB中点,直线MN经过点O,并且MN⊥AB M
则直线MN是线段AB的垂直平分线
(MN⊥AB,OA=OB)
A· · · B
N
2.定理:线段垂直平分线上的点到线段两个端点的距离相等。
如图,直线MN是线段AB的垂直平分线,点C是直线MN上的任意一点
则可得:CA=CB M
C
A B
N
3.定理:到线段两个端点的距离相等的点,必在线段的垂直平分线上。
如图,如果:CA=CB
则:点C肯定在线段AB的垂直平分线上
C
A B
4.把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,
那么就说这两个图形关于这条直线对称。这条直线叫对称轴,折叠
后重合的对应点,叫对称点。两个图形关于直线对称叫轴对称。
如图:△ABC沿直线MN折叠后,与△DEF完全重合,
那么就说△ABC与△DEF关于直线MN成轴对称。 M
直线MN是对称轴
点A与D、B与E、C与F是对称点 A D
定理:关于某条直线对称的两个图形是全等形。
(△ABC≌△DEF)
定理:如果两个图形关于某条直线对称,那么 B E
对称轴是对应点连线的垂直平分线。
(直线MN是线段AD的垂直平分线,同时也是线段 C F
BE、线段CF的垂直平分线) N
定理:两个图形关于某条直线对称,如果它们的对应线段 M
或延长线相交,那么交点在对称轴上。 A D
如图:△ABC与△DCB关于直线MN成轴对称,对应边 E
AC与DB相较于对称轴上的点E;对应边AB与DC
本身不相交,但它们的延长线相交于对称轴上
的点F。
N
5.如果一个图形沿着一条直线折叠,直线两旁的部分能够互相重合,
这个图形就叫轴对称图形。这条直线就是它的对称轴。 M
如图:把长方形ABCD沿它一边BC的垂直平分线MN折叠, A D
直线MN两旁的部分能够互相重合,则长方形ABCD
就是一个轴对称图形。BC边的垂直平分线MN B C
就是对称轴。 N
轴对称图形中的对称轴是对应点所连线段的垂直平分线。
(直线MN不仅是BC的垂直平分线,也是AD的垂直平分线。)
6.注意:轴对称是指两个图形之间的关系。轴对称图形是一个图形。
二、轴对称作图
1.如图,已知△ABC和直线m,作出△ABC关于直线m对称的图形。
作法:(1)过点A作AO⊥m于O,并延长AO到 B
D点,使OD=AO.点D就是点A关于
直线m的对称点。 A C
(2)同理可以作出点B和点C的对称点 m
(3)顺次连接点D、E、F
△DEF为所求 D
2. 如图,已知△ABC和直线m,作出△ABC关于直线m对称的图形。 m
A
C
B
3. 如图,已知△ABC和直线m,作出△ABC关于直线m对称的图形。
m
A
B C
4.尺规作图:(作线段的垂直平分线)
已知:线段AB
求作:线段AB的垂直平分线
作法:(1)分别以A、B为圆心,以大于AB
为半径作弧,两弧交于C、D两点
(2)作直线CD
则直线CD为所求
三、用坐标表示轴对称
1. 如图,分别作出△ABC关于x轴和y轴
对称的图形。并写出对称前后三角形各
顶点的坐标。
2.如图,分别作出△PQR关于直线x = 1(记为直线m)和直线y = -1(记为直线n)
对称的图形,并写出对称前后三角形各顶点的坐标。
y
x
四、等腰三角形
1.有两条边相等的三角形是等腰三角形。 A
如图,△ABC中,若AB=AC,
则它是一个等腰三角形
B C
2.定理:等腰三角形的两个底角相等。(简称:等边对等角)
如图,△ABC中,若AB=AC A
那么AB边的对角∠C和AC边的对角∠B也相等。
(即:由AB=AC 可得 ∠B=∠C)
B C
3.定理:等腰三角形的顶角平分线、底边上的中线、底边上的高重合。
(简称:等腰三角形“三线合一”) A
如图,等腰△ABC中,AB=AC
线段AD只要具有以下三个身份中的一个
① 顶角∠BAC的平分线,
② 底边BC的中线
③ 底边BC上的高
那么它同时也具备剩下的那两个身份。 B D C
4.定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等。
(简称:等角对等边) (则这个三角形就是一个等腰三角形)
如图,△ABC中,若∠B=∠C A
那么∠B的对边AC和∠C的对边AB也相等。
(即:由∠B=∠C 可得AB=AC)
B C
五、等边三角形
1.三条边都相等的三角形叫等边三角形。 A
如图,△ABC中,若AB=BC=CA
则它就是一个等边三角形,也叫正三角形
B C
2.定理:等边三角形的三个内角都相等,并且每一个角都等于60°
3.定理:有一个角是60°的等腰三角形是等边三角形。 A
4.定理:在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半。
如图,Rt△ACB中,∠C=90°
若∠A=30°,则可得BC=AB B C
第十三章 实数
一、平方根
1.因为3= 9 ,则9是3的平方。而3叫9的平方根。
又有(-3)= 9 ,则 -3也是9的平方根。
也就是说,9的平方根有两个,一个是3,另一个是 -3,它们一正一负,它们互为相反数
2.一般地,如果一个数x的平方等于a ,那么这个数x叫做a的平方根(或二次方根)。
就是说,如果x= a ,那么x叫a的平方根。
3.我们知道:正数有两个平方根。
又:因为:0= 0 所以:0的平方根是0
因为没有任何数的平方等于负数。所以:负数没有平方根
4. 一个正数a的正的平方根用+表示,读作:正的二次根号a (正号通常省略)
其中a叫被开方数,2叫根指数(根指数是2时通常省略)。如: =3
正数a的负的平方根用-表示,读作:负的二次根号a 如:-= -3
合起来:一个正数a的平方根用±表示。
如:9的平方根记为:±=±3 读作:正负根号9等于正负3
5.求一个数的平方根的运算叫做开平方。开平方的运算符号是“±2 ”
如:求16的平方根:±= ±4
6.正数有两个平方根,其中正的那一个平方根叫做这个正数的算术平方根。
如:9的平方根有两个,一个是3,另一个是 -3, 9的算术平方根是3
即:9的算术平方根:= 3 16的算术平方根:= 4
0的算术平方根:= 0
7.正数的算术平方根是正数;0的算术平方根0;负数没有算术平方根
a是非负数时(正数和0叫非负数),表示a的算术平方根。
8.比较大小
(1)因为:= 2 ,= 3 ,= 4 所以:<<
即:等于带根号的数来说,被开方数越大,它的值就越大。如:>
(2)在哪两个整数之间?因为4=,5= 而16<20<25
所以在4和5之间。
二、立方根
1.如果一个数x的立方等于a ,那么这个数x就叫做a的立方根或三次方根。
就是说:如果x= a ,那么x叫a的立方根。
如:2= 8 ,则2是8的立方根。 (-2)= -8 ,则-2是-8的立方根。
2.求一个数的立方根的运算叫做开立方;开立方的运算符号是:读作:三次根号
(根指数3不能省略) 如:8的立方根:= 2 读作:三次根号8等于2
-27的立方根: = 3 读作:三次根号负27等于负3
0的立方根:= 0
3.正数有一个正的立方根,负数有一个负的立方根,0的立方根是0
4.因为 = -2, -= -2 所以 = -
因为 = -3, -= -3 所以 = -
即: = - 如: = -, = -
三、关于逆运算
1.开平方与平方互为逆运算。如:3=9,=3
(1)所以:()= 4(把4开平方再平方,逆运算互相抵消,相当于4没有变化)
同样:()= 9 ,()= 2 ,()= 7 , ()= 11
注意:()是没有意义的【因为负数没有算术平方根,没有意义】
(2)还有:==3 ,=5 ,=6
但是要注意: ≠ - 5 ,而是:==5
2.开立方与立方互为逆运算。如:2= 8 ,= 2
所以:()= 8(把8开立方再立方,逆运算互相抵消,相当于8没有变化)
同样:()= 27 ,()= 5 , ()= -19
== 2 ,=4 ,= -5 ,= -6
四、实数
1.有理数包括整数和分数,而整数和分数都可以写成有限小数或无限循环小数的形式。
如:3=3.0 , -=-0.6 , =0.81
2. 无限不循环小数叫做无理数。如:,-,π,0.12345… ,2.1010010001…
3.有理数和无理数统称实数。
正有理数:2, 0.3,,…
有理数 0
负有理数:-3,-3.1,-…
正无理数:,π,0.12345…
负无理数:-,-π,-0.12345…
正实数:2, 0.1,,,π,0.12345…
实数 0
负实数:-2,-7.3,-,-,-π,-0.12345…
4.当数从有理数扩充到实数以后,有理数关于相反数和绝对值的意义同样适合于实数。
的相反数是 -, π-3.14的相反数是 -(π-3.14) , |-|=
五、实数运算
1. 3+2=(3+2)= 5 2. 3-2=(3-2)=
3. |- ︳+ 2 = - + 2 = +
4. (+2)= · + 2 =()+ 2 = 2 + 2
5. (+)=· +· =() + = 3 + 1 = 4
第十四章 一次函数
一、常量和变量、自变量与函数
1.汽车以60千米/小时的速度行驶,行驶里程为s千米,行驶时间为t小时,
用式子表达为:s=60t 。在这个变化过程中60是不变的,叫常量;s和t
的值是变化的,叫变量。给定一个t的值,就有唯一的一个s的值与t的
值对应。我们就说t是自变量,s是t的函数。
2.一般地,在一个变化过程中,有两个变量x与y,并且对于x的每一个确定
的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数。
3.在上例中,我们是用式子s=60t来表达s与t之间的函数关系的。这种用数学式子
表示函数的方法叫做解析式法(或叫关系式法)
4. 在函数s=60t中,当t=3时,s=180,那么180叫做自变量t的值等于3时的函数值。
5. 在上例s=60t中,因为自变量t是表示时间,它不会是负数,所以t≥0
那么t≥0叫做函数s=60t中自变量t的取值范围。
例如:函数y=2x+3 自变量的取值范围是:全体实数
函数y= 自变量的取值范围是:x≠1
函数y= 自变量的取值范围是:x≥2
确定函数自变量的取值范围注意两点:① 使解析式有意义。② 使实际问题有意义。
二、一次函数
1.一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数。
如:y=2x ,y=-2x(右边是自变量的一次单项式)
2.画出下列正比例函数的图象
(1)y = 2x
解:列表:(在自变量x的取值范围内选取适当的值,算出对应的函数值)
x … -3 -2 -1 0 1 2 3 …
y … -6 -4 -2 0 2 4 6 …
描点:(把每组对应值都看成点的坐标,在坐标系中描出这些点)
y y = 2x
连线:(顺次连接各点) 得一条直线, ·
这条直线叫函数y=2x的图象。 ·6
·
·4
·
·2
·
· · · · · · · · · · · · · · ·
· x
·-2
·
·-4
·
·-6
所以函数y=2x的图象也叫直线y=2x
y=-2x y
·6
(2)y=-2x ·
与上面画法一样,可以得到 ·4
函数y = - 2x的图象。 ·
·2
·
· · · · · · · · · · · · · x
·
·-2
·
·-4
·
·-6
3. 正比例函数y=kx(k≠0)的性质
(1)图象是一条经过原点的直线,称为直线y=kx
(2)当k>0时,直线y=kx经过第一、三象限。从左向右上升,即y随x的增大而增大。
当k<0时,直线y=kx经过第二、四象限。从左向右下降,即y随x的增大而减小。
4.一般地,形如y=kx+b(k,b是常数,k≠0)的函数,叫做一次函数。
当b=0时,就是正比例函数y=kx,即:正比例函数是特殊的一次函数。
5.画函数y = 2x + 1和y = -2x + 1的图像。
列表: x … -2 -1 0 1 2 …
y=2x+1 … -3 -1 1 3 5 …
x … -2 -1 0 1 2 …
y=-2x+1 … 5 3 1 -1 -3 …
描点,连线
y y=2x+1 y=-2x+1 y
· ·
· ·
·4 ·4
· ·
·2 ·2
· ·
· · · · · · · · · x · · · · · · · · · x
· ·
·-2 ·-2
· ·
·-4 ·-4
· ·
· ·
6.一次函数y=kx+b(k≠0)的性质
(1)图像是一条直线。
(2)当k>0时,从左向右上升,即y随x的增大而增大。
当k<0时,从左向右下降,即y随x的增大而减小。
三、正比例函数与一次函数的联系
1.画函数y = 2x , y = 2x + 3 , y = 2x - 3的图象。
列表:
x -2 -1 0 1 2
y=2x -4 -2 0 2 4
y=2x+3 -1 1 3 5 7
y=2x-3
y=2x+3
y=2x
·
·6
·
·4
·
·2
·
· · · · · · · · ·
·
·-2
·
·-4
·
·-6
·
① 对于每一个确定的x的值,函数y=2x+3的值都比函数y=2x的值大3,反映在图象
上就是点的位置高3个单位。
② 即直线y=2x+3上的所有点都比直线y=2x上相应的点高3个单位。(整体来说就是
直线y=2x+3比直线y=2x高3个单位)
③ 把直线y=2x向上平移3个单位就得直线y=2x+3
④ 直线y=2x+3与直线y=2x是平行,平行的原因是k值都等于2
猜想:直线y = 2x - 3在什么地方
(在表中算出y=2x-3的值,画出图象,进行观察、总结)
2. 画函数y = -2x , y = -2x + 3 , y = -2x - 3的图象。
列表:(因为一次函数的图像是直线,所以用两个点就够了)
x 0 1
y = -2x 0 -2
y = -2x + 3 3 1
y = -2x - 3 -3 -5
y=2x+3
y=2x
y=2x-3
2.归纳
(1)对于直线y=kx与直线y=kx+b ,若k= k ,则直线y∥直线y
直线y可以通过平移直线y来得到。b>0时,向上平移b个单位;
b<0时,向下平移∣b∣个单位。
(2)直线y=kx+b与y轴交于点(0,b),b叫直线y=kx+b在y轴上的截距。
(b有正负,即截距有正负)
(3)对于直线y=kx+b
当k>0 ,b>0时,经过第 象限。
当k>0 ,b>0时,经过第 象限。
当k>0 ,b>0时,经过第 象限。
当k>0 ,b>0时,经过第 象限。
四、用待定系数法求函数解析式
1.先设出式子中的未知系数,再根据条件求出未知系数,叫做待定系数法。
2.已知一次函数的图像过点(3,5)与(-4,-9),求这个一次函数的解析式。
解:设这个一次函数的解析式为y=kx+b(k、b这两个系数未知,待定)
得: 3k+b=5 解得: k=2
-4k+b=-9 b=-1
∴ 解析式为 y=2x-1
3.已知正比例函数y=kx ,当x=-2时,y=-1 。求解析式。
4.已知一次函数y=kx+b ,在x=4时,y的值为9 ,在x=6时的值为3 。求解析式。
5.已知y与x成正比例,且x=3时,y=4 ,求关系式。
6.已知y与x-1成正比例,且x=2时,y=-3 ,求y与x的函数关系式。
7.已知y-3与x成正比例,且x=2时,y=7 ,求y与x的函数关系式。
8.直线y=(2m-3)x+m-5与y轴交点的纵坐标为1 ,则m= 。
9.一次函数y=x+m-1的图象与x轴的交点到y轴的距离为4,则此一次函数的解析式为
五、一次函数与一元一次方程和一元一次不等式
1.函数y=2x-4的图象如图所示 y=2x-4
直线y=2x-4与x轴的交点是A(2,0)
(1)点A(2,0)在直线y=2x-4上,意味着
x=2时,可以使y=0 A(2,0)
(2)y=0就是2x-4=0 ,即x=2时,2x-4=0
就是:x=2是方程2x-4=0的解。
总结:函数y=2x-4的图象与x轴的交点A(2,0)
的横坐标x=2就是方程2x-4=0的解。
2.如图,方程mx+2=0的解是 ,m=
y
2 不等式mx+2>0的解集是
x 不等式组0≤mx+2≤2的解集是
y=mx+2
六、用图象法解二元一次方程组
解方程组 x+2y=4 ① y=2x-3
2x-y=3 ② y=-x+2
解:把方程①化为函数形式:y=-x+2
把方程②化为函数形式:y=2x-3
在坐标系中画出直线y=-x+2和直线y=2x-3
两直线交点的坐标为(2,1)
则 x=2 是方程组 x+2y=4 ①
y=1 2x-y=3 ② 的解 (交点坐标为什么就是方程组的解)
不等式mx+2>0的解集是 不等式-x+2>2x-3的解集是
七、一次函数应用题
第十五章 整式的乘除与因式分解
一、幂的运算公式
1.同底数幂相乘:底数不变,指数相加。·=
2.幂的乘方:底数不变,指数相乘。=
3.积的乘方:把积的每一个因式分别乘方,再把所得的幂相乘。=
4.商的乘方:分子、分母分别乘方,再把所得的幂相除。=
二、整式的乘法
1. 单项式乘以单项式:系数乘以系数,相同字母乘以相同字母。对于只在
一个单项式里含有的字母,则连同它的指数保留下来。
如,(2x)·(-5xy)=8x·(-5xy)=[8×(-5)]·(xx)·y=-40xy
2. 单项式乘以多项式:用单项式分别去乘以多项式的每一项。
如,(-4x)·(2x+3x-xy)=(-4x)·(2x)+(-4x)·(3x)+(-4x)·(-xy)
= -8x-12x+4xy
-2a·(ab-b)= -ab + 2ab
3.多项式乘以多项式:用一个多项式的每一项乘以另一个多项式的每一项。
如,(-5m+2)(4m-3) = -20m+ 15m + 8m - 6 = -20m+ 23m - 6
4.乘法公式
平方差公式:(a+b)(a-b)=a-b
如,(3m+2n)(3m-2n)=(3m)-(2n)= 9m-4n
(-4a-1)(4a-1)=(-1-4a)(-1+4a)=(-1)-(4a)=1-16a
完全平方和公式:(a + b)= a + 2ab + b
如,(4x+3y)=(4x)+ 2×4x×3y + (3y)= 16x+ 24xy + 9y
完全平方差公式:(a - b)= a - 2ab + b
如,(-2m-1)=(-2m)- 2×(-2m)×1 + 1= 4m+ 4m + 1
三、整式的除法
1.同底数幂相除:底数不变,指数相减。÷=(a≠0)
2. =1 (≠0) = (≠0 ,p是正整数)
如,(-3)=1 3= =
3.单项式除以单项式:系数除以系数,同底数幂和同底数幂相除。
对于只在被除式里含有的字母,则连同它的指数保留下来。
如,-15abc÷5ab=[(-15)÷5]·(a÷a)·(b÷b)·c =-3ac
4.多项式除以单项式:用多项式的每一项去除以单项式。
如,(25x+ 15xy - 20x)÷(-5x)
=[25x÷(-5x)]+15xy÷(-5x)+(-20x)÷(-5x)
= -5 -3xy + 4x
(-4a + 12ab - 8ab)÷(-4a) = a - 3b + 2ab
四、因式分解
1.把一个多项式化成几个整式的积的形式,叫做因式分解【也叫分解因式】。
2.因式分解的方法
(1)提公因式法:把多项式中各项的公因式提取出来。【提公因式就是做除法】
如,3a- 9ab中,3a和- 9ab这两项共同的因式是3a ,
从3a中提取3a就是做除法:=,即提取后剩下,同理:=-3b
∴3a- 9ab = 3a(a-3b) 【这个因式分解就完成了】
(2)运用公式法:把乘法公式反过来就是因式分解的过程。
乘法公式反过来就成了: a-b = (a+b)(a-b)
a + 2ab + b= (a + b)
a - 2ab + b= (a - b)
这三个公式从左到右就是因式分解的过程。它们可以用来进行因式分解。
如, 1-a=(1=a)(1-a) 8mn-2n=2n(4m-1)=2n(2m+1)(2m-1)
x+6x+9=(x+3) (m+n)-4(m+n)+4=[(m+n)-2]=(m+n-2)
(3)分组分解法:把多项式中能够提取公因式的项,或能够运用公式的项分成一组,
以便用提取公因式法和运用公式法进行因式分解。
如,xy-x+y-1=(xy-x)+(y-1)=x(y-1)+(y-1)=(y-1)(x+1)
-a+ 2ab + ac – bc - b= -( a-2ab+ b)+(ac-bc)
=-(a-b)+c(a-b)
=(a-b)[-(a-b)+c]
=(a-b)(-a+b+c)
(4)十字相乘法
如: 把x+5x+6因式分解:把第一项x和第三项6都分成两个因式的积:
把x分成x和x相乘,6分成2和3相乘,并且竖着写:
x 2
x 3
然后交叉相乘,再把乘得的积相加:3x+2x=5x,相加得到的5x与多项式x+5x+6
的中间项相等,说明算对了。最后横着写 ∴ x+5x+6 =(x+2)(x+3)
因式分解:① y-7y+12=(y -3)(y -4) ② 2x-x-6=(2x+3)(x-2)
y -3 2x 3
y -4 x -2
-4y - 3y = -7y -4x + 3x = - x
注意:第①题中的12不能分成-2乘以-6因为这样乘完后相加得不到-7x
第十六章 分 式
关于分式
1.一般地,如果A、B表示两个整式,并且B中含有字母,那么式子叫分式。
也就是说,分母中含有字母的式子是分式。
2.整式和分式统称为有理式。
3.分母不为0时分式才有意义。
如,当x≠0时,分式有意义。 当x≠2时,分式有意义。
当x≠-时,分式有意义。 当x≠y时,分式有意义。
4.分式的基本性质:分式的分子和分母都乘(或除以)不为0的整式,分式的值不变。
如:=(分子、分母都乘以) =(分子、分母都除以)
5.不改变分式的值,把下列各式的分子与分母中各项的系数都化为整数。
(1) = =
(2)==
6. 不改变分式的值,使下列各式的分子与分母都不含负号。
(1)==【分子、分母都乘以-1】
(2)=(-1)× = -【分式前面乘以-1就是乘到分子上】
(3)===
【总结:分式本身的符号、分子的符号、分母的符号,这三个符号中
任意改变其中两个,分式的值不变】
如:=【同时改变了分子和分母的符号】
=【同时改变了分子的符号和分式本身的符号】
=【同时改变了分子和分母的符号】
二、分式的乘除法
1.约分:把一个分式的分子与分母的公因式约去。【即:分子、分母同时除以公因式】
如: = 【约去公因式5abc】
= = 【约去公因式(x+3)】
= = 2(x-y)【约去公因式3(x-y)】
= = 【约去公因式(x+3)】
注意:分式中出现多项式时,要先因式分解,才容易看出公因式。
【分子、分母没有公因式的分式叫最简分式。约分后的分式应该是最简分式】
2.分式乘法:分子乘分子、分母乘分母。能约分的要约分。
如:(1)· = = 又:· = · =
【先约去公因式,再乘】
(2)· =
=
=
又:· = =
【先约去公因式,再乘】
3.分式的除法:除以一个分式,等于乘以它的倒数。
如:(1)÷ = · = = -
(2)÷ = ·( = -·(
= ·
= -
(3) ÷÷(x-2y)
= ··
= ··
=
4.分式的乘方:分子、分母分别乘方。
如:() = =
÷· = ·· = -
三、分式的加减法
1.同分母的分式相加减:分母不变,分子相加减。
如:+===
-===
2.异分母的分式相加减需要先通分,变成同分母的分式,再加减。
3.通分:把分母不相同的分式化成分母相同的分式。
4.通分需要先找最简公分母。找最简公分母的方法:
(1)最简公分母的的系数取各系数的最小公倍数。
(2)字母取指数大的。
(3)单独的字母参加最简公分母。
5.计算:(1)+=+=+=
(2)=
==
(3)(a+2)- =(a+2)+=+=
四、整数指数幂
1.我们以前学过幂的运算公式:
① 同底数幂相乘:底数不变,指数相加。·=
② 幂的乘方:底数不变,指数相乘。=
③ 积的乘方:把积的每一个因式分别乘方,再把所得的幂相乘。=
④ 商的乘方:分子、分母分别乘方,再把所得的幂相除。=
⑤ 同底数幂相除:底数不变,指数相减。÷=(a≠0)
⑥ =1 (≠0) ⑦ = (≠0 ,p是正整数)
上面公式中的指数m和n是负数时公式仍然成立。如:
( ==
2.科学记数法。
如:2300=2.3×10 420600=4.206×10 2304.23=2.30423×10
(指数=原数的整数位数减1)
又如:0.0023=2.3×10 -0.000205 = -2.05×10 0.01=1×10
0.0001=10
(绝对值小于1的数的科学记数法:指数是负的,到底是负几呢,
是第一个不是0的数前面所有的0的个数。 ( http: / / www.21cnjy.com )包括小数点前面的那个0)
五、分式方程
1.分母中含有未知数的方程叫分式方程。
2.解分式方程:方程两边同时乘以最简公分母,达到去分母的目的,
把分式方程化为整式方程再解方程。
3.最简公分母由各个分母的所有因式组成,相同的因式取指数大的。
4.解方程组:
(1)= (2)=
解:方程两边同时乘以最简公分母x(x-2) 解:=
x=3(x-2) 两边乘以(x+5)(x-5)得
解这个方程 x+5=10
x=3x-6 x=5
x=3 检验:把x=5代入最简公分母(x+5)(x-5)
检验:把x=3代入原方程: 得0
左边==1 ,右边==1 ∴ 原方程无解
左边=右边 【x=5是原方程的增根】
∴ x=3是原方程的解(根)
(3) (4)+=
解:方程两边乘以(x-1)(x+2)得 解:
x(x+2) - (x-1)(x+2)=3 7(x-1)+(x+1)=6x
x+2x-(x+2x-x-2)=3 7x-7+x+1=6x
x+2x-(x+x-2)=3 2x=6
x+2x-x-x+2=3 x=3
x+2=3 经检验x=3是原方程的解
x=1
检验:当x=1时,(x-1)(x+2)=0
∴ 原方程无解
【x=1是原方程的增根】
六、列分式方程解应用题
第十七章 反比例函数
一、反比例函数:一般地,形如(k为不等于0的常数)的函数叫反比例函数。
x是自变量,y是x的函数。自变量x的取值范围是:x≠0
二、反比例函数的图像和性质
1.画反比例函数和的图像
(1)列表
x -6 -4 -3 -2 -1 1 2 3 4 6
y= -1 -1.5 -2 -3 -6 6 3 2 1.5 1
(2)描点、连线
y
·6
·
·4
·
·2
·
· · · · · · · · · · · · · x
·
·-2
·
·-4
·
·
(1)列表:
x -6 -4 -3 -2 -1 1 2 3 4 6
y=- 1 1.5 2 3 6 -6 -3 -2 -1.5 -1
(2)描点、连线
y
·6
·
·4
·
·2
·
· · · · · · · · · · · · · x
·
·-2
·
·-4
·
· ·
2.反比例函数(k为不等于0的常数)的图像的性质:
(1)图像叫双曲线,有两个分支。
(2)当k>0时,图像分别在一、三象限,在每个分支内y随x的增大而减小。
【图像从左向右呈下降趋势】
(3)当k<0时,图像分别在二、四象限,在每个分支内y随x的增大而增大。
【图像从左向右呈上升趋势】
(4)双曲线的两个分支关于原点成中心对称。
(5)双曲线的两个分支无限接近x轴和y轴,但永远不能到达。
三、如图,点P(m,n)在双曲线上, y
过P点作PA⊥x轴,PB⊥y轴。
求长方形OAPB的面积 ( http: / / www.21cnjy.com )
∵ 点P(m,n)在双曲线上 0 x
∴ n= 即 mn=4
∴ S=OA×OB=mn=4 【实际上,在图像上任取一点, (比如H)向两坐标轴作垂线,所围成的长方形面积都等于4】
第十八章 勾股定理
一、勾股定理
1. 勾股定理:直角三角形中,两直角边的平方和等于斜边的平方。
如图,在直角三角形ABC中, A
a和b是直角边,c是斜边
有:
B C
2. 勾股定理公式的变形:
(1) (2) 等等。
3.利用勾股定理画无理数线段
如图,在数轴上画长度为的线段
① 在数轴上从原点向右截取线段OA=3
② 过A点作直线m⊥x轴
③ 在直线m上截取AB=2
④ 连接OB,
则线段OB=为所求。
二、勾股定理的逆定理
1.勾股定理的逆定理:如果一个三角形两边的平方和等于第三边的平方,
那么这个三角形就是直角三角形。【最长的边是斜边,它对的角是直角】
2.如图,在△ABC中, A
如果 AB=5,BC=3,AC=4
那么:
∵ 3
即:BC+AC=AB
则:△ABC是直角三角形,并且AB是斜边,∠C是直角。
3.象3,4,5这样的三个整数,其中两个数的平方和等于第三个数的平方,
则这样的三个整数叫勾股数。如:6,8,10; 5,12,13; 7,24,25;等等。
原命题和逆命题
1.看下面的两个命题:
(1)同位角相等,两直线平行。 (2)两直线平行,同位角相等。
这两个命题的题设和结论互相颠倒,这样的两个命题叫互为逆命题.【简称:互逆命题】
2. (1)同位角相等,两直线平行。(2)两直线平行,同位角相等。
上面的两个互逆命题都是定理,其中一个叫原定理另一个叫逆定理。
3.注意:并不是所有的定理都有逆定理【∵有的定理的逆命题是错误的】
第十九章 平行四边形
一、平行四边形
1.两组对边分别平行的四边形叫平行四边形。
如图,在四边形ABCD中
若,AD∥BC, AB∥DC, 则四边形ABCD是平行四边形 A D
记作:□ ABCD 读作:平行四边形ABCD
对边:AB和DC、AD和BC B C
对角:∠A和∠C、∠B和∠D A D
对角线:AC和BD(如图)
2.平行四边形的性质 B C
(1)平行四边形对边平行。 (2)平行四边形对边相等
(3)平行四边形对角相等。 (4)平行四边形邻角互补。
如图 A D
AB∥DC,AD∥BC(对边平行)
AB=DC,AD=BC(对边相等) B C
∠A=∠C,∠B=∠D(对角相等)
∠A+∠B=180°, ∠A+∠D=180°等(邻角互补)
(5)对角线互相平分
如图, ABCD中, A D
对角线AC和BD相交于O点, O
则有:OA=OC,OB=OD B C
3. 平行四边形的判定定理
(1)两组对边分别平行的四边形是平行四边形。
如图,若AB∥DC,AD∥BC,则四边形ABCD是平行四边形。
(2)两组对边分别相等的四边形是平行四边形。
如图,若AB=DC,AD=BC,则四边形ABCD是平行四边形。
(3)两组对角分别相等的四边形是平行四边形。
如图,若∠A=∠C,∠B=∠D,则四边形ABCD是平行四边形。
(4)对角线互相平分的四边形是平行四边形。
如图,若OA=OC,OB=OD,则四边形ABCD是平行四边形。
O
(5)一组对边平行且相等的四边形是平行四边形。
如图,若AB∥DC并且AB=DC,则四边形ABCD是平行四边形。
如图,若AD∥BC并且AD=BC,则四边形ABCD是平行四边形。
二、三角形的中位线
1.定义:连接三角形两边中点的线段叫三角形的中位线。
如图,△ABC中,点D、E分别是AB、AC的中点
则线段DE叫△ABC的中位线。
2. 三角形的中位线定理
三角形的中位线平行于第三边,并且等于第三边的一半。
如图,线段DE是△ABC的中位线,则DE∥BC,DE=BC
3.如图,点A是直线m外的一点,过A作AE⊥m于E,
则垂线段AE叫点A到直线m的距离。
4.如图,直线a∥b,点A是直线a上的一点,过A作AE⊥b于E,则垂线段AE叫
两条平行线间的距离。
平行线间的距离不只一处,过a上另一点B作BF⊥b于F,则垂线段BF也叫
两条平行线a、b间的距离。
平行线间的距离处处相等。即AE=BF
三、矩形
1.有一个角是直角的平行四边形叫矩形。
如图,若□ ABCD中, 有一个角∠B=90°,则它是矩形。
2.矩形的性质
(1)矩形具有平行四边形的所有性质(因为矩形首先是平行四边形,只不过
它是特殊的平行四边形,特殊在有一个角是直角)
(2)矩形的四个角都是直角,
(3)矩形的对角线相等。
3.定理:直角三角形斜边上的中线等于斜边的一半。
如图,已知,矩形ABCD。
∵ 矩形的对角线相等
∴ AC=BD
又∵ 矩形的对角线互相平分 看Rt△ABC:O为斜边AC的中点,
∴ OA=OC=AC,OB=OD=BD OB为斜边AC上的中线
∴ OA=OC=OB=OD=AC=BD 而OB=AC
4.矩形的判定
(1)有一个角是直角的平行四边形是矩形。
如图,若四边形ABCD是平行四边形,并且有一个角∠B=90°
则它是一个矩形
(2)有三个角是直角的四边形是矩形。
如图,四边形ABCD中,若∠A=∠B=∠C=90°,
则四边形ABCD是矩形。
(3)对角线相等的平行四边形是矩形。
如图,若四边形ABCD是平行四边形,
并且有一组邻边AC=BD,则它是一个矩形。
四、菱形
1.有一组邻边相等的平行四边形叫菱形。
如图,若□ABCD中,有一组邻边AB=BC
则它是一个菱形。
2.菱形的性质
(1)菱形具有平行四边形的所有性质。
(2)菱形的四条边都相等。
如图,若四边形ABCD是菱形,则AB=BC=CD=DA
(3)菱形对角线互相垂直平分,并且每一条对角线平分一组对角。
如图,若四边形ABCD是菱形,则AC⊥BD,OA=OC,OB=OD
并且,AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC
(4)菱形的面积等于对角线乘积的一半。
如上图,菱形ABCD的面积=AC·BD
3.菱形的判定
(1)有一组邻边相等的平行四边形是菱形。
如图,若四边形ABCD是平行四边形,
并且有一组邻边AB=BC,则它是一个菱形
(2)四边相等的四边形是菱形。
如图,四边形ABCD中,
若AB=BC=CD=DA,则它是一个菱形
(3)对角线互相垂直的平行四边形是菱形。
如图,若四边形ABCD是平行四边形,并且AC⊥BD
则它是一个菱形
五、正方形
1. 有一个角是直角,并且有一组邻边相等的平行四边形是正方形。
如图,若□ ABCD中, 有一个角∠B=90°,并且有一组邻边AB=BC
则它是一个正方形。
2.正方形的性质(正方形具有平行四边形、矩形、菱形的所有性质)
(1)正方形既是矩形又是菱形。
(2)正方形的对边平行,四边相等。
(3)正方形的四个角都是直角。
如图, AB∥DC,AD∥BC
正方形ABCD AB=BC=CD=DA
∠A=∠B=∠C=∠D=90°
(4)正方形的对角线互相垂直平分,且相等。每一条对角线平分一组对角。
如图,正方形ABCD中,
AC⊥BD,OA=OC=OB=OD=AC=BD,AC=BD
AC平分∠BAD和∠BCD,BD平分∠ABC和∠ADC
3.正方形的判定
(1)有一个角是直角,并且有一组邻边相等的平行四边形是正方形。
如图,若□ ABCD中, 有一个角∠B=90°,并且有一组邻边AB=BC
则它是一个正方形。
(2)有一组邻边相等的矩形是正方形。
如图,若四边形ABCD是矩形,并且有一组邻边AB=BC
则它是正方形。
(3)有一个角是直角的菱形是正方形。
如图,若四边形ABCD是菱形,并且有一个角∠B=90°
则它是正方形。
(4)对角线互相垂直的矩形是正方形。
如图,若四边形ABCD是矩形,并且对角线AC⊥BD
则它是正方形。
(5)对角线相等的菱形是正方形。
如图,若四边形ABCD是菱形,并且对角线AC=BD
则它是正方形。
(6)想证明一个四边形是正方形,就要证明它既是矩形又是菱形。
六、梯形
1.有一组对边平行,另一组对边不平行的四边形叫梯形。
如图,四边形ABCD中AD∥BC,AB不平行于DC
则四边形ABCD是一个梯形。
平行的两边叫做底,较短的上底,较长的叫下底。
不平行的两边叫腰。
两底之间的距离叫梯形的高。
2.有一个角是直角的梯形叫直角梯形。
如图,梯形ABCD中,AB⊥BC,
则梯形ABCD就是一个直角梯形。
3. 两腰相等的梯形叫等腰梯形。
如图,梯形ABCD中,AB=DC
则梯形ABCD就是一个等腰梯形。
4.等腰梯形的性质
(1)等腰梯形同一底上的两个角相等。
如图,等腰梯形ABCD中,∠A =∠D,∠B =∠C
(2)等腰梯形的对角线相等。
如图,等腰梯形ABCD中,AC=BD
5.梯形常用辅助线
【作高】
【平移腰,过点D 【平移对角线,过点D
【延长腰】 作DE∥AB,交BC于E】 作DE∥AC,交BC的
延长线于E】
6. 等腰梯形的判定
(1)同一底上的两个角相等梯形是等腰梯形。
如图,梯形ABCD中,AD∥BC
若∠B =∠C,(或∠A =∠D)
则梯形ABCD是等腰梯形。
(2)对角线相等的梯形是等腰梯形。
如图,梯形ABCD中,AD∥BC
若AC=BD,则梯形ABCD是等腰梯形。
7.梯形的中位线:连接梯形两腰中点的线段叫梯形的中位线。
(1)如图,梯形ABCD中,点D、E分别是两腰
AB和DC的中点,则线段DE叫梯形ABCD的中位线。
(2)梯形的中位线平行于两底,并且等于两底和的一半。
如上图,DE是梯形ABCD的中位线,则DE∥BC,并且DE=(AD+BC)
1
2
3
4
E
F
E
F
O
O
B
C
F
D
A
B
C
y
x
A
B
C
O
P
Q
R
O
m
n
实数
无理数
2
4
-2
-4
0
2
4
-2
-4
-2
-4
2
4
0
-2
-4
2
4
0
4
2
-4
-2
x
y
O
-4
-3
-2
-1
1
2
3
4
-4
-3
-2
-1
1
2
3
4
-5
x
y
O
-4
-3
-2
-1
1
2
3
4
-4
-3
-2
-1
1
2
3
4
-2
x
y
O
-4
-3
-2
-1
1
2
3
4
-4
-3
-2
-1
1
2
3
4
3x + 2x = 5x
0
2
4
6
-6
-2
-4
-6
y=
0
2
4
6
-6
-2
-4
-6
y= -
P
H
A
B
a
b
c
m
B
A
O
x
0
1
-5
-4
-3
-2
-1
2
3
4
5
3
4
5
B
C
ABCD
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
D
A
B
C
E
D
A
E
m
B
F
A
E
b
a
A
B
C
D
A
B
C
D
O
A
B
C
D
A
B
C
D
A
B
C
D
O
A
C
B
D
A
C
B
D
A
C
B
D
O
A
C
B
D
A
C
B
D
A
C
B
D
O
A
B
C
D
C
A
D
B
A
B
C
D
O
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
O
A
B
C
D
O
A
B
C
D
E
腰
腰
上底
下底
高
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
D
C
E
A
B
D
C
E
A
B
C
D
A
B
C
D
D
A
D
E
C
B
同课章节目录
