第6单元长方形和正方形的面积典例分析与精选好题(讲义)数学三年级下册苏教版(含解析)
文档属性
| 名称 | 第6单元长方形和正方形的面积典例分析与精选好题(讲义)数学三年级下册苏教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 406.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-18 14:31:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第6单元长方形和正方形的面积典例分析与精选好题(讲义)数学三年级下册苏教版
典例分析一
.导盲砖是一种为盲人铺设盲道的特殊地砖。现在要在一条长120米的人行道中间铺设宽为6分米的盲道,如果选用边长为3分米的正方形导盲砖,需要多少块这样的导盲砖?
【答案】解:120米=1200分米
(6÷3)×(1200÷3)
=2×400
=800(块)
答:需要800块这样的导盲砖。
典例分析二
.一根软铁丝能围成一个长是6cm,宽是2cm的长方形。如果用这根铁丝围成一个正方形,这个正方形的面积是多少平方厘米?
【答案】解:(6+2)×2÷4
=8×2÷4
=16÷4
=4(cm)
4×4=16(cm2)
答:这个正方形的面积是16平方厘米。
典例分析三
.一辆洒水车每分行驶50m,洒水的宽度是10m,如果洒水车行驶8分钟,洒过水的地面的面积是多大?
【答案】解:50×10=500(平方米)
500×8=4000(平方米)
答:洒过水的地面的面积是4000平方米。
精选好题
1.王大爷用篱笆靠墙围了一个长8米、宽6米的长方形菜园。如果每平方米种10棵大白菜,这个菜园一共可以种多少棵大白菜?
2.一个长方形花圃,长35米,宽28米。
(1)这个长方形花圃的面积是多少平方米?
(2)如果每平方米可以种3株凤仙花,这个花圃一共能种多少株凤仙花?
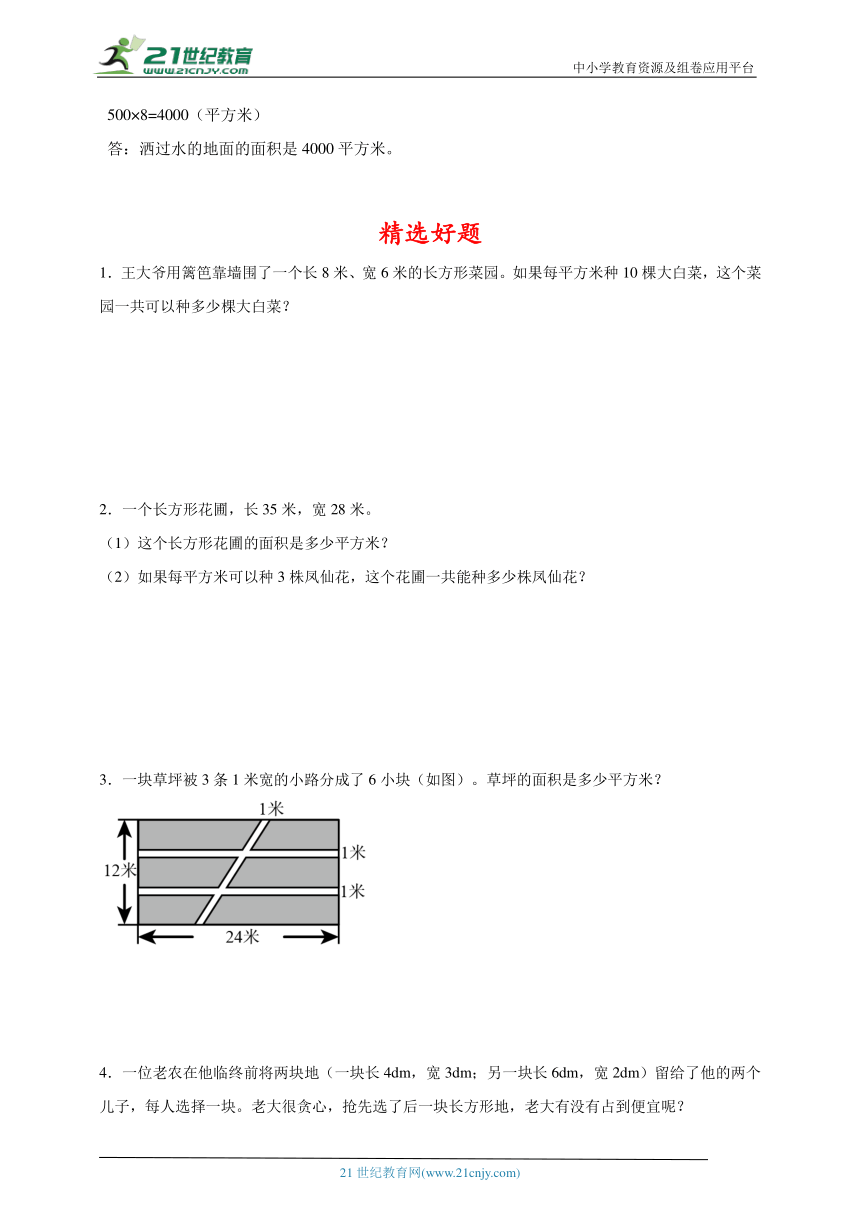
3.一块草坪被3条1米宽的小路分成了6小块(如图)。草坪的面积是多少平方米?
4.一位老农在他临终前将两块地(一块长4dm,宽3dm;另一块长6dm,宽2dm)留给了他的两个儿子,每人选择一块。老大很贪心,抢先选了后一块长方形地,老大有没有占到便宜呢?
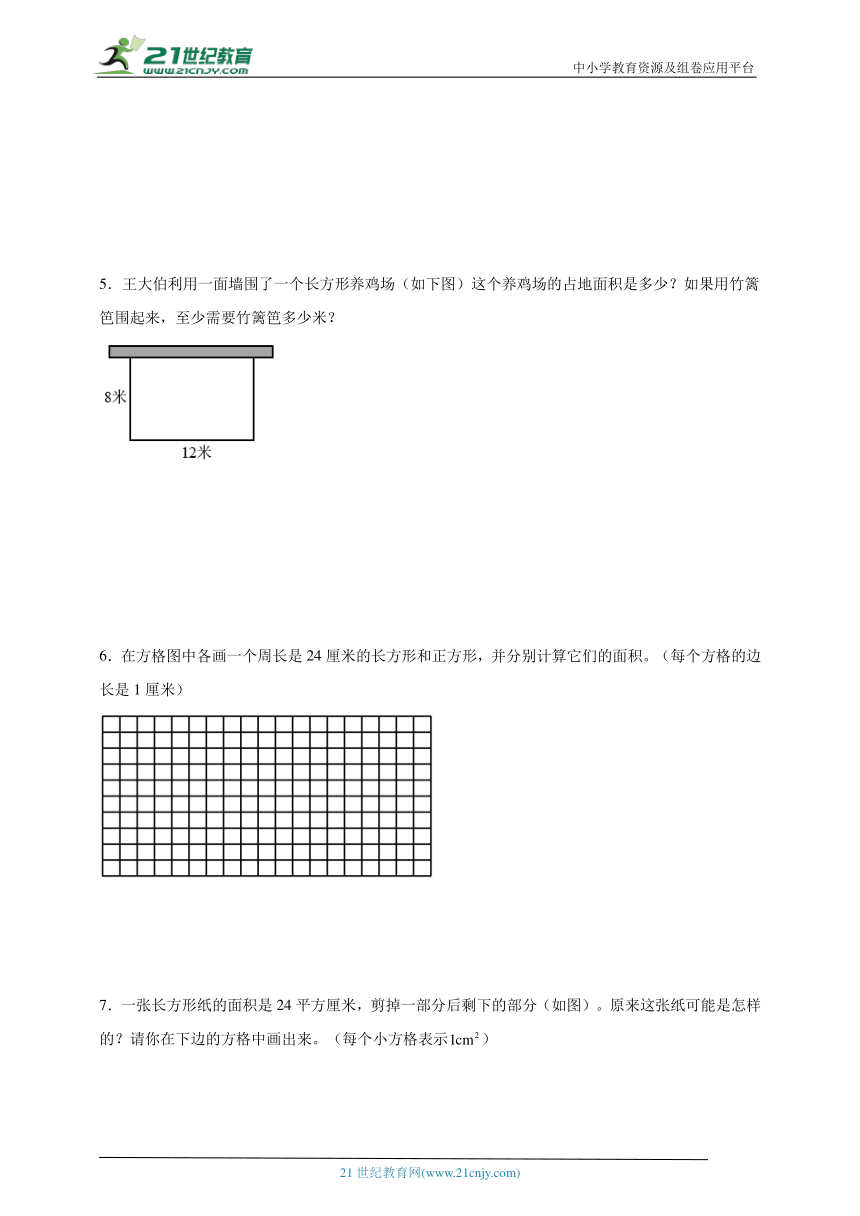
5.王大伯利用一面墙围了一个长方形养鸡场(如下图)这个养鸡场的占地面积是多少?如果用竹篱笆围起来,至少需要竹篱笆多少米?
6.在方格图中各画一个周长是24厘米的长方形和正方形,并分别计算它们的面积。(每个方格的边长是1厘米)
7.一张长方形纸的面积是24平方厘米,剪掉一部分后剩下的部分(如图)。原来这张纸可能是怎样的?请你在下边的方格中画出来。(每个小方格表示)
8.一张长60厘米的长方形纸,刚好可以剪成3个同样的小正方形(如下图)。
(1)这张长方形纸的面积是多少平方厘米?
(2)剪成3个同样的小正方形后,三个小正方形的周长总和比原来长方形纸的周长多多少厘米?
9.学校准备在一块长27米,宽21米的长方形空地上挖一个最大的正方形荷花池。那么剩余空地的面积是多少平方米?
10.一辆洒水车每分钟行驶60米,洒水的宽度是9米。洒水车行驶10分钟,洒水的面积一共是多少平方米?
11.从一张大长方形纸上剪下了一个最大的正方形(如下图),已知剩下的小长方形的面积是24平方厘米,又知小长方形和剪下的正方形的周长之和比原来大长方形的周长长16厘米。剪下的正方形的边长是多少厘米?原来大长方形的面积是多少平方厘米?
12.有一张长10厘米、宽5厘米的长方形纸。
(1)这张长方形纸的周长是多少厘米?
(2)沿着长方形的边剪下一个边长2厘米的正方形(如图)。请算出剩下图形的面积。
13.一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。现在这块木板的周长是多少厘米?
14.有一个小长方形,它和一个正方形拼成了一个大长方形ABCD(如下图),已知大长方形的面积是35平方厘米,且周长比原来小长方形的周长多10厘米。求原来小长方形的面积。
参考答案:
1.480棵
【分析】根据长方形的面积=长×宽,求出菜园的面积,再乘每平方米种大白菜的棵数,求出大白菜的总棵数。
【详解】8×6×10
=48×10
=480(棵)
答:这个菜园一共可以种480棵大白菜。
【点睛】本题考查长方形面积公式的应用,关键是熟记公式。
2.(1)980平方米
(2)2940株
【分析】(1)长方形的面积=长×宽,把数据代入公式计算即可。
(2)每平方米种凤仙花株数乘长方形面积可以算出这个花圃一共能种多少株凤仙花。
【详解】(1)35×28=980(平方米)
答:这个长方形花圃的面积是980平方米。
(3)3×980=2940(株)
答:这个花圃一共能种2940株凤仙花。
【点睛】此题考查了三位数乘一位数,两位数乘两位数乘法的实际应用,熟记长方形面积公式是解题关键。
3.230平方米
【分析】根据题意,把中间的小路向左、向上平移,6块小草坪可拼成一个长方形草坪,则草坪的面积就是长(24-1=23)米,宽(12-1-1=10)米的长方形面积,根据“长方形面积=长×宽”,代入数据,即可解答。
【详解】(24-1)×(12-1-1)
=23×10
=230(平方米)
答:草坪的面积是230平方米。
【点睛】此题的解题关键是通过平移拼成一个长方形,根据长方形的面积公式求解。
4.没有占到便宜
【分析】长方形的面积=长×宽,据此分别求出两块地的面积,再比较两个面积的大小解答。
【详解】4×3=12(dm2)
6×2=12(dm2)
12dm2=12dm2
答:两块地的面积相等,老大没有占到便宜。
【点睛】本题考查长方形面积公式的应用,关键是熟记公式。
5.96平方米;28米
【分析】(1)已知围成的养鸡场是一个长12米,宽8米的长方形,根据长方形的面积=长×宽,可求出它的面积;
(2)因一面靠墙,需要的篱笆最少,则应让长的一面靠墙,即2个宽与1个长,由此把三个边的长度加起来即可。
【详解】12×8=96(平方米)
12+8×2
=12+16
=28(米)
答:这个养鸡场占地面积96平方米,至少需要竹篱笆28米。
【点睛】本题主要考查了学生对长方形面积和周长计算方法的掌握。
6.图见详解;32平方厘米(不唯一);36平方厘米
【分析】长方形的周长是24厘米,24除以2得12,即长方形的长与宽的和是12厘米,再看哪两个数的和是12,如4加8得12,长可以是8厘米,宽是4厘米,再把4与8相乘即可求出其面积,并据此作图;正方形的周长是24厘米,24除以4得6,即正方形的边长是6厘米,据此画图,6乘6即可求出此正方形的面积。
【详解】长方形:24÷2=12(厘米)
12-4=8(厘米)
4×8=32(平方厘米)(答案不唯一)
正方形:24÷4=6(厘米)
6×6=36(平方厘米)
答:长方形的面积是32平方厘米,正方形的面积是36平方厘米。
【点睛】此题主要考查长方形、正方形周长与面积公式的应用,作长方形图时先确定其长与宽,这是重点。
7.见详解
【分析】因为1个方格的面积是1平方厘米,由此可知1个方格的边长是1厘米,而图中剩余纸的一边是4厘米,要使面积是24平方厘米,那么另一边是24÷4=6厘米,据此画图即可。
【详解】24÷4=6(厘米)
答:原来这张纸是长为6厘米,宽为4厘米的长方形。
【点睛】由图先找到长方形纸的宽,再根据“长=长方形面积÷宽”,求出长方形的长后再画图。
8.(1)1200平方厘米;(2)80厘米
【分析】(1)观察上图可知,长方形的长除以3等于小正方形的边长,长方形的宽与小正方形的边长相等,再用长乘宽即可求出长方形纸的面积;
(2)小正方形的边长乘4等于小正方形的周长,再乘3等于3个小正方形的周长和,减长方形的周长即可解答。
【详解】(1)60÷3=20(厘米)
60×20=1200(平方厘米)
答:这张长方形纸的面积是1200平方厘米。
(2)20×4×3-(60+20)×2
=240-160
=80(厘米)
答:三个小正方形的周长总和比原来长方形纸的周长多80厘米。
【点睛】本题主要考查学生对长方形、正方形的周长和面积公式的掌握,求出小正方形的边长是解答本题的关键。
9.126平方米
【分析】能挖的最大正方形的边长与长方形的宽相等,那么剩下的空地是长方形,剩下长方形的长是21米,原长方形的长减少21米后是6米,即剩余空地的宽是6米,再根据长方形的面积公式,长乘宽即可求出面积。
【详解】27-21=6(米)
21×6=126(平方米)
答:剩余空地的面积是126平方米。
【点睛】此题的重点是确定正方形最大时的边长,在长方形空地挖正方形荷花池,正方形边长最大与长方形较短的边长度相等。
10.5400平方米
【分析】根据题意,所洒地面是一个长方形,首先根据速度×时间=路程,求出10分钟洒水车行驶多少米,也就是所洒地面长方形的长,已知洒水的宽度是9米,利用长方形的面积公式解答即可。
【详解】60×10=600(米)
600×9=5400(平方米)
答:洒水的面积一共是5400平方米。
【点睛】本题考查长方形面积公式的实际应用,需要理解题意,得出洒水车走过的是一个长方形,求出洒水的长度是本题的关键。
11.8厘米;88平方厘米
【分析】把一张大长方形纸剪成一个最大的正方形和一个小长方形,增加了2条正方形的边,16厘米就是这2条边的长度和,用16除以2,求出剪下的正方形的边长,也就是大长方形的宽;用24除以剪下的正方形的边长,求出小长方形的宽;用剪下的正方形的边长加上小长方形的宽,求出大长方形的长;长方形的面积=长×宽,代入相关数据即可解答。
【详解】16÷2=8(厘米)
24÷8=3(厘米)
(8+3)×8
=11×8
=88(平方厘米)
答:剪下的正方形的边长是8厘米,原来大长方形的面积是88平方厘米。
【点睛】解答此题的关键是明白16厘米就是2条正方形边的长度和,再进一步解答。
12.(1)30厘米;
(2)46平方厘米
【分析】(1)根据长方形周长公式:C=(a+b)×2,据此计算得出这张长方形纸的周长。
(2)用长方形面积减去正方形面积即可求出剩下图形的面积,长方形面积公式:S=a×b,正方形面积公式:S=a×a;根据公式计算,求出剩下图形的面积。
【详解】(1)(10+5)×2
=15×2
=30(厘米)
答:这张长方形纸的周长是30厘米。
(2)10×5-2×2
=50-2×2
=50-4
=46(平方厘米)
答:剩下图形的面积是46平方厘米。
【点睛】本题考查长方形周长和面积公式以及正方形面积公式。
13.88厘米
【分析】观察图形可知,剪切掉的192平方厘米部分的图形,正好可以组成一个宽4厘米的长方形,据此利用长方形的面积公式求出它们的总长度是:192÷4=48厘米,把它减去4厘米,就是现在这块木板的一条长与宽的和,再乘2就是现在这块木板的周长。
【详解】(192÷4-4)×2
=(48-4)×2
=44×2
=88(厘米)
答:现在这块木板的周长是88厘米。
【点睛】根据剪切方法和剪切掉的面积,求出剪掉的小长方形的长度之和,进而得出现在这块木板的长与宽的和,是解决本题的关键。
14.10平方厘米
【分析】看图发现大长方形比小长方形多的周长部分是正方形的两个边长。据此,先利用除法求出正方形的边长,从而求出正方形的面积。再利用大长方形的面积减去正方形的面积,求出小长方形的面积即可。
【详解】10÷2=5(厘米)
35-5×5
=35-25
=10(平方厘米)
答:原来小长方形的面积是10平方厘米。
【点睛】本题考查了长方形和正方形,灵活运用正方形的面积公式,对长方形的周长有清晰的认识是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第6单元长方形和正方形的面积典例分析与精选好题(讲义)数学三年级下册苏教版
典例分析一
.导盲砖是一种为盲人铺设盲道的特殊地砖。现在要在一条长120米的人行道中间铺设宽为6分米的盲道,如果选用边长为3分米的正方形导盲砖,需要多少块这样的导盲砖?
【答案】解:120米=1200分米
(6÷3)×(1200÷3)
=2×400
=800(块)
答:需要800块这样的导盲砖。
典例分析二
.一根软铁丝能围成一个长是6cm,宽是2cm的长方形。如果用这根铁丝围成一个正方形,这个正方形的面积是多少平方厘米?
【答案】解:(6+2)×2÷4
=8×2÷4
=16÷4
=4(cm)
4×4=16(cm2)
答:这个正方形的面积是16平方厘米。
典例分析三
.一辆洒水车每分行驶50m,洒水的宽度是10m,如果洒水车行驶8分钟,洒过水的地面的面积是多大?
【答案】解:50×10=500(平方米)
500×8=4000(平方米)
答:洒过水的地面的面积是4000平方米。
精选好题
1.王大爷用篱笆靠墙围了一个长8米、宽6米的长方形菜园。如果每平方米种10棵大白菜,这个菜园一共可以种多少棵大白菜?
2.一个长方形花圃,长35米,宽28米。
(1)这个长方形花圃的面积是多少平方米?
(2)如果每平方米可以种3株凤仙花,这个花圃一共能种多少株凤仙花?
3.一块草坪被3条1米宽的小路分成了6小块(如图)。草坪的面积是多少平方米?
4.一位老农在他临终前将两块地(一块长4dm,宽3dm;另一块长6dm,宽2dm)留给了他的两个儿子,每人选择一块。老大很贪心,抢先选了后一块长方形地,老大有没有占到便宜呢?
5.王大伯利用一面墙围了一个长方形养鸡场(如下图)这个养鸡场的占地面积是多少?如果用竹篱笆围起来,至少需要竹篱笆多少米?
6.在方格图中各画一个周长是24厘米的长方形和正方形,并分别计算它们的面积。(每个方格的边长是1厘米)
7.一张长方形纸的面积是24平方厘米,剪掉一部分后剩下的部分(如图)。原来这张纸可能是怎样的?请你在下边的方格中画出来。(每个小方格表示)
8.一张长60厘米的长方形纸,刚好可以剪成3个同样的小正方形(如下图)。
(1)这张长方形纸的面积是多少平方厘米?
(2)剪成3个同样的小正方形后,三个小正方形的周长总和比原来长方形纸的周长多多少厘米?
9.学校准备在一块长27米,宽21米的长方形空地上挖一个最大的正方形荷花池。那么剩余空地的面积是多少平方米?
10.一辆洒水车每分钟行驶60米,洒水的宽度是9米。洒水车行驶10分钟,洒水的面积一共是多少平方米?
11.从一张大长方形纸上剪下了一个最大的正方形(如下图),已知剩下的小长方形的面积是24平方厘米,又知小长方形和剪下的正方形的周长之和比原来大长方形的周长长16厘米。剪下的正方形的边长是多少厘米?原来大长方形的面积是多少平方厘米?
12.有一张长10厘米、宽5厘米的长方形纸。
(1)这张长方形纸的周长是多少厘米?
(2)沿着长方形的边剪下一个边长2厘米的正方形(如图)。请算出剩下图形的面积。
13.一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。现在这块木板的周长是多少厘米?
14.有一个小长方形,它和一个正方形拼成了一个大长方形ABCD(如下图),已知大长方形的面积是35平方厘米,且周长比原来小长方形的周长多10厘米。求原来小长方形的面积。
参考答案:
1.480棵
【分析】根据长方形的面积=长×宽,求出菜园的面积,再乘每平方米种大白菜的棵数,求出大白菜的总棵数。
【详解】8×6×10
=48×10
=480(棵)
答:这个菜园一共可以种480棵大白菜。
【点睛】本题考查长方形面积公式的应用,关键是熟记公式。
2.(1)980平方米
(2)2940株
【分析】(1)长方形的面积=长×宽,把数据代入公式计算即可。
(2)每平方米种凤仙花株数乘长方形面积可以算出这个花圃一共能种多少株凤仙花。
【详解】(1)35×28=980(平方米)
答:这个长方形花圃的面积是980平方米。
(3)3×980=2940(株)
答:这个花圃一共能种2940株凤仙花。
【点睛】此题考查了三位数乘一位数,两位数乘两位数乘法的实际应用,熟记长方形面积公式是解题关键。
3.230平方米
【分析】根据题意,把中间的小路向左、向上平移,6块小草坪可拼成一个长方形草坪,则草坪的面积就是长(24-1=23)米,宽(12-1-1=10)米的长方形面积,根据“长方形面积=长×宽”,代入数据,即可解答。
【详解】(24-1)×(12-1-1)
=23×10
=230(平方米)
答:草坪的面积是230平方米。
【点睛】此题的解题关键是通过平移拼成一个长方形,根据长方形的面积公式求解。
4.没有占到便宜
【分析】长方形的面积=长×宽,据此分别求出两块地的面积,再比较两个面积的大小解答。
【详解】4×3=12(dm2)
6×2=12(dm2)
12dm2=12dm2
答:两块地的面积相等,老大没有占到便宜。
【点睛】本题考查长方形面积公式的应用,关键是熟记公式。
5.96平方米;28米
【分析】(1)已知围成的养鸡场是一个长12米,宽8米的长方形,根据长方形的面积=长×宽,可求出它的面积;
(2)因一面靠墙,需要的篱笆最少,则应让长的一面靠墙,即2个宽与1个长,由此把三个边的长度加起来即可。
【详解】12×8=96(平方米)
12+8×2
=12+16
=28(米)
答:这个养鸡场占地面积96平方米,至少需要竹篱笆28米。
【点睛】本题主要考查了学生对长方形面积和周长计算方法的掌握。
6.图见详解;32平方厘米(不唯一);36平方厘米
【分析】长方形的周长是24厘米,24除以2得12,即长方形的长与宽的和是12厘米,再看哪两个数的和是12,如4加8得12,长可以是8厘米,宽是4厘米,再把4与8相乘即可求出其面积,并据此作图;正方形的周长是24厘米,24除以4得6,即正方形的边长是6厘米,据此画图,6乘6即可求出此正方形的面积。
【详解】长方形:24÷2=12(厘米)
12-4=8(厘米)
4×8=32(平方厘米)(答案不唯一)
正方形:24÷4=6(厘米)
6×6=36(平方厘米)
答:长方形的面积是32平方厘米,正方形的面积是36平方厘米。
【点睛】此题主要考查长方形、正方形周长与面积公式的应用,作长方形图时先确定其长与宽,这是重点。
7.见详解
【分析】因为1个方格的面积是1平方厘米,由此可知1个方格的边长是1厘米,而图中剩余纸的一边是4厘米,要使面积是24平方厘米,那么另一边是24÷4=6厘米,据此画图即可。
【详解】24÷4=6(厘米)
答:原来这张纸是长为6厘米,宽为4厘米的长方形。
【点睛】由图先找到长方形纸的宽,再根据“长=长方形面积÷宽”,求出长方形的长后再画图。
8.(1)1200平方厘米;(2)80厘米
【分析】(1)观察上图可知,长方形的长除以3等于小正方形的边长,长方形的宽与小正方形的边长相等,再用长乘宽即可求出长方形纸的面积;
(2)小正方形的边长乘4等于小正方形的周长,再乘3等于3个小正方形的周长和,减长方形的周长即可解答。
【详解】(1)60÷3=20(厘米)
60×20=1200(平方厘米)
答:这张长方形纸的面积是1200平方厘米。
(2)20×4×3-(60+20)×2
=240-160
=80(厘米)
答:三个小正方形的周长总和比原来长方形纸的周长多80厘米。
【点睛】本题主要考查学生对长方形、正方形的周长和面积公式的掌握,求出小正方形的边长是解答本题的关键。
9.126平方米
【分析】能挖的最大正方形的边长与长方形的宽相等,那么剩下的空地是长方形,剩下长方形的长是21米,原长方形的长减少21米后是6米,即剩余空地的宽是6米,再根据长方形的面积公式,长乘宽即可求出面积。
【详解】27-21=6(米)
21×6=126(平方米)
答:剩余空地的面积是126平方米。
【点睛】此题的重点是确定正方形最大时的边长,在长方形空地挖正方形荷花池,正方形边长最大与长方形较短的边长度相等。
10.5400平方米
【分析】根据题意,所洒地面是一个长方形,首先根据速度×时间=路程,求出10分钟洒水车行驶多少米,也就是所洒地面长方形的长,已知洒水的宽度是9米,利用长方形的面积公式解答即可。
【详解】60×10=600(米)
600×9=5400(平方米)
答:洒水的面积一共是5400平方米。
【点睛】本题考查长方形面积公式的实际应用,需要理解题意,得出洒水车走过的是一个长方形,求出洒水的长度是本题的关键。
11.8厘米;88平方厘米
【分析】把一张大长方形纸剪成一个最大的正方形和一个小长方形,增加了2条正方形的边,16厘米就是这2条边的长度和,用16除以2,求出剪下的正方形的边长,也就是大长方形的宽;用24除以剪下的正方形的边长,求出小长方形的宽;用剪下的正方形的边长加上小长方形的宽,求出大长方形的长;长方形的面积=长×宽,代入相关数据即可解答。
【详解】16÷2=8(厘米)
24÷8=3(厘米)
(8+3)×8
=11×8
=88(平方厘米)
答:剪下的正方形的边长是8厘米,原来大长方形的面积是88平方厘米。
【点睛】解答此题的关键是明白16厘米就是2条正方形边的长度和,再进一步解答。
12.(1)30厘米;
(2)46平方厘米
【分析】(1)根据长方形周长公式:C=(a+b)×2,据此计算得出这张长方形纸的周长。
(2)用长方形面积减去正方形面积即可求出剩下图形的面积,长方形面积公式:S=a×b,正方形面积公式:S=a×a;根据公式计算,求出剩下图形的面积。
【详解】(1)(10+5)×2
=15×2
=30(厘米)
答:这张长方形纸的周长是30厘米。
(2)10×5-2×2
=50-2×2
=50-4
=46(平方厘米)
答:剩下图形的面积是46平方厘米。
【点睛】本题考查长方形周长和面积公式以及正方形面积公式。
13.88厘米
【分析】观察图形可知,剪切掉的192平方厘米部分的图形,正好可以组成一个宽4厘米的长方形,据此利用长方形的面积公式求出它们的总长度是:192÷4=48厘米,把它减去4厘米,就是现在这块木板的一条长与宽的和,再乘2就是现在这块木板的周长。
【详解】(192÷4-4)×2
=(48-4)×2
=44×2
=88(厘米)
答:现在这块木板的周长是88厘米。
【点睛】根据剪切方法和剪切掉的面积,求出剪掉的小长方形的长度之和,进而得出现在这块木板的长与宽的和,是解决本题的关键。
14.10平方厘米
【分析】看图发现大长方形比小长方形多的周长部分是正方形的两个边长。据此,先利用除法求出正方形的边长,从而求出正方形的面积。再利用大长方形的面积减去正方形的面积,求出小长方形的面积即可。
【详解】10÷2=5(厘米)
35-5×5
=35-25
=10(平方厘米)
答:原来小长方形的面积是10平方厘米。
【点睛】本题考查了长方形和正方形,灵活运用正方形的面积公式,对长方形的周长有清晰的认识是解题的关键。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
