2023-2024学年福建省南平市浦城县高二(下)期中数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年福建省南平市浦城县高二(下)期中数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 84.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-18 08:04:05 | ||
图片预览




文档简介
2023-2024学年福建省南平市浦城县高二(下)期中数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,集合且,则( )
A. B. C. D.
2.展开式中的第项为( )
A. B. C. D.
3.已知随机变量,且,则( )
A. B. C. D.
4.不等式解集为( )
A. B.
C. D.
5.某平台设有“人物”“视听学习”等多个栏目假设在这些栏目中,某时段“人物”更新了篇文章,“视听学习”更新了个视频一位学习者准备从更新的这项内容中随机选取个视频和篇文章进行学习,则这篇文章学习顺序相邻的学法有( )
A. 种 B. 种 C. 种 D. 种
6.函数的单调递增区间是( )
A. B. 和
C. D. 和
7.抛掷三枚质地均匀的硬币一次,在有一枚正面朝上的条件下,另外两枚也正面朝上的概率是( )
A. B. C. D.
8.已知函数,,以下结论正确的( )
A. 函数的图象关于直线对称
B. 函数的图象关于点中心对称
C. 函数没有最大值
D. 若方程有两个解,则
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.函数的图象可以是( )
A. B.
C. D.
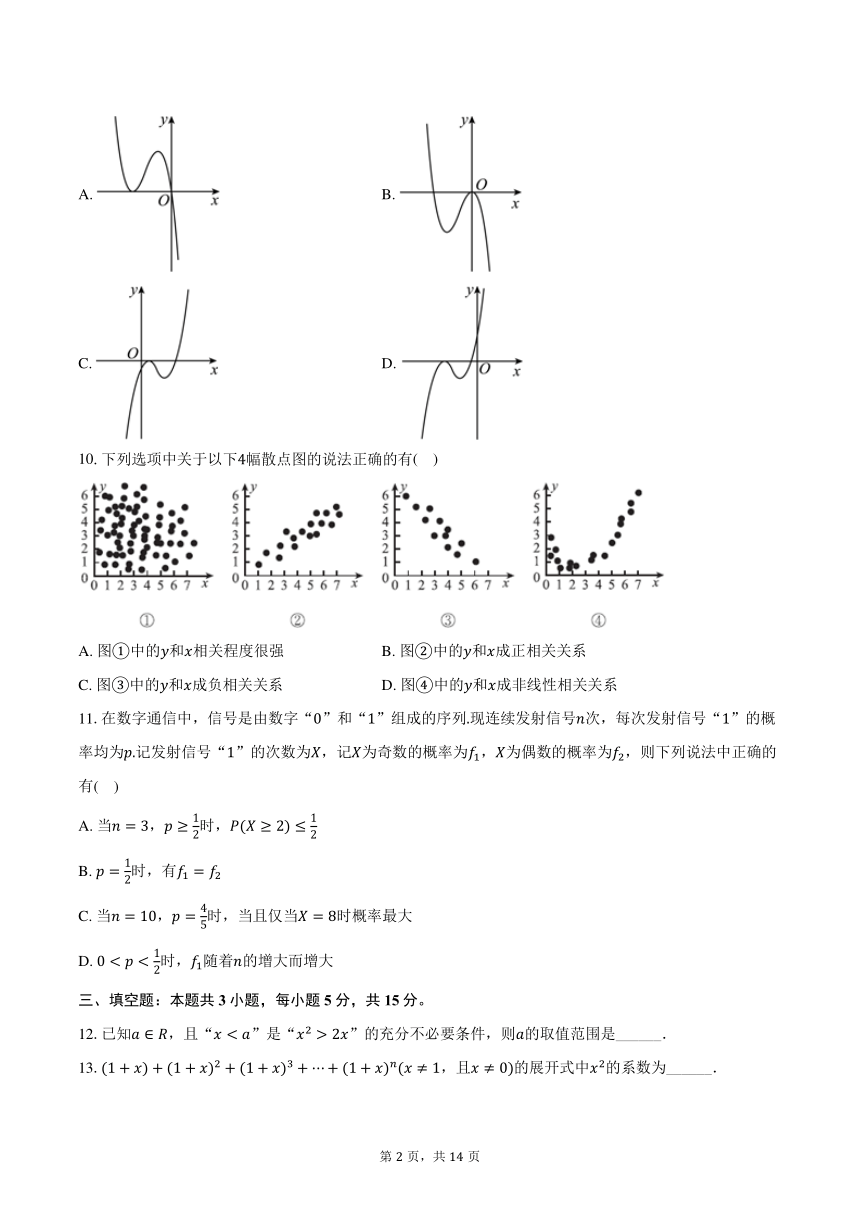
10.下列选项中关于以下幅散点图的说法正确的有( )
A. 图中的和相关程度很强 B. 图中的和成正相关关系
C. 图中的和成负相关关系 D. 图中的和成非线性相关关系
11.在数字通信中,信号是由数字“”和“”组成的序列现连续发射信号次,每次发射信号“”的概率均为记发射信号“”的次数为,记为奇数的概率为,为偶数的概率为,则下列说法中正确的有( )
A. 当,时,
B. 时,有
C. 当,时,当且仅当时概率最大
D. 时,随着的增大而增大
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,且“”是“”的充分不必要条件,则的取值范围是______.
13.,且的展开式中的系数为______.
14.近年来,我国外卖业发展迅猛,外卖小哥穿梭在城市的大街小巷成为一道道亮丽的风景线他们根据外卖平台提供的信息到外卖店取单某外卖小哥每天来往于个外卖店外卖店的编号分别为,,,,约定:每天他首先从号外卖店取单,叫做第次取单,之后,他等可能的前往其余个外卖店中的任何一个店取单叫做第次取单,依此类推假设从第次取单开始,他每次都是从上次取单的店之外的个外卖店取单,设事件第次取单恰好是从号店取单,是事件发生的概率,显然,,则 ______, ______第二空精确到.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知幂函数在定义域上不单调.
试问:函数是否具有奇偶性?请说明理由;
若,求实数的取值范围.
16.本小题分
某校为了解本校学生课间进行体育活动的情况,随机抽取了名男生和名女生,通过调查得到如下数据:名女生中有人课间经常进行体育活动,名男生中有人课间经常进行体育活动.
请补全列联表,试根据小概率值的独立性检验,判断性别与课间经常进行体育活动是否有关联;
性别 体育活动 合计
课间不经常进行体育活动 课间经常进行体育活动
男
女
合计
以样本的频率作为概率的值,在全校的男生中任取人,记其中课间经常进行体育活动的人数为,求的分布列、数学期望和方差.
附表:
则:,其中.
17.本小题分
若正数,满足,.
当时,求的最小值;
当时,求的取值范围.
18.本小题分
设某幼苗从观察之日起,第天的高度为,测得的一些数据如下表所示:
第天
高度
作出这组数据的散点图发现:与天之间近似满足关系式,其中,均为大于的常数试借助一元线性回归模型,根据所给数据,用最小二乘法对,作出估计,并求出关于的经验回归方程;
在作出的这组数据的散点图中,甲同学随机圈取了其中的个点,记这个点中幼苗的高度大于的点的个数为,其中为表格中所给的幼苗高度的平均数,试求随机变量的分布列和数学期望.
附:对于一组数据,,,,其回归直线方程的斜率和截距的最小二乘估计分别为:,.
19.本小题分
某人从地到地有路程接近的条路线可以选择,其中第一条路线上有个路口,第二条路线上有个路口.
若,,第一条路线的每个路口遇到红灯的概率均为;第二条路线的第一个路口遇到红灯的概率为,第二个路口遇到红灯的概率为,从“遇到红灯次数的期望”考虑,哪条路线更好?请说明理由.
已知:随机变量服从两点分布,且,则,且若第一条路线的第个路口遇到红灯的概率为,当选择第一条路线时,求遇到红灯次数的方差.
答案和解析
1.【答案】
【解析】解:,又且,
,,又,
,,,,
故选:.
先化简集合,再根据集合的条件化简即可得解.
本题考查集合表的描述表示法,属基础题.
2.【答案】
【解析】解:由二项式定理可知,展开式中的第项为.
故选:.
利用二项式定理求解.
本题主要考查了二项式定理的应用,属于基础题.
3.【答案】
【解析】解:,且,
,
.
故选:.
利用正态分布曲线的对称性求解.
本题主要考查了正态分布曲线的对称性,属于基础题.
4.【答案】
【解析】解:根据题意,不等式,
则有且,
解可得:或,
则不等式的解集为,;
故选:.
根据题意,分析可得原不等式变形可得且,解可得的取值范围,即可得答案.
本题考查分式不等式的解法,关键是将分式不等式转化为整式不等式.
5.【答案】
【解析】解:根据题意,分两步进行分析:
第一步:从个视频中选个有种方法,篇文章全选有种方法,篇文章要相邻则可以先“捆绑”看成个元素,
四个学习内容全排列有种方法,
第二步:需要对“捆绑”元素进行“松绑”全排列,
故满足题意的学法有种.
故选:.
利用“捆绑法”,结合排列组合知识求解.
本题主要考查了排列组合知识,属于基础题.
6.【答案】
【解析】解:因为,定义域为,
所以,
所以函数为偶函数,当时,,开口向上,对称轴的抛物线,
所以时,函数单调递减,时,函数单调递增,
由偶函数的对称性,可得函数的单调递增区间为和.
故选:.
由函数的解析式可得,即函数为偶函数,求出时,函数的单调递增区间,再由偶函数的对称性,可得函数在上的单调递增区间.
本题考查偶函数的性质及函数的单调递增区间的求法,属于基础题.
7.【答案】
【解析】解:根据题意可知抛掷三枚硬币,则其样本空间包含个等可能的样本点,其中有一枚正面朝上包含个样本点,
记事件表示“有一枚正面朝上”,事件表示“另外两枚也正面朝上”,
则为“三枚都正面朝上”,
所以,,
所以.
即在有一枚正面朝上的条件下,另外两枚也正面朝上的概率是.
故选:.
利用条件概率公式求解.
本题主要考查了条件概率公式,属于基础题.
8.【答案】
【解析】解:对于,因为,
,所以函数的图象不关于直线对称,故错误;
对于,因数,为奇函数,所以关于原点对称,所以函数的图象关于点中心对称,故正确;
对于,当时,,
当时,,
因为,所以,
所以,
所以的最大值为,故错误;
对于,因为,
由可得,
即,
若,则方程有唯一的解,,不满足题意,
若,则有,
解得且,故错误.
故选:.
对于,只需判断是否成立,即可判断;
对于,判断是否为奇函数,即可判断;
对于,将函数化简为,即可求出函数的值域为,即可判断;
对于,由可得,由一元二次方程的根可解得且,即可判断.
本题考查了函数的奇偶性、对称性及值域,属于中档题.
9.【答案】
【解析】解:由函数解析式可知,是不变号零点,是变号零点,
A.由图可知,变号零点是,则,则,不成立,故A错误;
B.由图可知,变号零点小于,不变号零点为,则,,此时,
当,,当,,当时,,满足图象,故B正确;
C.由图可知,,,当时,,当时,,当时,,满足图象,故C正确;
D.由图可知,,,当时,,与图象不符,所以D错误.
故选:.
首先根据解析式确定零点类型,再结合图象,判断选项.
本题主要考函数图象的判断,考查逻辑推理能力,属于中档题.
10.【答案】
【解析】解:对于图中的散点杂乱,无规律,所以和相关程度极弱,所以A错误;
对于图中,散点分布在某条直线的附近,且呈上升趋势,所以和成正相关关系,所以B正确,
对于图中,散点分布在某条直线的附近,且呈下降趋势,所以和成负相关关系,所以C正确,
对于图中,散点分布在某条曲线附近,所以和成非线性相关关系,所以D正确,
故选:.
根据散点图的分布逐个分析判断即可.
本题考查了变量相关关系的判断,属于基础题.
11.【答案】
【解析】解:由题意得发射信号“”的次数为,则,
选项,当,可取,,,,
所以,
因为,所以,,所以,故A项错误;
选项,当时,即每次发射信号“”和发射信号“”的概率相等,所以为奇数的概率和为偶数的概率相等,即,故B正确;
选项,当,,此时,,,
当取得概率最大时,即,即,解得,故C项正确;
选项,由题知当,发射信号“”的次数为,,
由二项式的均值公式,当概率一定时,越大,则的值越大,所以能够出现奇数的概率也增大,故D正确.
故选:.
由题意知发射信号“”的次数为和概率符合二项分布,然后对各项分别求解即可判断.
本题考查离散型随机变量的概率和期望,是中档题.
12.【答案】
【解析】解:根据题意,设集合,集合,则或,
若“”是“”的充分不必要条件,则,
则有,即的取值范围为.
故答案为:.
根据题意,设集合,集合,求出集合,分析可得,由此分析可得答案.
本题考查充分必要的判断,涉及集合间的包含关系,属于基础题.
13.【答案】
【解析】解:二项式的展开式中的系数为,
,且的展开式中的系数为:
.
故答案为:.
由题意可知,且的展开式中的系数为,再结合组合数的性质求解.
本题主要考查了二项式定理的应用,考查了组合数的性质,属于基础题.
14.【答案】
【解析】解:第次取单恰好是从号店取单,由于每天第一次取单都是从号店开始,根据题意,第次不可能从号店取单.
所以,第次取单恰好是从号店取单,
因此.
根据以上方法可得,.
根据上式可得,
,
以此类推,可得
.
故答案为:,.
本题利用对立事件概率计算公式、条件概率可解决.
本题考查概率的求法,考查对立事件概率计算公式、条件概率、等比数列的性质等基础知识,考查推理能力与计算能力,属于较难题.
15.【答案】解:由题意,解得或,
当时,,
函数在上单调递增,不合题意;
当时,,
函数的定义域为,
函数在上单调递减,在上单调递减,
但,,
所以函数在定义域上不单调,符合题意,
所以,
因为函数的定义域关于原点对称,
且,
所以为奇函数;
由及为奇函数,
可得,
即,
而在上递减且恒负,在上递减且恒正,
所以或或,
解得或
【解析】由幂函数的定义可得或,结合函数的单调性排除增根,由此确定的单调性,结合奇函数和偶函数的定义,判断函数的奇偶性;
利用奇函数的性质化简不等式,再结合函数的单调性通过讨论化简不等式求其解.
本题主要考查了幂函数性质的应用,还考查了单调性在不等式求解中的应用,属于中档题.
16.【答案】解:根据题意,补全列联表如下:
性别 体育活动 合计
课间不经常进行体育活动 课间经常进行体育活动
男
女
合计
设零假设:性别与课间经常进行体育活动没有关联,
则,
所以根据小概率值的独立性检验,我们推断不成立,即认为性别与课间经常进行体育活动是否有关联,此推断犯错误的概率不大于;
由题意可知,全校的男生中经常进行体育活动者的频率为,则,
所以的所有可能取值为,,,,,
则,,,,,
所以的分布列为:
所以,.
【解析】根据题意补全列联表,计算的值,再与临界值比较即可;
由题意可知,,所以的所有可能取值为,,,,,利用二项分布的概率公式、期望公式和方差公式求解.
本题主要考查了独立性检验的应用,考查了离散型随机变量的分布列和期望,属于中档题.
17.【答案】解:当时,,
所以,
所以,
当且仅当且,即时取等号;
当时,,当且仅当,即,时取等号,
解得,
故的取值范围为.
【解析】由已知可得,然后利用乘法,结合基本不等式可求;
由已知,结合基本不等式即可直接求解.
本题主要考查了基本不等式在最值求解中的应用,属于中档题.
18.【答案】解:令,则,根据已知数据表得到如下表:
,,
通过上表计算可得:,
因为回归直线过点,
所以,
故关于的回归方程;
这天中幼苗高度大于的有天,服从超几何分布,其中,,,
,,,,
所以随机变量的分布列为:
随机变量的期望值.
【解析】令,则,变为线型回归问题,先根据已知数据得到的对应数据表,计算样本中心,然后利用最小二乘估计公式依次计算和的估计值,求得关于的线性回归方程,进而得到关于的回归方程;
利用超几何分布概率公式计算,求得随机变量的分布列,并根据分布列,利用数学期望计算求得期望值.
本题主要考查线性回归方程,离散型随机变量分布列及数学期望,考查运算求解能力,属于中档题.
19.【答案】解:应选择第一条路线,理由如下:
设走第一、二条路线遇到的红灯次数分别为随机变量,,则,,;,,;
,,,
所以;
又因为,,;
所以;
因为,所以应选择第一条路线.
设选择第一条路线时遇到的红灯次数为,
所以,
.
设随机变量,取值为,其概率分别为,且,
,
所以;
又因为,所以.
【解析】设选择第一条路线和第二条路线遇到红灯次数分别为随机变量,,计算对应的概率,求出数学期望,比较大小即可.
设选择第一条路线时遇到的红灯次数为,计算和,设随机变量,取值为,其概率分别为,且,计算,,由,计算的值.
本题考查了离散型随机变量的应用问题,也考查了推理与运算能力,是难题.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知集合,集合且,则( )
A. B. C. D.
2.展开式中的第项为( )
A. B. C. D.
3.已知随机变量,且,则( )
A. B. C. D.
4.不等式解集为( )
A. B.
C. D.
5.某平台设有“人物”“视听学习”等多个栏目假设在这些栏目中,某时段“人物”更新了篇文章,“视听学习”更新了个视频一位学习者准备从更新的这项内容中随机选取个视频和篇文章进行学习,则这篇文章学习顺序相邻的学法有( )
A. 种 B. 种 C. 种 D. 种
6.函数的单调递增区间是( )
A. B. 和
C. D. 和
7.抛掷三枚质地均匀的硬币一次,在有一枚正面朝上的条件下,另外两枚也正面朝上的概率是( )
A. B. C. D.
8.已知函数,,以下结论正确的( )
A. 函数的图象关于直线对称
B. 函数的图象关于点中心对称
C. 函数没有最大值
D. 若方程有两个解,则
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.函数的图象可以是( )
A. B.
C. D.
10.下列选项中关于以下幅散点图的说法正确的有( )
A. 图中的和相关程度很强 B. 图中的和成正相关关系
C. 图中的和成负相关关系 D. 图中的和成非线性相关关系
11.在数字通信中,信号是由数字“”和“”组成的序列现连续发射信号次,每次发射信号“”的概率均为记发射信号“”的次数为,记为奇数的概率为,为偶数的概率为,则下列说法中正确的有( )
A. 当,时,
B. 时,有
C. 当,时,当且仅当时概率最大
D. 时,随着的增大而增大
三、填空题:本题共3小题,每小题5分,共15分。
12.已知,且“”是“”的充分不必要条件,则的取值范围是______.
13.,且的展开式中的系数为______.
14.近年来,我国外卖业发展迅猛,外卖小哥穿梭在城市的大街小巷成为一道道亮丽的风景线他们根据外卖平台提供的信息到外卖店取单某外卖小哥每天来往于个外卖店外卖店的编号分别为,,,,约定:每天他首先从号外卖店取单,叫做第次取单,之后,他等可能的前往其余个外卖店中的任何一个店取单叫做第次取单,依此类推假设从第次取单开始,他每次都是从上次取单的店之外的个外卖店取单,设事件第次取单恰好是从号店取单,是事件发生的概率,显然,,则 ______, ______第二空精确到.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
已知幂函数在定义域上不单调.
试问:函数是否具有奇偶性?请说明理由;
若,求实数的取值范围.
16.本小题分
某校为了解本校学生课间进行体育活动的情况,随机抽取了名男生和名女生,通过调查得到如下数据:名女生中有人课间经常进行体育活动,名男生中有人课间经常进行体育活动.
请补全列联表,试根据小概率值的独立性检验,判断性别与课间经常进行体育活动是否有关联;
性别 体育活动 合计
课间不经常进行体育活动 课间经常进行体育活动
男
女
合计
以样本的频率作为概率的值,在全校的男生中任取人,记其中课间经常进行体育活动的人数为,求的分布列、数学期望和方差.
附表:
则:,其中.
17.本小题分
若正数,满足,.
当时,求的最小值;
当时,求的取值范围.
18.本小题分
设某幼苗从观察之日起,第天的高度为,测得的一些数据如下表所示:
第天
高度
作出这组数据的散点图发现:与天之间近似满足关系式,其中,均为大于的常数试借助一元线性回归模型,根据所给数据,用最小二乘法对,作出估计,并求出关于的经验回归方程;
在作出的这组数据的散点图中,甲同学随机圈取了其中的个点,记这个点中幼苗的高度大于的点的个数为,其中为表格中所给的幼苗高度的平均数,试求随机变量的分布列和数学期望.
附:对于一组数据,,,,其回归直线方程的斜率和截距的最小二乘估计分别为:,.
19.本小题分
某人从地到地有路程接近的条路线可以选择,其中第一条路线上有个路口,第二条路线上有个路口.
若,,第一条路线的每个路口遇到红灯的概率均为;第二条路线的第一个路口遇到红灯的概率为,第二个路口遇到红灯的概率为,从“遇到红灯次数的期望”考虑,哪条路线更好?请说明理由.
已知:随机变量服从两点分布,且,则,且若第一条路线的第个路口遇到红灯的概率为,当选择第一条路线时,求遇到红灯次数的方差.
答案和解析
1.【答案】
【解析】解:,又且,
,,又,
,,,,
故选:.
先化简集合,再根据集合的条件化简即可得解.
本题考查集合表的描述表示法,属基础题.
2.【答案】
【解析】解:由二项式定理可知,展开式中的第项为.
故选:.
利用二项式定理求解.
本题主要考查了二项式定理的应用,属于基础题.
3.【答案】
【解析】解:,且,
,
.
故选:.
利用正态分布曲线的对称性求解.
本题主要考查了正态分布曲线的对称性,属于基础题.
4.【答案】
【解析】解:根据题意,不等式,
则有且,
解可得:或,
则不等式的解集为,;
故选:.
根据题意,分析可得原不等式变形可得且,解可得的取值范围,即可得答案.
本题考查分式不等式的解法,关键是将分式不等式转化为整式不等式.
5.【答案】
【解析】解:根据题意,分两步进行分析:
第一步:从个视频中选个有种方法,篇文章全选有种方法,篇文章要相邻则可以先“捆绑”看成个元素,
四个学习内容全排列有种方法,
第二步:需要对“捆绑”元素进行“松绑”全排列,
故满足题意的学法有种.
故选:.
利用“捆绑法”,结合排列组合知识求解.
本题主要考查了排列组合知识,属于基础题.
6.【答案】
【解析】解:因为,定义域为,
所以,
所以函数为偶函数,当时,,开口向上,对称轴的抛物线,
所以时,函数单调递减,时,函数单调递增,
由偶函数的对称性,可得函数的单调递增区间为和.
故选:.
由函数的解析式可得,即函数为偶函数,求出时,函数的单调递增区间,再由偶函数的对称性,可得函数在上的单调递增区间.
本题考查偶函数的性质及函数的单调递增区间的求法,属于基础题.
7.【答案】
【解析】解:根据题意可知抛掷三枚硬币,则其样本空间包含个等可能的样本点,其中有一枚正面朝上包含个样本点,
记事件表示“有一枚正面朝上”,事件表示“另外两枚也正面朝上”,
则为“三枚都正面朝上”,
所以,,
所以.
即在有一枚正面朝上的条件下,另外两枚也正面朝上的概率是.
故选:.
利用条件概率公式求解.
本题主要考查了条件概率公式,属于基础题.
8.【答案】
【解析】解:对于,因为,
,所以函数的图象不关于直线对称,故错误;
对于,因数,为奇函数,所以关于原点对称,所以函数的图象关于点中心对称,故正确;
对于,当时,,
当时,,
因为,所以,
所以,
所以的最大值为,故错误;
对于,因为,
由可得,
即,
若,则方程有唯一的解,,不满足题意,
若,则有,
解得且,故错误.
故选:.
对于,只需判断是否成立,即可判断;
对于,判断是否为奇函数,即可判断;
对于,将函数化简为,即可求出函数的值域为,即可判断;
对于,由可得,由一元二次方程的根可解得且,即可判断.
本题考查了函数的奇偶性、对称性及值域,属于中档题.
9.【答案】
【解析】解:由函数解析式可知,是不变号零点,是变号零点,
A.由图可知,变号零点是,则,则,不成立,故A错误;
B.由图可知,变号零点小于,不变号零点为,则,,此时,
当,,当,,当时,,满足图象,故B正确;
C.由图可知,,,当时,,当时,,当时,,满足图象,故C正确;
D.由图可知,,,当时,,与图象不符,所以D错误.
故选:.
首先根据解析式确定零点类型,再结合图象,判断选项.
本题主要考函数图象的判断,考查逻辑推理能力,属于中档题.
10.【答案】
【解析】解:对于图中的散点杂乱,无规律,所以和相关程度极弱,所以A错误;
对于图中,散点分布在某条直线的附近,且呈上升趋势,所以和成正相关关系,所以B正确,
对于图中,散点分布在某条直线的附近,且呈下降趋势,所以和成负相关关系,所以C正确,
对于图中,散点分布在某条曲线附近,所以和成非线性相关关系,所以D正确,
故选:.
根据散点图的分布逐个分析判断即可.
本题考查了变量相关关系的判断,属于基础题.
11.【答案】
【解析】解:由题意得发射信号“”的次数为,则,
选项,当,可取,,,,
所以,
因为,所以,,所以,故A项错误;
选项,当时,即每次发射信号“”和发射信号“”的概率相等,所以为奇数的概率和为偶数的概率相等,即,故B正确;
选项,当,,此时,,,
当取得概率最大时,即,即,解得,故C项正确;
选项,由题知当,发射信号“”的次数为,,
由二项式的均值公式,当概率一定时,越大,则的值越大,所以能够出现奇数的概率也增大,故D正确.
故选:.
由题意知发射信号“”的次数为和概率符合二项分布,然后对各项分别求解即可判断.
本题考查离散型随机变量的概率和期望,是中档题.
12.【答案】
【解析】解:根据题意,设集合,集合,则或,
若“”是“”的充分不必要条件,则,
则有,即的取值范围为.
故答案为:.
根据题意,设集合,集合,求出集合,分析可得,由此分析可得答案.
本题考查充分必要的判断,涉及集合间的包含关系,属于基础题.
13.【答案】
【解析】解:二项式的展开式中的系数为,
,且的展开式中的系数为:
.
故答案为:.
由题意可知,且的展开式中的系数为,再结合组合数的性质求解.
本题主要考查了二项式定理的应用,考查了组合数的性质,属于基础题.
14.【答案】
【解析】解:第次取单恰好是从号店取单,由于每天第一次取单都是从号店开始,根据题意,第次不可能从号店取单.
所以,第次取单恰好是从号店取单,
因此.
根据以上方法可得,.
根据上式可得,
,
以此类推,可得
.
故答案为:,.
本题利用对立事件概率计算公式、条件概率可解决.
本题考查概率的求法,考查对立事件概率计算公式、条件概率、等比数列的性质等基础知识,考查推理能力与计算能力,属于较难题.
15.【答案】解:由题意,解得或,
当时,,
函数在上单调递增,不合题意;
当时,,
函数的定义域为,
函数在上单调递减,在上单调递减,
但,,
所以函数在定义域上不单调,符合题意,
所以,
因为函数的定义域关于原点对称,
且,
所以为奇函数;
由及为奇函数,
可得,
即,
而在上递减且恒负,在上递减且恒正,
所以或或,
解得或
【解析】由幂函数的定义可得或,结合函数的单调性排除增根,由此确定的单调性,结合奇函数和偶函数的定义,判断函数的奇偶性;
利用奇函数的性质化简不等式,再结合函数的单调性通过讨论化简不等式求其解.
本题主要考查了幂函数性质的应用,还考查了单调性在不等式求解中的应用,属于中档题.
16.【答案】解:根据题意,补全列联表如下:
性别 体育活动 合计
课间不经常进行体育活动 课间经常进行体育活动
男
女
合计
设零假设:性别与课间经常进行体育活动没有关联,
则,
所以根据小概率值的独立性检验,我们推断不成立,即认为性别与课间经常进行体育活动是否有关联,此推断犯错误的概率不大于;
由题意可知,全校的男生中经常进行体育活动者的频率为,则,
所以的所有可能取值为,,,,,
则,,,,,
所以的分布列为:
所以,.
【解析】根据题意补全列联表,计算的值,再与临界值比较即可;
由题意可知,,所以的所有可能取值为,,,,,利用二项分布的概率公式、期望公式和方差公式求解.
本题主要考查了独立性检验的应用,考查了离散型随机变量的分布列和期望,属于中档题.
17.【答案】解:当时,,
所以,
所以,
当且仅当且,即时取等号;
当时,,当且仅当,即,时取等号,
解得,
故的取值范围为.
【解析】由已知可得,然后利用乘法,结合基本不等式可求;
由已知,结合基本不等式即可直接求解.
本题主要考查了基本不等式在最值求解中的应用,属于中档题.
18.【答案】解:令,则,根据已知数据表得到如下表:
,,
通过上表计算可得:,
因为回归直线过点,
所以,
故关于的回归方程;
这天中幼苗高度大于的有天,服从超几何分布,其中,,,
,,,,
所以随机变量的分布列为:
随机变量的期望值.
【解析】令,则,变为线型回归问题,先根据已知数据得到的对应数据表,计算样本中心,然后利用最小二乘估计公式依次计算和的估计值,求得关于的线性回归方程,进而得到关于的回归方程;
利用超几何分布概率公式计算,求得随机变量的分布列,并根据分布列,利用数学期望计算求得期望值.
本题主要考查线性回归方程,离散型随机变量分布列及数学期望,考查运算求解能力,属于中档题.
19.【答案】解:应选择第一条路线,理由如下:
设走第一、二条路线遇到的红灯次数分别为随机变量,,则,,;,,;
,,,
所以;
又因为,,;
所以;
因为,所以应选择第一条路线.
设选择第一条路线时遇到的红灯次数为,
所以,
.
设随机变量,取值为,其概率分别为,且,
,
所以;
又因为,所以.
【解析】设选择第一条路线和第二条路线遇到红灯次数分别为随机变量,,计算对应的概率,求出数学期望,比较大小即可.
设选择第一条路线时遇到的红灯次数为,计算和,设随机变量,取值为,其概率分别为,且,计算,,由,计算的值.
本题考查了离散型随机变量的应用问题,也考查了推理与运算能力,是难题.
第1页,共1页
同课章节目录
