北京市三帆中学2023~2024学年九年级下学期 5 月阶段练习二数学试卷(PDF版无答案)
文档属性
| 名称 | 北京市三帆中学2023~2024学年九年级下学期 5 月阶段练习二数学试卷(PDF版无答案) |  | |
| 格式 | |||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-18 15:52:33 | ||
图片预览


文档简介
班级 分层班级 学号 姓名
北京市三帆中学初三第二学期 5月数学阶段练习二
一、选择题(共 16分, 每小题 2分)
第 1~8题均有四个选项,符合题意的选项只有一个.
1. 右图是某几何体的展开图,该几何体是( )
A.圆柱 B. 圆锥 C. 长方体 D. 三棱锥
2. KN95型口罩能过滤空气中 95%的粒径约为 0.00 000 025 m的非油性颗粒,用科学记数法表
示 0.00 000 025是( )
A.2.5×10-7 B.0.25×10-6 C.2.5×10-6 D. 25×10-8
3. 在同一条数轴上分别用点表示实数 -2.5,0, 13, 4.5 ,则其中最左边的点表示的实
数是( )
A. -2.5 B. 0 C. 13 D. 4.5
x 2y 2 x 14. 已知方程组 ,则代数式 y的值是( )
2x y 1 3
1 1
A. 2 B. 1 C. D.
2 3
5. 如图,直线 AB∥CD,直线 EF分别交 AB,CD于点 E,F,∠BEF
的平分线交 CD于点 G,若∠BEF =118°,则∠EGC的大小是( )
A. 124 ° B. 118° C. 62° D.59°
6.小明计划到周口市体验民俗文化,想从“沈丘回族文狮舞”、“传统戏剧越调”、“八音楼子”、“泥
塑”四种民俗文化中任意选择两项,则小明选择体验“传统戏剧越调”、“泥塑”的概率为( )
1 1 1 3
A. B. C. D.
3 4 6 4
7. 一条观光船沿直线向码头前进,下表记录了 4个时间点观光船与码头的距离,其中 t表示时
间,y表示观光船与码头的距离. t / min 0 3 6 9
y / m 625 550 475 400
如果观光船保持这样的行进状态继续前进,那么从开始计时到观光船与码头的距离为
175 m时,所用时间为( )
A.21min B.18 min C. 15 min D. 13 min
第 1 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
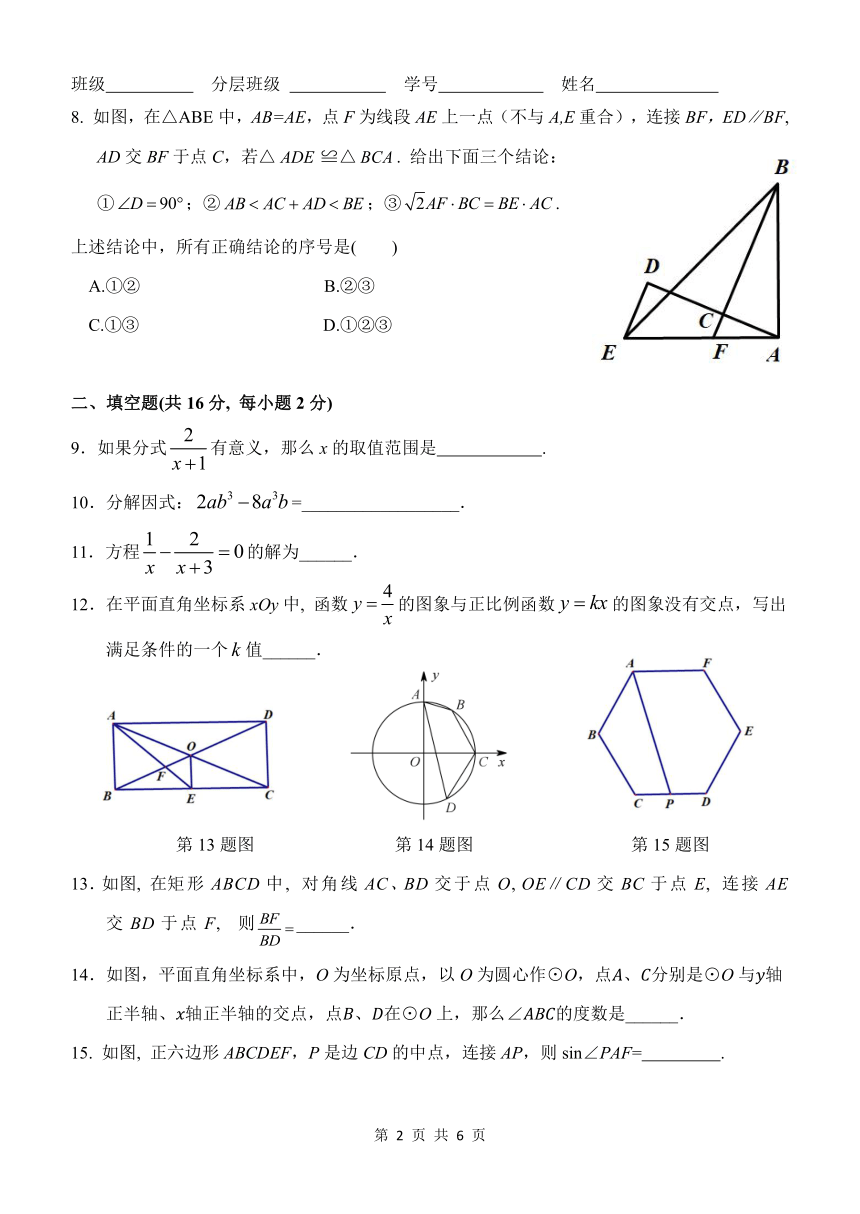
8. 如图,在△ABE 中,AB=AE,点 F为线段 AE上一点(不与 A,E重合),连接 BF,ED∥BF,
AD交 BF于点 C,若△ ADE≌△ BCA . 给出下面三个结论:
① D 90 ;② AB AC AD BE;③ 2AF BC BE AC .
上述结论中,所有正确结论的序号是( )
A.①② B.②③
C.①③ D.①②③
二、填空题(共 16分, 每小题 2分)
2
9.如果分式 有意义,那么 x的取值范围是 .
x 1
10 3 3.分解因式: 2ab 8a b =__________________.
1 2
11.方程 0的解为______.
x x 3
4
12.在平面直角坐标系 xOy中, 函数 y 的图象与正比例函数 y kx的图象没有交点,写出
x
满足条件的一个 k值______.
第 13题图 第 14题图 第 15题图
13.如图, 在矩形 ABCD 中 , 对角线 AC、BD 交于点 O, OE∥CD 交 BC 于点 E, 连接 AE
交 BD 于点 F, 则 BF ______.
BD
14.如图,平面直角坐标系中,O为坐标原点,以 O为圆心作⊙O,点 、 分别是⊙O与 轴
正半轴、 轴正半轴的交点,点 、 在⊙O上,那么∠ B 的度数是______.
15. 如图, 正六边形 ABCDEF,P是边 CD的中点,连接 AP,则 sin∠PAF= .
第 2 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
16.车间里有五台车床同时出现故障.已知第一台至第五台修复的时间如下表:
车床代号 A B C D E
修复时间(分钟) 8 31 11 6 17
若每台车床停产一分钟造成经济损失 10元,修复后即可投入生产.
(1)若只有一名修理工,且一名修理工每次只能修理一台机床,则下列三个修复车床
的顺序:①D→B→E→A→C;②D→A→C→E→B;③C→A→E→B→D中,经济
损失最少的是__________(填序号);
(2)若由两名修理工同时修复车床,且每台机床只由一名修理工修理,则最少经济损
失为 元.
三、解答题(共 68分,第 17-19题,每题 5分,第 20~21题,每题 6分,第 22~23题,每题 5
分,第 24题 6分,第 25题 5分,第 26题 6分,第 27~28题,每题 7分)
1 2
17. 计算: 2 tan 45 2 1 18;
2
2x 1 x 1
18. 解下列不等式: 1 ,并求出满足不等式的非负整数解.
3 6
19.已知: 2x2 5x 11 0 , 2求代数式 (2x 1)(x 4) (2x 3) 的值.
20. 如图,在△AOC中,OD垂直平分 AC.延长 AO至点 B,作∠COB的角平分线 OH,过点
C作 CF⊥OH 于点 F.
(1)求证:四边形 CDOF是矩形;
(2 4)连接 DF,若 = 5,DF=15,求 AC的长.
21. “母亲节”前夕,某商店依据市场调查,用 3000元购进第一批花束,上市后很快售完.接着又
用 5000元购进第二批花束。第二批所购花的数量是第一批的 2倍,且每束花的进价比第一批的
进价少 5元,求第一批每束花的进价是多少元?
第 3 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
22. 在平面直角坐标系 xOy 中,函数 y=kx+b(k≠0)的图象经过点 A(0,2)和 B(-2,5),
与过点(0,-1)且平行于 x 轴的直线交于点 C.
(1)求该函数的表达式及点 C 的坐标;
(2)当 x < 2时,对于 x 的每一个值,函数 y=-x+a的值于小于函数 y=kx+b(k≠0)的值
且大于-1,直接写出 a 的值.
23. 为了解某一路口汽车流量情况,小明同学在 10天的早、晚高峰时间段统计通过该路口的汽
车数量(单位:辆),将统计结果整理如下:
a :早高峰:
b :晚高峰:192, 189, 200, 190, 180, 192, 185, 173, 192, 181
(1)早高峰 10个数据的中位数是___________;晚高峰 10个数据的众数是__________
(2)若某时段的汽车数量方差越小,则认为该时段车流量越稳定,则早晚高峰时段车流量更稳
定的是 (填“早”或“晚”);
(3)若早高峰时段该路口通过的汽车数量高于 200辆则视为“拥堵”,试估计该路口一个月 30
天)早高峰时段拥堵的天数为多少天?
24.如图, AB为 O的直径,C是圆上一点,D是 B C的中点,弦 DE⊥AB,垂足为点 F.
(1)求证:BC DE;
4
(2)P是 AE上一点, AC=6, tan BPC = , 求 BF的长度;3
第 4 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
25. 依据《国家纺织产品基本安全技术规范》规定,服装标签上标示着 A、B、C三个类别.
A类:婴幼儿用品, 是指年龄在 36个月以内的婴幼儿使用的纺织产品,同时也包括指 100cm
身高以下的儿童. 包括了婴幼使用的相关服装产品等,其代表着服装最高的安全级别。其甲醛
含量必须低于 20mg/kg.
B类:直接接触皮肤的产品, 是正常人的衣服标准,也就是适中的安全级别,同时也是指
将会与身体直接接触的服装 ,包括大部面积与人体接触的衣服等. 其甲醛含量高于 20mg/kg,
但必须低于 75mg/kg.
C类:非直接接触皮肤的产品, 是安全级别最低的纺织产品,是指将不会与人体的皮肤有
直接的接触,或者是仅仅只有很小面积的接触,这类衣服的安全级别是最低的,包括了外套、
窗帘、裙子等. 其甲醛含量高于 75mg/kg,但必须低于 300mg/kg.
为了去除衣物上的甲醛(记作“P”),某小组研究了衣物上 P的含量(单位:mg/kg)与
浸泡时长(单位:h)的关系.该小组选取甲、乙两类服装样品,将样品分成多份,进行浸泡处
理,检测处理后样品中 P的含量.所得数据如下:
浸泡时长 甲类衣物中 P的含量 乙类衣物中 P的含量
(h) (mg/kg) (mg/kg)
0 79 80
2 32 37
4 25 31
6 21 29
8 18 28
10 17 27
12 16 27
(1)设浸泡时间为 x,甲,乙两类衣物中 P的含量分别为 y1, y2,在平面直角坐标系 xOy中,
描出表中各组数值所对应的点(x,y1),(x,y2),并画出 y1, y2的图象;
(2)结合实验数据,利用所画的函数图象可以推断,当浸泡时长为 5h时,甲,乙两类衣物中
P的含量的差约为_______ mg/kg(精确到 1);
(3)若浸泡时长不超过 12h,则经过浸泡处理后可能达到 A类标准的衣物为_______(填“甲
类”或“乙类”),该类衣物达到 A类标准至少需要浸泡_______h(精确到 1).
第 5 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
26. 已知抛物线 y ax2 2x c(a 0)经过点(-2,4).
(1)用含 a的式子表示 c及抛物线的顶点坐标;
(2)当 1 x 1时,所有 x对应的函数值 y都满足: y 4,求 a的取值范围.
27. 如图,∠OPQ=α,点 A在 PQ上,过点 A作 PO的平行线,与∠OPQ的平分线交于点 B,
M为 PB的中点,点 C在 PM上,(不与点 P,M重合),连接 AC,将线段 AC绕点 A顺时针
旋转 180°-α,得到线段 AD,连接 BD.
(1)①直接写出线段 AP与 AB之间的数量关系;
②用等式表示线段 BD,BM,MC之间的数量关系,并证明;
(2)连接 DC并延长,分别交 AB,PO于点 E,F,过点 M作 OP的垂线,交 DC于点 N.
依题意补全图形,用等式表示线段 CF,CN,NE之间的数量关系,并证明.
28. 在平面直角坐标系 xOy中,⊙O 的半径为 1,对于直线 l 和线段 PQ,给出如下定义:
若线段 PQ关于直线 l的对称图形是⊙O的弦 P'Q'(P',Q' 分别为 P,Q 的对应点),则
称线段 PQ是⊙O关于直线 l 的“对称弦”.
(1)如图,点 A1,A2,A3,B1,B2,B3 的横、纵坐标都是整数.线段 A1B1,A2 B2,A3 B3 中,是⊙O
关于直线 y = x+1 的“对称弦”的是
(2)CD是⊙O关于直线 y = kx(k ≠ 0)的“对称弦”,若点
1 3
C的坐标为(- , ),且 CD=1,直接写出点 D的坐标;
2 2
(3)已知直线 y 3x b和点M(2 3,3 ),若线段
MN是⊙O关于直线 y 3x b的“对称弦”,且MN=1,
直接写出 ON的最值和相应 b的值.
第 6 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
北京市三帆中学初三第二学期 5月数学阶段练习二
一、选择题(共 16分, 每小题 2分)
第 1~8题均有四个选项,符合题意的选项只有一个.
1. 右图是某几何体的展开图,该几何体是( )
A.圆柱 B. 圆锥 C. 长方体 D. 三棱锥
2. KN95型口罩能过滤空气中 95%的粒径约为 0.00 000 025 m的非油性颗粒,用科学记数法表
示 0.00 000 025是( )
A.2.5×10-7 B.0.25×10-6 C.2.5×10-6 D. 25×10-8
3. 在同一条数轴上分别用点表示实数 -2.5,0, 13, 4.5 ,则其中最左边的点表示的实
数是( )
A. -2.5 B. 0 C. 13 D. 4.5
x 2y 2 x 14. 已知方程组 ,则代数式 y的值是( )
2x y 1 3
1 1
A. 2 B. 1 C. D.
2 3
5. 如图,直线 AB∥CD,直线 EF分别交 AB,CD于点 E,F,∠BEF
的平分线交 CD于点 G,若∠BEF =118°,则∠EGC的大小是( )
A. 124 ° B. 118° C. 62° D.59°
6.小明计划到周口市体验民俗文化,想从“沈丘回族文狮舞”、“传统戏剧越调”、“八音楼子”、“泥
塑”四种民俗文化中任意选择两项,则小明选择体验“传统戏剧越调”、“泥塑”的概率为( )
1 1 1 3
A. B. C. D.
3 4 6 4
7. 一条观光船沿直线向码头前进,下表记录了 4个时间点观光船与码头的距离,其中 t表示时
间,y表示观光船与码头的距离. t / min 0 3 6 9
y / m 625 550 475 400
如果观光船保持这样的行进状态继续前进,那么从开始计时到观光船与码头的距离为
175 m时,所用时间为( )
A.21min B.18 min C. 15 min D. 13 min
第 1 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
8. 如图,在△ABE 中,AB=AE,点 F为线段 AE上一点(不与 A,E重合),连接 BF,ED∥BF,
AD交 BF于点 C,若△ ADE≌△ BCA . 给出下面三个结论:
① D 90 ;② AB AC AD BE;③ 2AF BC BE AC .
上述结论中,所有正确结论的序号是( )
A.①② B.②③
C.①③ D.①②③
二、填空题(共 16分, 每小题 2分)
2
9.如果分式 有意义,那么 x的取值范围是 .
x 1
10 3 3.分解因式: 2ab 8a b =__________________.
1 2
11.方程 0的解为______.
x x 3
4
12.在平面直角坐标系 xOy中, 函数 y 的图象与正比例函数 y kx的图象没有交点,写出
x
满足条件的一个 k值______.
第 13题图 第 14题图 第 15题图
13.如图, 在矩形 ABCD 中 , 对角线 AC、BD 交于点 O, OE∥CD 交 BC 于点 E, 连接 AE
交 BD 于点 F, 则 BF ______.
BD
14.如图,平面直角坐标系中,O为坐标原点,以 O为圆心作⊙O,点 、 分别是⊙O与 轴
正半轴、 轴正半轴的交点,点 、 在⊙O上,那么∠ B 的度数是______.
15. 如图, 正六边形 ABCDEF,P是边 CD的中点,连接 AP,则 sin∠PAF= .
第 2 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
16.车间里有五台车床同时出现故障.已知第一台至第五台修复的时间如下表:
车床代号 A B C D E
修复时间(分钟) 8 31 11 6 17
若每台车床停产一分钟造成经济损失 10元,修复后即可投入生产.
(1)若只有一名修理工,且一名修理工每次只能修理一台机床,则下列三个修复车床
的顺序:①D→B→E→A→C;②D→A→C→E→B;③C→A→E→B→D中,经济
损失最少的是__________(填序号);
(2)若由两名修理工同时修复车床,且每台机床只由一名修理工修理,则最少经济损
失为 元.
三、解答题(共 68分,第 17-19题,每题 5分,第 20~21题,每题 6分,第 22~23题,每题 5
分,第 24题 6分,第 25题 5分,第 26题 6分,第 27~28题,每题 7分)
1 2
17. 计算: 2 tan 45 2 1 18;
2
2x 1 x 1
18. 解下列不等式: 1 ,并求出满足不等式的非负整数解.
3 6
19.已知: 2x2 5x 11 0 , 2求代数式 (2x 1)(x 4) (2x 3) 的值.
20. 如图,在△AOC中,OD垂直平分 AC.延长 AO至点 B,作∠COB的角平分线 OH,过点
C作 CF⊥OH 于点 F.
(1)求证:四边形 CDOF是矩形;
(2 4)连接 DF,若 = 5,DF=15,求 AC的长.
21. “母亲节”前夕,某商店依据市场调查,用 3000元购进第一批花束,上市后很快售完.接着又
用 5000元购进第二批花束。第二批所购花的数量是第一批的 2倍,且每束花的进价比第一批的
进价少 5元,求第一批每束花的进价是多少元?
第 3 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
22. 在平面直角坐标系 xOy 中,函数 y=kx+b(k≠0)的图象经过点 A(0,2)和 B(-2,5),
与过点(0,-1)且平行于 x 轴的直线交于点 C.
(1)求该函数的表达式及点 C 的坐标;
(2)当 x < 2时,对于 x 的每一个值,函数 y=-x+a的值于小于函数 y=kx+b(k≠0)的值
且大于-1,直接写出 a 的值.
23. 为了解某一路口汽车流量情况,小明同学在 10天的早、晚高峰时间段统计通过该路口的汽
车数量(单位:辆),将统计结果整理如下:
a :早高峰:
b :晚高峰:192, 189, 200, 190, 180, 192, 185, 173, 192, 181
(1)早高峰 10个数据的中位数是___________;晚高峰 10个数据的众数是__________
(2)若某时段的汽车数量方差越小,则认为该时段车流量越稳定,则早晚高峰时段车流量更稳
定的是 (填“早”或“晚”);
(3)若早高峰时段该路口通过的汽车数量高于 200辆则视为“拥堵”,试估计该路口一个月 30
天)早高峰时段拥堵的天数为多少天?
24.如图, AB为 O的直径,C是圆上一点,D是 B C的中点,弦 DE⊥AB,垂足为点 F.
(1)求证:BC DE;
4
(2)P是 AE上一点, AC=6, tan BPC = , 求 BF的长度;3
第 4 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
25. 依据《国家纺织产品基本安全技术规范》规定,服装标签上标示着 A、B、C三个类别.
A类:婴幼儿用品, 是指年龄在 36个月以内的婴幼儿使用的纺织产品,同时也包括指 100cm
身高以下的儿童. 包括了婴幼使用的相关服装产品等,其代表着服装最高的安全级别。其甲醛
含量必须低于 20mg/kg.
B类:直接接触皮肤的产品, 是正常人的衣服标准,也就是适中的安全级别,同时也是指
将会与身体直接接触的服装 ,包括大部面积与人体接触的衣服等. 其甲醛含量高于 20mg/kg,
但必须低于 75mg/kg.
C类:非直接接触皮肤的产品, 是安全级别最低的纺织产品,是指将不会与人体的皮肤有
直接的接触,或者是仅仅只有很小面积的接触,这类衣服的安全级别是最低的,包括了外套、
窗帘、裙子等. 其甲醛含量高于 75mg/kg,但必须低于 300mg/kg.
为了去除衣物上的甲醛(记作“P”),某小组研究了衣物上 P的含量(单位:mg/kg)与
浸泡时长(单位:h)的关系.该小组选取甲、乙两类服装样品,将样品分成多份,进行浸泡处
理,检测处理后样品中 P的含量.所得数据如下:
浸泡时长 甲类衣物中 P的含量 乙类衣物中 P的含量
(h) (mg/kg) (mg/kg)
0 79 80
2 32 37
4 25 31
6 21 29
8 18 28
10 17 27
12 16 27
(1)设浸泡时间为 x,甲,乙两类衣物中 P的含量分别为 y1, y2,在平面直角坐标系 xOy中,
描出表中各组数值所对应的点(x,y1),(x,y2),并画出 y1, y2的图象;
(2)结合实验数据,利用所画的函数图象可以推断,当浸泡时长为 5h时,甲,乙两类衣物中
P的含量的差约为_______ mg/kg(精确到 1);
(3)若浸泡时长不超过 12h,则经过浸泡处理后可能达到 A类标准的衣物为_______(填“甲
类”或“乙类”),该类衣物达到 A类标准至少需要浸泡_______h(精确到 1).
第 5 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
班级 分层班级 学号 姓名
26. 已知抛物线 y ax2 2x c(a 0)经过点(-2,4).
(1)用含 a的式子表示 c及抛物线的顶点坐标;
(2)当 1 x 1时,所有 x对应的函数值 y都满足: y 4,求 a的取值范围.
27. 如图,∠OPQ=α,点 A在 PQ上,过点 A作 PO的平行线,与∠OPQ的平分线交于点 B,
M为 PB的中点,点 C在 PM上,(不与点 P,M重合),连接 AC,将线段 AC绕点 A顺时针
旋转 180°-α,得到线段 AD,连接 BD.
(1)①直接写出线段 AP与 AB之间的数量关系;
②用等式表示线段 BD,BM,MC之间的数量关系,并证明;
(2)连接 DC并延长,分别交 AB,PO于点 E,F,过点 M作 OP的垂线,交 DC于点 N.
依题意补全图形,用等式表示线段 CF,CN,NE之间的数量关系,并证明.
28. 在平面直角坐标系 xOy中,⊙O 的半径为 1,对于直线 l 和线段 PQ,给出如下定义:
若线段 PQ关于直线 l的对称图形是⊙O的弦 P'Q'(P',Q' 分别为 P,Q 的对应点),则
称线段 PQ是⊙O关于直线 l 的“对称弦”.
(1)如图,点 A1,A2,A3,B1,B2,B3 的横、纵坐标都是整数.线段 A1B1,A2 B2,A3 B3 中,是⊙O
关于直线 y = x+1 的“对称弦”的是
(2)CD是⊙O关于直线 y = kx(k ≠ 0)的“对称弦”,若点
1 3
C的坐标为(- , ),且 CD=1,直接写出点 D的坐标;
2 2
(3)已知直线 y 3x b和点M(2 3,3 ),若线段
MN是⊙O关于直线 y 3x b的“对称弦”,且MN=1,
直接写出 ON的最值和相应 b的值.
第 6 页 共 6 页
{#{QQABAYoUoggoAIBAABhCEwGQCkIQkAACAAoOxBAEoAAAyAFABAA=}#}
同课章节目录
