01押浙江卷第1-5题(实数、三视图、科学记数法、整式运算、统计)-2024年浙江省中考数学题号押题(含解析)
文档属性
| 名称 | 01押浙江卷第1-5题(实数、三视图、科学记数法、整式运算、统计)-2024年浙江省中考数学题号押题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-18 14:55:43 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
押题方向1:实数相关概念、运算及大小比较
2023年浙江真题 考点 命题趋势
2023年湖州、衢州、金华、台州、宁波卷第1题 实数的大小比较 从近几年浙江中考来看,实数的相关概念(正负数、数轴、相反数、绝对值、倒数、平方根、算术平方根、立方根)、实数的大小比较、有理数的运算以选择题形式考查,比较简单;预计2024年浙江卷还将继续重视对正负数的意义、相反数、绝对值、倒数、数轴、平方根、算术平方根、立方根等实数的相关概念及实数的大小比较和运算的考查。
2023年丽水卷第1题 相反数
2023年嘉兴、舟山卷第1题 立方根
2023年温州、绍兴卷第1题 有理数的加减
2023年杭州卷第2题 有理数的混合运算
1.(2023 衢州)手机信号的强弱通常采用负数来表示,绝对值越小表示信号越强(单位:dBm),则下列信号最强的是( )
A.﹣50 B.﹣60 C.﹣70 D.﹣80
2.(2023 温州)如图,比数轴上点A表示的数大3的数是( )
A.﹣1 B.0 C.1 D.2
3.(2023 舟山、嘉兴)下面四个数中,比1小的正无理数是( )
A. B.﹣ C. D.
4.(2023 丽水)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
5.(2023 浙江)﹣8的立方根是( )
A.﹣2 B.2 C.±2 D.不存在
6.(2023 绍兴)计算2﹣3的结果是( )
A.﹣1 B.﹣3 C.1 D.3
7.(2023 杭州)(﹣2)2+22=( )
A.0 B.2 C.4 D.8
8.(2023 金华)某一天,哈尔滨、北京、杭州、金华四个城市的最低气温分别是﹣20℃,﹣10℃,0℃,2℃,其中最低气温是( )
A.﹣20℃ B.﹣10℃ C.0℃ D.2℃
9.(2023 台州)下列各数中,最小的是( )
A.2 B.1 C.﹣1 D.﹣2
10.(2023 宁波)在﹣2,﹣1,0,π这四个数中,最小的数是( )
A.﹣2 B.﹣1 C.0 D.π
数轴、相反数、绝对值、倒数是核心考点,常在选择题和填空题中出现。对于数轴我们不仅要记住它的三要素,还要能借助它比较实数大小;对于相反数我们需要注意的是当用一个式子表示一个数量,求相反数时需要注意整体概念;对于绝对值需要注意情况不确定时,需要分类讨论;而对于倒数需要注意的是0没有倒数。
实数比较大小可以根据数的性质来比较,正数比负数大,两个负数比较大小,绝对大的反而小;也可通过数轴,数轴上的两个数比较大小,右边的数比左边的大。但对于一些复杂的式子,我们就需要用求差法或者求商法;对于含根号的数,我们还可以用平方法或者倒数法。
1.如果水位升高3m时水位变化记作+3m,那么水位不升不降时水位变化记作( )
A.+3m B.﹣3m C.0m D.±3m
2.在﹣4,﹣1,0,1这四个数中,比﹣2小的数是( )
A.﹣4 B.﹣1 C.0 D.1
3.下列算式中,运算结果最小的是( )
A.﹣2+3 B.﹣2﹣3 C.﹣2×3 D.﹣2÷3
4.(﹣2)3=( )
A.﹣6 B.6 C.﹣8 D.8
5.|﹣3|﹣(﹣2)=( )
A.﹣1 B.5 C.1 D.﹣5
6.﹣2024的倒数是( )
A.﹣2024 B.2024 C. D.
7.家用冰箱冷冻室的温度需控制在﹣4℃到﹣24℃之间,则可将冷冻室的温度设为( )
A.0℃ B.﹣3℃ C.﹣18℃ D.﹣25℃
8.把笔尖放在数轴的原点,沿数轴先向左(负方向)移动6个单位长度,再向右移动3个单位长度,用算式表示上述过程与结果,正确的是( )
A.﹣6+3=9 B.﹣6﹣3=﹣3 C.﹣6+3=﹣3 D.﹣6+3=3
9.已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.若在该快递公司寄一件9千克的物品,则需要付费( )
A.17元 B.19元 C.21元 D.23元
10.有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
A.a2>b2 B.a﹣b>0 C. D.a+b>0
押题方向2:投影与视图
20233年浙江真题 考点 命题趋势
2023年湖州、温州、金华、台州、舟山、嘉兴卷第2题 简单几何体的三视图 从近几年浙江中考来看,投影与视图以选择题形式考查,2023年浙江省10份中考试卷有9份试卷考查了投影与视图,比较简单,主要考查了简单几何体的三视图与由三视图判断几何体;预计2024年浙江卷还将继续重视对三视图的考查。
2023年绍兴卷第3题 简单几何体的三视图
2023年湖州、宁波、丽水卷第4题 简单几何体的三视图
2023年湖州卷第4题 由三视图判断几何体
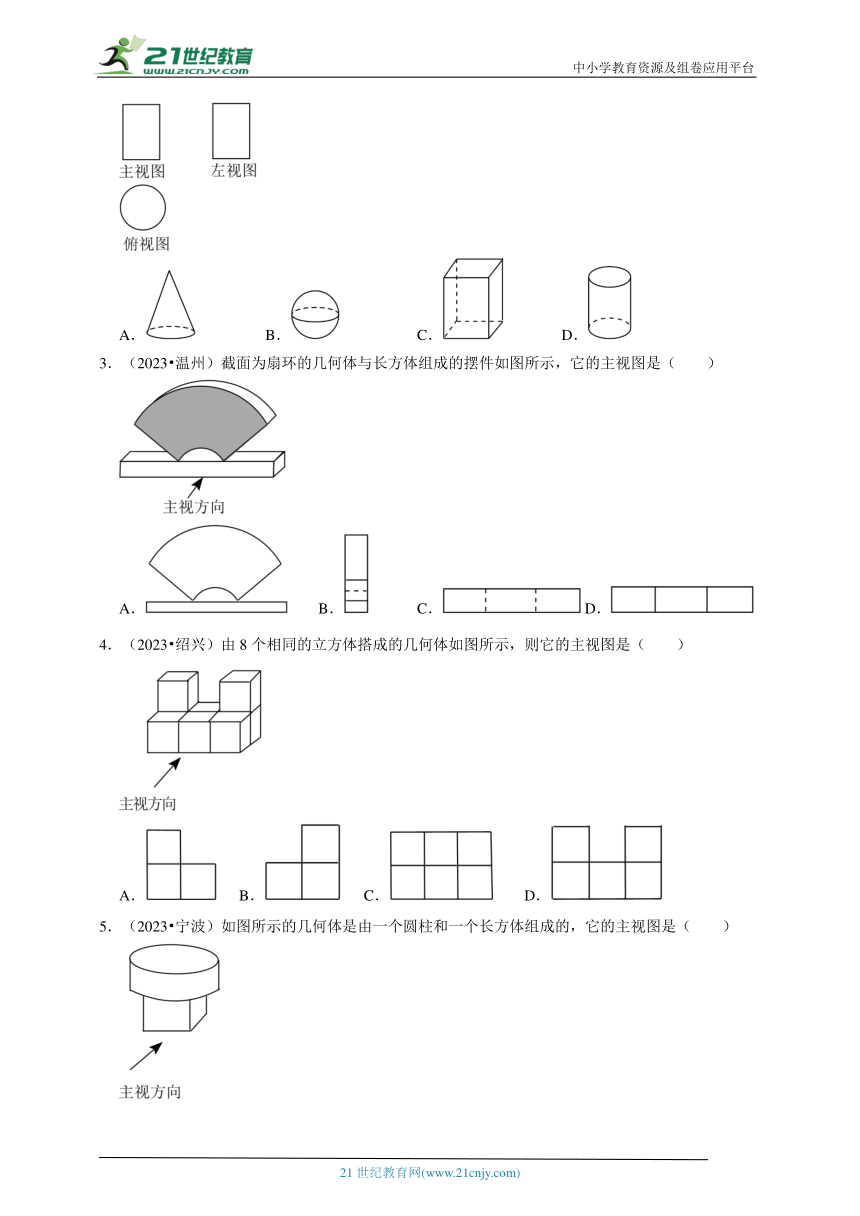
1.(2023 湖州)已知某几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
3.(2023 温州)截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )
A. B. C. D.
4.(2023 绍兴)由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B. C. D.
5.(2023 宁波)如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
A. B. C. D.
1.几何体的三视图:(1)主视图:物体在正投影面上的正投影.(2)左视图:物体在侧投影面上的正投影.(3)俯视图:物体在水平投影面上的正投影.
2.画“三视图”的原则:(1)大小:长对正,高平齐,宽相等.(2)虚实:在画图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.
3.由三视图确定几何体的方法:
1)由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:
① 根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;
② 从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;
③ 熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助.
1.如图是由5个大小相同的小正方体组成的几何体,该几何体的俯视图是( )
A. B. C. D.
2.如图是一个古建筑中常用的榫卯构件,其左视图为( )
A. B. C. D.
3.榫卯是我国古代木制建筑、家具等的主要结构方式,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
4.某物体如图所示,其左视图是( )
A. B. C. D.
5.在下面四个几何体中,主视图与俯视图都是圆的为( )
A. B. C. D.
6.下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
7.如图是一个几何体的三视图,则该几何体是( )
A.B.C. D.
8.如图,是一个几何体的三视图,则这个几何体是( )
A. B. C. D.
押题方向3:科学记数法
20233年浙江真题 考点 命题趋势
2023年杭州卷第1题 科学记数法 从近几年浙江中考来看,科学记数法、近似数以选择题形式考查,比较简单,科学记数法有大数和小数两种形式,有时带“亿”、“万”、“千万”等单位,做题时要仔细审题,切忽略单位;预计2024年浙江卷还将继续重视对科学记数法的考查。
2023年绍兴卷第2题 科学记数法
2023年湖州、温州、金华、宁波卷第3题 科学记数法
1.(2023 宁波)据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011 C.3.8018×1010 D.38.018×1010
2.(2023 湖州)国家互联网信息办公室2023年5月23日发布的《数字中国发展报告(2022年)》显示,2022年我国数字经济规模达502000亿元.用科学记数法表示502000,正确的是( )
A.0.502×106 B.5.02×106 C.5.02×105 D.50.2×104
3.(2023 杭州)杭州奥体中心体育场又称“大莲花”,里面有80800个座位.数据80800用科学记数法表示为( )
A.8.8×104 B.8.08×104 C.8.8×105 D.8.08×105
4.(2023 温州)苏步青来自“数学家之乡”,为纪念其卓越贡献,国际上将一颗距地球约218000000公里的行星命名为“苏步青星”.数据218000000用科学记数法表示为( )
A.0.218×109 B.2.18×108 C.21.8×102 D.218×106
5.(2023 绍兴)据报道,2023年“五一”假期全国国内旅游出游合计274000000人次.数字274000000用科学记数法表示是( )
A.27.4×107 B.2.74×108 C.0.274×109 D.2.74×109
科学记数法是中考高频考点,我们不仅要记住它的基本形式,更要记住表达式中a的取值范围;还要注意n,当表示一个绝对值大于10的数,n是正整数;当表示一个绝对值小于1的数时,指数为负整数。注意:1)单位的统一,尤其是带“万”或者“亿”的问题:含有万、亿等单位的数,用科学记数法表示时,要先还原成原数,再用科学记数法表示,最后按要求取近似值。
1.2023年5月28日,我国自主研发的C919国产大飞机商业首航取得圆满成功.C919可储存约186000升燃油,将数据186000用科学记数法表示为( )
A.0.186×105 B.1.86×105 C.18.6×104 D.186×103
2.我国自主研发的500m口径球面射电望远镜(FAST)有“中国天眼”之称,它的反射面面积约为250000m2.用科学记数法表示数据250000为( )
A.0.25×106 B.25×104 C.2.5×104 D.2.5×105
3.中国信通院预计未来2~3年内将实现5G的个人终端应用和数字内容的创新突破,预计2025年全球5G移动用户数将突破57亿户.数据57亿用科学记数法表示为( )
A.0.57×1010 B.5.7×1010 C.5.7×109 D.57×104
4.芯片是手机、电脑等高科技产品最核心的部件,更小的芯片意味着更高的性能,目前我国芯片的量产工艺已达到14纳米,已知14纳米等于0.000000014米,用科学记数法将0.000000014表示为( )
A.1.4×10﹣9 B.1.4×10﹣7 C.1.4×10﹣8 D.14×10﹣7
5.华为一部分Mate40手机将会搭载麒麟9000处理器,这是手机行业首批采用5nm工艺制式的芯片,1nm=0.000000001m,其中5nm用科学记数法表示为( )
A.5×109 B.5×10﹣10 C.5×10﹣8 D.5×10﹣9
押题方向4:整式运算
2023年浙江真题 考点 命题趋势
2023年湖州卷第2题 同底数幂的乘法 从近几年浙江中考来看,整式运算主要以考查整式的加减、乘除、乘法公式、幂的运算为主,也是考查重点,难度较低。预计2024年浙江卷还将继续考查幂的运算、整式混合运算(特别是乘法公式),为避免丢分,学生应扎实掌握。
2023年丽水卷第2题 合并同类项
2023年衢州卷第3题、宁波卷第2题 同底数幂的除法
2023年绍兴卷第4题 整式的混合运算
2023年绍兴卷第4题 完全平方公式
1.(2023 丽水)计算a2+2a2的正确结果是( )
A.2a2 B.2a4 C.3a2 D.3a4
2.(2023 温州)化简a4 (﹣a)3的结果是( )
A.a12 B.﹣a12 C.a7 D.﹣a7
3.(2023 台州)下列运算正确的是( )
A.2(a﹣1)=2a﹣2 B.(a+b)2=a2+b2 C.3a+2a=5a2 D.(ab)2=ab2
4.(2023 绍兴)下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7
C.(a+1)(a﹣1)=a2﹣1 D.(a+1)2=a2+1
5.(2023 衢州)下列运算,结果正确的是( )
A.3a+2a=5a2 B.3a﹣2a=1 C.a2 a3=a5 D.a÷a2=a
6.(2023 宁波)下列计算正确的是( )
A.x2+x=x3 B.x6÷x3=x2 C.(x3)4=x7 D.x3 x4=x7
1)幂的运算法则是进行整式乘除法的基础,要熟练掌握,解题时要明确运算的类型,正确运用法则;在运算的过程中,一定要注意指数、系数和符号的处理.
2)整式的加减,实质上就是合并同类项,有括号的,先去括号,只要算式中没有同类项,就是最后的结果;多项式乘多项式的运算中要做到不重不漏,应用乘法公式进行简便计算,另外去括号时,要注意符号的变化,最后把所得式子化简,即合并同类项.
1.计算(﹣a)3 a2的结果是( )
A.﹣a6 B.a6 C.﹣a5 D.a5
2.下列运算正确的是( )
A.2+4a=6a B.a3 a4=a12 C.(﹣2a)2=﹣4a2 D.a5÷a3=a2
3.下列计算正确的是( )
A.(a2)4=a6 B.(3a)2=6a2 C.a8÷a4=a2 D.(﹣ab3)2=a2b6
4.下列运算正确的是( )
A.(a2)3=a5 B.a3 a4=a12 C.a8÷a4=a2 D.(﹣3a2)2=9a4
5.下列计算正确的是( )
A.a3﹣a2=a B.a3 a2=a6 C.(a3)2=a6 D.(2a+1)(2a﹣1)=2a2﹣1
6.下列计算正确的是( )
A.a+2a=3a B.(a+b)2=a2+b2 C.(a2)3=a5 D.a2 a3=a6
7.下列计算正确的是( )
A.a6÷a3=a3 B.(a﹣b)2=a2﹣b2 C.(﹣3a2)3=﹣9a6 D.a2+a3=a5
8.下列运算正确的是( )
A.x4 x3=x12 B.(a6)2÷(a4)3=a C.(a3)2 a4=a10 D.(ab2)3÷(﹣ab)2=﹣ab4
押题方向五:统计
2023年浙江真题 考点 命题趋势
2023年湖州卷第7题 算术平均数 从近几年浙江中考来看,统计部分主要以考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差为主,有的结合统计图表考查,难度较低。预计2024年浙江卷还将继续考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差,为避免丢分,学生应扎实掌握。
2023年舟山、嘉兴卷第3题、台州卷第7题 全面调查与抽样调查
2023年金华卷第6题 众数
2023年宁波卷第6题、杭州卷第9题 方差
2023年温州卷第5题 样本估计总体
1.(2023 湖州)某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这5天平均每天的用水量是( )
A.25立方米 B.30立方米 C.32立方米 D.35立方米
2.(2023 台州)以下调查中,适合全面调查的是( )
A.了解全国中学生的视力情况 B.检测“神舟十六号”飞船的零部件
C.检测台州的城市空气质量 D.调查某池塘中现有鱼的数量
3.(2023 金华)上周双休日,某班8名同学课外阅读的时间如下(单位:时):1,4,2,4,3,3,4,5,这组数据的众数是( )
A.1时 B.2时 C.3时 D.4时
4.(2023 宁波)甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:
甲 乙 丙 丁
9 8 9 9
S2 1.2 0.4 1.8 0.4
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
5.某校计划组织研学活动,现有四个地点可供选择:南麂岛、百丈漈、楠溪江、雁荡山.
为了解学生想法,校方进行问卷调查(每人选一个地点),并绘制成如图所示统计图.已知选择雁荡山的有270人,那么选择楠溪江的有( )
A.90人 B.180人 C.270人 D.360人
6.(2023 杭州)一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字.根据下面的统计结果,能判断记录的这5个数字中一定没有出现数字6的是( )
A.中位数是3,众数是2 B.平均数是3,中位数是2
C.平均数是3,方差是2 D.平均数是3,众数是2
1.如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
2.平均数能充分利用各数据提供的信息,在实际生活中常用样本的平均数估计总体的平均数;中位数不受个别偏大或偏小数据的影响,当一组数据中的个别数据变动较大时,一般用中位数来描述数据的集中趋势;众数考察的是各数据所出现的频数,其大小只与部分数据有关,当一组数据中某些数据多次重复出现时,众数往往更能反映问题。
3.方差反映数据的离散程度,方差越大,数据的波动越大,数据越不稳定。
1.下列调查方式适合用普查的是( )
A.检测一批LED灯的使用寿命
B.检测一批家用汽车的抗撞击能力
C.测试2024神舟十八号载人飞船的零部件质量情况
D.中央电视台《2024年第九季诗词大会》的收视率
2.为加强交通安全教育,某校随机调查了九年级部分学生的上学方式(乘车、步行、骑车),并根据调查结果绘制了如图两幅不完整的统计图,下列判断错误的是( )
A.本次调查的总人数为60人 B.调查的学生中骑车上学的有8人
C.若该校九年级学生有1200人,则乘车上学的约有600人
D.扇形统计图中步行的学生人数所占的圆心角是122°
3.下列说法中,正确的是( )
A.一组数据4,4,2,3,1的中位数是2
B.反映空气的主要成分(氮气约占78%,氧气约占21%,其他微量气体约占1%)宜采用折线统计图
C.甲、乙两人各10次射击的平均成绩相同,方差分别是s甲2=2.2,s乙2=1.3,则乙的射击成绩较稳定
D.对载人航天器零部件的检查适合采用抽样凋查
4.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是3,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A.2,3 B.2,9 C.4,18 D.4,27
5.某店铺连续5天销售衬衣的件数分别为10,11,13,15,11.关于这组数据,以下结论错误的是( )
A.众数是11 B.平均数是12 C.方差是3.2 D.中位数是13
6.如图是描述某校篮球队员年龄的条形图,则这个篮球队员年龄的众数和中位数分别为( )
A.14,15 B.15,14 C.15,15 D.15,14.5
7.某班35位同学课外阅读物的数量统计如表所示,其中有两个数据被遮盖,下列关于课外阅读物的统计量中,与被遮盖的数据无关的是( )
课外阅读物的数量 2 3 4 5 6 7 8
人数 ■ ■ 9 7 9 3 2
A.平均数,方差 B.中位数,方差 C.平均数,众数 D.中位数,众数
8.已知5个正数a1,a2,a3,a4,a5的平均数是a,且a1>a2>a3>a4>a5,则数据a1,a2,a3,0,a4,a5的平均数和中位数是( )
A.a, B.a, C.a, D.a,
答案与解析
押题方向1:实数相关概念、运算及大小比较
2023年浙江真题 考点 命题趋势
2023年湖州、衢州、金华、台州、宁波卷第1题 实数的大小比较 从近几年浙江中考来看,实数的相关概念(正负数、数轴、相反数、绝对值、倒数、平方根、算术平方根、立方根)、实数的大小比较、有理数的运算以选择题形式考查,比较简单;预计2024年浙江卷还将继续重视对正负数的意义、相反数、绝对值、倒数、数轴、平方根、算术平方根、立方根等实数的相关概念及实数的大小比较和运算的考查。
2023年丽水卷第1题 相反数
2023年嘉兴、舟山卷第1题 立方根
2023年温州、绍兴卷第1题 有理数的加减
2023年杭州卷第2题 有理数的混合运算
1.(2023 衢州)手机信号的强弱通常采用负数来表示,绝对值越小表示信号越强(单位:dBm),则下列信号最强的是( )
A.﹣50 B.﹣60 C.﹣70 D.﹣80
【答案】A
【点拨】先求出各个选项中数的绝对值,然后进行比较,根据绝对值越小表示信号越强,找出信号最强的即可.
【解析】解:∵|﹣50|=50,|﹣60|=60,|﹣70|=70,|﹣80|=80,50<60<70<80,
∴信号最强的是﹣50,
故答案为:A.
【点睛】本题主要考查了绝对值,解题关键是熟练掌握绝对值的性质.
2.(2023 温州)如图,比数轴上点A表示的数大3的数是( )
A.﹣1 B.0 C.1 D.2
【答案】D
【点拨】结合数轴得出A对应的数,再利用有理数的加法计算得出答案.
【解析】解:由数轴可得:A表示﹣1,则比数轴上点A表示的数大3的数是:﹣1+3=2.
故选:D.
【点睛】此题主要考查了有理数的加法以及数轴,正确掌握有理数的加法是解题关键.
3.(2023 舟山、嘉兴)下面四个数中,比1小的正无理数是( )
A. B.﹣ C. D.
【答案】A
【点拨】无理数即无限不循环的小数,结合实数比较大小的方法进行判断即可.
【解析】解:A.∵1>,
∴>,
即1>,且是正无理数,
则A符合题意;
B.﹣是负数,
则B不符合题意;
C.是分数,不是无理数,
则C不符合题意;
D.∵π>3,
∴>1,
则D不符合题意;
故选:A.
【点睛】本题考查无理数的定义及实数的大小比较,此为基础且重要知识点,必须熟练掌握.
4.(2023 丽水)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
【答案】C
【点拨】根据相反数的定义判断即可.
【解析】解:﹣3的相反数是3,
故选:C.
【点睛】本题考查了相反数:只有符号不同的两个数是互为相反数,掌握其定义是解题的关键.
5.(2023 浙江)﹣8的立方根是( )
A.﹣2 B.2 C.±2 D.不存在
【答案】A
【点拨】根据立方根的定义求出的值,即可得出答案.
【解析】解:﹣8的立方根是==﹣2,
故选:A.
【点睛】本题考查了对立方根的定义的理解和运用,明确a的立方根是是解题的关键.
6.(2023 绍兴)计算2﹣3的结果是( )
A.﹣1 B.﹣3 C.1 D.3
【答案】A
【点拨】根据有理数减法法则:减去一个数,等于加上这个数的相反数.即:a﹣b=a+(﹣b),即可得出答案.
【解析】解:2﹣3=﹣1.
故选:A.
【点睛】此题主要考查了有理数的减法,正确掌握有理数的减法运算法则是解题关键.
7.(2023 杭州)(﹣2)2+22=( )
A.0 B.2 C.4 D.8
【答案】D
【点拨】根据有理数的混合运算顺序,先计算乘方,再计算加法即可.
【解析】解:(﹣2)2+22=4+4=8.
故选:D.
【点睛】本题考查了有理数的混合运算,掌握有理数的乘方的定义是解答本题的关键.
8.(2023 金华)某一天,哈尔滨、北京、杭州、金华四个城市的最低气温分别是﹣20℃,﹣10℃,0℃,2℃,其中最低气温是( )
A.﹣20℃ B.﹣10℃ C.0℃ D.2℃
【答案】A
【点拨】明确在实数中负数小于0小于正数,且负数之间比较大小绝对值越大负数越小.
【解析】解:由题可知:﹣20<﹣10<0<2,
所以最低气温是﹣20℃.
故选:A.
【点睛】本题考查了实数的比较大小,题目难度较小,一般出现在期末第一题.
9.(2023 台州)下列各数中,最小的是( )
A.2 B.1 C.﹣1 D.﹣2
【答案】D
【点拨】正数>0>负数,两个负数比较大小,绝对值大的反而小;据此进行判断即可.
【解析】解:∵|﹣1|=1,|﹣2|=2,1<2,
∴﹣1>﹣2,
则2>1>﹣1>﹣2,
那么最小的数为:﹣2,
故选:D.
【点睛】本题考查有理数的大小比较,此为基础且重要知识点,必须熟练掌握.
10.(2023 宁波)在﹣2,﹣1,0,π这四个数中,最小的数是( )
A.﹣2 B.﹣1 C.0 D.π
【答案】A
【点拨】正数>0>负数,两个负数比较大小,绝对值大的反而小,据此进行判断即可.
【解析】解:∵|﹣2|=2,|﹣1|=1,2>1,
∴﹣1>﹣2,
∴π>0>﹣1>﹣2,
则最小的数为:﹣2,
故选:A.
【点睛】本题考查实数的大小比较,此为基础且重要知识点,必须熟练掌握.
数轴、相反数、绝对值、倒数是核心考点,常在选择题和填空题中出现。对于数轴我们不仅要记住它的三要素,还要能借助它比较实数大小;对于相反数我们需要注意的是当用一个式子表示一个数量,求相反数时需要注意整体概念;对于绝对值需要注意情况不确定时,需要分类讨论;而对于倒数需要注意的是0没有倒数。
实数比较大小可以根据数的性质来比较,正数比负数大,两个负数比较大小,绝对大的反而小;也可通过数轴,数轴上的两个数比较大小,右边的数比左边的大。但对于一些复杂的式子,我们就需要用求差法或者求商法;对于含根号的数,我们还可以用平方法或者倒数法。
1.如果水位升高3m时水位变化记作+3m,那么水位不升不降时水位变化记作( )
A.+3m B.﹣3m C.0m D.±3m
【答案】C
【点拨】正数和负数是一组具有相反意义的量,据此即可求得答案.
【解析】解:水位升高3m时水位变化记作+3m,那么水位不升不降时水位变化记作0m,
故选:C.
【点睛】本题考查正数和负数,理解具有相反意义的量是解题的关键.
2.在﹣4,﹣1,0,1这四个数中,比﹣2小的数是( )
A.﹣4 B.﹣1 C.0 D.1
【答案】A
【点拨】有理数大小比较的法则:(1)正数都大于0;(2)负数都小于0;(3)正数大于一切负数;(4)两个负数,绝对值大的其值反而小,据此逐个判断即可.
【解析】解:∵﹣4<﹣2,﹣1>﹣2,0>﹣2,1>﹣2,
∴在﹣4,﹣1,0,1这四个数中,比﹣2小的数是﹣4.
故选:A.
【点睛】此题主要考查了有理数大小比较的方法,解答此题的关键是要明确:(1)正数都大于0;(2)负数都小于0;(3)正数大于一切负数;(4)两个负数,绝对值大的其值反而小.
3.下列算式中,运算结果最小的是( )
A.﹣2+3 B.﹣2﹣3 C.﹣2×3 D.﹣2÷3
【答案】C
【点拨】根据有理数混合运算的计算法则进行解答.
【解析】解:﹣2+3=1;
﹣2﹣3=﹣5;
﹣2×3=﹣6;
﹣2÷3=﹣,
﹣6.
故选:C.
【点睛】本题考查了有理数的混合运算,解题的关键是运用计算法则进行计算.
4.(﹣2)3=( )
A.﹣6 B.6 C.﹣8 D.8
【答案】C
【点拨】原式利用乘方的意义计算即可得到结果.
【解析】解:原式=﹣8,
故选:C.
【点睛】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.
5.|﹣3|﹣(﹣2)=( )
A.﹣1 B.5 C.1 D.﹣5
【答案】B
【点拨】﹣3的绝对值等于3,减去﹣2就相当于加上2.
【解析】解:|﹣3|﹣(﹣2)=3+2=5.
故选:B.
【点睛】本题考查了有理数的减法法则及绝对值的定义.减去一个数,等于加上这个数的相反数.一个负数的绝对值等于它的相反数.
6.﹣2024的倒数是( )
A.﹣2024 B.2024 C. D.
【答案】C
【点拨】根据题意利用倒数定义即可得出本题答案.
【解析】解:∵,
故选:C.
【点睛】本题考查倒数定义,解题的关键是掌握倒数的定义.
7.家用冰箱冷冻室的温度需控制在﹣4℃到﹣24℃之间,则可将冷冻室的温度设为( )
A.0℃ B.﹣3℃ C.﹣18℃ D.﹣25℃
【答案】C
【点拨】根据有理数大小比较方法解答即可.
【解析】解:∵﹣25<﹣24<﹣18<﹣4<﹣3<0,家用冰箱冷冻室的温度需控制在﹣4℃到﹣24℃之间,
∴可将冷冻室的温度设为﹣18℃.
故选:C.
【点睛】本题考查了有理数大小比较以及正数和负数,掌握有理数大小比较方法是解答本题的关键.
8.把笔尖放在数轴的原点,沿数轴先向左(负方向)移动6个单位长度,再向右移动3个单位长度,用算式表示上述过程与结果,正确的是( )
A.﹣6+3=9 B.﹣6﹣3=﹣3 C.﹣6+3=﹣3 D.﹣6+3=3
【答案】C
【点拨】根据有理数的运算法则即可求出答案.
【解析】解:由题意可知:﹣6+3=﹣3,
故选:C.
【点睛】本题考查有理数的运算,解题的关键是正确理解有理数的加法法则,本题属于基础题型.
9.(2024 余姚市一模)已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.若在该快递公司寄一件9千克的物品,则需要付费( )
A.17元 B.19元 C.21元 D.23元
【答案】C
【点拨】根据题意和题目中的数据,可以列出算式13+(9﹣5)×2,然后计算即可.
【解析】解:由题意可得,
13+(9﹣5)×2
=13+4×2
=13+8
=21(元),
故选:C.
【点睛】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.
10.(2024 宁波模拟)有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
A.a2>b2 B.a﹣b>0 C. D.a+b>0
【答案】A
【点拨】根据有理数a、b在数轴上的位置得出a、b的符号和绝对值,进而逐项进行判断即可.
【解析】解:由有理数a、b在数轴上的位置可知,
a<0<b,且|a|>|b|,
所以a2>b2,a﹣b<0,<0,a+b<0,
因此A是正确的,
故选:A.
【点睛】本题考查数轴表示数,理解符号和绝对值是确定有理数的必要条件,掌握有理数的运算法则是正确判断的前提.
押题方向2:投影与视图
20233年浙江真题 考点 命题趋势
2023年湖州、温州、金华、台州、舟山、嘉兴卷第2题 简单几何体的三视图 从近几年浙江中考来看,投影与视图以选择题形式考查,2023年浙江省10份中考试卷有9份试卷考查了投影与视图,比较简单,主要考查了简单几何体的三视图与由三视图判断几何体;预计2024年浙江卷还将继续重视对三视图的考查。
2023年绍兴卷第3题 简单几何体的三视图
2023年湖州、宁波、丽水卷第4题 简单几何体的三视图
2023年湖州卷第4题 由三视图判断几何体
1.(2023 湖州)已知某几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
【答案】D
【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形,从而得出答案.
【解析】解:∵主视图和左视图是矩形,
∴几何体是柱体,
∵俯视图是圆,
∴该几何体是圆柱,故D正确.
故选:D.
【点睛】本题主要考查了由三视图确定几何体的形状,主要考查学生空间想象能力.
3.(2023 温州)截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )
A. B. C. D.
【答案】A
【点拨】根据从正面看得到的图形是主视图,可得答案.
【解析】解:从正面看,可得选项A的图形.
故选:A.
【点睛】本题考查了简单组合体的三视图,从正面看得到的图形是主视图.
4.(2023 绍兴)由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B. C. D.
【答案】D
【点拨】主视图有3列,每列小正方形数目分别为2,1,2,据此判断即可.
【解析】解:如图所示:它的主视图是:
.
故选:D.
【点睛】此题主要考查了简单组合体的三视图,正确把握观察角度是解题关键.
5.(2023 宁波)如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
A. B. C. D.
【答案】A
【点拨】根据从正面看得到的图形是主视图判断即可.
【解析】解:从正面看,上边是一个长方形,下边也是一个长方形,
故选:A.
【点睛】本题考查了简单几何体的三视图,需掌握:从正面看得到的图形是主视图,从上面看得到的图形是俯视图,从左面看得到的图形是左视图.
1.几何体的三视图:(1)主视图:物体在正投影面上的正投影.(2)左视图:物体在侧投影面上的正投影.(3)俯视图:物体在水平投影面上的正投影.
2.画“三视图”的原则:(1)大小:长对正,高平齐,宽相等.(2)虚实:在画图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.
3.由三视图确定几何体的方法:
1)由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:
① 根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;
② 从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;
③ 熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助.
1.如图是由5个大小相同的小正方体组成的几何体,该几何体的俯视图是( )
A. B. C. D.
【答案】C
【点拨】根据从上边看得到的图形是俯视图,可得答案.
【解析】解:从上边看,一共有三列,从左到右正方形的个数分别为2、1、1.
故选:C.
【点睛】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.
2.如图是一个古建筑中常用的榫卯构件,其左视图为( )
A. B. C. D.
【答案】B
【点拨】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
【解析】解:从左面看,是一列三个新来的矩形.
故选:B.
【点睛】本题考查了三视图的知识,掌握主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图,俯视图是从物体的上面看得到的视图是解题的关键.
3.榫卯是我国古代木制建筑、家具等的主要结构方式,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
【答案】A
【点拨】从正面看到的平面图形是主视图,根据主视图的含义可得答案.
【解析】解:如图所示的几何体的主视图如下:
.
故选:A.
【点睛】此题主要考查了简单组合体的三视图;用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形.
4.某物体如图所示,其左视图是( )
A. B. C. D.
【答案】A
【点拨】根据左视图是从左边看得到的图形,可得答案.
【解析】解:从左边看,是一列两个相邻的矩形.
故选:A.
【点睛】本题考查了简单组合体的三视图,左视图是从左边看得到的图形.
5.在下面四个几何体中,主视图与俯视图都是圆的为( )
A. B. C. D.
【答案】D
【点拨】根据圆柱、圆锥、圆台和球的三视图进行判断.
【解析】解:(A)圆柱的主视图是长方形,俯视图是圆,故(A)错误;
(B)圆锥的主视图是等腰三角形,俯视图是圆,故(B)错误;
(C)圆台的主视图是等腰梯形,俯视图是两个同心圆,故(C)错误;
(D)球的主视图与俯视图都是圆,故(D)正确.
故选:D.
【点睛】本题主要考查了几何体的三视图,解决问题的关键是掌握几种简单几何体的特征.解题时注意,圆柱的左视图与主视图都是长方形,圆锥的左视图与主视图都是等腰三角形,圆台的左视图与主视图都是等腰梯形,而三种视图都一样的几何体有球和正方体等.
6.下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
【答案】A
【点拨】分别分析四种几何体的主视图和左视图,找出主视图和左视图不同的几何体.
【解析】解:A、正三棱柱的主视图是三角形,左视图是矩形,符合题意;
B、圆柱的主视图与左视图都是长方形,不合题意;
C、圆锥的主视图与左视图相同,都是等腰三角形,不合题意;
D、正方体的主视图和左视图相同,都是正方形,不合题意.
故选:A.
【点睛】本题考查了简单几何体的三视图,掌握主视图是从物体的正面看到的视图,左视图是从物体的左面看得到的视图是解答本题的关键.
7.如图是一个几何体的三视图,则该几何体是( )
A.B.C. D.
【答案】C
【点拨】由于主视图是从物体的正面看得到的视图,所以先得出四个选项中各几何体的主视图,再与题目图形进行比较即可.
【解析】解:A、主视图是,故选项错误;
B、主视图是,故选项错误;
C、主视图是,故选项正确;
D、主视图是, 故选项错误.
故选:C.
【点睛】本题考查由三视图判断几何体,掌握三视图定义是解题的关键.
8.如图,是一个几何体的三视图,则这个几何体是( )
A. B. C. D.
【答案】A
【点拨】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,即可判断出答案.
【解析】解:选项A的三视图符合题意,选项B的左视图和主视图都不符合题意,选项C、D的三视图都不符合题意.
故选:A.
【点睛】此题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
押题方向3:科学记数法
20233年浙江真题 考点 命题趋势
2023年杭州卷第1题 科学记数法 从近几年浙江中考来看,科学记数法、近似数以选择题形式考查,比较简单,科学记数法有大数和小数两种形式,有时带“亿”、“万”、“千万”等单位,做题时要仔细审题,切忽略单位;预计2024年浙江卷还将继续重视对科学记数法的考查。
2023年绍兴卷第2题 科学记数法
2023年湖州、温州、金华、宁波卷第3题 科学记数法
1.(2023 宁波)据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011 C.3.8018×1010 D.38.018×1010
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:380180000000=3.8018×1011.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.(2023 湖州)国家互联网信息办公室2023年5月23日发布的《数字中国发展报告(2022年)》显示,2022年我国数字经济规模达502000亿元.用科学记数法表示502000,正确的是( )
A.0.502×106 B.5.02×106 C.5.02×105 D.50.2×104
【答案】C
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正整数;当原数的绝对值小于1时,n是负整数.
【解析】解:502000=5.02×105,
故选:C.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,正确确定a的值以及n的值是解决问题的关键.
3.(2023 杭州)杭州奥体中心体育场又称“大莲花”,里面有80800个座位.数据80800用科学记数法表示为( )
A.8.8×104 B.8.08×104 C.8.8×105 D.8.08×105
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:80800=8.08×104,
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(2023 温州)苏步青来自“数学家之乡”,为纪念其卓越贡献,国际上将一颗距地球约218000000公里的行星命名为“苏步青星”.数据218000000用科学记数法表示为( )
A.0.218×109 B.2.18×108 C.21.8×102 D.218×106
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:将218000000用科学记数法表示为2.18×108.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
5.(2023 绍兴)据报道,2023年“五一”假期全国国内旅游出游合计274000000人次.数字274000000用科学记数法表示是( )
A.27.4×107 B.2.74×108 C.0.274×109 D.2.74×109
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【解析】解:274000000=2.74×108.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
科学记数法是中考高频考点,我们不仅要记住它的基本形式,更要记住表达式中a的取值范围;还要注意n,当表示一个绝对值大于10的数,n是正整数;当表示一个绝对值小于1的数时,指数为负整数。注意:1)单位的统一,尤其是带“万”或者“亿”的问题:含有万、亿等单位的数,用科学记数法表示时,要先还原成原数,再用科学记数法表示,最后按要求取近似值。
1.2023年5月28日,我国自主研发的C919国产大飞机商业首航取得圆满成功.C919可储存约186000升燃油,将数据186000用科学记数法表示为( )
A.0.186×105 B.1.86×105 C.18.6×104 D.186×103
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:将186000用科学记数法表示为:1.86×105.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.我国自主研发的500m口径球面射电望远镜(FAST)有“中国天眼”之称,它的反射面面积约为250000m2.用科学记数法表示数据250000为( )
A.0.25×106 B.25×104 C.2.5×104 D.2.5×105
【答案】D
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:250000=2.5×105,
故选:D.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.中国信通院预计未来2~3年内将实现5G的个人终端应用和数字内容的创新突破,预计2025年全球5G移动用户数将突破57亿户.数据57亿用科学记数法表示为( )
A.0.57×1010 B.5.7×1010 C.5.7×109 D.57×104
【答案】C
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:57亿=5700000000=5.7×109.
故选:C.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.芯片是手机、电脑等高科技产品最核心的部件,更小的芯片意味着更高的性能,目前我国芯片的量产工艺已达到14纳米,已知14纳米等于0.000000014米,用科学记数法将0.000000014表示为( )
A.1.4×10﹣9 B.1.4×10﹣7 C.1.4×10﹣8 D.14×10﹣7
【答案】C
【点拨】根据科学记数法的方法进行解题即可.
【解析】解:0.000000014=1.4×10﹣8.
故选:C.
【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
5.华为一部分Mate40手机将会搭载麒麟9000处理器,这是手机行业首批采用5nm工艺制式的芯片,1nm=0.000000001m,其中5nm用科学记数法表示为( )
A.5×109 B.5×10﹣10 C.5×10﹣8 D.5×10﹣9
【答案】D
【点拨】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解析】解:5nm=0.000000005m,
0.000000005=5×10﹣9.
故选:D.
【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
押题方向4:整式运算
2023年浙江真题 考点 命题趋势
2023年湖州卷第2题 同底数幂的乘法 从近几年浙江中考来看,整式运算主要以考查整式的加减、乘除、乘法公式、幂的运算为主,也是考查重点,难度较低。预计2024年浙江卷还将继续考查幂的运算、整式混合运算(特别是乘法公式),为避免丢分,学生应扎实掌握。
2023年丽水卷第2题 合并同类项
2023年衢州卷第3题、宁波卷第2题 同底数幂的除法
2023年绍兴卷第4题 整式的混合运算
2023年绍兴卷第4题 完全平方公式
1.(2023 丽水)计算a2+2a2的正确结果是( )
A.2a2 B.2a4 C.3a2 D.3a4
【答案】C
【点拨】根据合并同类项法则进行计算即可.
【解析】解:a2+2a2
=(1+2)a2
=3a2,
故选:C.
【点睛】本题考查了合并同类项法则,能熟记合并同类项法则是解此题的关键,把同类项的系数相加作为系数,字母和字母的指数不变.
2.(2023 温州)化简a4 (﹣a)3的结果是( )
A.a12 B.﹣a12 C.a7 D.﹣a7
【答案】D
【点拨】直接利用同底数幂的乘法运算法则计算得出答案.
【解析】解:a4 (﹣a)3=﹣a7.
故选:D.
【点睛】此题主要考查了同底数幂的乘法运算,正确掌握相关运算法则是解题关键.
3.(2023 台州)下列运算正确的是( )
A.2(a﹣1)=2a﹣2 B.(a+b)2=a2+b2 C.3a+2a=5a2 D.(ab)2=ab2
【答案】A
【点拨】根据去括号法则,完全平方公式,合并同类项法则,积的乘方法则将各项计算后进行判断即可.
【解析】解:A.2(a﹣1)
=2a﹣2×1
=2a﹣2,
则A符合题意;
B.(a+b)2=a2+2ab+b2,
则B不符合题意;
C.3a+2a
=(3+2)a
=5a,
则C不符合题意;
D.(ab)2=a2b2,
则D不符合题意;
故选:A.
【点睛】本题考查整式的运算,其相关运算法则是基础且重要知识点,必须熟练掌握.
4.(2023 绍兴)下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7
C.(a+1)(a﹣1)=a2﹣1 D.(a+1)2=a2+1
【答案】C
【思路点拨】直接利用整式的混合运算法则分别判断得出答案.
【解析】解:A.a6÷a2=a4,故此选项不合题意;
B.(﹣a2)5=﹣a10,故此选项不合题意;
C.(a+1)(a﹣1)=a2﹣1,故此选项符合题意;
D.(a+1)2=a2+2a+1,故此选项不合题意.
故选:C.
【点睛】此题主要考查了整式的混合运算,正确掌握相关运算法则是解题关键.
5.(2023 衢州)下列运算,结果正确的是( )
A.3a+2a=5a2 B.3a﹣2a=1 C.a2 a3=a5 D.a÷a2=a
【答案】C
【点拨】根据同底数幂的乘法法则和同底数幂的除法法则及合并同类项法则即可解决问题.
【解析】解:因为3a+2a=5a,所以A选项错误.
因为3a﹣2a=a,所以B选项错误.
因为a2 a3=a2+3=a5,所以C选项正确.
因为a÷a2=a1﹣2=a﹣1,所以D选项错误.
故选:C.
【点睛】本题考查同底数幂的运算及合并同类项,熟知同底数幂的运算法则及合并同类项法则是解题的关键.
6.(2023 宁波)下列计算正确的是( )
A.x2+x=x3 B.x6÷x3=x2 C.(x3)4=x7 D.x3 x4=x7
【答案】D
【点拨】根据合并同类项的法则、同底数幂除法、幂的乘方以及同底数幂乘法的运算法则计算即可.
【解析】解:A、x2和x不是同类项,不能进行合并,故选项不符合题意;
B、x6÷x3=x3,原式计算错误,故选项不符合题意;
C、(x3)4=x12,原式计算错误,故选项不符合题意;
D、x3 x4=x7,运算计算正确,故选项符合题意.
故选:D.
【点睛】本题考查了合并同类项的法则、同底数幂除法、幂的乘方以及同底数幂乘法的运算法则,解题的关键是熟记相关的运算法则并灵活运用.
1)幂的运算法则是进行整式乘除法的基础,要熟练掌握,解题时要明确运算的类型,正确运用法则;在运算的过程中,一定要注意指数、系数和符号的处理.
2)整式的加减,实质上就是合并同类项,有括号的,先去括号,只要算式中没有同类项,就是最后的结果;多项式乘多项式的运算中要做到不重不漏,应用乘法公式进行简便计算,另外去括号时,要注意符号的变化,最后把所得式子化简,即合并同类项.
1.计算(﹣a)3 a2的结果是( )
A.﹣a6 B.a6 C.﹣a5 D.a5
【答案】C
【点拨】利用同底数幂的乘法的法则对式子进行运算即可.
【解析】解:(﹣a)3 a2
=﹣a3 a2
=﹣a5,
故选:C.
【点睛】本题主要考查同底数幂的乘法,解答的关键是熟记同底数幂的乘法的法则.
2.下列运算正确的是( )
A.2+4a=6a B.a3 a4=a12 C.(﹣2a)2=﹣4a2 D.a5÷a3=a2
【答案】D
【点拨】A.根据同类项的定义判断即可;
B.根据同底数幂的乘法运算法则计算并判断即可;
C.根据积的乘方与幂的乘方运算法则计算并判断即可;
D.根据同底数幂的除法运算法则计算并判断即可.
【解析】解:2与4a不是同类项,无法合并,
∴A不正确,不符合题意;
a3 a4=a7,
∴B不正确,不符合题意;
(﹣2a)2=4a2,
∴C不正确,不符合题意;
a5÷a3=a2,
∴D正确,符合题意.
故选:D.
【点睛】本题考查同底数幂的乘除法、积的乘方与幂的乘方,掌握它们的运算法则是解题的关键.
3.下列计算正确的是( )
A.(a2)4=a6 B.(3a)2=6a2 C.a8÷a4=a2 D.(﹣ab3)2=a2b6
【答案】D
【点拨】根据同底数幂的除法法则、幂的乘方与积的乘方法则进行解题即可.
【解析】解:A、(a2)4=a8,故该项不正确,不符合题意;
B、(3a)2=9a2,故该项不正确,不符合题意;
C、a8÷a4=a4,故该项不正确,不符合题意;
D、(﹣ab3)2=a2b6,故该项正确,符合题意;
故选:D.
【点睛】本题考查同底数幂的除法、幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
4.下列运算正确的是( )
A.(a2)3=a5 B.a3 a4=a12 C.a8÷a4=a2 D.(﹣3a2)2=9a4
【答案】D
【点拨】根据幂的乘方,同底数幂的乘法,同底数幂的除法,积的乘方,逐一进行计算即可得到答案.
【解析】解:A、(a2)3=a6,原计算错误,不符合题意,选项错误;
B、a3 a4=a7,原计算错误,不符合题意,选项错误;
C、a8÷a4=a4,原计算错误,不符合题意,选项错误;
D、(﹣3a2)2=9a4,原计算正确,符合题意,选项正确,
故选:D.
【点睛】本题考查了幂的乘方,同底数幂的乘法,同底数幂的除法,积的乘方,熟练掌握相关运算法则是解题关键.
5.下列计算正确的是( )
A.a3﹣a2=a B.a3 a2=a6 C.(a3)2=a6 D.(2a+1)(2a﹣1)=2a2﹣1
【答案】C
【点拨】利用合并同类项法则,同底数幂乘法法则,幂的乘方法则,平方差公式逐项判断即可.
【解析】解:a3与a2不是同类项,无法合并,则A不符合题意;
a3 a2=a5,则B不符合题意;
(a3)2=a6,则C符合题意;
(2a+1)(2a﹣1)=4a2﹣1,则D不符合题意;
故选:C.
【点睛】本题考查整式的运算,熟练掌握相关运算法则是解题的关键.
6.下列计算正确的是( )
A.a+2a=3a B.(a+b)2=a2+b2 C.(a2)3=a5 D.a2 a3=a6
【答案】A
【点拨】根据合并同类项法则、完全平方公式、幂的乘方运算法则、整式的乘法运算即可求出答案.
【解析】解:A、原式=3a,故A符合题意.
B、原式=a2+2ab+b2,故B不符合题意.
C、原式=a6,故C不符合题意.
D、原式=a5,故D不符合题意.
故选:A.
【点睛】本题考查合并同类项法则、完全平方公式、幂的乘方运算法则、整式的乘法运算,本题属于基础题型.
7.下列计算正确的是( )
A.a6÷a3=a3 B.(a﹣b)2=a2﹣b2 C.(﹣3a2)3=﹣9a6 D.a2+a3=a5
【答案】A
【点拨】运用合并同类项、同底数幂除法、积的乘方、完全平方公式进行逐一计算辨别.
【解析】解:∵a6÷a3=a3,
∴选项A符合题意;
∵(a﹣b)2=a2﹣2ab+b2,
∴选项B不符合题意;
∵(﹣3a2)3=﹣27a6,
∴选项C不符合题意;
∵a2和a3不是同类项,不能合并,
∴选项D不符合题意,
故选:A.
【点睛】此题考查了合并同类项、同底数幂除法、积的乘方、完全平方公式的运算能力,关键是能准确理解并运用以上知识进行准确地计算.
8.下列运算正确的是( )
A.x4 x3=x12 B.(a6)2÷(a4)3=a C.(a3)2 a4=a10 D.(ab2)3÷(﹣ab)2=﹣ab4
【答案】C
【点拨】根据同底数幂乘除法,积的乘方,幂的乘方,单项式除以单项式等计算法则求解判断即可.
【解析】解:A、x4 x3=x7,原计算错误,不符合题意;
B、(a6)2÷(a4)3=a12÷a12=1,原计算错误,不符合题意;
C、(a3)2 a4=a6 a4=a10,正确,符合题意;
D、(ab2)3÷(﹣ab)2=a3b6÷a2b2=ab4,原计算错误,不符合题意.
故选:C.
【点睛】本题主要考查了同底数幂乘除法,积的乘方,幂的乘方,单项式除以单项式,熟知相关计算法则是解题的关键,注意同底数幂乘除法指数是相加减,积的乘方和幂的乘方指数是相乘.
押题方向五:统计
2023年浙江真题 考点 命题趋势
2023年湖州卷第7题 算术平均数 从近几年浙江中考来看,统计部分主要以考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差为主,有的结合统计图表考查,难度较低。预计2024年浙江卷还将继续考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差,为避免丢分,学生应扎实掌握。
2023年舟山、嘉兴卷第3题、台州卷第7题 全面调查与抽样调查
2023年金华卷第6题 众数
2023年宁波卷第6题、杭州卷第9题 方差
2023年温州卷第5题 样本估计总体
1.(2023 湖州)某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这5天平均每天的用水量是( )
A.25立方米 B.30立方米 C.32立方米 D.35立方米
【答案】B
【点拨】先确定每天的用水量,根据用水量的和除以用水天数,求出结果即可.
【解析】解:由折线图可知,该小区五天的用水量分别是:30、40、20、30、30.所以5天的平均用水量为:
=30(立方米).
故选:B.
【点睛】本题考查了折线图和算术平均数,掌握算术平均数的计算方法是解决本题的关键.
2.(2023 台州)以下调查中,适合全面调查的是( )
A.了解全国中学生的视力情况 B.检测“神舟十六号”飞船的零部件
C.检测台州的城市空气质量 D.调查某池塘中现有鱼的数量
【答案】B
【点拨】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【解析】解:A.了解全国中学生的视力情况,适合抽样调查,故本选项不合题意;
B.检测“神舟十六号”飞船的零部件,适合普查,故本选项符合题意;
C.检测台州的城市空气质量,适合抽样调查,故本选项不合题意;
D.调查某池塘中现有鱼的数量,适合抽样调查,故本选项不合题意.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.(2023 金华)上周双休日,某班8名同学课外阅读的时间如下(单位:时):1,4,2,4,3,3,4,5,这组数据的众数是( )
A.1时 B.2时 C.3时 D.4时
【答案】D
【点拨】根据众数的定义求解即可.
【解析】解:这组数据4出现的次数最多,故众数为4,
故选:D.
【点睛】本题考查了众数的知识,属于基础题,解答本题的关键是熟练掌握众数的定义.
4.(2023 宁波)甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:
甲 乙 丙 丁
9 8 9 9
S2 1.2 0.4 1.8 0.4
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
【答案】D
【点拨】根据平均环数比较成绩的优劣,根据方差比较数据的稳定程度.
【解析】解:由表知甲、丙、丁射击成绩的平均数相等,且大于乙的平均数,
∴从甲、丙、丁中选择一人参加竞赛,
∵甲、丙、丁三人中,丁的方差较小,
∴丁发挥最稳定,
∴选择丁参加比赛.
故选:D.
【点睛】本题考查的是方差和算术平均数,掌握方差反映了一组数据的波动大小,方差越大,波动性越大,方差越小,数据越稳定是解题的关键.
5.某校计划组织研学活动,现有四个地点可供选择:南麂岛、百丈漈、楠溪江、雁荡山.
为了解学生想法,校方进行问卷调查(每人选一个地点),并绘制成如图所示统计图.已知选择雁荡山的有270人,那么选择楠溪江的有( )
A.90人 B.180人 C.270人 D.360人
【答案】B
【点拨】先根据选择雁荡山的人数及其所占百分比求出被调查的总人数,再用总人数乘以选择楠溪江的人数所占百分比即可.
【解析】解:调查总人数:270÷30%=900(人),
选择楠溪江的人数:900×20%=180(人),
故选:B.
【点睛】本题考查的是扇形统计图.读懂统计图,从统计图中得到必要的信息是解决问题的关键;扇形统计图直接反映部分占总体的百分比大小.
6.(2023 杭州)一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字.根据下面的统计结果,能判断记录的这5个数字中一定没有出现数字6的是( )
A.中位数是3,众数是2 B.平均数是3,中位数是2
C.平均数是3,方差是2 D.平均数是3,众数是2
【答案】C
【点拨】根据中位数、众数、平均数、方差的定义,结合选项中设定情况,逐项判断即可.
【解析】解:当中位数是3,众数是2时,记录的5个数字可能为:2,2,3,4,5或2,2,3,4,6或2,2,3,5,6,故A选项不合题意;
当平均数是3,中位数是2时,5个数之和为15,记录的5个数字可能为1,1,2,5,6或1,2,2,5,5,故B选项不合题意;
当平均数是3,方差是2时,5个数之和为15,假设6出现了1次,方差最小的情况下另外4个数为:2,2,2,3,此时方差s2=×[3×(2﹣3)2+(3﹣3)2+(6﹣3)2]=2.4>2,因此假设不成立,即一定没有出现数字6,故C选项符合题意;
当平均数是3,众数是2时,5个数之和为15,2至少出现两次,记录的5个数字可能为1,2,2,4,6,故D选项不合题意;
故选:C.
【点睛】本题主要考查平均数、众数和中位数及方差,解题的关键是掌握平均数、众数和中位数及方差的定义.
1.如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
2.平均数能充分利用各数据提供的信息,在实际生活中常用样本的平均数估计总体的平均数;中位数不受个别偏大或偏小数据的影响,当一组数据中的个别数据变动较大时,一般用中位数来描述数据的集中趋势;众数考察的是各数据所出现的频数,其大小只与部分数据有关,当一组数据中某些数据多次重复出现时,众数往往更能反映问题。
3.方差反映数据的离散程度,方差越大,数据的波动越大,数据越不稳定。
1.下列调查方式适合用普查的是( )
A.检测一批LED灯的使用寿命
B.检测一批家用汽车的抗撞击能力
C.测试2024神舟十八号载人飞船的零部件质量情况
D.中央电视台《2024年第九季诗词大会》的收视率
【答案】C
【点拨】根据抽样调查和全面调查的区别判断即可.
【解析】解:A、检测一批LED灯的使用寿命,适合用抽样调查,不符合题意;
B、检测一批家用汽车的抗撞击能力,适合用抽样调查,不符合题意;
C、测试2024神舟十八号载人飞船的零部件质量情况,适合用普查,符合题意;
D、中央电视台《2024年第九季诗词大会》的收视率,适合用抽样调查,不符合题意;
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.为加强交通安全教育,某校随机调查了九年级部分学生的上学方式(乘车、步行、骑车),并根据调查结果绘制了如图两幅不完整的统计图,下列判断错误的是( )
A.本次调查的总人数为60人 B.调查的学生中骑车上学的有8人
C.若该校九年级学生有1200人,则乘车上学的约有600人
D.扇形统计图中步行的学生人数所占的圆心角是122°
【答案】D
【点拨】根据乘车人数以及百分比求出总人数,据此可判断选项A;
用总人数分别减去其它两种上学方式的人数,即可得出骑车上学的人数,据此可得判断选项B;
用样本估计总体的思想解决问题,即可判断选项C;
根据圆心角=360°×百分比计算,即可判断选项D.
【解析】解:本次调查的总人数为:30÷50%=60(人),故选项A说法正确,不符合题意;
调查的学生中骑车上学的有:60﹣30﹣22=8(人),故选项B说法正确,不符合题意;
若该校九年级学生有1200人,则乘车上学的约有:1200×50%=6008(人),故选项C说法正确,不符合题意;
扇形统计图中步行的学生人数所占的圆心角是:360°×=132°,故选项D说法错误,符合题意.
故选:D.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
3.下列说法中,正确的是( )
A.一组数据4,4,2,3,1的中位数是2
B.反映空气的主要成分(氮气约占78%,氧气约占21%,其他微量气体约占1%)宜采用折线统计图
C.甲、乙两人各10次射击的平均成绩相同,方差分别是s甲2=2.2,s乙2=1.3,则乙的射击成绩较稳定
D.对载人航天器零部件的检查适合采用抽样凋查
【答案】C
【点拨】选项A根据中位数的定义判断即可;选项B根据各种统计图的特点判断即可;选项C根据方差的意义判断即可;选项D根据全面调查和抽样调查的定义判断即可.
【解析】解:A.一组数据4,4,2,3,1的中位数是3,原说法错误,故本选项不符合题意;
B.反映空气的主要成分(氮气约占78%,氧气约占21%,其他微量气体约占1%)宜采用扇形统计图,原说法错误,故本选项不符合题意;
C.甲、乙两人各10次射击的平均成绩相同,方差分别是s甲2=2.2,s乙2=1.3,则乙的射击成绩较稳定,说法正确,故本选项符合题意;
D.对载人航天器零部件的检查适合采用全面调查,原说法错误,故本选项不符合题意.
故选:C.
【点睛】本题考查了全面调查和抽样调查,加权平均数,中位数以及方差,掌握相关定义是解答本题的关键.
4.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是3,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A.2,3 B.2,9 C.4,18 D.4,27
【答案】D
【点拨】利用平均数、方差的定义和性质直接求解.
【解析】解:∵数据x1,x2,x3,x4,x5的平均数是2,方差是3,
∴数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数为:3×2﹣2=4,方差为:32×3=27.
故选:D.
【点睛】本题主要考查方差和算术平均数,解题的关键是掌握若数据x1,x2,……,xn的平均数是,方差为s2,则新数据ax1+b,ax2+b,……,axn+b的平均数为a+b,方差为a2s2.
5.某店铺连续5天销售衬衣的件数分别为10,11,13,15,11.关于这组数据,以下结论错误的是( )
A.众数是11 B.平均数是12 C.方差是3.2 D.中位数是13
【答案】D
【点拨】根据众数、平均数、方差、中位数的计算方法分别求出结果再进行判断即可.
【解析】解:A、11出现了2次,出现的次数最多,则众数是11,故本选项不符合题意;
B、平均数是×(10+11+13+15+11)=12,
故本选项不符合题意;
C、方差是:×[(11﹣12)2+(10﹣12)2+(13﹣12)2+(15﹣12)2+(11﹣12)2]=3.2,故本选项不符合题意;
D、把这些数从小到大排列为:10,11,11,13,15,中位数是11,故本选项符合题意;
故选:D.
【点睛】本题考查中位数、众数、平均数、方差,掌握中位数、众数、平均数、方差的计算方法是解决问题的关键.
6.如图是描述某校篮球队员年龄的条形图,则这个篮球队员年龄的众数和中位数分别为( )
A.14,15 B.15,14 C.15,15 D.15,14.5
【答案】D
【点拨】根据中位数、众数的定义进行计算即可求解.
【解析】解:这20名篮球队员年龄出现次数最多的是15岁,共出现8次,因此众数是15岁;
将这20名篮球队员的年龄从小到大排列,处在中间位置的2个数是14岁和15岁,因此中位数是(岁).
故选:D.
【点睛】本题考查中位数、众数,掌握中位数、众数的计算方法是正确判断的关键.
7.某班35位同学课外阅读物的数量统计如表所示,其中有两个数据被遮盖,下列关于课外阅读物的统计量中,与被遮盖的数据无关的是( )
课外阅读物的数量 2 3 4 5 6 7 8
人数 ■ ■ 9 7 9 3 2
A.平均数,方差 B.中位数,方差 C.平均数,众数 D.中位数,众数
【答案】D
【点拨】通过计算课外阅读物的数量2、3分的人数之和,进行判断,不影响成绩出现次数最多的结果,因此不影响众数,同时不影响找第18位数据,因此不影响中位数的计算,进而进行选择.
【解析】解:由表格数据可知,课外阅读物的数量2、3分的人数之和为35﹣(9+7+9+3+2)=5(人),
课外阅读物的数量为4和6出现次数最多,因此课外阅读物的数量的众数是4和6,
成绩从小到大排列后处在第15位数都是5,因此中位数是5,
因此中位数和众数与被遮盖的数据无关,
故选:D.
【点睛】本题考查中位数、众数、方差、平均数的意义和计算方法,理解各个统计量的实际意义,以及每个统计量所反应数据的特征,是正确判断的前提.
8.已知5个正数a1,a2,a3,a4,a5的平均数是a,且a1>a2>a3>a4>a5,则数据a1,a2,a3,0,a4,a5的平均数和中位数是( )
A.a, B.a, C.a, D.a,
【答案】C
【点拨】对新数据按大小排列,然后根据平均数和中位数的定义计算即可.
【解析】解:由平均数定义可知:(a1+a2+a3+0+a4+a5)=×5a=a;
将这组数据按从小到大排列为0,a5,a4,a3,a2,a1;由于有偶数个数,取最中间两个数的平均数.
∴其中位数为.
故选:C.
【点睛】本题考查了平均数和中位数的定义.平均数是指在一组数据中所有数据之和再除以数据的个数;一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.
01 押浙江卷第1—5题
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
押题方向1:实数相关概念、运算及大小比较
2023年浙江真题 考点 命题趋势
2023年湖州、衢州、金华、台州、宁波卷第1题 实数的大小比较 从近几年浙江中考来看,实数的相关概念(正负数、数轴、相反数、绝对值、倒数、平方根、算术平方根、立方根)、实数的大小比较、有理数的运算以选择题形式考查,比较简单;预计2024年浙江卷还将继续重视对正负数的意义、相反数、绝对值、倒数、数轴、平方根、算术平方根、立方根等实数的相关概念及实数的大小比较和运算的考查。
2023年丽水卷第1题 相反数
2023年嘉兴、舟山卷第1题 立方根
2023年温州、绍兴卷第1题 有理数的加减
2023年杭州卷第2题 有理数的混合运算
1.(2023 衢州)手机信号的强弱通常采用负数来表示,绝对值越小表示信号越强(单位:dBm),则下列信号最强的是( )
A.﹣50 B.﹣60 C.﹣70 D.﹣80
2.(2023 温州)如图,比数轴上点A表示的数大3的数是( )
A.﹣1 B.0 C.1 D.2
3.(2023 舟山、嘉兴)下面四个数中,比1小的正无理数是( )
A. B.﹣ C. D.
4.(2023 丽水)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
5.(2023 浙江)﹣8的立方根是( )
A.﹣2 B.2 C.±2 D.不存在
6.(2023 绍兴)计算2﹣3的结果是( )
A.﹣1 B.﹣3 C.1 D.3
7.(2023 杭州)(﹣2)2+22=( )
A.0 B.2 C.4 D.8
8.(2023 金华)某一天,哈尔滨、北京、杭州、金华四个城市的最低气温分别是﹣20℃,﹣10℃,0℃,2℃,其中最低气温是( )
A.﹣20℃ B.﹣10℃ C.0℃ D.2℃
9.(2023 台州)下列各数中,最小的是( )
A.2 B.1 C.﹣1 D.﹣2
10.(2023 宁波)在﹣2,﹣1,0,π这四个数中,最小的数是( )
A.﹣2 B.﹣1 C.0 D.π
数轴、相反数、绝对值、倒数是核心考点,常在选择题和填空题中出现。对于数轴我们不仅要记住它的三要素,还要能借助它比较实数大小;对于相反数我们需要注意的是当用一个式子表示一个数量,求相反数时需要注意整体概念;对于绝对值需要注意情况不确定时,需要分类讨论;而对于倒数需要注意的是0没有倒数。
实数比较大小可以根据数的性质来比较,正数比负数大,两个负数比较大小,绝对大的反而小;也可通过数轴,数轴上的两个数比较大小,右边的数比左边的大。但对于一些复杂的式子,我们就需要用求差法或者求商法;对于含根号的数,我们还可以用平方法或者倒数法。
1.如果水位升高3m时水位变化记作+3m,那么水位不升不降时水位变化记作( )
A.+3m B.﹣3m C.0m D.±3m
2.在﹣4,﹣1,0,1这四个数中,比﹣2小的数是( )
A.﹣4 B.﹣1 C.0 D.1
3.下列算式中,运算结果最小的是( )
A.﹣2+3 B.﹣2﹣3 C.﹣2×3 D.﹣2÷3
4.(﹣2)3=( )
A.﹣6 B.6 C.﹣8 D.8
5.|﹣3|﹣(﹣2)=( )
A.﹣1 B.5 C.1 D.﹣5
6.﹣2024的倒数是( )
A.﹣2024 B.2024 C. D.
7.家用冰箱冷冻室的温度需控制在﹣4℃到﹣24℃之间,则可将冷冻室的温度设为( )
A.0℃ B.﹣3℃ C.﹣18℃ D.﹣25℃
8.把笔尖放在数轴的原点,沿数轴先向左(负方向)移动6个单位长度,再向右移动3个单位长度,用算式表示上述过程与结果,正确的是( )
A.﹣6+3=9 B.﹣6﹣3=﹣3 C.﹣6+3=﹣3 D.﹣6+3=3
9.已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.若在该快递公司寄一件9千克的物品,则需要付费( )
A.17元 B.19元 C.21元 D.23元
10.有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
A.a2>b2 B.a﹣b>0 C. D.a+b>0
押题方向2:投影与视图
20233年浙江真题 考点 命题趋势
2023年湖州、温州、金华、台州、舟山、嘉兴卷第2题 简单几何体的三视图 从近几年浙江中考来看,投影与视图以选择题形式考查,2023年浙江省10份中考试卷有9份试卷考查了投影与视图,比较简单,主要考查了简单几何体的三视图与由三视图判断几何体;预计2024年浙江卷还将继续重视对三视图的考查。
2023年绍兴卷第3题 简单几何体的三视图
2023年湖州、宁波、丽水卷第4题 简单几何体的三视图
2023年湖州卷第4题 由三视图判断几何体
1.(2023 湖州)已知某几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
3.(2023 温州)截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )
A. B. C. D.
4.(2023 绍兴)由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B. C. D.
5.(2023 宁波)如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
A. B. C. D.
1.几何体的三视图:(1)主视图:物体在正投影面上的正投影.(2)左视图:物体在侧投影面上的正投影.(3)俯视图:物体在水平投影面上的正投影.
2.画“三视图”的原则:(1)大小:长对正,高平齐,宽相等.(2)虚实:在画图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.
3.由三视图确定几何体的方法:
1)由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:
① 根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;
② 从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;
③ 熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助.
1.如图是由5个大小相同的小正方体组成的几何体,该几何体的俯视图是( )
A. B. C. D.
2.如图是一个古建筑中常用的榫卯构件,其左视图为( )
A. B. C. D.
3.榫卯是我国古代木制建筑、家具等的主要结构方式,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
4.某物体如图所示,其左视图是( )
A. B. C. D.
5.在下面四个几何体中,主视图与俯视图都是圆的为( )
A. B. C. D.
6.下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
7.如图是一个几何体的三视图,则该几何体是( )
A.B.C. D.
8.如图,是一个几何体的三视图,则这个几何体是( )
A. B. C. D.
押题方向3:科学记数法
20233年浙江真题 考点 命题趋势
2023年杭州卷第1题 科学记数法 从近几年浙江中考来看,科学记数法、近似数以选择题形式考查,比较简单,科学记数法有大数和小数两种形式,有时带“亿”、“万”、“千万”等单位,做题时要仔细审题,切忽略单位;预计2024年浙江卷还将继续重视对科学记数法的考查。
2023年绍兴卷第2题 科学记数法
2023年湖州、温州、金华、宁波卷第3题 科学记数法
1.(2023 宁波)据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011 C.3.8018×1010 D.38.018×1010
2.(2023 湖州)国家互联网信息办公室2023年5月23日发布的《数字中国发展报告(2022年)》显示,2022年我国数字经济规模达502000亿元.用科学记数法表示502000,正确的是( )
A.0.502×106 B.5.02×106 C.5.02×105 D.50.2×104
3.(2023 杭州)杭州奥体中心体育场又称“大莲花”,里面有80800个座位.数据80800用科学记数法表示为( )
A.8.8×104 B.8.08×104 C.8.8×105 D.8.08×105
4.(2023 温州)苏步青来自“数学家之乡”,为纪念其卓越贡献,国际上将一颗距地球约218000000公里的行星命名为“苏步青星”.数据218000000用科学记数法表示为( )
A.0.218×109 B.2.18×108 C.21.8×102 D.218×106
5.(2023 绍兴)据报道,2023年“五一”假期全国国内旅游出游合计274000000人次.数字274000000用科学记数法表示是( )
A.27.4×107 B.2.74×108 C.0.274×109 D.2.74×109
科学记数法是中考高频考点,我们不仅要记住它的基本形式,更要记住表达式中a的取值范围;还要注意n,当表示一个绝对值大于10的数,n是正整数;当表示一个绝对值小于1的数时,指数为负整数。注意:1)单位的统一,尤其是带“万”或者“亿”的问题:含有万、亿等单位的数,用科学记数法表示时,要先还原成原数,再用科学记数法表示,最后按要求取近似值。
1.2023年5月28日,我国自主研发的C919国产大飞机商业首航取得圆满成功.C919可储存约186000升燃油,将数据186000用科学记数法表示为( )
A.0.186×105 B.1.86×105 C.18.6×104 D.186×103
2.我国自主研发的500m口径球面射电望远镜(FAST)有“中国天眼”之称,它的反射面面积约为250000m2.用科学记数法表示数据250000为( )
A.0.25×106 B.25×104 C.2.5×104 D.2.5×105
3.中国信通院预计未来2~3年内将实现5G的个人终端应用和数字内容的创新突破,预计2025年全球5G移动用户数将突破57亿户.数据57亿用科学记数法表示为( )
A.0.57×1010 B.5.7×1010 C.5.7×109 D.57×104
4.芯片是手机、电脑等高科技产品最核心的部件,更小的芯片意味着更高的性能,目前我国芯片的量产工艺已达到14纳米,已知14纳米等于0.000000014米,用科学记数法将0.000000014表示为( )
A.1.4×10﹣9 B.1.4×10﹣7 C.1.4×10﹣8 D.14×10﹣7
5.华为一部分Mate40手机将会搭载麒麟9000处理器,这是手机行业首批采用5nm工艺制式的芯片,1nm=0.000000001m,其中5nm用科学记数法表示为( )
A.5×109 B.5×10﹣10 C.5×10﹣8 D.5×10﹣9
押题方向4:整式运算
2023年浙江真题 考点 命题趋势
2023年湖州卷第2题 同底数幂的乘法 从近几年浙江中考来看,整式运算主要以考查整式的加减、乘除、乘法公式、幂的运算为主,也是考查重点,难度较低。预计2024年浙江卷还将继续考查幂的运算、整式混合运算(特别是乘法公式),为避免丢分,学生应扎实掌握。
2023年丽水卷第2题 合并同类项
2023年衢州卷第3题、宁波卷第2题 同底数幂的除法
2023年绍兴卷第4题 整式的混合运算
2023年绍兴卷第4题 完全平方公式
1.(2023 丽水)计算a2+2a2的正确结果是( )
A.2a2 B.2a4 C.3a2 D.3a4
2.(2023 温州)化简a4 (﹣a)3的结果是( )
A.a12 B.﹣a12 C.a7 D.﹣a7
3.(2023 台州)下列运算正确的是( )
A.2(a﹣1)=2a﹣2 B.(a+b)2=a2+b2 C.3a+2a=5a2 D.(ab)2=ab2
4.(2023 绍兴)下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7
C.(a+1)(a﹣1)=a2﹣1 D.(a+1)2=a2+1
5.(2023 衢州)下列运算,结果正确的是( )
A.3a+2a=5a2 B.3a﹣2a=1 C.a2 a3=a5 D.a÷a2=a
6.(2023 宁波)下列计算正确的是( )
A.x2+x=x3 B.x6÷x3=x2 C.(x3)4=x7 D.x3 x4=x7
1)幂的运算法则是进行整式乘除法的基础,要熟练掌握,解题时要明确运算的类型,正确运用法则;在运算的过程中,一定要注意指数、系数和符号的处理.
2)整式的加减,实质上就是合并同类项,有括号的,先去括号,只要算式中没有同类项,就是最后的结果;多项式乘多项式的运算中要做到不重不漏,应用乘法公式进行简便计算,另外去括号时,要注意符号的变化,最后把所得式子化简,即合并同类项.
1.计算(﹣a)3 a2的结果是( )
A.﹣a6 B.a6 C.﹣a5 D.a5
2.下列运算正确的是( )
A.2+4a=6a B.a3 a4=a12 C.(﹣2a)2=﹣4a2 D.a5÷a3=a2
3.下列计算正确的是( )
A.(a2)4=a6 B.(3a)2=6a2 C.a8÷a4=a2 D.(﹣ab3)2=a2b6
4.下列运算正确的是( )
A.(a2)3=a5 B.a3 a4=a12 C.a8÷a4=a2 D.(﹣3a2)2=9a4
5.下列计算正确的是( )
A.a3﹣a2=a B.a3 a2=a6 C.(a3)2=a6 D.(2a+1)(2a﹣1)=2a2﹣1
6.下列计算正确的是( )
A.a+2a=3a B.(a+b)2=a2+b2 C.(a2)3=a5 D.a2 a3=a6
7.下列计算正确的是( )
A.a6÷a3=a3 B.(a﹣b)2=a2﹣b2 C.(﹣3a2)3=﹣9a6 D.a2+a3=a5
8.下列运算正确的是( )
A.x4 x3=x12 B.(a6)2÷(a4)3=a C.(a3)2 a4=a10 D.(ab2)3÷(﹣ab)2=﹣ab4
押题方向五:统计
2023年浙江真题 考点 命题趋势
2023年湖州卷第7题 算术平均数 从近几年浙江中考来看,统计部分主要以考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差为主,有的结合统计图表考查,难度较低。预计2024年浙江卷还将继续考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差,为避免丢分,学生应扎实掌握。
2023年舟山、嘉兴卷第3题、台州卷第7题 全面调查与抽样调查
2023年金华卷第6题 众数
2023年宁波卷第6题、杭州卷第9题 方差
2023年温州卷第5题 样本估计总体
1.(2023 湖州)某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这5天平均每天的用水量是( )
A.25立方米 B.30立方米 C.32立方米 D.35立方米
2.(2023 台州)以下调查中,适合全面调查的是( )
A.了解全国中学生的视力情况 B.检测“神舟十六号”飞船的零部件
C.检测台州的城市空气质量 D.调查某池塘中现有鱼的数量
3.(2023 金华)上周双休日,某班8名同学课外阅读的时间如下(单位:时):1,4,2,4,3,3,4,5,这组数据的众数是( )
A.1时 B.2时 C.3时 D.4时
4.(2023 宁波)甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:
甲 乙 丙 丁
9 8 9 9
S2 1.2 0.4 1.8 0.4
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
5.某校计划组织研学活动,现有四个地点可供选择:南麂岛、百丈漈、楠溪江、雁荡山.
为了解学生想法,校方进行问卷调查(每人选一个地点),并绘制成如图所示统计图.已知选择雁荡山的有270人,那么选择楠溪江的有( )
A.90人 B.180人 C.270人 D.360人
6.(2023 杭州)一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字.根据下面的统计结果,能判断记录的这5个数字中一定没有出现数字6的是( )
A.中位数是3,众数是2 B.平均数是3,中位数是2
C.平均数是3,方差是2 D.平均数是3,众数是2
1.如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
2.平均数能充分利用各数据提供的信息,在实际生活中常用样本的平均数估计总体的平均数;中位数不受个别偏大或偏小数据的影响,当一组数据中的个别数据变动较大时,一般用中位数来描述数据的集中趋势;众数考察的是各数据所出现的频数,其大小只与部分数据有关,当一组数据中某些数据多次重复出现时,众数往往更能反映问题。
3.方差反映数据的离散程度,方差越大,数据的波动越大,数据越不稳定。
1.下列调查方式适合用普查的是( )
A.检测一批LED灯的使用寿命
B.检测一批家用汽车的抗撞击能力
C.测试2024神舟十八号载人飞船的零部件质量情况
D.中央电视台《2024年第九季诗词大会》的收视率
2.为加强交通安全教育,某校随机调查了九年级部分学生的上学方式(乘车、步行、骑车),并根据调查结果绘制了如图两幅不完整的统计图,下列判断错误的是( )
A.本次调查的总人数为60人 B.调查的学生中骑车上学的有8人
C.若该校九年级学生有1200人,则乘车上学的约有600人
D.扇形统计图中步行的学生人数所占的圆心角是122°
3.下列说法中,正确的是( )
A.一组数据4,4,2,3,1的中位数是2
B.反映空气的主要成分(氮气约占78%,氧气约占21%,其他微量气体约占1%)宜采用折线统计图
C.甲、乙两人各10次射击的平均成绩相同,方差分别是s甲2=2.2,s乙2=1.3,则乙的射击成绩较稳定
D.对载人航天器零部件的检查适合采用抽样凋查
4.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是3,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A.2,3 B.2,9 C.4,18 D.4,27
5.某店铺连续5天销售衬衣的件数分别为10,11,13,15,11.关于这组数据,以下结论错误的是( )
A.众数是11 B.平均数是12 C.方差是3.2 D.中位数是13
6.如图是描述某校篮球队员年龄的条形图,则这个篮球队员年龄的众数和中位数分别为( )
A.14,15 B.15,14 C.15,15 D.15,14.5
7.某班35位同学课外阅读物的数量统计如表所示,其中有两个数据被遮盖,下列关于课外阅读物的统计量中,与被遮盖的数据无关的是( )
课外阅读物的数量 2 3 4 5 6 7 8
人数 ■ ■ 9 7 9 3 2
A.平均数,方差 B.中位数,方差 C.平均数,众数 D.中位数,众数
8.已知5个正数a1,a2,a3,a4,a5的平均数是a,且a1>a2>a3>a4>a5,则数据a1,a2,a3,0,a4,a5的平均数和中位数是( )
A.a, B.a, C.a, D.a,
答案与解析
押题方向1:实数相关概念、运算及大小比较
2023年浙江真题 考点 命题趋势
2023年湖州、衢州、金华、台州、宁波卷第1题 实数的大小比较 从近几年浙江中考来看,实数的相关概念(正负数、数轴、相反数、绝对值、倒数、平方根、算术平方根、立方根)、实数的大小比较、有理数的运算以选择题形式考查,比较简单;预计2024年浙江卷还将继续重视对正负数的意义、相反数、绝对值、倒数、数轴、平方根、算术平方根、立方根等实数的相关概念及实数的大小比较和运算的考查。
2023年丽水卷第1题 相反数
2023年嘉兴、舟山卷第1题 立方根
2023年温州、绍兴卷第1题 有理数的加减
2023年杭州卷第2题 有理数的混合运算
1.(2023 衢州)手机信号的强弱通常采用负数来表示,绝对值越小表示信号越强(单位:dBm),则下列信号最强的是( )
A.﹣50 B.﹣60 C.﹣70 D.﹣80
【答案】A
【点拨】先求出各个选项中数的绝对值,然后进行比较,根据绝对值越小表示信号越强,找出信号最强的即可.
【解析】解:∵|﹣50|=50,|﹣60|=60,|﹣70|=70,|﹣80|=80,50<60<70<80,
∴信号最强的是﹣50,
故答案为:A.
【点睛】本题主要考查了绝对值,解题关键是熟练掌握绝对值的性质.
2.(2023 温州)如图,比数轴上点A表示的数大3的数是( )
A.﹣1 B.0 C.1 D.2
【答案】D
【点拨】结合数轴得出A对应的数,再利用有理数的加法计算得出答案.
【解析】解:由数轴可得:A表示﹣1,则比数轴上点A表示的数大3的数是:﹣1+3=2.
故选:D.
【点睛】此题主要考查了有理数的加法以及数轴,正确掌握有理数的加法是解题关键.
3.(2023 舟山、嘉兴)下面四个数中,比1小的正无理数是( )
A. B.﹣ C. D.
【答案】A
【点拨】无理数即无限不循环的小数,结合实数比较大小的方法进行判断即可.
【解析】解:A.∵1>,
∴>,
即1>,且是正无理数,
则A符合题意;
B.﹣是负数,
则B不符合题意;
C.是分数,不是无理数,
则C不符合题意;
D.∵π>3,
∴>1,
则D不符合题意;
故选:A.
【点睛】本题考查无理数的定义及实数的大小比较,此为基础且重要知识点,必须熟练掌握.
4.(2023 丽水)实数﹣3的相反数是( )
A.﹣ B. C.3 D.﹣3
【答案】C
【点拨】根据相反数的定义判断即可.
【解析】解:﹣3的相反数是3,
故选:C.
【点睛】本题考查了相反数:只有符号不同的两个数是互为相反数,掌握其定义是解题的关键.
5.(2023 浙江)﹣8的立方根是( )
A.﹣2 B.2 C.±2 D.不存在
【答案】A
【点拨】根据立方根的定义求出的值,即可得出答案.
【解析】解:﹣8的立方根是==﹣2,
故选:A.
【点睛】本题考查了对立方根的定义的理解和运用,明确a的立方根是是解题的关键.
6.(2023 绍兴)计算2﹣3的结果是( )
A.﹣1 B.﹣3 C.1 D.3
【答案】A
【点拨】根据有理数减法法则:减去一个数,等于加上这个数的相反数.即:a﹣b=a+(﹣b),即可得出答案.
【解析】解:2﹣3=﹣1.
故选:A.
【点睛】此题主要考查了有理数的减法,正确掌握有理数的减法运算法则是解题关键.
7.(2023 杭州)(﹣2)2+22=( )
A.0 B.2 C.4 D.8
【答案】D
【点拨】根据有理数的混合运算顺序,先计算乘方,再计算加法即可.
【解析】解:(﹣2)2+22=4+4=8.
故选:D.
【点睛】本题考查了有理数的混合运算,掌握有理数的乘方的定义是解答本题的关键.
8.(2023 金华)某一天,哈尔滨、北京、杭州、金华四个城市的最低气温分别是﹣20℃,﹣10℃,0℃,2℃,其中最低气温是( )
A.﹣20℃ B.﹣10℃ C.0℃ D.2℃
【答案】A
【点拨】明确在实数中负数小于0小于正数,且负数之间比较大小绝对值越大负数越小.
【解析】解:由题可知:﹣20<﹣10<0<2,
所以最低气温是﹣20℃.
故选:A.
【点睛】本题考查了实数的比较大小,题目难度较小,一般出现在期末第一题.
9.(2023 台州)下列各数中,最小的是( )
A.2 B.1 C.﹣1 D.﹣2
【答案】D
【点拨】正数>0>负数,两个负数比较大小,绝对值大的反而小;据此进行判断即可.
【解析】解:∵|﹣1|=1,|﹣2|=2,1<2,
∴﹣1>﹣2,
则2>1>﹣1>﹣2,
那么最小的数为:﹣2,
故选:D.
【点睛】本题考查有理数的大小比较,此为基础且重要知识点,必须熟练掌握.
10.(2023 宁波)在﹣2,﹣1,0,π这四个数中,最小的数是( )
A.﹣2 B.﹣1 C.0 D.π
【答案】A
【点拨】正数>0>负数,两个负数比较大小,绝对值大的反而小,据此进行判断即可.
【解析】解:∵|﹣2|=2,|﹣1|=1,2>1,
∴﹣1>﹣2,
∴π>0>﹣1>﹣2,
则最小的数为:﹣2,
故选:A.
【点睛】本题考查实数的大小比较,此为基础且重要知识点,必须熟练掌握.
数轴、相反数、绝对值、倒数是核心考点,常在选择题和填空题中出现。对于数轴我们不仅要记住它的三要素,还要能借助它比较实数大小;对于相反数我们需要注意的是当用一个式子表示一个数量,求相反数时需要注意整体概念;对于绝对值需要注意情况不确定时,需要分类讨论;而对于倒数需要注意的是0没有倒数。
实数比较大小可以根据数的性质来比较,正数比负数大,两个负数比较大小,绝对大的反而小;也可通过数轴,数轴上的两个数比较大小,右边的数比左边的大。但对于一些复杂的式子,我们就需要用求差法或者求商法;对于含根号的数,我们还可以用平方法或者倒数法。
1.如果水位升高3m时水位变化记作+3m,那么水位不升不降时水位变化记作( )
A.+3m B.﹣3m C.0m D.±3m
【答案】C
【点拨】正数和负数是一组具有相反意义的量,据此即可求得答案.
【解析】解:水位升高3m时水位变化记作+3m,那么水位不升不降时水位变化记作0m,
故选:C.
【点睛】本题考查正数和负数,理解具有相反意义的量是解题的关键.
2.在﹣4,﹣1,0,1这四个数中,比﹣2小的数是( )
A.﹣4 B.﹣1 C.0 D.1
【答案】A
【点拨】有理数大小比较的法则:(1)正数都大于0;(2)负数都小于0;(3)正数大于一切负数;(4)两个负数,绝对值大的其值反而小,据此逐个判断即可.
【解析】解:∵﹣4<﹣2,﹣1>﹣2,0>﹣2,1>﹣2,
∴在﹣4,﹣1,0,1这四个数中,比﹣2小的数是﹣4.
故选:A.
【点睛】此题主要考查了有理数大小比较的方法,解答此题的关键是要明确:(1)正数都大于0;(2)负数都小于0;(3)正数大于一切负数;(4)两个负数,绝对值大的其值反而小.
3.下列算式中,运算结果最小的是( )
A.﹣2+3 B.﹣2﹣3 C.﹣2×3 D.﹣2÷3
【答案】C
【点拨】根据有理数混合运算的计算法则进行解答.
【解析】解:﹣2+3=1;
﹣2﹣3=﹣5;
﹣2×3=﹣6;
﹣2÷3=﹣,
﹣6.
故选:C.
【点睛】本题考查了有理数的混合运算,解题的关键是运用计算法则进行计算.
4.(﹣2)3=( )
A.﹣6 B.6 C.﹣8 D.8
【答案】C
【点拨】原式利用乘方的意义计算即可得到结果.
【解析】解:原式=﹣8,
故选:C.
【点睛】此题考查了有理数的乘方,熟练掌握乘方的意义是解本题的关键.
5.|﹣3|﹣(﹣2)=( )
A.﹣1 B.5 C.1 D.﹣5
【答案】B
【点拨】﹣3的绝对值等于3,减去﹣2就相当于加上2.
【解析】解:|﹣3|﹣(﹣2)=3+2=5.
故选:B.
【点睛】本题考查了有理数的减法法则及绝对值的定义.减去一个数,等于加上这个数的相反数.一个负数的绝对值等于它的相反数.
6.﹣2024的倒数是( )
A.﹣2024 B.2024 C. D.
【答案】C
【点拨】根据题意利用倒数定义即可得出本题答案.
【解析】解:∵,
故选:C.
【点睛】本题考查倒数定义,解题的关键是掌握倒数的定义.
7.家用冰箱冷冻室的温度需控制在﹣4℃到﹣24℃之间,则可将冷冻室的温度设为( )
A.0℃ B.﹣3℃ C.﹣18℃ D.﹣25℃
【答案】C
【点拨】根据有理数大小比较方法解答即可.
【解析】解:∵﹣25<﹣24<﹣18<﹣4<﹣3<0,家用冰箱冷冻室的温度需控制在﹣4℃到﹣24℃之间,
∴可将冷冻室的温度设为﹣18℃.
故选:C.
【点睛】本题考查了有理数大小比较以及正数和负数,掌握有理数大小比较方法是解答本题的关键.
8.把笔尖放在数轴的原点,沿数轴先向左(负方向)移动6个单位长度,再向右移动3个单位长度,用算式表示上述过程与结果,正确的是( )
A.﹣6+3=9 B.﹣6﹣3=﹣3 C.﹣6+3=﹣3 D.﹣6+3=3
【答案】C
【点拨】根据有理数的运算法则即可求出答案.
【解析】解:由题意可知:﹣6+3=﹣3,
故选:C.
【点睛】本题考查有理数的运算,解题的关键是正确理解有理数的加法法则,本题属于基础题型.
9.(2024 余姚市一模)已知某快递公司的收费标准为:寄一件物品不超过5千克,收费13元;超过5千克的部分每千克加收2元.若在该快递公司寄一件9千克的物品,则需要付费( )
A.17元 B.19元 C.21元 D.23元
【答案】C
【点拨】根据题意和题目中的数据,可以列出算式13+(9﹣5)×2,然后计算即可.
【解析】解:由题意可得,
13+(9﹣5)×2
=13+4×2
=13+8
=21(元),
故选:C.
【点睛】本题考查有理数的混合运算,熟练掌握运算法则是解答本题的关键.
10.(2024 宁波模拟)有理数a、b在数轴上的位置如图所示,则下列结论正确的是( )
A.a2>b2 B.a﹣b>0 C. D.a+b>0
【答案】A
【点拨】根据有理数a、b在数轴上的位置得出a、b的符号和绝对值,进而逐项进行判断即可.
【解析】解:由有理数a、b在数轴上的位置可知,
a<0<b,且|a|>|b|,
所以a2>b2,a﹣b<0,<0,a+b<0,
因此A是正确的,
故选:A.
【点睛】本题考查数轴表示数,理解符号和绝对值是确定有理数的必要条件,掌握有理数的运算法则是正确判断的前提.
押题方向2:投影与视图
20233年浙江真题 考点 命题趋势
2023年湖州、温州、金华、台州、舟山、嘉兴卷第2题 简单几何体的三视图 从近几年浙江中考来看,投影与视图以选择题形式考查,2023年浙江省10份中考试卷有9份试卷考查了投影与视图,比较简单,主要考查了简单几何体的三视图与由三视图判断几何体;预计2024年浙江卷还将继续重视对三视图的考查。
2023年绍兴卷第3题 简单几何体的三视图
2023年湖州、宁波、丽水卷第4题 简单几何体的三视图
2023年湖州卷第4题 由三视图判断几何体
1.(2023 湖州)已知某几何体的三视图如图所示,则该几何体可能是( )
A. B. C. D.
【答案】D
【点拨】主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的图形,从而得出答案.
【解析】解:∵主视图和左视图是矩形,
∴几何体是柱体,
∵俯视图是圆,
∴该几何体是圆柱,故D正确.
故选:D.
【点睛】本题主要考查了由三视图确定几何体的形状,主要考查学生空间想象能力.
3.(2023 温州)截面为扇环的几何体与长方体组成的摆件如图所示,它的主视图是( )
A. B. C. D.
【答案】A
【点拨】根据从正面看得到的图形是主视图,可得答案.
【解析】解:从正面看,可得选项A的图形.
故选:A.
【点睛】本题考查了简单组合体的三视图,从正面看得到的图形是主视图.
4.(2023 绍兴)由8个相同的立方体搭成的几何体如图所示,则它的主视图是( )
A. B. C. D.
【答案】D
【点拨】主视图有3列,每列小正方形数目分别为2,1,2,据此判断即可.
【解析】解:如图所示:它的主视图是:
.
故选:D.
【点睛】此题主要考查了简单组合体的三视图,正确把握观察角度是解题关键.
5.(2023 宁波)如图所示的几何体是由一个圆柱和一个长方体组成的,它的主视图是( )
A. B. C. D.
【答案】A
【点拨】根据从正面看得到的图形是主视图判断即可.
【解析】解:从正面看,上边是一个长方形,下边也是一个长方形,
故选:A.
【点睛】本题考查了简单几何体的三视图,需掌握:从正面看得到的图形是主视图,从上面看得到的图形是俯视图,从左面看得到的图形是左视图.
1.几何体的三视图:(1)主视图:物体在正投影面上的正投影.(2)左视图:物体在侧投影面上的正投影.(3)俯视图:物体在水平投影面上的正投影.
2.画“三视图”的原则:(1)大小:长对正,高平齐,宽相等.(2)虚实:在画图时,看得见部分的轮廓线通常画成实线,看不见部分的轮廓线通常画成虚线.
3.由三视图确定几何体的方法:
1)由三视图想象几何体的形状,首先应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,然后综合起来考虑整体形状.
2)由物体的三视图想象几何体的形状是有一定难度的,可以从以下途径进行分析:
① 根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状,以及几何体的长、宽、高;
② 从实线和虚线想象几何体看得见部分和看不见部分的轮廓线;
③ 熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助.
1.如图是由5个大小相同的小正方体组成的几何体,该几何体的俯视图是( )
A. B. C. D.
【答案】C
【点拨】根据从上边看得到的图形是俯视图,可得答案.
【解析】解:从上边看,一共有三列,从左到右正方形的个数分别为2、1、1.
故选:C.
【点睛】本题考查了简单组合体的三视图,从上边看得到的图形是俯视图.
2.如图是一个古建筑中常用的榫卯构件,其左视图为( )
A. B. C. D.
【答案】B
【点拨】找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在视图中.
【解析】解:从左面看,是一列三个新来的矩形.
故选:B.
【点睛】本题考查了三视图的知识,掌握主视图是从物体的正面看得到的视图,左视图是从物体的左面看得到的视图,俯视图是从物体的上面看得到的视图是解题的关键.
3.榫卯是我国古代木制建筑、家具等的主要结构方式,凸出部分叫榫,凹进部分叫卯.如图是某个部件“卯”的实物图,它的主视图是( )
A. B. C. D.
【答案】A
【点拨】从正面看到的平面图形是主视图,根据主视图的含义可得答案.
【解析】解:如图所示的几何体的主视图如下:
.
故选:A.
【点睛】此题主要考查了简单组合体的三视图;用到的知识点为:主视图,左视图,俯视图分别是从物体的正面,左面,上面看得到的图形.
4.某物体如图所示,其左视图是( )
A. B. C. D.
【答案】A
【点拨】根据左视图是从左边看得到的图形,可得答案.
【解析】解:从左边看,是一列两个相邻的矩形.
故选:A.
【点睛】本题考查了简单组合体的三视图,左视图是从左边看得到的图形.
5.在下面四个几何体中,主视图与俯视图都是圆的为( )
A. B. C. D.
【答案】D
【点拨】根据圆柱、圆锥、圆台和球的三视图进行判断.
【解析】解:(A)圆柱的主视图是长方形,俯视图是圆,故(A)错误;
(B)圆锥的主视图是等腰三角形,俯视图是圆,故(B)错误;
(C)圆台的主视图是等腰梯形,俯视图是两个同心圆,故(C)错误;
(D)球的主视图与俯视图都是圆,故(D)正确.
故选:D.
【点睛】本题主要考查了几何体的三视图,解决问题的关键是掌握几种简单几何体的特征.解题时注意,圆柱的左视图与主视图都是长方形,圆锥的左视图与主视图都是等腰三角形,圆台的左视图与主视图都是等腰梯形,而三种视图都一样的几何体有球和正方体等.
6.下列常见的几何体中,主视图和左视图不同的是( )
A. B. C. D.
【答案】A
【点拨】分别分析四种几何体的主视图和左视图,找出主视图和左视图不同的几何体.
【解析】解:A、正三棱柱的主视图是三角形,左视图是矩形,符合题意;
B、圆柱的主视图与左视图都是长方形,不合题意;
C、圆锥的主视图与左视图相同,都是等腰三角形,不合题意;
D、正方体的主视图和左视图相同,都是正方形,不合题意.
故选:A.
【点睛】本题考查了简单几何体的三视图,掌握主视图是从物体的正面看到的视图,左视图是从物体的左面看得到的视图是解答本题的关键.
7.如图是一个几何体的三视图,则该几何体是( )
A.B.C. D.
【答案】C
【点拨】由于主视图是从物体的正面看得到的视图,所以先得出四个选项中各几何体的主视图,再与题目图形进行比较即可.
【解析】解:A、主视图是,故选项错误;
B、主视图是,故选项错误;
C、主视图是,故选项正确;
D、主视图是, 故选项错误.
故选:C.
【点睛】本题考查由三视图判断几何体,掌握三视图定义是解题的关键.
8.如图,是一个几何体的三视图,则这个几何体是( )
A. B. C. D.
【答案】A
【点拨】根据主视图、左视图、俯视图是分别从物体正面、左面和上面看,所得到的图形,即可判断出答案.
【解析】解:选项A的三视图符合题意,选项B的左视图和主视图都不符合题意,选项C、D的三视图都不符合题意.
故选:A.
【点睛】此题主要考查了学生对三视图掌握程度和灵活运用能力,同时也体现了对空间想象能力方面的考查.
押题方向3:科学记数法
20233年浙江真题 考点 命题趋势
2023年杭州卷第1题 科学记数法 从近几年浙江中考来看,科学记数法、近似数以选择题形式考查,比较简单,科学记数法有大数和小数两种形式,有时带“亿”、“万”、“千万”等单位,做题时要仔细审题,切忽略单位;预计2024年浙江卷还将继续重视对科学记数法的考查。
2023年绍兴卷第2题 科学记数法
2023年湖州、温州、金华、宁波卷第3题 科学记数法
1.(2023 宁波)据中国宁波网消息:2023年一季度宁波全市实现地区生产总值380180000000元,同比增长4.5%.数380180000000用科学记数法表示为( )
A.0.38018×1012 B.3.8018×1011 C.3.8018×1010 D.38.018×1010
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:380180000000=3.8018×1011.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.(2023 湖州)国家互联网信息办公室2023年5月23日发布的《数字中国发展报告(2022年)》显示,2022年我国数字经济规模达502000亿元.用科学记数法表示502000,正确的是( )
A.0.502×106 B.5.02×106 C.5.02×105 D.50.2×104
【答案】C
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值大于10时,n是正整数;当原数的绝对值小于1时,n是负整数.
【解析】解:502000=5.02×105,
故选:C.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,正确确定a的值以及n的值是解决问题的关键.
3.(2023 杭州)杭州奥体中心体育场又称“大莲花”,里面有80800个座位.数据80800用科学记数法表示为( )
A.8.8×104 B.8.08×104 C.8.8×105 D.8.08×105
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:80800=8.08×104,
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.(2023 温州)苏步青来自“数学家之乡”,为纪念其卓越贡献,国际上将一颗距地球约218000000公里的行星命名为“苏步青星”.数据218000000用科学记数法表示为( )
A.0.218×109 B.2.18×108 C.21.8×102 D.218×106
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:将218000000用科学记数法表示为2.18×108.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
5.(2023 绍兴)据报道,2023年“五一”假期全国国内旅游出游合计274000000人次.数字274000000用科学记数法表示是( )
A.27.4×107 B.2.74×108 C.0.274×109 D.2.74×109
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.
【解析】解:274000000=2.74×108.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
科学记数法是中考高频考点,我们不仅要记住它的基本形式,更要记住表达式中a的取值范围;还要注意n,当表示一个绝对值大于10的数,n是正整数;当表示一个绝对值小于1的数时,指数为负整数。注意:1)单位的统一,尤其是带“万”或者“亿”的问题:含有万、亿等单位的数,用科学记数法表示时,要先还原成原数,再用科学记数法表示,最后按要求取近似值。
1.2023年5月28日,我国自主研发的C919国产大飞机商业首航取得圆满成功.C919可储存约186000升燃油,将数据186000用科学记数法表示为( )
A.0.186×105 B.1.86×105 C.18.6×104 D.186×103
【答案】B
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正数;当原数的绝对值<1时,n是负数.
【解析】解:将186000用科学记数法表示为:1.86×105.
故选:B.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
2.我国自主研发的500m口径球面射电望远镜(FAST)有“中国天眼”之称,它的反射面面积约为250000m2.用科学记数法表示数据250000为( )
A.0.25×106 B.25×104 C.2.5×104 D.2.5×105
【答案】D
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:250000=2.5×105,
故选:D.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
3.中国信通院预计未来2~3年内将实现5G的个人终端应用和数字内容的创新突破,预计2025年全球5G移动用户数将突破57亿户.数据57亿用科学记数法表示为( )
A.0.57×1010 B.5.7×1010 C.5.7×109 D.57×104
【答案】C
【点拨】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值≥10时,n是正整数;当原数的绝对值<1时,n是负整数.
【解析】解:57亿=5700000000=5.7×109.
故选:C.
【点睛】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.
4.芯片是手机、电脑等高科技产品最核心的部件,更小的芯片意味着更高的性能,目前我国芯片的量产工艺已达到14纳米,已知14纳米等于0.000000014米,用科学记数法将0.000000014表示为( )
A.1.4×10﹣9 B.1.4×10﹣7 C.1.4×10﹣8 D.14×10﹣7
【答案】C
【点拨】根据科学记数法的方法进行解题即可.
【解析】解:0.000000014=1.4×10﹣8.
故选:C.
【点睛】此题主要考查了用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
5.华为一部分Mate40手机将会搭载麒麟9000处理器,这是手机行业首批采用5nm工艺制式的芯片,1nm=0.000000001m,其中5nm用科学记数法表示为( )
A.5×109 B.5×10﹣10 C.5×10﹣8 D.5×10﹣9
【答案】D
【点拨】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
【解析】解:5nm=0.000000005m,
0.000000005=5×10﹣9.
故选:D.
【点睛】本题考查用科学记数法表示较小的数,一般形式为a×10﹣n,其中1≤|a|<10,n为由原数左边起第一个不为零的数字前面的0的个数所决定.
押题方向4:整式运算
2023年浙江真题 考点 命题趋势
2023年湖州卷第2题 同底数幂的乘法 从近几年浙江中考来看,整式运算主要以考查整式的加减、乘除、乘法公式、幂的运算为主,也是考查重点,难度较低。预计2024年浙江卷还将继续考查幂的运算、整式混合运算(特别是乘法公式),为避免丢分,学生应扎实掌握。
2023年丽水卷第2题 合并同类项
2023年衢州卷第3题、宁波卷第2题 同底数幂的除法
2023年绍兴卷第4题 整式的混合运算
2023年绍兴卷第4题 完全平方公式
1.(2023 丽水)计算a2+2a2的正确结果是( )
A.2a2 B.2a4 C.3a2 D.3a4
【答案】C
【点拨】根据合并同类项法则进行计算即可.
【解析】解:a2+2a2
=(1+2)a2
=3a2,
故选:C.
【点睛】本题考查了合并同类项法则,能熟记合并同类项法则是解此题的关键,把同类项的系数相加作为系数,字母和字母的指数不变.
2.(2023 温州)化简a4 (﹣a)3的结果是( )
A.a12 B.﹣a12 C.a7 D.﹣a7
【答案】D
【点拨】直接利用同底数幂的乘法运算法则计算得出答案.
【解析】解:a4 (﹣a)3=﹣a7.
故选:D.
【点睛】此题主要考查了同底数幂的乘法运算,正确掌握相关运算法则是解题关键.
3.(2023 台州)下列运算正确的是( )
A.2(a﹣1)=2a﹣2 B.(a+b)2=a2+b2 C.3a+2a=5a2 D.(ab)2=ab2
【答案】A
【点拨】根据去括号法则,完全平方公式,合并同类项法则,积的乘方法则将各项计算后进行判断即可.
【解析】解:A.2(a﹣1)
=2a﹣2×1
=2a﹣2,
则A符合题意;
B.(a+b)2=a2+2ab+b2,
则B不符合题意;
C.3a+2a
=(3+2)a
=5a,
则C不符合题意;
D.(ab)2=a2b2,
则D不符合题意;
故选:A.
【点睛】本题考查整式的运算,其相关运算法则是基础且重要知识点,必须熟练掌握.
4.(2023 绍兴)下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7
C.(a+1)(a﹣1)=a2﹣1 D.(a+1)2=a2+1
【答案】C
【思路点拨】直接利用整式的混合运算法则分别判断得出答案.
【解析】解:A.a6÷a2=a4,故此选项不合题意;
B.(﹣a2)5=﹣a10,故此选项不合题意;
C.(a+1)(a﹣1)=a2﹣1,故此选项符合题意;
D.(a+1)2=a2+2a+1,故此选项不合题意.
故选:C.
【点睛】此题主要考查了整式的混合运算,正确掌握相关运算法则是解题关键.
5.(2023 衢州)下列运算,结果正确的是( )
A.3a+2a=5a2 B.3a﹣2a=1 C.a2 a3=a5 D.a÷a2=a
【答案】C
【点拨】根据同底数幂的乘法法则和同底数幂的除法法则及合并同类项法则即可解决问题.
【解析】解:因为3a+2a=5a,所以A选项错误.
因为3a﹣2a=a,所以B选项错误.
因为a2 a3=a2+3=a5,所以C选项正确.
因为a÷a2=a1﹣2=a﹣1,所以D选项错误.
故选:C.
【点睛】本题考查同底数幂的运算及合并同类项,熟知同底数幂的运算法则及合并同类项法则是解题的关键.
6.(2023 宁波)下列计算正确的是( )
A.x2+x=x3 B.x6÷x3=x2 C.(x3)4=x7 D.x3 x4=x7
【答案】D
【点拨】根据合并同类项的法则、同底数幂除法、幂的乘方以及同底数幂乘法的运算法则计算即可.
【解析】解:A、x2和x不是同类项,不能进行合并,故选项不符合题意;
B、x6÷x3=x3,原式计算错误,故选项不符合题意;
C、(x3)4=x12,原式计算错误,故选项不符合题意;
D、x3 x4=x7,运算计算正确,故选项符合题意.
故选:D.
【点睛】本题考查了合并同类项的法则、同底数幂除法、幂的乘方以及同底数幂乘法的运算法则,解题的关键是熟记相关的运算法则并灵活运用.
1)幂的运算法则是进行整式乘除法的基础,要熟练掌握,解题时要明确运算的类型,正确运用法则;在运算的过程中,一定要注意指数、系数和符号的处理.
2)整式的加减,实质上就是合并同类项,有括号的,先去括号,只要算式中没有同类项,就是最后的结果;多项式乘多项式的运算中要做到不重不漏,应用乘法公式进行简便计算,另外去括号时,要注意符号的变化,最后把所得式子化简,即合并同类项.
1.计算(﹣a)3 a2的结果是( )
A.﹣a6 B.a6 C.﹣a5 D.a5
【答案】C
【点拨】利用同底数幂的乘法的法则对式子进行运算即可.
【解析】解:(﹣a)3 a2
=﹣a3 a2
=﹣a5,
故选:C.
【点睛】本题主要考查同底数幂的乘法,解答的关键是熟记同底数幂的乘法的法则.
2.下列运算正确的是( )
A.2+4a=6a B.a3 a4=a12 C.(﹣2a)2=﹣4a2 D.a5÷a3=a2
【答案】D
【点拨】A.根据同类项的定义判断即可;
B.根据同底数幂的乘法运算法则计算并判断即可;
C.根据积的乘方与幂的乘方运算法则计算并判断即可;
D.根据同底数幂的除法运算法则计算并判断即可.
【解析】解:2与4a不是同类项,无法合并,
∴A不正确,不符合题意;
a3 a4=a7,
∴B不正确,不符合题意;
(﹣2a)2=4a2,
∴C不正确,不符合题意;
a5÷a3=a2,
∴D正确,符合题意.
故选:D.
【点睛】本题考查同底数幂的乘除法、积的乘方与幂的乘方,掌握它们的运算法则是解题的关键.
3.下列计算正确的是( )
A.(a2)4=a6 B.(3a)2=6a2 C.a8÷a4=a2 D.(﹣ab3)2=a2b6
【答案】D
【点拨】根据同底数幂的除法法则、幂的乘方与积的乘方法则进行解题即可.
【解析】解:A、(a2)4=a8,故该项不正确,不符合题意;
B、(3a)2=9a2,故该项不正确,不符合题意;
C、a8÷a4=a4,故该项不正确,不符合题意;
D、(﹣ab3)2=a2b6,故该项正确,符合题意;
故选:D.
【点睛】本题考查同底数幂的除法、幂的乘方与积的乘方,熟练掌握运算法则是解题的关键.
4.下列运算正确的是( )
A.(a2)3=a5 B.a3 a4=a12 C.a8÷a4=a2 D.(﹣3a2)2=9a4
【答案】D
【点拨】根据幂的乘方,同底数幂的乘法,同底数幂的除法,积的乘方,逐一进行计算即可得到答案.
【解析】解:A、(a2)3=a6,原计算错误,不符合题意,选项错误;
B、a3 a4=a7,原计算错误,不符合题意,选项错误;
C、a8÷a4=a4,原计算错误,不符合题意,选项错误;
D、(﹣3a2)2=9a4,原计算正确,符合题意,选项正确,
故选:D.
【点睛】本题考查了幂的乘方,同底数幂的乘法,同底数幂的除法,积的乘方,熟练掌握相关运算法则是解题关键.
5.下列计算正确的是( )
A.a3﹣a2=a B.a3 a2=a6 C.(a3)2=a6 D.(2a+1)(2a﹣1)=2a2﹣1
【答案】C
【点拨】利用合并同类项法则,同底数幂乘法法则,幂的乘方法则,平方差公式逐项判断即可.
【解析】解:a3与a2不是同类项,无法合并,则A不符合题意;
a3 a2=a5,则B不符合题意;
(a3)2=a6,则C符合题意;
(2a+1)(2a﹣1)=4a2﹣1,则D不符合题意;
故选:C.
【点睛】本题考查整式的运算,熟练掌握相关运算法则是解题的关键.
6.下列计算正确的是( )
A.a+2a=3a B.(a+b)2=a2+b2 C.(a2)3=a5 D.a2 a3=a6
【答案】A
【点拨】根据合并同类项法则、完全平方公式、幂的乘方运算法则、整式的乘法运算即可求出答案.
【解析】解:A、原式=3a,故A符合题意.
B、原式=a2+2ab+b2,故B不符合题意.
C、原式=a6,故C不符合题意.
D、原式=a5,故D不符合题意.
故选:A.
【点睛】本题考查合并同类项法则、完全平方公式、幂的乘方运算法则、整式的乘法运算,本题属于基础题型.
7.下列计算正确的是( )
A.a6÷a3=a3 B.(a﹣b)2=a2﹣b2 C.(﹣3a2)3=﹣9a6 D.a2+a3=a5
【答案】A
【点拨】运用合并同类项、同底数幂除法、积的乘方、完全平方公式进行逐一计算辨别.
【解析】解:∵a6÷a3=a3,
∴选项A符合题意;
∵(a﹣b)2=a2﹣2ab+b2,
∴选项B不符合题意;
∵(﹣3a2)3=﹣27a6,
∴选项C不符合题意;
∵a2和a3不是同类项,不能合并,
∴选项D不符合题意,
故选:A.
【点睛】此题考查了合并同类项、同底数幂除法、积的乘方、完全平方公式的运算能力,关键是能准确理解并运用以上知识进行准确地计算.
8.下列运算正确的是( )
A.x4 x3=x12 B.(a6)2÷(a4)3=a C.(a3)2 a4=a10 D.(ab2)3÷(﹣ab)2=﹣ab4
【答案】C
【点拨】根据同底数幂乘除法,积的乘方,幂的乘方,单项式除以单项式等计算法则求解判断即可.
【解析】解:A、x4 x3=x7,原计算错误,不符合题意;
B、(a6)2÷(a4)3=a12÷a12=1,原计算错误,不符合题意;
C、(a3)2 a4=a6 a4=a10,正确,符合题意;
D、(ab2)3÷(﹣ab)2=a3b6÷a2b2=ab4,原计算错误,不符合题意.
故选:C.
【点睛】本题主要考查了同底数幂乘除法,积的乘方,幂的乘方,单项式除以单项式,熟知相关计算法则是解题的关键,注意同底数幂乘除法指数是相加减,积的乘方和幂的乘方指数是相乘.
押题方向五:统计
2023年浙江真题 考点 命题趋势
2023年湖州卷第7题 算术平均数 从近几年浙江中考来看,统计部分主要以考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差为主,有的结合统计图表考查,难度较低。预计2024年浙江卷还将继续考查全面调查与抽样调查、样本估计总体、中位数、众数、平均数、方差,为避免丢分,学生应扎实掌握。
2023年舟山、嘉兴卷第3题、台州卷第7题 全面调查与抽样调查
2023年金华卷第6题 众数
2023年宁波卷第6题、杭州卷第9题 方差
2023年温州卷第5题 样本估计总体
1.(2023 湖州)某住宅小区6月1日~6月5日每天用水量情况如图所示,那么这5天平均每天的用水量是( )
A.25立方米 B.30立方米 C.32立方米 D.35立方米
【答案】B
【点拨】先确定每天的用水量,根据用水量的和除以用水天数,求出结果即可.
【解析】解:由折线图可知,该小区五天的用水量分别是:30、40、20、30、30.所以5天的平均用水量为:
=30(立方米).
故选:B.
【点睛】本题考查了折线图和算术平均数,掌握算术平均数的计算方法是解决本题的关键.
2.(2023 台州)以下调查中,适合全面调查的是( )
A.了解全国中学生的视力情况 B.检测“神舟十六号”飞船的零部件
C.检测台州的城市空气质量 D.调查某池塘中现有鱼的数量
【答案】B
【点拨】根据普查得到的调查结果比较准确,但所费人力、物力和时间较多,而抽样调查得到的调查结果比较近似进行判断.
【解析】解:A.了解全国中学生的视力情况,适合抽样调查,故本选项不合题意;
B.检测“神舟十六号”飞船的零部件,适合普查,故本选项符合题意;
C.检测台州的城市空气质量,适合抽样调查,故本选项不合题意;
D.调查某池塘中现有鱼的数量,适合抽样调查,故本选项不合题意.
故选:B.
【点睛】本题考查了抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
3.(2023 金华)上周双休日,某班8名同学课外阅读的时间如下(单位:时):1,4,2,4,3,3,4,5,这组数据的众数是( )
A.1时 B.2时 C.3时 D.4时
【答案】D
【点拨】根据众数的定义求解即可.
【解析】解:这组数据4出现的次数最多,故众数为4,
故选:D.
【点睛】本题考查了众数的知识,属于基础题,解答本题的关键是熟练掌握众数的定义.
4.(2023 宁波)甲、乙、丙、丁四名射击运动员进行射击测试,每人10次射击成绩的平均数(单位:环)及方差S2(单位:环2)如下表所示:
甲 乙 丙 丁
9 8 9 9
S2 1.2 0.4 1.8 0.4
根据表中数据,要从中选择一名成绩好且发挥稳定的运动员参加比赛,应选择( )
A.甲 B.乙 C.丙 D.丁
【答案】D
【点拨】根据平均环数比较成绩的优劣,根据方差比较数据的稳定程度.
【解析】解:由表知甲、丙、丁射击成绩的平均数相等,且大于乙的平均数,
∴从甲、丙、丁中选择一人参加竞赛,
∵甲、丙、丁三人中,丁的方差较小,
∴丁发挥最稳定,
∴选择丁参加比赛.
故选:D.
【点睛】本题考查的是方差和算术平均数,掌握方差反映了一组数据的波动大小,方差越大,波动性越大,方差越小,数据越稳定是解题的关键.
5.某校计划组织研学活动,现有四个地点可供选择:南麂岛、百丈漈、楠溪江、雁荡山.
为了解学生想法,校方进行问卷调查(每人选一个地点),并绘制成如图所示统计图.已知选择雁荡山的有270人,那么选择楠溪江的有( )
A.90人 B.180人 C.270人 D.360人
【答案】B
【点拨】先根据选择雁荡山的人数及其所占百分比求出被调查的总人数,再用总人数乘以选择楠溪江的人数所占百分比即可.
【解析】解:调查总人数:270÷30%=900(人),
选择楠溪江的人数:900×20%=180(人),
故选:B.
【点睛】本题考查的是扇形统计图.读懂统计图,从统计图中得到必要的信息是解决问题的关键;扇形统计图直接反映部分占总体的百分比大小.
6.(2023 杭州)一枚质地均匀的正方体骰子(六个面分别标有数字1,2,3,4,5,6),投掷5次,分别记录每次骰子向上的一面出现的数字.根据下面的统计结果,能判断记录的这5个数字中一定没有出现数字6的是( )
A.中位数是3,众数是2 B.平均数是3,中位数是2
C.平均数是3,方差是2 D.平均数是3,众数是2
【答案】C
【点拨】根据中位数、众数、平均数、方差的定义,结合选项中设定情况,逐项判断即可.
【解析】解:当中位数是3,众数是2时,记录的5个数字可能为:2,2,3,4,5或2,2,3,4,6或2,2,3,5,6,故A选项不合题意;
当平均数是3,中位数是2时,5个数之和为15,记录的5个数字可能为1,1,2,5,6或1,2,2,5,5,故B选项不合题意;
当平均数是3,方差是2时,5个数之和为15,假设6出现了1次,方差最小的情况下另外4个数为:2,2,2,3,此时方差s2=×[3×(2﹣3)2+(3﹣3)2+(6﹣3)2]=2.4>2,因此假设不成立,即一定没有出现数字6,故C选项符合题意;
当平均数是3,众数是2时,5个数之和为15,2至少出现两次,记录的5个数字可能为1,2,2,4,6,故D选项不合题意;
故选:C.
【点睛】本题主要考查平均数、众数和中位数及方差,解题的关键是掌握平均数、众数和中位数及方差的定义.
1.如果数据的个数是奇数,则处于中间位置的数就是这组数据的中位数;如果数据的个数是偶数,则中间两个数据的平均数就是这组数据的中位数。
2.平均数能充分利用各数据提供的信息,在实际生活中常用样本的平均数估计总体的平均数;中位数不受个别偏大或偏小数据的影响,当一组数据中的个别数据变动较大时,一般用中位数来描述数据的集中趋势;众数考察的是各数据所出现的频数,其大小只与部分数据有关,当一组数据中某些数据多次重复出现时,众数往往更能反映问题。
3.方差反映数据的离散程度,方差越大,数据的波动越大,数据越不稳定。
1.下列调查方式适合用普查的是( )
A.检测一批LED灯的使用寿命
B.检测一批家用汽车的抗撞击能力
C.测试2024神舟十八号载人飞船的零部件质量情况
D.中央电视台《2024年第九季诗词大会》的收视率
【答案】C
【点拨】根据抽样调查和全面调查的区别判断即可.
【解析】解:A、检测一批LED灯的使用寿命,适合用抽样调查,不符合题意;
B、检测一批家用汽车的抗撞击能力,适合用抽样调查,不符合题意;
C、测试2024神舟十八号载人飞船的零部件质量情况,适合用普查,符合题意;
D、中央电视台《2024年第九季诗词大会》的收视率,适合用抽样调查,不符合题意;
故选:C.
【点睛】本题考查的是抽样调查和全面调查的区别,选择普查还是抽样调查要根据所要考查的对象的特征灵活选用,一般来说,对于具有破坏性的调查、无法进行普查、普查的意义或价值不大,应选择抽样调查,对于精确度要求高的调查,事关重大的调查往往选用普查.
2.为加强交通安全教育,某校随机调查了九年级部分学生的上学方式(乘车、步行、骑车),并根据调查结果绘制了如图两幅不完整的统计图,下列判断错误的是( )
A.本次调查的总人数为60人 B.调查的学生中骑车上学的有8人
C.若该校九年级学生有1200人,则乘车上学的约有600人
D.扇形统计图中步行的学生人数所占的圆心角是122°
【答案】D
【点拨】根据乘车人数以及百分比求出总人数,据此可判断选项A;
用总人数分别减去其它两种上学方式的人数,即可得出骑车上学的人数,据此可得判断选项B;
用样本估计总体的思想解决问题,即可判断选项C;
根据圆心角=360°×百分比计算,即可判断选项D.
【解析】解:本次调查的总人数为:30÷50%=60(人),故选项A说法正确,不符合题意;
调查的学生中骑车上学的有:60﹣30﹣22=8(人),故选项B说法正确,不符合题意;
若该校九年级学生有1200人,则乘车上学的约有:1200×50%=6008(人),故选项C说法正确,不符合题意;
扇形统计图中步行的学生人数所占的圆心角是:360°×=132°,故选项D说法错误,符合题意.
故选:D.
【点睛】本题考查的是条形统计图和扇形统计图的综合运用.读懂统计图,从不同的统计图中得到必要的信息是解决问题的关键.条形统计图能清楚地表示出每个项目的数据;扇形统计图直接反映部分占总体的百分比大小.
3.下列说法中,正确的是( )
A.一组数据4,4,2,3,1的中位数是2
B.反映空气的主要成分(氮气约占78%,氧气约占21%,其他微量气体约占1%)宜采用折线统计图
C.甲、乙两人各10次射击的平均成绩相同,方差分别是s甲2=2.2,s乙2=1.3,则乙的射击成绩较稳定
D.对载人航天器零部件的检查适合采用抽样凋查
【答案】C
【点拨】选项A根据中位数的定义判断即可;选项B根据各种统计图的特点判断即可;选项C根据方差的意义判断即可;选项D根据全面调查和抽样调查的定义判断即可.
【解析】解:A.一组数据4,4,2,3,1的中位数是3,原说法错误,故本选项不符合题意;
B.反映空气的主要成分(氮气约占78%,氧气约占21%,其他微量气体约占1%)宜采用扇形统计图,原说法错误,故本选项不符合题意;
C.甲、乙两人各10次射击的平均成绩相同,方差分别是s甲2=2.2,s乙2=1.3,则乙的射击成绩较稳定,说法正确,故本选项符合题意;
D.对载人航天器零部件的检查适合采用全面调查,原说法错误,故本选项不符合题意.
故选:C.
【点睛】本题考查了全面调查和抽样调查,加权平均数,中位数以及方差,掌握相关定义是解答本题的关键.
4.已知一组数据x1,x2,x3,x4,x5的平均数是2,方差是3,那么另一组数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数和方差分别是( )
A.2,3 B.2,9 C.4,18 D.4,27
【答案】D
【点拨】利用平均数、方差的定义和性质直接求解.
【解析】解:∵数据x1,x2,x3,x4,x5的平均数是2,方差是3,
∴数据3x1﹣2,3x2﹣2,3x3﹣2,3x4﹣2,3x5﹣2的平均数为:3×2﹣2=4,方差为:32×3=27.
故选:D.
【点睛】本题主要考查方差和算术平均数,解题的关键是掌握若数据x1,x2,……,xn的平均数是,方差为s2,则新数据ax1+b,ax2+b,……,axn+b的平均数为a+b,方差为a2s2.
5.某店铺连续5天销售衬衣的件数分别为10,11,13,15,11.关于这组数据,以下结论错误的是( )
A.众数是11 B.平均数是12 C.方差是3.2 D.中位数是13
【答案】D
【点拨】根据众数、平均数、方差、中位数的计算方法分别求出结果再进行判断即可.
【解析】解:A、11出现了2次,出现的次数最多,则众数是11,故本选项不符合题意;
B、平均数是×(10+11+13+15+11)=12,
故本选项不符合题意;
C、方差是:×[(11﹣12)2+(10﹣12)2+(13﹣12)2+(15﹣12)2+(11﹣12)2]=3.2,故本选项不符合题意;
D、把这些数从小到大排列为:10,11,11,13,15,中位数是11,故本选项符合题意;
故选:D.
【点睛】本题考查中位数、众数、平均数、方差,掌握中位数、众数、平均数、方差的计算方法是解决问题的关键.
6.如图是描述某校篮球队员年龄的条形图,则这个篮球队员年龄的众数和中位数分别为( )
A.14,15 B.15,14 C.15,15 D.15,14.5
【答案】D
【点拨】根据中位数、众数的定义进行计算即可求解.
【解析】解:这20名篮球队员年龄出现次数最多的是15岁,共出现8次,因此众数是15岁;
将这20名篮球队员的年龄从小到大排列,处在中间位置的2个数是14岁和15岁,因此中位数是(岁).
故选:D.
【点睛】本题考查中位数、众数,掌握中位数、众数的计算方法是正确判断的关键.
7.某班35位同学课外阅读物的数量统计如表所示,其中有两个数据被遮盖,下列关于课外阅读物的统计量中,与被遮盖的数据无关的是( )
课外阅读物的数量 2 3 4 5 6 7 8
人数 ■ ■ 9 7 9 3 2
A.平均数,方差 B.中位数,方差 C.平均数,众数 D.中位数,众数
【答案】D
【点拨】通过计算课外阅读物的数量2、3分的人数之和,进行判断,不影响成绩出现次数最多的结果,因此不影响众数,同时不影响找第18位数据,因此不影响中位数的计算,进而进行选择.
【解析】解:由表格数据可知,课外阅读物的数量2、3分的人数之和为35﹣(9+7+9+3+2)=5(人),
课外阅读物的数量为4和6出现次数最多,因此课外阅读物的数量的众数是4和6,
成绩从小到大排列后处在第15位数都是5,因此中位数是5,
因此中位数和众数与被遮盖的数据无关,
故选:D.
【点睛】本题考查中位数、众数、方差、平均数的意义和计算方法,理解各个统计量的实际意义,以及每个统计量所反应数据的特征,是正确判断的前提.
8.已知5个正数a1,a2,a3,a4,a5的平均数是a,且a1>a2>a3>a4>a5,则数据a1,a2,a3,0,a4,a5的平均数和中位数是( )
A.a, B.a, C.a, D.a,
【答案】C
【点拨】对新数据按大小排列,然后根据平均数和中位数的定义计算即可.
【解析】解:由平均数定义可知:(a1+a2+a3+0+a4+a5)=×5a=a;
将这组数据按从小到大排列为0,a5,a4,a3,a2,a1;由于有偶数个数,取最中间两个数的平均数.
∴其中位数为.
故选:C.
【点睛】本题考查了平均数和中位数的定义.平均数是指在一组数据中所有数据之和再除以数据的个数;一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.
01 押浙江卷第1—5题
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
