04押浙江卷第11-14题(因式分解、平行线的性质、概率、圆与正多边形)-2024年浙江省中考数学题号押题(含解析)
文档属性
| 名称 | 04押浙江卷第11-14题(因式分解、平行线的性质、概率、圆与正多边形)-2024年浙江省中考数学题号押题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-18 15:06:53 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
押题方向1:因式分解
2023年浙江真题 考点 命题趋势
2023年温州、绍兴、金华、台州第11题 因式分解-提公因式 从近几年浙江各地中考来看,因式分解以填空题形式考查比较多,比较简单,主要考查提公因式法、运用公式法(平方差公式、完全平方公式)及因式分解的应用;预计2024年浙江卷必考因式分解。
2023年宁波、丽水卷第11题 因式分解-运用公式法
2023年舟山、嘉兴卷第12题 因式分解的应用
1.(2023 丽水)分解因式:x2﹣9= .
2.(2023 金华)因式分解:x2+x= .
3.(2023 浙江)一个多项式,把它因式分解后有一个因式为(x+1),请你写出一个符合条件的多项式: .
4.(2023 温州)分解因式:2a2﹣2a= .
5.(2023 绍兴)因式分解:m2﹣3m= .
因式分解步骤:
1)如果多项式各项有公因式,应先提取公因式;
2)如果各项没有公因式,可以尝试使用公式法:为两项时,考虑平方差公式;为三项时,考虑完全平方公式;
3)检查分解因式是否彻底,必须分解到每一个多项式都不能再分解为止。
1.因式分解: .
2.因式分解: .
3.分解因式: .
4.因式分解: .
5.分解因式的结果是 .
6.分解因式: .
7.已知实数,满足,则的值为 .
押题方向2:平行线的性质与判定
2023年浙江真题 考点 命题趋势
2023年金华卷第7题、杭州卷第12题、台州卷第13题 平行线的性质 从近几年浙江各地中考来看,有关平行线的判定与性质的试题经常出现在选择题或填空题中,题目比较简单;预计2024年浙江卷还将继续对平行线的判定与性质进行考查。
2022年台州卷第4题 平行线的判定
2022年杭州卷第3题 平行线的性质
1.(2023 金华)如图,已知∠1=∠2=∠3=50°,则∠4的度数是( )
A.120° B.125° C.130° D.135°
2.(2023 杭州)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= .
3.(2023 台州)用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 .
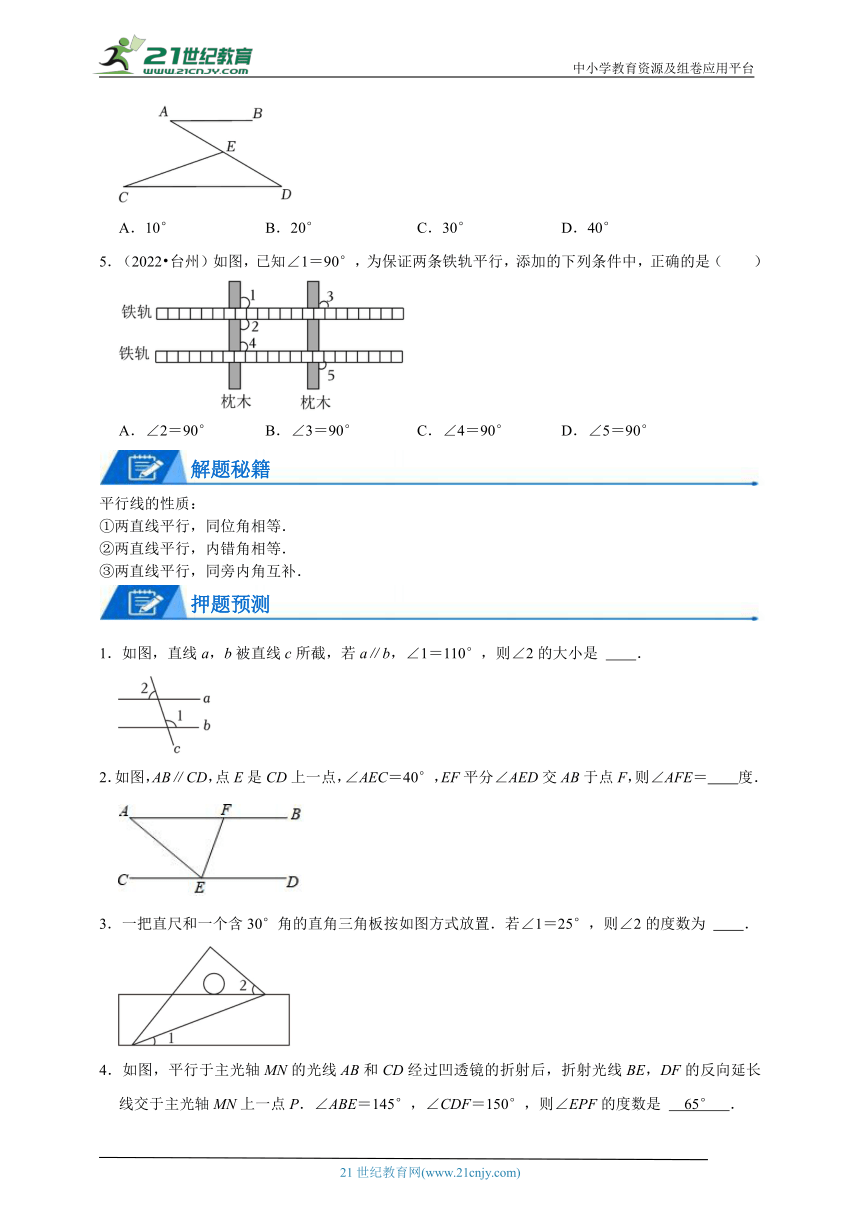
4.(2022 杭州)如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
5.(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
平行线的性质:
①两直线平行,同位角相等.
②两直线平行,内错角相等.
③两直线平行,同旁内角互补.
1.如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2的大小是 .
2.如图,AB∥CD,点E是CD上一点,∠AEC=40°,EF平分∠AED交AB于点F,则∠AFE= 度.
3.一把直尺和一个含30°角的直角三角板按如图方式放置.若∠1=25°,则∠2的度数为 .
4.如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.∠ABE=145°,∠CDF=150°,则∠EPF的度数是 65° .
5.如图,已知AB∥CD,直线EF分别与AB,CD相交于E,F两点,∠EFD的平分线交AB于点G.如果∠GEF=40°,则∠EGF等于 .
6.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于 .
押题方向3:概率
2023年浙江真题 考点 命题趋势
2023年湖州卷、衢州卷、台州卷第12题 随机事件的概率 从近几年浙江各地中考来看,随机事件的概率每年都有考查,难度较低。预计2024年浙江卷还将继续考查随机事件的概率、几何概型、用树状图或列表法求概率,为避免丢分,学生应扎实掌握。
2023年杭州卷、金华卷、舟山、嘉兴第13题 随机事件的概率
1.(2023 湖州)在一个不透明的箱子里放有7个红球和3个黑球,它们除颜色外其余都相同.从这个箱子里随机摸出一个球,摸出的球是红球的概率是 .
2.(2023 金华)如表为某中学统计的七年级500名学生体重达标情况(单位:人),在该年级随机抽取一名学生,该生体重“标准”的概率是 .
“偏瘦” “标准” “超重” “肥胖”
80 350 46 24
3.(2023 杭州)一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= .
4.(2023 衢州)衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都,如果他们可以选择其中任一航班,则他们选择同一航班的概率等于 .
5.(2023 台州)一个不透明的口袋中有5个除颜色外完全相同的小球,其中2个红球,3个白球.随机摸出一个小球,摸出红球的概率是 .
6.(2023 浙江)现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是 .
1.公式法:P(A)=,其中n为所有事件的总数,m为事件A发生的总次数。
2.列举法:
1)列表法:当一次试验要涉及两个因素,并且可能出现的结果数目较多时,应不重不漏地列出所有可能的结果,通常采用列表法求事件发生的概率。
2)画树状图法:当一次试验要涉及2个或更多的因素时,通常采用画树状图来求事件发生的概率。
1.一个不透明的袋里装有个白球,个黑球,个红球,它们除颜色外其余都相同.从袋中任意摸出一个球是黑球的概率为 .
2.五张分别印有“仁”、“义”、“礼”、“智”、“信”的卡片(除卡片上的字不同外,其余均相同),将它们洗匀后随机抽取两张,则恰好是“仁”和“义”的概率是 .
3.有四张正面分别标有数字,,0,2的卡片,它们除数字不同外其余全部相同.现将四张卡片背面朝上,洗匀后从中随机抽取两张,则抽取的两张卡片上的数字之积为负数的概率是 .
4.袋子里装有红、黄、白三种颜色的小球,除了颜色之外小球的形状、大小、材质完全相同,搅拌均匀后从袋中随机摸出一个球是红球的概率为,如果袋中红球有3个,则袋中的黄球和白球共有 个.
5.袋中装有个黑球和个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
6.今年春节电影《热辣滚烫》《飞驰人生2》《逆转时空》《第二十条》在网络上持续引发热议,根据国家电影局2月18日发布数据,我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录.甲、乙两位同学打算去观看这四部影片的其中一部,则这两位同学选择观看相同影片的概率为 .
7.已知二次函数的解析式为,从数字0,1,2中随机选取一个数作为的值,得到的二次函数图像的顶点在坐标轴上的概率是 .
8.紫色石蕊试剂遇到酸性液体变成红色,遇到碱性液体变成蓝色,现有3瓶无标记液体,其中有两瓶酸性液体、一瓶碱性液体,现取一滴紫色石蕊试剂随机滴入一瓶试剂中,液体变为红色的概率为 .
押题方向4:圆与正多边形
2023年浙江真题 考点 命题趋势
2023年宁波卷第14题 圆锥的计算 从近几年浙江中考来看,圆与正多边形主要考查圆的内接正多边形、垂径定理、切线的性质、弧长与扇形的面积的计算、圆锥的计算,试题以填空题形式呈现,整体难度中等;预计2024年浙江卷还将重视圆与正多边形、弧长与扇形的面积的相关计算、切线的性质的考查。
2023年湖州卷第13题 垂径定理
2023年绍兴卷第12题 圆内接四边形的性质
2023年温州卷第14题、金华卷第15题 弧长的计算
2023年杭州卷第14题 正多边形和圆
2023年温州卷、舟山嘉兴卷第16题 扇形面积的计算
2023年衢州卷、舟山嘉兴卷第14题 切线的性质
1.(2023 宁波)如图,圆锥形烟囱帽的底面半径为30cm,母线长为50cm,则烟囱帽的侧面积为 1500π cm2.(结果保留π)
2.(2023 温州)若扇形的圆心角为40°,半径为18,则它的弧长为 .
3.(2023 舟山、嘉兴)如图,点A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,点D在上.已知∠A=50°,则∠D的度数是 .
4.(2023 衢州)如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当餐盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于 cm.
5.(2023 金华)如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为 cm.
6.(2023 浙江)一副三角板ABC和DEF中,∠C=∠D=90°,∠B=30°,∠E=45°,BC=EF=12.将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 .现将△DEF绕点C(F)按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转0°到60°的过程中,线段DH扫过的面积是 .
7.(2023 杭州)如图,六边形ABCDEF是⊙O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= .
掌握圆的基本性质:垂径定理、圆周角定理、圆内接四边形的性质、切线的性质、弧长公式、扇形面积公式、圆锥的计算公式、正多边形的性质是解决这一类问题的关键。
1.如图,点A、B、C在半径为1的⊙O上,∠ACB=70°,则的长等于 .
2.如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
3.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为 .
4.若圆锥的侧面积为25π,底面半径为5,则该圆锥的母线长是 .
5.如图,在⊙O中,弦BC⊥半径OA于点D,连接OB.若OB=5cm,AD=2cm,则BC的长是 cm.
6.如图,⊙O的切线PA交半径OB的延长线于点P,A为切点.若∠P=30°,OB=2,则PB= .
7.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为 .
8.如图,过⊙O外一点P作圆的切线PA,PB,点A,B为切点,AC为直径,设∠P=m°,∠C=n°,则m,n的等量关系为 .
答案与解析
押题方向1:因式分解
2023年浙江真题 考点 命题趋势
2023年温州、绍兴、金华、台州第11题 因式分解-提公因式 从近几年浙江各地中考来看,因式分解以填空题形式考查比较多,比较简单,主要考查提公因式法、运用公式法(平方差公式、完全平方公式)及因式分解的应用;预计2024年浙江卷必考因式分解。
2023年宁波、丽水卷第11题 因式分解-运用公式法
2023年舟山、嘉兴卷第12题 因式分解的应用
1.(2023 丽水)分解因式:x2﹣9= (x+3)(x﹣3) .
【点拨】本题中两个平方项的符号相反,直接运用平方差公式分解因式.
【解析】解:x2﹣9=(x+3)(x﹣3).
故答案为:(x+3)(x﹣3).
【点睛】主要考查平方差公式分解因式,熟记能用平方差公式分解因式的多项式的特征,即“两项、异号、平方形式”是避免错用平方差公式的有效方法.
2.(2023 金华)因式分解:x2+x= x(x+1) .
【点拨】根据观察可知原式公因式为x,直接提取可得.
【解析】解:x2+x=x(x+1).
【点睛】本题考查了提公因式法分解因式,通过观察可直接得出公因式,直接观察法是解此类题目的常用的方法.
3.(2023 浙江)一个多项式,把它因式分解后有一个因式为(x+1),请你写出一个符合条件的多项式: x2﹣1(答案不唯一). .
【点拨】根据题意,可以写出分解因式中含有(x+1)的一个多项式,本题答案不唯一,符合题意即可.
【解析】解:∵x2﹣1=(x+1)(x﹣1),
∴符合条件的一个多项式是x2﹣1,
故答案为:x2﹣1(答案不唯一).
【点睛】本题考查因式分解的应用,解答本题的关键是明确题意,写出符合题意的一个多项式.
4.(2023 温州)分解因式:2a2﹣2a= 2a(a﹣1) .
【点拨】直接提取公因式2a,进而分解因式即可.
【解析】解:2a2﹣2a=2a(a﹣1).
故答案为:2a(a﹣1).
【点睛】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.
5.(2023 绍兴)因式分解:m2﹣3m= m(m﹣3) .
【点拨】直接提取公因式m,进而分解因式即可.
【解析】解:m2﹣3m=m(m﹣3).
故答案为:m(m﹣3).
【点睛】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.
因式分解步骤:
1)如果多项式各项有公因式,应先提取公因式;
2)如果各项没有公因式,可以尝试使用公式法:为两项时,考虑平方差公式;为三项时,考虑完全平方公式;
3)检查分解因式是否彻底,必须分解到每一个多项式都不能再分解为止。
1.因式分解: .
【点拨】本题考查了分解因式.根据式子的特点将公因数提取出来即可.
【解析】解:式子中含有公因数,
∴,
故答案为:.
【点睛】本题考查了提公因式法分解因式,通过观察可直接得出公因式,直接观察法是解此类题目的常用的方法.
2.因式分解: .
【点拨】此题主要考查了提取公因式法因式分解,直接提取公因式,即可求解.
【解析】解:,
故答案为:.
【点睛】本题考查了提公因式法分解因式,通过观察可直接得出公因式,直接观察法是解此类题目的常用的方法.
3.分解因式: .
【点拨】本题主要考查了分解因式,直接根据平方差公式分解因式即可.
【解析】解:,
故答案为:.
【点睛】主要考查平方差公式分解因式,熟记能用平方差公式分解因式的多项式的特征,即“两项、异号、平方形式”是避免错用平方差公式的有效方法.
4.因式分解: .
【点拨】本题主要考查了多项式的因式分解,熟练掌握多项式的因式分解方法是解题的关键.先提出公因式,再利用平方差公式进行因式分解,即可求解.
【解析】解:,
故答案为:.
【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
5.分解因式的结果是 .
【点拨】本题主要考查用公式法分解因式,掌握完全平方公式是解题的关键.利用完全平方公式分解因式即可.
【解析】解:,
故答案为:.
【点睛】此题主要考查了用完全平方公式分解因式,熟练应用乘法公式是解题关键.
6.分解因式:.
【点拨】本题考查因式分解.先提取公因式,然后利用完全平方公式进行因式分解即可.
【解析】解:,
故答案为:.
【点睛】此题主要考查了提取公因式法以及公式法分解因式,熟练应用乘法公式是解题关键.
7.已知实数,满足,则的值为 72 .
【点拨】本题考查了求代数式的值,将变形为,整体代入计算即可得出答案.
【解析】解:,
,
故答案为:.
【点睛】本题考查了因式分解的运用.
押题方向2:平行线的性质与判定
2023年浙江真题 考点 命题趋势
2023年金华卷第7题、杭州卷第12题、台州卷第13题 平行线的性质 从近几年浙江各地中考来看,有关平行线的判定与性质的试题经常出现在选择题或填空题中,题目比较简单;预计2024年浙江卷还将继续对平行线的判定与性质进行考查。
2022年台州卷第4题 平行线的判定
2022年杭州卷第3题 平行线的性质
1.(2023 金华)如图,已知∠1=∠2=∠3=50°,则∠4的度数是( )
A.120° B.125° C.130° D.135°
【点拨】由同位角相等两直线平行得到a与b平行,再由两直线平行同旁内角互补,求出∠5的度数,根据对顶角相等即可求出∠4的度数.
【解析】解:∵∠1=∠3=50°,
∴a∥b,
∴∠5+∠2=180°,
∵∠2=50°,
∴∠5=130°,
∴∠4=∠5=130°.
故选:C.
【点睛】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
2.(2023 杭州)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= 90° .
【点拨】由平行线的性质得到∠B=∠ADE=28°,由三角形外角的性质得到∠A=∠ACF﹣∠B=118°﹣28°=90°.
【解析】解:∵DE∥BC,
∴∠B=∠ADE=28°,
∵∠ACF=∠A+∠B,
∴∠A=∠ACF﹣∠B=118°﹣28°=90°.
故答案为:90°.
【点睛】本题考查平行线的性质,三角形外角的性质,关键是由平行线的性质求出∠B的度数,由三角形外角的性质即可求出∠A的度数.
3.(2023 台州)用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 140° .
【点拨】利用平行线的性质和各角之间的关系即可求解.
【解析】解:如图,标注三角形的三个顶点A、B、C.
∠2=∠BAC=180°﹣∠ABC﹣∠ACB.
∵图案是由一张等宽的纸条折成的,
∴AB=AC,
∴∠ABC=∠ACB.
又∵纸条的长边平行,
∴∠ABC=∠1=20°,
∴∠2=∠BAC=180°﹣2∠ABC=180°﹣2∠1=180°﹣2×20°=140°.
故答案为:140°.
【点睛】本题比较简单,主要考查了平行线的性质的运用.
4.(2022 杭州)如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
【点拨】由∠AEC为△CED的外角,利用外角性质求出∠D的度数,再利用两直线平行内错角相等即可求出∠A的度数.
【解析】解:∵∠AEC为△CED的外角,且∠C=20°,∠AEC=50°,
∴∠AEC=∠C+∠D,即50°=20°+∠D,
∴∠D=30°,
∵AB∥CD,
∴∠A=∠D=30°.
故选:C.
【点睛】此题考查了平行线的性质,以及外角性质,熟练掌握平行线的性质是解本题的关键.
5.(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
【点拨】根据平行线的判定逐项分析即可得到结论.
【解析】解:A.由∠2=90°不能判定两条铁轨平行,故该选项不符合题意;
B.由∠3=90°=∠1,可判定两枕木平行,故该选项不符合题意;
C.∵∠1=90°,∠4=90°,
∴∠1=∠4,
∴两条铁轨平行,故该选项符合题意;
D.由∠5=90°不能判定两条铁轨平行,故该选项不符合题意;
故选:C.
【点睛】本题主要考查了平行线的判定,熟练掌握平行线的判定方法是解决问题的关键.
平行线的性质:
①两直线平行,同位角相等.
②两直线平行,内错角相等.
③两直线平行,同旁内角互补.
1.如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2的大小是 70° .
【点拨】根据对顶角相等求出∠3的度数,根据平行线的性质得到答案.
【解析】解:∵a∥b,
∴∠1=∠3=110°,∠2+∠3=180°,
∴∠2=180°﹣∠3=70°,
故答案为:70°.
【点睛】本题考查的是平行线的性质和对顶角的性质,掌握两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补是解题的关键.
2.如图,AB∥CD,点E是CD上一点,∠AEC=40°,EF平分∠AED交AB于点F,则∠AFE= 70 度.
【点拨】由平角求出∠AED的度数,由角平分线得出∠DEF的度数,再由平行线的性质即可求出∠AFE的度数.
【解析】解:∵∠AEC=40°,
∴∠AED=180°﹣∠AEC=140°,
∵EF平分∠AED,
∴∠DEF=∠AED=70°,
又∵AB∥CD,
∴∠AFE=∠DEF=70°.
故答案为:70
【点睛】本题考查的是平行线的性质以及角平分线的定义.熟练掌握平行线的性质,求出∠DEF的度数是解决问题的关键.
3.一把直尺和一个含30°角的直角三角板按如图方式放置.若∠1=25°,则∠2的度数为 35° .
【点拨】由平行线的性质推出∠ABC=∠1=25°,即可求出∠2=60°﹣25°=35°.
【解析】解:∵AB∥CD,
∴∠ABC=∠1=25°,
∴∠2=60°﹣25°=35°.
故答案为:35°.
【点睛】本题考查平行线的性质,关键是由平行线的性质推出∠ABC=∠1.
4.如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.∠ABE=145°,∠CDF=150°,则∠EPF的度数是 65° .
【点拨】由平角得∠ABP=30°,∠CDP=20°,由平行线性质得∠BPN=∠ABP=30°,∠NPD=∠CDP=20°,故∠EPF=∠EPN+∠NPF=50°.
【解析】解:∵∠ABE=145°,
∴∠ABP=35°,
∵∠CDF=150°,
∴∠CDP=30°,
∵AB∥MN∥CD,
∴∠BPN=∠ABP=35°,∠NPD=∠CDP=30°,
∴∠EPF=∠EPN+∠NPF=65°,
故答案为:65°.
【点睛】本题考查了平行线的性质,会利用平行线性质是解题关键.
5.如图,已知AB∥CD,直线EF分别与AB,CD相交于E,F两点,∠EFD的平分线交AB于点G.如果∠GEF=40°,则∠EGF等于 70° .
【点拨】根据平行线的性质推出∠EGF=∠DFG,求出∠EFD=140°,由角平分线的定义求出∠DFG=70°,即可求出∠EGF.
【解析】解:∵AB∥CD,
∴∠EFD+∠GEF=180°,∠EGF=∠DFG,
∵∠GEF=40°,
∴∠EFD=180°﹣∠GEF=180°﹣40°=140°,
∵FG平分∠EFD,
∴∠EFG=∠DFG=∠EFD=×140°=70°,
∴∠EGF=70°,
故答案为:70°.
【点睛】本题考查了平行线的性质,角平分线的定义,掌握平行线的性质:两直线平行,同旁内角互补是解题的关键.
6.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于 65° .
【点拨】由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠BEF的度数,又由EG平分∠BEF,根据角平分线的定义,即可求得∠BEG的度数,又由两直线平行,内错角相等,即可求得∠2的度数.
【解析】解:∵AB∥CD,
∴∠1+∠BEF=180°,
∵∠1=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠BEG=∠BEF=65°,
∴∠2=∠BEG=65°,
故答案为:65°.
【点睛】此题考查了平行线的性质与角平分线的定义.解题的关键是掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理以及数形结合思想的应用.
押题方向3:概率
2023年浙江真题 考点 命题趋势
2023年湖州卷、衢州卷、台州卷第12题 随机事件的概率 从近几年浙江各地中考来看,随机事件的概率每年都有考查,难度较低。预计2024年浙江卷还将继续考查随机事件的概率、几何概型、用树状图或列表法求概率,为避免丢分,学生应扎实掌握。
2023年杭州卷、金华卷、舟山、嘉兴第13题 随机事件的概率
1.(2023 湖州)在一个不透明的箱子里放有7个红球和3个黑球,它们除颜色外其余都相同.从这个箱子里随机摸出一个球,摸出的球是红球的概率是 .
【点拨】直接由概率公式求解即可.
【解析】解:从这个箱子里随机摸出一个球,摸出的球是红球的概率是=,
故答案为:.
【点睛】本题考查了概率公式:概率=所求情况数与总情况数之比.熟记概率公式是解题的关键.
2.(2023 金华)如表为某中学统计的七年级500名学生体重达标情况(单位:人),在该年级随机抽取一名学生,该生体重“标准”的概率是 .
“偏瘦” “标准” “超重” “肥胖”
80 350 46 24
【点拨】根据概率公式计算即可.
【解析】解:七年级共有500名学生,体重“标准”的学生有350名,
∴.
故答案为:.
【点睛】本题主要考查了概率的计算.某事件的概率=这个事件发生的结果数除以总的结果数.
3.(2023 杭州)一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= 9 .
【点拨】根据红球的概率公式,列出方程求解即可.
【解析】解:根据题意,=,
解得n=9,
经检验n=9是方程的解.
∴n=9.
故答案为:9.
【点睛】本题考查概率公式,根据公式列出方程求解则可.用到的知识点为:概率=所求情况数与总情况数之比.
4.(2023 衢州)衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都,如果他们可以选择其中任一航班,则他们选择同一航班的概率等于 .
【点拨】根据概率公式即可得到结论.
【解析】解:如图所示,
选择航班从衢州飞往成都共有4种情况:(A,A)(A,B)(B,A)(B,B),其中选择同一航班从衢州市飞往成都市的有两种情况:
(A,A),(B,B).
∴P(选择同一航班从N市飞往S市)=.
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
5.(2023 台州)一个不透明的口袋中有5个除颜色外完全相同的小球,其中2个红球,3个白球.随机摸出一个小球,摸出红球的概率是 .
【点拨】利用红球的个数÷球的总个数可得红球的概率.
【解析】解:∵一个口袋里有5个除颜色外完全相同的小球,其中2个红球,3个白球,
∴摸到红球的概率是.
故答案为:.
【点睛】此题主要考查了概率公式,关键是掌握概率=所求情况数与总情况数之比.
6.(2023 浙江)现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是 .
【点拨】直接根据概率公式求解即可.
【解析】解:从这三张卡片中随机挑选一张,是“琮琮”的概率是,
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
1.公式法:P(A)=,其中n为所有事件的总数,m为事件A发生的总次数。
2.列举法:
1)列表法:当一次试验要涉及两个因素,并且可能出现的结果数目较多时,应不重不漏地列出所有可能的结果,通常采用列表法求事件发生的概率。
2)画树状图法:当一次试验要涉及2个或更多的因素时,通常采用画树状图来求事件发生的概率。
1.一个不透明的袋里装有个白球,个黑球,个红球,它们除颜色外其余都相同.从袋中任意摸出一个球是黑球的概率为 .
【点拨】本题考查了概率,根据概率公式直接计算即可求解,掌握概率公式是解题的关键.
【解析】解:∵一个不透明的袋里装有个白球,个黑球,个红球,
∴从袋中任意摸出一个球是黑球的概率为,
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
2.五张分别印有“仁”、“义”、“礼”、“智”、“信”的卡片(除卡片上的字不同外,其余均相同),将它们洗匀后随机抽取两张,则恰好是“仁”和“义”的概率是 .
【点拨】本题考查了用树状图或列表法求概率,先画出树状图,再利用概率公式即可求解,根据题意画出树状图是解题的关键.
【解析】解:用A、B、C、D、E分别表示“仁”、“义”、“礼”、“智”、“信”的卡片,
画树状图如图:
共有20种等可能事件,其中抽到恰好是“仁”和“义”的有2种情况,
恰好是“仁”和“义”的概率是,
故答案为:.
【点睛】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
3.有四张正面分别标有数字,,0,2的卡片,它们除数字不同外其余全部相同.现将四张卡片背面朝上,洗匀后从中随机抽取两张,则抽取的两张卡片上的数字之积为负数的概率是 .
【点拨】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
列表可得出所有等可能的结果数以及抽取的两张卡片上的数字之积为负数的结果数,再利用概率公式可得出答案.
【解析】解:列表如下:
0 2
0
2
共有12种等可能的结果,其中抽取的两张卡片上的数字之积为负数的结果有:,,,,共4种,
抽取的两张卡片上的数字之积为负数的概率是.
故答案为:.
【点睛】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
4.袋子里装有红、黄、白三种颜色的小球,除了颜色之外小球的形状、大小、材质完全相同,搅拌均匀后从袋中随机摸出一个球是红球的概率为,如果袋中红球有3个,则袋中的黄球和白球共有 个.
【点拨】本题考查的是已知概率求数量,设袋中的黄球和白球共有个,再建立方程求解即可.
【解析】解:设袋中的黄球和白球共有个,则
,
解得;,经检验符合题意;
∴袋中的黄球和白球共有个;
故答案为:
【点睛】本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
5.袋中装有个黑球和个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
【点拨】此题考查了概率公式的应用,注意用到的知识点为:概率=所求情况数与总情况数之比.
用黑球的个数除以球的总个数等于0.75列出关于n的方程,解之即可.
【解析】解:根据题意知 ,
解得,
经检验,是该分式方程的解,
∴这个袋中白球大约有3个,
故答案为:3.
【点睛】本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
6.今年春节电影《热辣滚烫》《飞驰人生2》《逆转时空》《第二十条》在网络上持续引发热议,根据国家电影局2月18日发布数据,我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录.甲、乙两位同学打算去观看这四部影片的其中一部,则这两位同学选择观看相同影片的概率为 .
【点拨】本题考查了用列表或画树状图法求概率和概率公式.画树状图,共有16种等可能的结果,甲、乙两人选择同一部电影的结果有4种,再利用概率公式进行计算即可.
【解析】解:A表示《热辣滚烫》、B表示《飞驰人生2》、C表示《逆转时空》、D表示《第二十条》,
画树状图如下:
共由16种等可能的结果,其中,甲、乙两人选择同一部电影的结果有4种,
甲、乙两人选择观看相同影片的概率为:.
故答案为:.
【点睛】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
7.已知二次函数的解析式为,从数字0,1,2中随机选取一个数作为的值,得到的二次函数图像的顶点在坐标轴上的概率是 .
【点拨】本题主要考查了二次函数的图像与性质,简单概率计算等知识,熟练掌握相关知识是解题关键.首先确定当、和时二次函数的顶点坐标,然后根据简单概率计算公式求解即可.
【解析】解:当时,该二次函数的解析式为,其顶点坐标为,在轴上;
当时,该二次函数的解析式为,其顶点坐标为,不在坐标轴上;
当时,该二次函数的解析式为,其顶点坐标为,在轴上.
综上可知,从数字0,1,2中随机选取一个数作为的值,得到的二次函数图像的顶点在坐标轴上的是0,2,
所以,得到的二次函数图像的顶点在坐标轴上的概率.
故答案为:.
【点睛】本题考查概率公式,解答本题的关键是明确题意,求出相应的概率.
8.紫色石蕊试剂遇到酸性液体变成红色,遇到碱性液体变成蓝色,现有3瓶无标记液体,其中有两瓶酸性液体、一瓶碱性液体,现取一滴紫色石蕊试剂随机滴入一瓶试剂中,液体变为红色的概率为 .
【点拨】此题考查了概率的知识,解题的关键是熟练掌握概率的求解方法.
【解析】解:取一滴紫色石蕊试剂随机滴入一瓶试剂中共有3种等可能情况,
其中滴入酸性液体有2种可能情况,即液体变为红色有2种,
∴液体变为红色的概率为,
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
押题方向4:圆与正多边形
2023年浙江真题 考点 命题趋势
2023年宁波卷第14题 圆锥的计算 从近几年浙江中考来看,圆与正多边形主要考查圆的内接正多边形、垂径定理、切线的性质、弧长与扇形的面积的计算、圆锥的计算,试题以填空题形式呈现,整体难度中等;预计2024年浙江卷还将重视圆与正多边形、弧长与扇形的面积的相关计算、切线的性质的考查。
2023年湖州卷第13题 垂径定理
2023年绍兴卷第12题 圆内接四边形的性质
2023年温州卷第14题、金华卷第15题 弧长的计算
2023年杭州卷第14题 正多边形和圆
2023年温州卷、舟山嘉兴卷第16题 扇形面积的计算
2023年衢州卷、舟山嘉兴卷第14题 切线的性质
1.(2023 宁波)如图,圆锥形烟囱帽的底面半径为30cm,母线长为50cm,则烟囱帽的侧面积为 1500π cm2.(结果保留π)
【点拨】根据扇形面积公式计算即可.
【解析】解:烟囱帽的侧面积为:×2π×30×50=1500π(cm2),
故答案为:1500π.
【点睛】本题考查的是圆锥的计算,熟记圆锥的侧面展开图是扇形以及扇形面积公式是解题的关键.
2.(2023 温州)若扇形的圆心角为40°,半径为18,则它的弧长为 4π .
【点拨】根据弧长公式计算即可.
【解析】解:由弧长公式得,
故答案为:4π.
【点睛】本题考查了弧长的计算,熟记弧长的公式,即(l表示弧长,n是弧所对圆心角的度数,r表示半径).
3.(2023 舟山、嘉兴)如图,点A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,点D在上.已知∠A=50°,则∠D的度数是 65° .
【点拨】连接OC,OB,根据切线的性质得到∠ACO=∠ABO=90°,求得∠COB=360°﹣∠A﹣∠ACO﹣∠ABO=130°,根据圆周角定理即可得到结论.
【解析】解:连接OC,OB,
∵AB,AC分别与⊙O相切于点B,C,
∴∠ACO=∠ABO=90°,
∵∠A=50°,
∴∠COB=360°﹣∠A﹣∠ACO﹣∠ABO=130°,
∴∠D=,
故答案为:65°.
【点睛】本题考查了切线的性质,圆周角定理,正确地作出辅助线是解题的关键.
4.(2023 衢州)如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当餐盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于 10 cm.
【点拨】连接OA,过点O作OE⊥BC,交BC于点E,交AD于点F,则点E为餐盘与BC边的切点,由矩形的性质得AD=BC=16cm,AD∥BC,∠BCD=∠ADC=90°,则四边形CDFE是矩形,OE⊥AD,得CD=EF=4cm,∠AFO=90°,AF=DF=8cm,设餐盘的半径为x cm,则OA=OE=x cm,OF=(x﹣4)cm,然后由勾股定理列出方程,解方程即可.
【解析】解:由题意得:BC=16cm,CD=4cm,
如图,连接OA,过点O作OE⊥BC,交BC于点E,交AD于点F,
则∠OEC=90°,
∵餐盘与BC边相切,
∴点E为切点,
∵四边形ABCD是矩形,
∴AD=BC=16cm,AD∥BC,∠BCD=∠ADC=90°,
∴四边形CDFE是矩形,OE⊥AD,
∴CD=EF=4cm,∠AFO=90°,AF=DF=AD=×16=8(cm),
设餐盘的半径为x cm,
则OA=OE=x cm,
∴OF=OE﹣EF=(x﹣4)cm,
在Rt△AFO中,由勾股定理得:AF2+OF2=OA2,
即82+(x﹣4)2=x2,
解得:x=10,
∴餐盘的半径为10cm,
故答案为:10.
【点睛】本题考查了切线的性质、矩形的判定与性质、勾股定理等知识,熟练掌握勾股定理是解题的关键.
5.(2023 金华)如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为 π cm.
【点拨】连接OE,OD,由等腰三角形的性质推出∠C=∠ODB,得到OD∥AC,推出∠EOD=∠AEO,由OE=OA,∠OEA=∠BAC=50°,因此∠∠EOD=∠BAC=50°,由弧长公式即可求出的长.
【解析】解:连接OE,OD,
∵OD=OB,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠EOD=∠AEO,
∵OE=OA,
∴∠OEA=∠BAC=50°,
∴∠EOD=∠BAC=50°,
∵OD=AB=×6=3(cm),
∴的长==π(cm).
故答案为:π.
【点睛】本题考查弧长的计算,等腰三角形的性质,平行线的性质,关键是由等腰三角形的性质推出OD∥AC,从而求出∠EOD的度数.
6.(2023 浙江)一副三角板ABC和DEF中,∠C=∠D=90°,∠B=30°,∠E=45°,BC=EF=12.将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 6﹣6 .现将△DEF绕点C(F)按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转0°到60°的过程中,线段DH扫过的面积是 18+12π﹣18 .
【点拨】如图1,过点G作GK⊥BC于K,则∠CKG=∠BKG=90°,由等腰直角三角形性质可得CK=GK=CG,进而得出BK=BC﹣CK=12﹣CG,利用解直角三角形可得BK=GK,建立方程求解即可得出答案;如图2,以C为圆心,CD为半径作圆,当△CDE绕点C旋转60°时,CE′交AB于H′,连接DD′,过点D作DM⊥AB于M,过点C作CN⊥DD′于N,则∠BCE′=∠DCD′=60°,点D的运动轨迹为,点H的运动轨迹为线段BH′,因此在旋转0°到60°的过程中,线段DH扫过的面积为S△BDD′+S扇形CDD′﹣S△CDD′,再利用等腰直角三角形性质、相似三角形的判定和性质、扇形面积公式即可求得答案.
【解析】解:如图1,过点G作GK⊥BC于K,则∠CKG=∠BKG=90°,
∵∠BCD=45°,
∴△CGK是等腰直角三角形,
∴CK=GK=CG,
∵BC=12,
∴BK=BC﹣CK=12﹣CG,
在Rt△BGK中,∠GBK=30°,
∴=tan∠GBK=tan30°=,
∴BK=GK,
即12﹣CG=×CG,
∴CG=6﹣6;
如图2,以C为圆心,CD为半径作圆,当△CDE绕点C旋转60°时,CE′交AB于H′,连接DD′,过点D作DM⊥AB于M,过点C作CN⊥DD′于N,
则∠BCE′=∠DCD′=60°,点D的运动轨迹为,点H的运动轨迹为线段BH′,
∴在旋转0°到60°的过程中,线段DH扫过的面积为S△BDD′+S扇形CDD′﹣S△CDD′,
∵CD=BC cosCBD=12cos45°=6,
∴DG=CD﹣CG=6﹣(6﹣6)=12﹣6,
∵∠BCD+∠ABC=60°+30°=90°,
∴∠BH′C=90°,
在Rt△BCH′中,CH′=BC sin30°=12×=6,BH′=BC cos30°=12×=6,
∵△CD′E′是等腰直角三角形,∠CD′E′=90°,D′H′⊥CE′,
∴D′H′=CE′=6,
∴BD′=6+6,
∵DM⊥AB,
∴∠DMG=90°,
∴∠DMG=∠CH′G,
∵∠DGM=∠CGH′,
∴△DGM∽△CGH′,
∴=,即=,
∴DM=3﹣3,
∵CD′=CD=6,∠DCD′=60°,
∴△CDD′是等边三角形,
∴∠CDD′=60°,
∵CN⊥DD′,
∴CN=CD sin∠CDD′=6sin60°=3,
∴S△BDD′+S扇形CDD′﹣S△CDD′=×(6+6)×(3﹣3)+﹣×6×3=18+12π﹣18;
故答案为:6﹣6;18+12π﹣18.
【点睛】本题是三角形综合题,考查了直角三角形性质,等腰直角三角形性质,等边三角形的判定和性质,解直角三角形,相似三角形的判定和性质等,得出DH扫过的面积为S△BDD′+S扇形CDD′﹣S△CDD′是解题关键.
7.(2023 杭州)如图,六边形ABCDEF是⊙O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= 2 .
【点拨】连接OA,OC,OE,首先证明出△ACE 是⊙O的内接正三角形,然后证明出△BAC≌△OAC(ASA),得到 S△ABC=S△AEE=S△CDE S△AOC=S△OAE=S△OCE,进而求解即可.
【解析】解:如图所示,连接OA,OC,OE.
∵六边形ABCDEF是⊙O的内接正六边形,
∴AC=AE=CE,
∴△ACE是⊙O的内接正三角形,
∵∠B=120°,AB=BC,
∴∠BAC=∠BCA=(180°﹣∠B)=30°,
∵∠CAE=60°,
∴∠OAC=∠OAE=30°,
∴∠BAC=∠OAC=30°,
同理可得,∠BCA=∠OCA=30°,
又∵AC=AC,
∴△BAC≌△OAC(ASA),
∴S△BAC=S△AOC,
圆和正六边形的性质可得,S△BAC=S△AFE=S△CDE,
由圆和正三角形的性质可得,S△OAC=S△OAE=S△OCE,
∵S1=S△BAC+S△AEF+S△CDE+S△OAC+S△OAE+S△OCE=2(S△OAC+S△OAE+S△OCE)=2S2,
∴,
故答案为:2
【点睛】此题考查了圆内接正多边形的性质,正六边形和正三角形的性质,全等三角形的性质和判定等知 识,解题的关键是熟练掌握以上知识点.
掌握圆的基本性质:垂径定理、圆周角定理、圆内接四边形的性质、切线的性质、弧长公式、扇形面积公式、圆锥的计算公式、正多边形的性质是解决这一类问题的关键。
1.如图,点A、B、C在半径为1的⊙O上,∠ACB=70°,则的长等于 .
【点拨】根据圆周角定理求出∠AOB,再根据弧长公式计算,得到答案.
【解析】解:∵∠ACB=70°,
∴∠AOB=2∠ACB=140°,
∴的长为:=,
故答案为:.
【点睛】本题考查的是弧长计算、圆周角定理,熟记弧长公式是解题的关键.
2.如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
【点拨】根据莱洛三角形的周长,可求出等边△ABC的边长,进而可求出莱洛三角形的面积.
【解析】解:由题知,
莱洛三角形的周长可转化为半径长为AB的圆周长的一半.
又因为莱洛三角形的周长为2π,
所以,
则AB=2,
所以等边△ABC的边长为2.
过点A作BC的垂线,垂足为M,
则BM=.
在Rt△ABM中,
AM=.
所以莱洛三角形的面积为:.
故答案为:.
【点睛】本题考查扇形面积的计算,能根据所给莱洛三角形的周长得出等边三角形的边长是解题的关键.
3.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为 12π .
【点拨】先确定扇形的圆心角的度数,然后利用扇形的面积公式计算即可.
【解析】解:∵正六边形的外角和为360°,
∴每一个外角的度数为360°÷6=60°,
∴正六边形的每个内角为180°﹣60°=120°,
∵正六边形的边长为6,
∴S阴影==12π,
故答案为:12π.
【点睛】考查了正多边形和圆及扇形的面积的计算的知识,解题的关键是求得正六边形的内角的度数并牢记扇形的面积计算公式,难度不大.
4.若圆锥的侧面积为25π,底面半径为5,则该圆锥的母线长是 5 .
【点拨】根据圆锥的侧面积=πrl,列出方程求解即可.
【解析】解:∵圆锥的侧面积为25π,底面半径为5,
∴5πl=25π.
解得:l=5,
故答案为:5.
【点睛】本题考查了圆锥的侧面积,解题关键是熟记圆锥的侧面积公式,列出方程进行求解.
5.如图,在⊙O中,弦BC⊥半径OA于点D,连接OB.若OB=5cm,AD=2cm,则BC的长是 8 cm.
【点拨】由垂径定理得BC=2BD,在Rt△OBD中可由勾股定理求出BD=4cm,由此可得BC的长.
【解析】解:∵弦BC⊥半径OA于点D,
∴BD=CD,
∴BC=2BD,
∵OB=OA=5cm,AD=2cm,
∴OD=OA﹣AD=5﹣2=3(cm),
在Rt△OBD中,OB=5cm,OD=3cm,
由勾股定理得:BD==4(cm),
∴BC=2BD=8(cm).
故答案为:8.
【点睛】此题主要考查了垂径定理,勾股定理,熟练掌握垂径定理及勾股定理是解决问题的关键.
6.如图,⊙O的切线PA交半径OB的延长线于点P,A为切点.若∠P=30°,OB=2,则PB= 2 .
【点拨】根据切线的性质得到∠OAP=90°,再利用含30度角的直角三角形三边的关系得到OP=4,然后计算OP﹣OB即可.
【解析】解:∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵∠P=30°,
∴OP=2OA=4,
∴PB=OP﹣OB=4﹣2=2.
故答案为:2.
【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.
7.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为 3 .
【点拨】过A作AM⊥OB于M,求得∠AOB=360°÷12=30°,根据直角三角形的性质得到AM=OA=,根据三角形的面积公式得到S△AOB=,于是得到正十二边形的面积为12×=3,根据圆的面积公式即可得到结论.
【解析】解:如图,AB是正十二边形的一条边,点O是正十二边形的中心,
过A作AM⊥OB于M,
在正十二边形中,∠AOB=360°÷12=30°,
∴AM=OA=,
∴S△AOB=OB AM=×=,
∴正十二边形的面积为12×=3,
∴3=12×π,
∴π=3,
∴π的近似值为3,
故答案为:3.
【点睛】本题考查了正多边形与圆,三角形的面积的计算,正确地作出辅助线是解题的关键.
8.如图,过⊙O外一点P作圆的切线PA,PB,点A,B为切点,AC为直径,设∠P=m°,∠C=n°,则m,n的等量关系为 m+2n=180° .
【点拨】连接OB,由切线的性质得到∠PAO=∠PBO=90°,由四边形内角和为360°得到∠P+∠AOB=180°,根据圆内角定理得到∠AOB=2∠C,代入上式即可得到结论.
【解析】解:连接OB,
∵PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
∵∠PAO+∠PBO+∠P+∠AOB=360°,
∴∠P+∠AOB=180°,
∵∠AOB=2∠C,
∴∠P+2∠C=180°,
∴m+2n=180°.
故答案为:m+2n=180°.
【点睛】本题主要考查了切线的性质,四边形内角和为360°,圆内角定理,熟练掌握相关知识是解决问题的关键.
04 押浙江卷第11—14题
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
押题方向1:因式分解
2023年浙江真题 考点 命题趋势
2023年温州、绍兴、金华、台州第11题 因式分解-提公因式 从近几年浙江各地中考来看,因式分解以填空题形式考查比较多,比较简单,主要考查提公因式法、运用公式法(平方差公式、完全平方公式)及因式分解的应用;预计2024年浙江卷必考因式分解。
2023年宁波、丽水卷第11题 因式分解-运用公式法
2023年舟山、嘉兴卷第12题 因式分解的应用
1.(2023 丽水)分解因式:x2﹣9= .
2.(2023 金华)因式分解:x2+x= .
3.(2023 浙江)一个多项式,把它因式分解后有一个因式为(x+1),请你写出一个符合条件的多项式: .
4.(2023 温州)分解因式:2a2﹣2a= .
5.(2023 绍兴)因式分解:m2﹣3m= .
因式分解步骤:
1)如果多项式各项有公因式,应先提取公因式;
2)如果各项没有公因式,可以尝试使用公式法:为两项时,考虑平方差公式;为三项时,考虑完全平方公式;
3)检查分解因式是否彻底,必须分解到每一个多项式都不能再分解为止。
1.因式分解: .
2.因式分解: .
3.分解因式: .
4.因式分解: .
5.分解因式的结果是 .
6.分解因式: .
7.已知实数,满足,则的值为 .
押题方向2:平行线的性质与判定
2023年浙江真题 考点 命题趋势
2023年金华卷第7题、杭州卷第12题、台州卷第13题 平行线的性质 从近几年浙江各地中考来看,有关平行线的判定与性质的试题经常出现在选择题或填空题中,题目比较简单;预计2024年浙江卷还将继续对平行线的判定与性质进行考查。
2022年台州卷第4题 平行线的判定
2022年杭州卷第3题 平行线的性质
1.(2023 金华)如图,已知∠1=∠2=∠3=50°,则∠4的度数是( )
A.120° B.125° C.130° D.135°
2.(2023 杭州)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= .
3.(2023 台州)用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 .
4.(2022 杭州)如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
5.(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
平行线的性质:
①两直线平行,同位角相等.
②两直线平行,内错角相等.
③两直线平行,同旁内角互补.
1.如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2的大小是 .
2.如图,AB∥CD,点E是CD上一点,∠AEC=40°,EF平分∠AED交AB于点F,则∠AFE= 度.
3.一把直尺和一个含30°角的直角三角板按如图方式放置.若∠1=25°,则∠2的度数为 .
4.如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.∠ABE=145°,∠CDF=150°,则∠EPF的度数是 65° .
5.如图,已知AB∥CD,直线EF分别与AB,CD相交于E,F两点,∠EFD的平分线交AB于点G.如果∠GEF=40°,则∠EGF等于 .
6.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于 .
押题方向3:概率
2023年浙江真题 考点 命题趋势
2023年湖州卷、衢州卷、台州卷第12题 随机事件的概率 从近几年浙江各地中考来看,随机事件的概率每年都有考查,难度较低。预计2024年浙江卷还将继续考查随机事件的概率、几何概型、用树状图或列表法求概率,为避免丢分,学生应扎实掌握。
2023年杭州卷、金华卷、舟山、嘉兴第13题 随机事件的概率
1.(2023 湖州)在一个不透明的箱子里放有7个红球和3个黑球,它们除颜色外其余都相同.从这个箱子里随机摸出一个球,摸出的球是红球的概率是 .
2.(2023 金华)如表为某中学统计的七年级500名学生体重达标情况(单位:人),在该年级随机抽取一名学生,该生体重“标准”的概率是 .
“偏瘦” “标准” “超重” “肥胖”
80 350 46 24
3.(2023 杭州)一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= .
4.(2023 衢州)衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都,如果他们可以选择其中任一航班,则他们选择同一航班的概率等于 .
5.(2023 台州)一个不透明的口袋中有5个除颜色外完全相同的小球,其中2个红球,3个白球.随机摸出一个小球,摸出红球的概率是 .
6.(2023 浙江)现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是 .
1.公式法:P(A)=,其中n为所有事件的总数,m为事件A发生的总次数。
2.列举法:
1)列表法:当一次试验要涉及两个因素,并且可能出现的结果数目较多时,应不重不漏地列出所有可能的结果,通常采用列表法求事件发生的概率。
2)画树状图法:当一次试验要涉及2个或更多的因素时,通常采用画树状图来求事件发生的概率。
1.一个不透明的袋里装有个白球,个黑球,个红球,它们除颜色外其余都相同.从袋中任意摸出一个球是黑球的概率为 .
2.五张分别印有“仁”、“义”、“礼”、“智”、“信”的卡片(除卡片上的字不同外,其余均相同),将它们洗匀后随机抽取两张,则恰好是“仁”和“义”的概率是 .
3.有四张正面分别标有数字,,0,2的卡片,它们除数字不同外其余全部相同.现将四张卡片背面朝上,洗匀后从中随机抽取两张,则抽取的两张卡片上的数字之积为负数的概率是 .
4.袋子里装有红、黄、白三种颜色的小球,除了颜色之外小球的形状、大小、材质完全相同,搅拌均匀后从袋中随机摸出一个球是红球的概率为,如果袋中红球有3个,则袋中的黄球和白球共有 个.
5.袋中装有个黑球和个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
6.今年春节电影《热辣滚烫》《飞驰人生2》《逆转时空》《第二十条》在网络上持续引发热议,根据国家电影局2月18日发布数据,我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录.甲、乙两位同学打算去观看这四部影片的其中一部,则这两位同学选择观看相同影片的概率为 .
7.已知二次函数的解析式为,从数字0,1,2中随机选取一个数作为的值,得到的二次函数图像的顶点在坐标轴上的概率是 .
8.紫色石蕊试剂遇到酸性液体变成红色,遇到碱性液体变成蓝色,现有3瓶无标记液体,其中有两瓶酸性液体、一瓶碱性液体,现取一滴紫色石蕊试剂随机滴入一瓶试剂中,液体变为红色的概率为 .
押题方向4:圆与正多边形
2023年浙江真题 考点 命题趋势
2023年宁波卷第14题 圆锥的计算 从近几年浙江中考来看,圆与正多边形主要考查圆的内接正多边形、垂径定理、切线的性质、弧长与扇形的面积的计算、圆锥的计算,试题以填空题形式呈现,整体难度中等;预计2024年浙江卷还将重视圆与正多边形、弧长与扇形的面积的相关计算、切线的性质的考查。
2023年湖州卷第13题 垂径定理
2023年绍兴卷第12题 圆内接四边形的性质
2023年温州卷第14题、金华卷第15题 弧长的计算
2023年杭州卷第14题 正多边形和圆
2023年温州卷、舟山嘉兴卷第16题 扇形面积的计算
2023年衢州卷、舟山嘉兴卷第14题 切线的性质
1.(2023 宁波)如图,圆锥形烟囱帽的底面半径为30cm,母线长为50cm,则烟囱帽的侧面积为 1500π cm2.(结果保留π)
2.(2023 温州)若扇形的圆心角为40°,半径为18,则它的弧长为 .
3.(2023 舟山、嘉兴)如图,点A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,点D在上.已知∠A=50°,则∠D的度数是 .
4.(2023 衢州)如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当餐盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于 cm.
5.(2023 金华)如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为 cm.
6.(2023 浙江)一副三角板ABC和DEF中,∠C=∠D=90°,∠B=30°,∠E=45°,BC=EF=12.将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 .现将△DEF绕点C(F)按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转0°到60°的过程中,线段DH扫过的面积是 .
7.(2023 杭州)如图,六边形ABCDEF是⊙O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= .
掌握圆的基本性质:垂径定理、圆周角定理、圆内接四边形的性质、切线的性质、弧长公式、扇形面积公式、圆锥的计算公式、正多边形的性质是解决这一类问题的关键。
1.如图,点A、B、C在半径为1的⊙O上,∠ACB=70°,则的长等于 .
2.如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
3.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为 .
4.若圆锥的侧面积为25π,底面半径为5,则该圆锥的母线长是 .
5.如图,在⊙O中,弦BC⊥半径OA于点D,连接OB.若OB=5cm,AD=2cm,则BC的长是 cm.
6.如图,⊙O的切线PA交半径OB的延长线于点P,A为切点.若∠P=30°,OB=2,则PB= .
7.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为 .
8.如图,过⊙O外一点P作圆的切线PA,PB,点A,B为切点,AC为直径,设∠P=m°,∠C=n°,则m,n的等量关系为 .
答案与解析
押题方向1:因式分解
2023年浙江真题 考点 命题趋势
2023年温州、绍兴、金华、台州第11题 因式分解-提公因式 从近几年浙江各地中考来看,因式分解以填空题形式考查比较多,比较简单,主要考查提公因式法、运用公式法(平方差公式、完全平方公式)及因式分解的应用;预计2024年浙江卷必考因式分解。
2023年宁波、丽水卷第11题 因式分解-运用公式法
2023年舟山、嘉兴卷第12题 因式分解的应用
1.(2023 丽水)分解因式:x2﹣9= (x+3)(x﹣3) .
【点拨】本题中两个平方项的符号相反,直接运用平方差公式分解因式.
【解析】解:x2﹣9=(x+3)(x﹣3).
故答案为:(x+3)(x﹣3).
【点睛】主要考查平方差公式分解因式,熟记能用平方差公式分解因式的多项式的特征,即“两项、异号、平方形式”是避免错用平方差公式的有效方法.
2.(2023 金华)因式分解:x2+x= x(x+1) .
【点拨】根据观察可知原式公因式为x,直接提取可得.
【解析】解:x2+x=x(x+1).
【点睛】本题考查了提公因式法分解因式,通过观察可直接得出公因式,直接观察法是解此类题目的常用的方法.
3.(2023 浙江)一个多项式,把它因式分解后有一个因式为(x+1),请你写出一个符合条件的多项式: x2﹣1(答案不唯一). .
【点拨】根据题意,可以写出分解因式中含有(x+1)的一个多项式,本题答案不唯一,符合题意即可.
【解析】解:∵x2﹣1=(x+1)(x﹣1),
∴符合条件的一个多项式是x2﹣1,
故答案为:x2﹣1(答案不唯一).
【点睛】本题考查因式分解的应用,解答本题的关键是明确题意,写出符合题意的一个多项式.
4.(2023 温州)分解因式:2a2﹣2a= 2a(a﹣1) .
【点拨】直接提取公因式2a,进而分解因式即可.
【解析】解:2a2﹣2a=2a(a﹣1).
故答案为:2a(a﹣1).
【点睛】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.
5.(2023 绍兴)因式分解:m2﹣3m= m(m﹣3) .
【点拨】直接提取公因式m,进而分解因式即可.
【解析】解:m2﹣3m=m(m﹣3).
故答案为:m(m﹣3).
【点睛】此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.
因式分解步骤:
1)如果多项式各项有公因式,应先提取公因式;
2)如果各项没有公因式,可以尝试使用公式法:为两项时,考虑平方差公式;为三项时,考虑完全平方公式;
3)检查分解因式是否彻底,必须分解到每一个多项式都不能再分解为止。
1.因式分解: .
【点拨】本题考查了分解因式.根据式子的特点将公因数提取出来即可.
【解析】解:式子中含有公因数,
∴,
故答案为:.
【点睛】本题考查了提公因式法分解因式,通过观察可直接得出公因式,直接观察法是解此类题目的常用的方法.
2.因式分解: .
【点拨】此题主要考查了提取公因式法因式分解,直接提取公因式,即可求解.
【解析】解:,
故答案为:.
【点睛】本题考查了提公因式法分解因式,通过观察可直接得出公因式,直接观察法是解此类题目的常用的方法.
3.分解因式: .
【点拨】本题主要考查了分解因式,直接根据平方差公式分解因式即可.
【解析】解:,
故答案为:.
【点睛】主要考查平方差公式分解因式,熟记能用平方差公式分解因式的多项式的特征,即“两项、异号、平方形式”是避免错用平方差公式的有效方法.
4.因式分解: .
【点拨】本题主要考查了多项式的因式分解,熟练掌握多项式的因式分解方法是解题的关键.先提出公因式,再利用平方差公式进行因式分解,即可求解.
【解析】解:,
故答案为:.
【点睛】本题考查了用提公因式法和公式法进行因式分解,一个多项式有公因式首先提取公因式,然后再用其他方法进行因式分解,同时因式分解要彻底,直到不能分解为止.
5.分解因式的结果是 .
【点拨】本题主要考查用公式法分解因式,掌握完全平方公式是解题的关键.利用完全平方公式分解因式即可.
【解析】解:,
故答案为:.
【点睛】此题主要考查了用完全平方公式分解因式,熟练应用乘法公式是解题关键.
6.分解因式:.
【点拨】本题考查因式分解.先提取公因式,然后利用完全平方公式进行因式分解即可.
【解析】解:,
故答案为:.
【点睛】此题主要考查了提取公因式法以及公式法分解因式,熟练应用乘法公式是解题关键.
7.已知实数,满足,则的值为 72 .
【点拨】本题考查了求代数式的值,将变形为,整体代入计算即可得出答案.
【解析】解:,
,
故答案为:.
【点睛】本题考查了因式分解的运用.
押题方向2:平行线的性质与判定
2023年浙江真题 考点 命题趋势
2023年金华卷第7题、杭州卷第12题、台州卷第13题 平行线的性质 从近几年浙江各地中考来看,有关平行线的判定与性质的试题经常出现在选择题或填空题中,题目比较简单;预计2024年浙江卷还将继续对平行线的判定与性质进行考查。
2022年台州卷第4题 平行线的判定
2022年杭州卷第3题 平行线的性质
1.(2023 金华)如图,已知∠1=∠2=∠3=50°,则∠4的度数是( )
A.120° B.125° C.130° D.135°
【点拨】由同位角相等两直线平行得到a与b平行,再由两直线平行同旁内角互补,求出∠5的度数,根据对顶角相等即可求出∠4的度数.
【解析】解:∵∠1=∠3=50°,
∴a∥b,
∴∠5+∠2=180°,
∵∠2=50°,
∴∠5=130°,
∴∠4=∠5=130°.
故选:C.
【点睛】此题考查了平行线的判定与性质,熟练掌握平行线的判定与性质是解本题的关键.
2.(2023 杭州)如图,点D,E分别在△ABC的边AB,AC上,且DE∥BC,点F在线段BC的延长线上.若∠ADE=28°,∠ACF=118°,则∠A= 90° .
【点拨】由平行线的性质得到∠B=∠ADE=28°,由三角形外角的性质得到∠A=∠ACF﹣∠B=118°﹣28°=90°.
【解析】解:∵DE∥BC,
∴∠B=∠ADE=28°,
∵∠ACF=∠A+∠B,
∴∠A=∠ACF﹣∠B=118°﹣28°=90°.
故答案为:90°.
【点睛】本题考查平行线的性质,三角形外角的性质,关键是由平行线的性质求出∠B的度数,由三角形外角的性质即可求出∠A的度数.
3.(2023 台州)用一张等宽的纸条折成如图所示的图案,若∠1=20°,则∠2的度数为 140° .
【点拨】利用平行线的性质和各角之间的关系即可求解.
【解析】解:如图,标注三角形的三个顶点A、B、C.
∠2=∠BAC=180°﹣∠ABC﹣∠ACB.
∵图案是由一张等宽的纸条折成的,
∴AB=AC,
∴∠ABC=∠ACB.
又∵纸条的长边平行,
∴∠ABC=∠1=20°,
∴∠2=∠BAC=180°﹣2∠ABC=180°﹣2∠1=180°﹣2×20°=140°.
故答案为:140°.
【点睛】本题比较简单,主要考查了平行线的性质的运用.
4.(2022 杭州)如图,已知AB∥CD,点E在线段AD上(不与点A,点D重合),连接CE.若∠C=20°,∠AEC=50°,则∠A=( )
A.10° B.20° C.30° D.40°
【点拨】由∠AEC为△CED的外角,利用外角性质求出∠D的度数,再利用两直线平行内错角相等即可求出∠A的度数.
【解析】解:∵∠AEC为△CED的外角,且∠C=20°,∠AEC=50°,
∴∠AEC=∠C+∠D,即50°=20°+∠D,
∴∠D=30°,
∵AB∥CD,
∴∠A=∠D=30°.
故选:C.
【点睛】此题考查了平行线的性质,以及外角性质,熟练掌握平行线的性质是解本题的关键.
5.(2022 台州)如图,已知∠1=90°,为保证两条铁轨平行,添加的下列条件中,正确的是( )
A.∠2=90° B.∠3=90° C.∠4=90° D.∠5=90°
【点拨】根据平行线的判定逐项分析即可得到结论.
【解析】解:A.由∠2=90°不能判定两条铁轨平行,故该选项不符合题意;
B.由∠3=90°=∠1,可判定两枕木平行,故该选项不符合题意;
C.∵∠1=90°,∠4=90°,
∴∠1=∠4,
∴两条铁轨平行,故该选项符合题意;
D.由∠5=90°不能判定两条铁轨平行,故该选项不符合题意;
故选:C.
【点睛】本题主要考查了平行线的判定,熟练掌握平行线的判定方法是解决问题的关键.
平行线的性质:
①两直线平行,同位角相等.
②两直线平行,内错角相等.
③两直线平行,同旁内角互补.
1.如图,直线a,b被直线c所截,若a∥b,∠1=110°,则∠2的大小是 70° .
【点拨】根据对顶角相等求出∠3的度数,根据平行线的性质得到答案.
【解析】解:∵a∥b,
∴∠1=∠3=110°,∠2+∠3=180°,
∴∠2=180°﹣∠3=70°,
故答案为:70°.
【点睛】本题考查的是平行线的性质和对顶角的性质,掌握两直线平行,同位角相等,两直线平行,内错角相等,两直线平行,同旁内角互补是解题的关键.
2.如图,AB∥CD,点E是CD上一点,∠AEC=40°,EF平分∠AED交AB于点F,则∠AFE= 70 度.
【点拨】由平角求出∠AED的度数,由角平分线得出∠DEF的度数,再由平行线的性质即可求出∠AFE的度数.
【解析】解:∵∠AEC=40°,
∴∠AED=180°﹣∠AEC=140°,
∵EF平分∠AED,
∴∠DEF=∠AED=70°,
又∵AB∥CD,
∴∠AFE=∠DEF=70°.
故答案为:70
【点睛】本题考查的是平行线的性质以及角平分线的定义.熟练掌握平行线的性质,求出∠DEF的度数是解决问题的关键.
3.一把直尺和一个含30°角的直角三角板按如图方式放置.若∠1=25°,则∠2的度数为 35° .
【点拨】由平行线的性质推出∠ABC=∠1=25°,即可求出∠2=60°﹣25°=35°.
【解析】解:∵AB∥CD,
∴∠ABC=∠1=25°,
∴∠2=60°﹣25°=35°.
故答案为:35°.
【点睛】本题考查平行线的性质,关键是由平行线的性质推出∠ABC=∠1.
4.如图,平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.∠ABE=145°,∠CDF=150°,则∠EPF的度数是 65° .
【点拨】由平角得∠ABP=30°,∠CDP=20°,由平行线性质得∠BPN=∠ABP=30°,∠NPD=∠CDP=20°,故∠EPF=∠EPN+∠NPF=50°.
【解析】解:∵∠ABE=145°,
∴∠ABP=35°,
∵∠CDF=150°,
∴∠CDP=30°,
∵AB∥MN∥CD,
∴∠BPN=∠ABP=35°,∠NPD=∠CDP=30°,
∴∠EPF=∠EPN+∠NPF=65°,
故答案为:65°.
【点睛】本题考查了平行线的性质,会利用平行线性质是解题关键.
5.如图,已知AB∥CD,直线EF分别与AB,CD相交于E,F两点,∠EFD的平分线交AB于点G.如果∠GEF=40°,则∠EGF等于 70° .
【点拨】根据平行线的性质推出∠EGF=∠DFG,求出∠EFD=140°,由角平分线的定义求出∠DFG=70°,即可求出∠EGF.
【解析】解:∵AB∥CD,
∴∠EFD+∠GEF=180°,∠EGF=∠DFG,
∵∠GEF=40°,
∴∠EFD=180°﹣∠GEF=180°﹣40°=140°,
∵FG平分∠EFD,
∴∠EFG=∠DFG=∠EFD=×140°=70°,
∴∠EGF=70°,
故答案为:70°.
【点睛】本题考查了平行线的性质,角平分线的定义,掌握平行线的性质:两直线平行,同旁内角互补是解题的关键.
6.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2等于 65° .
【点拨】由AB∥CD,根据两直线平行,同旁内角互补,即可求得∠BEF的度数,又由EG平分∠BEF,根据角平分线的定义,即可求得∠BEG的度数,又由两直线平行,内错角相等,即可求得∠2的度数.
【解析】解:∵AB∥CD,
∴∠1+∠BEF=180°,
∵∠1=50°,
∴∠BEF=130°,
∵EG平分∠BEF,
∴∠BEG=∠BEF=65°,
∴∠2=∠BEG=65°,
故答案为:65°.
【点睛】此题考查了平行线的性质与角平分线的定义.解题的关键是掌握两直线平行,同旁内角互补与两直线平行,内错角相等定理以及数形结合思想的应用.
押题方向3:概率
2023年浙江真题 考点 命题趋势
2023年湖州卷、衢州卷、台州卷第12题 随机事件的概率 从近几年浙江各地中考来看,随机事件的概率每年都有考查,难度较低。预计2024年浙江卷还将继续考查随机事件的概率、几何概型、用树状图或列表法求概率,为避免丢分,学生应扎实掌握。
2023年杭州卷、金华卷、舟山、嘉兴第13题 随机事件的概率
1.(2023 湖州)在一个不透明的箱子里放有7个红球和3个黑球,它们除颜色外其余都相同.从这个箱子里随机摸出一个球,摸出的球是红球的概率是 .
【点拨】直接由概率公式求解即可.
【解析】解:从这个箱子里随机摸出一个球,摸出的球是红球的概率是=,
故答案为:.
【点睛】本题考查了概率公式:概率=所求情况数与总情况数之比.熟记概率公式是解题的关键.
2.(2023 金华)如表为某中学统计的七年级500名学生体重达标情况(单位:人),在该年级随机抽取一名学生,该生体重“标准”的概率是 .
“偏瘦” “标准” “超重” “肥胖”
80 350 46 24
【点拨】根据概率公式计算即可.
【解析】解:七年级共有500名学生,体重“标准”的学生有350名,
∴.
故答案为:.
【点睛】本题主要考查了概率的计算.某事件的概率=这个事件发生的结果数除以总的结果数.
3.(2023 杭州)一个仅装有球的不透明布袋里只有6个红球和n个白球(仅有颜色不同).若从中任意摸出一个球是红球的概率为,则n= 9 .
【点拨】根据红球的概率公式,列出方程求解即可.
【解析】解:根据题意,=,
解得n=9,
经检验n=9是方程的解.
∴n=9.
故答案为:9.
【点睛】本题考查概率公式,根据公式列出方程求解则可.用到的知识点为:概率=所求情况数与总情况数之比.
4.(2023 衢州)衢州飞往成都每天有2趟航班.小赵和小黄同一天从衢州飞往成都,如果他们可以选择其中任一航班,则他们选择同一航班的概率等于 .
【点拨】根据概率公式即可得到结论.
【解析】解:如图所示,
选择航班从衢州飞往成都共有4种情况:(A,A)(A,B)(B,A)(B,B),其中选择同一航班从衢州市飞往成都市的有两种情况:
(A,A),(B,B).
∴P(选择同一航班从N市飞往S市)=.
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
5.(2023 台州)一个不透明的口袋中有5个除颜色外完全相同的小球,其中2个红球,3个白球.随机摸出一个小球,摸出红球的概率是 .
【点拨】利用红球的个数÷球的总个数可得红球的概率.
【解析】解:∵一个口袋里有5个除颜色外完全相同的小球,其中2个红球,3个白球,
∴摸到红球的概率是.
故答案为:.
【点睛】此题主要考查了概率公式,关键是掌握概率=所求情况数与总情况数之比.
6.(2023 浙江)现有三张正面印有2023年杭州亚运会吉祥物琮琮、宸宸和莲莲的不透明卡片,卡片除正面图案不同外,其余均相同.将三张卡片正面向下洗匀,从中随机抽取一张卡片,则抽出的卡片图案是琮琮的概率是 .
【点拨】直接根据概率公式求解即可.
【解析】解:从这三张卡片中随机挑选一张,是“琮琮”的概率是,
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
1.公式法:P(A)=,其中n为所有事件的总数,m为事件A发生的总次数。
2.列举法:
1)列表法:当一次试验要涉及两个因素,并且可能出现的结果数目较多时,应不重不漏地列出所有可能的结果,通常采用列表法求事件发生的概率。
2)画树状图法:当一次试验要涉及2个或更多的因素时,通常采用画树状图来求事件发生的概率。
1.一个不透明的袋里装有个白球,个黑球,个红球,它们除颜色外其余都相同.从袋中任意摸出一个球是黑球的概率为 .
【点拨】本题考查了概率,根据概率公式直接计算即可求解,掌握概率公式是解题的关键.
【解析】解:∵一个不透明的袋里装有个白球,个黑球,个红球,
∴从袋中任意摸出一个球是黑球的概率为,
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
2.五张分别印有“仁”、“义”、“礼”、“智”、“信”的卡片(除卡片上的字不同外,其余均相同),将它们洗匀后随机抽取两张,则恰好是“仁”和“义”的概率是 .
【点拨】本题考查了用树状图或列表法求概率,先画出树状图,再利用概率公式即可求解,根据题意画出树状图是解题的关键.
【解析】解:用A、B、C、D、E分别表示“仁”、“义”、“礼”、“智”、“信”的卡片,
画树状图如图:
共有20种等可能事件,其中抽到恰好是“仁”和“义”的有2种情况,
恰好是“仁”和“义”的概率是,
故答案为:.
【点睛】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
3.有四张正面分别标有数字,,0,2的卡片,它们除数字不同外其余全部相同.现将四张卡片背面朝上,洗匀后从中随机抽取两张,则抽取的两张卡片上的数字之积为负数的概率是 .
【点拨】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
列表可得出所有等可能的结果数以及抽取的两张卡片上的数字之积为负数的结果数,再利用概率公式可得出答案.
【解析】解:列表如下:
0 2
0
2
共有12种等可能的结果,其中抽取的两张卡片上的数字之积为负数的结果有:,,,,共4种,
抽取的两张卡片上的数字之积为负数的概率是.
故答案为:.
【点睛】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
4.袋子里装有红、黄、白三种颜色的小球,除了颜色之外小球的形状、大小、材质完全相同,搅拌均匀后从袋中随机摸出一个球是红球的概率为,如果袋中红球有3个,则袋中的黄球和白球共有 个.
【点拨】本题考查的是已知概率求数量,设袋中的黄球和白球共有个,再建立方程求解即可.
【解析】解:设袋中的黄球和白球共有个,则
,
解得;,经检验符合题意;
∴袋中的黄球和白球共有个;
故答案为:
【点睛】本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
5.袋中装有个黑球和个白球,经过若干次试验,发现“若从袋中任摸出一个球,恰是黑球的概率为”,则这个袋中白球大约有 个.
【点拨】此题考查了概率公式的应用,注意用到的知识点为:概率=所求情况数与总情况数之比.
用黑球的个数除以球的总个数等于0.75列出关于n的方程,解之即可.
【解析】解:根据题意知 ,
解得,
经检验,是该分式方程的解,
∴这个袋中白球大约有3个,
故答案为:3.
【点睛】本题主要考查概率公式,解题的关键是掌握随机事件A的概率P(A)=事件A可能出现的结果数÷所有可能出现的结果数.
6.今年春节电影《热辣滚烫》《飞驰人生2》《逆转时空》《第二十条》在网络上持续引发热议,根据国家电影局2月18日发布数据,我国2024年春节档电影票房达80.16亿元,创造了新的春节档票房纪录.甲、乙两位同学打算去观看这四部影片的其中一部,则这两位同学选择观看相同影片的概率为 .
【点拨】本题考查了用列表或画树状图法求概率和概率公式.画树状图,共有16种等可能的结果,甲、乙两人选择同一部电影的结果有4种,再利用概率公式进行计算即可.
【解析】解:A表示《热辣滚烫》、B表示《飞驰人生2》、C表示《逆转时空》、D表示《第二十条》,
画树状图如下:
共由16种等可能的结果,其中,甲、乙两人选择同一部电影的结果有4种,
甲、乙两人选择观看相同影片的概率为:.
故答案为:.
【点睛】本题考查列表法与树状图法,熟练掌握列表法与树状图法以及概率公式是解答本题的关键.
7.已知二次函数的解析式为,从数字0,1,2中随机选取一个数作为的值,得到的二次函数图像的顶点在坐标轴上的概率是 .
【点拨】本题主要考查了二次函数的图像与性质,简单概率计算等知识,熟练掌握相关知识是解题关键.首先确定当、和时二次函数的顶点坐标,然后根据简单概率计算公式求解即可.
【解析】解:当时,该二次函数的解析式为,其顶点坐标为,在轴上;
当时,该二次函数的解析式为,其顶点坐标为,不在坐标轴上;
当时,该二次函数的解析式为,其顶点坐标为,在轴上.
综上可知,从数字0,1,2中随机选取一个数作为的值,得到的二次函数图像的顶点在坐标轴上的是0,2,
所以,得到的二次函数图像的顶点在坐标轴上的概率.
故答案为:.
【点睛】本题考查概率公式,解答本题的关键是明确题意,求出相应的概率.
8.紫色石蕊试剂遇到酸性液体变成红色,遇到碱性液体变成蓝色,现有3瓶无标记液体,其中有两瓶酸性液体、一瓶碱性液体,现取一滴紫色石蕊试剂随机滴入一瓶试剂中,液体变为红色的概率为 .
【点拨】此题考查了概率的知识,解题的关键是熟练掌握概率的求解方法.
【解析】解:取一滴紫色石蕊试剂随机滴入一瓶试剂中共有3种等可能情况,
其中滴入酸性液体有2种可能情况,即液体变为红色有2种,
∴液体变为红色的概率为,
故答案为:.
【点睛】本题考查了概率公式,熟练掌握概率公式是解题的关键.
押题方向4:圆与正多边形
2023年浙江真题 考点 命题趋势
2023年宁波卷第14题 圆锥的计算 从近几年浙江中考来看,圆与正多边形主要考查圆的内接正多边形、垂径定理、切线的性质、弧长与扇形的面积的计算、圆锥的计算,试题以填空题形式呈现,整体难度中等;预计2024年浙江卷还将重视圆与正多边形、弧长与扇形的面积的相关计算、切线的性质的考查。
2023年湖州卷第13题 垂径定理
2023年绍兴卷第12题 圆内接四边形的性质
2023年温州卷第14题、金华卷第15题 弧长的计算
2023年杭州卷第14题 正多边形和圆
2023年温州卷、舟山嘉兴卷第16题 扇形面积的计算
2023年衢州卷、舟山嘉兴卷第14题 切线的性质
1.(2023 宁波)如图,圆锥形烟囱帽的底面半径为30cm,母线长为50cm,则烟囱帽的侧面积为 1500π cm2.(结果保留π)
【点拨】根据扇形面积公式计算即可.
【解析】解:烟囱帽的侧面积为:×2π×30×50=1500π(cm2),
故答案为:1500π.
【点睛】本题考查的是圆锥的计算,熟记圆锥的侧面展开图是扇形以及扇形面积公式是解题的关键.
2.(2023 温州)若扇形的圆心角为40°,半径为18,则它的弧长为 4π .
【点拨】根据弧长公式计算即可.
【解析】解:由弧长公式得,
故答案为:4π.
【点睛】本题考查了弧长的计算,熟记弧长的公式,即(l表示弧长,n是弧所对圆心角的度数,r表示半径).
3.(2023 舟山、嘉兴)如图,点A是⊙O外一点,AB,AC分别与⊙O相切于点B,C,点D在上.已知∠A=50°,则∠D的度数是 65° .
【点拨】连接OC,OB,根据切线的性质得到∠ACO=∠ABO=90°,求得∠COB=360°﹣∠A﹣∠ACO﹣∠ABO=130°,根据圆周角定理即可得到结论.
【解析】解:连接OC,OB,
∵AB,AC分别与⊙O相切于点B,C,
∴∠ACO=∠ABO=90°,
∵∠A=50°,
∴∠COB=360°﹣∠A﹣∠ACO﹣∠ABO=130°,
∴∠D=,
故答案为:65°.
【点睛】本题考查了切线的性质,圆周角定理,正确地作出辅助线是解题的关键.
4.(2023 衢州)如图是一个圆形餐盘的正面及其固定支架的截面图,凹槽ABCD是矩形.当餐盘正立且紧靠支架于点A,D时,恰好与BC边相切,则此餐盘的半径等于 10 cm.
【点拨】连接OA,过点O作OE⊥BC,交BC于点E,交AD于点F,则点E为餐盘与BC边的切点,由矩形的性质得AD=BC=16cm,AD∥BC,∠BCD=∠ADC=90°,则四边形CDFE是矩形,OE⊥AD,得CD=EF=4cm,∠AFO=90°,AF=DF=8cm,设餐盘的半径为x cm,则OA=OE=x cm,OF=(x﹣4)cm,然后由勾股定理列出方程,解方程即可.
【解析】解:由题意得:BC=16cm,CD=4cm,
如图,连接OA,过点O作OE⊥BC,交BC于点E,交AD于点F,
则∠OEC=90°,
∵餐盘与BC边相切,
∴点E为切点,
∵四边形ABCD是矩形,
∴AD=BC=16cm,AD∥BC,∠BCD=∠ADC=90°,
∴四边形CDFE是矩形,OE⊥AD,
∴CD=EF=4cm,∠AFO=90°,AF=DF=AD=×16=8(cm),
设餐盘的半径为x cm,
则OA=OE=x cm,
∴OF=OE﹣EF=(x﹣4)cm,
在Rt△AFO中,由勾股定理得:AF2+OF2=OA2,
即82+(x﹣4)2=x2,
解得:x=10,
∴餐盘的半径为10cm,
故答案为:10.
【点睛】本题考查了切线的性质、矩形的判定与性质、勾股定理等知识,熟练掌握勾股定理是解题的关键.
5.(2023 金华)如图,在△ABC中,AB=AC=6cm,∠BAC=50°,以AB为直径作半圆,交BC于点D,交AC于点E,则弧DE的长为 π cm.
【点拨】连接OE,OD,由等腰三角形的性质推出∠C=∠ODB,得到OD∥AC,推出∠EOD=∠AEO,由OE=OA,∠OEA=∠BAC=50°,因此∠∠EOD=∠BAC=50°,由弧长公式即可求出的长.
【解析】解:连接OE,OD,
∵OD=OB,
∴∠B=∠ODB,
∵AB=AC,
∴∠B=∠C,
∴∠C=∠ODB,
∴OD∥AC,
∴∠EOD=∠AEO,
∵OE=OA,
∴∠OEA=∠BAC=50°,
∴∠EOD=∠BAC=50°,
∵OD=AB=×6=3(cm),
∴的长==π(cm).
故答案为:π.
【点睛】本题考查弧长的计算,等腰三角形的性质,平行线的性质,关键是由等腰三角形的性质推出OD∥AC,从而求出∠EOD的度数.
6.(2023 浙江)一副三角板ABC和DEF中,∠C=∠D=90°,∠B=30°,∠E=45°,BC=EF=12.将它们叠合在一起,边BC与EF重合,CD与AB相交于点G(如图1),此时线段CG的长是 6﹣6 .现将△DEF绕点C(F)按顺时针方向旋转(如图2),边EF与AB相交于点H,连结DH,在旋转0°到60°的过程中,线段DH扫过的面积是 18+12π﹣18 .
【点拨】如图1,过点G作GK⊥BC于K,则∠CKG=∠BKG=90°,由等腰直角三角形性质可得CK=GK=CG,进而得出BK=BC﹣CK=12﹣CG,利用解直角三角形可得BK=GK,建立方程求解即可得出答案;如图2,以C为圆心,CD为半径作圆,当△CDE绕点C旋转60°时,CE′交AB于H′,连接DD′,过点D作DM⊥AB于M,过点C作CN⊥DD′于N,则∠BCE′=∠DCD′=60°,点D的运动轨迹为,点H的运动轨迹为线段BH′,因此在旋转0°到60°的过程中,线段DH扫过的面积为S△BDD′+S扇形CDD′﹣S△CDD′,再利用等腰直角三角形性质、相似三角形的判定和性质、扇形面积公式即可求得答案.
【解析】解:如图1,过点G作GK⊥BC于K,则∠CKG=∠BKG=90°,
∵∠BCD=45°,
∴△CGK是等腰直角三角形,
∴CK=GK=CG,
∵BC=12,
∴BK=BC﹣CK=12﹣CG,
在Rt△BGK中,∠GBK=30°,
∴=tan∠GBK=tan30°=,
∴BK=GK,
即12﹣CG=×CG,
∴CG=6﹣6;
如图2,以C为圆心,CD为半径作圆,当△CDE绕点C旋转60°时,CE′交AB于H′,连接DD′,过点D作DM⊥AB于M,过点C作CN⊥DD′于N,
则∠BCE′=∠DCD′=60°,点D的运动轨迹为,点H的运动轨迹为线段BH′,
∴在旋转0°到60°的过程中,线段DH扫过的面积为S△BDD′+S扇形CDD′﹣S△CDD′,
∵CD=BC cosCBD=12cos45°=6,
∴DG=CD﹣CG=6﹣(6﹣6)=12﹣6,
∵∠BCD+∠ABC=60°+30°=90°,
∴∠BH′C=90°,
在Rt△BCH′中,CH′=BC sin30°=12×=6,BH′=BC cos30°=12×=6,
∵△CD′E′是等腰直角三角形,∠CD′E′=90°,D′H′⊥CE′,
∴D′H′=CE′=6,
∴BD′=6+6,
∵DM⊥AB,
∴∠DMG=90°,
∴∠DMG=∠CH′G,
∵∠DGM=∠CGH′,
∴△DGM∽△CGH′,
∴=,即=,
∴DM=3﹣3,
∵CD′=CD=6,∠DCD′=60°,
∴△CDD′是等边三角形,
∴∠CDD′=60°,
∵CN⊥DD′,
∴CN=CD sin∠CDD′=6sin60°=3,
∴S△BDD′+S扇形CDD′﹣S△CDD′=×(6+6)×(3﹣3)+﹣×6×3=18+12π﹣18;
故答案为:6﹣6;18+12π﹣18.
【点睛】本题是三角形综合题,考查了直角三角形性质,等腰直角三角形性质,等边三角形的判定和性质,解直角三角形,相似三角形的判定和性质等,得出DH扫过的面积为S△BDD′+S扇形CDD′﹣S△CDD′是解题关键.
7.(2023 杭州)如图,六边形ABCDEF是⊙O的内接正六边形,设正六边形ABCDEF的面积为S1,△ACE的面积为S2,则= 2 .
【点拨】连接OA,OC,OE,首先证明出△ACE 是⊙O的内接正三角形,然后证明出△BAC≌△OAC(ASA),得到 S△ABC=S△AEE=S△CDE S△AOC=S△OAE=S△OCE,进而求解即可.
【解析】解:如图所示,连接OA,OC,OE.
∵六边形ABCDEF是⊙O的内接正六边形,
∴AC=AE=CE,
∴△ACE是⊙O的内接正三角形,
∵∠B=120°,AB=BC,
∴∠BAC=∠BCA=(180°﹣∠B)=30°,
∵∠CAE=60°,
∴∠OAC=∠OAE=30°,
∴∠BAC=∠OAC=30°,
同理可得,∠BCA=∠OCA=30°,
又∵AC=AC,
∴△BAC≌△OAC(ASA),
∴S△BAC=S△AOC,
圆和正六边形的性质可得,S△BAC=S△AFE=S△CDE,
由圆和正三角形的性质可得,S△OAC=S△OAE=S△OCE,
∵S1=S△BAC+S△AEF+S△CDE+S△OAC+S△OAE+S△OCE=2(S△OAC+S△OAE+S△OCE)=2S2,
∴,
故答案为:2
【点睛】此题考查了圆内接正多边形的性质,正六边形和正三角形的性质,全等三角形的性质和判定等知 识,解题的关键是熟练掌握以上知识点.
掌握圆的基本性质:垂径定理、圆周角定理、圆内接四边形的性质、切线的性质、弧长公式、扇形面积公式、圆锥的计算公式、正多边形的性质是解决这一类问题的关键。
1.如图,点A、B、C在半径为1的⊙O上,∠ACB=70°,则的长等于 .
【点拨】根据圆周角定理求出∠AOB,再根据弧长公式计算,得到答案.
【解析】解:∵∠ACB=70°,
∴∠AOB=2∠ACB=140°,
∴的长为:=,
故答案为:.
【点睛】本题考查的是弧长计算、圆周角定理,熟记弧长公式是解题的关键.
2.如图,分别以等边△ABC的顶点A,B,C为圆心,以AB长为半径画弧,我们把这三条弧组成的封闭图形叫做莱洛三角形.若莱洛三角形的周长为2π,则莱洛三角形的面积为 .
【点拨】根据莱洛三角形的周长,可求出等边△ABC的边长,进而可求出莱洛三角形的面积.
【解析】解:由题知,
莱洛三角形的周长可转化为半径长为AB的圆周长的一半.
又因为莱洛三角形的周长为2π,
所以,
则AB=2,
所以等边△ABC的边长为2.
过点A作BC的垂线,垂足为M,
则BM=.
在Rt△ABM中,
AM=.
所以莱洛三角形的面积为:.
故答案为:.
【点睛】本题考查扇形面积的计算,能根据所给莱洛三角形的周长得出等边三角形的边长是解题的关键.
3.如图,正六边形ABCDEF的边长为6,以顶点A为圆心,AB的长为半径画圆,则图中阴影部分的面积为 12π .
【点拨】先确定扇形的圆心角的度数,然后利用扇形的面积公式计算即可.
【解析】解:∵正六边形的外角和为360°,
∴每一个外角的度数为360°÷6=60°,
∴正六边形的每个内角为180°﹣60°=120°,
∵正六边形的边长为6,
∴S阴影==12π,
故答案为:12π.
【点睛】考查了正多边形和圆及扇形的面积的计算的知识,解题的关键是求得正六边形的内角的度数并牢记扇形的面积计算公式,难度不大.
4.若圆锥的侧面积为25π,底面半径为5,则该圆锥的母线长是 5 .
【点拨】根据圆锥的侧面积=πrl,列出方程求解即可.
【解析】解:∵圆锥的侧面积为25π,底面半径为5,
∴5πl=25π.
解得:l=5,
故答案为:5.
【点睛】本题考查了圆锥的侧面积,解题关键是熟记圆锥的侧面积公式,列出方程进行求解.
5.如图,在⊙O中,弦BC⊥半径OA于点D,连接OB.若OB=5cm,AD=2cm,则BC的长是 8 cm.
【点拨】由垂径定理得BC=2BD,在Rt△OBD中可由勾股定理求出BD=4cm,由此可得BC的长.
【解析】解:∵弦BC⊥半径OA于点D,
∴BD=CD,
∴BC=2BD,
∵OB=OA=5cm,AD=2cm,
∴OD=OA﹣AD=5﹣2=3(cm),
在Rt△OBD中,OB=5cm,OD=3cm,
由勾股定理得:BD==4(cm),
∴BC=2BD=8(cm).
故答案为:8.
【点睛】此题主要考查了垂径定理,勾股定理,熟练掌握垂径定理及勾股定理是解决问题的关键.
6.如图,⊙O的切线PA交半径OB的延长线于点P,A为切点.若∠P=30°,OB=2,则PB= 2 .
【点拨】根据切线的性质得到∠OAP=90°,再利用含30度角的直角三角形三边的关系得到OP=4,然后计算OP﹣OB即可.
【解析】解:∵PA为⊙O的切线,
∴OA⊥PA,
∴∠OAP=90°,
∵∠P=30°,
∴OP=2OA=4,
∴PB=OP﹣OB=4﹣2=2.
故答案为:2.
【点睛】本题考查了切线的性质:圆的切线垂直于经过切点的半径.
7.我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的割圆术:“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”.“割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416.如图,⊙O的半径为1,运用“割圆术”,以圆内接正六边形面积近似估计⊙O的面积,可得π的估计值为,若用圆内接正十二边形作近似估计,可得π的估计值为 3 .
【点拨】过A作AM⊥OB于M,求得∠AOB=360°÷12=30°,根据直角三角形的性质得到AM=OA=,根据三角形的面积公式得到S△AOB=,于是得到正十二边形的面积为12×=3,根据圆的面积公式即可得到结论.
【解析】解:如图,AB是正十二边形的一条边,点O是正十二边形的中心,
过A作AM⊥OB于M,
在正十二边形中,∠AOB=360°÷12=30°,
∴AM=OA=,
∴S△AOB=OB AM=×=,
∴正十二边形的面积为12×=3,
∴3=12×π,
∴π=3,
∴π的近似值为3,
故答案为:3.
【点睛】本题考查了正多边形与圆,三角形的面积的计算,正确地作出辅助线是解题的关键.
8.如图,过⊙O外一点P作圆的切线PA,PB,点A,B为切点,AC为直径,设∠P=m°,∠C=n°,则m,n的等量关系为 m+2n=180° .
【点拨】连接OB,由切线的性质得到∠PAO=∠PBO=90°,由四边形内角和为360°得到∠P+∠AOB=180°,根据圆内角定理得到∠AOB=2∠C,代入上式即可得到结论.
【解析】解:连接OB,
∵PA,PB是⊙O的切线,
∴∠PAO=∠PBO=90°,
∵∠PAO+∠PBO+∠P+∠AOB=360°,
∴∠P+∠AOB=180°,
∵∠AOB=2∠C,
∴∠P+2∠C=180°,
∴m+2n=180°.
故答案为:m+2n=180°.
【点睛】本题主要考查了切线的性质,四边形内角和为360°,圆内角定理,熟练掌握相关知识是解决问题的关键.
04 押浙江卷第11—14题
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
命题探究
真题回顾
解题秘籍
押题预测
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
