22.3实际问题与二次函数课件
文档属性
| 名称 | 22.3实际问题与二次函数课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 314.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-11-27 22:47:12 | ||
图片预览




文档简介
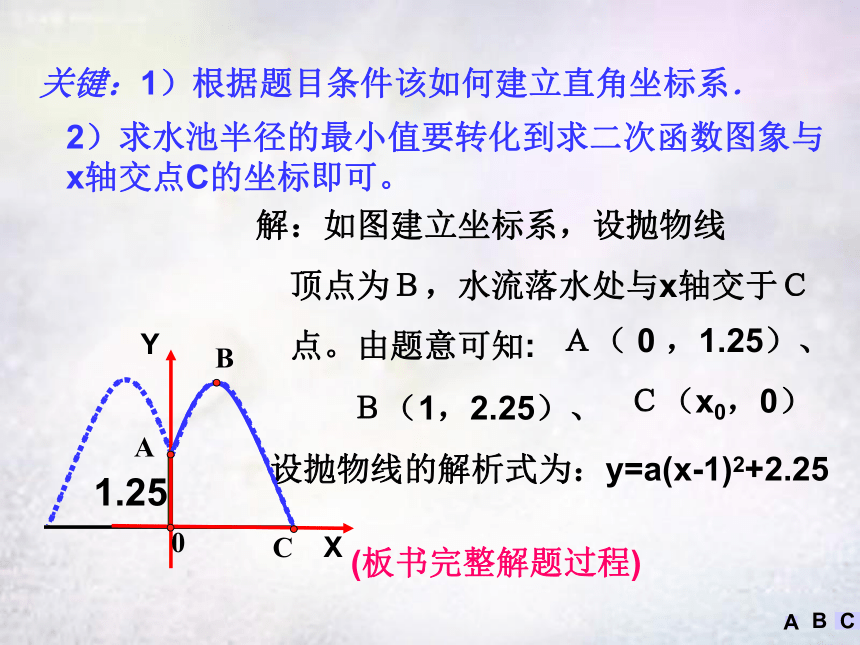
课件16张PPT。二次函数的应用联想到抛物线的生活实际问题0A问题1:公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下。为使水流较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米。如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流落不到池外?BAC1.250A问题1:公园要建造圆形的喷水池,在水池中央垂直于水面处安装一个柱子OA,O点恰在水面中心,OA=1.25米,由柱子顶端A处的喷头向外喷水,水流在各个方向沿形状相同的抛物线路线落下。为使水流较为漂亮,要求设计成水流在离OA距离为1米处达到距水面最大高度2.25米。如果不计其他因素,那么水池的半径至少要多少米,才能使喷出的水流落不到池外?BAC1.25关键:1)根据题目条件该如何建立直角坐标系. 解:如图建立坐标系,设抛物线
顶点为B,水流落水处与x轴交于C
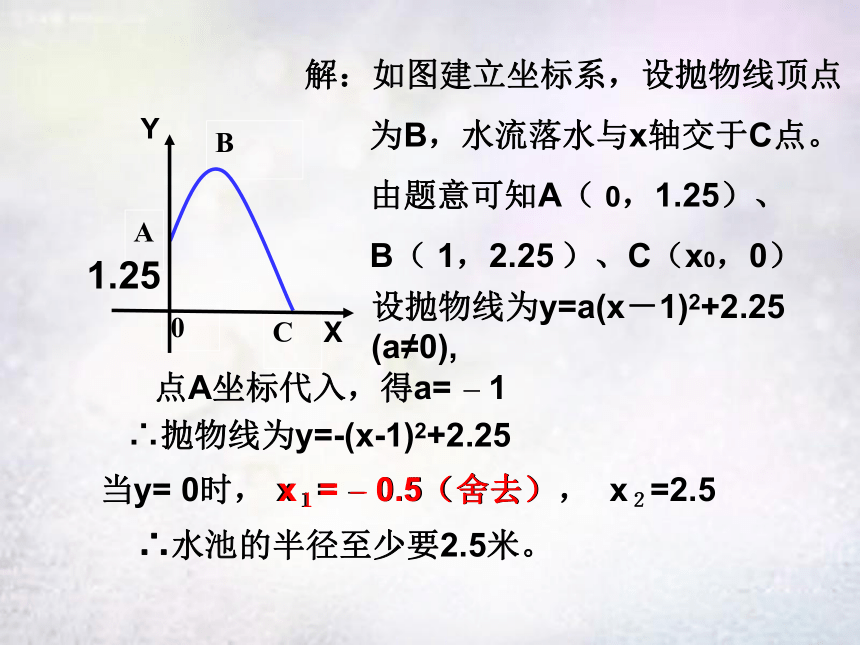
点。由题意可知:0A设抛物线的解析式为:y=a(x-1)2+2.25A( 0 ,1.25)、B(1,2.25)、C(x0,0) BAC2)求水池半径的最小值要转化到求二次函数图象与x轴交点C的坐标即可。(板书完整解题过程)1.250A解:如图建立坐标系,设抛物线顶点
为B,水流落水与x轴交于C点。
由题意可知A( 0,1.25)、
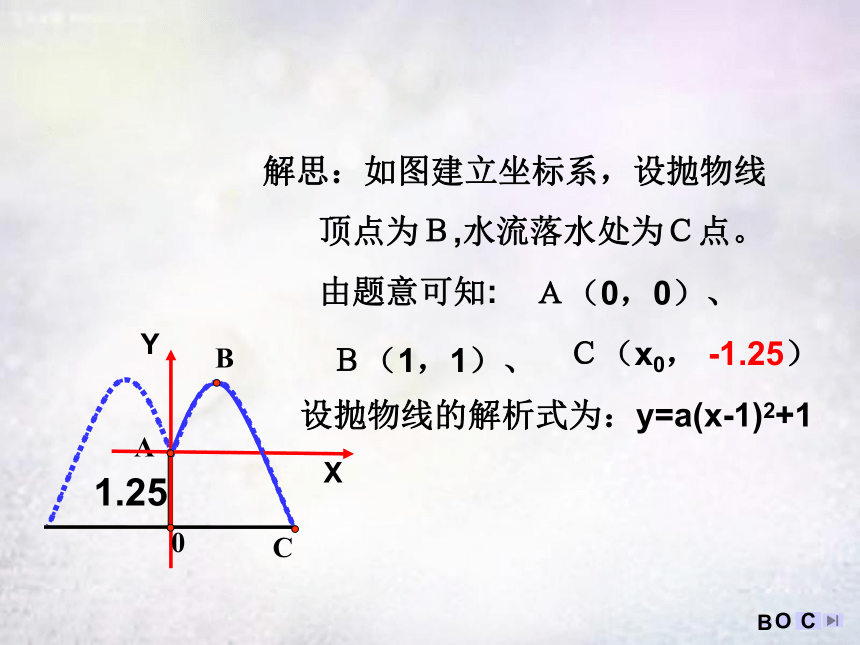
B( 1,2.25 )、C(x0,0) XY设抛物线为y=a(x-1)2+2.25 (a≠0), 点A坐标代入,得a= - 1当y= 0时, x1= - 0.5(舍去), x2=2.5∴水池的半径至少要2.5米。x1= - 0.5(舍去)∴抛物线为y=-(x-1)2+2.25 1.250A解思:如图建立坐标系,设抛物线
顶点为B,水流落水处为C点。
由题意可知:A(0,0)、B(1,1)、C(x0, -1.25)设抛物线的解析式为:y=a(x-1)2+1OBC1.250A解思:如图建立坐标系,设抛物线
顶点为B,水流落水处为C点。
由题意可知:C(x0, -2.25 )B(0,0)、A(-1,-1)、设抛物线的解析式为:y=ax2AC1.25解思:如图建立坐标系,设抛物线
顶点为B,水流落水处为C点。
由题意可知:0AB( x0+1, 2.25 )C(0,0)、A( x0 ,1.25)、设抛物线的解析式为:y=ax2+bxA1.25辨一辨0A1.250A1.250A1.250AXY1.25YYXX 借助二次函数的图象和性质解决有关生活实际问题的基本方法: 数学模型
(二次函数的图象和性质)实际问题转化关键点:1)能够将实际距离(准确的)转化为点的坐标; 2)选择运算简便的方法。师生小结:正确建立直角坐标系数学是来源于生活又服务于生活的. 1.小燕去参观一个蔬菜大棚,大棚的横截面为抛物线,有关数据如图所示。小燕身高1.40米,在她不弯腰的情况下,横向活动范围是多少?巩固练习(2)在某次试跳中,测得运动员在空中
的运动路线是(1)中的抛物线,且
运动员在空中调整好入水姿势时,距
池边的水平距离为3.6米,问此次跳
水会不会失误?(1)求如图所示坐标系下经过原点 的这条抛物线的解析式;5m? 二次函数的图象和性质不仅可以用来解决数学问题,还可以用来解决一些生活实际问题,同学们要善于观察和思考,要有意识的提高自己应用数学知识解决实际问题的能力,做到学数学用数学. 布置作业: 1、学诊
2、第二道巩固练习(用简单的建系方法解决问题)谢谢!
顶点为B,水流落水处与x轴交于C
点。由题意可知:0A设抛物线的解析式为:y=a(x-1)2+2.25A( 0 ,1.25)、B(1,2.25)、C(x0,0) BAC2)求水池半径的最小值要转化到求二次函数图象与x轴交点C的坐标即可。(板书完整解题过程)1.250A解:如图建立坐标系,设抛物线顶点
为B,水流落水与x轴交于C点。
由题意可知A( 0,1.25)、
B( 1,2.25 )、C(x0,0) XY设抛物线为y=a(x-1)2+2.25 (a≠0), 点A坐标代入,得a= - 1当y= 0时, x1= - 0.5(舍去), x2=2.5∴水池的半径至少要2.5米。x1= - 0.5(舍去)∴抛物线为y=-(x-1)2+2.25 1.250A解思:如图建立坐标系,设抛物线
顶点为B,水流落水处为C点。
由题意可知:A(0,0)、B(1,1)、C(x0, -1.25)设抛物线的解析式为:y=a(x-1)2+1OBC1.250A解思:如图建立坐标系,设抛物线
顶点为B,水流落水处为C点。
由题意可知:C(x0, -2.25 )B(0,0)、A(-1,-1)、设抛物线的解析式为:y=ax2AC1.25解思:如图建立坐标系,设抛物线
顶点为B,水流落水处为C点。
由题意可知:0AB( x0+1, 2.25 )C(0,0)、A( x0 ,1.25)、设抛物线的解析式为:y=ax2+bxA1.25辨一辨0A1.250A1.250A1.250AXY1.25YYXX 借助二次函数的图象和性质解决有关生活实际问题的基本方法: 数学模型
(二次函数的图象和性质)实际问题转化关键点:1)能够将实际距离(准确的)转化为点的坐标; 2)选择运算简便的方法。师生小结:正确建立直角坐标系数学是来源于生活又服务于生活的. 1.小燕去参观一个蔬菜大棚,大棚的横截面为抛物线,有关数据如图所示。小燕身高1.40米,在她不弯腰的情况下,横向活动范围是多少?巩固练习(2)在某次试跳中,测得运动员在空中
的运动路线是(1)中的抛物线,且
运动员在空中调整好入水姿势时,距
池边的水平距离为3.6米,问此次跳
水会不会失误?(1)求如图所示坐标系下经过原点 的这条抛物线的解析式;5m? 二次函数的图象和性质不仅可以用来解决数学问题,还可以用来解决一些生活实际问题,同学们要善于观察和思考,要有意识的提高自己应用数学知识解决实际问题的能力,做到学数学用数学. 布置作业: 1、学诊
2、第二道巩固练习(用简单的建系方法解决问题)谢谢!
同课章节目录
