14.5 等腰三角形的性质(教学课件)-七年级数学下册同步精品课堂(沪教版)
文档属性
| 名称 | 14.5 等腰三角形的性质(教学课件)-七年级数学下册同步精品课堂(沪教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览










文档简介
(共42张PPT)
14.5 等腰三角形的性质
2023-2024学年沪教版七年级下册数学课件
3、在你们的印象里,什么样的三角形叫做等腰三角形?
有两条边相等的三角形叫做等腰三角形
2、上面三个三角形按边分类是什么样的三角形
1、上面三个三角形按角分类是什么样的三角形
复习回顾:
如图:在△ABC中,AB=AC,则△ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫做腰。
腰
腰
底边
(2)另一边叫底边。
顶角
底角
底角
(3)两腰的夹角∠A叫顶角。
(4)腰与底边夹角∠B、∠C叫底角。
等腰三角形再认识
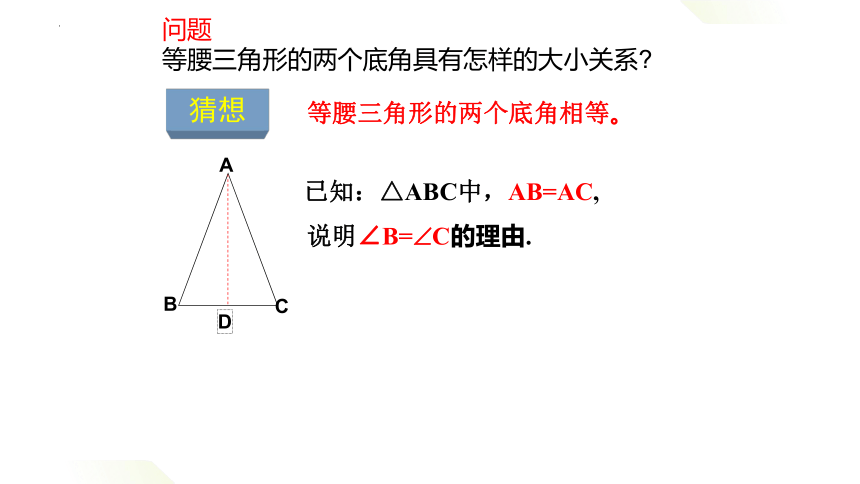
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC,
说明∠B= C的理由.
猜想
A
B
C
D
问题
等腰三角形的两个底角具有怎样的大小关系
操作
在纸上画一个等腰三角形ABC,其中AB=AC,再画出顶角的平分线AD,设AD与BC 相交于点 D(图14-37)
把 △ABC 纸片剪下,将△ABD 沿着直线AD翻折因为∠BAD= ∠ CAD,所以将 △ABC 沿着AD翻折后射线AB与射线AC 叠合由于 AB=AC,因此线段AB与线段AC 重合,于是点 B 与点 C 重合。又因为点 D 与点 D重合,所以线段BD与线段CD也重合(图14 -38)因此∠ B= ∠ C.
归纳结论
等腰三角形的两个底角相等。
性质1
(简称“等边对等角”)
用符号语言表示为:
A
B
C
∵AB=AC(已知)
∴∠B=∠C( )
等边对等角
A
B
C
则有∠1= ∠2(角平分线的意义)
D
1
2
在△ABD和△ACD中
证明: 过点A作∠BAC的角平分
线AD,交BC于点D.
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
我们可以直接利用全等三角形对等腰三角形的性质进行说理。
A
B
C
则有 BD= CD(中线的意义)
D
在△ABD和△ACD中
证明:过点A作BC边上的中线AD,
交BC于点D.
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
想一想:
由△BAD≌△CAD除了能得到∠B=∠C,你还能发现什么
相等的线段 相等的角
B
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠1 = ∠2
A
D
∠ADB =∠ADC
1 2
= 90°
AD是 ;
AD是 ;
AD是 .
底边上的中线
顶角平分线
底边上的高
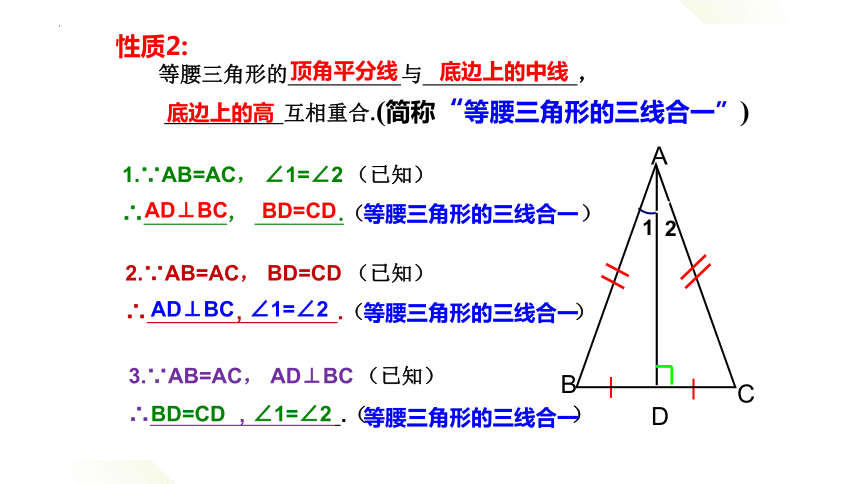
性质2:
三角形的 , ,
互相重合.
顶角平分线
等腰
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
1.∵AB=AC, ∠1=∠2 (已知)
∴ , .( )
2.∵AB=AC, BD=CD (已知)
∴ , .( )
3.∵AB=AC, AD⊥BC (已知)
∴ , .( )
A
B
C
1
2
D
等腰三角形的 与 ,
互相重合.
顶角平分线
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
等腰三角形的三线合一
性质2:
AD⊥BC
BD=CD
BD=CD
∠1=∠2
等腰三角形的三线合一
等腰三角形的三线合一
∠1=∠2
AD⊥BC
等腰三角形是轴对称图形.它的对称轴是:
性质3:
所在的直线.
底边上的中线(或顶角平分线,底边上的高)
等腰三角形的对称轴是底边的垂直平分线 . ( )
判断题:
√
D
思考:等腰三角形是轴对称图形吗?如果是,它的对称
轴是什么?
例题1、已知等腰△ABC中,AB=AC,∠B=70 ,求∠C和∠A的度数.
A
C
B
70
70
解(1) 因为 AB=AC(已知),
所以 ∠C= ∠ B(等边对等角)
由 ∠ B=70°(已知),
得 ∠ C=70°.
(2)因为 ∠ B= ∠ C=70°
又∠ A+ ∠ B+ ∠ C=180°(三角形的内角和等于180°).
所以 ∠ A=180°-70°-70°=40°
例题2:已知,AB=AC,∠BAC=110 ,
AD是△ABC的中线.
⑴求∠1的度数;
⑵求∠ADC的度数
解(1)∵AB=AC,AD是△ABC底边上的中线(已知)
∴∠1= ∠BAC (等腰三角形的三线合一)
∵∠BAC=110 (已知)
∴∠1= ×110 =55 (等式性质)
⑵∵ AB=AC,AD是△ABC底边上的中线(已知)
∴AD⊥BC(等腰三角形的三线合一)
∴∠ADC=90°(垂直的意义)
B
C
D
1
2
A
关于撑伞的数学问题
已知:如图,AB=AC,DB=DC
问: AD与BC有什么关系?
猜想:AD垂直平分BC
∴△ABD≌△ACD(SSS)
∴∠BAD=∠CAD
∴AD垂直平分BC
在⊿ABD和⊿ACD中
证明:
A
B
C
D
1.下列判断错误的是( ____ )
A.等腰三角形是轴对称图形
B.有两条边相等的三角形是等腰三角形
C.等腰三角形的两个底角相等
D.等腰三角形的角平分线、中线、高互相重合
【解析】解:A、等腰三角形是轴对称图形,正确;
B、两条边相等的三角形叫做等腰三角形,正确;
C、等腰三角形的两腰相等,两个底角相等,正确;
D、等腰三角形顶角的角平分线与底边上的中线、底边上的高线互相重合,故本选项错误;
D
2.等腰三角形的底角为35°,则一腰上的高与另一腰的夹角是( ____ )
A.55°
B.35°
C.20°
D.以上都不对
【解析】解:如图,BD⊥AC于点D,
____
∵∠C=35°,∠D=90°,
C
∴∠DBC=90°-35°=55°,
∵∠ABC=35°,
∴∠DBA=55°-35°=20°,
即一腰上的高与另一腰的夹角是20°,
故选:C.
3.下列说法错误的有( ____ )
①底边和顶角分别相等的两个等腰三角形全等
②含有100°内角且腰为3cm的两个等腰三角形全等
③腰长和底边长分别相等的两个等腰三角形全等
④含有80°内角且腰长是3cm的两个等腰三角形全等
A.1个
B.2个
C.3个
D.4个
【解析】解:①两个等腰三角形顶角相等,
A
∴两个等腰三角形底角相等,
∴根据ASA可证底边和顶角分别相等的两个等腰三角形全等,
故①不符合题意;
②等腰三角形100°内角为顶角,
∴根据SAS可证含有100°内角且腰为3cm的两个等腰三角形全等,
故②不符合题意;
③根据SSS可证腰长和底边长分别相等的两个等腰三角形全等,
故③不符合题意;
④等腰三角形80°内角不确定是顶角还是底角,
∴不能判定含有80°内角且腰长是3cm的两个等腰三角形全等,
故④符合题意,
4.在等腰三角形中,一个内角为40°,则另两个内角的大小分别是 _________________________ .
【解析】解;当顶角为40°时,其底角为 =70°
当底角为40°时,则顶角为180°-40°×2=100°,
所以有两种情况:当顶角为40°时,它的另外两个内角分别是70°,70°;
当底角为40°时,它的另外两个内角分别是40°,100°.
故答案为70°,70°或40°,100°.
70°,70°或40°,100°
5.等腰三角形的一个内角等于110°,则另两个内角的度数分别是 ___________ .
【解析】解:∵三角形内角和为180°,
∴110°不能为底角,
∴剩下两个角为底角,且他们之和为180°-110°=70°,
∵70°÷2=35°,
∴另两个内角的度数分别是35°,35°,
故答案为:35°,35°.
35°,35°
6.等腰三角形底角的度数是顶角度数的2倍,底角的度数是 _____ .
【解析】解:设等腰三角形的顶角度数为x,
∵等腰三角形的底角是顶角的2倍,
∴底角度数为2x,
根据三角形内角和定理得:x+2x+2x=180°,
解得x=36°,
则底角的度数为72°.
故答案为:72°.
72°
7.等腰三角形一腰上的高与另一腰的夹角是30°,这个三角形三个内角的度数是 _____________________________________ .
【解析】解:当等腰三角形为锐角三角形时,如图1,
___
由已知可知,∠ABD=30°,
又∵BD⊥AC,
60°,60°,60°或30°,30°,120°
∴∠ADB=90°,
∴∠A=60°,
∵AB=AC,
∴∠ABC=∠C=60°.
当等腰三角形为钝角三角形时,如图2,
_____
由已知可知,∠ACD=30°,
又∵CD⊥AB,
∴∠DAC=60°,
∴∠B=∠ACB=30°,∠BAC=120°.
故答案为:60°,60°,60°或30°,30°,120°.
8.已知等腰三角形的一边长为3cm,另一边长为7cm,则这个三角形的周长是 ______ .
【解析】解:①当腰长为3cm时,等腰三角形三边长为3cm、3cm、7cm,3+3<7,不符合三角形三边关系,不能构成三角形;
②当腰长为7cm时,等腰三角形三边长为3cm、7cm、7cm,符合三角形三边关系,
则三角形的周长为:3+7+7=17cm.
因此这个三角形的周长为17cm.
故答案为:17cm.
17cm
9.已知等腰三角形的周长为20,一边长为6,另两边长分别是 ____________ .
【解析】解:当腰为6时,另一腰也为6,则底为20-2×6=8,
∵6+6=12>8,
∴三边能构成三角形.
当底为6时,腰为(20-6)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故答案为:6,8或7,7.
6,8或7,7
10.若等腰三角形的底边长为8,则它的腰长x的取值范围是 _____ .
【解析】解:等腰三角形的底边长为8,腰长为x,
则2x>8,
解得x>4.
综上所述,该三角形的腰长x的取值范围是x>4.
故答案为:x>4.
x>4
11.如图,在△ABC中,AB=AD=DC,AE⊥BD,如果△ABC的面积是12,那么△ABE的面积是 ____ .
【解析】解:∵AB=AD=AC,
∴D是△ABC的中线,
∴S△ABD= S△ABC= 12=6,
∵△ABD是等腰三角形,AE⊥BD,
∴点E是BD的中点,
∴S△ABE= S△ABD= 6=3.
故答案为:3.
3
12.已知,△ABC中,AB=AC,点M在AC上,且 MA=MB,∠C=65°,求∠BMC的度数.
解:因为△ABC中,AB=AC (已知),
所以∠ _____ =∠ ____ ( _____________ )
因为∠C=65°( _____ ),
所以∠ABC= ____ °( __________ )
又因为∠A+∠C+∠ABC=180°( ________________________ ),
所以∠A=180°- ____ °- ____ °= ____ °.
又因为MA=MB (已知),
所以∠ _____ =∠A= ____ °( _____________ ),
ABC
C
等边对等角
已知
65
等量关系
三角形内角和为180°
65
65
50
ABM
50
等边对等角
而∠BMC=∠ ____ +∠ _____ ( ____________________ ),
所以∠BMC= ____ °+ ____ °= _____ °.
【解析】解:因为△ABC中,AB=AC(已知),
所以∠ABC=∠C(等边对等角),
因为∠C=65°(已知),
所以∠ABC=65°(等量关系),
又因为∠A+∠C+∠ABC=180°(三角形内角和为180°),
所以∠A=180°-65°-65°=50°.
又因为MA=MB(已知),
所以∠ABM=∠A=50°(等边对等角),
A
ABM
三角形外角的性质
50
50
100
而∠BMC=∠A+∠ABM(三角形外角的性质),
所以∠BMC=50°+50°=100°.
故答案为:ABC,C,等边对等角,已知,等量关系,三角形内角和为180°,65,65,50,ABM,50,等边对等角,A,ABM,三角形外角的性质,50,50,100.
13.如图,四边形ABCD中,AB=AD,BC=DC,试说明∠B=∠D的理由.(要求不用全等三角形说明)
【解析】解:如图,连接BD,
在△ABD中,∵AB=AD,
∴∠ABD=∠ADB,
在△CBD中,∵BC=DC,
∴∠CBD=∠CDB,
∴∠ABD+∠CBD=∠ADB+∠CDB,
即∠ABC=∠ADC.
14.如图,△ABC中,AB=AC,BE=CE,延长AE交BC于点D,试说明AD⊥BC的理由.
【解析】证明:∵AB=AC,
∴点A在BC的垂直平分线上,
∵BE=CE,
∴点E在BC的垂直平分线上,
∴A、E都在BC的垂直平分线上,
∵延长AE交BC边于点D,
∴AD⊥BC.
15.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,E、F分别为边AB、AC上的点,且EB=FC,连接EF,交AD于点O,那么OE=OF,且AO⊥EF,为什么?
【解析】解:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵BE=CF,
∴AB-BE=AC-CF,即AE=AF,
∴△AEF是等腰三角形,
∵∠EAO=∠FAO,
∴OE=OF,且AO⊥EF.
16.如图,已知:点D,E在△ABC的边BC上,AB=AC,AD=AE.请说明BD=CE的理由.
【解析】证明:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE.
17.如图,在△ABC中,AB=AC,AH⊥BC,BC=6,D为直线BC上一动点(不与点B、点C重合),向AB的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
______
(1)当点D在线段BC上时,求证:△BAD≌△CAE;
(2)在(1)的条件下,当AC⊥DE时,求BD的长;
(3)当CE∥AB时,若△ABD中有最小的内角为23°,试求∠AEC的度数.(直接写结果,无需写出求解过程)
【解析】(1)证明:①如图1,
___
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS);
(2)解:∵AE=AD,AC⊥DE,
∴∠DAC=∠EAC,
∵△BAD≌△CAE,
∴∠BAD=∠EAC,
∴∠DAC=∠BAD,
∵AB=AC,
∴BD=DC
∵BC=6,
∴BD= BC=3;
(3)如图2,当D在线段BC上时,
∵CE∥AB,
∴∠ACE=∠BAC,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,∠ADB=∠AEC,
∴∠ABD=∠BAC,又∠ABC=∠ACB,
∴△ABC为等边三角形,
∴∠ABC=60°,
∴∠AEC=∠ADB=180°-60°-23°=97°;
如图3,当点D在CB的延长线上时,同理可得,∠ABC=60°,
∴∠AEC=37°,
即当△ABD中的最小角是∠DAB时,∠ADB=∠AEC=37°,
当点D在BC的延长线上时,只能∠ADB=23°,则∠AEC=23°.
∴∠AEC的度数为97°或37°或23°.
谢谢
14.5 等腰三角形的性质
2023-2024学年沪教版七年级下册数学课件
3、在你们的印象里,什么样的三角形叫做等腰三角形?
有两条边相等的三角形叫做等腰三角形
2、上面三个三角形按边分类是什么样的三角形
1、上面三个三角形按角分类是什么样的三角形
复习回顾:
如图:在△ABC中,AB=AC,则△ABC就是等腰三角形
它的各部分名称分别是什么?
A
B
C
(1)相等的两条边都叫做腰。
腰
腰
底边
(2)另一边叫底边。
顶角
底角
底角
(3)两腰的夹角∠A叫顶角。
(4)腰与底边夹角∠B、∠C叫底角。
等腰三角形再认识
等腰三角形的两个底角相等。
已知:△ABC中,AB=AC,
说明∠B= C的理由.
猜想
A
B
C
D
问题
等腰三角形的两个底角具有怎样的大小关系
操作
在纸上画一个等腰三角形ABC,其中AB=AC,再画出顶角的平分线AD,设AD与BC 相交于点 D(图14-37)
把 △ABC 纸片剪下,将△ABD 沿着直线AD翻折因为∠BAD= ∠ CAD,所以将 △ABC 沿着AD翻折后射线AB与射线AC 叠合由于 AB=AC,因此线段AB与线段AC 重合,于是点 B 与点 C 重合。又因为点 D 与点 D重合,所以线段BD与线段CD也重合(图14 -38)因此∠ B= ∠ C.
归纳结论
等腰三角形的两个底角相等。
性质1
(简称“等边对等角”)
用符号语言表示为:
A
B
C
∵AB=AC(已知)
∴∠B=∠C( )
等边对等角
A
B
C
则有∠1= ∠2(角平分线的意义)
D
1
2
在△ABD和△ACD中
证明: 过点A作∠BAC的角平分
线AD,交BC于点D.
AB=AC
∠1=∠2
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SAS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法一
我们可以直接利用全等三角形对等腰三角形的性质进行说理。
A
B
C
则有 BD= CD(中线的意义)
D
在△ABD和△ACD中
证明:过点A作BC边上的中线AD,
交BC于点D.
AB=AC
BD=CD
AD=AD
(公共边)
∴ △ABD≌ △ACD
(SSS)
∴ ∠B=∠C
(全等三角形对应角相等)
方法二
想一想:
由△BAD≌△CAD除了能得到∠B=∠C,你还能发现什么
相等的线段 相等的角
B
C
AB=AC
BD=CD
AD=AD
∠B = ∠C.
∠1 = ∠2
A
D
∠ADB =∠ADC
1 2
= 90°
AD是 ;
AD是 ;
AD是 .
底边上的中线
顶角平分线
底边上的高
性质2:
三角形的 , ,
互相重合.
顶角平分线
等腰
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
1.∵AB=AC, ∠1=∠2 (已知)
∴ , .( )
2.∵AB=AC, BD=CD (已知)
∴ , .( )
3.∵AB=AC, AD⊥BC (已知)
∴ , .( )
A
B
C
1
2
D
等腰三角形的 与 ,
互相重合.
顶角平分线
底边上的中线
底边上的高
(简称“等腰三角形的三线合一”)
等腰三角形的三线合一
性质2:
AD⊥BC
BD=CD
BD=CD
∠1=∠2
等腰三角形的三线合一
等腰三角形的三线合一
∠1=∠2
AD⊥BC
等腰三角形是轴对称图形.它的对称轴是:
性质3:
所在的直线.
底边上的中线(或顶角平分线,底边上的高)
等腰三角形的对称轴是底边的垂直平分线 . ( )
判断题:
√
D
思考:等腰三角形是轴对称图形吗?如果是,它的对称
轴是什么?
例题1、已知等腰△ABC中,AB=AC,∠B=70 ,求∠C和∠A的度数.
A
C
B
70
70
解(1) 因为 AB=AC(已知),
所以 ∠C= ∠ B(等边对等角)
由 ∠ B=70°(已知),
得 ∠ C=70°.
(2)因为 ∠ B= ∠ C=70°
又∠ A+ ∠ B+ ∠ C=180°(三角形的内角和等于180°).
所以 ∠ A=180°-70°-70°=40°
例题2:已知,AB=AC,∠BAC=110 ,
AD是△ABC的中线.
⑴求∠1的度数;
⑵求∠ADC的度数
解(1)∵AB=AC,AD是△ABC底边上的中线(已知)
∴∠1= ∠BAC (等腰三角形的三线合一)
∵∠BAC=110 (已知)
∴∠1= ×110 =55 (等式性质)
⑵∵ AB=AC,AD是△ABC底边上的中线(已知)
∴AD⊥BC(等腰三角形的三线合一)
∴∠ADC=90°(垂直的意义)
B
C
D
1
2
A
关于撑伞的数学问题
已知:如图,AB=AC,DB=DC
问: AD与BC有什么关系?
猜想:AD垂直平分BC
∴△ABD≌△ACD(SSS)
∴∠BAD=∠CAD
∴AD垂直平分BC
在⊿ABD和⊿ACD中
证明:
A
B
C
D
1.下列判断错误的是( ____ )
A.等腰三角形是轴对称图形
B.有两条边相等的三角形是等腰三角形
C.等腰三角形的两个底角相等
D.等腰三角形的角平分线、中线、高互相重合
【解析】解:A、等腰三角形是轴对称图形,正确;
B、两条边相等的三角形叫做等腰三角形,正确;
C、等腰三角形的两腰相等,两个底角相等,正确;
D、等腰三角形顶角的角平分线与底边上的中线、底边上的高线互相重合,故本选项错误;
D
2.等腰三角形的底角为35°,则一腰上的高与另一腰的夹角是( ____ )
A.55°
B.35°
C.20°
D.以上都不对
【解析】解:如图,BD⊥AC于点D,
____
∵∠C=35°,∠D=90°,
C
∴∠DBC=90°-35°=55°,
∵∠ABC=35°,
∴∠DBA=55°-35°=20°,
即一腰上的高与另一腰的夹角是20°,
故选:C.
3.下列说法错误的有( ____ )
①底边和顶角分别相等的两个等腰三角形全等
②含有100°内角且腰为3cm的两个等腰三角形全等
③腰长和底边长分别相等的两个等腰三角形全等
④含有80°内角且腰长是3cm的两个等腰三角形全等
A.1个
B.2个
C.3个
D.4个
【解析】解:①两个等腰三角形顶角相等,
A
∴两个等腰三角形底角相等,
∴根据ASA可证底边和顶角分别相等的两个等腰三角形全等,
故①不符合题意;
②等腰三角形100°内角为顶角,
∴根据SAS可证含有100°内角且腰为3cm的两个等腰三角形全等,
故②不符合题意;
③根据SSS可证腰长和底边长分别相等的两个等腰三角形全等,
故③不符合题意;
④等腰三角形80°内角不确定是顶角还是底角,
∴不能判定含有80°内角且腰长是3cm的两个等腰三角形全等,
故④符合题意,
4.在等腰三角形中,一个内角为40°,则另两个内角的大小分别是 _________________________ .
【解析】解;当顶角为40°时,其底角为 =70°
当底角为40°时,则顶角为180°-40°×2=100°,
所以有两种情况:当顶角为40°时,它的另外两个内角分别是70°,70°;
当底角为40°时,它的另外两个内角分别是40°,100°.
故答案为70°,70°或40°,100°.
70°,70°或40°,100°
5.等腰三角形的一个内角等于110°,则另两个内角的度数分别是 ___________ .
【解析】解:∵三角形内角和为180°,
∴110°不能为底角,
∴剩下两个角为底角,且他们之和为180°-110°=70°,
∵70°÷2=35°,
∴另两个内角的度数分别是35°,35°,
故答案为:35°,35°.
35°,35°
6.等腰三角形底角的度数是顶角度数的2倍,底角的度数是 _____ .
【解析】解:设等腰三角形的顶角度数为x,
∵等腰三角形的底角是顶角的2倍,
∴底角度数为2x,
根据三角形内角和定理得:x+2x+2x=180°,
解得x=36°,
则底角的度数为72°.
故答案为:72°.
72°
7.等腰三角形一腰上的高与另一腰的夹角是30°,这个三角形三个内角的度数是 _____________________________________ .
【解析】解:当等腰三角形为锐角三角形时,如图1,
___
由已知可知,∠ABD=30°,
又∵BD⊥AC,
60°,60°,60°或30°,30°,120°
∴∠ADB=90°,
∴∠A=60°,
∵AB=AC,
∴∠ABC=∠C=60°.
当等腰三角形为钝角三角形时,如图2,
_____
由已知可知,∠ACD=30°,
又∵CD⊥AB,
∴∠DAC=60°,
∴∠B=∠ACB=30°,∠BAC=120°.
故答案为:60°,60°,60°或30°,30°,120°.
8.已知等腰三角形的一边长为3cm,另一边长为7cm,则这个三角形的周长是 ______ .
【解析】解:①当腰长为3cm时,等腰三角形三边长为3cm、3cm、7cm,3+3<7,不符合三角形三边关系,不能构成三角形;
②当腰长为7cm时,等腰三角形三边长为3cm、7cm、7cm,符合三角形三边关系,
则三角形的周长为:3+7+7=17cm.
因此这个三角形的周长为17cm.
故答案为:17cm.
17cm
9.已知等腰三角形的周长为20,一边长为6,另两边长分别是 ____________ .
【解析】解:当腰为6时,另一腰也为6,则底为20-2×6=8,
∵6+6=12>8,
∴三边能构成三角形.
当底为6时,腰为(20-6)÷2=7,
∵7+7>6,
∴三边能构成三角形.
故答案为:6,8或7,7.
6,8或7,7
10.若等腰三角形的底边长为8,则它的腰长x的取值范围是 _____ .
【解析】解:等腰三角形的底边长为8,腰长为x,
则2x>8,
解得x>4.
综上所述,该三角形的腰长x的取值范围是x>4.
故答案为:x>4.
x>4
11.如图,在△ABC中,AB=AD=DC,AE⊥BD,如果△ABC的面积是12,那么△ABE的面积是 ____ .
【解析】解:∵AB=AD=AC,
∴D是△ABC的中线,
∴S△ABD= S△ABC= 12=6,
∵△ABD是等腰三角形,AE⊥BD,
∴点E是BD的中点,
∴S△ABE= S△ABD= 6=3.
故答案为:3.
3
12.已知,△ABC中,AB=AC,点M在AC上,且 MA=MB,∠C=65°,求∠BMC的度数.
解:因为△ABC中,AB=AC (已知),
所以∠ _____ =∠ ____ ( _____________ )
因为∠C=65°( _____ ),
所以∠ABC= ____ °( __________ )
又因为∠A+∠C+∠ABC=180°( ________________________ ),
所以∠A=180°- ____ °- ____ °= ____ °.
又因为MA=MB (已知),
所以∠ _____ =∠A= ____ °( _____________ ),
ABC
C
等边对等角
已知
65
等量关系
三角形内角和为180°
65
65
50
ABM
50
等边对等角
而∠BMC=∠ ____ +∠ _____ ( ____________________ ),
所以∠BMC= ____ °+ ____ °= _____ °.
【解析】解:因为△ABC中,AB=AC(已知),
所以∠ABC=∠C(等边对等角),
因为∠C=65°(已知),
所以∠ABC=65°(等量关系),
又因为∠A+∠C+∠ABC=180°(三角形内角和为180°),
所以∠A=180°-65°-65°=50°.
又因为MA=MB(已知),
所以∠ABM=∠A=50°(等边对等角),
A
ABM
三角形外角的性质
50
50
100
而∠BMC=∠A+∠ABM(三角形外角的性质),
所以∠BMC=50°+50°=100°.
故答案为:ABC,C,等边对等角,已知,等量关系,三角形内角和为180°,65,65,50,ABM,50,等边对等角,A,ABM,三角形外角的性质,50,50,100.
13.如图,四边形ABCD中,AB=AD,BC=DC,试说明∠B=∠D的理由.(要求不用全等三角形说明)
【解析】解:如图,连接BD,
在△ABD中,∵AB=AD,
∴∠ABD=∠ADB,
在△CBD中,∵BC=DC,
∴∠CBD=∠CDB,
∴∠ABD+∠CBD=∠ADB+∠CDB,
即∠ABC=∠ADC.
14.如图,△ABC中,AB=AC,BE=CE,延长AE交BC于点D,试说明AD⊥BC的理由.
【解析】证明:∵AB=AC,
∴点A在BC的垂直平分线上,
∵BE=CE,
∴点E在BC的垂直平分线上,
∴A、E都在BC的垂直平分线上,
∵延长AE交BC边于点D,
∴AD⊥BC.
15.如图,△ABC中,AB=AC,AD⊥BC,垂足为D,E、F分别为边AB、AC上的点,且EB=FC,连接EF,交AD于点O,那么OE=OF,且AO⊥EF,为什么?
【解析】解:∵AB=AC,AD⊥BC,
∴∠BAD=∠CAD,
∵BE=CF,
∴AB-BE=AC-CF,即AE=AF,
∴△AEF是等腰三角形,
∵∠EAO=∠FAO,
∴OE=OF,且AO⊥EF.
16.如图,已知:点D,E在△ABC的边BC上,AB=AC,AD=AE.请说明BD=CE的理由.
【解析】证明:∵AB=AC,AD=AE,
∴∠B=∠C,∠ADE=∠AED,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∴BD=CE.
17.如图,在△ABC中,AB=AC,AH⊥BC,BC=6,D为直线BC上一动点(不与点B、点C重合),向AB的右侧作△ADE,使得AE=AD,∠DAE=∠BAC,连接CE.
______
(1)当点D在线段BC上时,求证:△BAD≌△CAE;
(2)在(1)的条件下,当AC⊥DE时,求BD的长;
(3)当CE∥AB时,若△ABD中有最小的内角为23°,试求∠AEC的度数.(直接写结果,无需写出求解过程)
【解析】(1)证明:①如图1,
___
∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
在△BAD和△CAE中,
,
∴△BAD≌△CAE(SAS);
(2)解:∵AE=AD,AC⊥DE,
∴∠DAC=∠EAC,
∵△BAD≌△CAE,
∴∠BAD=∠EAC,
∴∠DAC=∠BAD,
∵AB=AC,
∴BD=DC
∵BC=6,
∴BD= BC=3;
(3)如图2,当D在线段BC上时,
∵CE∥AB,
∴∠ACE=∠BAC,
∵△BAD≌△CAE,
∴∠ABD=∠ACE,∠ADB=∠AEC,
∴∠ABD=∠BAC,又∠ABC=∠ACB,
∴△ABC为等边三角形,
∴∠ABC=60°,
∴∠AEC=∠ADB=180°-60°-23°=97°;
如图3,当点D在CB的延长线上时,同理可得,∠ABC=60°,
∴∠AEC=37°,
即当△ABD中的最小角是∠DAB时,∠ADB=∠AEC=37°,
当点D在BC的延长线上时,只能∠ADB=23°,则∠AEC=23°.
∴∠AEC的度数为97°或37°或23°.
谢谢
