14.6 等腰三角形的判定(第1课时)(教学课件)-七年级数学下册同步精品课堂(沪教版五四学制)
文档属性
| 名称 | 14.6 等腰三角形的判定(第1课时)(教学课件)-七年级数学下册同步精品课堂(沪教版五四学制) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 00:00:00 | ||
图片预览





文档简介
(共25张PPT)
14.6 等腰三角形的判定(第1课时)
2023-2024学年沪教版七年级下册数学课件
复习引入
等腰三角形的
性质定理1、
等腰三角形的两个底角相等。
简记为:
(等边对等角)
性质定理2、
等腰三角形的顶角平分线、底边
上的中线和高线互相重合。
定义:
有两边相等的三角形是等腰三角形。
(等腰三角形三线合一)
简记为:
探究新知
A
B
C
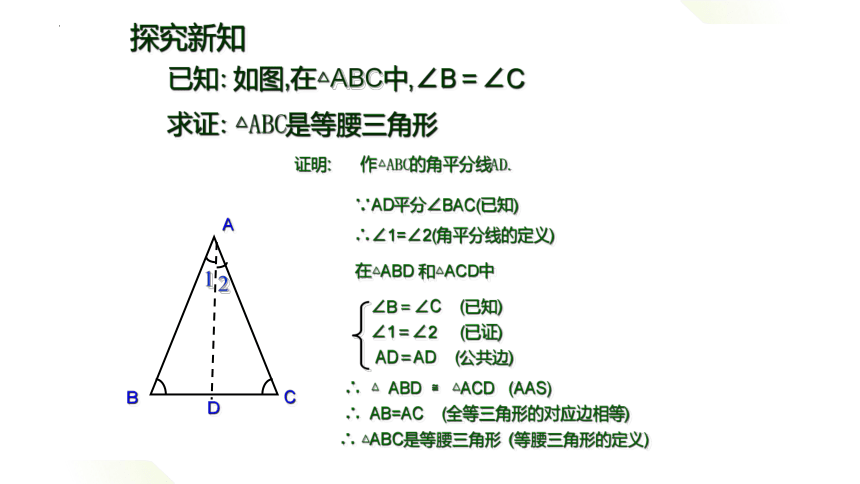
已知:
如图,在△ABC中,∠B=∠C
求证:
△ABC是等腰三角形
D
1
2
证明:
作△ABC的角平分线AD.
在△ABD 和△ACD中
∠B=∠C (已知)
AD=AD (公共边)
∠1=∠2 (已证)
∴ △ ABD ≌ △ACD (AAS)
∴ AB=AC (全等三角形的对应边相等)
∴ △ABC是等腰三角形 (等腰三角形的定义)
∵AD平分∠BAC(已知)
∴∠1=∠2(角平分线的定义)
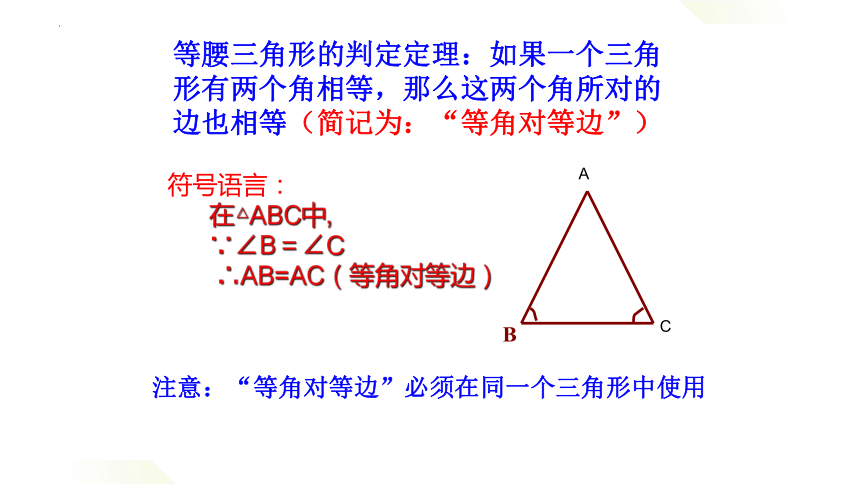
等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简记为:“等角对等边”)
B
A
C
符号语言:
在△ABC中,
∵∠B=∠C
∴AB=AC(等角对等边)
注意:“等角对等边”必须在同一个三角形中使用
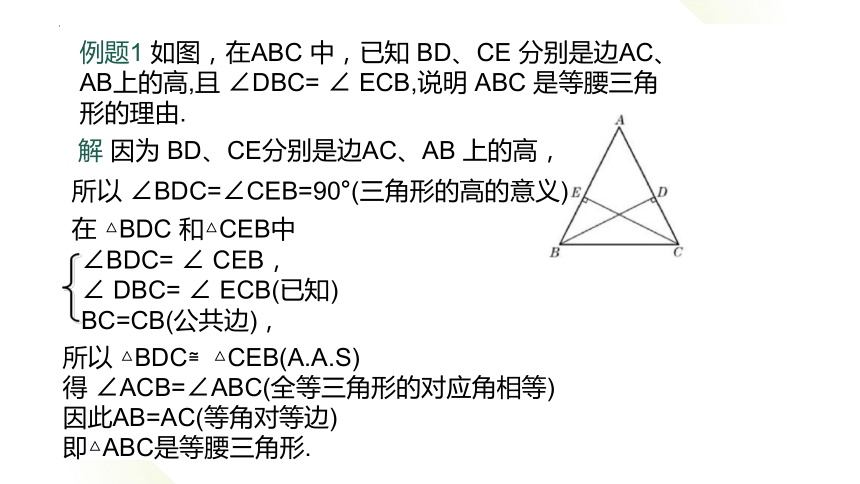
例题1 如图,在ABC 中,已知 BD、CE 分别是边AC、AB上的高,且 ∠DBC= ∠ ECB,说明 ABC 是等腰三角形的理由.
解 因为 BD、CE分别是边AC、AB 上的高,
所以 ∠BDC=∠CEB=90°(三角形的高的意义)
在 △BDC 和△CEB中
∠BDC= ∠ CEB,
∠ DBC= ∠ ECB(已知)
BC=CB(公共边),
所以 △BDC≌△CEB(A.A.S)
得 ∠ACB=∠ABC(全等三角形的对应角相等)
因此AB=AC(等角对等边)
即△ABC是等腰三角形.
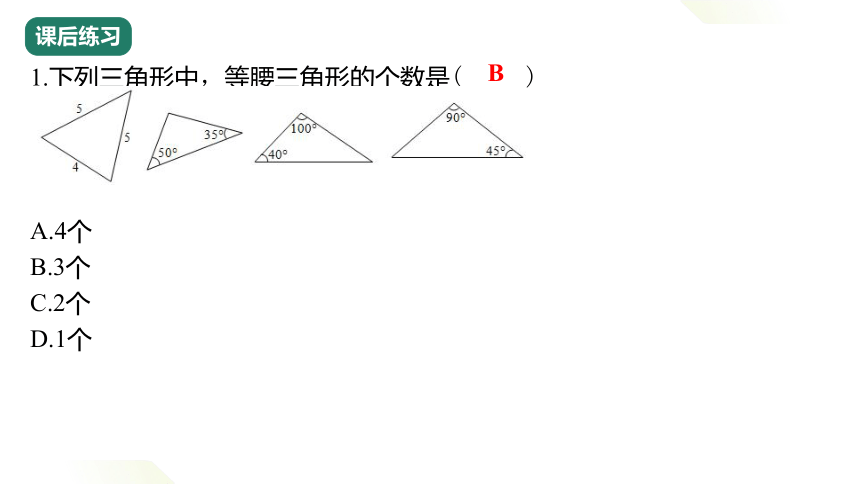
1.下列三角形中,等腰三角形的个数是( ____ )
____________
A.4个
B.3个
C.2个
D.1个
B
2.如图,下列条件不能推出△ABC是等腰三角形的是( ____ )
A.∠B=∠C
B.AD⊥BC,∠BAD=∠CAD
C.BD=AD=CD
D.AD⊥BC,BD=CD
【解析】解:A、∵∠B=∠C,
∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;
B、∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ADB和△ADC中,
C
,
∴△ADB≌△ADC(ASA),
∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;
C、根据AD=BD=CD不能推出△ABC是等腰三角形,故本选项符合题意;
D、∵AD⊥BC,BD=CD,
∴AD垂直平分BC,
∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;
故选:C.
3.在△ABC中,∠A=36°,∠ABC=72°,BD 是△ABC的平分线,则图中的等腰三角形一共有( ____ )
A.1个
B.2个
C.3个
D.4个
【解析】解:∵∠A=36°,∠ABC=72°,
∴∠ABC=∠ACB=72°,
∴AB=AC,
∵BD是∠ABC的角的平分线,
C
∴∠ABD=∠DBC= ∠ABC=36°=∠A,
∴AD=BD,
∵∠DBC=36°,∠ACB=72°,
∴∠BDC=180°-72°-36°=72°,
∴BD=BC,
∴△ABC,△ADB,△BDC都是等腰三角形,共3个.
故选:C.
4.如图,△ABC中,AB=AC,∠A=36°,BD 平分∠ABC,DE⊥AB于点E,则∠C= _____ ,∠BDE= _____ ;若△BDC的周长为24,CD=4,则BC= ____ ,△ABD的周长为 ____ ,△ABC的周长为 ____ .
【解析】解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
72°
54°
10
34
38
∴∠CBD=∠ABD=36°,
∴∠BDC=∠C=72°,∠BDE=54°,
∴BC=BD,
∴BC=BD=AD,
∵△BDC的周长为24,CD=4,
∴△BDC的周长为BC+CD+BD=BC+CD+AD=AC+BC=AB+BC=24,
∴BC+BD=AD=10,
∴AB=AC=14,
∴△ABD的周长为10+10+14=34,△ABC的周长为14+14+10=38.
故答案为:72°,54°,10,34,38.
5.如图,下列3个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是 ____ (填序号).
【解析】解:由题意知,要求“被一条直线分成两个小等腰三角形”,
①中分成的两个等腰三角形的角的度数分别为:36°,36°,108°和36°,72°,72°,能;
②不能;
③显然原等腰直角三角形的斜边上的高把它还分为了两个小等腰直角三角形,能;
②
故答案为:②.
6.在△ABC中∠B=20°,∠A=110°,点P在△ABC的三边上运动,当△PAC成为等腰三角形时,顶角是 ___________________ °.
【解析】解:①如图1,点P在AB上时,AP=AC,顶角为∠A=110°,
②∵∠B=20°,∠A=110°,
∴∠C=180°-20°-110°=50°,
如图2,点P在BC上时,若AC=PC,顶角为∠C=50°,
110°或50°或80
如图3,若AC=AP,则顶角为∠CAP=180°-2∠C=180°-2×50°=80°,
如图3中,P点在BC上,AP=CP的,顶角也是80°.
综上所述,顶角为110°或50°或80°.
故答案为:110°或50°或80.
7.如图,∠B=∠E,AB=FE,BC=ED,那么△GDC是等腰三角形吗?
解:因为BC=ED(已知),
所以BC+CD=ED+CD( _____________ ),
即BD=EC,
在△ABD和△FEC中,
所以 ______ ≌ ______ ( _____ ),
等式的性质
△ABD
△FEC
SAS
所以∠DCG=∠ _____ ( ____________________________ ),
所以DG= ____ ( _____________ ),
所以△GDC是等腰三角形.
【解析】解:△GDC是等腰三角形,理由如下:
因为BC=ED(已知),
所以BC+CD=ED+CD(等式的性质),
即BD=EC,
在△ABD和△FEC中,
CDG
全等三角形的对应角相等
CG
等角对等边
,
∴△ABD≌△FEC(SAS),
∴∠DCG=∠CDG(全等三角形的对应角相等),
∴DG=CG(等角对等边),
∴△GDC是等腰三角形,
故答案为:等式的性质,△ABD,△FEC,SAS,∠CDG,全等三角形的对应角相等,CG,等角对等边.
8.如图,点D是△ABC中BC边上一点,E是AD上一点,EB=EC,且∠ABE=∠ACE,那么△ABC是否是等腰三角形?为什么?
【解析】解:△ABC是等腰三角形,理由如下:
∵EB=EC,
∴∠EBC=∠ECB,
∵∠ABE=∠ACE,
∴∠EBC+∠ABE=∠ECB+∠ACE,即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
9.如图,在△ABC中,AM=CM,AD=CD,DM∥BC,判断△CMB的形状,并说明理由.
【解析】解:在△AMC中,因为AM=CM,AD=CD,(已知),
所以∠AMD=∠CMD(等腰三角形三线合一),
因为DM∥BC( 已知),
所以∠AMD=∠B(两直线平行,同位角相等),∠CMD=∠MCB(两直线平行,内错角角相等),
所以∠B=∠MCB(等量代换),
所以MC=MB(等角对等边),
即△CMB是等腰三角形.
10.如图,已知直线AB∥CD,∠ACD的平分线CE交AB于点F,∠AFE的平分线交CA延长线于点G.
(1)说明△ACF是等腰三角形的理由;
(2)当∠FCD等于多少度时,△AFG是等腰三角形?
【解析】(1)证明:∵∠ACD的平分线CE交AB于点F,
∴∠ACF=∠DCF,
∵AB∥CD,
∴∠AFC=∠DCF,
∴∠ACF=∠AFC,
∴AC=AF,
∴△ACF是等腰三角形;
(2)解:∵AB∥CD,
∴∠GAF=∠ACD,∠FCD=∠AFC,
∵∠ACD的平分线CE交AB于点F,
∴∠ACF=∠FCD= ∠ACD,
∴∠ACD=∠GAF=2∠FCD,
设∠GAF=2x,∠FCD=∠AFC=x,
∵∠AFE的平分线交CA延长线于点G,
∴∠AFG=∠EFG= (180°-∠AFC),
∴∠AFG= (180°-x),
∵△AFG为等腰三角形,
∴ (180°-x)2x,
解得:x=36°,
∴∠FCD=36°.
∴当∠FCD等于36度时,△AFG是等腰三角形.
谢谢
14.6 等腰三角形的判定(第1课时)
2023-2024学年沪教版七年级下册数学课件
复习引入
等腰三角形的
性质定理1、
等腰三角形的两个底角相等。
简记为:
(等边对等角)
性质定理2、
等腰三角形的顶角平分线、底边
上的中线和高线互相重合。
定义:
有两边相等的三角形是等腰三角形。
(等腰三角形三线合一)
简记为:
探究新知
A
B
C
已知:
如图,在△ABC中,∠B=∠C
求证:
△ABC是等腰三角形
D
1
2
证明:
作△ABC的角平分线AD.
在△ABD 和△ACD中
∠B=∠C (已知)
AD=AD (公共边)
∠1=∠2 (已证)
∴ △ ABD ≌ △ACD (AAS)
∴ AB=AC (全等三角形的对应边相等)
∴ △ABC是等腰三角形 (等腰三角形的定义)
∵AD平分∠BAC(已知)
∴∠1=∠2(角平分线的定义)
等腰三角形的判定定理:如果一个三角形有两个角相等,那么这两个角所对的边也相等(简记为:“等角对等边”)
B
A
C
符号语言:
在△ABC中,
∵∠B=∠C
∴AB=AC(等角对等边)
注意:“等角对等边”必须在同一个三角形中使用
例题1 如图,在ABC 中,已知 BD、CE 分别是边AC、AB上的高,且 ∠DBC= ∠ ECB,说明 ABC 是等腰三角形的理由.
解 因为 BD、CE分别是边AC、AB 上的高,
所以 ∠BDC=∠CEB=90°(三角形的高的意义)
在 △BDC 和△CEB中
∠BDC= ∠ CEB,
∠ DBC= ∠ ECB(已知)
BC=CB(公共边),
所以 △BDC≌△CEB(A.A.S)
得 ∠ACB=∠ABC(全等三角形的对应角相等)
因此AB=AC(等角对等边)
即△ABC是等腰三角形.
1.下列三角形中,等腰三角形的个数是( ____ )
____________
A.4个
B.3个
C.2个
D.1个
B
2.如图,下列条件不能推出△ABC是等腰三角形的是( ____ )
A.∠B=∠C
B.AD⊥BC,∠BAD=∠CAD
C.BD=AD=CD
D.AD⊥BC,BD=CD
【解析】解:A、∵∠B=∠C,
∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;
B、∵AD⊥BC,
∴∠ADB=∠ADC=90°,
在△ADB和△ADC中,
C
,
∴△ADB≌△ADC(ASA),
∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;
C、根据AD=BD=CD不能推出△ABC是等腰三角形,故本选项符合题意;
D、∵AD⊥BC,BD=CD,
∴AD垂直平分BC,
∴AB=AC,即△ABC是等腰三角形,故本选项不符合题意;
故选:C.
3.在△ABC中,∠A=36°,∠ABC=72°,BD 是△ABC的平分线,则图中的等腰三角形一共有( ____ )
A.1个
B.2个
C.3个
D.4个
【解析】解:∵∠A=36°,∠ABC=72°,
∴∠ABC=∠ACB=72°,
∴AB=AC,
∵BD是∠ABC的角的平分线,
C
∴∠ABD=∠DBC= ∠ABC=36°=∠A,
∴AD=BD,
∵∠DBC=36°,∠ACB=72°,
∴∠BDC=180°-72°-36°=72°,
∴BD=BC,
∴△ABC,△ADB,△BDC都是等腰三角形,共3个.
故选:C.
4.如图,△ABC中,AB=AC,∠A=36°,BD 平分∠ABC,DE⊥AB于点E,则∠C= _____ ,∠BDE= _____ ;若△BDC的周长为24,CD=4,则BC= ____ ,△ABD的周长为 ____ ,△ABC的周长为 ____ .
【解析】解:∵AB的垂直平分线DE交AC于D,交AB于E,
∴AD=BD,
∴∠ABD=∠A=36°,
∵AB=AC,
∴∠ABC=∠C=72°,
∵BD平分∠ABC,
72°
54°
10
34
38
∴∠CBD=∠ABD=36°,
∴∠BDC=∠C=72°,∠BDE=54°,
∴BC=BD,
∴BC=BD=AD,
∵△BDC的周长为24,CD=4,
∴△BDC的周长为BC+CD+BD=BC+CD+AD=AC+BC=AB+BC=24,
∴BC+BD=AD=10,
∴AB=AC=14,
∴△ABD的周长为10+10+14=34,△ABC的周长为14+14+10=38.
故答案为:72°,54°,10,34,38.
5.如图,下列3个三角形中,均有AB=AC,则经过三角形的一个顶点的一条直线不能够将这个三角形分成两个小等腰三角形的是 ____ (填序号).
【解析】解:由题意知,要求“被一条直线分成两个小等腰三角形”,
①中分成的两个等腰三角形的角的度数分别为:36°,36°,108°和36°,72°,72°,能;
②不能;
③显然原等腰直角三角形的斜边上的高把它还分为了两个小等腰直角三角形,能;
②
故答案为:②.
6.在△ABC中∠B=20°,∠A=110°,点P在△ABC的三边上运动,当△PAC成为等腰三角形时,顶角是 ___________________ °.
【解析】解:①如图1,点P在AB上时,AP=AC,顶角为∠A=110°,
②∵∠B=20°,∠A=110°,
∴∠C=180°-20°-110°=50°,
如图2,点P在BC上时,若AC=PC,顶角为∠C=50°,
110°或50°或80
如图3,若AC=AP,则顶角为∠CAP=180°-2∠C=180°-2×50°=80°,
如图3中,P点在BC上,AP=CP的,顶角也是80°.
综上所述,顶角为110°或50°或80°.
故答案为:110°或50°或80.
7.如图,∠B=∠E,AB=FE,BC=ED,那么△GDC是等腰三角形吗?
解:因为BC=ED(已知),
所以BC+CD=ED+CD( _____________ ),
即BD=EC,
在△ABD和△FEC中,
所以 ______ ≌ ______ ( _____ ),
等式的性质
△ABD
△FEC
SAS
所以∠DCG=∠ _____ ( ____________________________ ),
所以DG= ____ ( _____________ ),
所以△GDC是等腰三角形.
【解析】解:△GDC是等腰三角形,理由如下:
因为BC=ED(已知),
所以BC+CD=ED+CD(等式的性质),
即BD=EC,
在△ABD和△FEC中,
CDG
全等三角形的对应角相等
CG
等角对等边
,
∴△ABD≌△FEC(SAS),
∴∠DCG=∠CDG(全等三角形的对应角相等),
∴DG=CG(等角对等边),
∴△GDC是等腰三角形,
故答案为:等式的性质,△ABD,△FEC,SAS,∠CDG,全等三角形的对应角相等,CG,等角对等边.
8.如图,点D是△ABC中BC边上一点,E是AD上一点,EB=EC,且∠ABE=∠ACE,那么△ABC是否是等腰三角形?为什么?
【解析】解:△ABC是等腰三角形,理由如下:
∵EB=EC,
∴∠EBC=∠ECB,
∵∠ABE=∠ACE,
∴∠EBC+∠ABE=∠ECB+∠ACE,即∠ABC=∠ACB,
∴AB=AC,
∴△ABC是等腰三角形.
9.如图,在△ABC中,AM=CM,AD=CD,DM∥BC,判断△CMB的形状,并说明理由.
【解析】解:在△AMC中,因为AM=CM,AD=CD,(已知),
所以∠AMD=∠CMD(等腰三角形三线合一),
因为DM∥BC( 已知),
所以∠AMD=∠B(两直线平行,同位角相等),∠CMD=∠MCB(两直线平行,内错角角相等),
所以∠B=∠MCB(等量代换),
所以MC=MB(等角对等边),
即△CMB是等腰三角形.
10.如图,已知直线AB∥CD,∠ACD的平分线CE交AB于点F,∠AFE的平分线交CA延长线于点G.
(1)说明△ACF是等腰三角形的理由;
(2)当∠FCD等于多少度时,△AFG是等腰三角形?
【解析】(1)证明:∵∠ACD的平分线CE交AB于点F,
∴∠ACF=∠DCF,
∵AB∥CD,
∴∠AFC=∠DCF,
∴∠ACF=∠AFC,
∴AC=AF,
∴△ACF是等腰三角形;
(2)解:∵AB∥CD,
∴∠GAF=∠ACD,∠FCD=∠AFC,
∵∠ACD的平分线CE交AB于点F,
∴∠ACF=∠FCD= ∠ACD,
∴∠ACD=∠GAF=2∠FCD,
设∠GAF=2x,∠FCD=∠AFC=x,
∵∠AFE的平分线交CA延长线于点G,
∴∠AFG=∠EFG= (180°-∠AFC),
∴∠AFG= (180°-x),
∵△AFG为等腰三角形,
∴ (180°-x)2x,
解得:x=36°,
∴∠FCD=36°.
∴当∠FCD等于36度时,△AFG是等腰三角形.
谢谢
