19.3 课题学习 选择方案(同步课件)-八年级数学下册同步精品课堂(人教版)
文档属性
| 名称 | 19.3 课题学习 选择方案(同步课件)-八年级数学下册同步精品课堂(人教版) |

|
|
| 格式 | pptx | ||
| 文件大小 | 39.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-05-20 11:01:01 | ||
图片预览





文档简介
(共26张PPT)
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
19.3
课题学习
选择方案
情景引入
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
让哪家公司制作这批
宣传材料比较合算?
这节课我们结合这个问题来
学习怎样选择最佳方案.
新知探究
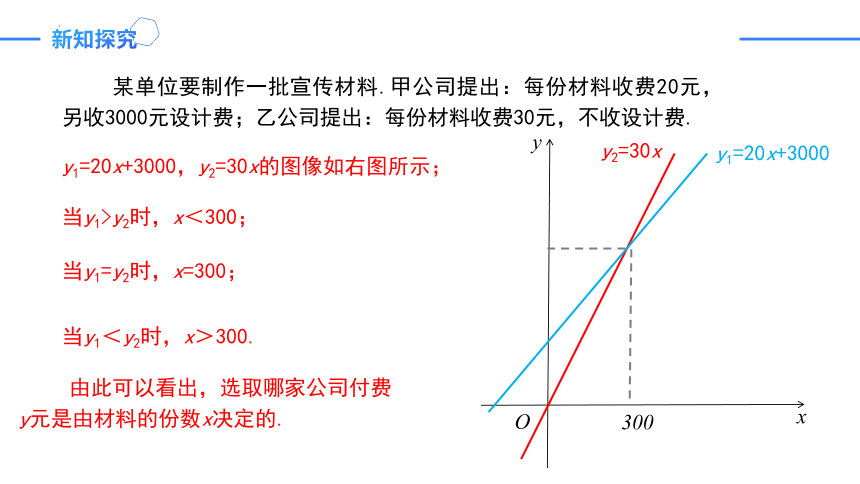
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
思考:两家公司的收费都与什么有关?
两家公司的收费都与材料的份数有关
设共有x份材料,两家公司的收费分别
为y1(元)、y2(元),则有:
y1=20x+3000,
y2=30x;
那么如何去比较两种收费的大小呢?
新知探究
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
y1=20x+3000,y2=30x的图像如右图所示;
x
y
O
y2=30x
y1=20x+3000
当y1>y2时,x<300;
当y1=y2时,x=300;
当y1<y2时,x>300.
由此可以看出,选取哪家公司付费
y元是由材料的份数x决定的.
300
新知探究
数形本是相倚依,怎能分作两边飞;
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休。
——华罗庚
新知探究
为了贯彻落实市委市政府提出的“精准扶 贫”精神,某校特制定了一系列关于帮扶A,B两贫困村的计划,现决定从某地运送152箱鱼苗到A,B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼 苗.已知这两种大小货车的载货能力分别为12箱/辆和8 箱/辆,其运往A,B两村的运费如下表:
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
新知探究
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
(1)求这15辆车中大小货车各多少辆?
解:(1)设大货车有a辆,小货车有b辆,根据题意得
解得
所以这15辆车中大货车有8辆,小货车有7辆.
新知探究
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
(2)现安排其中的10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A,B两村总费用为y元, 试求出y与x之间的函数解析式.
解:(2)由前往A村的大货车为x辆,知前往B村的大货车为(8-x)辆,
前往A村的小货车为(10-x)辆,前往B村的小货车为[7-(10-x)]辆,
由此可得
y=800x+900(8-x)+400(10-x)+600[7-(10-x)]
=100x+9 400(3≤x≤8,且x为整数).
新知探究
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少总费用.
解:(3)由题意得12x+8(10-x)≥100,解得x≥5.
因为3≤x≤8且x为整数,所以5≤x≤8且x为整数.
对于y=100x+9 400,100>0,所以y随x的增大而增大,
所以当x=5时,y有最小值100×5+9 400=9 900.
所以使总费用最少的货车调配方案是:5辆大货车、 5辆小货车前往A村;3辆大货车、2辆小货车前往B村,最少总费用为9 900元.
新知探究
小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?
解:(1)设购进甲种服装x件,由题意可知:
80x+60(100-x)≤7 500,解得x≤75.
答:甲种服装最多购进75件.
新知探究
小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
(2)设总利润为w元,则
w=(120-80-a)x+(90-60)(100-x)
=(10-a)x+3 000.
因为甲种服装不少于65件,所以65≤x≤75,x为整数.
新知探究
方案1:当00,w随x的增大而增大,
所以当x=75时,w有最大值,则购进甲种服装75件,乙种服装25件才能获得最大利润;
方案2:当a=10时,所有65≤x≤75,x为整数的方案获利相同,所以按哪种方案进货都可以;
方案3:当10所以当x=65时,w有最大值,则购进甲种服装65件,乙种服装35件才能获得最大利润.
新知探究
实际问题
一次函数问题
设变量
找对应关系
一次函数问题的解
实际问题的解
解释实
际意义
这个实际问题的解决过程中是怎样思考的?
新知探究
某校准备组织师生共60人,从宜昌乘高铁前往汉口参加夏令营活动,动车票价格如下表:(教师按成人票价购买,学生按学生票价购买).
运行区间 成人票价 /(元/张) 学生票价
/(元/张)
出发站 终点站 一等座 二等座 二等座
宜昌 汉口 147 92 46
若师生均购买二等座票,则共需3220元.
(1)参加活动的教师有____人,学生有____人.
10 50
新知探究
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票的全部费用为y元.①求y关于x的函数解析式;
②若购买一、二等座票的全部费用不多于3385元,则提早前往的教师最多只能有多少人?
解:(2)①依题意有
y=147x+92(10-x)+46×50=55x+3220.
故y关于x的函数解析式是y=55x+3220.
②依题意有55x+3220≤3385,
解得x≤3.
答:提早前往的教师最多只能有3人.
新知探究
一种节能灯的功率为10瓦(即0.01千瓦)售价为60元,一种白炽灯功率为60瓦(即0.06千瓦)售价为3元.两种灯的照明效果一样,使用寿命也相同(3000小时以上)如果电费价格为0.5元/千瓦·时,消费者选用哪种灯省钱?
解析:费用=电费+灯的售价
设照明时间为x小时,则节能灯的总费用为
y1=0.5×0.01x+60
用白炽灯的总费用为
y2=0.5×0.06x+3
令y1=y2,即0.5×0.01x+60=0.5×0.06x+3 解得x=2280
令y1>y2,即0.5×0.01x+60>0.5×0.06x+3 解得 x<2280
令y1答:当x=2280时选用两种灯总费用一样
当x<2280时选用白炽灯总费用省
当x>2280时选用节能灯总费用省
新知探究
下表给出A,B,C 三种上宽带网的收费方式:
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
在A,B两种方式中,影响上网费用的变量是 ,
方式C中的上网费用是 .
上网时间
常量
A,B,C三种收费方式的函数表达式分别是什么?
新知探究
方式C的上网费用确定吗?需要多少钱?
方式C的上网费用是确定的,需要120元
方式A、B的上网费用确定吗?影响费用的因素是什么?
方式A、B的上网费用与上网时间有什么关系?
当上网时间不超过规定时间时:
方式A、B的上网费用是不确定的,与上网时间有关
当上网时间超过规定时间时:
上网费
=
月使用费
上网费
=
月使用费
+
超时费
超时使用价格
=
×
超时时间
思考
思考
思考
新知探究
设月上网时间为xh,方案A,方案B,方案C的收费金额分别为y1,y2,y3,则有:
方案A费用:
y1=
30, 0≤t≤25;
3t-45, t>25.
方案B费用:
y2=
50, 0≤t≤50;
3t-100,t>50.
方案C费用:
y3=120.
120
50
30
25
50
75
O
t
y
y1
y2
y3
新知探究
120
50
30
25
50
75
O
t
y
y1
y2
y3
由函数图象可知:
31小时40分
73小时20分
(1)当上网时间不超过 ,
选择方案A最省钱;
31小时40分
(2)当上网时间为为 ,选择方案B最省钱;
31小时40分至73小时20分
(3)当上网时间 ,
选择方案C最省钱.
超过73小时20分
方案选择的步骤:
在解决方案选择问题时,常常要通过建立函数模型来完成.
1.模型思想——建立函数关系;
2.图形直观——画出函数图象;
3.数形结合——利用函数图象选择方案.
归纳总结
当堂检测
1.小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,但甲商店的优惠条件是:购买10本以上,从第11本开始以按标价的70﹪卖;乙商店的优惠条件是:从第1本开始就按标价的85﹪卖.
(1)小明要买20本时,到哪个商店购买较省钱?
(2)分别写出甲乙两商店中,收款y(元)与购买本数x(本)(x>10)的函数关系式.
(3)小明现有24元钱,最多可买多少本?
一样
y1=3+0.7x
y2=0.85x
30
当堂检测
解:设有学生x人,则甲旅行社收费y1元,乙旅行社收费y2元,则
y1=240+0.5×240x=240+120x,y2=240×0.6x=144x
当y1=y2时,有x=10;当y1>y2时,有x<10;当y110,
∴当学生的人数是10时,两家旅行社收费一样,当学生为9人时,乙旅行社收费低,当学生为11人时,甲旅行社收费低.
2.我校校长暑期带领学校市级“三好学生”去北京旅游,甲旅行社说:“如果校长买全票一张,则其余的学生可以享受半价优惠”.乙旅行社说:“包括校长全部按全票价的6折优惠”.已知全票价为240元.
(1)当学生人数是多少时,两家旅行社的收费一样?
(2)若学生人数为9人时,哪家收费低?
(3)若学生人数为11人时,哪家收费低?
当堂检测
3.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
类别 电视机 洗衣机
进价(元/台) 1800 1500
售价(元/台) 2000 1600
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
解:(1)设电视机进货x台,则洗衣机进货(100-x)台.
则由题意得:1800x+1500×(100-x)≤161800.解得x≤39.
又∵x≥ (100-x),∴x≥34,∴34≤x≤39.
∴商店一共有6种进货方案.
当堂检测
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
设利润为y元,则由题意得:
y=(2000-1800)·x+(1600-1500)(100-x)
=100x+10000.
∵34≤x≤39,
∴当x=39时,ymax=100×39+10000=13900.
∴当商店购进电视机39台、洗衣机61台时,获得的利润最多,为13900元.
第19章
一次函数
八年级数学下册同步精品课堂(人教版)
人教版 数学
八年级 下册
19.3
课题学习
选择方案
情景引入
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
让哪家公司制作这批
宣传材料比较合算?
这节课我们结合这个问题来
学习怎样选择最佳方案.
新知探究
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
思考:两家公司的收费都与什么有关?
两家公司的收费都与材料的份数有关
设共有x份材料,两家公司的收费分别
为y1(元)、y2(元),则有:
y1=20x+3000,
y2=30x;
那么如何去比较两种收费的大小呢?
新知探究
某单位要制作一批宣传材料.甲公司提出:每份材料收费20元,另收3000元设计费;乙公司提出:每份材料收费30元,不收设计费.
y1=20x+3000,y2=30x的图像如右图所示;
x
y
O
y2=30x
y1=20x+3000
当y1>y2时,x<300;
当y1=y2时,x=300;
当y1<y2时,x>300.
由此可以看出,选取哪家公司付费
y元是由材料的份数x决定的.
300
新知探究
数形本是相倚依,怎能分作两边飞;
数缺形时少直观,形少数时难入微;
数形结合百般好,隔离分家万事休。
——华罗庚
新知探究
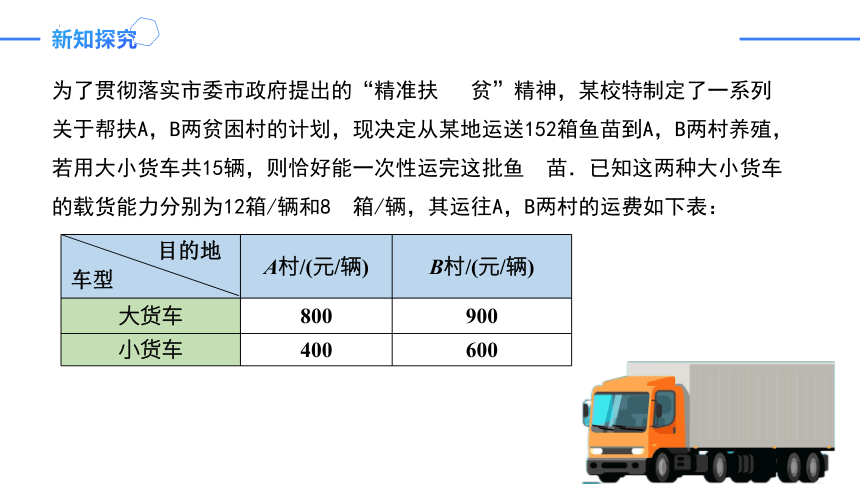
为了贯彻落实市委市政府提出的“精准扶 贫”精神,某校特制定了一系列关于帮扶A,B两贫困村的计划,现决定从某地运送152箱鱼苗到A,B两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼 苗.已知这两种大小货车的载货能力分别为12箱/辆和8 箱/辆,其运往A,B两村的运费如下表:
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
新知探究
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
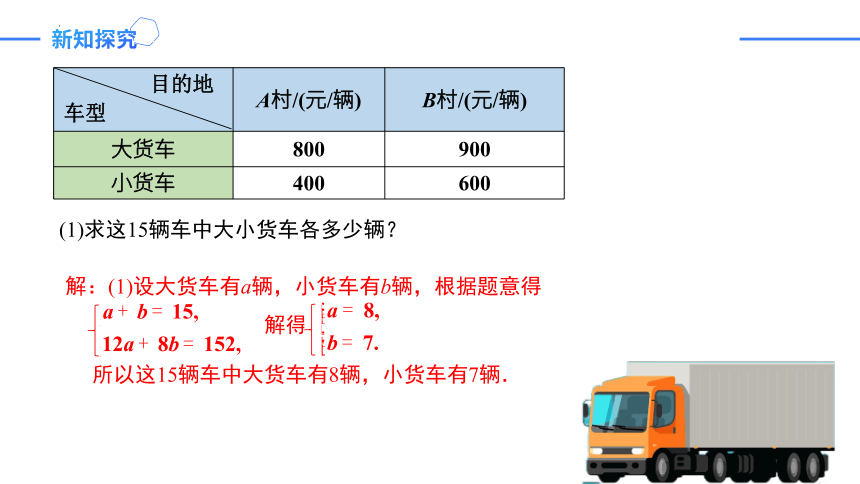
(1)求这15辆车中大小货车各多少辆?
解:(1)设大货车有a辆,小货车有b辆,根据题意得
解得
所以这15辆车中大货车有8辆,小货车有7辆.
新知探究
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
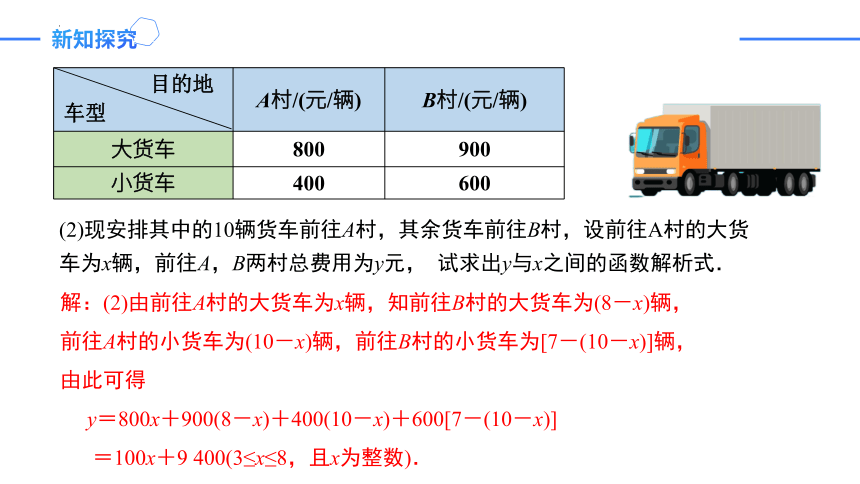
(2)现安排其中的10辆货车前往A村,其余货车前往B村,设前往A村的大货车为x辆,前往A,B两村总费用为y元, 试求出y与x之间的函数解析式.
解:(2)由前往A村的大货车为x辆,知前往B村的大货车为(8-x)辆,
前往A村的小货车为(10-x)辆,前往B村的小货车为[7-(10-x)]辆,
由此可得
y=800x+900(8-x)+400(10-x)+600[7-(10-x)]
=100x+9 400(3≤x≤8,且x为整数).
新知探究
A村/(元/辆) B村/(元/辆)
大货车 800 900
小货车 400 600
车型
目的地
(3)在(2)的条件下,若运往A村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少总费用.
解:(3)由题意得12x+8(10-x)≥100,解得x≥5.
因为3≤x≤8且x为整数,所以5≤x≤8且x为整数.
对于y=100x+9 400,100>0,所以y随x的增大而增大,
所以当x=5时,y有最小值100×5+9 400=9 900.
所以使总费用最少的货车调配方案是:5辆大货车、 5辆小货车前往A村;3辆大货车、2辆小货车前往B村,最少总费用为9 900元.
新知探究
小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(1)若购进这100件服装的费用不得超过7 500元,则甲种服装最多购进多少件?
解:(1)设购进甲种服装x件,由题意可知:
80x+60(100-x)≤7 500,解得x≤75.
答:甲种服装最多购进75件.
新知探究
小明到服装店参加社会实践活动,服装店经理让小明帮助解决以下问题:
服装店准备购进甲、乙两种服装,甲种每件进价80元,售价120元;乙种每件进价60元,售价90元.计划购进两种服装共100件,其中甲种服装不少于65件.
(2)在(1)的条件下,该服装店对甲种服装以每件优惠a(0<a<20)元的价格进行优惠促销活动,乙种服装价格不变,那么该服装店应如何调整进货方案才能获得最大利润?
(2)设总利润为w元,则
w=(120-80-a)x+(90-60)(100-x)
=(10-a)x+3 000.
因为甲种服装不少于65件,所以65≤x≤75,x为整数.
新知探究
方案1:当0
所以当x=75时,w有最大值,则购进甲种服装75件,乙种服装25件才能获得最大利润;
方案2:当a=10时,所有65≤x≤75,x为整数的方案获利相同,所以按哪种方案进货都可以;
方案3:当10
新知探究
实际问题
一次函数问题
设变量
找对应关系
一次函数问题的解
实际问题的解
解释实
际意义
这个实际问题的解决过程中是怎样思考的?
新知探究
某校准备组织师生共60人,从宜昌乘高铁前往汉口参加夏令营活动,动车票价格如下表:(教师按成人票价购买,学生按学生票价购买).
运行区间 成人票价 /(元/张) 学生票价
/(元/张)
出发站 终点站 一等座 二等座 二等座
宜昌 汉口 147 92 46
若师生均购买二等座票,则共需3220元.
(1)参加活动的教师有____人,学生有____人.
10 50
新知探究
(2)由于部分教师需提早前往做准备工作,这部分教师均购买一等座票,而后续前往的教师和学生均购买二等座票.设提早前往的教师有x人,购买一、二等座票的全部费用为y元.①求y关于x的函数解析式;
②若购买一、二等座票的全部费用不多于3385元,则提早前往的教师最多只能有多少人?
解:(2)①依题意有
y=147x+92(10-x)+46×50=55x+3220.
故y关于x的函数解析式是y=55x+3220.
②依题意有55x+3220≤3385,
解得x≤3.
答:提早前往的教师最多只能有3人.
新知探究
一种节能灯的功率为10瓦(即0.01千瓦)售价为60元,一种白炽灯功率为60瓦(即0.06千瓦)售价为3元.两种灯的照明效果一样,使用寿命也相同(3000小时以上)如果电费价格为0.5元/千瓦·时,消费者选用哪种灯省钱?
解析:费用=电费+灯的售价
设照明时间为x小时,则节能灯的总费用为
y1=0.5×0.01x+60
用白炽灯的总费用为
y2=0.5×0.06x+3
令y1=y2,即0.5×0.01x+60=0.5×0.06x+3 解得x=2280
令y1>y2,即0.5×0.01x+60>0.5×0.06x+3 解得 x<2280
令y1
当x<2280时选用白炽灯总费用省
当x>2280时选用节能灯总费用省
新知探究
下表给出A,B,C 三种上宽带网的收费方式:
收费方式 月使用费/元 包时上网时间/h 超时费/(元/min)
A 30 25 0.05
B 50 50 0.05
C 120 不限时
选取哪种方式能节省上网费?
该问题要我们做什么?选择方案的依据是什么?
在A,B两种方式中,影响上网费用的变量是 ,
方式C中的上网费用是 .
上网时间
常量
A,B,C三种收费方式的函数表达式分别是什么?
新知探究
方式C的上网费用确定吗?需要多少钱?
方式C的上网费用是确定的,需要120元
方式A、B的上网费用确定吗?影响费用的因素是什么?
方式A、B的上网费用与上网时间有什么关系?
当上网时间不超过规定时间时:
方式A、B的上网费用是不确定的,与上网时间有关
当上网时间超过规定时间时:
上网费
=
月使用费
上网费
=
月使用费
+
超时费
超时使用价格
=
×
超时时间
思考
思考
思考
新知探究
设月上网时间为xh,方案A,方案B,方案C的收费金额分别为y1,y2,y3,则有:
方案A费用:
y1=
30, 0≤t≤25;
3t-45, t>25.
方案B费用:
y2=
50, 0≤t≤50;
3t-100,t>50.
方案C费用:
y3=120.
120
50
30
25
50
75
O
t
y
y1
y2
y3
新知探究
120
50
30
25
50
75
O
t
y
y1
y2
y3
由函数图象可知:
31小时40分
73小时20分
(1)当上网时间不超过 ,
选择方案A最省钱;
31小时40分
(2)当上网时间为为 ,选择方案B最省钱;
31小时40分至73小时20分
(3)当上网时间 ,
选择方案C最省钱.
超过73小时20分
方案选择的步骤:
在解决方案选择问题时,常常要通过建立函数模型来完成.
1.模型思想——建立函数关系;
2.图形直观——画出函数图象;
3.数形结合——利用函数图象选择方案.
归纳总结
当堂检测
1.小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,但甲商店的优惠条件是:购买10本以上,从第11本开始以按标价的70﹪卖;乙商店的优惠条件是:从第1本开始就按标价的85﹪卖.
(1)小明要买20本时,到哪个商店购买较省钱?
(2)分别写出甲乙两商店中,收款y(元)与购买本数x(本)(x>10)的函数关系式.
(3)小明现有24元钱,最多可买多少本?
一样
y1=3+0.7x
y2=0.85x
30
当堂检测
解:设有学生x人,则甲旅行社收费y1元,乙旅行社收费y2元,则
y1=240+0.5×240x=240+120x,y2=240×0.6x=144x
当y1=y2时,有x=10;当y1>y2时,有x<10;当y1
∴当学生的人数是10时,两家旅行社收费一样,当学生为9人时,乙旅行社收费低,当学生为11人时,甲旅行社收费低.
2.我校校长暑期带领学校市级“三好学生”去北京旅游,甲旅行社说:“如果校长买全票一张,则其余的学生可以享受半价优惠”.乙旅行社说:“包括校长全部按全票价的6折优惠”.已知全票价为240元.
(1)当学生人数是多少时,两家旅行社的收费一样?
(2)若学生人数为9人时,哪家收费低?
(3)若学生人数为11人时,哪家收费低?
当堂检测
3.某商店需要购进一批电视机和洗衣机,根据市场调查,决定电视机进货量不少于洗衣机进货量的一半.电视机与洗衣机的进价和售价如下表:
类别 电视机 洗衣机
进价(元/台) 1800 1500
售价(元/台) 2000 1600
计划购进电视机和洗衣机共100台,商店最多可筹集资金161800元.
(1)请你帮助商店算一算有多少种进货方案?(不考虑除进价之外的其他费用)
解:(1)设电视机进货x台,则洗衣机进货(100-x)台.
则由题意得:1800x+1500×(100-x)≤161800.解得x≤39.
又∵x≥ (100-x),∴x≥34,∴34≤x≤39.
∴商店一共有6种进货方案.
当堂检测
(2)哪种进货方案待商店销售购进的电视机与洗衣机完毕后获得利润最多?并求出最多利润.(利润=售价-进价)
设利润为y元,则由题意得:
y=(2000-1800)·x+(1600-1500)(100-x)
=100x+10000.
∵34≤x≤39,
∴当x=39时,ymax=100×39+10000=13900.
∴当商店购进电视机39台、洗衣机61台时,获得的利润最多,为13900元.
